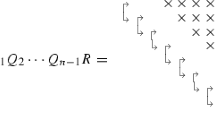Skip to main content

Advertisement

SpringerLink
Log in

An extended Hessenberg form for Hamiltonian matrices

  • Published:
Calcolo Aims and scope Submit manuscript

Abstract

A unitary symplectic similarity transformation for a special class of Hamiltonian matrices to extended Hamiltonian Hessenberg form is presented. Whereas the classical Hessenberg form links to Krylov subspaces, the extended Hessenberg form links to extended Krylov subspaces. The presented algorithm generalizes thus the classic reduction to Hamiltonian Hessenberg form and offers more freedom in the choice of Hamiltonian condensed forms, to be used within an extended Hamiltonian QR algorithm. Theoretical results identifying the structure of the extended Hamiltonian Hessenberg form and proofs of uniqueness of the reduction process are included. Numerical experiments confirm the validity of the approach.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3

Similar content being viewed by others

Notes

  1. The name extended refers to the link with extended Krylov subspaces, see [12] for details.

  2. If the matrix exhibits particular structure, core transformations could equal the identity and are therefore not shown in the pyramidal structure.

References

  1. Ammar G., Mehrmann V.: A geometric perspective on condensed forms for Hamiltonian matrices. In: Computation and control, II (Bozeman, MT, 1990), vol. 11 of Progr. Systems Control Theory, pp. 1–11. Birkhäuser, Boston (1991)

  2. Ammar, G., Mehrmann, V.: On Hamiltonian and symplectic Hessenberg forms. Linear Algebra Appl. 149, 55–72 (1991)

    Article  MathSciNet  MATH  Google Scholar 

  3. Beckermann, B., Güttel, S., Vandebril, R.: On the convergence of rational Ritz-values. SIAM J. Matrix Anal. A. 31, 1740–1774 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  4. Bini, D.A., Iannazzo, B., Meini, B.: Numerical Solution of Algebraic Riccati Equations, Fundamentals of Algorithms. SIAM (2012)

  5. Byers, R.: A Hamiltonian \({QR}\)-algorithm. SIAM J. Sci. Stat. Comp. 7, 212–229 (986)

  6. Ferranti, M., Iannazzo, B., Mach, T., Vandebril, R.: An extended Hamiltonian QR algorithm (2016) (in preparation)

  7. Ferranti, M., Mach, T., Vandebril, R.: Extended Hamiltonian Hessenberg matrices arise in projection based model order reduction. Proc. Appl. Math. Mech. 15, 583–584 (2015)

    Article  Google Scholar 

  8. Francis, J.G.F.: The QR Transformation a unitary analogue to the LR transformation-Part 1. Comput. J. 4, 265–271 (1961)

    Article  MathSciNet  MATH  Google Scholar 

  9. Francis, J.G.F.: The QR transformation-part 2. Comput. J. 4, 332–345 (1962)

    Article  MathSciNet  Google Scholar 

  10. Kuijlaars, A.B.J.: Which eigenvalues are found by the Lanczos method? SIAM J. Matrix Anal. A. 22, 306–321 (2000)

    Article  MathSciNet  MATH  Google Scholar 

  11. Kuijlaars, A.B.J.: Convergence analysis of Krylov subspace iterations with methods from potential theory. SIAM Rev. 48, 3–40 (2006)

    Article  MathSciNet  MATH  Google Scholar 

  12. Mach, T., Pranić, M.S., Vandebril, R.: Computing approximate extended Krylov subspaces without explicit inversion. Electron. T. Numer. Anal. 40, 414–435 (2013)

    MathSciNet  MATH  Google Scholar 

  13. Paige, C., Van Loan, C.: A Schur decomposition for Hamiltonian matrices. Linear Algebra Appl. 41, 11–32 (1981)

    Article  MathSciNet  MATH  Google Scholar 

  14. Raines, A.C.I.I.I., Watkins, D.S.: A class of Hamiltonian-symplectic methods for solving the algebraic Riccati equation. Linear Algebra Appl. 205(206), 1045–1060 (1994)

    Article  MathSciNet  MATH  Google Scholar 

  15. Vandebril, R.: Chasing bulges or rotations? A metamorphosis of the QR-algorithm. SIAM J. Matrix Anal. A. 32, 217–247 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  16. Watkins, D.S.: Bulge exchanges in algorithms of \({QR}\) type. SIAM J. Matrix Anal. A. 19, 1074–1096 (1998)

    Article  MathSciNet  MATH  Google Scholar 

  17. Watkins, D.S.: Francis’s algorithm. Am. Math. Mon. 118, 387–403 (2011)

    Article  MathSciNet  MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Computer Science, KU Leuven, Celestijnenlaan 200A, 3001, Leuven, Belgium

    Micol Ferranti, Thomas Mach & Raf Vandebril

  2. Dipartimento di Matematica e Informatica, Università degli studi di Perugia, Via Vanvitelli 1, 06123, Perugia, Italy

    Bruno Iannazzo

Authors
  1. Micol Ferranti
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Bruno Iannazzo
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Thomas Mach
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Raf Vandebril
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Micol Ferranti.

Additional information

The research was partially supported by the Research Council KU Leuven, Projects CREA-13-012 Can Unconventional Eigenvalue Algorithms Supersede the State of the Art, OT/11/055 Spectral Properties of Perturbed Normal Matrices and their Applications, and CoE EF/05/006 Optimization in Engineering (OPTEC); by the Fund for Scientific Research–Flanders (Belgium) Project G034212N Reestablishing Smoothness for Matrix Manifold Optimization via Resolution of Singularities; and by the Interuniversity Attraction Poles Programme, initiated by the Belgian State, Science Policy Office, Belgian Network DYSCO (Dynamical Systems, Control, and Optimization). The Bruno Iannazzo was partly supported by INdAM through GNCS Project 2015.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Ferranti, M., Iannazzo, B., Mach, T. et al. An extended Hessenberg form for Hamiltonian matrices. Calcolo 54, 423–453 (2017). https://doi.org/10.1007/s10092-016-0192-1

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10092-016-0192-1

Keywords

Mathematics Subject Classification

Search

Navigation