Abstract
We study two-stage all-pay contests in which synergy exists between the stages. The value of winning for each contestant is fixed in the first stage while it is effort-dependent in the second one. We assume that a player’s effort in the first stage either increases (positive synergy) or decreases (negative synergy) his value of winning in the second stage. The subgame perfect equilibrium of this contest is analyzed with either positive or negative synergy. We show, in particular, that whether the contestants are symmetric or asymmetric their expected payoffs may be higher under negative synergy than under positive synergy. Consequently, they prefer smaller values of winning (negative synergy) over higher ones (positive synergy).



Similar content being viewed by others
Notes
The one-stage all-pay contest with discrimination in the form of a head-start advantage has been analyzed by Konrad (2002).
In contrast to Ryvkin (2011) who assumed that fatigue has an indirect effect on the contestant’s ability such that it changes his success function, we assume that fatigue has a direct effect on the contestant’s ability such that it changes his value of winning.
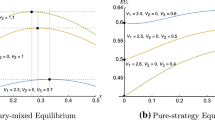
In the second stage the contestants are asymmetric and then their expected total effort does not necessarily increase in their values of winning. In fact, it increases in the lower value of winning, but decreases in the higher value of winning.
The analysis of an all-pay contest with a contestant’s utility function \( u^{i}=v^{i}-x^{i}\) is equivalent to the analysis with a contestant’s utility function \(u^{i}=v^{i}-\frac{x^{i}}{a^{i}}\) where \(a^{i}\) is the contestant’s ability. Thus, we can ignore the contestants’ abilities and assume that they are included in their values of winning.
If the marginal increasing rate \(\alpha \) is larger than one there is no equilibrium since the optimal effort for every contestant in the first stage is infinite.
The contests in both stages are not the same and therefore the contestants might be symmetric in one stage but asymmetric in another one.
Note that if \(v_{1}^{1}>v_{1}^{2}\) then \(\frac{d\pi _{p}^{1}}{d\alpha }\) is strictly positive.
It can be verified that this result holds regardless of whether the contestants are symmetric or asymmetric.
It can be verified that this result holds regardless of whether the contestants are symmetric or asymmetric.
References
Amegashie J, Cadsby C, Song Y (2007) Competitive burnout: theory and experimental evidence. Games Econ Behav 59:213–239
Amman E, Leininger W (1996) Asymmetric all-pay auctions with incomplete information: the two-player case. Games Econ Behav 14:1–18
Baye M, Kovenock D, de Vries C (1993) Rigging the lobbying process: an application of the all-pay auction. Am Econ Rev 83:289–294
Baye M, Kovenock D, de Vries C (1996) The all-pay auction with complete information. Econ Theory 8:291–305
Baye M, Kovenock D, de Vries C (2012) Contests with rank-order spillovers. Econ Theory 51(2):315–350
Che Y-K, Gale I (1998) Caps on political lobbying. Am Econ Rev 88:643–651
Cohen C, Kaplan T, Sela A (2008) Optimal rewards in contests. Rand J Econ 39(2):434–451
Fu Q, Lu J (2012) The optimal multi-stage contest. Econ Theory 51(2):351–382
Gavious A, Moldovanu B, Sela A (2003) Bid costs and endogenous bid caps. Rand J Econ 33(4):709–722
Gradstein M, Konrad K (1999) Orchestrating rent seeking contests. Econ J 109:536–545
Groh C, Moldovanu B, Sela A, Sunde U (2012) Optimal seedings in elimination tournaments. Econ Theory 49:59–80
Harris C, Vickers J (1987) Racing with uncertainty. Rev Econ Stud 54(1):1–21
Hart S (2008) Discrete Colonel Blotto and general lotto games. Int J Game Theory 36:441–460
Hilman A, Riley J (1989) Politically contestable rents and transfers. Econ Polit 1:17–39
Kaplan T, Wettstein D (2015) The optimal design of rewards in contests. Rev Econ Des 19(4):327–339
Kaplan T, Luski I, Sela A, Wettstein D (2002) All-pay auctions with variable rewards. J Ind Econ 50(4):417–430
Kaplan T, Luski I, Wettstein D (2003) Innovative activity and sunk costs. Int J Ind Organ 21(8):1111–1133
Klumpp T, Polborn M (2006) Primaries and the New Hampshire effect. J Public Econ 90:1073–1114
Konrad K (2002) Investment in the absence of property rights. Eur Econ Rev 46:1521–1537
Konrad K, Kovenock D (2009) Multi-battle contests. Games Econ Behav 66:256–274
Kovenock D, Roberson B (2009) Is the 50-state strategy optimal? J Theor Polit 21(2):213–236
Krishna V, Morgan J (1997) An analysis of the war of attrition and the all-pay auction. J Econ Theory 72(2):343–362
Kvasov D (2007) Contests with limited resources. J Econ Theory 136:738–748
Moldovanu B, Sela A (2001) The optimal allocation of prizes in contests. Am Econ Rev 91:542–558
Moldovanu B, Sela A (2006) Contest architecture. J Econ Theory 126(1):70–97
Roberson B (2006) The Colonel Blotto game. Econ Theory 29:1–24
Ryvkin D (2011) Fatigue in dynamic tournaments. J Econ Manag Strategy 20(4):1011–1041
Sela A (2012) Sequential two-prize contests. Econ Theory 51:383–395
Sela A, Erez E (2013) Dynamic contests with resource constraints. Soc Choice Welf 41(4):863–882
Siegel R (2009) All-pay contests. Econometrica 77(1):71–92
Snyder JM (1989) Election goals and the allocation of campaign resources. Econometrica 57:637–660
Author information
Authors and Affiliations
Corresponding author
Appendix
Appendix
1.1 Proof of Proposition 1
We can see that the functions \(F_{p}^{i}(x)\), \(i=1,2\), are well defined, strictly increasing on \(\left[ 0,x_{\max -p}\right] \), continuous, and that \( F_{p}^{1}(0)=0\), \(F_{p}^{2}(0)=\frac{1}{\alpha }-\frac{(1-\alpha )^{\frac{ v_{1}^{1}-v_{1}^{2}}{v_{1}^{1}}}}{\alpha }>0\) and \(F_{p}^{1}(x_{\max -p})=F_{p}^{2}(x_{\max -p})=1\). Thus, \(F_{p}^{i}(x)\), \(i=1,2\) are cumulative distribution functions of continuous probability distributions supported on \(\left[ 0,x_{\max -p}\right] \). In order to see that the above strategies are an equilibrium, note that when contestant 2 uses the mixed strategy \(F_{p}^{2}(x)\), contestant 1’s expected payoff is
for any effort \(x\in [0,x_{\max -p}]\). Since it can be easily shown that for contestant 1, efforts above \(x_{\max -p_{a}}\) would lead to a lower expected payoff than \(v_{1}^{1}(\frac{1}{\alpha }-\frac{(1-\alpha )^{\frac{ v_{1}^{1}-v_{1}^{2}}{v_{1}^{1}}}}{\alpha })\), any effort in \([0,x_{\max -p}]\) is a best response of contestant 1 to \(F_{p}^{2}(x)\). Similarly, when contestant 1 uses the mixed strategy \(F_{p}^{1}(x)\), contestant 2’s expected payoff is
for any effort \(x\in [0,x_{\max -p_{a}}]\). Since it can be easily shown that for contestant 2, efforts above \(x_{\max -p}\) would result in a non-positive expected payoff, any effort in \([0,x_{\max -p}]\) is a best response of contestant 2 to \(F_{p}^{1}(x)\). Hence, the pair \(\left( F_{p}^{1}(x),F_{p}^{2}(x)\right) \) is a mixed strategy equilibrium.
1.2 Proof of Proposition 2
It is clear that the functions \(F_{n}^{i}(x)\), \(i=1,2\), are well defined, strictly increasing on \(\left[ 0,x_{\max -n}\right] \), continuous, and that \( F_{n}^{1}(0)=0\), \(F_{n}^{2}(0)=\frac{1+\alpha }{\alpha }-\frac{(1+\alpha )^{ \frac{v_{1}^{2}}{v_{1}^{1}}}}{\alpha }\) and \(F_{n}^{1}(x_{\max -n})=F_{n}^{2}(x_{\max -n})=1\). Thus, \(F_{n}^{i}(x)\), \(i=1,2\) are cumulative distribution functions of continuous probability distributions supported on \(\left[ 0,x_{\max -n}\right] \).
In order to see that the above strategies are an equilibrium, note that when contestant 2 uses the mixed strategy \(F_{n}^{2}(x)\), contestant 1’s expected payoff is
for any effort \(x\in [0,x_{\max -n}]\). Since it can be easily shown that for contestant 1, efforts above \(x_{\max -n}\) would lead to a lower expected payoff than \(v_{1}^{1}-\frac{v_{1}^{2}}{\alpha }\ln (1+\alpha )\), any effort in \([0,x_{\max -n}]\) is a best response of contestant 1 to \( F_{n}^{2}(x)\). Similarly, when contestant 1 uses the mixed strategy \( F_{n}^{1}(x)\), contestant 2’s expected payoff is
for any effort \(x\in [0,x_{\max -n}]\). Since it can be easily shown that for contestant 2, efforts above \(x_{\max -n}\) would result in a lower expected payoff than \(v_{1}^{2}-\frac{v_{1}^{2}}{\alpha }\ln (1+\alpha )\), any effort in \([0,x_{\max -n}]\) is a best response of contestant 2 to \( F_{n}^{1}(x)\). Hence, the pair \(\left( F_{n}^{1}(x),F_{n}^{2}(x)\right) \) is a mixed strategy equilibrium.
1.3 Proof of Proposition 4
By (11), when the synergy is negative we have that \( \frac{d\pi _{n}^{1}}{d\alpha }\ge 0\), and
On the other hand, by (5), when the synergy is positive we have that \(\frac{d\pi _{p}^{1}}{d\alpha }\ge 0\) and
Thus, when \(\alpha \) is sufficiently close to 1, we obtain that \(\pi _{p}^{1}-\pi _{n}^{1}>0\).
1.4 Proof of Proposition 5
By (6), if the contestants are symmetric, a contestant’s expected effort in the first stage of the contest under positive synergy is
And, by (12), if the contestants are symmetric, a contestant’s expected effort in the first stage of the contest under negative synergy is
Thus we have
In order to show that \(E_{p}-E_{n}>0\), we define
Then, we have
Since \(g(0)=g^{\prime }(0)=0\) and
we obtain that \(g^{\prime }(\alpha )>0\) and therefore \(g(\alpha )>0\) for all \(0<\alpha <1\). Thus, \(E_{p}-E_{n}>0\).
Rights and permissions
About this article
Cite this article
Sela, A. Two-stage contests with effort-dependent values of winning. Rev Econ Design 21, 253–272 (2017). https://doi.org/10.1007/s10058-017-0205-9
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10058-017-0205-9