Evaluation of spectral dispersion of optical constants of a-Se films from their normal-incidence transmittance spectra using Swanepoel algebraic envelope approach

Abstract

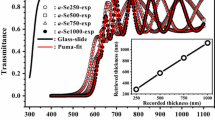
Spectral dispersions of index of refraction ${n(\lambda )}$ and extinction coefficient ${\kappa (\lambda )}$ of undoped amorphous selenium (a-Se) films of three thicknesses (d ≈ 0.5, 0.75, and 1.0 µm) were evaluated by analyzing experimental room-temperature normal-incidence transmittance-wavelength (${{T_{{\text{exp}}}}(\lambda )} - \lambda$) data (λ = 400–1100 µm) of their air-supported {a-Se film/thick glass slide}-stacks using Swanepoel’s transmission envelope theory of uniform films. Above a wavelength ${{\lambda _c}\,\, \approx \,\,640\;{\text{nm}}}$, as-measured ${{T_{{\text{exp}}}}(\lambda )}\,\, - \,\lambda$ spectra display well-resolved maxima and minima, with minor shrinkage in transparent and weak absorption regions (750–1100 nm). Below ${\lambda _{\text{c}}}$, a smeared sharp decline of ${{T_{{\text{exp}}}}(\lambda )}$ with decreasing λ, signifying strong absorption in a-Se films and existence of band-tail localized states. For λ > λ _c, the ${n\,(\lambda )}\, - \,\lambda$ data retrieved from algebraic envelope procedures followed a Sellmeier-like dispersion relation, with the best-fit values of high-frequency dielectric constant ${{\varepsilon _\infty }\, \approx \,\,{\text{4.9}}}$, static index of refraction ${{n_{\text{0}}} = n\left( {E\, \to \,{\text{0}}} \right)\,\, \approx \,\,{\text{2.43}}}$, and resonance wavelength ${{\lambda _0}\, \approx \,490\,\,{\text{nm}}}$, which may be assigned to onset of photogeneration in a-Se. Urbach-like dependency of absorption coefficient ${\alpha (h{{\nu }})}$ of a-Se films on photon energy ${h{{\nu }}}$ was realized with an Urbach-tail breadth of 85 meV. All achieved optical parameters were found to be slightly dependent on film thickness. Findings of present algebraic analysis are consistent with reported literature results obtained on the basis of other optical analytical approaches.

Appendices

Appendix A: Swanepoel’s transmission envelope theory of uniform films

The Swanepoel’s transmission envelope theory of uniform films is based on the theoretical formulas describing normal-incidence transmittance of a transparent slab standing freely in the air and of an ideal {air/thin uniform film/thick transparent substrate/air}-stack [21–24, 31, 41, 51–58]. Theoretical formulas, features of Swanepoel transmission envelope method and procedures underlying its application to analyze normal-incidence transmittance spectra of ideal air-supported 4-layered stacks will be briefed.

1.1 Theoretical formulas of transmittance and reflectance of a thick slab standing freely in the air

Let a quasi-monochromatic light of wavelength λ and spectral bandwidth (SBW) Δλ travelling in the air to hit normally a partially-absorbing slab immersed in the air. For incoherently thick slab with smooth surfaces, geometric thickness d _s and complex index of refraction ${{{\hat n}_{\text{s}}}(\lambda ) = {n_{\text{s}}}(\lambda ) + j\,{\kappa _{\text{s}}}(\lambda )}$, ${\Delta \lambda \,\,>> \,\,{{{\lambda ^{\text{2}}}} \mathord{\left/ {\vphantom {{{\lambda ^{\text{2}}}} {{\text{2}}\,{{\pi }}\,{n_{\text{s}}}\,{d_{\text{s}}}}}} \right. \kern-\nulldelimiterspace} {{\text{2}}\,{{\pi }}\,{n_{\text{s}}}\,{d_{\text{s}}}}}}$, so light intensities of multiple internal reflections at its interfaces with the air (v) (${{{\hat n}_v}(\lambda ) \cong 1.0\, + \,j\,0}$) are added algebraically (incoherently), to get its specular reflectance R(λ) and transmittance T(λ) [22, 31, 41, 55–58]:

$${T_{{\text{vsv}}}}(\lambda ) = \frac{{{{\left( {{\text{1}}\, - \,{R_{{\text{vs}}}}} \right)}^{\text{2}}}\left( {{\text{1}}\, + \,\frac{{\kappa _{\text{s}}^{\text{2}}}}{{n_{\text{s}}^{\text{2}}}}} \right)\,{e^{ - \,{\alpha _{\text{s}}}\,{d_{\text{s}}}}}}}{{{\text{1}}\,{\text{ - }}\,R_{{\text{vs}}}^{\text{2}}\,{e^{ - \,{\text{2}}\,{\alpha _{\text{s}}}\,{d_{\text{s}}}}}}},$$

(6)

$${{R_{{\text{vsv}}}}(\lambda ) = {R_{{\text{vs}}}}\, + \,\frac{{{R_{{\text{vs}}}}\,{{\left( {{\text{1}}\, - \,{R_{{\text{vs}}}}} \right)}^{\text{2}}}\left( {{\text{1}}\, + \,\frac{{\kappa _{\text{s}}^{\text{2}}}}{{n_{\text{s}}^{\text{2}}}}} \right)\,{e^{ - \,{\text{2}}\,{\alpha _{\text{s}}}\,{d_{\text{s}}}}}}}{{{\text{1}} - R_{{\text{vs}}}^{\text{2}}\,{e^{ - \,{\text{2}}\,{\alpha _{\text{s}}}\,{d_{\text{s}}}}}}}}.$$

(7)

The absorption coefficient α _s(λ) of the slab is related to its extinction coefficient κ _s(λ) as ${{\alpha _{\text{s}}}(\lambda ) \equiv {{{\text{4}}\,{{\pi }}\,{\kappa _{\text{s}}}(\lambda )} \mathord{\left/ {\vphantom {{{\text{4}}\,{{\pi }}\,{\kappa _{\text{s}}}(\lambda )} \lambda }} \right. \kern-\nulldelimiterspace} \lambda }}$. The intensity reflection coefficient R _vs (=R _sv) at vacuum–slab (vs-) interface is given by

$${R_{{{\text{vs}}}} (\lambda ) = \frac{{\left[ {n_{{\text{s}}} (\lambda )\, - \,{\text{1}}} \right]^{{\,{\text{2}}}} \, + \,\left[ {\kappa _{{\text{s}}} (\lambda )} \right]^{{\,{\text{2}}}} }}{{\left[ {n_{{\text{s}}} (\lambda )\, + \,{\text{1}}} \right]^{{\,{\text{2}}}} \, + \,\left[ {\kappa _{{\text{s}}} (\lambda )} \right]^{{\,{\text{2}}}} }}}.$$

(8)

For the model approximation ${\kappa _{\text{s}}^2\, < < \,n_{\text{s}}^2}$, the T _vsv(λ) and R _vsv(λ) formulas become simple, so they can be used to calculate, at each λ, n _s(λ) and κ _s(λ) of a slab standing freely in the air from its measured T _exp(λ) and R _exp(λ) [58]. If the slab is transparent (${{\kappa _{\text{s}}}(\lambda ) \cong {\alpha _{\text{s}}} \cong {\text{0}}}$), its normal-incidence specular transmittance T _s(λ) and reflectance R _s(λ) are expressed in terms of its index of refraction n _s(λ) only, viz.

$$R_{{\text{s}}} (\lambda ) = \frac{{\left[ {n_{{\text{s}}} (\lambda )\, - \,1} \right]^{{\,2}} }}{{\left[ {n_{{\text{s}}} (\lambda )} \right]^{{\,2}} \, + \,1}};\quad T_{{\text{s}}} (\lambda ) = 1 - R_{{\text{s}}} (\lambda ) = \frac{{2\,n_{{\text{s}}} (\lambda )}}{{\left[ {n_{{\text{s}}} \,(\lambda )} \right]^{{\,2}} \, + \,1}}$$

(9)

One can use Eq. (9) to calculate directly n _s (λ) of a thick dielectric slab at each λ from its T _s(λ) − λ or R _s(λ) − λ data; hence its n _s(λ)-dispersion above its absorption edge.

1.2 Theoretical formula of normal-incidence transmittance of air-supported {film/slab}-stacks

Consider an {air/thin film/thick substrate/air}-stack, with ${{{\hat n}_{\text{s}}}(\lambda )\, = \,\,{n_{\text{s}}}(\lambda ) + \,j\,{\kappa _{\text{s}}}(\lambda )}$, ${{\alpha _{\text{s}}}\,\, \equiv \,\,{{{\text{4}}\,{{\pi }}\,{\kappa _{\text{s}}}} \mathord{\left/ {\vphantom {{{\text{4}}\,{{\pi }}\,{\kappa _{\text{s}}}} \lambda }} \right. \kern-\nulldelimiterspace} \lambda }}$, ${{{\hat n}_{\text{f}}}(\lambda ) = \hat n(\lambda ) = n(\lambda ) + j\kappa (\lambda )}$, and ${{\alpha _{\text{f}}}\,\, = \,\,\alpha \,\, \equiv \,\,{{{\text{4}}\,{{\pi }}\,\kappa } \mathord{\left/ {\vphantom {{{\text{4}}\,{{\pi }}\,\kappa } \lambda }} \right. \kern-\nulldelimiterspace} \lambda }},$ on which quasi-monochromatic light is incident normally on its air (v)–film (f) interface. For a coherently thin film (${\Delta \lambda \,\, < < \,\,{{{\lambda ^{\text{2}}}} \mathord{\left/ {\vphantom {{{\lambda ^{\text{2}}}} {{\text{2}}\,{{\pi }}\,nd}}} \right. \kern-\nulldelimiterspace} {{\text{2}}\,{{\pi }}\,nd}}}$, d is its geometric thickness) with smooth, plane-parallel surfaces, both multiple internal reflections in the film and interference among them are important, but only internal reflections in its incoherently thick substrate of finite thickness d _s (>>d) are essential, and the theoretical transmission ${{T_{{\text{vfsv}}}}(\lambda )}$ formula is [40, 41, 56, 57]:

$${{T_{{\text{vfsv}}}}(\lambda ) = \frac{{\left( {\tau _{{\text{vf}}}^{\text{2}}\,\tau _{{\text{fs}}}^{\text{2}}\,{e^{ - \,\alpha \,d}}} \right)\left( {\tau _{{\text{sv}}}^{\text{2}}\,{e^{ - \,{\alpha _{\text{s}}}\,{d_{\text{s}}}}}} \right)}}{{{\text{1}} - \frac{{\rho _{{\text{fs}}}^{\text{2}}\, + \,\rho _{{\text{vf}}}^{\text{2}}\,{e^{ - \,2\,\alpha \,d}}\, + \,{\text{2}}\,{\rho _{{\text{vf}}}}\,{\rho _{{\text{fs}}}}\,{e^{ - \,\alpha \,d}}{\text{cos}}\left( {{\text{2}}\,\delta _{\text{f}}^{\prime}\, + \,{\varphi _{{\text{vf}}}}\, - \,{\varphi _{{\text{fs}}}}} \right)}}{{{\text{1}}\, + \,\rho _{{\text{vf}}}^{\text{2}}\rho _{{\text{fs}}}^{\text{2}}\,{e^{ - \,2\,\alpha \,d}}\, + \,{\text{2}}\,{\rho _{{\text{vf}}}}\,{\rho _{{\text{fs}}}}\,{e^{ - \,\alpha \,d}}{\text{cos}}\left( {{\text{2}}\,\delta _{\text{f}}^{\prime}\, + \,{\varphi _{{\text{vf}}}}\, + \,{\varphi _{{\text{fs}}}}} \right)}}\left( {\rho _{{\text{sv}}}^{\text{2}}\,{e^{ - \,{\text{2}}\,{\alpha _{\text{s}}}\,{d_{\text{s}}}}}} \right)}}},$$

(10)

where ${{{\hat \delta }_{\text{f}}}\,\, \equiv \,\,\delta _{\text{f}}^{\prime}\, + \,j\,\delta _{\text{f}}^{''}\,\, = \,\,\left( {{{{\text{2}}\,{{\pi }}\,d} \mathord{\left/ {\vphantom {{{\text{2}}\,{{\pi }}\,d} \lambda }} \right. \kern-\nulldelimiterspace} \lambda }} \right)\,\,\left( {n\, + \,j\,\kappa } \right)\,\, = \,\,{{\left( {\phi \, + \,j\,\alpha \,d} \right)} \mathord{\left/ {\vphantom {{\left( {\phi \, + \,j\,\alpha \,d} \right)} 2}} \right. \kern-\nulldelimiterspace} 2}}$ is normal-incidence complex phase angle produced upon a single traversal of light waves in the film, ϕ is an interference phase angle [31, 41, 57], ρ _lm and τ _lm are real scalar reflection and transmission coefficients at interfaces of the adjacent l–m layers and φ _lm is phase angle produced upon wave reflection at the l–m interface. The normal-incidence expressions of ρ _lm , φ _lm , and τ _lm are given by [31, 57]

$$\begin{array}{*{20}{c}} {\rho _{lm}^{\text{2}}\,\, \equiv \,\,\frac{{{{\left( {{n_l}\, - \,{n_m}} \right)}^{\text{2}}} + {{\left( {{\kappa _l}\, - \,{\kappa _m}} \right)}^{\text{2}}}}}{{{{\left( {{n_l}\, + \,{n_m}} \right)}^{\text{2}}} + {{\left( {{\kappa _l}\, + \,{\kappa _m}} \right)}^{\text{2}}}}}\,\,\,;}&{{\text{tan}}\,{\varphi _{lm}}\,\, = \,\,\frac{{ - \,{\text{2}}\,\left( {{n_l}\,{\kappa _m}\, - \,{n_m}{\kappa _l}} \right)}}{{\left( {n_l^{\text{2}}\, + \,\kappa _l^{\text{2}}} \right) - \left( {n_m^{\text{2}}\, + \,\kappa _m^{\text{2}}} \right)}}} \end{array}$$

(11)

$${\tau _{lm}^{\text{2}}\,\, \equiv \,\,\frac{{{\text{4}}\,\left( {n_l^{\text{2}}\, + \,\kappa _l^{\text{2}}} \right)}}{{{{\left( {{n_l}\, + \,{n_m}} \right)}^{\text{2}}}\, + \,{{\left( {{\kappa _l} + \,{\kappa _m}} \right)}^{\text{2}}}}}}.$$

(12)

Equation (10) becomes less involved for κ ² << n ², ${\kappa \,\, \cong \,\,{\text{0}}}$ and ${{\kappa _{\text{s}}}(\lambda )\,\, = \,\,{\text{0}}}$; so, for n > n _s, ${{T_{{\text{vfsv}}}}(\lambda ) = T\left( {\lambda \,;\,n\,,\,\kappa \,,\,d\,,\,{n_{\text{s}}}} \right)}$ can be written in the form of Swanepoel T(λ)-formula, in terms of n, κ, ${x \equiv {\text{exp}}\left( { - \,\alpha \,d} \right)}$ and ${\phi \,\, \equiv \,\,{{{\text{4}}\,{{\pi }}\,n\,d} \mathord{\left/ {\vphantom {{{\text{4}}\,{{\pi }}\,n\,d} \lambda }} \right. \kern-\nulldelimiterspace} \lambda }}$ as [31, 38]

$${T\left( {\lambda \,;\,n\,,\,\kappa \,,\,d\,,\,{n_{\text{s}}}} \right)\,\, = \,\,\frac{{A\,x}}{{B\, - \,C\,x\,{\text{cos}}\phi \, + \,D\,{x^{\text{2}}}}}},$$

(13a)

$$A\,\, = \,\,{\text{16}}\,{n^{\text{2}}}\,{n_{\text{s}}},$$

(13b)

$$B\,\, = \,\,{\left( {n\, + \,{\text{1}}} \right)^{\,{\text{3}}}} \times \,\left( {n\, + \,n_{\text{s}}^{\text{2}}} \right),$$

(13c)

$$C\,\, = \,\,{\text{2}}\,\left( {{n^{\text{2}}}\, - \,{\text{1}}} \right) \times \left( {{n^{\text{2}}}\, - \,n_{\text{s}}^{\text{2}}} \right),$$

(13d)

$$D\,\, = \,\,{\left( {n\, - \,{\text{1}}} \right)^{\,{\text{3}}}} \times \left( {n\, - \,n_{\text{s}}^{\text{2}}} \right).$$

(13e)

Equation (13a) forms the basis for deriving the analytical formulas used in the arithmetic procedures underlying Swanepoel’s envelope method of normal-incidence transmittance spectrum of a uniform thin film placed onto a thick dielectric slab, with n _s(λ) constant (=n _s) or slightly dispersive with a pre-determined numeric n _s(λ) − λ relation.

1.2.1 Swanepoel transmission envelope method for air-supported {thin film/thick transparent substrate}-stacks

Swanepoel [38] overcome curbs of Manifacier’s envelope approach [37] to a uniform dielectric film on an infinitely-thick transparent slab (κ _s = 0 and n _s < n) to get n(λ) and κ(λ) of the films from their normal-incidence transmission spectra displaying interference-fringe maxima and minima via supposing that the substrate has instead an incoherent finite thickness d _s (>>d) and smooth surfaces; so ignored multiple back and forth light-wave reflections inside it contribute to the stack’s specular transmission. With model approximations κ ² << n ² and κ ~ 0 and no interference between multiple internal reflections in the substrate, Swanepoel used the $T\left( {\lambda \,;\,n\,,\,\kappa \,,\,d\,,\,{n_{\text{s}}}} \right)$-Eq. (13a) to develop series of algebraic procedures of an envelope approach to extract n(λ), κ(λ), and d of a uniform film from its normal-incidence T _exp(λ) − λ spectrum only. Yet, execution of Swanepoel’s analytical envelope procedures is solely relied on the presence of many maxima and minima in transparent and weak/medium absorbing parts of transmission spectrum and on the ability to construct continuous envelope curves around these maxima and minima. Many workers used Swanepoel transmission envelope method to analyze the transmittance T _exp(λ) − λ spectra of air-supported structures embracing coherent uniform thin films on incoherent thick transparent substrates at which a light beam of small SBWs is normally incident to retrieve geometric thicknesses of films and spectral dispersion of their optical constants n(λ) and κ(λ) [22, 23, 38]. Effects due to light-wave polarization and incidence angles are not important in envelope analyses of transmission spectra of uniform thin films measured at normal incidence of quasi-monochromatic light with small SBW. The main formulas and procedures of Swanepoel’s transmission envelope approach are summarized in the next subsections.

The transmission spectrum of an air-supported {thin film/thick non-absorbing substrate}-stack can be divided into four main spectral regimes. In the transparency region, the film’s absorption coefficient α(λ) = 0 (x(λ) = 1), so the transmission of such an air-supported {film-substrate}-stack is determined by n(λ) and n _s(λ). In the weak absorption region, α(λ) is small but causes a slight reduction in the stack’s transmission, which often unveils a fair decrease in its medium absorption region due to a substantial absorption coefficient of the film. At λ smaller than a specific wavelength λ _c, which designates the onset of the film’s absorption edge, the optical absorption in the film is strong and the transmission of this {air/film/substrate/air}-stack will decrease drastically because of large values of α(λ) = 0 (x(λ) < < 1) due to light-induced band-to-band electronic transitions [21, 59–61]. If the film has geometric thickness d with smooth, parallel-plane surfaces, and is uniform, homogeneous and amply thin, its optical thickness nd satisfies the coherency criterion ${n\,d < < {{{\lambda ^{\text{2}}}} \mathord{\left/ {\vphantom {{{\lambda ^{\text{2}}}} {{\text{2}}\,\pi \,\Delta \lambda }}} \right. \kern-\nulldelimiterspace} {{\text{2}}\,\pi \,\Delta \lambda }}}$ [41], with Δλ being the spectral band width (SBW) of the light beam normally incident on it, and the measured T _exp(λ) − λ spectrum of its structure often exhibits a pattern of maxima and minima at the long-wavelength side arising from interference of multiple internal reflections in the film, whose optical thickness governs their number and spectral spacing. The implementation of analytical procedures of Swanepoel transmission envelope method requires numerous and well-resolved interference-fringe maxima and minima. The transmission spectra of air-supported {thin film/thick transparent substrate}-stacks can be analyzed by assuming a constant substrate’s index of refraction n _s(λ) or using a numeric dispersion n _s(λ)-relation, which may be deduced from measured transmission T _s(λ) or reflection R _s(λ) of a bare substrate standing freely in the air via Eq. (9) or via Eqs. (6) to (8) with ${\left[ {\kappa _{{\text{s}}} (\lambda )} \right]^{{\,{\text{2}}}} \,<< \,\left[ {n_{{\text{s}}} (\lambda )} \right]^{{\,{\text{2}}}} }$ [58].

1.2.2 Transmission maxima and minima envelope curves

It is more convenient to re-write the $T\left( {\lambda \,,{n_{\text{s}}};\,n,\,\kappa ,\,\phi } \right)$-formula given in Eq. (13a) in terms of the unknowns index of refraction n(λ) and absorbance parameter ${x(\lambda )\, \equiv {\text{exp}}\left[ { - \,\alpha (\lambda )\,d} \right]}$ of the film—that is, ${T(\lambda )\, = \,\,T\left\{ {\lambda ;\,n(\lambda )\,,\,x(\lambda )} \right\}}$, with ${\alpha \left( \lambda \right)\,\, \equiv \,\,{{{\text{4}}\,{{\pi }}\,\kappa (\lambda )} \mathord{\left/ {\vphantom {{{\text{4}}\,{{\pi }}\,\kappa (\lambda )} \lambda }} \right. \kern-\nulldelimiterspace} \lambda }}$ and ${\phi \,\, \equiv \,\,{{{\text{4}}\,{{\pi }}\,n\,d} \mathord{\left/ {\vphantom {{{\text{4}}\,{{\pi }}\,n\,d} \lambda }} \right. \kern-\nulldelimiterspace} \lambda }}$. Set the first derivative of this ${T\left( {\lambda \,,\,{n_{\text{s}}}\,;\,n\,,\,\kappa \,,\,\phi } \right)}$-formula with respect to ϕ to zero to get cosϕ = +1 for a maximum in transmission spectrum at a wavelength λ _M and cosϕ = −1 for a minimum at a different wavelength λ _m. For small SBWs and uniform films, the transmission maxima and minima are, respectively, labeled by ${{T_{{\text{M0}}}}({\lambda _{\text{M}}})}$ and ${{T_{{\text{m0}}}}({\lambda _{\text{m}}})}$, which are the T(λ) values at λ-positions that are tangent to maxima and minima of the as-measured normal-incidence transmittance T _exp(λ) − λ spectrum, and are given by [38]

$$ {T_{{{\text{M0}}}} (\lambda _{{\text{M}}} )\,\, = \,\,\left. {\frac{{A\,x(\lambda )}}{{B\, - \,C\,x(\lambda )\, + \,D\,\left[ {x(\lambda )} \right]^{{\text{2}}} }}} \right|_{{\lambda \, = \,\lambda _{{\text{M}}} }} \,\, ; } {\left. {T_{{{\text{m0}}}} (\lambda _{{\text{m}}} )\,\, = \,\,\frac{{A\,x(\lambda )}}{{B\, + \,C\,x(\lambda )\, + \,D\,\left[ {x(\lambda )} \right]^{{\,{\text{2}}}} }}} \right|_{{\lambda \, = \,\lambda _{{\text{m}}} }} } \\$$

(14)

The transmission envelope approach does rely on the ability to construct two virtual ${{T_{{\text{M0}}}}(\lambda )}$ and ${{T_{{\text{m0}}}}(\lambda )}$ envelope curves that should be monotonic continuous functions in λ from the ${{T_{{\text{M0}}}}({\lambda _{\text{M}}})}$ and ${{T_{{\text{m0}}}}({\lambda _{\text{m}}})}$ transmittances measured at λ _M and λ _m can be shown to satisfy the basic interference condition [38]:

$${{\text{2}}\,n\left( {\lambda _{i} } \right)\,d \equiv p\,\lambda _{i} }.$$

(15)

In transmission case, the interference-fringe order p is an integer (1, 2, 3,...) for maxima and half-integer (1/2, 3/2, 5/2,...) for minima, where n(λ _i ) is the film’s index of refraction at wavelength λ _i at which tangent points of maxima or minima of measured transmission spectrum are located. Equation (15) contains information on the product of film’s index of refraction n and thickness d (optical thickness nd), but there is no way of obtaining information on either n or d separately using this equation only. The underlying computational procedures of the analytical envelope method are modeled to calculate directly the optical constants and geometric thickness of the film, but such calculation is only feasible if constructed transmission ${{T_{{\text{M0}}}}(\lambda )}$ and ${{T_{{\text{m0}}}}(\lambda )}$ envelope curves are used to calculate transmittance values ${T_{{\text{m0}}}^{\prime}({\lambda _{\text{M}}})}$ at wavelengths λ _M , for maxima of measured transmittances ${{T_{{\text{M0}}}}({\lambda _{\text{M}}})}$, and transmittance values ${T_{{\text{M0}}}^{\prime}({\lambda _{\text{m}}})}$ at wavelengths λ _m , for minima of measured transmittances ${{T_{{\text{m0}}}}({\lambda _{\text{m}}})}$.

The sets of maxima and minima transmittances at the measured wavelengths λ _M and λ _m and calculated ones—that is, ${\left\{ {{T_{{\text{M0}}}}({\lambda _{\text{M}}})\,,\,T_{{\text{m0}}}^{\prime}({\lambda _{\text{M}}})} \right\}}$ and ${\left\{ {\,T_{{\text{M0}}}^{\prime}({\lambda _{\text{m}}})\,,\,{T_{{\text{m0}}}}({\lambda _{\text{m}}})\,} \right\}},$ form the basis for retrieving film’s n(λ) and κ(λ) at each λ _M and λ _m and its geometric thickness d by the Swanepoel transmission envelope approach, the main features and analytical expressions of which its applicability limits will now be discussed. Its formulation is involved for non-uniform (wedge-shaped) films [38, 41–45] and large SBWs [38], determined by the inherent (natural) bandwidth of emitted photons and by the slits’ widths: two factors that affect the spectral contour and magnitudes of maxima and minima pattern (fringe shrinkage) of as-measured transmission spectra in transparent and weak absorption regions. The effect slit width is under experimental control and can be reduced by choosing small slit widths that yield an output light beam of good signal-to-noise ratio; otherwise, one has to obtain slit-free maxima and minima transmittance values before using Swanepoel analytical transmission envelope method [38]. The as-measured shrunk transmission maxima and minima must be manipulated to get a couple of closed-form analytical transcendental formulas to get the ${{T_{{\text{M0}}}}({\lambda _{\text{M}}})}$ and ${{T_{{\text{m0}}}}(\lambda )}$ envelope curves of uniform films [23].

1.2.3 Transmission envelope analytical expressions of optical constants

The formulations and computational procedures that can be used to directly calculate, at each wavelength λ, the optical constants of a thin uniform film laid onto a thick transparent substrate from its as-measured normal-incidence transmission spectrum using the measured and calculated ${\left\{ {{T_{{\text{M0}}}}({\lambda _{\text{M}}})\,,\,T_{{\text{m0}}}^{\prime}({\lambda _{\text{M}}})} \right\}}$ and ${\left\{ {\,T_{{\text{M0}}}^{\prime}({\lambda _{\text{m}}})\,,\,{T_{{\text{m0}}}}({\lambda _{\text{m}}})\,} \right\}}$-pairs will be summarized below for three main optical absorption regions.

1.2.3.1 Optically transparent region

In the transparent part of normal-incidence transmission spectrum of an air-supported {uniform film/transparent slab}-stack, ${\alpha (\lambda ) \cong {\text{0}}}$ (${x(\lambda ) = {\text{1}}}$). Putting ${x(\lambda ) = {\text{1}}}$ in the ${{T_{{\text{M0}}}}({\lambda _{\text{M}}})}$- and ${{T_{{\text{m0}}}}({\lambda _{\text{m}}})}\text{-}$formulas of Eq. (14) and substituting A, B, C, and D given in Eqs. (13b)–(13e) into these formulas to get a formula for ${{T_{{\text{M0}}}}({\lambda _{\text{M}}})\,\, = \,\,{T_{\text{s}}}(\lambda )}$, in terms of n _s(λ) Eq. (9) and ${{T_{{\text{m0}}}}({\lambda _{\text{m}}})}$, in terms of n(λ) and n _s(λ), from which an n (λ)-formula is found [38]:

$$\begin{array}{*{20}c} {n\,\, = \,\,\left\{ {M\, + \,\left[ {M^{{\text{2}}} \, - \,n_{{\text{s}}}^{{\text{2}}} } \right]^{{\,{{\text{1}} \mathord{\left/ {\vphantom {{\text{1}} {\text{2}}}} \right. \kern-\nulldelimiterspace} {\text{2}}}}} } \right\}^{{\,{{\text{1}} \mathord{\left/ {\vphantom {{\text{1}} {\text{2}}}} \right. \kern-\nulldelimiterspace} {\text{2}}}}} \,\,;} & {M\,\, = \,\,\frac{{{\text{2}}\,n_{{\text{s}}} }}{{T_{{{\text{m0}}}} }}\, - \,\frac{{n_{{\text{s}}}^{{\text{2}}} \, + \,{\text{1}}}}{{\text{2}}}} \\ \end{array} .$$

(16)

For known n _s(λ), Eq. (16) can be used to calculate n of the film in the transparency region at λ _m and λ _M using the observed (measured) ${{T_{{\text{m0}}}}({\lambda _{\text{m}}})}$- and calculated ${T_{{\text{m0}}}^{\prime}({\lambda _{\text{M}}})}$-minima transmittances only.

1.2.3.2 Weak and medium optical absorption regions

In regions of weak and medium optical absorption of the film, ${\alpha (\lambda ) \ne {\text{0}}}$ and ${x(\lambda ) < {\text{1}}}$, and one can get a formula in terms of ${{T_{{\text{M0}}}}({\lambda _{\text{M}}})}$ and ${{T_{{\text{m0}}}}({\lambda _{\text{m}}})}$ that is independent of x(λ), but is a function of n and n _s, viz. [38]:

$${\frac{{\text{1}}}{{{T_{{\text{m0}}}}}}\, - \,\frac{{\text{1}}}{{{T_{{\text{M0}}}}}}\,\, = \,\,\frac{{{\text{2}}\,C}}{A}\,\, = \,\,\frac{{\left( {{n^{\text{2}}}\, - \,{\text{1}}} \right) \times \left( {{n^{\text{2}}}\, - \,n_{\text{s}}^{\text{2}}} \right)}}{{{\text{4}}\,{n^{\text{2}}}\,{n_{\text{s}}}}}}.$$

(17)

Solve Eq. (17) for the film’s index of refraction n to get

$$\begin{array}{*{20}c} {n\,\, = \,\,\left\{ {N\, + \,\left[ {N^{{\text{2}}} \, - \,n_{{\text{s}}}^{{\text{2}}} } \right]^{{{{\,1} \mathord{\left/ {\vphantom {{\,1} 2}} \right. \kern-\nulldelimiterspace} 2}}} } \right\}^{{{{\,1} \mathord{\left/ {\vphantom {{\,1} 2}} \right. \kern-\nulldelimiterspace} 2}}} ;} & {N\,\, = \,\,{\text{2}}\,n_{{\text{s}}} \,\frac{{T_{{{\text{M0}}}} \, - \,T_{{{\text{m0}}}} }}{{T_{{{\text{M0}}}} \,T_{{{\text{m0}}}} }}\, + \,\frac{{n_{{\text{s}}}^{{\text{2}}} \, + \,{\text{1}}}}{{\text{2}}}} \\ \end{array} .$$

(18)

Given ${{n_{\text{s}}}(\lambda )\, - \,\lambda }$ data, Eq. (18) can be utilized to calculate directly the film’s index of refraction n(λ) from measured and calculated transmittance maxima and minima pairs: ${\left\{ {{T_{{\text{M0}}}}({\lambda _{\text{M}}})\,,\,T_{{\text{m0}}}^{\prime}({\lambda _{\text{M}}})} \right\}}$ and ${\left\{ {T_{{\text{M0}}}^{\prime}({\lambda _{\text{m}}})\,,\,{T_{{\text{m0}}}}({\lambda _{\text{m}}})} \right\}}$ at λ _M and λ _m in weak and medium absorption regions of the transmission spectrum. In transparent part of ${T(\lambda ) - \lambda }$ spectrum of an {air/uniform film/transparent substrate/air}-stack, ${x(\lambda )\,\, \cong \,\,{\text{1}}}$ and ${\alpha (\lambda )\,\, \cong \,\,{\text{0}}}$; however, in its weak and medium absorption regions, where a number of interference-fringe extremes are displayed, ${{\text{0}}\,\, < \,\,x(\lambda )\, < \,\,{\text{1}}}$ and ${x(\lambda )\,}$ can be evaluated from measured and calculated values of transmission maxima and minima at same λ _M and λ _m . In these absorption regions, ${x(\lambda )\,}$ can be given by a variety of algebraic analytical expressions [38]. As the ${{T_{{\text{M0}}}}(\lambda )\,}$ and ${{T_{{\text{m0}}}}(\lambda )\,}$ formulas of Eq. (14) are quadratic functions in ${x(\lambda )\,},$ they can be solved for ${x(\lambda )\,}$ to obtain compact analytical closed-form ${x(\lambda )\,}$-expressions in terms of ${{T_{{\text{M0}}}}(\lambda )\,}$ and/or ${{T_{{\text{m0}}}}(\lambda )\,}$, in addition to n and n _s, one of which is written in terms of ${{T_{{\text{M0}}}}(\lambda )\,}$ only as [38]

$$\begin{gathered} x{\mkern 1mu} {\mkern 1mu} = {\mkern 1mu} {\mkern 1mu} \frac{{E_{M} {\mkern 1mu} - {\mkern 1mu} \left[ {E_{M}^{{\text{2}}} {\mkern 1mu} - {\mkern 1mu} \left( {n^{{\text{2}}} {\mkern 1mu} - {\mkern 1mu} {\text{1}}} \right)^{{{\kern 1pt} {\text{3}}}} \times \left( {n^{{\text{2}}} {\mkern 1mu} - {\mkern 1mu} n_{{\text{s}}}^{{\text{4}}} } \right)} \right]^{{{\kern 1pt} 1/2}} }}{{\left( {n{\mkern 1mu} - {\mkern 1mu} {\text{1}}} \right)^{{{\kern 1pt} {\text{3}}}} \times \left( {n{\mkern 1mu} - {\mkern 1mu} n_{{\text{s}}}^{{\text{2}}} } \right)}}; \hfill \\ E_{M} {\mkern 1mu} {\mkern 1mu} = {\mkern 1mu} {\mkern 1mu} \frac{{{\text{8}}{\mkern 1mu} n^{{\text{2}}} {\mkern 1mu} n_{{\text{s}}} }}{{T_{{{\text{M0}}}} }}{\mkern 1mu} + {\mkern 1mu} \left( {n^{{\text{2}}} {\mkern 1mu} - {\mkern 1mu} {\text{1}}} \right) \times \left( {n^{{\text{2}}} {\mkern 1mu} - {\mkern 1mu} n_{{\text{s}}}^{{\text{2}}} } \right). \hfill \\ \end{gathered}$$

(19)

Using the n(λ) values, determined from Eq. (18) and known values of n _s(λ), the corresponding values of x(λ) ${\left( {\, \equiv {\text{exp}}\left[ { - \,\alpha (\lambda )\,d} \right]\,} \right)}$ can be calculated, at wavelength λ, from Eq. (19), which yields reliable values for the film’s absorption coefficient α(λ), since it is less sensitive to errors in n(λ) and n _s(λ), and α(λ) is less sensitive to errors in ${{T_{{\text{M0}}}}(\lambda )}$, compared with other x(λ)-expressions [38]. The x(λ)-expression in ${{T_{{\text{M0}}}}(\lambda )}$ is feasible in weak and medium absorption parts of normal-incidence ${T(\lambda )\, - \,\lambda }$ spectrum onto which many maxima and minima are displayed, since the ${{T_{{\text{M0}}}}}$-envelope is the easiest and reliable monotonic envelope curve to construct. The geometric thickness d of the film is required for the calculation of its absorption coefficient α(λ) at the wavelength λ from the respective calculated values of x(λ). Once the values of α(λ) at each λ in weak and medium optical absorption regions are found, the λ-dependence of the film’s extinction coefficient κ(λ) can be computed from ${\kappa (\lambda )\,\, \equiv \,\,{{\lambda \,\alpha (\lambda )} \mathord{\left/ {\vphantom {{\lambda \,\alpha (\lambda )} {4\,\pi }}} \right. \kern-\nulldelimiterspace} {4\,\pi }}}$. In Swanepoel’s analytical envelope approach, rough values of d, n(λ) and κ(λ) are first calculated and then improved via a series of computational procedures based on the above-cited formulas [38].

1.2.3.3 Strong optical absorption region

In the strong absorption region of as-measured transmission ${{T_{{\text{exp}}}}(\lambda )\,\, - \,\lambda }$ spectrum, the interference fringes disappear; thus, there is no way to find closed-form analytical expressions for calculating n(λ) and x(λ) independently from transmission spectrum alone. One can estimate n(λ) in this region by extrapolating the n(λ) − λ data calculated in transparency, weak, and medium absorption parts of the ${{T_{{\text{exp}}}}(\lambda )\,\, - \,\lambda }$ spectrum using a dispersion formula that fits n(λ) − λ data at all wavelengths and no absorption bands exist. For very large α(λ) (${x(\lambda ) < < {\text{1}}}$), the ${{T_{{\text{M0}}}}(\lambda )}$, ${{T_{{\text{m0}}}}(\lambda )}$, and ${{T_\alpha }(\lambda )\,\, \equiv \,\,\sqrt {{T_{{\text{M0}}}}(\lambda ) \times {T_{{\text{m0}}}}(\lambda )} }$ curves all converge to a single transmission curve ${{T_{\text{0}}}(\lambda )}$, which matches as-measured ${T(\lambda )\,\, - \,\lambda }$ spectrum, and the ${T(\lambda )}$-formula of Eq. (13a) reduces to [38]

$$T_{{\text{0}}} \,\, \cong \,\,\frac{{A\,x}}{B};\quad x\,\, \cong \,\,\frac{{\left( {n\, + \,{\text{1}}} \right)^{{\,{\text{3}}}} \times \left( {n\, + \,n_{{\text{s}}}^{{\text{2}}} } \right)}}{{{\text{16}}\,n^{{\text{2}}} n_{{\text{s}}} }}T_{{\text{0}}} .$$

(20)

Given n _s(λ) and n(λ) at each λ in the strong absorbing region, α(λ) can be computed from ${{T_{{\text{exp}}}}(\lambda )\,\, - \,\lambda }$ data using Eq. (20), which works well for values of T(λ) below 0.2 or so; however, this computational procedure is questionable for larger values of T(λ) [38].

The applicability of Swanepoel’s transmission analytical envelope method is based on the ability of constructing, from ${{T_{{\text{M0}}}}({\lambda _{\text{M}}})}$ and ${{T_{{\text{m0}}}}({\lambda _{\text{m}}})}$ values at tangent points to interference-fringe maxima and minima of as-measured normal-incidence transmission spectrum of an ideal air-supported {thin uniform film/thick transparent substrate}-stack, two “virtual” envelope curves that are reliable, monotonic functions in λ around its maxima and minima. This can be attained using quadratic or exponential-like formula, or computer software like that of McClain et al. [46]. Furthermore, in the transparency region of this four-layered structure, α(λ) = 0 and the transmittances of film and substrate coincide. For incident light beam of small SBW, deviation of maxima of its as-measured normal-incidence transmission spectrum from ${{T_{\text{s}}}(\lambda )}$ with decreasing wavelength indicates onset of optical absorption inside the film itself.

Appendix B: dispersion functions of index of refraction of dielectric and semiconducting films

There are many empirical and theoretical dispersion and absorption functions that can be used to describe optical behavior of dielectric and semiconducting samples, but most of which are intricate and involve many parameters to be determined, thus require a large number of data, besides rigorous non-linear curve-fitting programs [19–21, 32, 61]. Unwieldy dispersion functions are impractical in case of limited number of dispersion data and it would be more instructive to use simpler dispersion formulas [21–23].

The spectral dispersion of index of refraction n(λ) of numerous dielectric and pure semiconducting materials is often analyzed by the Cauchy dispersion relation with multi-constant parameters, the three-constant Sellmeier dispersion relation, and the two-constant Wemple–DiDominco (WDD) dispersion function to discuss wavelength (photon energy) dependency of their indices of refraction in spectral part above their absorption edges [50]. The Sellmeier and WDD dispersion functions incorporate more physically informative parameters than the purely empirical Cauchy relation. More details on the formulations of these dispersion functions can be found elsewhere [19–24, 49, 50, 61]; here, we shall only quote their common mathematical forms. The Cauchy’s dispersion relation is a multi-constant polynomial function of n(λ) in λ given by [21–24]

$${n\left( \lambda \right)\,\, = \,\,{A_{\text{1}}}\, + \,\frac{{{A_{\text{2}}}}}{{{\lambda ^{\text{2}}}}}\, + \,\frac{{{A_{\text{3}}}}}{{{\lambda ^{\text{4}}}}}\, + \, \cdots }$$

(21)

The constants A ₁, A ₂, A ₃,… etc are usually treated as adjustable parameters to be found by non-linear curve-fitting of n(λ) − λ data to Eq. (21), with the number of constants being two or three. The first-order (three-constant) Sellmeier dispersion relation is often expressed in terms of three constant parameters C ₀(>1), which is equal to unity in original Sellmeier dispersion formula [18–24], C ₁(>1), and a threshold wavelength λ ₀ (<<λ) that is an inherent characteristic of the material [18], viz.

$${\left[ {n\left( \lambda \right)} \right]^{{\,2}} \,= \,C_{{\text{0}}} \, + \,\frac{{C_{{\text{1}}} \,\lambda ^{{\text{2}}} }}{{\lambda ^{{\text{2}}} \, - \,\lambda _{0}^{2} }}}$$

(22)

The constant C ₀ is taken to represent the dielectric constant ${{\varepsilon _\infty }}$ arising from contributions at very high frequencies, while the index of refraction ${n\left( {\lambda \to \infty } \right)}$ at infinite spectral wavelength (zero photon energy) represents static index of refraction of the material, with ${n\left( {\lambda \to \infty } \right)\,\, = \,\,{n_{\text{0}}}\,\, \approx \sqrt {{C_{\text{0}}}\, + \,{C_{\text{1}}}} }$. The wavelength λ ₀ is much less than the lowermost wavelength λ of spectral range over which the n(λ) − λ data is taken, and is related to the threshold photon energy required for onset of photogeneration process in material [18]. The Wemple and DiDominco (WDD) describes a zero-broadening single-oscillator dielectric function, written in terms of the photon energy E (${ \cong {\text{1240}}\,\,{{{\text{eV}}} \mathord{\left/ {\vphantom {{{\text{eV}}} {\lambda \left( {{\text{nm}}} \right)}}} \right. \kern-\nulldelimiterspace} {\lambda \left( {{\text{nm}}} \right)}}}$) and two-constant parameters: the single-oscillator energy E ₀ and dispersion energy (oscillator strength) E _d in the form (for E ₀ >> E) [50]:

$${\left[ {n(E)} \right]^{{\,{\text{2}}}} \,\, = \,\,{\text{1}}\, + \,\frac{{E_{{\text{0}}} \,E_{{\text{d}}} }}{{E_{{\text{0}}}^{{\text{2}}} \, - \,E^{{\text{2}}} }}}$$

(23)

A model approximation that is viable to the three-constant Sellmeier and the two-constant WDD dispersion formulations, where they match, is at photon energies E→ 0 (λ → ∞); in this spectral limit, both dispersion relations asymptotically yields the static index of refraction of the material ${{n_{\text{0}}}\,\, \approx \,\,\sqrt {{C_{\text{0}}}\, + \,{C_{\text{1}}}} \,\, \approx \,\,\sqrt {{\text{1}}\, + \,{{{E_{\text{d}}}} \mathord{\left/ {\vphantom {{{E_{\text{d}}}} {{E_{\text{0}}}}}} \right. \kern-\nulldelimiterspace} {{E_{\text{0}}}}}} \cong \sqrt {{\varepsilon _{\text{s}}}} }$, where ${\varepsilon _{\text{s}}}$ is its static dielectric constant.