1 Introduction

Recently, mobile robots with special leg mechanisms have been developed [1, 2]. We have studied mobile robots with rimless wheels. A rimless wheel has only a hub and spokes without a rim [3, 4]. Instead of rolling movement, a wheel essentially undergoes a walking motion without a rim. Therefore, such a wheel can travel uneven terrain similar to a general walking robot, and this, particularly, gives researchers an interest in its ability to overcome the steps.

Robots with the wheels are called “rimless wheel robots” and have been studied [5,6,7,8]. Moreover, rimless wheel robots with elastic telescopic legs have been proposed. Based on the numerical simulation results, Asano et al. presented that rimless wheel robots have a high adaptability to steps due to the elasticity of the telescopic legs [9,10,11].

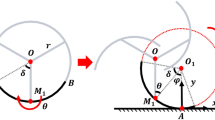
However, experimental studies are required on the rolling motion of rimless wheels with elastic telescopic legs to confirm their adaptability. Similar robotics research has developed a robot that can climb high steps with actively moving telescopic legs [12]. Furthermore, we want to realize a robot that can move fast and passively handle steps. This means moving at high speed on a stepped surface in a concrete real-life situation. Figure 1 shows a schematic of the rimless wheel robot. The robot has a torso and legs that can stretch and contract due to the elastic spring.

However, no developments on rimless wheel robots that can walk on level ground with steps. Altough rimless wheel robots with elastic telescopic legs is being developed, the elasticity of their legs aims shock absorption rather than traversing steps [13, 14]. To better understand the performance of such robots, it is required to investigate their behavior while climbing up and down steps through walking experiments with actual robots.

It is necessary to determine the parameters of the robot to develop an experimental machine, particularly the elasticity of the telescopic leg with a substantial effect on gait. Additionally, although simple two-dimensional (2D) walking simulations were reported, there is still a need for gait analysis using three-dimensional (3D) walking simulations, which were closely simulated in real environments.

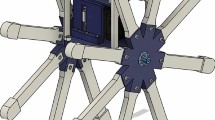
In this study, we first developed a robot model and simulated its walking on level ground and surfaces with steps, and built the actual robot. Figures 2, 3 and 4 demonstrate the 3D model of the rimless wheel robot built using 3D computer-aided design (CAD) software. The 3D walking of a rimless wheel robot with telescopic legs shows very complex dynamics and it is unrealistic to create such a model after deriving all the equations of motion and impact equations as in previous studies. Thus, we simulated the walking of the robot in Unity [15]. We obtained the optimum elasticity of the legs suitable to overcoming steps. Based on the simulation results, we constructed a rimless wheel robot with elastic legs, optimized for overcoming steps. Finally, we conducted walking experiments using a rimless wheel robot with the optimum elasticity to overcome steps. The rest of this paper is organized as follows. Section 2 introduces the model of the rimless wheel robot in Unity. Section 3 presents the output-zeroing control method. Section 4 displays the numerical simulation results of the walking simulator. Section 5 highlights the constructed rimless wheel robot and the experimental results. Finally, Sect. 6 presents the conclusion and discusses future directions.

Fig. 1
figure 1

Schematic illustrating a rimless wheel robot with elastic telescopic legs

Full size image
Fig. 2
figure 2

3D model representation of the rimless wheel robot with elastic telescopic legs: an overview

Full size image
Fig. 3
figure 3

Frontal perspective of 3D model of the rimless wheel robot

Full size image
Fig. 4
figure 4

Lateral perspective of 3D model of the rimless wheel robot

Full size image

2 Model of the rimless wheel robot in unity

In this section, we detail of the rimless wheel robot model with elastic telescopic legs developed in Unity. We constructed a 3D model of the robot (Fig. 5) which is less complex than the 3D model of the actual robot (Fig. 2). The parameters were determined using 3D CAD software.

Fig. 5
figure 5

Unity-based 3D model of the rimless wheel robot

Full size image
Fig. 6
figure 6

Specified parameters of rimless wheel robot with elastic telescopic legs

Full size image

Initially, we equipped the robot’s tiptoe with a sphere collider to detect collisions. However, we observed certain phenomena, such as skidding. To address this, we employed a capsule collider. Additionally, a slider-joint asset was used to represent the telescopic legs. The asset allows the user to set the telescoping length, spring constant, and damper constant. We used numerical simulations to optimize the elastic parameters of the robot (Fig. 6) shows the robot and its physical parameters, which we set according to Table 1. We set the Unity simulation parameters, listed in Table 2, to produce accurate a result while increasing the computational complexity.

Table 1 Physical parameters of the robot
Full size table
Table 2 Unity simulation parameters
Full size table

3 Control method

We utilized input–output linearization and output-zeroing control to achieve the desired angle to control attitude of the torso. Despite the robot was 3D, the mathematical model for the control was defined as follows. 2D as the rimless wheel robot performed 2D motion while moving in the sagittal plane. If the leg extension/contraction is small, the robot’s dynamics should be similar to a rimless wheel robot without leg extension/contraction. The following equation describes the motion of the rimless wheel robot without leg extension/contraction:

$$\begin{aligned} \varvec{M}(\varvec{q})\ddot{\varvec{q}}+\varvec{H}(\varvec{q},\dot{\varvec{q}})=\varvec{S}u, \end{aligned}$$
(1)

where \(\varvec{q}=[\theta _{1},~\theta _{2}]^{\textrm{T}}\) is the generalized coordinate vector. Inertial matrix \(\varvec{M}(\varvec{q})\in \mathbb {R}^{2\times 2}\) is expressed as follows:

$$\begin{aligned} \varvec{M}(\varvec{q})=\left[ \begin{array}{cc} I_{1zz} + (m_{1} + m_{2})l_{1}^{2} &{} m_{2}dl_{1}\textrm{cos}(\theta _1 - \theta _2) \\ m_{2}dl_{1}\textrm{cos}(\theta _1 - \theta _2) &{} I_{2zz} + m_{2}d^{2} \\ \end{array}\right] , \end{aligned}$$

the Coriolis, centrifugal, and gravitational force vectors \(\varvec{H}(\varvec{q},\dot{\varvec{q}})\in \mathbb {R}^{2}\) is expressed as follows:

$$\begin{aligned} \varvec{H}(\varvec{q},\dot{\varvec{q}})=\left[ \begin{array}{c} m_{2}dl_{1}\sin (\theta _{1}-\theta _{2})\dot{\theta }_{2}^{2} -(m_{1}+m_{2})l_{1}g \sin \theta _{1} \\ -m_{2}dl_{1}\sin (\theta _{1}-\theta _{2})\dot{\theta }_{1}^{2} -m_{2}dg \sin \theta _{2} \\ \end{array}\right] , \end{aligned}$$

u is the input, and the driving matrix \(\varvec{S} \in \mathbb {R}^{2}\) is expressed as

$$\begin{aligned} \varvec{S}=\left[ \begin{array}{c} -1 \\ 1 \\ \end{array}\right] . \end{aligned}$$

The equation for the affine system is defined as follows:

$$\begin{aligned} \frac{d}{dt} \begin{bmatrix} \varvec{q} \\ \varvec{\dot{q}} \end{bmatrix}&:=f_A(\varvec{q} , \varvec{\dot{q}}) + g_A(\varvec{q})u.\nonumber \\ f_A(\varvec{q},\varvec{\dot{q}})&= \begin{bmatrix} \varvec{\dot{q}} \\ \varvec{M}^{-1}(\varvec{q})~(-\varvec{H}(\varvec{q},\dot{\varvec{q}})) \end{bmatrix} \nonumber \\ g_A(\varvec{q})&= \begin{bmatrix} 0 \\ \varvec{M}^{-1}(\varvec{q}) \varvec{S} \end{bmatrix} \end{aligned}$$
(2)

To converge the torso angle \(\theta _{2}\) to the desired value \(\theta _{2d}\), the output function is defined as follows:

$$\begin{aligned} y := h(q) = \theta _2 - \theta _{2d} = 0. \end{aligned}$$
(3)

Differentiating this function with time yields the following functions [16].

$$\begin{aligned} \frac{dy}{dt}&= \begin{bmatrix} \frac{\partial h}{\partial q}&0 \end{bmatrix} \begin{bmatrix} \varvec{ \dot{q}} \\ \varvec{M}^{-1}(\varvec{q})~(-\varvec{H}(\varvec{q},\dot{\varvec{q}})) \end{bmatrix} \nonumber \\&\quad +\begin{bmatrix} \frac{\partial h}{\partial q}&0 \end{bmatrix} \begin{bmatrix} 0 \\ \varvec{M}^{-1}(\varvec{q}) \varvec{S} \end{bmatrix} u \nonumber \\&= L_fh + L_gh, \end{aligned}$$
(4)
$$\begin{aligned} \frac{d^2y}{dt^2}&= \begin{bmatrix} \frac{\partial }{\partial q}\left( \frac{\partial h}{\partial q} \dot{q}\right)&\frac{\partial h}{\partial q} \end{bmatrix} \begin{bmatrix} \varvec{\dot{q}} \\ \varvec{M}^{-1}(\varvec{q})~(-\varvec{H}(\varvec{q},\dot{\varvec{q}})) \end{bmatrix} \nonumber \\&\quad +\frac{\partial h}{\partial q} \varvec{M}^{-1}(\varvec{q}) \varvec{S}u \nonumber \\&= L^2_fh + L_gL_fhu. \end{aligned}$$
(5)

As the relative order of the system is two, the partially linearized feedback input for input–output linearization is given by

$$\begin{aligned} u = -\frac{1}{L_{g}L_{f}h}(L_{f}^2h - v), \end{aligned}$$
(6)

where \(L_gL_fh\) and \(L_{f}^2h\) are provided by

$$\begin{aligned} L_{g}L_{f}h&= \varvec{C}\varvec{M}^{-1}(\varvec{q})\varvec{S}, \\ L_{f}^2h&= -\varvec{C}\varvec{M}^{-1}(\varvec{q})\varvec{H} (\varvec{q},\dot{\varvec{q}}), \\ \varvec{C}&= \begin{bmatrix} 0&1 \end{bmatrix}. \end{aligned}$$

Finally, we set a new control input v as

$$\begin{aligned} v = -K_P(\theta _2 - \theta _{2d})-K_d\dot{\theta }_2. \end{aligned}$$
(7)
Table 3 Control parameters of the robot
Full size table
Fig. 7
figure 7

Walking environment with a green object as a step

Full size image

4 Walking analysis in unity

Figure 7 shows the walking environment of the rimless wheel. The robot model was placed in Unity space. Moreover, the floor and a step (the green object) were set. We first analyzed the walking speed and energy efficiency of the robot with respect to the spring constant of the legs on level ground. Table 3 presents the list of the control parameters of the robot. The initial condition of the robot was \(\varvec{x}_0=[0.0,0.30,~0.0,~0.0]^{\textrm{T}}\), and the index of energy efficiency and specific resistance (SR) was calculated as follows:

$$\begin{aligned} \textrm{SR}:= \frac{p}{Mgv_a}, \end{aligned}$$
(8)

where p [J/s] is the average input power, \(M = m_{1} + m_{2}\) [kg] is the total mass of the robot, and \(v_a\) is the average walking speed. The average input power of the robot is given by

$$\begin{aligned} p:=\frac{1}{T}\int _0^T |u(\dot{\theta }_2-\dot{\theta }_1)|\textrm{d}t, \end{aligned}$$

where T [s] is the total walking time.

Initially, Fig. 8 demonstrate the walking speed of the robot on level ground (i.e. no step case) with respect to the spring constant of the legs. The robot’s walking speed depended on the spring constant, and it reached the maximum speed when the spring constant was 340 N/m. Figure 9 presents the variation in the SR of the robot while walking on level ground with respect to the spring constant of the legs. The spring constant is also correlated with SR. When the spring constant of the legs was 370 N/m, the robot walked most energy-efficiency with the lowest SR value.

Fig. 8
figure 8

Walking speeds on level ground with respect to the spring constant of the legs

Full size image
Fig. 9
figure 9

Relation of Specific resistance on level ground with the spring constant of the legs

Full size image

Furthermore, we investigated the robot’s ability to overcome different heights based on variation of the leg’s spring constant. The ease of overcoming heights varied with the position between the legs and the step to be overcome. To divede stride length was into four parts, the following formula is employed: (i.e., 0.5 \(\times l_1 \times \sin (\pi /16)\)) when the legs were not stretched or contracted, and the initial position before walking was categorized into four patterns. Then, when three of the four patterns overcame a step, it was defined as walking over a step. Figure 10 presents the heights of the steps overcome by the robot with respect to the spring constant of the legs. The spring constant affected the height of the steps that the robot could overcome, and there was a spring constant that enabled the robot to overcome the highest step. With the leg extension/retraction setting, the rimless wheel would overcome could overcome a 0.035 m high step. Figure 11 presents the results based on a more detailed examination of the steps between 380 and 450 N/m. The robot with spring constants 420 and 430 N/m overcame a step height of 0.0356 m.

Comparing level walking at 420 and 430 N/m in terms of walking speed (Fig. 8) and energy efficiency (Fig. 9), it was found that level walking at 420 N/m was superior in terms of walking speed and energy efficiency. Therefore, a spring constant of 420 N/m is optimum for the rimless wheel robot.

Fig. 10
figure 10

Heights of steps overcome by the robot with respect to the spring constant of the legs

Full size image
Fig. 11
figure 11

More detailed analysis of the height of steps exceeded by the robot

Full size image

5 Walking experiments

First, we performed a walking experiment with the robot (Fig. 12) on level ground. However, as the developed robot cannot accurately gather the angle of the support legs, PD control was conducted using only the torso posture. Then, we made the experiment on the ground without and with a 0.03 m step (Approx. 20% of leg length). Figures 13 and 14 display the torso angles of the robot walking on level ground without and with a step, respectively. Comparing the two figures, the angle of the torso changed considerably during the period when the steps were overcome. Figures 15 and 16 present the sequential photos of walking on level ground without and with a step, respectively. These figures demonstrate that the robot walked on level-ground and overcame the step.

Fig. 12
figure 12

Rimless wheel robot with elastic telescopic-legs

Full size image
Fig. 13
figure 13

Torso angle while walking on level ground

Full size image
Fig. 14
figure 14

Torso angle while walking on level ground with a step

Full size image
Fig. 15
figure 15

Sequential photos of walking on level ground

Full size image
Fig. 16
figure 16

Sequential photos of walking on level ground with a step

Full size image

6 Conclusion and future work

We simulated and analyzed the walking performance of a 3D model of a rimless-wheel robot with elastic telescopic legs in Unity. The leg’s spring constant affected the robot’s walking performance. The analyses revealed an optimum spring constant that enabled the robot to overcome the steps. Employing the optimal parameters, we constructed a rimless-wheel robot with elastic telescopic legs that could overcome steps. The robot could walk on level ground and surfaces with 0.03 m step. This rimless wheeled robot with leg elasticity optimization could cope passively with stepped environments and move at fast on stepped surfaces.

In the future, we will implement advanced control and optimize the robot’s energy consumption during walking. We intend to develop a one-wheeled rimless wheeled robot so that the single-wheeled version can move in more confined spaces and consequently enhance the robot’s versatility.