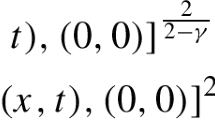Perturbation Theory for Second Order Elliptic Operators with BMO Antisymmetric Part

Abstract

In the present paper we study perturbation theory for the $L^p$ Dirichlet problem on bounded chord arc domains for elliptic operators in divergence form with potentially unbounded antisymmetric part in BMO. Specifically, given elliptic operators $L_0 = \text {div}(A_0\nabla )$ and $L_1 = \text {div}(A_1\nabla )$ such that the $L^p$ Dirichlet problem for $L_0$ is solvable for some $p>1$; we show that if $A_0 - A_1$ satisfies certain Carleson condition, then the $L^q$ Dirichlet problem for $L_1$ is solvable for some $q \ge p$. Moreover if the Carleson norm is small then we may take $q=p$. We use the approach first introduced in Fefferman–Kenig–Pipher ’91 on the unit ball, and build on Milakis–Pipher–Toro ’11 where the large norm case was shown for symmetric matrices on bounded chord arc domains. We then apply this to solve the $L^p$ Dirichlet problem on a bounded Lipschitz domain for an operator $L = \text {div}(A\nabla )$, where A satisfies a Carleson condition similar to the one assumed in Kenig–Pipher ’01 and Dindoš–Petermichl–Pipher ’07 but with unbounded antisymmetric part.

1 Introduction

The study of perturbations of elliptic operators in divergence form $L:=\text {div}(A\nabla \cdot )$ goes back to a result of Dahlberg [5]. Specifically, given elliptic operators $L_0 = \text {div}(A_0\nabla )$ and $L_1 = \text {div}(A_1\nabla )$, where we know that the $L^p$ Dirichlet problem for $L_0$ is solvable, he considered the discrepancy function $\varepsilon (X):=|A_0(X)-A_1(X)|$, and showed that if the measure

$$\begin{aligned} d\mu (Z)=\sup _{X\in B(Z,\delta (Z)/2))}\frac{\varepsilon (X)^2}{\delta (X)}dZ, \qquad \text {with }~\delta (Z):=\text {dist}(Z,\partial \Omega ), \end{aligned}$$

(1.1)

is a Carleson measure with vanishing Carleson norm, then the solvability of the $L^p$ Dirichlet problem is transferred to $L_1:=\text {div}(A_1\nabla \cdot )$ with the same exponent p.

Actually this was formulated in terms of properties of the corresponding elliptic measures $\omega _0$ and $\omega _1$ since we know that the $L^p$ Dirichlet problem for $L = \text {div}(A\nabla \cdot )$ is solvable iff the elliptic measure $\omega$ associated with L belongs to the reverse Hölder space $B_p(d\sigma )$, where $d\sigma$ is surface measure on $\partial \varOmega$. In this language Dahlberg has shows that if the Carleson norm of $\mu$ is small, then $\omega _0\in B_p(d\sigma )$ implies $\omega _1\in B_p(d\sigma )$.

A natural question that arose was whether the condition on $\mu$ could be relaxed to draw the weaker conclusion that $\omega _0\in A_\infty (d\sigma )$ implies $\omega _1\in A_{\infty }(d\sigma )$, where $A_{\infty }(d\sigma ) = \bigcup _{q>1} B_q(d\sigma )$; i.e. transferring solvability to $L_1$ but not necessarily with the same exponent. After some progress was made in [11] this important results was finally established in [12].

To summarize two different types of results were established

• (L) If the Carleson norm of $\mu$ is bounded then $\omega _0\in A_\infty (d\sigma )$ implies $\omega _1\in A_{\infty }(d\sigma )$.

• (S) If the Carleson norm of $\mu$ is small then $\omega _0\in B_p(d\sigma )$ implies $d\omega _1\in B_p(d\sigma )$.

In [5] and [12] the results were only proved for symmetric matrices in the case $\Omega = \mathbb {B}^n \subset \mathbb {R}^n$. The symmetry assumption in these papers is not really necessary and the new techniques established there works with some modifications also in the non-symmetric case. Regarding the assumptions on the domain, there has been some work to extend this result to more general domains. In [23] the authors extend (L) to the case where $\Omega$ is a bounded chord-arc domain (see Definition 2.4).

These results were recently generalized to 1-sided chord-arc domains in [2] where the authors show both type (L) and (S) results. In the second part [3] they also prove a type (L) results for non-symmetric bounded matrices. Finally an (S) type result for bounded matrices was obtained in [1].

In this paper we relax the boundedness hypothesis on the coefficients and assume that an elliptic matrix A has (potentially unbounded) antisymmetric part. Operators with BMO coefficients were considered previously in [24] and more results were considered for elliptic boundary value problems by Li and Pipher in [22], where they have shown that under the assumption that the antisymmetric part of the matrix A belongs to BMO space (and the symmetric part is bounded) then the usual elliptic theory holds for such operators and in particular we have the usual Harnack’s inequality, interior and boundary Hölder continuity, etc.

We note that in our approach we need to assume that $\Omega$ is a chord-arc domain as we currently require the exterior cone condition (see Remark 2.18) to hold. There is an opportunity that new techniques as in [1, 3] will remove this assumption in the future.

Recall that a matrix A is elliptic if there exists $\lambda _0$ such that

$$\begin{aligned} \lambda _0 |\xi |^2 \le \xi ^T A(X) \xi \le \lambda _0^{-1} |\xi |^2, \quad \forall \xi \in \mathbb {R}^n, ~\text { a.e. } X \in \Omega . \end{aligned}$$

(1.2)

Note that even in the case where the matrix A is not symmetric, ellipticity is only a condition on the symmetric part of the matrix $A^s$.

For the antisymmetric part $A^a$ we ask that $\Vert A^a\Vert _{\text {BMO}(\Omega )} \le \Lambda _0$, i.e.

(1.3)

Our main results are as follows. We generalize (L) and (S) type results to operators as above in Theorems 1.5 and 1.6. Instead of using the Carleson measure $\mu$ defined as in (1.1) which uses the $L^\infty$ norm, we introduce a more generalized version that allows A to be unbounded, namely that

$$\begin{aligned} d\mu '(Z):=\frac{\beta _r(Z)^2}{\delta (Z)}dZ \end{aligned}$$

where

(1.4)

for some large fixed $1\le r<\infty$ which only depends on $n,\lambda _0$ and $\Lambda _0$. Recall that by the John–Nirenberg inequality a function in BMO belongs to all $L^r$ spaces $r<\infty$.

Observe that even if we restrict ourselves to bounded matrices A this new Carleson measure $\mu '$ has smaller Carleson norm than the original measure $\mu$. In particular, it follows that perturbation result [23, Theorem 8.1] is a special case of Theorem 1.5.

We are ready to state two perturbation results:

Theorem 1.5

Let $\Omega \subset \mathbb {R}^n$ be a bounded chord arc domain and $L_0=\textrm{div}(A_0\nabla \cdot )$ and $L_1=\textrm{div}(A_1\nabla \cdot )$ two elliptic operators that satisfy (1.2) and (1.3). Let $\omega _0$ and $\omega _1$ be the corresponding elliptic measures. Then there exists $1\le r=r(n,\lambda _0,\Lambda _0)<\infty$ such that if $d\mu '(Z):=\frac{\beta _r(Z)^2}{\delta (Z)}dZ$ is a Carleson measure then $\omega _0 \in A_\infty (d\sigma )$ implies $\omega _1 \in A_\infty (d\sigma )$. Thus if the $L^p$ Dirichlet problem for $L_0$ is solvable this implies solvability of the $L^q$ Dirichlet problem for $L_1$, for some $q \ge p$.

Theorem 1.6

Let $\Omega \subset \mathbb {R}^n$ be a bounded chord arc domain and $L_0=\textrm{div}(A_0\nabla \cdot )$ and $L_1=\textrm{div}(A_1\nabla \cdot )$ two elliptic operators that satisfy (1.2) and (1.3). Let $\omega _0$ and $\omega _1$ be the corresponding elliptic measures. Let $1<p<\infty$ and assume that $\omega _0 \in B_{p'}(d\sigma )$ for $p'=p/(p-1)$. Then there exists $1\le r=r(n,\lambda _0,\Lambda _0)<\infty$ and $\gamma =\gamma (n,p,[\omega _0]_{B_p},\lambda _0,\Lambda _0) > 0$ such that if $\Vert \mu '\Vert _{\mathcal {C}} \le \gamma$ then $\omega _1 \in B_p(d\sigma )$. Thus if the $L^p$ Dirichlet problem for $L_0$ is solvable this implies solvability of the $L^p$ Dirichlet problem for $L_1$, for the same exponent p.

(The Carleson norm $\Vert \cdot \Vert _{\mathcal {C}}$ is defined below in Definition 2.5.)

When we started to develop the above perturbation theory for unbounded operators we had in mind one particular application in the spirit of papers by Kenig and Pipher [21] and Dindoš, Petermichl and Pipher [9] and extend such results to unbounded matrices.

From [9, 21], it follows that if $\Omega$ is a Lipschitz domain and $A:\Omega \rightarrow \mathbb R^{n\times n}$ is a bounded elliptic matrix such that

$$\begin{aligned} d\tilde{\mu }(X):= \delta (X)^{-1} \underset{B(X, \delta (X)/2)}{\textrm{osc}} \sup _{ij} |a_{ij}(Z)|^2 \end{aligned}$$

is a Carleson measure then the $L^p$ Dirichlet problem is solvable for some large $p<\infty$. Additionally, if $p\in (1,\infty )$ is given and both the Lipschitz character of our domain and the Carleson norm of $\tilde{\mu }$ is sufficiently small then we can conclude solvability of the $L^p$ Dirichlet problem for this given value of p. So again we have one large-Carleson and one small-Carleson type result.

To obtain this one needs perturbation results since in the paper [9] mollification procedure is used to replace above Carleson condition with

$$\begin{aligned} d\hat{\mu }(X):= \sup _{B(X, \delta (X)/2)}|\nabla A(Z)|^2\delta (Z). \end{aligned}$$

This gives the authors better matrix to work with and get the conclusions. To deduce the same for the original matrix we apply our Theorems 1.5 and 1.6 and improve conclusions of [9, 21] to unbounded matrices.

We note that under a different assumption of so-called t-independence of the coefficients on A the solvability of the $L^p$ Dirichlet problem for matrices with BMO antisymmetric part was shown in [16].

Theorem 1.7

Let $\Omega$ be a bound ed Lipschitz domain with Lipschitz character $K>0$ (that is the Lipschitz constant of graphs describing $\partial \Omega$ is bounded by K). Let $L_0=\textrm{div}(A\nabla \cdot )$ be an elliptic operator satisfying (1.2) and (1.3) let $\alpha _r$ be

(1.8)

Then for every $1<p<\infty$ there exists $r=r(n,\lambda _0,\Lambda _0)>1$ and $\varepsilon = \varepsilon (p) > 0$ such that if

$$\begin{aligned} \Vert \alpha _r(Z)^2 \delta (Z)^{-1} dZ\Vert _{\mathcal {C}}< \varepsilon \quad \text {and}\quad K<\varepsilon , \end{aligned}$$

then $\omega \in B_{p'}(\sigma )$, i.e. the $L^p$ Dirichlet problem is solvable for the operator $L_0$ in $\Omega$.

Similarly, [21] can be improved as follows:

Theorem 1.9

Let $\Omega$ be a bounded Lipschitz domain and $L_0=\textrm{div}(A\nabla \cdot )$ an elliptic operator satisfying (1.2) and (1.3). Consider $\alpha _r$ defined as above in (1.8). Then there exists $r=r(n,\lambda _0,\Lambda _0)>1$ such that if

$$\begin{aligned} \Vert \alpha _r(Z)^2 \delta (Z)^{-1} dZ \Vert _{\mathcal {C}} < \infty \end{aligned}$$

then the corresponding elliptic measure of $L_0$ belongs to $\omega \in A_\infty (d\sigma )$, i.e. the $L^p$ Dirichlet problem for $L_0$ is solvable for all $p\in (p_0,\infty )$ where some $p_0 >1$ is sufficiently large.

It follows that we now have a larger class of elliptic operators that solve the $L^p$ Dirichlet problem on bounded Lipschitz domains than was previously known, since we are replacing the oscillation of A measured in $L^\infty$ norm by an $L^p$ mean oscillation for some large $p > 2$.

It is worth noting that the study of boundary value problems for scalar elliptic operators has a long history. The reader might be interested to read more in the survey paper [8].

The paper is organized as follows: We start with Section 2 containing definitions and other preliminaries. In Section 3, we outline the proof of Theorem 1.5, which closely follows that of [23] and [12]; this contains a subsection with results needed to prove the key identity

$$\begin{aligned} F(X) := u_1(X) - u_0(X) = \int _{\Omega } \varepsilon \nabla u_1(Y) \nabla _Y G_0(X,Y) dY. \end{aligned}$$

(1.10)

We note that the formula (1.10) for F comes from the paper [12] and was also carried over to [23]. We have realized that the proof that (1.10) holds in our case does not follow immediately from the properties of the Green’s function since the difference $u_1-u_0$ does not have sufficient regularity (c.f. Proposition 2.21). This observation also applies to [12] and [23] but a rather simple approximation argument can close this gap in the case of bounded coefficients. In our case we had to work a bit harder to show that (1.10) is indeed true.

The meat of the proof of Theorem 1.5 consists of proving Lemmas 3.3 and 5.3, which is done in Sections 4 and 5 respectively. With these results established, Theorem 1.6 follows (Section 6). Finally, in Section 7 we prove Theorems 1.9 and 1.7.

2 Preliminaries

Here and in the following sections we implicitly allow all constants to depend on n, $\lambda _0$ and $\Lambda _0$.

Definition 2.1

$\Omega \subset \mathbb R^n$ satisfies the corkscrew condition with parameters $M > 1$, $r_0 > 0$ if, for each boundary ball $\Delta := \Delta (Q,r)$ with $Q \in \partial \Omega$ and $0< r < r_0$, there exists a point $A(Q,r) \in \Omega$, called a corkscrew point relative to $\Delta$, such that $B(A(Q,r),M^{-1}r) \subset T(Q,r)$.

Definition 2.2

$\Omega$ is said to satisfy the Harnack chain condition if there is a constant $c_0$ such that for each $\rho > 0$, $\Lambda \ge 1$, $X_1,X_2 \in \Omega$ with $\delta (X_j) \ge \rho$ and $|X_1 - X_2| \le \Lambda \rho$, there exists a chain of open balls $B_1,\dots ,B_N \subset \Omega$ with $N \lesssim _{\Lambda } 1$, $X_1 \in B_1$, $X_2 \in B_N$, $B_i \cap B_{i+1} \ne \emptyset$ and $c_0^{-1} r(B_i) \le \text {dist}(B_i,\partial \Omega ) \le c_0 r(B_i)$. The chain of balls is called a Harnack chain.

Definition 2.3

(NTA) $\Omega$ is an Non-Tangentially Accessible domain if it satisfies the Harnack chain condition and $\Omega$, $\mathbb {R}^n \setminus \bar{\Omega }$ both satisfy the corkscrew condition. If only $\Omega$ satisfied the corkscrew condition then it is called a 1-sided NTA domain or uniform domain.

Definition 2.4

(CAD) Let $\Omega \subset \mathbb {R}^n$. $\Omega$ is called chord arc domain (CAD) if $\Omega$ is a NTA set of locally finite perimeter and Ahlfors regular boundary, i.e. there exists $C\ge 1$ so that for $r\in (0,\text {diam}(\Omega ))$ and $Q\in \partial \Omega$

$$\begin{aligned} C^{-1}r^{n-1}\le \sigma (B(Q,r))\le Cr^{n-1}. \end{aligned}$$

Here B(Q, r) denotes the n-dimensional ball with radius r and center Q and $\sigma$ denotes the surface measure. The best constant C in the condition above is called the Ahlfors regularity constant.

If we replace NTA domain with 1-sided NTA domain in the above definition then $\Omega$ is called a 1-sided chord arc domain (1-sided CAD).

Throughout this paper $\Omega$ will denote a bounded CAD.

Definition 2.5

For a measure $\mu$ on $\Omega$ if the quantity

$$\begin{aligned} \Vert \mu \Vert _{\mathcal {C}}:= \sup _{\Delta \subset \partial \Omega } \frac{1}{\sigma (\Delta )}\int _{T(\Delta )}d\mu , \end{aligned}$$

is finite then $\mu$ is said to be the Carleson measure and $\Vert \mu \Vert _{\mathcal {C}}$ its Carleson norm. Here the Carleson region $T(\Delta )$ of a boundary ball $\Delta =\Delta (Q,r) := B(Q,r) \cap \partial \Omega$ is defined as $T(\Delta (Q,r))=\overline{B(Q,r)}\cap \Omega$.

Proposition 2.6

Let b be a constant anti-symmetric matrix and let $u \in W^{1,2}(E)$ and $v \in W_0^{1,2}(E)$, with $E \subset \Omega$ measurable. Then

$$\begin{aligned} \int _{E} b\nabla u \cdot \nabla v = 0. \end{aligned}$$

Proof

Note that if b is a constant anti-symmetric matrix and $E \subset \Omega$, then for $u \in W^{1,2}(E)$ and $\phi \in C_c^\infty (E)$ we have

$$\begin{aligned} \int _{E} b\nabla u \cdot \nabla \phi= & {} \int _{E} b_{ij} \partial _i u \partial _j \phi = \int _{E} u \partial _{i}(b_{ij} \partial _j \phi ) = \int _{E} u b_{ij} \partial _{ij} \phi = \int _{E} u b_{ji}^T \partial _{ij} \phi \\= & {} - \int _{E} u b_{ji} \partial _{ji} \phi = - \int _{E} u b_{ij} \partial _{ij} \phi = - \int _{E} \partial _i (b_{ij} u) \partial _{j} \phi \\= & {} - \int _{E} b_{ij} \partial _i u \partial _{i} \partial _{j} \phi = - \int _{E} b\nabla u \cdot \nabla \phi . \end{aligned}$$

$\square$

Denoting by $(A_i^a)_E$ the constant matrix of component-wise means of A on E. It follows that for u, v as above

$$\begin{aligned} \int _{E} A_i \nabla u \cdot \nabla v = \int _{E} (A_i-(A_i^a)_E)\nabla u \cdot \nabla v. \end{aligned}$$

(2.7)

2.1 Muckenhoupt and Reverse Hölder Spaces

Let $\mu$ be a doubling measure on $\partial \Omega$ and let $w:\partial \Omega \rightarrow [0,\infty )$. Furthermore, let $1<p<\infty$ and let $p'$ denote its Hölder conjugate i.e. $\frac{1}{p} + \frac{1}{p'} = 1$.

Definition 2.8

(Muckenhoupt spaces) We define the Muckenhoupt spaces $A_1(\mu )$, $A_p(\mu )$, $A_\infty (\mu )$ by:

• $w \in A_p(\mu )$ if and only if there exists $C>0$ such that for all balls $B\subset \mathbb {R}^n$

  $$\begin{aligned} \left( \frac{1}{\mu (B)}\int _B wd\mu \right) \left( \frac{1}{\mu (B)}\int _B w^{1-p'}d\mu \right) ^{p-1}\le C<\infty . \end{aligned}$$

• $w \in A_1(\mu )$ if and only if there exists $C>0$ such that for $\mu$-a.e. $x\in \mathbb {R}^n$ and balls $B=B(x)\subset \mathbb {R}^n$ centered at x

  $$\begin{aligned} \frac{1}{\mu (B)}\int _{B(x)} wd\mu \le Cw(x). \end{aligned}$$

• Finally, we set $A_\infty (\mu ) :=\bigcup _{1\le p<\infty }A_p(\mu )$.

Definition 2.9

(Reverse Hölder spaces) We define the Reverse Hölder spaces $B_p(\mu )$, $B_\infty (\mu )$ by:

• $w \in B_p(\mu )$ if and only if there exists $C>0$ such that for all balls $B\subset \mathbb {R}^n$

  $$\begin{aligned} \left( \frac{1}{\mu (B)}\int _B w^p d\mu \right) ^{1/p}\le \frac{C}{\mu (B)}\int _B wd\mu . \end{aligned}$$

  The best constant in the above estimate we shall denote by $[w]_{B_p}$.

• $w \in B_\infty (\mu )$ if and only if there exists $c>0$ such that for a.e. $x\in \mathbb {R}^n$ and balls $B=B(x)\subset \mathbb {R}^n$ centered at x

  $$\begin{aligned} cw(x)\le \frac{1}{\mu (B)}\int _{B(x)}wd\mu . \end{aligned}$$

It is easy to see that the following hold:

• $A_1(\mu )\subset A_p(\mu )\subset A_q(\mu )\subset A_\infty (\mu )$ for $1\le p<q<\infty$,

• $B_q(\mu )\subset B_p(\mu )$ for $1<p<q \le \infty$, and

• $A_\infty (\mu )=\bigcup _{p>1}B_p(\mu )$.

For more properties of these spaces we refer the reader to [13].

Suppose now that $\nu$ is another doubling measure on $\partial \Omega$. We say that $\nu \in A_p(\mu ) \; [B_q(\mu )]$ if $\nu \ll \mu$ and the Radon–Nikodym $w := \frac{d\nu }{d\mu } \in A_p(\mu ) \; [B_q(\mu )]$.

2.2 The $L^p$ Dirichlet Boundary Value Problem

Definition 2.10

Let $u:\Omega \rightarrow \mathbb {R}$. The nontangential maximal function $N[u] : \partial \Omega \rightarrow \mathbb {R}$ is defined as

$$\begin{aligned} N_\alpha [u](Q):=\sup _{X\in \Gamma _\alpha (Q)}|u(X)|, \end{aligned}$$

where

$$\begin{aligned} \Gamma _\alpha (Q) := \{Y\in \Omega ; |Y-Q|<\alpha \delta (Y)\}, \end{aligned}$$

is the cone of aperture $\alpha$ (for $\alpha >1$). Here $\delta$ denotes the distance function to the boundary $\partial \Omega$.

Let $L = \text {div}(A\nabla \cdot )$, where $A(X)\in \mathbb {R}^{n\times n}$ is a matrix, satisfying (1.2) and (1.3). We say that $u\in W_{\text {loc}}^{1,2}(\Omega )$ is weak solution to the equation $Lu=0$ in $\Omega$ if

$$\begin{aligned} \int _\Omega A \nabla u \nabla \varphi dx = 0, \quad \forall \varphi \in C^\infty _0(\Omega ), \end{aligned}$$

where $C^\infty _0(\Omega )$ denotes the space of all smooth functions with compact support. We know (see e.g. [22]) that if $f \in C^0(\partial \Omega )$ then there exists a $u \in W^{1,2}(\Omega ) \cap C^0(\bar{\Omega })$ such that

$$\begin{aligned} \left\{ \begin{array}{ll} Lu=0&{} \quad \text {in } \Omega ,\\ u=f&{} \quad \text {on } \partial \Omega . \end{array}\right. \end{aligned}$$

Definition 2.11

Let $\alpha > 0$. We say the $L^p$ Dirichlet problem for the operator L is solvable, if for all boundary data $f\in L^p(\partial \Omega )\cap C(\partial \Omega )$ the solution u as defined above satisfies the estimate

$$\begin{aligned} \Vert N_\alpha (u)\Vert _{L^p(\partial \Omega )}\lesssim _{\alpha } \Vert f\Vert _{L^p(\partial \Omega )}. \end{aligned}$$

2.3 Elliptic Measure

Recall that there exists a measure $\omega ^X$ such that that for u as above

$$\begin{aligned} u(X) = \int _{\Omega } f d\omega ^X. \end{aligned}$$

This is called the elliptic measure with pole at X. As noted in the introduction the $L^p$ Dirichlet problem is solvable if and only if $\omega \in B_{p'}(d\sigma )$. For a proof see e.g. [19] and the references therein.

2.4 Properties of Solutions

In this sections we include some important results from Li’s thesis [22] that will be used later. These results hold for solutions on NTA domains. First we have reverse Hölder and Caccioppoli’s inequalities for the gradient:

Proposition 2.12

(Lemma 3.1.2) Let $u \in W_{\textrm{loc}}^{1,2}(\Omega )$ be a weak solution. Let $X \in \Omega$ and let $B_R = B_R(X)$ be such that $\overline{B}_R \subset \Omega$ and let $0< \sigma < 1$. Then there exists $p>2$ such that

Proposition 2.13

For a $C=C(n,\lambda ,\Lambda _0)<\infty$ we have for a solution u and $B(X,2R)\subset \Omega$

Proposition 2.14

(Lemma 3.1.4) Let $u\in W^{1,2}_{\textrm{loc}}(\Omega )$ be a weak solution of $Lu=0$ and $\overline{B(X,2R)}\subset \Omega$. Then

Harnack’s inequality also does hold:

Proposition 2.15

(Lemma 3.1.8) Let $u\in W^{1,2}_{\textrm{loc}}(\Omega )$ be a nonnegative weak solution and $\overline{B(X,2R)}\subset \Omega$. Then

$$\begin{aligned} \sup _{B(X,R)} |u| \le C(n,\lambda ,\Lambda _0) \inf _{B(X,R)} |u|. \end{aligned}$$

We also have the comparison principle.

Proposition 2.16

(Proposition 4.3.6) Let $u,v \in W^{1,2}(T_{2r}(Q)) \cap C^0(\overline{(T_{2r}(Q))})$ be non-negative such that $Lu=Lv=0$ in $T_{2r}(Q)$ and $u,v \equiv 0$ on $\Delta (Q,2r)$. Then

$$\begin{aligned} \frac{u(X)}{v(X)} \approx \frac{u(A_r(Q))}{v(A_r(Q))}, \quad X \in T_r(Q). \end{aligned}$$

And the boundary Hölder estimate also holds.

Proposition 2.17

(Lemma 3.2.5) Let $u \in W^{1,2}(\Omega )$ be a solution in $\Omega$ and $P \in \partial \Omega$. Suppose that u vanishes on $\Delta (P,R)$. Then for $0 < r \le R$ we have

$$\begin{aligned} \underset{T(P,r)}{\textrm{osc}} u \lesssim _{\Omega } \left( \frac{r}{R} \right) ^{\alpha } \sup \limits _{T(P,R)} |u|. \end{aligned}$$

Remark 2.18

The proof of this result uses the exterior corkscrew condition, i.e., that $\mathbb {R}^n \setminus \bar{\Omega }$ satisfies Definition 2.1 and it is the reason why in the paper we assume that $\Omega$ is a CAD rather than a 1-sided CAD domain.

An important corollary of the result above is the following lemma:

Proposition 2.19

Let $u \ge 0$ be a solution in $\Omega$ that vanishes on $\Delta (Q,2r)$. Then

$$\begin{aligned} \sup _{T(\Delta (Q,r))} u \lesssim u(A(Q,r)). \end{aligned}$$

Here A(Q, r) is a corkscrew point inside $\Omega$ w.r.t Q and r as defined by Definition 2.1.

This is Lemma 4.4 of [17], the only difference in our setting is that equation (4.5) in [17] follows from Proposition 2.17. After combining Proposition 2.19 with Proposition 2.17 we have:

Proposition 2.20

Let $u\ge 0$ be a solution that vanishes on $\Delta (Q,R)$. Then there are $C>0$, $1>\alpha >0$ such that

$$\begin{aligned} \sup _{T(\Delta (Q,r))} u \le C\left( \frac{r}{R}\right) ^\alpha u(A(Q,R)). \end{aligned}$$

2.5 Properties of the Green’s Function

The paper [22] also gives us information on some properties of the Green’s function.

Proposition 2.21

(Theorem 4.1.1) There exists a unique function (the Green’s function) $G : \Omega \times \Omega \rightarrow \mathbb {R} \cup \{ \infty \}$, such that

$$\begin{aligned} G(\cdot ,Z) \in W^{1,2}(\Omega \setminus B(Z,r)) \cap W_0^{1,1}(\Omega ), \quad Z \in \Omega ,~ r > 0, \end{aligned}$$

and

$$\begin{aligned} \int _{\Omega } A(Y) \nabla _{Y} G(Y,Z) \nabla \phi (Y) dY = \phi (Z), \quad \phi \in W_0^{1,p}(\Omega ) \cap C^0(\Omega ), \quad p>n. \end{aligned}$$

(2.22)

Proposition 2.23

$$\begin{aligned} G(X,Y) \lesssim |X-Y|^{2-n}, \quad X,Y \in \Omega , \end{aligned}$$

and for any $0<\theta <1$ we have

$$\begin{aligned} G(X,Y) \gtrsim _{n,\lambda _0,\Lambda _0,\theta } |X-Y|^{2-n}, \quad X,Y \in \Omega : |X-Y| < \theta \delta (Y). \end{aligned}$$

Proposition 2.24

Let $L^*$ be the adjoint operator to L and let $G^*$ be its Green’s function. Then

$$\begin{aligned} G^*(X,Y) = G(Y,X), \quad X,Y \in \Omega . \end{aligned}$$

Finally we have the following relation between the Green’s function and the elliptic measure $\omega ^X$ which gives us that the elliptic measure must be doubling.

Proposition 2.25

(Corollary 4.3.1)

$$\begin{aligned} \omega ^X(\Delta (Q,r)) \approx r^{n-2} G(X,A(Q,r)), \quad X \in \Omega \setminus B(Q,2r). \end{aligned}$$

Proposition 2.26

(Corollary 4.3.2)

$$\begin{aligned} \omega ^X(\Delta (Q,2r)) \lesssim \omega ^X(\Delta (Q,r)), \quad X \in \Omega \setminus B(Q,2r). \end{aligned}$$

As $\delta (X)$ is a continuous function on $\overline{\Omega }$, without loss of generality assume that $0\in \Omega$ and that $\delta (0)\ge \delta (X)$ for all $X\in \Omega$. Let $\omega ^0=\omega$.

Lemma 2.27

Then

$$\begin{aligned} \omega (\Delta (X^*,\delta (X))) \approx \delta (X)^{n-2} G(0,X), \quad X \in \Omega \setminus B(0, \tfrac{1}{2}\delta (0)). \end{aligned}$$

Proof

Let $X \in \Omega \setminus B(0, \tfrac{1}{2}\delta (0))$. To begin with note that if $\delta (X) < \frac{1}{2}\delta (0)$, then $0\notin B(X^*,2\delta (X))$ and hence the result immediately follows from Proposition 2.25. Assume therefore that $\delta (X) \ge \frac{1}{2}\delta (0)$. Let Z be the point given by $\partial B(X^*,\frac{1}{4}\delta (0)) \cap [X^*,X]$. Then $\delta (Z) = |Z-X^*| = \frac{1}{4}\delta (0)$ and we may choose $Z^*= X^*$. Thus $0 \notin T(Z^*,2\delta (Z))$ so Proposition 2.25 applies. We get that

$$\begin{aligned} \omega (\Delta (Z^*,\delta (Z))) \approx \delta (Z)^{n-2} G(0,Z). \end{aligned}$$

(2.28)

Next as our domain is CAD, there clearly exists a finite Harnack chain, from X to Y in $B(X,\delta (X)) \setminus B(0,\delta (0)/4)$ whose length is independent of X. Thus by Proposition 2.15 we deduce that

$$\begin{aligned} G(0,X) \approx G(0,Z). \end{aligned}$$

(2.29)

Finally we note that since $\omega$ is doubling and $4\delta (Z) = \delta (X) \le \delta (0)$ we have

$$\begin{aligned} \omega (\Delta (X^*,\delta (X))) \approx \omega (\Delta (Z^*,\delta (Z))). \end{aligned}$$

(2.30)

Thus combining (2.28), (2.29) and (2.30) yields the desired result.$\square$

Throughout this work $G_i$ will denote the Green’s function of $L_i$ for $i=0,1$. Furthermore, as above, we assume $0\in \Omega$ and declare this to be the special point that is the “center of the domain” $\Omega$ in the sense that $\delta (0)=\max \{\delta (X);X\in \Omega \}$. We shorten notation and set $G_0(Y):=G_0(0,Y)$.

2.6 Nontangential Behaviour and the Square Function in Chord Arc Domains

Recall that the nontangential maximal function is given by

$$\begin{aligned} N_\alpha [u](Q):=\sup \limits _{X\in \Gamma _\alpha (Q)}|u(X)|, \end{aligned}$$

and the mean-valued nontangential maximal function is defined by

It is immediately clear that

$$\begin{aligned} \tilde{N}^\eta _\alpha [u](Q) \le N_{\alpha +\eta /2}[u](Q). \end{aligned}$$

We write $\tilde{N}_\alpha [u]=\tilde{N}^1_\alpha [u]$ and drop the aperture $\alpha$ when it is clear from the context.

Lemma 2.31

(Remark 7.2 in [23]) Let $\mu$ be a doubling measure on $\partial \Omega$, where $\Omega$ is a NTA domain. Let $v : \Omega \rightarrow \mathbb {R}$ and let $0< p < \infty$, $\alpha ,\beta >0$, $2>\eta >0$. Then

$$\begin{aligned} \Vert \tilde{N}_\alpha [v] \Vert _{L^p(d\mu )} \approx \Vert \tilde{N}_\beta [v] \Vert _{L^p(d\mu )} \approx \Vert \tilde{N}^\eta _\alpha [v] \Vert _{L^p(d\mu )}, \end{aligned}$$

where the implied constant depends on the character of $\Omega$, the doubling constant of $\mu$ and $\beta /\alpha$.

Now for $L_i = \text {div}(A_i\nabla )$, $i=0,1$, where $A_i$ satisfies (1.2) and (1.3), let $u_i$ be the solution to the Dirichlet problem for $L_i$ with boundary data $f \in L^p(\partial \Omega )\cap C(\partial \Omega )$. We set $F:= u_1-u_0$ and note that clearly $F = 0$ on $\partial \Omega$.

Lemma 2.32

Let $0< \eta < 2$. For any solution u of an elliptic PDE we have

$$\begin{aligned} N_\alpha [u](Q)\lesssim \tilde{N}^{\eta }_\alpha [u](Q) \end{aligned}$$

and furthermore

$$\begin{aligned} N_\alpha [F](Q)\lesssim \tilde{N}^{\eta }_{\alpha }[F](Q) + \tilde{N}^{\eta }_\alpha [u_0](Q). \end{aligned}$$

(2.33)

Proof

First, note that by Proposition 2.14 we have, for any solution u:

and hence

$$\begin{aligned} N_\alpha [u](Q) \lesssim \tilde{N}^{\eta }_\alpha [u](Q). \end{aligned}$$

Using this and the triangle inequality we then have

$$\begin{aligned} N_\alpha [F](Q)\le & {} N_\alpha [u_1](Q) + N_\alpha [u_0](Q) \lesssim \tilde{N}^{\eta }_\alpha [u_1](Q) + \tilde{N}^{\eta }_\alpha [u_0](Q)\\\lesssim & {} \tilde{N}^{\eta }_\alpha [F](Q) + \tilde{N}^{\eta }_\alpha [u_0](Q). \end{aligned}$$

$\square$

We also have an “almost Caccioppoli inequality” for F.

Lemma 2.34

$$\begin{aligned} \int _{B(X,R)} |\nabla F |^2dZ \lesssim \frac{1}{R^2}\int _{B(X,2R)} (F^2 + u_0^2) dZ. \end{aligned}$$

To see this one simply uses Caccioppoli for $u_0$ and $u_1$, and the triangle inequality

$$\begin{aligned} \int _{B(X,R)} |\nabla F |^2dZ\lesssim & {} \int _{B(X,R)} (|\nabla u_1^2| + |\nabla u_0|^2) dZ \lesssim \frac{1}{R^2}\int _{B(X,2R)} (u_1^2 + u_0^2) dZ\\\lesssim & {} \frac{1}{R^2}\int _{B(X,2R)} (F^2 + u_0^2) dZ. \end{aligned}$$

As is customary, we can define the square function of a function $u\in W^{1,2}_{\text {loc}}(\Omega )$ by

$$\begin{aligned} S_\alpha [u](Q):=\left( \int _{\Gamma _\alpha (Q)}|\nabla u(X)|^2\delta (X)^{2-n}dX\right) ^{1/2}. \end{aligned}$$

If we set $f := |\nabla u|\delta$, the square function can be considered to be a restriction of a more general operator

$$\begin{aligned} A^{(\alpha )}[f](Q):=\left( \int _{\Gamma _\alpha (Q)}\frac{|f|^2}{\delta (X)^{n}}dX\right) ^{1/2}. \end{aligned}$$

More results on this operator can be found in [23], in particular their Proposition 4.5:

Proposition 2.35

We have for $0<p<\infty$ and two apertures $\alpha ,\beta \ge 1$

$$\begin{aligned} \Vert A^{(\alpha )}[f]\Vert _{L^p(d\sigma )}\approx \Vert A^{(\beta )}[f]\Vert _{L^p(d\sigma )}. \end{aligned}$$

This holds for any doubling measure $\mu$ and in our case it means that the $L^p$ norms of square functions for cones of different aperture are comparable.

2.7 Dyadic Decomposition of $\partial \Omega$ and Definition of Decomposition $(\partial \Omega ,4R_0)$

Recall that $0\in \Omega$ and set $R_0=\min (\frac{1}{2^{30}}\delta (0), 1)$. As in [23] we consider a matrix $A'$ with $A'=A_1$ on $(\partial \Omega ,R_0/2) := \{Y\in \Omega : \delta (Y)<R_0/2\}$ and $A'=A_0$ on $\Omega \setminus (\partial \Omega ,2R_0)$. Then the following holds

Lemma 2.36

(cf. Lemma 7.5 in [23]) If $\omega '$ denotes the elliptic measure associated to $L'=\textrm{div}(A'\nabla \cdot )$. Then $\omega _1\in B_p(\omega _0)$ if and only if $\omega '\in B_p(\omega _0)$.

Thus without loss of generality we may assume that $\beta _r(Y)=0$ for $Y\in \Omega$, $\delta (Y)> 4R_0$.

Recall the famous decomposition of M. Christ. By [4] there exists a family of “cubes” $\{Q_\alpha ^k\subset \partial \Omega ; k\in \mathbb {Z},\alpha \in I_k \subset \mathbb {N}\}$ where each scale k decomposes $\partial \Omega$ such that for every $k\in \mathbb {Z}$:

$$\begin{aligned} \sigma \left( \partial \Omega \setminus \bigcup _{\alpha \in I_k}Q_\alpha ^k\right) =0 \qquad \text {and}\qquad \omega _0\left( \partial \Omega \setminus \bigcup _{\alpha \in I_k}Q_\alpha ^k\right) =0. \end{aligned}$$

Furthermore, the following properties hold:

• 1. If $l\ge k$ then either $Q_\beta ^l\subset Q_\alpha ^k$ or $Q_\beta ^l\cap Q_\alpha ^k=\emptyset$.

• 2. For each $(k,\alpha )$ and $l<k$ there is a unique $\beta$ so that $Q_\alpha ^k\subset Q_\beta ^l$.

• 3. Each $Q_\alpha ^k$ contains a ball $\Delta (Z_\alpha ^k,8^{-k-1})$.

• 4. There exists a constant $C_0>0$ such that $8^{-k-1}\le \text {diam}(Q_\alpha ^k)\le C_08^{-k}$.

The last listed property implies together with the Ahlfors regularity of the surface measure that $\sigma (Q_\alpha ^k)\approx 8^{-k(n-1)}$. Similarly, the doubling property Proposition 2.26 of the elliptic measure guarantees us $\omega _0(Q_\alpha ^k)\approx \omega _0(B(Z_\alpha ^k, 8^{-k-1}))$.

Now we can define a decomposition of $(\partial \Omega ,4R_0)$. For $k\in \mathbb {Z}$, $\alpha \in I_k$, set

$$\begin{aligned} I_\alpha ^k := \left\{ Y\in \Omega ; \lambda 8^{-k-1}<\delta (Y)<\lambda 8^{-k+1}, \exists P\in Q_\alpha ^k: \lambda 8^{-k-1}<|P-Y|<\lambda 8^{-k+1}\right\} , \end{aligned}$$

where $\lambda$ is chosen so small that the $\{I_\alpha ^k\}_{\alpha \in I_k}$ have finite overlaps and

$$\begin{aligned} (\partial \Omega ,4R_0)\subset \bigcup _{\alpha ,k\ge k_0}I^k_\alpha . \end{aligned}$$

The scale $k_0$ is chosen such that $k_0$ is the largest integer with $4R_0<\lambda 8^{-k_0+1}$. Additionally, for $\varepsilon >0$ we set the scale $k_\varepsilon$ as the smallest integer such that $I^k_\alpha \subset (\partial \Omega ,\varepsilon )$ for all $k\ge k_\varepsilon$. The choices of $k_0$ and $k_\varepsilon$ guarantee that

$$\begin{aligned} (\partial \Omega ,4R_0)\setminus (\partial \Omega ,\varepsilon )\subset \bigcup _{\alpha , k_0\le k\le k_\varepsilon } I_\alpha ^k \subset (\partial \Omega ,32R_0)\setminus (\partial \Omega ,\varepsilon /8). \end{aligned}$$

(2.37)

Furthermore, we define the following enlarged decomposition

$$\begin{aligned} \hat{I}_\alpha ^k=\left\{ Y\in \Omega ; \lambda 8^{-k-2}<\delta (Y)<\lambda 8^{-k+2}, \exists P\in Q_\alpha ^k: \lambda 8^{-k-2}<|P-Y|<\lambda 8^{-k+2}\right\} , \end{aligned}$$

and it is clear that that $I_\alpha ^k\subset \hat{I}_\alpha ^k$ and that the $\hat{I}_\alpha ^k$ have finite overlap. Observe that we can cover $I_\alpha ^k$ by balls $\{B(X_i,\lambda 8^{-k-3})\}_{1\le i\le N}$ with $X_i\in I_\alpha ^k$ such that $|X_i-X_l|\ge \lambda 8^{-k-3}/2$. Note here that N is independent of k and $\alpha$. Furthermore, we have for each $Z\in B(X_i,2\lambda 8^{-k-3})$ that

$$\begin{aligned} \lambda 8^{-k+2}>\delta (Z)> \lambda 8^{-k-1}-2\lambda 8^{-k-3}=\frac{62}{8}\lambda 8^{-k-2}, \end{aligned}$$

and hence

$$\begin{aligned}{} & {} B(X_i,\lambda 8^{-k-3})\subset B(Z,3\lambda 8^{-k-3})\subset B(Z,\frac{62}{8}\lambda 8^{-k-3})\subset B(Z,\delta (Z)/8),\end{aligned}$$

(2.38)

$$\begin{aligned}{} & {} |B(X_i,\lambda 8^{-k-3})|\approx |I_\alpha ^k|\approx B(Z,\delta (Z)/2), \end{aligned}$$

(2.39)

and

$$\begin{aligned} I_\alpha ^k\subset \bigcup _{i=1}^NB(X_i,\lambda 8^{-k-3})\subset \bigcup _{i=1}^NB(X_i,2\lambda 8^{-k-3}) \subset \hat{I}_\alpha ^k. \end{aligned}$$

Note also that for $Z\in (\partial \Omega ,4R_0)$ there exists $Z^*\in \partial \Omega$ with $|Z^*-Z|=\delta (Z)$ and an $I_\alpha ^k$ such that $Z^*\in Q^k_\alpha$ and

$$\begin{aligned} 2\lambda 8^{-k-1}\le \delta (Z)\le \frac{1}{2}8^{k+1}. \end{aligned}$$

Thus, for every $X\in B(Z,\delta (Z)/4)$

$$\begin{aligned} \lambda 8^{-k-1}\le \delta (X)\le \lambda 8^{-k+1}\qquad \text {and}\qquad \lambda 8^{-k-1}\le |Z^*-X| \le \lambda 8^{k+1}. \end{aligned}$$

Hence

$$\begin{aligned} B(Z,\delta (Z)/4)\subset I_\alpha ^k. \end{aligned}$$

(2.40)

Next, we note that

$$\begin{aligned} \hat{I}_\alpha ^k\subset T\left( \Delta (Z_\alpha ^k, C_0+16\lambda )8^{-k}\right) . \end{aligned}$$

Lastly, we also observe that if $P\in Q_\alpha ^k$ and $Z\in \hat{I}_\alpha ^k$ then, for $M=8^4$,

$$\begin{aligned} Z\in \Gamma _M(P). \end{aligned}$$

We are also going to need an intermediate decomposition in cubes $\tilde{I}_\alpha ^k$ defined by

$$\begin{aligned} \tilde{I}_\alpha ^k:= & {} \left\{ Y\in \Omega : \lambda \frac{14}{16}8^{-k-1}<\delta (Y)<\lambda \frac{18}{16}8^{-k+1},\right. \\{} & {} \quad \qquad \qquad \left. \exists P\in Q_\alpha ^k: \lambda \frac{14}{16}8^{-k-1}<|P-Y|<\lambda \frac{18}{16}8^{-k+1}\right\} . \end{aligned}$$

The enlargement compared to $I_\alpha ^k$ here is chosen such that

$$\begin{aligned} I_\alpha ^k\subset \bigcup _{i=1}^NB(X_i,\lambda 8^{-k-3})\subset \bigcup _{i=1}^NB(X_i,2\lambda 8^{-k-3})\subset \tilde{I}_\alpha ^k\subset \bigcup _{i=1}^NB(X_i,4\lambda 8^{-k-3})\subset \hat{I}_\alpha ^k. \end{aligned}$$

All of this will be used to prove the following important proposition:

Proposition 2.41

With $I_\alpha ^k$, $\tilde{I}_\alpha ^k$ as above we have:

In particular, if $\big \Vert \frac{\beta _r(Z)^2G_0(Z)}{\delta (Z)^2}\big \Vert _{\mathcal {C}}\le \varepsilon _0^2$, then

Proof

Using the covering of $I_\alpha ^k$ by balls defined above we have

Furthermore, for the second part under the assumption that $\big \Vert \frac{\beta _r(Z)^2G_0(Z)}{\delta (Z)^2}\big \Vert _{\mathcal {C}}\le \varepsilon _0^2$, we have that

$$\begin{aligned}{} & {} \left( \frac{1}{\omega _0(Q_\alpha ^k)} \int _{\hat{I}^k_\alpha }\delta (Z)^{-2}G_0(Z)\beta _r(Z)^2dZ\right) ^{1/2}\\{} & {} \;\qquad \lesssim \left( \frac{1}{\omega _0(\Delta (Z_\alpha ^k, C_0+16\lambda )8^{-k})}\int _{T(\Delta (Z_\alpha ^k, (C_0+16\lambda )8^{-k}))}\frac{\beta _r(Z)^2G_0(Z)}{\delta (Z)^{2}}dZ\right) ^{1/2}\\{} & {} \;\qquad \lesssim \varepsilon _0. \end{aligned}$$

$\square$

3 Proof of Theorem 1.5

We use a method inspired by [23]. Recall that $A_0$ and $A_1$ satisfy (1.2) and (1.3), and that $\omega _0$ and $\omega _1$ denote their elliptic measures. Furthermore, $F=u_1-u_0$ and $\beta _r$ are as in (1.4). First, we need to prove

Theorem 3.1

Let $\Omega$ be a bounded CAD. There exists $\varepsilon _0=\varepsilon _0(n,\lambda _0,\Lambda _0)>0$ and $r>0$, such that if

$$\begin{aligned} \sup _{\Delta \subset \partial \Omega } \left( \frac{1}{\omega _0(\Delta )}\int _{T(\Delta )}\beta _r^2(X)\frac{G_0(X)}{\delta (X)^2}dX\right) ^{1/2}<\varepsilon _0, \end{aligned}$$

then $\omega _1\in B_2(\omega _0)$.

This theorem corresponds to Theorem 2.9 in [23] but with the discrepancy function $\alpha$ instead of $\beta _r$. Using this the authors of [23] first prove

Theorem 3.2

(Theorem 8.2) Let $\Omega$ be a bounded CAD and let

$$\begin{aligned} A(a)(Q)=\left( \int _{\Gamma (Q)}\frac{\alpha ^2(X)}{\delta (X)^n}dX\right) ^{1/2}. \end{aligned}$$

If $\Vert A(a)\Vert _{L^{\infty }}\le C<\infty$ and $\omega _0\in A_\infty (\sigma )$ then $\omega _1\in A_\infty (\sigma )$.

After that, they establish Theorem 1.5 (which is Theorem 8.1 in their notation). If we replace $\alpha$ by $\beta _r$, we can conclude Theorem 1.5 from Theorems 3.2 and 3.2 from Theorem 3.1 in the same way as in [23]. The only modification is the substitution of their discrepancy function $\alpha$ by $\beta _r$.

Hence it remains to prove Theorem 3.1. We first establish the following two lemmas.

Lemma 3.3

Let $\mu$ be a doubling measure on $\partial \Omega$. Under the assumptions of Theorem 3.1 we have for every $0<p<\infty$

$$\begin{aligned} \int _{\partial \Omega }\tilde{N}_{\alpha }[F]^pd\mu \lesssim _{p} \varepsilon _0\int _{\partial \Omega } M_{\omega _0}[S_{\bar{M}}u_1]^pd\mu , \end{aligned}$$

where the aperture $\bar{M}=2^8$ is at least twice as large as $\alpha$.

In particular this lemma holds with $\mu \in \{\omega _0,\sigma \}$.

Lemma 3.4

Under the assumptions of Theorem 3.1 we have for any aperture $\alpha >0$

$$\begin{aligned} \int _{\partial \Omega } S_{\bar{M}}[F]^2 d\omega _0 \lesssim \int _{\partial \Omega } \left( \tilde{N}_{\alpha }[F]^2 + f^2 \right) d\omega _0. \end{aligned}$$

These lemmas are versions of Lemmas 2.9 and 2.10 in [12] or Lemmas 7.7 and 7.8 in [23].

Proof of Theorem 3.1

Assume that Lemmas 3.3 and 3.4 hold. Since

$$\begin{aligned} \Vert S_{\alpha }[u_0]\Vert _{L^2(d\omega _0)} \lesssim \Vert f \Vert _{L^2(d\omega _0)}, \end{aligned}$$

we have that

$$\begin{aligned} \int _{\partial \Omega } \tilde{N}_{\alpha }[F]^2 d\omega _0\lesssim & {} \int _{\partial \Omega } \varepsilon _0^2 M_{\omega _0}[S_{\bar{M}}u_1]^2 d\omega _0 \lesssim \varepsilon _0^2 \int _{\partial \Omega } S_{\bar{M}}[u_1]^2 d\omega _0\\\le & {} \varepsilon _0^2 \int _{\partial \Omega } S_{\bar{M}}[F]^2 d\omega _0 + \varepsilon _0^2 \int _{\partial \Omega } S_{\bar{M}}[u_0]^2 d\omega _0 \\\lesssim & {} \varepsilon _0^2 \int _{\partial \Omega } S_{\bar{M}}[F]^2 d\omega _0 + \varepsilon _0^2 \int _{\partial \Omega } f^2 d\omega _0 \\\lesssim & {} \varepsilon _0^2\int _{\partial \Omega } \tilde{N}_{\alpha }[F]^2 d\omega _0 + \varepsilon _0^2 \int _{\partial \Omega } f^2 d\omega _0. \end{aligned}$$

Thus, with $\varepsilon _0$ small enough we can hide the term $\tilde{N}_\alpha [F]^2$ and absorb it by the left-hand side. We get

$$\begin{aligned} \Vert \tilde{N}_{\alpha }[F] \Vert _{L^2(d\omega _0)} \lesssim \Vert f \Vert _{L^2(d\omega _0)}. \end{aligned}$$

By Lemma 2.32 we obtain

$$\begin{aligned} \int _{\partial \Omega } N_{\alpha }[u_1]^2 d\omega _0\lesssim \int _{\partial \Omega } \tilde{N}_{\alpha }[F]^2 d\omega _0+\int _{\partial \Omega } \tilde{N}_{\alpha }[u_0]^2 d\omega _0\lesssim \int _{\partial \Omega } f^2 d\omega _0. \end{aligned}$$

Therefore $\omega _1 \in B_2(\omega _0)$ as desired. $\square$

3.1 The Difference Function F

Our first proposition is a generalization of Lemma 3.12 in [2] using the same strategy for its proof.

Proposition 3.5

Suppose that $\Omega \subset \mathbb {R}^{n}$ is a bounded CAD and let $L_0$, $L_1$ be two elliptic operators. Let $u_0\in W^{1,2}(\Omega )$ be a weak solution of $L_0u_0=0$ in $\Omega$, and let $G_1$ be the Green’s function of $L_1$. Then

$$\begin{aligned} \int _\Omega A_0^*(Y)\nabla _Y G_1(Y,X) \cdot \nabla u_0(Y)dY=0 \qquad \text {for a.e. } X\in \Omega . \end{aligned}$$

Proof

We begin by fixing a point $X_0\in \Omega$ and considering a cut-off function $\varphi \in C_c([-2,2])$ such that $0\le \varphi \le 1$ and $\varphi \equiv 1$ on $[-1,1]$. For each $0<\varepsilon <\delta (X_0)/16$ we set $\varphi _\varepsilon (X)=\varphi (|X-X_0|/\varepsilon )$ and $\psi _\varepsilon =1-\varphi _\varepsilon$. Furthermore, let $G_1^{X_0} = G_1(Y,X_0)$. We see that

$$\begin{aligned} \int _\Omega A_0^*\nabla G_1^{X_0} \cdot \nabla u_0 dY = \int _\Omega A_0^*\nabla (G_1^{X_0} \psi _\varepsilon ) \cdot \nabla u_0 dY + \int _\Omega A_0^*\nabla (G_1^{X_0} \varphi _\varepsilon ) \cdot \nabla u_0dY. \end{aligned}$$

Thanks to Proposition 2.21 we have that $G_1(\cdot ,X_0)\psi _\varepsilon \in W_0^{1,2}(\Omega )$, which gives us (as $L_0u_0=0$) that

$$\begin{aligned} \int _\Omega A_0^*(Y)\nabla (G_1(Y,X_0)\psi _\varepsilon (Y)) \cdot \nabla u_0(Y)dY=0. \end{aligned}$$

Next we note that

$$\begin{aligned} \int _\Omega A_0^*\nabla (G_1^{X_0} \varphi _\varepsilon ) \cdot \nabla u_0dY= & {} \int _\Omega A_0^*\nabla G_1^{X_0} \cdot \nabla u_0 \varphi _\varepsilon dY + \int _\Omega A_0^*\nabla \varphi _\varepsilon \cdot G_1^{X_0} \nabla u_0dY\\=: & {} I_\varepsilon (X_0) +II_\varepsilon (X_0). \end{aligned}$$

Thus if we can show that $I_\varepsilon (X_0) + II_\varepsilon ^k(X_0) \rightarrow 0$ as $\varepsilon \rightarrow 0$ for a.e. $X_0 \in \Omega$, then we have shown our claim. We start by considering the first term. Clearly,

$$\begin{aligned} |I_\varepsilon (X_0)|\le & {} \int _{B(X_0,2\varepsilon )}|A_0| |\nabla G_1^{X_0}| |\nabla u_0| dY\\\le & {} \left( \int _{B(X_0,\delta (X_0/8))}|A_0|^r dY\right) ^{1/r}\left( \int _{B(X_0,2\varepsilon )} \left( |\nabla G_1^{X_0}||\nabla u_0|\right) ^{r'}dY\right) ^{1/r'}, \end{aligned}$$

for some $r>2$ to be determined later. Notice that the first term is bounded since $A_0\in L^r_{\textrm{loc}}(\Omega )$. To deal with the second term we decompose the ball $B(X_0,2\varepsilon )$ into family of annuli $C_j(X_0,\varepsilon )=B(X_0,2^{-j+1}\varepsilon )\setminus B(X_0,2^{-j}\varepsilon )$, $j\ge 0$. This gives us

Using Proposition 2.12, Caccioppoli’s inequality and Proposition 2.23 we get that for r sufficiently large we have:

and

Hence

$$\begin{aligned} |I_\varepsilon (X_0)|\lesssim & {} \sum _{j=0}^\infty (2^{-j}\varepsilon )^{1-(n-n/r')}M[|\nabla u_0|^2\chi _\Omega ](X_0)^{1/2} \\= & {} \sum _{j=0}^\infty (2^{-j}\varepsilon )^{1-n/r}M[|\nabla u_0|^2\chi _\Omega ](X_0)^{1/2}. \end{aligned}$$

Choosing $r > 2n$ we get that

$$\begin{aligned} |I_\varepsilon (X_0)|\lesssim \sum _{j=0}^\infty 2^{-j/2}\sqrt{\varepsilon }M[|\nabla u_0|^2\chi _\Omega ](X_0)^{1/2} \lesssim \sqrt{\varepsilon }M[|\nabla u_0|^2\chi _\Omega ](X_0)^{1/2}. \end{aligned}$$

For the second term we note that $\Vert \nabla \varphi _\varepsilon \Vert _\infty \approx \varepsilon ^{-1}$. Then Proposition 2.23 and Hölder’s inequality give us:

Combining both integrals we have

$$\begin{aligned} \int _\Omega A_0\nabla (G_1^{X_0}\varphi _\varepsilon ) \cdot \nabla u_0dY\le |I_\varepsilon (X_0)|+|II_\varepsilon (X_0)|\lesssim \sqrt{\varepsilon }M[|\nabla u_0|^2\chi _\Omega ](X_0)^{1/2} \end{aligned}$$

for all $\varepsilon >0$. Since $\nabla u_0\in L^2(\Omega )$ we have $M[|\nabla u_0|^2\chi _\Omega ]\in L^{1,\infty }(\Omega )$ and thus $M[|\nabla$ $u_0|^2\chi _\Omega ] <\infty$ a.e. on $\Omega$. Thus letting $\varepsilon \rightarrow 0+$ finishes the proof.$\square$

Next we prove a result similar to Lemma 3.18 in [2]. However, we note that the proof of this result is not actually given in [2], the paper instead cites [15] which was not available to us as it has not yet appeared anywhere.

Proposition 3.6

Suppose that $\Omega \subset \mathbb {R}^{n}$ is a bounded CAD. Let $L_0$, $L_1$ be two elliptic operators, $u_0,u_1\in W^{1,2}(\Omega )$ be a pair of weak solutions of $L_0u_0=0$, $L_1u_1=0$ in $\Omega$, with $u_0-u_1\in W_0^{1,2}(\Omega )$ and $G_0$ be the Green’s function of $L_0$. Then for a.e. $X\in \Omega$ we have

$$\begin{aligned} F(X) := u_0(X)-u_1(X) = \int _\Omega A_0(Y)\nabla _Y G_0(Y,X) \cdot \nabla (u_0-u_1)(Y)dY. \end{aligned}$$

Proof

Fix $X_0\in \Omega$ and consider a cut-off function $\vartheta \in C_c([-2,2])$ such that $0\le \vartheta \le 1$ and $\vartheta \equiv 1$ on $[-1,1]$. For each $0<\varepsilon <\delta (X_0)/16$ we set $\vartheta _\varepsilon (X)=\vartheta (|X-X_0|/\varepsilon )$ and $\psi _\varepsilon =1-\vartheta _\varepsilon$. Consider a sequence of functions $\varphi _k\in C_0^\infty (\Omega )$ such that $\varphi _k \rightarrow u_0-u_1$ in $W^{1,2}(\Omega )$ with

$$\begin{aligned} \Vert \varphi _{k+1}-( u_0-u_1)\Vert _{W^{1,2}(\Omega )} \le \frac{1}{2}\Vert \varphi _k-(u_0-u_1)\Vert _{W^{1,2}(\Omega )}, \quad \forall k\ge 1. \end{aligned}$$

By Proposition 2.21

$$\begin{aligned} \varphi _k(X_0) = \int _\Omega A_0(Y)\nabla _Y G_0(Y,X_0) \cdot \nabla \varphi _k(Y)dY. \end{aligned}$$

Notice that, by taking a subsequence, we may assume that $\varphi _k \rightarrow u_0-u_1$ a.e. It follows that

$$\begin{aligned}{} & {} \int _\Omega A_0(Y) \nabla _Y G_0(Y,X_0) \nabla (\varphi _k-(u_0-u_1))(Y) dY\\{} & {} =\int _\Omega A_0(Y) \nabla _Y (G_0(Y,X_0)\psi _\varepsilon (Y)) \nabla (\varphi _k-(u_0-u_1))(Y)dY\\{} & {} \quad +\int _\Omega A_0(Y) \nabla _Y G_0(Y,X_0) \nabla (\varphi _k-(u_0-u_1))(Y)\vartheta _\varepsilon (Y) dY \\{} & {} \quad +\int _\Omega A_0(Y) \nabla \vartheta _\varepsilon (Y) \nabla (\varphi _k-(u_0-u_1))(Y)G_0(Y,X_0)dY\\{} & {} =: I_\varepsilon ^k(X_0) +II_\varepsilon ^k(X_0) +III_\varepsilon ^k(X_0). \end{aligned}$$

We aim to show that

$$\begin{aligned} I_\varepsilon ^{k}(X_0) + II_\varepsilon ^k(X_0) + III_\varepsilon ^k(X_0) \rightarrow 0, \quad \varepsilon \rightarrow 0, \end{aligned}$$

(3.7)

for a well chosen sequence $k=k(\varepsilon )$ with property that $k(\varepsilon )\rightarrow \infty$ as $\varepsilon \rightarrow 0$.

Analogous to the proof of Proposition 3.5 we get that for a large k

$$\begin{aligned} |I_\varepsilon ^k| \lesssim \Vert G_0(\cdot ,X_0)\psi _\varepsilon \Vert _{W^{1,2}(\Omega )}\Vert \varphi _k-(u_0-u_1)\Vert _{W^{1,2}(\Omega )} \le \sqrt{\varepsilon }, \end{aligned}$$

and

$$\begin{aligned} |II_\varepsilon ^k|,|II_\varepsilon ^k|\lesssim \sqrt{\varepsilon } M[g_k](X_0)^{1/2}, \end{aligned}$$

where $g_k := |\nabla (\varphi _k-(u_0-u_1))|^2\chi _\Omega$. Thus

$$\begin{aligned} |I_\varepsilon ^k|+|II_\varepsilon ^k|+|III_\varepsilon ^k| \lesssim \sqrt{\varepsilon } \max \left\{ 1, \sup _{k} M[g_k]^{1/2}\right\} \end{aligned}$$

(3.8)

Now, since $g_k \in L^1(\mathbb {R}^n)$ we have that $M[g_k]\in L^{1,\infty }(\mathbb {R}^n)$ with the bound

$$\begin{aligned} \Vert M[g_k]\Vert _{L^{1,\infty }(\mathbb {R}^n)} \lesssim \Vert g_k\Vert _{L^1(\Omega )} \le \Vert \varphi _k-(u_0-u_1)\Vert _{W^{1,2}(\Omega )}^2 \lesssim 2^{-k}, \end{aligned}$$

Thus $\sup _{k} M[g_k]^{1/2} <\infty$ a.e. allowing us to let $\varepsilon \rightarrow 0$ in (3.8) and yielding (3.7) for a.e. $X_0$ as desired.$\square$

4 Proof of Lemma 3.3

Let $Q\in \partial \Omega$ and $X\in \Gamma _\alpha (Q)$. Let $G_0$ be the Green’s function corresponding to $L_0$ and $G_0^*$ its adjoint. As before let $F = u_1 - u_0$ and note that by Propositions 3.6, 3.5 and 2.24 we have

$$\begin{aligned} F(X)= & {} u_1(X) - u_0(X) = \int _{\Omega } A_0^T \nabla _Y G_0^*(Y,X) \nabla (u_1-u_0)(Y) dY\\= & {} \int _{\Omega } A_0 \nabla u_1(Y) \nabla _Y G_0(X,Y) dY - \int _{\Omega } A_0 \nabla u_0(Y) \nabla _Y G_0(X,Y) dY\\= & {} \int _{\Omega } A_0 \nabla u_1(Y) \nabla _Y G_0(X,Y) dY - \int _{\Omega } A_1 \nabla u_1(Y) \nabla _Y G_0(X,Y) dY\\= & {} \int _{\Omega } \varepsilon \nabla u_1(Y) \nabla _Y G_0(X,Y) dY. \end{aligned}$$

Remark 4.1

Note that the Green’s function property (2.22) only holds for $\varphi \in W_{0}^{1,p}(\Omega )$ with $p > n \ge 2$ and so cannot be applied directly unless we have shown statements such as Propositions 3.5 and 3.6. This is true even if $A_0$, $A_1$ are bounded and symmetric. This was perhaps overlooked in [23] and [12] but can be fortunately fixed via an approximation argument similar to the one we have given in the previous section.

We split F into two terms (first of which is the near part close to X).

$$\begin{aligned} F = F_1 + F_2, \quad F_1(Z) = \int _{B(X)} \nabla _{Y} G_0(Z,Y)\cdot \varepsilon (Y) \nabla u_1(Y) dY, \end{aligned}$$

and then split $F_1$ further and write it as

$$\begin{aligned} F_1 = \tilde{F}_1 + \tilde{\tilde{F}}_1, \quad \tilde{F}_1(Z) = \int _{B(X)} \nabla _Y \tilde{G}_0(Z,Y) \cdot \varepsilon (Y) \nabla u_1(Y) dY. \end{aligned}$$

Here $B(X):=B(X,\delta (X)/4)$ and $\tilde{G}_0$ denotes the “local Green function” for $L_0$ on 2B(X). We also set $K(Z,Y) := G_0(Z,Y) - \tilde{G}_0(Z,Y)$. Since $\mu$ is a doubling measure we have by Lemma 2.31 that

$$\begin{aligned} \Vert \tilde{N}_\alpha [F]\Vert _{L^p(d\mu )}\le & {} \Vert \tilde{N}_\alpha [\tilde{F_1}]\Vert _{L^p(d\mu )} + \Vert \tilde{N}_\alpha [\tilde{\tilde{F}}_1]\Vert _{L^p(d\mu )} + \Vert \tilde{N}_\alpha [F_2]\Vert _{L^p(d\mu )}\\\lesssim & {} \Vert \tilde{N}_\alpha ^{1/2}[\tilde{F_1}]\Vert _{L^p(d\mu )} + \Vert \tilde{N}_\alpha ^{1/2}[\tilde{\tilde{F}}_1]\Vert _{L^p(d\mu )} + \Vert \tilde{N}_\alpha ^{1/4}[F_2]\Vert _{L^p(d\mu )}. \end{aligned}$$

Hence to conclude that Lemma 3.3 holds it is enough to show that the pointwise bound

is true for almost every $Q\in \partial \Omega$ and $X\in \Gamma _\alpha (Q)$. We shall consider each of the terms above separately.

4.1 The “local term” $F_1$

Consider $\phi \in C_c^\infty (\mathbb {B}^n)$ non-negative with $\int _{\mathbb {R}^n} \phi = 1$ and set $\phi _m = (\frac{2m}{\delta (X)})^{n}\phi (2mX/\delta (X))$. Define

$$\begin{aligned} \hat{A}^m := A_{1} *\phi _m, \quad \hat{\varepsilon }^m := \varepsilon *\phi _m, \quad \hat{L}_m := \text {div}(\hat{A}^m \nabla ), \end{aligned}$$

and let $r >1$ be large enough that Proposition 2.12 holds with $p = \frac{2r}{r-2}$. Let $\hat{u}_m$ be the weak solution to the Dirichlet problem

$$\begin{aligned} \hat{L}_m v = 0, \text { in } 2B(X), \quad u_1-v \in W_0^{1,2}(2B(X)). \end{aligned}$$

We know that $A_{0},A_{1} \in L^{r}(2B(X))$, wherefore

$$\begin{aligned} \hat{A}^m \rightarrow A_{1}, \quad \hat{\varepsilon }^m \rightarrow \varepsilon , \quad \text {in } L^{r}(2B(X)). \end{aligned}$$

Moreover $A_{1}^s \in L^{\infty }(2B(X))$, hence by the ellipticity of our original $A_1$ for large m there exists $\lambda _{0,m} > 0$ such that

$$\begin{aligned} \lambda _{0,m} |\xi |^2 \le \xi ^T \hat{A}^m \xi \le \lambda _{0,m}^{-1} |\xi |^2, \quad \forall \xi \in \mathbb {R}^n, ~\text { a.e. } X \in 2B(X), \end{aligned}$$

with $\lambda _{0,m} \rightarrow \lambda _{0}$ as $m \rightarrow \infty$ and so the ellipticity constant does not depend on m. Next we will show that

$$\begin{aligned} \Vert \nabla (\hat{u}_m - u_1) \Vert _{L^2(2B(X))} \lesssim \Vert \hat{A}^m - A_1 \Vert _{L^r(2B(X))}^2, \end{aligned}$$

(4.2)

and in particular it follows that $\nabla \hat{u}_m \rightarrow \nabla u_1$ in $L^2(2B(X))$. Clearly for m large enough we have that

$$\begin{aligned} \int _{2B(X)}|\nabla (\hat{u}_m - u_1)|^2\lesssim & {} 2\lambda _0^{-1} \int _{2B(X)}\hat{A}^m\nabla (\hat{u}_m - u_1)\cdot \nabla (\hat{u}_m - u_1) \\= & {} - 2\lambda _0^{-1} \int _{2B(X)}(\hat{A}^m)\nabla u_1\cdot \nabla (\hat{u}_m - u_1)\\= & {} 2\lambda _0^{-1} \int _{2B(X)}(A_1 - \hat{A}^m)\nabla u_1\cdot \nabla (\hat{u}_m - u_1)\\\le & {} 2\lambda _0^{-1} \Vert \hat{A}^m - A_1 \Vert _{L^r(2B(X))} \Vert \nabla u_1 \Vert _{L^{\frac{2r}{r-2}}(2B(X))}\\{} & {} \quad \cdot \left( \int _{2B(X)} |\nabla \hat{u}_m-\nabla u_1|^2\right) ^{1/2}\\\le & {} 2\lambda _0^{-2} \Vert \hat{A}^m - A_1 \Vert _{L^r(2B(X))}^2 \Vert \nabla u_1 \Vert _{L^{\frac{2r}{r-2}}(2B(X))}^2\\{} & {} \quad + \frac{1}{2} \left( \int _{2B(X)} |\nabla \hat{u}_m-\nabla u_1|^2\right) \\\lesssim & {} \Vert \hat{A}^m - A_1 \Vert _{L^r(2B(X))}^2 \Vert \nabla u_1 \Vert _{L^{\frac{2r}{r-2}}(2B(X))}^2. \end{aligned}$$

By Proposition 2.12 we have that

$$\begin{aligned} \Vert \nabla u_1 \Vert _{L^{\frac{2r}{r-2}}(2B(X))}^2 \lesssim _X \Vert \nabla u_1 \Vert _{L^{2}(3B(X))}^2 \le \Vert \nabla u_1 \Vert _{L^{2}(\Omega )}^2 < \infty , \end{aligned}$$

and hence (4.2) follows.

The reason we consider approximations of $\tilde{F}_1$, namely

$$\begin{aligned} \hat{F}_m(Z) := \int _{B(X)} \nabla _Y \tilde{G}_0(Z,Y) \cdot \hat{\varepsilon }^m(Y) \nabla \hat{u}_m(Y) dY, \end{aligned}$$

and

$$\begin{aligned} \hat{F}_m^{\rho }(Z)&:= \int _{B(X)} \nabla _Y \tilde{G}^{\rho }_0(Z,Y) \cdot \hat{\varepsilon }^m(Y) \nabla \hat{u}_m(Y) dY\nonumber \\&= - \int _{B(X)} \text {div}(\hat{\varepsilon }^m \nabla \hat{u}_m) \tilde{G}_{0}^{\rho }(Z,Y)dY + \int _{\partial B(X)} \hat{\varepsilon }^m \nabla \hat{u}_m \cdot \nu \tilde{G}_{0}^{\rho }(Z,Y)dY. \end{aligned}$$

(4.3)

is that for the term $\tilde{F}_1$ we have few situations where derivative hit terms that do not have required regularity. This is not true for mollified coefficients as those are smooth. Here, in the formula above $\tilde{G}_0^\rho (Z,Y)\in W^{1,2}_0(2B(X))$ is the unique function that satisfies

which exists by the Lax–Milgram theorem. From (4.3), it is clear that $\hat{F}_m^{\rho }$ is continuous on $2B(X) \setminus \frac{3}{2}B(X)$ with $\hat{F}_m^{\rho } = 0$ on $\partial 2B(X)$. Next note that by [14]

$$\begin{aligned} \Vert \tilde{G}_0^{\rho }\Vert _{L^{\frac{n}{n-2},\infty }(2B(X))} \lesssim 1, \end{aligned}$$

where the implied constant is independent of $\rho$. Hence $\Vert \tilde{G}_0^{\rho }\Vert _{L^{1}(2B(X))} \lesssim 1$ and therefore

$$\begin{aligned} |\hat{F}_m^{\rho }| \lesssim \Vert \text {div}(\hat{\varepsilon }^m \nabla \hat{u}_m) \Vert _{\infty } + \Vert \hat{\varepsilon }^m \nabla \hat{u}_m \Vert _{\infty } \lesssim _m 1. \end{aligned}$$

(4.4)

This allows us to claim that $\hat{F}_m^{\rho } \in L^{\infty }(2B(X))$. Finally by Minkowski’s integral inequality

$$\begin{aligned}{} & {} \left\| \int _{B(X)} |\text {div}(\hat{\varepsilon }^m \nabla \hat{u}_m)| |\nabla _Z \tilde{G}_{0}^{\rho }(Z,Y)|dY \right\| _{L_Z^2(2B(X))}\\{} & {} \le \int _{B(X)} |\text {div}(\hat{\varepsilon }^m \nabla \hat{u}_m)| \Vert \nabla _Z\tilde{G}_{0}^{\rho }(\cdot ,Y) \Vert _{L^2(2B(X))} dY\\{} & {} \lesssim _{\rho } \int _{B(X)} |\text {div}(\hat{\varepsilon }^m \nabla \hat{u}_m)| dY \lesssim _m |B(X)| \lesssim _X 1, \end{aligned}$$

and similarly

$$\begin{aligned} \left\| \int _{\partial B(X)} |\hat{\varepsilon }^m \nabla \hat{u}_m| |\nabla _Z \tilde{G}_{0}^{\rho }(Z,Y)|dY \right\| _{L_Z^2(2B(X))} \lesssim _{\rho ,X} 1. \end{aligned}$$

Thus $\Vert \nabla \hat{F}_m^{\rho } \Vert _{L^2(2B(X))} \lesssim _{\rho ,X} 1$ and we can conclude that $\hat{F}_m^{\rho } \in W_0^{1,2}(2B(X))$. Next,

Therefore

Since the term

it can be absorbed by the left-hand side of the expression above and thus giving us that

We also note that

We know that if $\delta (X)\ge 4R_0$, then $\varepsilon =0$ on B(X) and there is nothing to show. Hence may assume that $\delta (X)\le 4R_0$ and use (2.40) and Proposition 2.41, to obtain

For the remaining term we have by Proposition 2.12

and by the Poincare inequality for $\hat{F}^\rho _m$ we have

(4.5)

Collecting all terms together then yields:

$$\begin{aligned} \lim _{m\rightarrow \infty }\left( \delta (X)^{2-n} \int _{2B(X)} |\nabla \hat{F}^\rho _m|^2\right)&\lesssim \varepsilon _0^2 \int _{2B(X)} |\nabla \hat{u}_1|^2 \delta (Z)^{2-n} dZ \nonumber \\&\le \varepsilon _0^2 S_{\bar{M}}[u_1](Q_0)^2. \end{aligned}$$

(4.6)

To get statement on the original $\tilde{F}_1$ we let $\rho \rightarrow 0$ and then $m\rightarrow \infty$. We claim that

(4.7)

and

(4.8)

Having this (4.5) and (4.6) combined give us

as desired.

We start by proving (4.7). As this is a claim at every X we allow the implicit constants below to depend on X. We know from [22] that for a fixed Z, $\tilde{G}_{0}^{\rho }(Z,\cdot ) \rightarrow \tilde{G}_{0}(Z,\cdot )$ weakly in $W_0^{1,1+\eta }(2B(X))$ for small $\eta > 0$. Hence we also have weak convergence in $W^{1,1+\eta }(B(X))$. For any $v \in W^{1,1+\eta }(B(X))$

$$\begin{aligned} \left| \int _{B(X)} \nabla v \cdot \hat{\varepsilon }^m \nabla \hat{u}_m dY \right| \le \Vert \hat{\varepsilon }^m \nabla \hat{u}_m \Vert _{L^\infty (B(X))} \Vert \nabla v \Vert _{L^1(B(X))} \lesssim _{m,X} \Vert v \Vert _{W^{1,1+\eta }(B(X))}, \end{aligned}$$

and in particular, this means that

$$\begin{aligned} \int _{B(X)} \nabla \tilde{G}_{0}^{\rho }(Z,\cdot ) \cdot \hat{\varepsilon }^m \nabla \hat{u}_m dY \rightarrow \int _{B(X)} \nabla \tilde{G}_{0}(Z,\cdot ) \cdot \hat{\varepsilon }^m \nabla \hat{u}_m dY, \quad \rho \rightarrow 0, \end{aligned}$$

i.e., $\hat{F}_m^{\rho }(Z) \rightarrow \hat{F}_m(Z)$. Thus using (4.4) and the dominated convergence theorem we conclude that

To establish (4.8) we consider the pointwise difference of the two functions at $Z\in B(X)$. We have that

$$\begin{aligned} (\hat{F}_m-\tilde{F}_1)(Z)= & {} \int _{B(X)} \nabla _Y \tilde{G}_0(Z,Y) \cdot (\hat{\varepsilon }^m-\varepsilon )(Y) \nabla \hat{u}_m(Y) dY\\{} & {} + \int _{B(X)} \nabla _Y \tilde{G}_0(Z,Y) \cdot \varepsilon (Y) \nabla (\hat{u}_m-u_1)(Y) dY\\=: & {} I^m(Z)+II^m(Z). \end{aligned}$$

We proceed as in the proof of Proposition 3.6 and consider a cut-off function $\vartheta \in C_c([-2,2])$ such that $0\le \vartheta \le 1$ and $\vartheta \equiv 1$ on $[-1,1]$. For each $0< s <\delta (X)/16$ we set $\vartheta _s(Y) := \vartheta (|Y-Z|/s)$ and $\psi _s := 1-\vartheta _s$. This allows us to write

$$\begin{aligned} I^m(Z)= & {} \int _{B(X)} \nabla _Y (\tilde{G}_0(Z,Y)\psi _s(Y)) \cdot (\hat{\varepsilon }^m-\varepsilon )(Y) \nabla \hat{u}_m(Y) dY \\{} & {} +\int _{B(X)} \nabla _Y \tilde{G}_0(Z,Y)\vartheta _s(Y) \cdot (\hat{\varepsilon }^m-\varepsilon )(Y) \nabla \hat{u}_m(Y) dY\\{} & {} +\int _{B(X)} \tilde{G}_0(Z,Y)\nabla \vartheta _s(Y) \cdot (\hat{\varepsilon }^m-\varepsilon )(Y) \nabla \hat{u}_m(Y) dY\\=: & {} \tilde{I}_s^m(Z)+\hat{I}_s^m(Z)+\bar{I}_s^m(Z), \end{aligned}$$

and

$$\begin{aligned} II^m(Z)= & {} \int _{B(X)} \nabla _Y (\tilde{G}_0(Z,Y)\psi _s(Y)) \cdot \varepsilon (Y) \nabla (\hat{u}_m-u_1)(Y) dY\\{} & {} +\int _{B(X)} \nabla _Y \tilde{G}_0(Z,Y)\vartheta _s(Y) \cdot \varepsilon (Y) \nabla (\hat{u}_m-u_1)(Y) dY\\{} & {} +\int _{B(X)} \tilde{G}_0(Z,Y)\nabla \vartheta _s(Y) \cdot \varepsilon (Y) \nabla (\hat{u}_m-u_1)(Y) dY\\=: & {} \tilde{II}^m_s(Z) +\hat{II}_s^m(Z)+\bar{II}_s^m(Z). \end{aligned}$$

For $\tilde{I}_s^m$ and $\tilde{II}_s^m$ we can use Hölder’s inequality to get

$$\begin{aligned} \tilde{I}_s^m(Z)\lesssim & {} \Vert \nabla (\tilde{G}_0(Z,\cdot )\psi _s)\Vert _{L^{\frac{2r}{2-r}}(B(X)\setminus B(Z,s))} \Vert \hat{\varepsilon }_m-\varepsilon \Vert _{L^r(B(X))} \Vert \nabla \hat{u}_m\Vert _{L^{2}(B(X))}\\\lesssim & {} \Vert \nabla (\tilde{G}_0(Z,\cdot )\psi _s)\Vert _{L^{\frac{2r}{2-r}}(B(X)\setminus B(Z,s))} \Vert \hat{\varepsilon }_m-\varepsilon \Vert _{L^r(B(X))}, \end{aligned}$$

and

$$\begin{aligned} \tilde{II}_s^m(Z)\lesssim & {} \Vert \nabla (\tilde{G}_0(Z,\cdot )\psi _s)\Vert _{L^{\frac{2r}{2-r}}(B(X)\setminus B(Z,s))} \Vert \varepsilon \Vert _{L^r(B(X))} \Vert \nabla (\hat{u}_m-u_1)\Vert _{L^{2}(B(X))}\\\lesssim & {} \Vert \nabla (\tilde{G}_0(Z,\cdot )\psi _s)\Vert _{L^{\frac{2r}{2-r}}(B(X)\setminus B(Z,s))} \Vert \nabla (\hat{u}_m-u_1)\Vert _{L^{2}(B(X))}. \end{aligned}$$

By the chain rule we see that

$$\begin{aligned} \Vert \nabla (\tilde{G}_0(Z,\cdot )\psi _s)\Vert _{L^{\frac{2r}{2-r}}(B(X)\setminus B(Z,s))}\le & {} \Vert \nabla (\tilde{G}_0(Z,\cdot ))\Vert _{L^{\frac{2r}{2-r}}(B(X)\setminus B(Z,s))} \\{} & {} + \Vert \nabla \psi _s\Vert _{\infty } \Vert \tilde{G}_0(Z,\cdot )\Vert _{L^{\frac{2r}{2-r}}(B(X)\setminus B(Z,s))}. \end{aligned}$$

Since $\Vert \nabla \psi _s \Vert _{\infty } \lesssim \frac{1}{s}$ by Proposition 2.23$\Vert \tilde{G}_0(Z,\cdot )\Vert _{L^{\frac{2r}{2-r}}(B(X)\setminus B(Z,s))} \lesssim _{s} 1$ and therefore by Propositions 2.12 and 2.21

$$\begin{aligned} \Vert \nabla \tilde{G}_0(Z,\cdot )\Vert _{L^{\frac{2r}{2-r}}(2B(X)\setminus B(Z,s))}&\lesssim _{s}&\Vert \nabla \tilde{G}_0(Z,\cdot )\Vert _{L^{2}(\frac{3}{2}B(X)\setminus \frac{1}{2}B(Z,s))} \\&\lesssim _{s}&\Vert \tilde{G}_0(Z,\cdot )\Vert _{L^{2}(2B(X)\setminus \frac{1}{3}B(Z,s))} \lesssim _{s} 1. \end{aligned}$$

Since $\Vert \hat{\varepsilon }_m-\varepsilon \Vert _{L^r(B(X))}, \Vert \nabla (\hat{u}_m-u_1)\Vert _{L^{2}(B(X))} \rightarrow 0$ for a fixed $s>0$ we may therefore choose $m=m(s)$ so that

$$\begin{aligned} |\tilde{I}_s^{m(s)}|+|\tilde{II}_s^{m(s)}|\lesssim \sqrt{s}. \end{aligned}$$

For the remaining terms, estimates similar to the ones in the proofs of Propositions 3.6 and 3.5 give us:

$$\begin{aligned} |\hat{I}_s^m(Z)|,|\bar{I}_s^m(Z)| \lesssim \sqrt{s}M[|\nabla \hat{u}_m|^2\chi _{\frac{3}{2}B(X)}](Z)^{1/2}, \end{aligned}$$

and

$$\begin{aligned} |\hat{II}_s^m(Z)|,|\bar{II}_s^m|\lesssim & {} \sqrt{s}M[|\nabla (\hat{u}_m-u_1)|^2\chi _{\frac{3}{2}B(X)}](Z)^{1/2} \\\lesssim & {} \sqrt{s}M[|\nabla \hat{u}_m|^2\chi _{\frac{3}{2}B(X)}](Z)^{1/2} + \sqrt{s}M[|\nabla u_1|^2\chi _{\frac{3}{2}B(X)}](Z)^{1/2}. \end{aligned}$$

Putting everything together, we get for some $m=m(s)$

Since $\nabla u_1,\nabla \hat{u}_m\in L^{\frac{2r}{r-2}}(\frac{3}{2}B(X))$, by Hölder and the fact that the maximal function $\Vert M \Vert _{L^p \rightarrow L^p} < \infty$ for $p>1$ is bounded we may conclude that

and similarly

Hence

Because the implicit constant in this inequality depends on m or s we conclude that (4.8) must hold. Thus

as desired.

Remark 4.9

This involved approximation argument is not shown in either [23] nor [12]. Instead they argue that $\tilde{F}_1$ satisfies the equation

$$\begin{aligned} \left\{ \begin{array}{ll} L_0 \tilde{F}_1 = \text {div}[\varepsilon \nabla u_1 \chi _{B(X)}] \quad &{}\text {in } 2B(X),\\ \tilde{F}_1 = 0 &{}\text {on } 2B(X). \end{array}\right. \end{aligned}$$

There are two problems with this. The first one is that it is not clear if the weak derivative $\nabla \tilde{F}_1$ even exists in $L_{\text {loc}}^1(2B(X))$ due to the low regularity of the Green’s function. The second issue is that even if we could claim that $\tilde{F}_1 \in W_{0}^{1,2}(2B(X))$, the Green’s function property (2.22) only holds for $\varphi \in W_{0}^{1,p}(2B(X))$ with $p > n \ge 2$ and so it would not apply for this case.

Next we consider bounds for $\tilde{\tilde{F}}_1(Z)$. For a large $r>1$ and $Z\in B(X)$ we have that

The first two terms are handled as we did above for $\tilde{F}_1$. Note that $L_0K(Z,\cdot )=0$ in 2B(X) and $K(Z,\cdot )\ge 0$, so we may use Caccioppoli (Proposition 2.13) and Harnack (Proposition 2.15) to deduce that

Bounds in Proposition 2.23 apply on K as it is the sum of two Green’s functions. Hence

$$\begin{aligned} \int _{\frac{3}{2}B(X)} |K(Z,Y)| \lesssim \int _{\frac{3}{2}B(X)} |Z-Y|^{2-n}dY = \int _{0}^{\frac{3}{2}B(X)} t dt \approx \delta (X)^2/2. \end{aligned}$$

Combining this with the previous estimate we obtain

4.2 The “away” Term F ₂

The aim is to consider a fixed point $Z \in B(X, \delta (X)/8)$. We integrate over $Y\in \Omega \setminus B(X)$ and by triangle inequality we therefore must have $|Z-Y|\ge \delta (X)/8$ for all such points Y. We would like to obtain a pointwise bound

$$\begin{aligned} F_2(Z)\lesssim C \varepsilon _0 M_{\omega _0}S_{\bar{M}}(u_1)(Q). \end{aligned}$$

Let $X^*\in \partial \Omega$ be a point such that $|X^*-X|=\delta (X)$. We consider the following decompositions of the boundary and the domain:

$$\begin{aligned} \Delta _j:= & {} \Delta (X^*, 2^{j-1}\delta (X)), \quad \Omega _j := \Omega \cap B(X^*,\delta (X)2^{j-1}), \quad R_j:= \Omega _j \setminus (\Omega _{j-1}\cup B(X)),\\ A^j:= & {} A(X^*, 2^{j-1}\delta (X)) \end{aligned}$$

for $j=-1,0,1,\dots ,N$ where N is chosen so that $2^{14}R_0\le 2^{N-1}\delta (X)<2^{15}R_0$. Let

$$\begin{aligned} \left\{ \begin{array}{l} F_2^0(Z) := \displaystyle \int _{\Omega _0} \varepsilon (Y) \nabla _{Y} G_0(Z,Y) \cdot \nabla u_1(Y) dY,\\ F_2^j(Z) := \displaystyle \int _{R_j} \varepsilon (Y) \nabla _{Y} G_0(Z,Y) \cdot \nabla u_1(Y) dY. \end{array}\right. \end{aligned}$$

This decomposes $F_2$ into the following terms:

$$\begin{aligned} |F_2(Z)|= & {} \left| \int _{\Omega \setminus B(X)} \varepsilon (Y) \nabla _{Y} G_0(Z,Y) \cdot \nabla u_1(Y) dY\right| \\\le & {} \left| \int _{\Omega _0} \varepsilon (Y) \nabla _{Y} G_0(Z,Y) \cdot \nabla u_1(Y) dY\right| \\{} & {} +\sum _{j=1}^N\left| \int _{R_j} \varepsilon (Y) \nabla _{Y} G_0(Z,Y) \cdot \nabla u_1(Y) dY\right| \\{} & {} + \int _{(\partial \Omega ,4R_0)\setminus (B(X)\cup B(X^*,2^{15}R_0))} |\varepsilon (Y) ||\nabla _{Y} G_0(Z,Y)|| \nabla u_1(Y)| dY\\= & {} |F_2^0(Z)| + \sum _{j=1}^N|F_2^j(Z)|+J. \end{aligned}$$

Starting with estimating $F_2^0(Z)$ we have that

$$\begin{aligned} |F_2^0(Z)|\le & {} \int _{\Omega _0\cap (\partial \Omega ,4R_0)}|\varepsilon (Y)||\nabla _Y G_0(Z,Y)||\nabla u_1(Y)|dY\\= & {} \lim _{\varepsilon \rightarrow 0}\int _{(\Omega _0\cap (\partial \Omega ,4R_0))\setminus (\partial \Omega ,\varepsilon )}|\varepsilon (Y)||\nabla _Y G_0(Z,Y)||\nabla u_1(Y)|dY. \end{aligned}$$

Since we can cover $(\partial \Omega ,4R_0)\setminus (\partial \Omega ,\varepsilon )$ by the decomposition introduced in Section 2.7, by (2.37), we can write

(4.10)

Using the ball covering that we have introduced in Section 2.7 and its properties (2.39) and (2.38) together with Proposition 2.12 we obtain

(4.11)

We estimate the Green’s function using Caccioppoli’s inequality

For the last term we further use the comparison principle and the doubling property of the elliptic measure:

Since we can cover $5\Delta _0$ with N balls $B(Q_i,\delta (X)/4)$ such that $|Q_i-Q_j|<\delta (X)/4$, $Q_i\in 5\Delta _0$ we see that $\Omega _0\cap (\partial \Omega ,\delta (X)/8)\subset \bigcup _i B(Q_i,\delta (X)/4)$. Note that N here is independent of X and $\delta (X)$. Let $\tilde{A}_i=A(Q_i, \delta (X)/4)$. By the comparison principle for $Y\in B(Q_i,\delta (X)/4)$ we have that

$$\begin{aligned} \frac{|G_0(Z,Y)|}{|G_0(Y)|}\approx \frac{|G_0(Z,\tilde{A}_i)|}{|G_0(\tilde{A}_i)|}. \end{aligned}$$

By the Harnack’s inequality for all $Y\in \Omega _0\setminus (\partial \Omega ,\delta (X)/16)$

$$\begin{aligned} \frac{|G_0(Z,Y)|}{|G_0(Y)|}\approx \frac{|G_0(Z,A_0)|}{|G_0(A_0)|}. \end{aligned}$$

Since $\tilde{A}_i\in \Omega _0\setminus (\partial \Omega ,\delta (X)/16)$ also have the same estimates for all $Y\in \Omega _0\cap (\partial \Omega ,\delta (X)/16)$, that is

$$\begin{aligned} \frac{|G_0(Z,Y)|}{|G_0(Y)|}\approx \frac{|G_0(Z,\tilde{A}_i)|}{|G_0(\tilde{A}_i)|}\approx \frac{|G_0(Z,A_0)|}{|G_0(A_0)|}. \end{aligned}$$

Hence we may use the comparison principle for the Green’s function to obtain

$$\begin{aligned} \frac{|G_0(Z,A_0)|}{|G_0(A_0)|} \lesssim \frac{\omega ^Z_0(\Delta (X^*, \delta (X)/2))}{\omega _0(\Delta (X^*, \delta (X)/2))}\lesssim \frac{1}{\omega _0(\Delta _0)}. \end{aligned}$$

After we put all pieces together we finally have for the gradient of $G_0$:

(4.12)

Next, we consider the term of (4.10) containing $\varepsilon$ function. By Proposition 2.41 we have

and hence (4.10) can be further estimated by

(4.13)

For the purposes of the stopping time argument below we define

$$\begin{aligned} T u_1 (Z)=|\nabla u_1(Z)|^2\delta (Z)^{2-n} \end{aligned}$$

and the super-level sets

$$\begin{aligned} O_j=\left\{ P\in 3\Delta _0; T_\varepsilon u_1(P)=\left( \int _{(\Gamma _M(P)\setminus B_{\varepsilon }(0))\cap (\partial \Omega ,4R_0)}T u_1(Z)dZ\right) ^{1/2}>2^j\right\} . \end{aligned}$$

We say a dyadic boundary cube $Q_\alpha ^k$, $k_{R_0}\le k\le k_\varepsilon$ belongs to $J_j$, if

$$\begin{aligned} \omega _0(O_j\cap Q_\alpha ^k)\ge \frac{1}{2}\omega _o(Q_\alpha ^k)\qquad \text {and}\qquad \omega _0(O_{j+1}\cap Q_\alpha ^k)< \frac{1}{2}\omega _o(Q_\alpha ^k), \end{aligned}$$

and belongs to $J_\infty$, if

$$\begin{aligned} \omega _0(Q_\alpha ^k\cap \{T_\varepsilon u_1=0\})\ge \frac{1}{2}\omega _o(Q_\alpha ^k). \end{aligned}$$

Furthermore, let $M_{\omega _0}$ be the uncentered Hardy–Littlewood maximal function and let

$$\begin{aligned} \tilde{O}_j=\{M_{\omega _0}(\chi _{O_j})>1/2\} \end{aligned}$$

and observe that for $Z\in Q_\alpha ^k\in J_j$

$$\begin{aligned} M_{\omega _0}(\chi _{O_j})(Z)\ge \frac{\omega _0(Q_\alpha ^k\cap O_j)}{\omega _0(Q_\alpha ^k)}\ge \frac{1}{2} \end{aligned}$$

and hence $Q_\alpha ^k\subset \tilde{O}_j$. Thus, we also have

$$\begin{aligned} \omega _0(Q_\alpha ^k\cap \tilde{O}_j\setminus O_{j+1})=\omega _0(Q_\alpha ^k\setminus O_{j+1})\ge \frac{1}{2}\omega _o(Q_\alpha ^k). \end{aligned}$$

The weak $L^1$ boundedness of the maximal function therefore implies that

$$\begin{aligned} \omega _0(\tilde{O}_j\setminus O_{j+1})\le \omega _0(\tilde{O}_j)=\omega _0(\{M_{\omega _0}(\chi _{O_j})>1/2\})\lesssim \Vert \chi _{O_j}\Vert _{L^1(d\omega _0)}=\omega _0(O_j). \end{aligned}$$

We use this to further estimate (4.13). Applying the above decomposition and the Cauchy–Schwarz inequality we get

$$\begin{aligned}{} & {} \underset{\underset{k_0\le k\le k_{\varepsilon }}{Q_\alpha ^k\subset 3\Delta _0}}{\sum }\!\!\!\omega _0(Q_\alpha ^k)^{1/2}\!\!\left( \!\int _{\hat{I}^k_\alpha }\frac{G_0(Z)\beta _r(Z)^2}{\delta (Z)^2}dZ\right) ^{1/2}\left( \int _{\hat{I}_\alpha ^k}|\nabla u_1|^2\delta ^{2-n} dY\right) ^{1/2}\\{} & {} \lesssim \frac{1}{\omega _0(\Delta _0)}\!\sum _{j}\!\!\left( \underset{\underset{k_0\le k\le k_{\varepsilon }}{Q_\alpha ^k\in J_j}}{\sum } \!\!\!\int _{\hat{I}^k_\alpha }\frac{G_0(Z)\beta _r(Z)^2}{\delta (Z)^2}dZ\!\!\right) ^{1/2}\!\!\!\!\!\left( \underset{\underset{k_0\le k\le k_{\varepsilon }}{Q_\alpha ^k\in J_j}}{\sum }\!\!\! \omega _0(Q_\alpha ^k)\!\!\int _{\hat{I}_\alpha ^k}|\nabla u_1|^2\delta ^{2-n} dY\!\!\right) ^{1/2}\!\!\!. \end{aligned}$$

Since for every two cubes $Q_\alpha ^k$, $Q_\beta ^l$, $l\le k$ either contain each other, i.e., $Q_\beta ^l\subset Q_\alpha ^{k}$ or are disjoint $Q_\beta ^l\cap Q_\alpha ^{k}=\emptyset$, there is a disjoint collection of cubes in $J_j$ such that their union covers all the other cubes. We call them the top cubes. We observe that for any such top cube $Q_\alpha ^k$ and its subcube $Q_\beta ^l\subset Q_\alpha ^k$ we have $\hat{I}_\beta ^l\subset T(\Delta (Z_\alpha ^k, (C_0+16\lambda )8^{-k}))$ and the overlap of these Carleson regions of different top cubes $Q_\alpha ^k$ is finite. We also know that the overlap of the $\hat{I}_\beta ^l$ is finite. Hence

$$\begin{aligned} \sum _{Q_\alpha ^k\in J_j}\int _{\hat{I}^k_\alpha }\frac{G_0(Z)\beta _r(Z)^2}{\delta (Z)^2}dZ= & {} \underset{\underset{\text {disj. top cubes}}{Q_\alpha ^k\in J_j}}{\sum } \sum _{Q_\beta ^l\in J_j, Q_\beta ^l\subset Q_\alpha ^k} \int _{\hat{I}^l_\beta }\frac{G_0(Z)\beta _r(Z)^2}{\delta (Z)^2}dZ\\\lesssim & {} \underset{\underset{\text {disj. top cubes}}{Q_\alpha ^k\in J_j}}{\sum } \int _{T(\Delta (Z_\alpha ^k, (C_0+16\lambda )8^{-k}))}\frac{G_0(Z)\beta _r(Z)^2}{\delta (Z)^2}dZ\\\lesssim & {} \underset{\underset{\text {disj. top cubes}}{Q_\alpha ^k\in J_j}}{\sum } \varepsilon _0^2 \omega _0(Q_\alpha ^{k})\le 2\varepsilon _0^2\omega _0(O_j). \end{aligned}$$

Here we have used Proposition 2.41 in the penultimate step and the property of cubes in $J_j$ in the last step. Denote $S_M^{\varepsilon }(Q)=\Gamma _M(Q)\setminus B_{2\varepsilon (Q)}\cap (\partial \Omega ,4R_0)$. Then

$$\begin{aligned}{} & {} \sum _{Q_\alpha ^k\in J_j} \omega _0(Q_\alpha ^k)\int _{\hat{I}_\alpha ^k}Tu_1(Z)dZ = \underset{\underset{\text {disj. top cubes}}{Q_\alpha ^k\in J_j}}{\sum } \sum _{Q_\beta ^l\in J_j, Q_\beta ^l\subset Q_\alpha ^k} \omega _0(Q_\beta ^l)\int _{\hat{I}_\beta ^l}Tu_1(Z)dZ\\{} & {} \qquad \lesssim \underset{\underset{\text {disj. top cubes}}{Q_\alpha ^k\in J_j}}{\sum }\sum _{Q_\beta ^l\in J_j, Q_\beta ^l\subset Q_\alpha ^k} \omega _0((\tilde{O}_j\setminus O_{j+1})\cap Q_\beta ^l)\int _{\hat{I}_\beta ^l}Tu_1(Z)dZ\\{} & {} \qquad \lesssim \underset{\underset{\text {disj. top cubes}}{Q_\alpha ^k\in J_j}}{\sum } \sum _{Q_\beta ^l\in J_j, Q_\beta ^l\subset Q_\alpha ^k} \int _{(\tilde{O}_j\setminus O_{j+1})\cap Q_\beta ^l}\int _{\hat{I}_\beta ^l}Tu_1(Z)dZd\omega _0(P)\\{} & {} \qquad \lesssim \underset{\underset{\text {disj. top cubes}}{Q_\alpha ^k\in J_j}}{\sum } \sum _{Q_\beta ^l\in J_j, Q_\beta ^l\subset Q_\alpha ^k} \int _{(\tilde{O}_j\setminus O_{j+1})\cap Q_\alpha ^k}\int _{\hat{I}_\beta ^l}Tu_1(Z)dZd\omega _0(P)\\{} & {} \qquad \lesssim \underset{\underset{\text {disj. top cubes}}{Q_\alpha ^k\in J_j}}{\sum } \int _{(\tilde{O}_j\setminus O_{j+1})\cap Q_\alpha ^k}\sum _{Q_\beta ^l\in J_j, Q_\beta ^l\subset Q_\alpha ^k}\int _{\hat{I}_\beta ^l}Tu_1(Z)dZd\omega _0(P)\\{} & {} \qquad \lesssim \underset{\underset{\text {disj. top cubes}}{Q_\alpha ^k\in J_j}}{\sum } \int _{(\tilde{O}_j\setminus O_{j+1})\cap Q_\alpha ^k}\int _{S_M^\varepsilon (P)}Tu_1(Z)dZd\omega _0(P)\\{} & {} \qquad \le \int _{(\tilde{O}_j\setminus O_{j+1})}\int _{S_M^\varepsilon (P)}Tu_1(Z)dZd\omega _0(P)\\{} & {} \qquad \le \int _{(\tilde{O}_j\setminus O_{j+1})}T_\varepsilon u_1(P)^2d\omega _0(P). \end{aligned}$$

We put everything together to finally get the following estimate for (4.10):

$$\begin{aligned}{} & {} \int _{\Omega _0\setminus (\partial \Omega ,\varepsilon )} |\varepsilon ||G_0||\nabla F||\nabla u_1|dY \lesssim \frac{1}{\omega _0(\Delta _0)}\sum _j \varepsilon _0 \omega _0(O_j)^{1/2} \left( \int _{(\tilde{O}_j\setminus O_{j+1})}T_\varepsilon u_1^2d\omega _0 \right) ^{1/2} \\{} & {} \qquad \le \varepsilon _0\frac{1}{\omega _0(\Delta _0)}\sum _j 2^{j+1}\omega _0(O_j)^{1/2}\omega _0(\tilde{O}_j\setminus O_{j+1})^{1/2} \\{} & {} \qquad \le \varepsilon _0\frac{1}{\omega _0(\Delta _0)}\sum _j 2^{j+1}\omega _0(O_j)\\{} & {} \qquad \le \varepsilon _0\frac{1}{\omega _0(\Delta _0)}\int _{3\Delta _0} T_\varepsilon u_1 d\omega _0\\{} & {} \qquad = \varepsilon _0\frac{1}{\omega _0(\Delta _0)}\int _{3\Delta _0} \left( \int _{(\Gamma _M(P)\setminus B_\varepsilon (P))\cap (\partial \Omega ,4R_0)}|\nabla u_1(Z)|^2\delta (Z)^{2-n}dZ\right) ^{1/2} d\omega _0(P). \end{aligned}$$

Taking $\varepsilon \rightarrow 0$ finally yields

$$\begin{aligned} F_2^0(Z)=\int _{\Omega _0}|\varepsilon ||\nabla G_0||\nabla u_1|dY \lesssim \varepsilon _0\frac{1}{\omega _0(\Delta _0)}\int _{3\Delta _0} S_M u_1 \omega _0 \le M_{\omega _0}[S_M(u)](Q_0). \end{aligned}$$

Our next objective are the terms $F_2^j$ for $j\ge 1$. We split the region $R_j$ and write it as a union of two subregions:

$$\begin{aligned} R_j=(R_j\cap (\partial \Omega ,2^{j-6}\delta (X)))\cup (R_j\setminus (\partial \Omega ,2^{j-6}\delta (X))):= V_j \cup W_j. \end{aligned}$$

For $Y\in R_j$, we observe that $|A_{-1}-Y|\ge \delta (X)/4$ since $A_{-1}\in \overline{\Omega _{-1}}$. Now, by the Harnack’s inequality $G_0(Z,Y)\approx G_0(A_{-1},Y)$ where the implicit constants in the Harnack’s inequality are independent of the points Z and X. Using the boundary Hölder continuity of the nonnegative solution $G_0(\cdot , Y)$ in $\Omega _{j-2}$ in Proposition 2.20 we get that

$$\begin{aligned} G_0(Z,Y){} & {} \approx G_0(A_{-1},Y)\le \sup _{\tilde{Z}\in T(\Omega _{-1})} G_0(\tilde{Z},Y) \lesssim \left( \frac{2^{-2}\delta (X)}{2^{j-3}\delta (X)}\right) ^\beta G_0(A_{j-2}, Y)\nonumber \\{} & {} \lesssim 2^{-j\alpha }G_0(A_{j-2}, Y). \end{aligned}$$

(4.14)

Assume now that $Y\in V_j$. We proceed similarly to the above case for $\Omega _0$. We have a bound analogous to (4.10), namely that

Instead of (4.12) we have a similar argument. By Caccioppoli’s inequality we have

We can cover $\frac{3}{2}\Delta _j\setminus \frac{3}{2}\Delta _{j-2}$ with at most N balls $B(Q_i,2^{j-5}\delta (X))$ such that $|Q_i-Q_j|<2^{j-5}\delta (X)$, $Q_i\in \frac{3}{2}\Delta _j\setminus \frac{3}{2}\Delta _{j-2}$ and $I_\alpha ^k\subset \bigcup _i B(Q_i,2^{j-5}\delta (X))$ when $Q_\alpha ^k\subset \frac{3}{2}\Delta _j\setminus \frac{3}{2}\Delta _{j-2}$. Note that N is again independent of X and $\delta (X)$. Let $\tilde{A}_i=A(Q_i, 2^{j-5}\delta (X))$ and since $\text {dist}(I_\alpha ^k,A_{j-2})\ge 2^{j-3}-2^{-3}-2^{j-5}\ge 2^{j-5}\delta (X)$ the comparison principle applies and gives us for $Y\in B(Q_i,2^{j-5}\delta (X))$:

$$\begin{aligned} \frac{|G_0(A_{j-2},Y)|}{|G_0(Y)|}\approx \frac{|G_0(A_{j-2},\tilde{A}_i)|}{|G_0(\tilde{A}_i)|}. \end{aligned}$$

Since $\delta (\tilde{A}_i)=2^{j-5}\delta (X)$ we can use Harnack to obtain

$$\begin{aligned} \frac{|G_0(A_{j-2},\tilde{A}_i)|}{|G_0(\tilde{A}_i)|}\approx \frac{|G_0(A_{j-2},A_j)|}{|G_0(A_j)|}. \end{aligned}$$

Hence by Proposition 2.25 we have that

$$\begin{aligned} \frac{|G_0(A_{j-2},A_j)|}{|G_0(A_j)|} \lesssim \frac{\omega ^{A_{j}}_0(\Delta _{j-2})}{\omega _0(\Delta _j)} \lesssim \frac{1}{\omega _0(\Delta _j)}. \end{aligned}$$

Combined with the above estimate with (4.14) we therefore have

$$\begin{aligned} \frac{G_0(Z,Y)}{G_0(Y)}\approx 2^{-j\beta }\frac{G_0(A_{j-2},Y)}{G_0(Y)}\lesssim 2^{-j\beta }\frac{1}{\omega _0(\Delta _j)}, \end{aligned}$$

and hence

We again apply the stopping time argument but this time with the sets $O_j=\{P\in \frac{3}{2}\Delta _j$ $\setminus \frac{3}{2}\Delta _{j-2}; T_\varepsilon u_1(P)>2^j\}$. This leads to the estimate

$$\begin{aligned}{} & {} \int _{V_j\setminus (\partial \Omega ,\varepsilon )}|\varepsilon (Y)||\nabla _Y G_0(Z,Y)||\nabla u_1(Y)|dY\\{} & {} \qquad \lesssim 2^{-j\alpha }\varepsilon _0\frac{1}{\omega _0(\Delta _j)}\int _{\frac{3}{2}\Delta _j\setminus \frac{3}{2}\Delta _{j-2}}\left( \int _{D_{M,\varepsilon ,R_0}}|\nabla u_1(Z)|^2\delta (Z)^{2-n}dZ\right) ^{1/2}d\omega _0(P), \end{aligned}$$

where $D_{M,\varepsilon ,R_0} = (\Gamma _M(P)\setminus B_\varepsilon (P))\cap (\partial \Omega ,4R_0)$. Again, taking $\varepsilon \rightarrow 0$ yields:

$$\begin{aligned} \int _{V_j}|\varepsilon ||\nabla _Y G_0||\nabla u_1|dY\lesssim & {} \varepsilon _0\frac{1}{\omega _0(\Delta _j)}\int _{\frac{3}{2}\Delta _j\setminus \frac{3}{2}\Delta _{j-2}} S_M u_1(P)d\omega _0(P) \\\le & {} M_{\omega _0}[S_M(u)](Q_0). \end{aligned}$$

This takes care of the subregion $V_j$. When $Y\in W_j$ we cover $W_j$ by at most N balls $B_{jl}$ $:= B(X^j_l, 2^{j-9}\delta (X))$ with $X_l^j\in W_j$. Again, N is independent of j. Using the comparison principle for the Green’s function, the doubling of the elliptic measure and the fact that $G_0(A_{j-2})\approx G_0(Y)$ using Harnack we have

$$\begin{aligned} G_0(A_{j-2}, Y)= & {} \frac{G_0(A_{j-2}, Y)}{G_0(A_{j-2})}G_0(Y) = \frac{G_0^*(Y, A_{j-2})}{G_0(A_{j-2})}G_0(Y)\\\lesssim & {} \frac{{\omega ^*}^Y_0(\Delta (X^*, 2^{j-3}\delta (X)))}{\omega _0(\Delta (X^*, 2^{j-3}\delta (X)))}G_0(Y) \lesssim \frac{1}{\omega _0(\Delta _j)}G_0(Y). \end{aligned}$$

Since (4.14) still applies we therefore have $G_0(Z,Y)\lesssim 2^{-j\alpha }\frac{1}{\omega _0(\Delta _j)}G_0(Y)$. By Proposition 2.19 we have $G_0(Y)\lesssim G_0(A_{j+1})$ and therefore

For every $Y\in B_{jl}$ we have estimates $\delta (Y)\ge (2^{j-6}-2^{j-8})\delta (X)\ge 2^{j-7}\delta (X)$ and $|Y-X^*|\le (2^{j}+2^{j-8})\delta (X)\le 2^{j+1}\delta (X)$ therefore have for $\bar{M}=2^8$

$$\begin{aligned} B_{jl}\subset \tilde{B}_{jl}\subset \Gamma _{\bar{M}}(X^*)\subset \Gamma _{\bar{M}}(Q_0), \end{aligned}$$

where $\tilde{B}_{jl}=B(X_l^j,2^{j-8}\delta (X))$ is an enlarged ball. Since the finite ball covers $(B_{jl})$ and $\tilde{B}_{jl}$ can be chosen to have finite overlap. This implies an estimate similar to (4.10), namely that

By Proposition 2.12 we get a statement analogous to (4.11):

Next we consider term containing the function $\varepsilon$. We see that $|B_{jl}|\approx \delta (Y)^n\approx (2^{j}\delta (X))^n$ and $B_{jl}\subset B(Y,\delta (Y)/2)$ for $Y\in B_{jl}$. Hence by the Harnack $G_0(Y)\approx G_0(A_{j+1})$ and therefore

and therefore

Next, by the comparison principle, Proposition 2.25, Cauchy–Schwarz inequality, and the assumptions of Theorem 3.1 we have

Combining together the estimates for the subregions $V_j$ and $W_j$ and summing over j’s we get

$$\begin{aligned} \sum _{j=1}^N |F_2^j(Z)|\lesssim & {} \sum _{j=1}^N \int _{R_j}|\varepsilon (Y)||\nabla _Y G(Z,Y)||\nabla u_1(Y)|dY\\\lesssim & {} \sum _{j=1}^N 2^{-j\beta }\varepsilon _0 M_{\omega _0}[S_{\bar{M}}(u_1)](Q_0)\lesssim \varepsilon _0 M_{\omega _0}[S_{\bar{M}}(u_1)](Q_0). \end{aligned}$$

We still have one more term J to tackle. First, we observe that

$$\begin{aligned} (\partial \Omega ,4R_0)\setminus (B(X)\cup B(X^*,2^{15}R_0))\subset \underset{\underset{k_0\le k}{Q_\alpha ^k\subset \partial \Omega \setminus \Delta _{2^{14}R_0}}}{\bigcup } I_\alpha ^k. \end{aligned}$$

To see this consider any $Y\in (\partial \Omega ,4R_0)\setminus (B(X)\cup B(X^*,2^{15}R_0))$. Since the collection $\{I_\alpha ^k\}_{\alpha ,k}$ covers $(\partial \Omega ,4R_0)$ we have that $Y\in I_\alpha ^k$. We know that that there exists $P_\alpha ^k\in Q_\alpha ^k$ such that $8/\lambda \le |P_\alpha ^k-Y|8^k\le 8\lambda$. For such $P\in I_\alpha ^k$ we have

$$\begin{aligned} |P-X^*|\ge & {} |Y-X^*|-|P-P_\alpha ^k|-|P_\alpha ^k-Y| \ge 2^{15}R_0- C_08^{-k}-\lambda 8^{-k+1}\\\ge & {} 2^{15}R_0-8R_0-8R_0\ge 2^{14}R_0, \end{aligned}$$

and hence $Q_\alpha ^k\subset \partial \Omega \setminus \Delta _{2^{14}R_0}$. We again start with an estimate analogous to (4.10):

Since $Y\in I_\alpha ^k$ is far away from Z and 0 we can use Harnack’s inequality to conclude that $G_0(Z,Y)\approx G_0(Y)$, where the implicit constants are independent of Y. Again, using the Caccioppoli’s inequality, Proposition 2.25 and the fact that $\omega _0$ is doubling we have as a replacement of (4.12):

Next step is again the stopping time argument analogous to the case $F_2^0$ with sets $O_j=\{P\in \partial \Omega \setminus \Delta _{2^{14}R_0}; T_\varepsilon u_1(P)>2^j\}$. This gives us the final estimate of this section:

$$\begin{aligned} J= & {} \int _{(\partial \Omega ,4R_0)\setminus (B(X)\cup B(X^*,2^{15}R_0))} |\varepsilon (Y) ||\nabla _{Y} G_0(Z,Y)|| \nabla u_1(Y)| dY\\\lesssim & {} \varepsilon _0\int _{\partial \Omega \setminus \Delta _{2^{13}R_0}}S_M(u_1)dP \lesssim \varepsilon _0\frac{1}{\omega _0(\partial \Omega )}\int _{\partial \Omega }S_M(u_1)dP\\\lesssim & {} \varepsilon _0 M_{\omega _0}[S_M(u_1)](Q_0). \end{aligned}$$

5 Proof of Lemma 3.4

To prove Lemma 3.4 we need establish a “good-$\lambda$” inequality. To shorten our notation let

$$\begin{aligned} h[F,u_1] := N_{\hat{M}}[F]S_{\hat{M}}[F] + N_{\hat{M}}[F]S_{\hat{M}}[u_1] + \tilde{N}_{\hat{M}}[u_0]S_{\hat{M}}[u_1], \quad \hat{M}:=8\bar{M}. \end{aligned}$$

Lemma 5.1

There exists $0<\gamma <1$ such that for all $\lambda >0$

$$\begin{aligned} \omega _0 \left( \left\{ S_{\bar{M}}[F]>2\lambda , \; h[F,u_1]\le (\lambda \gamma )^2 \right\} \right) \lesssim \gamma ^2\omega _0 \left( \{S_{\bar{M}}[F]>\lambda \} \right) . \end{aligned}$$

Also, because $\omega _0\in A_\infty (d\sigma )$ a similar “good-$\lambda$” inequality holds for $\sigma$ as well:

Corollary 5.2

There exists $0<\eta <1$, $C>0$ and $0<\gamma <1$ such that for all $\lambda >0$

$$\begin{aligned} \sigma \left( \left\{ S_{\bar{M}}[F]>2\lambda , \; h[F,u_1]\le (\lambda \gamma )^2 \right\} \right) \lesssim \gamma ^\eta \sigma \left( \{S_{\bar{M}}[F]>\lambda \} \right) . \end{aligned}$$

Proof

Consider q for which $\omega _0\in A_q(d\sigma )$. Then

$$\begin{aligned} \frac{\sigma (E)}{\sigma (\Delta )} \lesssim \bigg ( \frac{\omega _0(E)}{\omega _0(\Delta )} \bigg )^{1/q}, \quad E \subset \Delta \subset \partial \Omega , \quad \Delta \text { cube}. \end{aligned}$$

Next take a Whitney decomposition of $\{S_{\bar{M}}[F]>\lambda \} = \bigcup _j \Delta _j$, where $\Delta _j \subset \partial \Omega$ are cubes, and set

$$\begin{aligned} E_j :=\Delta _j\cap \left\{ S_{\bar{M}}[F]>2\lambda , \; h[F,u_1]\le (\lambda \gamma )^2 \right\} . \end{aligned}$$

Then

$$\begin{aligned} \sigma (E_j)= & {} \sigma (\Delta _j)\frac{\sigma (E_j )}{\sigma (\Delta _j)} \lesssim \sigma (\Delta _j)\left( \frac{\omega _0(E_j )}{\omega _0(\Delta _j)}\right) ^{1/q} \lesssim \sigma (\Delta _j) \left( \frac{\gamma \omega _0(\Delta _j)}{\omega _0(\Delta _j)}\right) ^{1/q}\\\lesssim & {} \gamma ^{1/q} \sigma (\Delta _j). \end{aligned}$$

This proves our corollary.$\square$

Lemma 3.4 is a consequence of the following lemma.

Lemma 5.3

$$\begin{aligned} \int _{\partial \Omega }S_{\bar{M}}[F]^2d\omega _0\lesssim \int _{\partial \Omega }f^2d\omega _0+\int _{\partial \Omega }N_{\alpha }[F]^2d\omega _0. \end{aligned}$$

(5.4)

Moreover if $\omega _0\in B_p(d\sigma )$ we have

$$\begin{aligned} \int _{\partial \Omega }S_{\bar{M}}[F]^qd\sigma \lesssim \int _{\partial \Omega }f^qd\sigma +\int _{\partial \Omega }N_{\alpha }[F]^qd\sigma . \end{aligned}$$

(5.5)

Proof

We take $\mu \in \{\sigma ,\omega _0\}$ since the proof works analogously for both measures. The “good-$\lambda$-inequality” of Lemma  5.1 or Corollary 5.2 implies that

$$\begin{aligned} \int _{\partial \Omega }S_{\bar{M}}[F]^qd\mu= & {} q2^{q-1}\int _0^\infty \lambda ^{q-1}\mu (\{S_{\bar{M}}[F]>2\lambda \})d\lambda \\\lesssim & {} \int _0^\infty \lambda ^{q-1}\mu \left( \left\{ S_{\bar{M}}[F]>2\lambda , \; h[F,u_1]\le (\lambda \gamma )^2 \right\} \right) d\lambda \\{} & {} +\int _0^\infty \lambda ^{q-1}\mu (\{N_{\hat{M}}[F]S_{\hat{M}}[F]> (\lambda \gamma )^2\})d\lambda \\{} & {} +\int _0^\infty \lambda ^{q-1}\mu (\{N_{\hat{M}}[F]S_{\hat{M}}[u_1]> (\lambda \gamma )^2\})d\lambda \\{} & {} +\int _0^\infty \lambda ^{q-1}\mu (\{\tilde{N}_{\hat{M}}[u_0]S_{\hat{M}}[u_1]> (\lambda \gamma )^2\})d\lambda \\\le & {} \gamma ^\eta \int _{\partial \Omega }S_{\hat{M}}[F]^q d\mu +C_\gamma \left( \int _{\partial \Omega }(S_{\hat{M}}[F]N_{\hat{M}}[F])^{q/2}d\mu \right. \\{} & {} \left. +\int _{\partial \Omega }(N_{\hat{M}}[F]S_{\hat{M}}[u_1])^{q/2}d\mu + \int _{\partial \Omega }(\tilde{N}_{\hat{M}}[u_0]S_{\hat{M}}[u_1])^{q/2}d\mu \right) . \end{aligned}$$

Because $\Vert S_{\bar{M}}[F]\Vert _{L^q(d\mu )}\approx \Vert S_{\hat{M}}[F]\Vert _{L^q(d\mu )}$ thanks to Proposition 2.35, we choose $\gamma$ sufficiently small so that the first term of the last line can be absorbed by the left-hand side. Next,

$$\begin{aligned} \int _{\partial \Omega }(S_{\hat{M}}[F]N_{\hat{M}}[F])^{q/2}d\mu \le \rho \int _{\partial \Omega }S_{\bar{M}}[F]^qd\mu + C_\rho \int _{\partial \Omega }N_{\hat{M}}[F]^q d\mu . \end{aligned}$$

Hence again for a sufficiently small $\rho$ the square function term can be hidden on the left-hand side. We treat the other terms similarly, using the fact that $S_{\hat{M}}[u_1] \lesssim S_{\hat{M}}[F] + S_{\hat{M}}[u_0]$, and then apply (2.33) to obtain

$$\begin{aligned} \int _{\partial \Omega }S_{\bar{M}}[F]^qd\mu \lesssim \int _{\partial \Omega }\tilde{N}_{\hat{M}}[u_0]^qd\mu + \int _{\partial \Omega }N_{\hat{M}}[F]^qd\mu + \int _{\partial \Omega }S_{\hat{M}}[u_0]^qd\mu . \end{aligned}$$

Finally, note that $\omega _0\in B_p(\mu )$ which implies

$$\begin{aligned} \Vert S_{\hat{M}}[u_0]\Vert _{L^q(d\mu )} \approx \Vert \tilde{N}_{\hat{M}}[u_0]\Vert _{L^q(d\mu )} \lesssim \Vert f\Vert _{L^q(d\mu )}, \end{aligned}$$

therefore with the help of Lemma 2.31 we have

$$\begin{aligned} \int _{\partial \Omega }S_{\hat{M}}[F]^qd\mu \lesssim \int _{\partial \Omega }f^qd\mu +\int _{\partial \Omega }N_{\hat{M}}[F]^qd\mu \lesssim \int _{\partial \Omega }f^qd\mu +\int _{\partial \Omega }N_{\alpha }[F]^qd\mu . \end{aligned}$$

This means that (5.5) and (5.4) holds.$\square$

It remains to establish Lemma 5.1.

5.1 Proof of Lemma 5.1

Consider a decomposition of $\{S_{\bar{M}}[F]>\lambda \}$ into a union of Whitney balls $\Delta _j$. We set

$$\begin{aligned} E_j :=\Delta _j\cap \left\{ \begin{matrix}S_{\bar{M}}[F]>2\lambda \\ N_{\hat{M}}[F]S_{\hat{M}}(F), N_{\hat{M}}[F]S_{\hat{M}}(u_1), \tilde{N}_{\hat{M}}[u_0]S_{\hat{M}}[u_1]\le (\lambda \gamma )^2 \end{matrix}\right\} \end{aligned}$$

and in what follows we drop the subscript j. By Lemma 1 of [6] we know that for every $\tau >0$ there exists a $\gamma >0$ such that for the truncated square function

$$\begin{aligned} S_{\tau r}[F]^2(Q) := \int _{\Gamma _{\bar{M}}^{\tau r}(Q)} |\nabla F(X)|^2\delta (X)^{2-n}dX>\frac{\lambda ^2}{4} \end{aligned}$$

holds for all points $Q\in E$, where $\Gamma _{\bar{M}}^{\tau r}(Q):= \Gamma _{\bar{M}}(Q)\cap B(Q,\tau r)$. Let $\tilde{\Omega }=\bigcup _{Q\in E}\Gamma _{\bar{M}}^{\tau r}$ be a sawtooth region. We would like to define a partition of unity on it. Recall from Section 2.7 the family of balls $B(X_l,\lambda 8^{-k-3})_{1\le l\le N}$ covering $I_\alpha ^k$ and denote their center points by $X^{k,l}_\alpha$. We claim the existence of a family $(\eta ^{k,l}_\alpha )_{k,l,\alpha }$ with the following properties

• 1. $\eta _\alpha ^{k,l}\in C_0^\infty (\tilde{I}_\alpha ^k)$,

• 2. $0\le \eta ^{k,l}_\alpha \le 1$,

• 3. $\eta ^{k,l}_\alpha \equiv 1$ on $B(X_{\alpha }^{k,l},\lambda 8^{-k-3})$ and $\eta ^{k,l}_\alpha \equiv 0$ outside of $B(X_{\alpha }^{k,l},2\lambda 8^{-k-3})$,

• 4. $\Vert \nabla \eta ^{k,l}_\alpha \Vert _{L^\infty }\approx \frac{1}{\text {diam}(Q_\alpha ^k)}$,

• 5.
  $$\begin{aligned} \sum _{\alpha ,k,l}\eta _\alpha ^{k,l}\equiv 1\quad \text {on }~ \Gamma _{\bar{M}}^{\tau r}(Q) \qquad \text {and}\qquad \sum _{\alpha ,k,l}\eta _\alpha ^{k,l}\equiv 0 \quad \text {on }~\Omega \setminus \Gamma ^{\tau r}_{8\bar{M}}(Q). \end{aligned}$$

Let ${\mathcal {D}}_k(Q):=\{I_\alpha ^k|I_\alpha ^k\cap \Gamma _{\bar{M}}^{\tau r}(Q)\ne \emptyset \}$, ${\mathcal {D}}(Q)=\bigcup _k {\mathcal {D}}_k(Q)$, where we let $k_0$ be the scale from which on ${\mathcal {D}}_k(Q)=\emptyset$ for all $k\ge k_0$. We can observe that for the choice $\hat{M}:=8\bar{M}$ and for all $I_\alpha ^k\in {\mathcal {D}}(Q)$ we have $\hat{I}_\alpha ^k\subset \Gamma _{\hat{M}}(Q)$. Therefore

$$\begin{aligned} \omega _0(E)\lesssim & {} \frac{1}{\lambda ^2}\int _E S_{\tau r}[F]^2d\omega _0 = \frac{1}{\lambda ^2}\int _E\int _{\tilde{\Omega }}|\nabla F|^2\delta ^{2-n}\chi _{\Gamma _{\bar{M}}^{\tau r}(Q)}dXd\omega (Q)\\= & {} \frac{1}{\lambda ^2}\int _{\tilde{\Omega }}|\nabla F|^2\delta ^{2-n}\left( \int _E\chi _{\Gamma _{\bar{M}}^{\tau r}(Q)}d\omega (Q)\right) dX\\\lesssim & {} \frac{1}{\lambda ^2}\int _{\tilde{\Omega }}|\nabla F|^2\delta ^{2-n}\omega _0(\Delta (X^*,\delta (X)))dX\\\lesssim & {} \frac{1}{\lambda ^2}\int _{\tilde{\Omega }}|\nabla F|^2G_0dX. \end{aligned}$$

In the last line we have used the comparison principle, Proposition 2.25 and writing $G_0(X)=G(0,X)$. Continuing our estimate we have

$$\begin{aligned} \frac{1}{\lambda ^2}\int _{\tilde{\Omega }}|\nabla F|^2G_0dX\approx & {} \frac{1}{\lambda ^2}\int _E\int _{\Gamma _{\bar{M}}^{\tau r}(Q)}\delta ^{1-n}|\nabla F|^2G_0dXd\sigma (Q)\\\le & {} \frac{1}{\lambda ^2}\int _E\int _{\Gamma _{8\bar{M}}^{\tau r}(Q)}\delta ^{1-n}|\nabla F|^2 \left( G_0 \underset{\underset{I^k_\alpha \in {\mathcal {D}}(Q)}{k,l,\alpha }}{\sum } \eta ^{k,l}_\beta \right) dXd\sigma (Q)\\\lesssim & {} \frac{1}{\lambda ^2}\int _E \underset{\underset{I^k_\alpha \in {\mathcal {D}}(Q)}{k,l,\alpha }}{\sum } \int _{\tilde{I}_\alpha ^k}\delta (X)^{1-n}|\nabla F|^2 \left( G_0\eta ^{k,l}_\alpha \right) dXd\sigma (Q)\\\lesssim & {} \frac{1}{\lambda ^2}\int _E \underset{\underset{I^k_\alpha \in {\mathcal {D}}(Q)}{k,l,\alpha }}{\sum } \text {diam}(Q_\alpha ^k)^{1-n}\int _{\tilde{I}_\alpha ^k}|\nabla F|^2 \left( G_0\eta ^{k,l}_\alpha \right) dXd\sigma (Q)\\\lesssim & {} \frac{1}{\lambda ^2}\int _E \underset{\underset{I^k_\alpha \in {\mathcal {D}}(Q)}{k,l,\alpha }}{\sum } \text {diam}(Q_\alpha ^k)^{1-n}\int _{\tilde{I}_\alpha ^k}A_0\nabla F\cdot \nabla F \left( G_0\eta ^{k,l}_\alpha \right) dXd\sigma (Q). \end{aligned}$$

In the penultimate line we have used the fact that $\delta (X)\approx \text {diam}(Q_\alpha ^k)$. Consider some fixed k, l, $\alpha$. Since $G_0\eta ^{k,l}_\alpha , FG_0\eta ^{k,l}_\alpha \in W^{1,2}_0(\tilde{I}_\alpha ^{k})$ we have

$$\begin{aligned} \int _{\tilde{I}_\alpha ^k}A_0\nabla F \cdot \nabla F (G_0\eta ^{k,l}_\alpha )= & {} \int _{\tilde{I}_\alpha ^k}\text {div}(A_0\nabla (F^2)) G_0\eta ^{k,l}_\alpha -F\text {div}(A_0\nabla u_0) G_0\eta ^{k,l}_\alpha \\{} & {} +F\text {div}(A_1\nabla u_1) G_0\eta ^{k,l}_\alpha +\text {div}(\varepsilon \nabla u_1)FG_0\eta ^{k,l}_\alpha \\= & {} \int _{\tilde{I}_\alpha ^k}\text {div}(A_0\nabla (F^2)) G_0\eta ^{k,l}_\alpha + \int _{\tilde{I}_\alpha ^k}\text {div}(\varepsilon \nabla u_1)FG_0\eta ^{k,l}_\alpha , \end{aligned}$$

and therefore

$$\begin{aligned}{} & {} \text {diam}(Q_\alpha ^k)^{1-n}\int _{\tilde{I}_\alpha ^k}A_0\nabla F \cdot \nabla F (G_0\eta ^{m,l}_\beta )\\{} & {} \quad =\text {diam}(Q_\alpha ^k)^{1-n}\int _{\tilde{I}_\alpha ^k}\text {div}(A_0\nabla (F^2)) G_0\eta ^{k,l}_\alpha +\text {diam}(Q_\alpha ^k)^{1-n}\int _{\tilde{I}_\alpha ^k}\text {div}(\varepsilon \nabla u_1)FG_0\eta _\alpha ^{k,l}\\{} & {} \quad =:I^{k,l,\alpha }+II^{k,l,\alpha }. \end{aligned}$$

The term $I^{k,l,\alpha }$ we handle using integration by parts

$$\begin{aligned} |I^{k,l,\alpha }|= & {} \left| \text {diam}(Q_\alpha ^k)^{1-n}\int _{\tilde{I}_\alpha ^k}\text {div}(A_0\nabla (F^2)) G_0\eta ^{k,l}_\alpha \right| \\= & {} \text {diam}(Q_\alpha ^k)^{1-n}\left| \int _{\tilde{I}_\alpha ^k}A_0\nabla (F^2) \nabla (G_0\eta ^{k,l}_\alpha ) \right| \\\le & {} \text {diam}(Q_\alpha ^k)^{1-n}N_{\hat{M}}[F](Q)\left| \int _{\tilde{I}_\alpha ^k}A_0\nabla F \nabla (G_0\eta ^{k,l}_\alpha ) \right| . \end{aligned}$$

By (2.7) we may assume that $(A_0^a)_{\tilde{I_\alpha ^k}}=0$ and therefore

We use the fact that $\Vert \nabla \eta ^{k,l}_\alpha \Vert _{L^\infty }\approx \frac{1}{\text {diam}(Q_\alpha ^k)}$, and apply Propositions 2.13 and 2.25:

(5.6)

The definition of F and Proposition 2.12 then give us

Finally, after putting all terms together we have

$$\begin{aligned} |I^{k,l,\alpha }|\lesssim N_{\hat{M}}[F](Q)M[k](Q) \left( \left( \int _{\hat{I}_\alpha ^k}|\nabla F|^{2}\delta ^{2-n}\right) ^{1/2} + \left( \int _{\hat{I}_\alpha ^k}|\nabla u_1|^{2}\delta ^{2-n}\right) ^{1/2}\right) . \end{aligned}$$

Next, consider $II^{k,l,\alpha }$. Again, by integration by parts

First, we consider $II_1^{k,l,\alpha }$. For $X\in \tilde{I}_\alpha ^k$ by Propositions 2.25 and 2.26 we obtain

Hence we have

For the last term by Lemma 2.34 and Proposition 2.12 we have

In the previous calculation we have chosen $s>1$ (independent of k and $\alpha$) to be a small constant such that the enlargement $s\tilde{I}_\alpha ^k$ of $\tilde{I}_\alpha ^k$ is a sufficiently small enlargements, so that it is between the sets $\tilde{I}_\alpha ^k$ and $\hat{I}_\alpha ^k$; that is

$$\begin{aligned} \tilde{I}_\alpha ^k\subset s\tilde{I}_\alpha ^k\subset s^2\tilde{I}_\alpha ^k\subset \hat{I}_\alpha ^k. \end{aligned}$$

Since is bounded by Propositions 2.41 and 7.1 of [23] we then get

$$\begin{aligned} |II^{k,l,\alpha }_1|\lesssim (\tilde{N}_{\hat{M}}(F)+\tilde{N}_{\hat{M}}(u_0))(Q)M[k](Q)\left( \int _{\hat{I}_\alpha ^k}|\nabla u_1|^2\delta ^{2-n}\right) ^{1/2}. \end{aligned}$$

Next, we consider $II^{k,l,\alpha }_2$. We have

The term is again bounded, and using Proposition 2.12 and (5.6) we then have

$$\begin{aligned} |II^{k,l,\beta }_2|\lesssim N_{\hat{M}}[F](Q)M[k](Q)\left( \int _{\hat{I}_\alpha ^k}|\nabla u_1|^2\delta ^{2-n}\right) ^{1/2}. \end{aligned}$$

It remains to add up together all terms.

$$\begin{aligned}{} & {} \omega _0(E)\lesssim \frac{1}{\lambda ^2}\int _E \underset{\underset{I_\alpha ^k\in {\mathcal {D}}(Q)}{k,l,\alpha }}{\sum } I^{k,l,\alpha }+II^{k,l,\alpha }d\sigma (Q)\\{} & {} \lesssim \frac{1}{\lambda ^2}\int _E \Bigg [ \underset{\underset{I_\alpha ^k\in {\mathcal {D}}(Q)}{k,l,\alpha }}{\sum } N_{\hat{M}}[F](Q)M[k](Q)\left( \!\!\!\left( \int _{\hat{I}_\alpha ^k}\!\!|\nabla F|^{2}\delta ^{2-n} \right) ^{1/2} +\left( \int _{\hat{I}_\alpha ^k}|\nabla u_1|^{2}\delta ^{2-n} \right) ^{1/2}\right) \\{} & {} \quad +(N_{\hat{M}}[F])+\tilde{N}_{\hat{M}}[u_0]))(Q)M[k](Q)\left( \int _{\hat{I}_\alpha ^k}|\nabla u_1|^2\delta ^{2-n}\right) ^{1/2}\\{} & {} \quad +N_{\hat{M}}[F](Q)M[k](Q)\left( \int _{\hat{I}_\alpha ^k}|\nabla u_1|^2\delta ^{2-n}\right) ^{1/2} \Bigg ] d\sigma (Q) \\{} & {} \lesssim \frac{1}{\lambda ^2}\int _E M[k] \cdot \big [N_{\hat{M}}[F]S_{\hat{M}}(F)+N_{\hat{M}}[F]S_{\hat{M}}(u_1)+\tilde{N}_{\hat{M}}[u_0]S_{\hat{M}}(u_1)\big ]d\sigma (Q)\\{} & {} \lesssim \gamma ^2\int _E M[k](Q)d\sigma (Q). \end{aligned}$$

In the last line we used the properties of the set E. For the last step we use the fact that $k\in B_p(d\sigma )$, the Hölder’s inequality and boundedness of the maximal function.

Hence we have $\omega _0(E)\lesssim \gamma ^2\omega _0(\Delta )$, or more precisely $\omega _0(E_j)\lesssim \gamma ^2\omega _0(\Delta _j)$ as this is true for all j. Summing up in j gives us the desired good-$\lambda$ inquality.

6 Proof of Theorem 1.6

Most of the work to prove Theorem 1.6 is already done. Recall that we want to show that $\omega _1\in B_p(d\sigma )$ which is equivalent to

$$\begin{aligned} \Vert \tilde{N}_\alpha (u_1)\Vert _{L^q(\partial \Omega ,d\sigma )} \lesssim \Vert f\Vert _{L^q(\partial \Omega ,d\sigma )}\qquad \text{ for } ~\frac{1}{q} + \frac{1}{p} = 1. \end{aligned}$$

We assume that $\omega _0 \in B_p(d\sigma )$ which is equivalent to $\sigma \in A_{q}(d\omega )$. Using this, Lemmas 3.3 and 5.3 imply:

$$\begin{aligned} \!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\int _{\partial \Omega } \tilde{N}_{\alpha }[F]^q d\sigma\lesssim & {} \int _{\partial \Omega } \varepsilon _0^q M_{\omega _0}[S_{\bar{M}}u_1]^q d\sigma \\\lesssim & {} \varepsilon _0^q \int _{\partial \Omega } S_{\bar{M}}[u_1]^q d\sigma \\\lesssim & {} \varepsilon _0^q\int _{\partial \Omega } S_{\bar{M}}[F]^q d\sigma + \varepsilon _0^q \int _{\partial \Omega } S_{\bar{M}}[u_0]^q d\sigma \\\lesssim & {} \varepsilon _0^q \int _{\partial \Omega } S_{\bar{M}}[F]^q d\sigma + \int _{\partial \Omega } f^q d\sigma \\\lesssim & {} \varepsilon _0^q\int _{\partial \Omega } \tilde{N}_{\alpha }[F]^q d\sigma + \int _{\partial \Omega }\tilde{N}_{\alpha }[u_0]^qd\sigma + \int _{\partial \Omega } f^q d\sigma \\\lesssim & {} \varepsilon _0^q\int _{\partial \Omega } \tilde{N}_{\alpha }[F]^q d\sigma + \int _{\partial \Omega } f^q d\sigma . \end{aligned}$$

By Lemma 2.31, and with $\varepsilon _0$ sufficiently small, we can hide the first term of the right-hand side by moving it to the left-hand side. Hence

$$\begin{aligned} \Vert \tilde{N}_{\alpha }[F] \Vert _{L^q(d\sigma )} \lesssim \Vert f \Vert _{L^q(d\sigma )}. \end{aligned}$$

Moreover, we also have $\Vert \tilde{N}_{\alpha }[u_0] \Vert _{L^q(d\sigma )} \lesssim \Vert f \Vert _{L^q(d\sigma )}$ because $\omega _0\in B_p(d\sigma )$. Thus

$$\begin{aligned} \int _{\partial \Omega } \tilde{N}_{\alpha }[u_1]^q d\sigma\lesssim & {} \int _{\partial \Omega } \tilde{N}_{\alpha }[F]^q d\sigma + \int _{\partial \Omega } \tilde{N}_{\alpha }[u_0]^q d\sigma \lesssim \int _{\partial \Omega } \tilde{N}_{\alpha }[F]^q d\sigma + \int _{\partial \Omega } f^q d\sigma \\\lesssim & {} \int _{\partial \Omega } f^q d\sigma . \end{aligned}$$

From this $\omega _1 \in B_p(d\sigma )$.

7 Operators with Coefficients Satisfying Carleson Condition

In this section $\Omega$ will be a bounded Lipschitz domain with Lipschitz constant K. We consider the operator $L=\text {div}(A\nabla \cdot )$, where A is $\lambda _0$-elliptic with $\Vert A^a\Vert _{\text {BMO}(\Omega )} \le \Lambda _0$ and recall that

The aim of this section is to prove Theorems 1.7 and 1.9. But first we prove a similar slightly weaker result:

Theorem 7.1

Let $\Omega$ be a bounded Lipschitz domain with Lipschitz constant K and suppose that $\hat{A}$ is elliptic with BMO antisymmetric part. Moreover, suppose that the weak derivative of coefficients exists and consider

$$\begin{aligned} \hat{\alpha }^{\eta }(Z) := \delta (Z) \sup _{X\in B(Z,\eta \delta (Z))}|\nabla \hat{A}(X)|, \quad 0<\eta <1/2. \end{aligned}$$

• (i) If

  $$\begin{aligned} \Vert \hat{\alpha }^{\eta }(Z)^2\delta (Z)^{-1}dZ \Vert _{\mathcal {C}} < \infty \end{aligned}$$

  then the $L^p$ Dirichlet problem is solvable for some $1< p < \infty$.

• (ii) For each $1< p < \infty$, there exists an $\varepsilon = \varepsilon (p) > 0$, such that if

  $$\begin{aligned} \Vert \hat{\alpha }^{\eta }(Z)^2 \delta (Z)^{-1}dZ \Vert _{\mathcal {C}}< \varepsilon \quad \text {and}\quad K < \varepsilon , \end{aligned}$$

  then the $L^p$ Dirichlet problem is solvable.

Statement (ii) follows from [9, Theorem 2.2]; though it is stated there for bounded matrices it holds in our case as well. To prove (i) we apply the following theorem (see [10, Theorem 1.3] or [20, Theorem 4.1]):

Theorem 7.2

If

$$\begin{aligned} \Vert |\nabla u|^2 \delta (X) dX \Vert _{\mathcal {C}} \lesssim \Vert f\Vert _{L^\infty (\partial \Omega )}^2, \quad \forall f \in C(\partial \Omega ), \end{aligned}$$

(7.3)

then $\omega \in A_{\infty }(d\sigma )$.

It remains to show (7.3). Let $\Delta \subset \partial \Omega$ be a boundary ball with $\text {diam}\,\Delta \le \gamma$, where $\gamma$ is taken small enough that $T(\Delta )$ lies above a Lipschitz graph. Note that by [7, Corollary 5.2] we have

$$\begin{aligned} \int _{T(\Delta )} |\nabla u(X)|^2\delta (X) dX \lesssim \int _{2\Delta } (|f|^2 + N_{\alpha }(u)^2)d\sigma . \end{aligned}$$

(Again although $\hat{A}$ is assumed to be bounded in [7] this assumption is not necessary this corollary to hold as it only uses ellipticity and boundedness of the symmetric part of the matrix). Thus $f \in C(\partial \Omega )$ and the maximum principle implies

$$\begin{aligned} \int _{T(\Delta )} |\nabla u(X)|^2\delta (X) dX \lesssim \Vert f\Vert _{L^\infty }^2 \sigma (2\Delta ) \lesssim \Vert f\Vert _{L^\infty }^2 \sigma (\Delta ). \end{aligned}$$

Dividing both sides by $\sigma (\Delta )$ and taking supremum over $\Delta$ yields (7.3).

7.1 Proofs of Theorems 1.7 and 1.9

In order to prove Theorems 1.7 and 1.9 we have the following strategy.

First we construct a matrix $\hat{A}$ from A. The objective is to improve regularity of coefficients in order to use Theorem  7.1 for $\hat{A}$. We then deduce solvability for the original matrix A by applying our perturbation results.

To begin with, let $B(X) = B(X,\delta (X)/2)$ and set

$$\begin{aligned} \hat{B}(X) := B\left( X,\tfrac{2}{5} \tfrac{\delta (X)}{2}\right) , \end{aligned}$$

so that

$$\begin{aligned} \bigcup _{X\in \hat{B}(Z)} \hat{B}(X) \subset B(Z). \end{aligned}$$

In order to apply Theorem 7.1 our matrix needs to be differentiable. Thus we define $\hat{A}$ from A using a mollification procedure.

Consider $\phi \in C_c^\infty (\frac{1}{5}\mathbb {B}^n)$ to be nonnegative with $\int _{\mathbb {R}^n} \phi = 1$, and $\phi _t(X) = t^{-n}\phi (X/t)$. Let $\delta (X)$ be a smooth version of the distance function and

$$\begin{aligned} \hat{A}(X) := (\phi _{\delta (X)} *A)(X). \end{aligned}$$

Clearly $\hat{A}(X)$ is differentiable with

$$\begin{aligned} \nabla \hat{A}(X)=\int _\Omega (A(Y)-b) \nabla _X \phi _{\delta (X)}(X-Y)dY \quad \text{ for } \text{ any } b \in \mathbb {R}^{n\times n}. \end{aligned}$$

(7.4)

If we can show that

$$\begin{aligned} \Vert \hat{\alpha }(Z)^2 \delta (Z)^{-1} dZ \Vert _{\mathcal {C}} \lesssim \Vert \alpha _r(Z)^2 \delta (Z)^{-1} dZ \Vert _{\mathcal {C}}, \end{aligned}$$

(7.5)

holds for $\hat{\alpha }:=\hat{\alpha }^{\frac{2}{5}}$ clearly Theorem 7.1 implies that:

Lemma 7.6

Let $\Omega$ be a bounded Lipschitz domain with Lipschitz constant $K>0$. Let $\alpha _r$ be defined like in (1.8) and let $\omega$ be the elliptic measure of the operator $L=\textrm{div}(\hat{A}\nabla \cdot )$. Then there exists $1<r=r(n,\lambda _0,\Lambda _0)<\infty$ such that

• (i) If

  $$\begin{aligned} \Vert \alpha _r(Z)^2 \delta (Z)^{-1} dZ \Vert _{\mathcal {C}} < \infty \end{aligned}$$

  then $\omega \in A_\infty (\sigma )$, i.e. the $L^p$ Dirichlet problem for $\hat{A}$ is solvable for some $1< p < \infty$.

• (ii) For every $1< p < \infty$ there exists an $\varepsilon = \varepsilon (p) > 0$, such that if

  $$\begin{aligned} \Vert \alpha _r(Z)^2 \delta (Z)^{-1} dZ \Vert _{\mathcal {C}}< \varepsilon \quad \text {and}\quad K < \varepsilon , \end{aligned}$$

  then $\omega \in B_p(\sigma )$, i.e., the $L^p$ Dirichlet problem for $\hat{A}$ is solvable.

To prove (7.5) it suffices to show that

$$\begin{aligned} \hat{\alpha }(Z) \lesssim \alpha _r(Z). \end{aligned}$$

Take $b = (A)_{B(Z)}$ in (7.4). Then

$$\begin{aligned} |\nabla \hat{A}(X)| \le \int _{\hat{B}(X)} |A(Y)-(A)_{B(Z)}| |\nabla \phi _{\delta (X)}(X-Y)|dY. \end{aligned}$$

Let us estimate the gradient term inside the integral.

$$\begin{aligned} \delta (X)^{n+1} |\nabla _X \phi _{\delta (X)}|\lesssim & {} |\nabla \delta (X)| \phi \left( \frac{X-Y}{\delta (X)}\right) + \left| \nabla \phi \left( \frac{X-Y}{\delta (X)}\right) \right| \left( |\nabla \delta (X)| \frac{|X-Y|}{\delta (X)} + 1 \right) \\\le & {} \Vert \phi \Vert _{L^\infty } + 2\Vert \nabla \phi \Vert _{L^\infty } \lesssim 1, \end{aligned}$$

since $|X-Y| \le \delta (X)$ and $|\nabla \delta | \le 1$. It follows that

$$\begin{aligned} |\nabla _X \phi _{\delta (X)}| \lesssim \delta (X)^{-(n+1)}. \end{aligned}$$

This implies that for any $X\in \hat{B}(Z)$ we have that

From this

$$\begin{aligned} \hat{\alpha }(Z) = \delta (Z) \sup _{X \in \hat{B}(Z)} |\nabla \hat{A}| \lesssim \alpha _r(Z), \end{aligned}$$

as desired.

It remains to apply our two perturbation results for $A_0 = \hat{A}$ and $A_1 = A$. Clearly $\hat{A}$ is $\lambda _0$-elliptic. Moreover, we can see that $\Vert \hat{A}\Vert _{\text {BMO}(\Omega )}\lesssim \Lambda _0$.

To see this we distinguish two cases. First, consider a ball $B\subset \Omega$ such that $B\not \subset \hat{B}(X)$ is true for all $X\in \Omega$. Then we can find a cover with balls $(\hat{B}(X_i))_{i}$ such that the balls $\hat{B}(X_i)$ have finite overlap, and $|\bigcup _i \hat{B}(X_i)|\lesssim |B|$. The constants in the last inequality are independent of B. By Lemma 2.1 of [18] we know that $|(A)_{\hat{B}(X)}-(A)_{B(Z)}|\lesssim \Lambda _0$ for all $X\in \hat{B}(Z)$. Hence

The second case is if $B\subset \hat{B}(X_1)$ for some $X_1\in \Omega$. Then we have

Thus we can conclude that

which implies $\Vert \hat{A}\Vert _{\text {BMO}(\Omega )}\lesssim \Lambda _0$. It follows that we indeed may apply our perturbation results.

Let

Our next objective is to show that

$$\begin{aligned} \Vert \beta _r(Z)^2 \delta ^{-1}(Z) dZ \Vert _{\mathcal {C}} \lesssim \Vert \alpha _r(Z)^2 \delta (Z)^{-1} dZ \Vert _{\mathcal {C}}. \end{aligned}$$

(7.7)

Assume for the moment this is indeed true. Then Lemma 7.6 and Theorem 1.5 imply Theorem 1.9. Similarly, Lemma 7.6 and Theorem 1.6 imply Theorem 1.7. Thus if we establish (7.7) we are done.

We start by observing that the following estimate holds:

The last term already has the required form. For the first term we see that