1 Introduction

The cooling of a wall by a convective flow is a fundamental engineering issue present in a multitude of instruments and machines [1]. Often practical designs are too complex to allow direct analytical modelling. Nevertheless fundamental approaches combining heat transfer laws with fluid mechanics help to grasp the underlying effects of parameters like Prandtl or Reynolds number. One of the most fundamental cases is the heat transfer from a flat plate to a passing flow which can be a free stream or a jet emanating from a wall bound nozzle.

The three flow cases flat plate, free jet and wall jet as sketched in Fig. 1 present a family of similar solutions based on Prandtl’s boundary layer equations. In [2] we have regrouped these solutions and shown experimentally that the laminar wall jet coincides perfectly with predicted velocity profiles. Other than in the flat plate boundary layer, where the leading edge fixes the origin of the coordinate system, the free jet and the wall jet have to deal with a virtual origin which moves with flow conditions. To account for this problem in the wall jet case we have included a factor C in the theory [2] which basically defines the virtual origin for otherwise measured or known flow parameters.

Fig. 1
figure 1

Three related flow cases featuring similarity solutions. Indicated velocity profiles and similarity coordinates, see Eq. 1

Full size image

Presently we extend the flow theory to the wall jet heat transfer in terms of a similarity solution for constant wall temperature. The real jet evolves from a gap flow which is strictly kept laminar (Re < 3000). The gap consists of an inner cylinder and a surrounding outer cylinder rendering possible a small ratio of gap width to cylinder diameter (order of 1:100). Such a design allows the plane wall assumption and avoids the flat plate problems in terms of edges and plate thickness.

The laminar parabolic profile exiting the gap at the mean velocity \(U_{\infty}\) develops into a boundary layer along a cylinder of uniform temperature above ambient room temperature. The virtual origin settles upstream of the gap mouth. A perfect laminar case can only be achieved at very low Reynolds numbers where natural and forced convection blend which is neither covered by the present theory nor the experiments. In realistic forced convection cases disturbances will occur at the outer side of the wall jet and enlarge in flow direction. (Visualizations to this effect are shown in [2]). The heat transfer is dominated by the laminar sublayer at the wall which is supposed to follow laminar theory. Thus far it seems a reasonable motivation to check whether the laminar wall jet solutions are capable of representing heat transfer data obtained from a benchmark experiment.

The paper uses the wall jet flow solution from [2] and, going from there, develops the heat transfer solution. In the experimental part the solution is specified to the given flow and boundary conditions. Finally, individual heat transfer rates in Watt in the temperature range 50 to 90 °C are plotted vs Reynolds number and compared with the theoretical predictions. The results are also shown in terms of Nusselt number.

2 The wall jet solution for the velocity

The transformation from the real coordinates y and x to the similarity coordinates η and x applies to all three cases flat plate, free jet and wall jet in the form

$$\eta =\frac{y}{g(x)}=\frac{y}{\left(\nu /U_{\infty}\right)^{1-m}x^{m}}$$
(1)

with m = 1/2 for the flat plate, m = 2/3 for the free jet and m = 3/4 for the wall jet [2]. The ordinary differential equation resulting from the boundary layer partial differential equations takes the general form

$$C\frac{2m-1}{m}f'^{2}+C\frac{1-m}{m}ff''+f'''=0$$
(2)

with the velocity components

$$u=\frac{C\nu }{\left(\frac{\nu }{U_{\infty }}\right)^{2-2m}mx^{2m-1}}f'\left(\eta \right)$$
(3)
$$\mathrm{v}=\frac{C\nu }{\left(\frac{\nu }{U_{\infty }}\right)^{1-m}mx^{m}}\left[m\eta f'-\left(1-m\right)f\right]$$
(4)

The constant C emerges in the derivation subject to the requirement of constant coefficients [2]. For the flat plate \(C=\textit{const}.=1/2\). It reflects that the leading edge is the origin of the coordinate system for any \(\nu /U_{\infty }\). In case of the free and the wall jet C is not universal. It means that the real source (normally a nozzle) cannot be identical with the virtual origin. Therefore C needs to be determined in an experimental situation in order to evaluate the final results for the boundary layer variables.

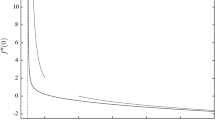
Other than in the flat plate case the wall jet allows analytical solutions for the streamfunction f, the velocity \(f'\) and its derivative \(f''\:\)[2]. They are

$$\begin{aligned} \eta \sqrt{C}=3\kappa &\left[\ln\frac{\sqrt{f\sqrt{C}\kappa +\sqrt{f\sqrt{C}\kappa }+1}}{1-\sqrt{f\sqrt{C}\kappa }}\right.\\ &\left. +\sqrt{3}\tan ^{-1}\frac{\sqrt{3}\sqrt{f\sqrt{C}\kappa }}{2+\sqrt{f\sqrt{C}\kappa }}\right] \end{aligned}$$
(5)
$$f'=\frac{2}{9}\sqrt{f\sqrt{C}}\left[\kappa ^{-3/2}-\left(\sqrt{f\sqrt{C}}\right)^{3}\right]$$
(6)
$$\begin{aligned} f''=&\,\sqrt{C}\left(\kappa ^{-3/2}\sqrt{f\sqrt{C}}-f^{2}C\right)\\ &\frac{2}{81}\left[\frac{1}{\kappa ^{3/2}\,\sqrt{f\sqrt{C}}}-4f\sqrt{C}\right] \end{aligned}$$
(7)

\(f'andf''\)are explicit in f while f is implicit in η. We show \(f\sqrt{C}\) and \(f'\) as function of \(\eta \sqrt{C}\) in Fig. 2. Notable features are the following. The velocity \(f'\) exhibits its maximum \(f'=1\) at

$$\eta _{\max }\sqrt{C}=1.972$$
(8)

where

$$f_{\max }\sqrt{C}=\sqrt{3/2}$$
(9)

\(f\sqrt{C}\) approaches a maximum for \(\eta \rightarrow \infty\)

$$f_{\infty }\sqrt{C}=\frac{1}{\kappa }=3.086$$
(10)
Fig. 2
figure 2

The analytical solutions of the wall jet stream function \(f\sqrt{C}\) and velocity f \('\)

Full size image

The derivative of \(f'\) at the wall takes the universal value

$$f''\left(\eta \sqrt{C}=0\right)=0.7256$$
(11)

For numerical calculations it is useful to fit \(f\sqrt{C}\) by some numerical expression of \(\overline{\eta }=\eta \sqrt{C}\) to allow \(fandf'\) to be written explicitly. It turns out that a polynomial of sixth order qualifies quite well up to \(\overline{\eta }=\eta \sqrt{C}=5.54\) where \(f\sqrt{C}\left(\eta \right)=3.0\) falling a bit short of the maximum.

$$\begin{aligned} f\sqrt{C}\left(\overline{\eta }\right)=&-0.0009921\overline{\eta }^{6}+0.017023\overline{\eta }^{5}\\ &-0.098441\overline{\eta }^{4}+0.164387\overline{\eta }^{3}\\ &+0.242910\overline{\eta }^{2}+0.030085\overline{\eta } \end{aligned}$$
(12)

3 The wall jet solution for the temperature

As described in [3] the transport equation of the temperature T (ignoring self-heating) is analog to the transport equation of momentum

$$u\frac{\partial T}{\partial x}+\mathrm{v}\frac{\partial T}{\partial y}=a\frac{\partial ^{2}T}{\partial y^{2}}$$
(13)

Inserting the flat plate solutions for the velocities the differential equation for the temperature at the flat plate comes to

$$T''+\frac{Pr}{2}fT'=0$$
(14)

the solution of which was given by Pohlhausen [3].

In the following steps we derive the equivalent equations for the wall jet. Equation 1 for m = 3/4 and its derivative read

$$\eta =\frac{y}{g\left(x\right)}=\frac{y}{\left(\nu /U_{\infty }\right)^{1/4}x^{3/4}}$$
(15)
$$\frac{\partial \eta }{\partial x}=-\frac{3\eta }{4x}$$
(16)

Observing that T is to be constant on \(\eta =\textit{const}.\) the partial derivatives amount to

$$\frac{\partial T}{\partial x}=\frac{\partial T}{\partial \xi }\frac{\partial \xi }{\partial x}+\frac{\partial T}{\partial \eta }\frac{\partial \eta }{\partial x}=-\frac{\partial T}{\partial \eta }\frac{3\eta }{4x}$$
(17a)
$$\frac{\partial T}{\partial y}=\frac{\partial T}{\partial \xi }\frac{\partial \xi }{\partial y}+\frac{\partial T}{\partial \eta }\frac{\partial \eta }{\partial y}=\frac{\partial T}{\partial \eta }\frac{1}{g}$$
(17b)
$$\frac{\partial ^{2}T}{\partial y^{2}}=\frac{1}{g^{2}}\frac{\partial ^{2}T}{\partial \eta ^{2}}$$
(17c)

and the velocities (Eqs. 3 and 4) yield

$$u=\frac{4\,C\nu }{3\left(\frac{\nu x}{U_{\infty }}\right)^{1/2}}f'\left(\eta \right)=\frac{4\,C\nu }{3g^{2}}x^{1/4}f'\left(\eta \right)$$
(18)
$$\mathrm{v}=\frac{\:C\nu }{\left(\frac{\nu x}{U_{\infty }}\right)^{1/4}x^{1/2}}\left[\eta f'-\frac{1}{3}f\right]=\frac{\:C\nu }{g\:}\left[\eta f'-\frac{1}{3}f\right]$$
(19)

Inserting everything into the differential equation (Eq. 13) leads to the final equation (Eq. 20)

$$-\frac{4\,C\nu x}{3\,g^{2}}f'\:T'\frac{3\eta }{4x}+\;\frac{\:C\nu }{g\:}\left[\eta f'-\frac{1}{3}f\right]\frac{T'}{g}=a\frac{T''}{g^{2}}$$
$$T''+C\frac{Pr}{3}fT'=0$$
$$T''+\sqrt{C}\frac{Pr}{3}f\sqrt{C}T'=0$$
$$\frac{d^{2}T}{d\left(\eta \sqrt{C}\right)^{2}}+\frac{Pr}{3}\left(f\sqrt{C}\right)\frac{dT}{d\left(\eta \sqrt{C}\right)}=0$$
(20)

We see that C acts as a stretching parameter of  η and that the equation deviates formally from the equation of the flat plate by the denominator 3 instead of 2.

In case of a heated wall the normalized temperature Θ

$$\Uptheta =\frac{T-T\infty }{Tw-T\infty }$$
(21)

serves to express the boundary conditions and Eq. 20 accordingly

$$\Uptheta =1\quad\mathrm{at}\quad\upeta =0$$
$$\Uptheta =0\quad\mathrm{at}\quad\upeta =\mathrm{\infty }$$
(22)
$$\frac{d^{2}\Uptheta }{d\left(\eta \sqrt{C}\right)^{2}}+\frac{Pr}{3}\left(f\sqrt{C}\right)\frac{d\Uptheta }{d\left(\eta \sqrt{C}\right)}=0$$
(23)

Inserting the solution for \(f\sqrt{C}\) of Eq. 12 we find numerically at \(\eta \sqrt{C}=0\) when e.g. Pr = 0.7

$$\left.\frac{d\Uptheta }{d\left(\eta \sqrt{C}\right)}\right| _{w}=-0.304$$
(24)

Figure 3 displays the wall gradient for Prandtl numbers from 0.6 to 7. A best fit to the data obeys

$$\left.\frac{d\Uptheta }{d\left(\eta \sqrt{C}\right)}\right| _{w}=-0.349Pr^{0.38}$$
(25)
Fig. 3
figure 3

The wall gradient of the normalized temperature vs distinct Prandtl numbers as numerically calculated from Eq. 23. The inserted expression represents the fitted curve

Full size image

For the specific heat flux \(\dot{q}\) at the wall (\(\upeta =0)\) we write with Fourier’s law

$$\begin{aligned} \dot{q}=&-\lambda \frac{\partial \Uptheta }{\partial y}\left(T_{w}-T_{\infty }\right)\\ =&-\lambda \left.\frac{\partial \Uptheta }{\partial \left(\eta \sqrt{C}\right)}\right| _{w}\frac{\left(T_{w}-T_{\infty }\right)\sqrt{C}}{\left(\nu /U_{\infty }\right)^{1/4}x^{3/4}} \end{aligned}$$
(26)

Here λ is the heat conductivity of air at the wall. The effect of C will be evaluated in context with experiments presented in the following.

4 Experiments

4.1 The experimental set-up

The set-up follows Fig. 4 with all measures given in mm. A blower feeds air into a plenum chamber at controllable flow rates (nozzle). After some homogenizing the air passes a circular gap of width s encompassing a solid cylinder made of PVC. At the gap’s exit this cylinder merges into a thin-walled aluminum cylinder which holds hot water up to the top where a PVC block serves as a lid. A digital thermometer and a rotating propeller shaft are fed through the lid. PVC and aluminum are chosen for their low and high heat conductivity, respectively. The water temperature is kept uniform by the propeller such that water temperature equals wall temperature (neglecting the gradient in the thin wall).

Fig. 4
figure 4

Experimental set-up. All measures in mm

Full size image

A series is run for a pre-set water temperature Tw0 at varying flow rates. The mean velocity \(U_{\infty }\) in the gap is calculated from the flow rate. The corresponding heat flux is determined through the cooling gradient  dTw∕dt at Tw0 multiplied by the product of the heat capacity of the water (and the aluminum).

The heat flux has to be corrected for losses at the top lid and the bottom. Using the lid assembly on an appropriate dewer (perfect insulation) the heat loss at the top is found separately. It runs from 5 Watts at 50 °C to 20 Watts at 90 °C with linear interpolation for the intermediate temperatures. The bottom loss is almost negligible between 1 and 3 Watts.

4.2 Determination of the cooling gradient at T w0

The experimental heat flux in Watt across the cylinder wall equals the heat loss in the water/aluminum system

$$\dot{Q}_{ex}=-K\frac{dT_{w}}{dt}$$
(27)

Here K stands for the combined heat content of water and aluminum. This gradient is needed at the pre-set temperature Tw0. It is obtained by recording the time elapsing for the temperature to drop in the interval \(T_{w0}\pm 1\,{^{\circ}}C\). The drop is linear for small times based on the following argument. Theory asks \(\dot{Q}_{th}\) to be proportional to the temperature difference

$$\dot{Q}_{th}=K_{1}\left(T_{w}-T_{\infty }\right)$$
(28)

where K1 models the overall pre-factor. Equating the two expressions yields the exponential decay function

$$\frac{T_{w}-T_{\infty }}{T_{w0}-T_{\infty }}=\exp \left(-\frac{K_{1}}{K}t\right)$$
(29)

For our experimental conditions the exponent stays very small for sufficiently small t. Therefore, the gradient at the wall approaches

$$\frac{dT_{w}}{dt}=-\left(T_{w0}-T_{\infty }\right)\frac{K_{1}}{K}\left(1-\frac{K_{1}}{K}t\right)$$
(30)

It means that the linear temperature drop that we see is basically the initial slope of an exponential decay function of diminishing argument.

4.3 Laminar gap flow

The experiment is operated in the laminar regime of the gap flow (and a bit further). In order to identify the transition we measure the maximal Pitot-pressure at the gap mouth against the flow rate as plotted in Fig. 5. Clearly, the Pitot pressure collapses where the laminar profile switches to a turbulent one. The associated critical Reynolds number is found at 2610 which is consistent with a reported upper limit of 3000 [4].

Fig. 5
figure 5

Laminar gap flow. Pitot pressure (Pa) and Reynolds number (based on laminar flow). Transition shows close to Re = 2610

Full size image

4.4 Adaptation of Eq. 26 to experimental conditions

We integrate the theoretical specific heat flux of Eq. 26 over the surface of the cylinder with circumference B and length L to give the absolute heat flux

$$\begin{aligned} \dot{Q}_{th}=&\, 4B\lambda \left(0.349Pr^{0.38}\right)\sqrt{C}\times\\ &\left(\frac{U_{\infty }L}{\nu }\right)^{\frac{1}{4}}\left(T_{w0}-T_{\infty }\right) \end{aligned}$$
(31)

It remains to deal with C. In [2] we suggested and demonstrated a straightforward way that includes the determination of the location of two velocity maxima in the flow field. Presently the method is too elaborate to be practicable. A more viable method is the following. From Eqs. (7 and 2.30) in [2] C can be extracted in the form

$$C=\frac{y_{\max }}{1.972}\frac{1}{{\nu U_{\infty }}^{1/2}}\left(\frac{3}{4}U_{\max }\right)^{3/2}$$
(32)

Generally Umax is the maximal velocity at any location (x,ymax). Assuming that the parabolic profile at the gap’s mouth approximates the similarity profile (see Fig. 6) we identify Umax with \(\frac{3}{2}\:U_{\infty }\) which is the peak velocity in the parabolic profile. The corresponding ymax is then s∕2. This leads to C and \(\dot{Q}_{th}\) in the form

$$\sqrt{C}=\sqrt{\frac{0.5\:s}{1.972L}\left(\frac{9}{8}\right)^{3/2}}\left(\frac{U_{\infty }L}{\nu }\right)^{1/2}$$
(33)
$$\begin{aligned} \dot{Q}_{th}=&\,4B\lambda \left(0.349Pr^{0.38}\right)\sqrt{\frac{0.5\,s}{1.972L}\left(\frac{9}{8}\right)^{3/2}}\times\\ &\left(\frac{U_{\infty }L}{\nu }\right)^{\frac{3}{4}}\left(T_{w0}-T_{\infty }\right) \end{aligned}$$
(34)
Fig. 6
figure 6

The boundary layer profile at the location of the gap’s mouth is equated with the parabolic profile of the gap flow

Full size image

Equation 34 shows that the Reynolds number dependence changes from ½ (flat plate) to ¾. In addition a geometry parameter s/L arises. The Prandtl number dependence remains almost unchanged.

Alternatively \(\dot{Q}_{th}\) of Eq. 34 may be written in normalized form as the Nusselt number

$$Nu=4\left(0.349Pr^{0.38}\right)\sqrt{\frac{0.5\,s}{1.972L}\left(\frac{9}{8}\right)^{3/2}}\:\left(\frac{U_{\infty }L}{\nu }\right)^{\frac{3}{4}}$$
(35)

Before comparing these analytical results with experimental data the significance of L needs attention. The derivation of Eq. 34 was based on the analogy of flow and temperature boundary layers. Both layers have the same origin and similarity coordinates. By the above setting of ymax the flow coordinates are fixed relative to the gap mouth. The upstream part is virtual while the downstream part is real with the boundary condition \(f'=0\). For the thermal boundary layer we have a constant wall temperature downstream as indicated in Fig. 6. Yet, we cannot, like in the flow case, start with an approximate temperature profile at the mouth because the heating starts only right there. For L this means that even if we integrate correctly over x to L the result cannot be expected to be consistent. Therefore, in a rigorous sense, the similarity solution cannot map the present boundary conditions. To test the significance of the solution anyhow we simply use the length of the heated cylinder for L considering it as a matching parameter if necessary.

5 Experimental results

Experiments were performed at room temperature at \(21.8\pm 0.3\,{^{\circ}}C\). The wall temperature Tw0 was set to 90, 80, 70, 60 and 50 °C. The results are collected in Fig. 7, top to bottom. The open symbols present the measured heat transfer rates in Watt plotted vs the Reynolds number \((U_{\infty }L/\nu )\). The solid lines denote the analytical solutions. The overall agreement confirms clearly the ¾ Reynolds number dependence and also the temperature dependence. There is no data fitting of L or any other parameter. The increasing deviation towards higher Reynolds numbers seems to be due to two simultaneously arising effects which means that the gap flow and the boundary layer approach transition to turbulence. While this is evident from Fig. 5 for the gap flow it remains a supposition for the boundary layer based on flat plate facts and indications drawn from [2].

Fig. 7
figure 7

Heat transfer from the heated cylinder to the wall jet for five different wall temperatures 90, 80, 70, 60, 50 °C, top to bottom. The circles stand for individual measurements. The lines represents the theory according to Eq. 34

Full size image

One obvious objection relates to the effect of free convection. We measured 50 W at 90 °C and less for lower temperatures when the wall jet is off. Although, on its own, this appears relatively high it becomes totally suppressed in the flow case if the Grashof number complies with Gr < < Re2 (see e.g. [5]) which is satisfied in our data range.

Figure 8 presents an alternative data display in terms of the Nusselt number. The line stands for Eq. 35 while the circles provide all experimental data. For perfect measurements the data would be expected to collapse onto a common line. Therefore, the data scattering represents the measuring uncertainty among various runs at different temperatures. Here the main source of uncertainty is not the temperature itself. It rather roots in imperfections of experimental conditions like stability of flow rate, adjustment of the gap, thermal expansion of materials, heat loss at feed throughs and alike, effects which can hardly be prevented by reasonable experimental effort.

Fig. 8
figure 8

Alternative display of all data of Fig. 7 in terms of Nusselt number. The line refers to Eq. 35. The lower line represents the corresponding Nusselt number for the flat plate

Full size image

The Nusselt number representation underscores the consistent deviation of data from the ¾ line with growing Reynolds number. For practical reasons one could fiddle with the exponent to get a better fit. This would, however, require a better understanding of the flow which tends to turbulence.

The lower line in Fig. 8 shows the Nusselt number of the flat plate for comparison. The benefit of the wall jet set-up clearly stands out against the standard flat plate arrangement.

6 Summary and conclusion

The thermal boundary layer of the laminar wall jet was presented in terms of a similarity solution based on the velocity solution. A constant C allows the adaptation of the similarity coordinate system with its virtual origin to the real wall jet flow. From there Fourier’s law yields the heat transfer at an isothermal wall. In relation to the flat plate one observes the following. The effect of the Prandtl number remains almost unchanged. The Reynolds number exponent changes from ½ to ¾. In addition to the Reynolds number a geometry parameter s/L results. The virtual origin of the coordinate system moves with the flow conditions. We fix it successfully by assuming that the parabolic flow profile of the real source resembles the similarity profile. Adversely the thermal boundary layer cannot be initialized in the same way because it has no forerun and only starts at this point. In comparing with experimental data we ignore this fact and accept L as the integration length.

A set of experimental data in terms of wall heat transfer in Watt vs Reynolds number confirms the ¾ dependence of the Reynolds number clearly. The overall agreement with the prediction is satisfying with no data fitting necessary. An obvious trend evolves for higher Reynolds number which shows even better in the Nusselt number representation. Beyond 105 the experimental data fall increasingly short of the theory.

Concluding, we may say that the laminar wall jet solution is capable of predicting heat transfer within limits. The covered range is quite practical, not just academic. Especially when the heat transfer of the wall jet is related to the one of the flat plate as pointed out in Fig. 8.

This study was restricted to the effect of the Reynolds number in terms of the velocity. Further studies should extend the range of variables with a focus on the geometry parameter s/L which could have a potential for optimization.

7 List of symbols

The list of Symbols is shown in Table 1.

Table 1 List of Symbols
Full size table