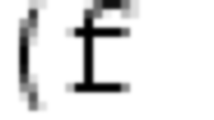1 Introduction

The B-method [2] is a correct-by-construction approach for software development based on formal refinement. Its foundation is an expressive formal language rooted in set-theory, integer arithmetic, and first-order logic. The B language supports higher order data types such as functions or arbitrarily nested relations and is nowadays referred to as classical B. Event-B [3] is its successor which, e.g., puts the focus on systems modeling by extending refinement. In this article, we only refer to the B language which covers predicates and expressions that are present in classical B and Event-B. In particular, there is no need to differentiate between classical B and Event-B in the context of constraint solving.

ProB [51, 52] is an animator, model checker, and constraint solver for the B-method. The constraint solver is used for many tasks and is the foundation of the ProB tool. For instance, the constraint solver has to compute the effect of state changes during animation, find counter examples to proof obligations during disproving or solve constraints for symbolic model checking or program synthesis. One key feature of ProB is that it computes all solutions of a constraint. For instance, this is important for a complete state-space exploration during model checking or when computing set comprehensions. This search is performed using chronological backtracking. A set comprehension in B is a quantified formula describing the elements of a set using a constraint that has to be satisfied by each element. The core of ProB is implemented in SICStus Prolog [18] using its library for constraint solving over the finite domain integers (CLP(FD)) [19] and other features such as coroutines for deterministic propagation and constraint reification. Coroutines in Prolog can be used to suspend computations until a certain condition is met. Constraint logic programming (CLP) generally uses algorithms to reduce the domain of variables when new constraints are posted and identifies a contradiction if a domain becomes empty. After the phase of domain reduction, solutions can be found by enumerating the remaining domains (aka grounding). ProB’s constraint solver handles integer overflow by custom implementations to overcome the limited range of CLP(FD) and deal with unbounded domains. It also supports symbolic representations for infinite values. Of course, the ProB constraint solver might fail to solve constraints over unbounded domains, e.g., due to a timeout or a virtual timeout, which is the case when ProB detects that a domain cannot be enumerated exhaustively and all solutions are required.

Other prominent constraint solvers such as Z3 [26] implement a conflict-driven clause learning modulo theories (CDCL(T)) architecture, which combines SAT and theory solving called Satisfiability Modulo Theories (SMT). In contrast to CLP(FD) and ProB’s constraint solver, SMT solvers are able to learn from contradictions [65, 66] and possibly leave dead-end parts of the search tree earlier and more aggressively by applying backjumping instead of chronological backtracking. The SMT-LIB standard [10, 11] defines the input language for SMT solvers.

In prior work, Krings and Leuschel presented a high-level translation from B to SMT-LIB to integrate the Z3 SMT solver into ProB [45]. The authors have shown that, on the one hand, Z3 can be superior to ProB when disproving formulas, especially over unbounded domains. On the other hand, Z3 often fails to find solutions for satisfiable constraints involving relations or set comprehensions. The translation uses existing operators in SMT-LIB or Z3 wherever possible [45]. Unfortunately, SMT-LIB does not have native support for set comprehensions, which are frequently used in the B language. The authors thus suggested translating B set comprehensions using a universal quantification which constrains all the members of a set variable. Unfortunately, this axiomatic translation often leads to complex constraints for which Z3 fails to find a solution. Several other B operators are also not supported by the SMT-LIB standard like relational composition, iteration and closure, or quantified union \(\bigcup _{\textrm{x}\in \textrm{S}}\) and intersection \(\bigcap _{\textrm{x}\in \textrm{S}}\). As their axiomatic translation to SMT-LIB using universal quantifiers is complex, these operators were not supported in [45].

While trying to improve Z3’s performance and analyzing satisfiable B constraints which can be solved by ProB’s constraint solver but not by Z3, we found an alternate translation using lambda functions instead of quantifiers. It turned out that this alternate approach can considerably improve performance. Take for example, the (right) relational override operator , which joins two relations by adding tuples of \(\textrm{s}\) to \(\textrm{r}\). A tuple in \(\textrm{r}\) is replaced by a tuple in \(\textrm{s}\) if both tuples have the same first element. For instance, a simple satisfiable constraint is given by , which has the solution \(\textrm{g} = \{1 \mapsto 2, 2 \mapsto 3\}\). With the axiomatic translation Z3 is not able to solve this constraint while Z3 can solve it when encoding the override operator using a lambda function. Z3 supports such lambda functions, even though they are not part of the latest SMT-LIB standard 2.6. Note that from version 3.0 lambda functions will be part of the SMT-LIB standard as well. Nevertheless, we observed that the axiomatic translation from B to SMT-LIB has benefits. In order to achieve the best performance, we decided to run several configurations of the Z3 solver with both translations in parallel.

While our empirical evaluation in Sect. 7 shows that the new integration of Z3 improves performance and coverage compared to the prior integration [45], it still has limitations. For example, it cannot deal well with constraints involving set cardinalities, which are frequently used in B. B sets are translated as characteristic functions using Z3’s array theory [25]. This array theory allows defining nested and infinite sets, which is important in the context of the B language. Unfortunately, Z3 does not provide a cardinality constraint. B’s set cardinality is thus translated as a total bijection, which itself is rewritten using universal quantification. For instance, the B predicate \(\textrm{c} = \textrm{card}(\textrm{s})\) is encoded as an existentially quantified total bijection ( is the symbol for a total bijection in B) [45]. A simple constraint for which the integration of Z3 spends a disproportional amount of time to find a solution is \(\textrm{x} \in \mathbb {P}(\mathbb {Z}) \wedge \textrm{card}(\textrm{x})>10\). The reason for this is that Z3 often has trouble solving formulas that contain many quantifiers. Other examples of constraints which have no direct counterpart in SMT-LIB and exhibit similar performance issues are the power set or maximum and minimum of a set of integers.

In this article, we thus also investigated a third approach to SMT solving. We additionally implemented state-of-the-art SMT solving techniques directly in ProB to tightly connect ProB’s constraint solving core for finding solutions with a CDCL(T)-based learning scheme to prune the search space early and improve the identification of contradictions. The ProB constraint solver is particularly strong in solving set cardinalities which are encoded using bit vectors and coroutines while a constraint of CLP(FD) that computes the sum of a list of integers is used to compute the actual cardinality from a corresponding bit vector. Our expectations are thus that the use of ProB’s constraint solver as the theory solver for an SMT solver enables to overcome the aforementioned shortcomings of the integration of Z3. Furthermore, our implementation can be of interest in the SMT community since the B language entails well-definedness conditions which are not considered in common SMT solvers.

The presented constraint solving backends are integrated into ProB which is available at:

https://prob.hhu.de

This article is the extended version of our original submission to the FMICS conference [64]. We extend the former work in different aspects by providing

  • a brief introduction to B and SMT-LIB (Sect. 2),

  • a more formal description of the translation from B to SMT-LIB by providing constructive definitions for sorts in SMT-LIB (Sect. 4.1.2),

  • a decomposition of B constraints into independent components to investigate the impact on constraint solving for the integration of Z3 (Sect. 4.3),

  • a direct implementation of SMT solving for B and Event-B in Prolog using ProB’s constraint solver as a theory solver (Sect. 5),

  • an integration of an additional theory solver for integer difference logic alongside ProB’s constraint solver (Sect. 6),

  • and an extended empirical evaluation including a justification for the decision of running different Z3 solvers in parallel, more benchmarks from bounded model checking, and benchmarks from constraint-based proofs of inductive invariants as well as for deadlock freedom (Sect. 7).

2 Background

In the following, we will give a brief introduction to the basics of SAT and SMT solving, the B formal specification language, and the SMT-LIB language. We focus on the parts of the languages that we use for our translation from B to SMT-LIB as well as our empirical evaluation.

2.1 Basics of SAT and SMT solving

Propositional logic allows defining relations between literals by providing the common sentential connectives as well as the logical negation. A literal is either a proposition or the negation of a proposition, which is said to have a positive or negative polarity. Satisfiability (SAT) solving is the process of deciding whether a propositional logic formula is satisfiable, which is NP-complete. Modern SAT solvers are based on the Davis–Putnam–Logemann–Loveland algorithm (DPLL) [22, 23] as well as conflict-driven clause learning (CDCL) [65, 66]. The input to the algorithm is a propositional logic formula in the conjunctive normal form (CNF), i.e., a conjunction of disjunctions. The algorithm has two main steps which are unit-propagation and variable branching. The unit-propagation eliminates all clauses with a singleton variable by assigning the variable to its polarity. If a formula in conjunctive normal form does not contain a unit-clause, the algorithm selects an arbitrary variable and sets it to either true or false. Furthermore, the algorithm decides which polarity to assign to a variable first. Both of these decisions are usually guided by some heuristic. For instance, a simple heuristic is to assign the most frequent variable among all clauses first. Each variable assignment is connected to a level in the search tree of the SAT solver. After each decision, the level is increased by one while unit propagations are conducted on the level of a decision. The set of clauses is simplified after each assignment of a variable by applying Boolean resolution. For instance, the clause \(\textrm{A} \vee \textrm{B}\) is simplified to the unit clause \(\textrm{A}\) after assigning \(\textrm{B}\) to false. If a clause becomes satisfiable, it is removed from the set of clauses. A model of a propositional logic formula is an assignment of SAT variables which makes the formula true. A propositional logic formula is unsatisfiable if there exists no model. We refer to a model as partial if it does not assign all variables.

Predicate logic is an extension of propositional logic which enables reasoning over domain specific objects, predicates, and to quantify variables. First-order logic restricts predicate logic to only quantify over domain specific objects but not predicates. Satisfiability Modulo Theories (SMT) [34, 60, 67] defines the problem of deciding whether a logical formula is satisfiable for some background theories. SMT solvers distinguish in their underlying logic, e.g., first-order or temporal logic, as well as the supported background theories, e.g., integers or arrays. There are two approaches to SMT solving which are the eager and lazy approach. In eager SMT solving, all constraints are translated to propositional logic and solved solely by a SAT solver. For instance, finite sets can be encoded as bit vectors. The lazy approach to SMT solving first creates a Boolean abstraction of a logical formula which introduces literals for theory formulas. A SAT solver then interacts with theory specific solvers using a conflict-driven clause learning scheme to decide for the satisfiability of an SMT formula. For instance, the formula \(x> y \wedge y > x\) can be abstracted to \(A \wedge B\) where \(A \equiv x > y\) and \(B \equiv y > x\) are set up to reify the SAT and theory solver. If the SAT solver finds a model, the theory specific constraints which are reified with the SAT variables are sent to theory solvers according to their polarity in the found model. For the above formula, a SAT solver finds the only solution \(A = B = \top \) which induces the SMT solver to send both corresponding first-order logic formulas to an appropriate theory solver. The algorithm has found a solution if all the theory solvers report satisfiability. Otherwise, the procedure learns from the conflicting assignment and backtracks to the SAT solver which searches for another solution of the Boolean abstraction. An SMT formula is identified to be unsatisfiable if the SAT solver reports unsatisfiability for the Boolean abstraction. This lazy approach to SMT solving is also referred to as DPLL(T) [34, 60, 67] or CDCL(T). There are many sophisticated implementation details and improvements to these two decision procedures which are discussed in Sect. 5 along our implementation in ProB.

2.2 Primer on B

The formal specification language B [2] is rooted in set-theory, integer arithmetic, and first-order logic and follows the correct-by-construction approach. B has been developed for the specification and design of software systems. Specific properties can be proven mathematically using theorem provers, e.g., using AtelierB [20], or be checked using a model checker such as ProB [50,51,52]. The B language supports unbounded domains and higher order data types such as arbitrarily nested relations. Nowadays, the B language is referred to as classical B. Event-B [3] is the successor of classical B which improves the language in several aspects and puts the focus on systems modeling by extending refinement. Note again that in this article we only refer to the B language for the sake of simplicity, which covers predicates and expressions that are present in classical B and Event-B.

The development in classical B and Event-B is incremental starting with a high-level abstract specification which is successively refined and decomposed to increase the maintainability and ease the specification of complex models. A model thus consists of a collection of so-called machines. All refinement steps are linked by proof obligations which have to be discharged in order to ensure that the refinement does not diverge from the prior specification. A machine consists of variable and type definitions as well as initial values. A state is defined by the current values of the machine variables. One can specify transitions between states by defining machine operations (called events in Event-B) that compute successor states including all variables. An operation (or event) can have a precondition (called guard in Event-B), allowing or prohibiting execution based on the current state. Certain behavior can be ensured by defining machine invariants, which are safety properties that have to hold in every reachable state. The correctness of a formal model thus refers to its specified invariants.

In addition to native B types such as \(\mathbb {Z}\) or \(\mathbb {B}\), one can provide user-defined sets. These sets can be defined by a finite enumeration of distinct elements (enumerated sets) or left open (deferred sets). For instance, \(\textrm{S} = \{\textrm{s}\}\) defines an element \(\textrm{s}\) of type \(\textrm{S}\), which both can be accessed by name within the machine. Deferred sets are assumed to be non-empty during proof and also finite for animation in ProB.

A set comprehension in B is a quantified formula constraining the elements of a set. If quantifying two variables, the elements of a set comprehension are tuples. For instance, the equations \(\{\textrm{x} \mid \textrm{x} \in 1..2\} = \{1,2\}\) and \(\{\textrm{x},\textrm{y} \mid \textrm{x} \in 1..2 \wedge \textrm{y}=0\} = \{(1 \mapsto 0),(2 \mapsto 0)\}\) are true in B. There is no limit to the amount of quantified variables other than that it is a finite number. For instance, the elements of a set corresponding to a set comprehension quantifying three variables are triples.

B is statically and strongly typed while ProB further executes runtime checks to ensure well-definedness. For instance, a function application \(\textrm{f}(1)\) is well-defined if 1 is an element of the domain of the function \(\textrm{f}\). Other exemplary B operators that entail a well-definedness condition are the minimum and maximum of a set of integers which has to be non-empty or integer division. Type domains can be unbounded, possibly resulting in a model with an infinite state space. While B has a strict type system, there is no distinction between sets of pairs, relations, functions, and sequences. For instance, the sequence \([-1]\) is the function \(\{1\mapsto -1\}\), which is also a relation, which in turn is a set of pairs. It is thus possible that sequences interact with sets of pairs resulting in a set of pairs which is not a sequence anymore. For instance, the equation \([-1] \cup \{3\mapsto 2\} = \{1\mapsto -1, 3\mapsto 2\}\) is true in B, but the right-hand side of the equation is not a well-defined sequence since the domain is not enumerated coherently.

2.3 Primer on SMT-LIB

The SMT-LIB foundationFootnote 1 defines a standard input language for common SMT solvers called SMT-LIB [10] as well as a set of benchmarks for different background theories.

The SMT-LIB language is based on many-sorted first-order logic with equality [10] that allows defining sorts, i.e., types, and sorted terms. Its syntax is defined in a Lisp style. Exemplary sorts are the integers (), the Booleans () or arrays (). For instance, defines an array sort that maps integers to Booleans. SMT-LIB allows defining function symbols that are associated with a rank. The rank of a function symbol defines the sorts of the inputs as well as the output. In general, a function symbol with rank \(\sigma _1 \cdots \sigma _{\textrm{n}} \sigma \) has \(\textrm{n}\) inputs of sort \(\sigma _1 \cdots \sigma _{\textrm{n}}\) and one output of sort \(\sigma \) [10]. One is able to introduce uninterpreted functions using the keyword, or interpreted functions using . For instance, declares an uninterpreted function \(\textrm{x}\) that returns an integer, i.e., \(\textrm{x}\) is an integer variable, and defines a function \(\textrm{f}\) that adds two integers. All functions in SMT-LIB are total which entails that every function call is well-defined. In fact, there is no concept of well-definedness in SMT-LIB. For instance, the equality is true for an arbitrary integer symbol \(\textrm{x}\) although the division by zero is not defined in mathematics. It is possible to define recursive functions using the keyword. Furthermore, the SMT-LIB language allows defining algebraic data types along arbitrary function declarations that have to hold for a data type using the keyword. For instance, a tuple type that provides two projection functions to access its first and second element can be declared as follows:

Formulas in SMT-LIB are terms of sort that can be asserted to hold using the keyword. Such formulas can reason over function symbols that have been declared beforehand. A dedicated SMT solver holds a stack of assertions that consists of formulas, declarations, and definitions. Besides reasoning over globally declared function symbols within an SMT formula, it is possible to reason over local function symbols using different kinds of binders such as , or . The scoping is defined to refer to the last declaration of a function symbol. For instance, the following example shows a simple SMT-LIB model that defines a global integer symbol as well as an existential quantifier that reasons over a local integer symbol :

The keywords and instruct a solver to check for the satisfiability of all assertions and return a model for all global function symbols if the assertions are satisfiable. For the above example, we receive a model stating that \(\textrm{x}\) is equal to 1 which is represented in SMT-LIB as well. In particular, we receive a list of function definitions for global function symbols as a model.

3 Former Z3 integration

In the following, we revise the workflow of the former integration of Z3 in ProB as well as the high-level translation from B to SMT-LIB presented by Krings and Leuschel [45].

3.1 High-level translation

The former high-level translation [45] uses corresponding operators of SMT-LIB wherever possible. B sets are translated as characteristic functions in SMT-LIB mapping set elements to either true or false as defined by Z3’s array theory [25]. This theory allows defining nested and infinite sets. For instance, for the predicate \(\textrm{x} \subseteq \mathbb {P}(\mathbb {Z})\), the variable \(\textrm{x}\) is defined as a characteristic function of sort . All logical B predicates (\(\wedge \), \(\vee \), \(\Rightarrow \), \(\Leftrightarrow \)), all integer expressions except for division (\(+\), −, \(\textrm{mod}\), \(**\), \(\ge \), >, <, \(\le \)), simple set expressions (\(\in \), \(\subset \), \(\subseteq \), \(\cup \), \(\cap \), −), and quantifiers (\(\forall \), \(\exists \)) are supported by SMT-LIB and can be translated with equivalent operators.

Since the B language does not distinguish between sets of pairs, relations, functions, and sequences, all of these data types are translated as sets of pairs as is defined in B. Unfortunately, this prevents us from using certain features of Z3 which would probably be more efficient. For instance, B sequences could be directly translated as arrays in SMT-LIB instead of rewriting them to sets of pairs beforehand. Yet, this translation to arrays could only be performed if sequences only interoperate with other sequences since B set operators can be called on sequences yielding a relation which is not a sequence anymore.

Another difference between B and SMT-LIB is that B implements a concept of well-definedness [4] which is not present in SMT-LIB. Axioms for well-definedness ensure that certain operators are only applied when they make sense and that the proof rules of classical two-valued logic can be applied. For instance, B prohibits division by zero while in SMT-LIB integer division is a total function, e.g., is true in SMT-LIB and not well-defined in B. Another difference is that B’s integer division rounds toward zero while SMT-LIB follows Boute’s euclidean definition [16]. Boute defined division as rounding to positive infinity when the divisor is negative and rounding to negative infinity otherwise. B’s integer division \(\textrm{a}/\textrm{b}\) is thus translated to SMT-LIB as follows:

For the well-definedness of \(\textrm{a}/\textrm{b}\), we assert that \(\textrm{b}\) is not equal to zero. Other operators with a well-definedness condition are, e.g., B’s function application or minimum and maximum of a set of integers. For the translation of these operators, additional well-definedness conditions are added.

A frequently used construct in B is set comprehension which has no direct counterpart in SMT-LIB. Set comprehensions are thus rewritten as axiomatized formulas using quantifiers [45]. In particular, an existentially quantified variable is defined for each quantified variable of a set comprehension. For instance, the set comprehension \(\{\textrm{x} \mid \textrm{x} \in \mathbb {Z} \wedge \textrm{x} > 0\}\) is encoded as a fresh existential integer set variable \(\textrm{tmp}\) alongside the axiom \(\forall \textrm{v}.(\textrm{v} \in \textrm{tmp} \Leftrightarrow \textrm{v} > 0)\) [45].

Several B set operators which cannot be directly translated to SMT-LIB such as the domain of a relation are rewritten as set comprehensions. For instance, \(\textrm{dom}(\textrm{r})\) is rewritten as \(\{\textrm{x} \mid \exists \textrm{y}.(\textrm{x} \mapsto \textrm{y} \in \textrm{r})\}\). Yet, the operators \(\textrm{min}(\textrm{s})\), \(\textrm{max}(\textrm{s})\), and \(\textrm{card}(\textrm{s})\) cannot be rewritten as set comprehensions. These operators are instead translated as identifiers which are axiomatized accordingly. For instance, the minimum of an integer set \(\textrm{min}(\textrm{s})\) is replaced by an identifier \(\textrm{m}\) which is axiomatized by \(\forall \textrm{x}.(\textrm{x}: \textrm{s} \Rightarrow \textrm{m} \le \textrm{x}) \wedge \exists \textrm{x}.(\textrm{x} \in \textrm{s} \wedge \textrm{m} = \textrm{x})\). The maximum of an integer set is encoded analogously.

Computing the cardinality of a set in SMT-LIB is expensive due to the employed encoding of sets as characteristic functions. A total bijection has to be computed mapping the elements of a set to a coherent interval of indices starting at 1 while the largest index corresponds to the cardinality of the set. For instance, the B predicate \(\textrm{c} = \textrm{card}(\textrm{s})\) is encoded as an existentially quantified total bijection [45]. It has to be ensured that the variable \(\textrm{c}\) is greater than or equal to zero since the empty set could have any negative cardinality otherwise. The authors refer to such rewritten predicates as normalized B. A normalized predicate is then passed to the actual translator to SMT-LIB.

B supports user-defined types in the form of deferred sets and enumerated sets as described in Sect. 2.2. Such B types are translated to corresponding sorts in SMT-LIB. Deferred sets are not limited in size but assumed to be non-empty for proof and also finite for animation in ProB. For enumerated sets, the actual instances are given which are defined as function symbols in SMT-LIB and axiomatized to be distinct.

The authors point out that several operators such as the relational closure or the general union \(\bigcup _{\textrm{x}\in \textrm{S}}\) and intersection \(\bigcap _{\textrm{x}\in \textrm{S}}\) of a nested set \(\textrm{S}\) cannot be translated effectively to SMT-LIB using quantifiers [45], which is why they are not supported.

3.2 Workflow

The former integration [45] of Z3 in ProB provides two interfaces. First, full B predicates can be translated to SMT-LIB and be solved by Z3. As described in Sect. 3.1, several B operators are not supported by the former translation to SMT-LIB and thus, are filtered before the translation. In particular, all top-level conjuncts that contain an unsupported operator are removed. If a predicate uses unsupported operators, the result of Z3 can thus only be used if a contradiction has been found. For instance, consider the predicate \(\textrm{P} \wedge \textrm{Q}\) where \(\textrm{P}\) is any unsatisfiable predicate and \(\textrm{Q}\) contains any predicate that is not supported by the former integration of Z3, e.g., the quantified union. We remove the top-level conjunct \(\textrm{Q}\) and only translate the contradicting predicate \(\textrm{P}\) to SMT-LIB. The unsatisfiability of the overall formula is identified if Z3 is able to identify the contradiction in \(\textrm{P}\). Yet, if \(\textrm{P}\) is satisfiable, we cannot use the partial model since \(\textrm{Q}\) has not been evaluated.

The second interface intertwines Z3 with ProB’s constraint solver by setting up constraints simultaneously and sharing intermediate results. All clauses learned by Z3 are fed to ProB’s constraint solver as well, which lifts ProB’s search capabilities from backtracking to backjumping. The call to Z3 is delayed after the deterministic propagation phase of ProB [45] since ProB’s constraint solver generally shows better performance in model finding over B constraints than Z3. During this phase, ProB might infer new constraints which are then added to Z3.

4 New Z3 integration

In the following, we describe the new high-level translation from B to SMT-LIB as supported by Z3 as well as the new parallel solver integration.

4.1 High-level translation

For the formal description of the translation, we provide two semantic functions for B expressions representing values and predicates representing a truth value. In particular, \(E \llbracket \textrm{e} \rrbracket {i}\) is the Z3 encoding of the B expression \(\textrm{e}\), and \(P \llbracket \textrm{p} \rrbracket {i}\) is the Z3 encoding of the B predicate \(\textrm{p}\). The variable i is an environment which stores specific information of a translation. The following example shows a series of rewriting steps, applying the rules of \(E \llbracket \textrm{e} \rrbracket {i}\) and \(P \llbracket \textrm{e} \rrbracket {i}\) (shown further below):

Global B variables such as \(E \llbracket \textrm{x} \rrbracket {i}\) are translated as functions using the same name. That means, \(E \llbracket \textrm{x} \rrbracket {i} ~\mathrel {\widehat{=}}~ \textrm{x}\) but as a side effect a global function symbol for the variable \(\textrm{x}\) has been introduced in SMT-LIB. Locally quantified B variables are translated in the same way but do not introduce a global function symbol in SMT-LIB.

The environment i contains a list of translated Z3 expressions and function declarations, a mapping from B expressions to B types \(\varPsi _{i}\), e.g., \(\varPsi _{i}(-1) = \mathbb {Z}\), and a mapping from Z3 expressions to Z3 sorts \(\varPhi _{i}\), e.g., \(\varPhi _{i}(-1)\) . For sets, i.e., arrays in SMT-LIB, we introduce the operator \(\mathbb {P}^{-1}\) yielding the type of the elements of a set. For instance, for a basic set of integers, and   for a nested set of integers.

Furthermore, the environment stores a mapping from B tuple types to Z3 functions \(\varOmega _{i}\), which allow accessing the elements of tuples in SMT-LIB. For instance, \(\varOmega _{i}(\varPsi _{i}(1 \mapsto 2)) = [\textrm{first}_{i,\varPhi _{i}(E \llbracket 1 \mapsto 2 \rrbracket {i})},\textrm{second}_{i,\varPhi _{i}(E \llbracket 1 \mapsto 2 \rrbracket {i})}]\), where \(\textrm{first}_{i,\varPhi _{i}(E \llbracket 1 \mapsto 2 \rrbracket {i})}\) and \(\textrm{second}_{i,\varPhi _{i}(E \llbracket 1 \mapsto 2 \rrbracket {i})}\) are the projection functions of the Z3 tuple sort corresponding to the B type \(\varPsi _{i}(1 \mapsto 2)\). For better readability, we use the abbreviations and with \(\textrm{c} = E \llbracket \textrm{x} \mapsto \textrm{y} \rrbracket {i}\) for the projection functions of the Z3 tuple sort that has been introduced for the B type \(\varPsi _{i}(\textrm{x} \mapsto \textrm{y})\). For instance, and . Furthermore, we drop the type information of the projection functions if their argument is given. For instance, with \(\textrm{c} = E \llbracket \textrm{x} \mapsto \textrm{y} \rrbracket {i}\). We refer to the Z3 sort of a tuple in SMT-LIB using \(\varTheta _i\), e.g., corresponds to the Z3 sort of a tuple of integers. The types of the elements of a tuple can be accessed using \(\theta _1\) and \(\theta _2\), e.g., and . Last but not least, we allow calling the semantic functions on partially defined B operators, e.g., \(E \llbracket \textrm{dom}(\textrm{S}) \rrbracket {i}~ ~\mathrel {\widehat{=}}~ \) \((E \llbracket \textrm{dom} \rrbracket {i}~ E \llbracket \textrm{S} \rrbracket {i})\).

4.1.1 Tuples

In B, tuples are encoded as nested pairs. Thus, several encodings of tuples exist and the modeler has to know which one is being used. For instance, a triple can be represented as either \((\textrm{x}\mapsto (\textrm{y}\mapsto \textrm{z}))\) or \(((\textrm{x}\mapsto \textrm{y})\mapsto \textrm{z})\). We use the first left-associative encoding and introduce a unique Z3 sort for each tuple type occurring in a B predicate when translating to SMT-LIB. For this, we declare a new data type using as described in Sect. 2.3. B tuples are then translated using their corresponding Z3 sort’s constructor which is defined as follows:

The Z3 function is the constructor of the Z3 tuple sort which has been introduced for B tuples of type \(\varPsi _{i}(\mathrm {x_1} \times \dots \times \mathrm {x_n})\), where \(\textrm{n} \in \mathbb {N}\). For the sake of readability, we drop the type information of the tuple constructor since the types are implicitly given by the constructor’s arguments. In particular, we use .

B provides two projection functions to access the elements of a tuple which are translated as follows:

4.1.2 Set notation

As described in Sect. 3.2, the former high-level translation rewrites many set operators to B set comprehensions since they are not directly supported by SMT-LIB. Set comprehensions themselves are then rewritten using B quantifiers which can be directly translated to SMT-LIB. However, using many quantifiers can lead to unnecessarily complex constraints for which Z3 is not able to find a model. Fortunately, Z3 provides lambda functions which allow defining a set of variables that are constrained by an expression. In general, a lambda function in Z3 returns an expression of the sort where \(\textrm{range}\) is the sort of \(\textrm{body}\). For instance, the lambda function describes the set of integers \(\{0,1,2\}\) as an array that maps integers to either true or false, i.e., the output has the sort . For our translations, we consistently use such lambda functions that constrain a single variable by a Boolean expression.

First and foremost, we suggest translating B set comprehensions using Z3’s lambda function which we define as follows:

The first case is a special case for a B set comprehension with a singleton result variable since no tuple has to be created here. In the second case, \(R^{*}\) is a semantic function that replaces the translated variables \(\mathrm {x_1},\dots ,\mathrm {x_n}\) in the predicate \(\textrm{p}\) corresponding to the position in the tuple \(\textrm{c}\). For instance, as can be seen in the following example, where \(\textrm{x}\) is translated as , \(\textrm{y}\) as , and \(\textrm{z}\) as :

A formal description of our syntax-directed translation rules for a subset of B’s set operators can be seen in Fig. 1.

Fig. 1
figure 1

A formal description of our syntax-directed translation rules for translating a subset of B’s set operators to SMT-LIB as understood by Z3. In particular, lambda functions are not part of the latest SMT-LIB standard version 2.6, but are supported by Z3. The environment i and the functions \(\varTheta _i\), \(\theta _1\), \(\theta _2\), \(\varPhi _{i}\), and \(\mathbb {P}^{-1}\) are defined in the introduction of Sect. 4.1

Full size image

For the translation of the direct product \(\mathbin \otimes \), let \(\textrm{T1}\) be the sort \(\varTheta _i(\theta _2(\mathbb {P}^{-1}(\varPhi _i(E \llbracket \textrm{p} \rrbracket {i}))),\theta _2(\mathbb {P}^{-1}(\varPhi _i(E \llbracket \textrm{q} \rrbracket {i}))))\) and \(\textrm{T2}\) be \(\varTheta _i(\theta _1(\mathbb {P}^{-1}(\varPhi _i(E \llbracket \textrm{p} \rrbracket {i}))),\textrm{T1}))\):

To translate the parallel product \(\mathbin \Vert \), let \(\textrm{T1}\) be the sort \(\varTheta _i(\theta _1(\mathbb {P}^{-1}(\varPhi _i(E \llbracket \textrm{p} \rrbracket {i}))),\theta _1(\mathbb {P}^{-1}(\varPhi _i(E \llbracket \textrm{q} \rrbracket {i}))))\) and \(\textrm{T2}\) be \(\varTheta _i(\theta _2(\mathbb {P}^{-1}(\varPhi _i(E \llbracket \textrm{p} \rrbracket {i}))),\theta _2(\mathbb {P}^{-1}(\varPhi _i(E \llbracket \textrm{q} \rrbracket {i}))))\):

4.1.3 Finite subsets

The finite set operators \(\textrm{min}\), \(\textrm{max}\), and \(\textrm{card}\) cannot be expressed efficiently using lambda functions. We thus stick to the axiomatic translation using quantifiers for these operators [45] as described in Sect. 3.1. While the same applies for the Event-B operator \(\textrm{finite}\), the operators describing all finite subsets \(\mathbb {F}\) and all finite non-empty subsets \(\mathbb {F}_{1}\) can be expressed using lambda functions as is formalized in the following:

4.1.4 Rewriting set cardinality and power set

Since Z3 often lacks performance when solving quantified formulas [45], we provide special rewriting rules for B set cardinality and power set constraints to equivalent representations which do not lead to quantified formulas in SMT-LIB. In particular, we provide the following rewriting rules:

$$\begin{aligned}{} & {} \textrm{S} \in \mathbb {P}(\textrm{R}) \equiv \textrm{S} \subset \textrm{R} \\{} & {} \textrm{S} \in \mathbb {P}_{1}(\textrm{R}) \equiv \textrm{S} \subset \textrm{R} \wedge \textrm{S} \ne \emptyset \\{} & {} \textrm{S} \in \mathbb {F}(\textrm{R}) \equiv \textrm{S} \subset \textrm{R}~ \mathrm {if\ R\ is\ finite} \\{} & {} \textrm{S} \in \mathbb {F}_{1}(\textrm{R}) \equiv \textrm{S} \subset \textrm{R} \wedge \textrm{S} \ne \emptyset ~ \mathrm {if\ R\ is\ finite} \\{} & {} \textrm{card}(\textrm{S}) > 0 \equiv \textrm{card}(\textrm{S}) \ge 1 \equiv \textrm{S} \ne \emptyset \\{} & {} \textrm{card}(\textrm{S}) = 0 \equiv \textrm{card}(\textrm{S}) < 1 \equiv \textrm{S} = \emptyset \\{} & {} \textrm{card}(\{\mathrm {x_1}, \dots , \mathrm {x_n}\}) = \textrm{n} \equiv \mathrm {all\_different}(\{\mathrm {x_1}, \dots , \mathrm {x_n}\}) \\{} & {} \textrm{q} \in 1\mathrel {{.}\,{.}}\textrm{n} \mathbin \rightarrow 1\mathrel {{.}\,{.}}\textrm{n} \wedge \textrm{card}(\textrm{ran}(\textrm{q}))=\textrm{n} \equiv \\{} & {} \quad \quad \quad \bigwedge _{i \in 1\mathrel {{.}\,{.}}\textrm{n}-1} \textrm{q}(\textrm{i}) \ne \textrm{q}(\textrm{i}+1) \end{aligned}$$

Here, \(\mathrm {all\_different}\) is a constraint that sets up a pairwise distinction between all elements. Furthermore, we replace set cardinality constraints of enumerated sets with integer values. For instance, we can simplify the B constraint \(\textrm{s} = 1\mathrel {{.}\,{.}}4 \wedge \textrm{card}(\textrm{s}) > 1 \wedge \textrm{i} = \textrm{card}(\textrm{s})-1\) to \(\textrm{s} = 1\mathrel {{.}\,{.}}4 \wedge \textrm{i} = 3\) to prevent sending any cardinality constraint to Z3. Such formulas might not be written by hand but do often occur when using an automated translation backend of ProB such as the integration [36] of \(\textrm{TLA}^{+}\) [47] in B.

4.1.5 Relational composition, iteration, and closure

Some relational B operators such as the transitive and reflexive closure are more complex to translate to SMT-LIB and will be discussed in the following. The transitive and reflexive closure \(\textrm{r}^*\) of a relation \(\textrm{r} \in \textrm{S} \mathbin \leftrightarrow \textrm{S}\) can be mathematically defined as \(\bigcup _{\textrm{n} \in \mathbb {N}} \textrm{r}^\textrm{n}\) and the transitive and not reflexive closure \(\textrm{r}^+\) as \(\bigcup _{\textrm{n} \in \mathbb {N}_1} \textrm{r}^\textrm{n}\). Here, the transitive and reflexive closure is defined by the union of a relation’s iterations for all natural numbers.

The iteration of a relation \(\textrm{r} \in \textrm{S} \mathbin \leftrightarrow \textrm{S}\) can be defined recursively using B’s forward composition. This conforms to the formula \(\textrm{r}^{\textrm{n}} = \textrm{r}^{\textrm{n}-1}; \textrm{r}^1\), where the base case is \(\textrm{r}^1 = \textrm{r}\). One special case of the relational iteration’s definition in B is \(\textrm{r}^0 = \textrm{id}(\textrm{S})\), which is rewritten before the translation. B’s forward composition of two relations \(\textrm{p} \mathbin ;\textrm{q}\) is defined by the set comprehension \(\{\textrm{x},\textrm{y} \mid \exists \textrm{z}.(\textrm{x} \mapsto \textrm{z} \in \textrm{p} \wedge \textrm{z} \mapsto \textrm{y} \in \textrm{q})\}\) which can be straightforwardly translated to SMT-LIB using lambda functions. Let \(\textrm{T1}\) be the sort \(\varPhi _{i}(E \llbracket \textrm{p} \rrbracket {i})\) and \(\textrm{T2}\) be \(\varPhi _{i}(E \llbracket \textrm{q} \rrbracket {i})\). We then translate the forward composition \(\textrm{p} \mathbin ;\textrm{q}\) as follows:

Note that a relational backward composition can be described by a forward composition, i.e., \(\textrm{p} \circ \textrm{q} \equiv \textrm{q} \mathbin ;\textrm{p}\). We are able to define the iteration of a relation \(\textrm{r}\) as a recursive function using the encoding of B’s forward composition in SMT-LIB as follows:

Due to the employed encoding of sets in SMT-LIB that introduces a sort for each type of set, e.g., a set of the integers or a set of the Booleans, we have to define the functions and for each type that they are applied to. We thus define unique names for the different functions differing in the relation’s type and case split on these types before translating to SMT-LIB.

Let be a function passing its only argument to the lambda function for the translation of B’s general union as defined in Sect. 4.1.2. The transitive and reflexive closure of a relation \(\textrm{r}\) can then be translated to SMT-LIB straightforwardly:

B’s transitive and not reflexive closure \(\textrm{r}^+\) is translated analogously but using \(\textrm{n} \in \mathbb {N}_1\).

4.2 New workflow

The new workflow of ProB’s Z3 interface is supposed to replace the former interface which sends full predicates to Z3 as described in Sect. 3.2. Note that ProB also has an interface to Z3 where both solvers share constraints which we do not consider here. A diagram of the workflow is presented in Fig. 2.

Fig. 2
figure 2

A workflow diagram of the new integration of Z3 in ProB running two Z3 constraint solvers in parallel using the former and new translation from B to SMT-LIB

Full size image

4.2.1 Preprocessing

First, a formula is simplified by ProB as was the case for the former integration [45] of Z3. For instance, formulas are rewritten to use a subset of operators such as only using \(\le \) but not \(\ge \).

We decided to apply a static analysis to check syntactically for contradictions before translating to SMT-LIB. The goal is to prevent that those contradictions are no longer detected by Z3, e.g., after adding quantifiers. For this, we extended the simplification rules of ProB to more aggressively replace variables by their value if this value is explicitly given. For instance, the formula \(\textrm{s}=\emptyset \wedge \textrm{card}(\textrm{s}) > 1\) can be rewritten as \(\textrm{s}=\emptyset \wedge \textrm{card}(\emptyset ) > 1\) in a first phase. Afterward, the cardinality constraint can be replaced by the integer 0 which makes it obvious that the integer comparison is not satisfied. We thus prevented the translation of a cardinality constraint to SMT-LIB.

To further extend the static syntax analysis, we decided to abstract a B formula to a SAT formula as is done by lazy SMT solvers [59] and only translate a formula to SMT-LIB if its SAT abstraction is satisfiable as can be seen in Fig. 2. If it is not satisfiable, we have avoided the overhead of translating B to SMT-LIB and calling the external constraint solver. For instance, the formula \(\textrm{x} = \textrm{y} \wedge \textrm{x} \ne \textrm{y}\) can be abstracted to \(\textrm{A} \wedge \lnot \textrm{A}\) where \(\textrm{A} \equiv \textrm{x} = \textrm{y}\). Note that this is not an eager SMT solving [59] where all semantics are translated to propositional logic. We are now able to call a SAT solver to find a solution for an abstracted B formula. For this, we use a small timeout of 50 ms to prevent adding too much overhead due to SAT solving. In particular, a SAT solver should be able to identify simple static contradictions fast.

4.2.2 Z3 solver integration

If the SAT abstraction is satisfiable, we apply both translations from B to SMT-LIB: the preexisting one proposed by Krings and Leuschel [45] (Sect. 3.1), and the new one described in Sect. 4.1.

The former integration of Z3 always used the incremental solver where constraints can be pushed on to the solver stack. While this is required when both ProB and Z3 run simultaneously, this is not the case for the integration presented in this article, where we send full predicates to Z3 only. In particular, using the incremental solver incurs an additional overhead since constraints are internalized. We thus decided to run two non-incremental Z3 solvers in parallel with the two different translations as described above. Unfortunately, Z3’s incremental solver does not support an existential quantifier at the top-level of a lambda expression.Footnote 2 This makes some of our new translation not applicable for running ProB’s constraint solver and Z3 simultaneously and sharing constraints.

We use the result of the solver which answers first if a solution or a contradiction has been found. The other solvers are then interrupted. If the fastest solver answers unknown, we do not use this result but wait for another solver. The solver integration returns unknown if all solvers did so as well, or if a formula cannot be translated to SMT-LIB, e.g., because of a missing implementation. The return of unknown is not shown in Fig. 2.

Note that it is simple to add a Z3 solver configuration to the workflow. Our implementation is able to create a deep copy of a translation with all of its referenced Z3 objects, which are stored in a so-called context in Z3. We then just have to create a new solver object for a copied context and set the desired options.

4.2.3 Postprocessing of models

A model found by Z3 is represented in SMT-LIB. We parse a model and translate it to B as was the case for the former workflow integration described in Sect. 3.2. Unfortunately, Z3 often fails to compute explicit values from lambda functions or quantifiers while it is able to find contradictions. For instance, for the formula \(\textrm{s}=\textrm{union}(\{\{1\},\{2\}\})\), Z3 returns a model containing the translated lambda function of the general union defined in Sect. 4.1 while \(\textrm{s}\) could be set to \(\{1,2\}\). However, Z3 is able to find contradictions using the general union such as for \(\emptyset = \textrm{union}(\{\{1\},\{2\}\})\). We thus extend the translation from SMT-LIB to B and the processing of found models to compute remaining quantifiers and lambda functions with ProB’s constraint solver. For instance, the lambda function in the above example’s model returned by Z3 is translated as a set comprehension in B which results in \(\textrm{s} = \{\textrm{e} \mid \exists \textrm{f}.(\textrm{e} \in \textrm{f} \wedge (\textrm{f} = \{1\} \vee \textrm{f} = \{2\}))\}\). The ProB constraint solver is then called to compute an explicit value which results in \(\textrm{s} = \{1,2\}\).

4.3 Decomposition of constraints

In recent work [64], we observed that Z3 often lacks performance for constraints containing many quantifiers.

We mainly attribute these performance issues to the use of set cardinality constraints as well as the definition of functions, which are translated using quantifiers in SMT-LIB to axiomatize their behavior. While Z3 is able to solve many constraints involving such axiomatized translations, it often fails to solve constraints with many quantifiers. In particular, the Z3 solver often answers unknown.

figure a

We thus decided to decompose constraints into components that use a distinct set of variables prior to the translation to SMT-LIB and solve each of these components independently using Z3. For instance, the B constraint can be decomposed into two independent components and \(y \in \mathbb {N} \mathbin \rightarrow \mathbb {N} \wedge y \ne \emptyset \). We suppose that Z3 is able to solve several small constraints better than is the case for one large constraint. Furthermore, the performance should increase for unsatisfiable constraints if a single component is already unsatisfiable in which case not all components have to be solved.

Algorithm 1 shows a pseudocode implementation of the solving routine that decomposes constraints into independent components prior to the translation to SMT-LIB. The function \(\textsc {decompose}\) used in line 2 is a function that decomposes a B constraint into independent components where the output is a set of constraints. We iterate over the set of components and solve each component with Z3 after translating a B constraint to SMT-LIB (line 6 of Algorithm 1) by applying the workflow described in Sect. 4.2. If a component is unsatisfiable, we return from the solving routine by stating that a contradiction has been found. In this case, we do not have to solve possibly remaining components since the unsatisfiability of a single component implies the unsatisfiability of the overall constraint. If a component is satisfiable, we combine the variable assignments of this component’s solutions with the overall satisfiable variable assignments (line 12 of Algorithm 1). This combination of solutions results in appending the lists of variable bindings since each component refers to an independent set of variables.

The Z3 solver possibly answers unknown when solving a constraint. However, if Z3 is unable to decide for the satisfiability of a single component, it might be able to detect the unsatisfiability of a remaining component which determines the unsatisfiability of the overall constraint. We thus store the information that Z3 was unable to solve a single component in a Boolean variable introduced in line 3 of Algorithm 1 and do not terminate the solving routine if Z3 is unable to decide for the satisfiability of a single component (line 9 and 10 of Algorithm 1). We return \(\textrm{unknown}\) if all components have been solved and Z3 was unable to decide for the satisfiability of a single component (line 13 and 14 of Algorithm 1). Otherwise, the overall result is returned in line 15 of Algorithm 1.

5 SMT solving in ProB

The integration of Z3 in ProB has shown benefits for solving B and Event-B constraints [64]. Yet, the encoding of sets as characteristic functions in SMT-LIB is suboptimal for several constraints such as the set cardinality or the minimum and maximum of a set of integers. We thus decided to implement state-of-the-art SMT solving techniques directly in ProB to tightly connect ProB’s constraint solving core for finding solutions with a CDCL(T)-based learning scheme to prune the search space early and improve the identification of contradictions. In the following, we describe our implementation of the lazy SMT approach for the B language in ProB. In the process, we also describe the standard techniques of SMT solving that we have implemented to address a broad audience.

5.1 SMT workflow in ProB

In Fig. 3, we present the main workflow diagram of our integration of SMT solving in ProB. The input to the SMT solver is a B formula, and ProB’s constraint solver (ProB CLP) is the only theory solver by default. Note that our SMT solver does not support the SMT-LIB language as input like other SMT solvers usually do. The dashed paths in the workflow diagram represent an optional static syntax analysis and symmetry breaking. Both techniques are independent and can be applied together, alone or not at all. The result of the workflow can be a satisfying assignment of variables (sat), a contradiction (unsat) or a timeout, which can either be caused by the SAT or theory solver. The specific stages and applied techniques of the workflow as well as our implementation are discussed in the remainder of this section.

Fig. 3
figure 3

A generalized workflow diagram of the direct implementation of SMT solving in ProB. The dashed paths represent an optional static syntax analysis and symmetry breaking. The workflow diagram does not show the use of features such as early pruning

Full size image

5.2 Preprocessing

First and foremost, B formulas need to be abstracted to SAT formulas for the Boolean satisfiability part of the SMT solver. We transform a propositional logic formula to conjunctive normal form as is the case for most SAT solvers. Additionally, we try to improve SMT solving by deducing different constraints that minimize the search space as explained in the following.

5.2.1 SAT abstraction

First, we rewrite formulas to only use conjunctions and disjunctions by rewriting implications and equivalences. We define two functions \(\textrm{T2B}(\alpha )\) and \(\textrm{B2T}(\beta )\) which translate a theory formula to propositional logic and vice versa. The function \(\textrm{T2B}\) replaces conjuncts and disjuncts by unique Boolean variables. For instance, let \(\alpha \) be the B predicate \(\textrm{x} \ne \textrm{y} \wedge \textrm{x} = \textrm{y}\). The Boolean abstraction is defined as \(\textrm{T2B}(\alpha ) = \lnot \textrm{A} \wedge \textrm{A}\) where \(\textrm{A} \equiv \textrm{x} = \textrm{y}\). The negation has been lifted from the inequality to reduce the amount of introduced Boolean variables. Furthermore, contradictions are possibly shifted from the theory level to the Boolean level which improves the performance by preventing unnecessary calls to a theory solver. We deem this to be one of the main improvements of SMT solving compared to saturation-based solving as performed by ProB’s constraint solver since the enumeration of theory domains is possibly prevented. This is desirable in the context of the B language and especially ProB’s constraint solver since domains can be unbounded, which possibly makes exhaustive domain enumeration and disproving infeasible. In order to reduce the amount of introduced Boolean variables, we normalize a formula by applying ProB’s internal rewriting rules for optimization before calling the function \(\textrm{T2B}\). For instance, the arguments of commutative operators are sorted lexicographically, obvious tautologies and contradictions are removed, and a subset of operators is used such as only using \(\le \) but not \(\ge \). Note that a quantifier in an SMT formula is abstracted by a single Boolean variable, e.g., introducing a variable \(\textrm{A} \equiv \forall \textrm{x}.(\textrm{x} \in \mathbb {N} \Rightarrow \textrm{x} \ge 0)\). A resulting SAT abstraction thus does not contain any quantifier.

A Boolean formula using only conjunctions and disjunctions can be transformed to conjunctive normal form by applying DeMorgan’s laws as well as the distributive law. Yet, rewriting disjunctions of nested conjunctions can lead to an exponential growth in the amount of clauses of a conjunctive normal form [69], which obviously can impact solver performance. Tseitin [69] has shown that the amount of clauses can be reduced by introducing artificial Boolean variables for specific formulas, which we implement as well. For instance, the distributive formula \((A \wedge B \wedge C) \vee (D \wedge E \wedge F)\) can be rewritten as \(((A \wedge B \wedge C) \vee P) \wedge (P \Leftrightarrow (D \wedge E \wedge F))\). Furthermore, nested equivalences and equivalences under disjunctions are rewritten in the same manner because they also expand to disjunctions of conjunctions.

5.2.2 Static symmetry breaking

A lot of logical formulas contain symmetries which lead to redundant paths in the search space [29]. In general, a logical formula is a symmetry of another formula if both formulas are syntactically equal except for variable permutations which maintain satisfiability. The size of the search space can be reduced by breaking symmetries either statically before the search or dynamically during the search. For instance, we can deduce the symmetry breaking constraint \(\textrm{x} \le \textrm{y}\) for the formula \(\textrm{x}< \textrm{y} \wedge \textrm{y} < \textrm{x}\) since the variables \(\textrm{x}\) and \(\textrm{y}\) can be exchanged without changing the semantics. We assume that B formulas often contain symmetries since the language is based on set theory and integer arithmetic, which provide several commutative operators. Static symmetry breaking is also capable of shifting theory contradictions to the Boolean level of an SMT solver which again prevents unnecessary enumerations of theory domains. Furthermore, breaking symmetries supports the theory solver. We thus deem symmetry breaking to be a valuable technique for an SMT solver in the context of the B language. While there exist techniques to break symmetries for SAT formulas, it is a pitfall to use such techniques in the context of SMT solving. The resulting symmetry breaking predicates for a SAT formula neglect the theory and can thus lead to spurious contradictions. For instance, consider the formula \(\textrm{A} \wedge (\textrm{B} \vee \textrm{C})\) with \(\textrm{A} \equiv \textrm{x} \in \mathbb {Z}\), \(\textrm{B} \equiv \textrm{x} > 1\), and \(\textrm{C} \equiv \textrm{x} \bmod 2 = 0\). It is valid to break the symmetry for the variables \(\textrm{B}\) and \(\textrm{C}\) in propositional logic, e.g., allowing the partial model \(\textrm{B} = \top \wedge \textrm{C} = \bot \) but forbidding \(\textrm{B} = \bot \wedge \textrm{C} = \top \). Yet, it is not correct to break this symmetry in the context of SMT solving since the corresponding theory constraints \(\textrm{x} > 1\) and \(\textrm{x} \bmod 2 = 0\) are not symmetric.

Fig. 4
figure 4

A colored graph to find static symmetry breaking predicates for the formula \(\textrm{x}< \textrm{y} \wedge \textrm{y} < \textrm{x}\) by computing graph automorphisms as proposed by Areces et al. [5]

Full size image

Areces et al. [5] presented an algorithm to statically compute symmetry breaking constraints for SMT formulas. The idea is to encode an SMT formula as a colored, directed, and acyclic graph where symmetries of the formula are described by automorphism groups. A graph automorphism is an isomorphism from a graph onto itself, i.e., a bijective mapping such that \((\textrm{v},\textrm{w}) \in \textrm{E} \Leftrightarrow (\textrm{h}(\textrm{v}), \textrm{h}(\textrm{w})) \in \textrm{E}\) for all edges \((\textrm{v},\textrm{w}) \in \textrm{E}\). There exist polynomial algorithms for detecting automorphisms in graphs with a bounded degree (number of a node’s incident edges) [53].

The process of symmetry breaking is split in two stages which are the creation and coloring of the graph [5]. A node is introduced for each interpreted and uninterpreted symbol as well as for constants. For instance, the colored graph for the above example \(\textrm{x}< \textrm{y} \wedge \textrm{y} < \textrm{x}\) can be seen in Fig. 4. We prefixed each node by a number as our implementation works with numbers instead of names for nodes. For the given example, we add one node for the uninterpreted symbols of the conjunction (number 0) and integer comparison (number 2), one node for the complete interpreted conjunction (number 1) and both integer comparisons (number 3 and 4), and one node for each argument (number 7 to 10) as well as the identifiers (number 5 and 6), which are treated as constants. The edges in the graph are set depending on the commutativity of operators. If an operator is not commutative, its arguments are ordered by adding one edge from the interpreted symbol node to the first argument’s node as well as an edge from the first argument’s node to the second one and so on. For instance, the integer comparisons in Fig. 4 are not commutative so that the second argument can only be reached through the first argument in the graph. Otherwise, one edge from the interpreted symbol node to each argument’s node is added as is the case for the conjunction in Fig. 4. The colors of the nodes are split into three classes for interpreted and uninterpreted symbols as well as nodes for interpreted symbols’ arguments. Each uninterpreted symbol is assigned a unique color, e.g., nodes number 0 and 2 in Fig. 4. We implemented this technique for B in ProB’s Prolog core and interface bliss [42] using its C++ API to compute graph automorphisms. Each automorphism group is represented as a set of generators by bliss. A symmetry breaking predicate is generated for each set of generators, which allows for only one symmetric solution. For the above example, bliss computes one automorphism group which is represented by the set of generators \(\{((3,4),(5,6),(7,9),(8,10))\}\). We can now generate a symmetry breaking predicate by deciding a variable ordering, e.g., lexicographic, and computing the image of each variable under the automorphism group. Here, the nodes with number 5 and 6 correspond to the variables \(\textrm{x}\) and \(\textrm{y}\). The image of \(\textrm{x}\) under the automorphism group is \(\textrm{y}\) so that we add the symmetry breaking constraint \(\textrm{x} \le \textrm{y}\). No symmetry breaking predicate is added for the variable \(\textrm{y}\) since its image under the automorphism group is the same variable \(\textrm{y}\).

Note that this technique also ensures finding nested symmetries. For instance, consider the predicate \(\textrm{z}> 1 \vee (\textrm{x}> \textrm{y} \wedge \textrm{y} > \textrm{x})\). The colored graph for symmetry breaking contains a top-level disjunction which right-hand side is the colored graph presented in Fig. 4. The disjunction’s left-hand side is a colored graph for the integer comparison constraint pointing to a node for the variable \(\textrm{z}\), which is independent of the disjunction’s right-hand side. We thus find the same graph automorphism as before. Now, consider that the disjunction’s left-hand side is the constraint \(\textrm{x} > 1\). We then add an edge from the disjunction’s left-hand side to the node of the variable \(\textrm{x}\) in the graph presented in Fig. 4. This breaks the graph automorphism since the variables \(\textrm{x}\) and \(\textrm{y}\) cannot be exchanged anymore without changing the semantics of the predicate. The described technique thus correctly recognizes that this predicate does not contain any symmetries between variables.

5.2.3 Static syntax analysis

Besides applying static symmetry breaking, we extend the static syntax analysis to deduce constraints which imply one another but do not necessarily break symmetries. For instance, we can deduce the constraint \(\textrm{x}< \textrm{y} \Rightarrow \lnot (\textrm{y} < \textrm{x})\) for the formula \(\textrm{x}< \textrm{y} \wedge \textrm{y} < \textrm{x}\). This constraint moves the contradiction from the theory level to the SAT level of the SMT solver which is not the case for the symmetry breaking constraint \(\textrm{x} \le \textrm{y}\). We thus deem this additional static analysis to be valuable for SMT solving in the context of B and ProB’s constraint solver since possibly more enumerations of domains in the theory solver are prevented. Note that this syntax analysis only considers subformulas that are present in the input formula and does not introduce new formulas. For instance, we do not deduce the constraint \(\textrm{x} < \textrm{y} \Rightarrow \lnot (\textrm{y} \le \textrm{x})\) since \(\textrm{y} \le \textrm{x}\) is not part of the input formula.

For this analysis, we only consider direct implications of pairs of formulas which share at least one variable. Due to performance regards, we do not consider transitive or other variable dependencies between formulas. Furthermore, we define a set of operators which we want to check for whether they imply one another. In particular, we use the equality, set membership, subset relations, and integer comparisons. We collect all candidate constraints and group them by their types as well as the amount of used variables, which is either one or two. Afterward, we check for all pairs of constraints \(\mathrm {c_1}\), \(\mathrm {c_2}\) with \(\mathrm {c_1} \ne \mathrm {c_2}\) in each set of candidates if \(\mathrm {c_1} \Rightarrow \mathrm {c_2}\), \(\mathrm {c_1} \Rightarrow \lnot \mathrm {c_2}\), \(\mathrm {c_2} \Rightarrow \mathrm {c_1}\), and/or \(\mathrm {c_2} \Rightarrow \lnot \mathrm {c_1}\). For the above example, this results in solving the constraint \(\forall (\textrm{x},\textrm{y}).(\textrm{x} \in \mathbb {Z} \wedge \textrm{y} \in \mathbb {Z} \Rightarrow (\textrm{x}< \textrm{y} \Rightarrow \lnot (\textrm{y} < \textrm{x})))\). Alternatively, a counter example can be searched for the negated formula resulting in an existentially quantified formula. To prevent possible performance issues due to the enumeration of (unbounded) domains, we use ProB’s prover [49] to prove such constraints instead of its constraint solver. Therewith, we are able to drop the universal or existential quantifier to prove the actual constraint.

5.3 SAT solving

The problem of satisfiability solving is NP-completeness and many possible improvements of decision procedures have been suggested to date. The basis of our SAT solver is the solver presented by Howe and King [40] which implements the watched literals scheme [58] by using coroutines in Prolog. We extend this implementation by different variable selection heuristics, conflict-driven clause learning with the reduction of learned clauses, and restarts with phase saving.

5.3.1 Watched literals

The DPLL algorithm simplifies the clauses of a conjunctive normal form and searches for unit propagations after each variable decision. This results in traversing the complete set of clauses in the worst case, which is a bottleneck for performance. The watched literals scheme [58] improves this issue by storing pointers to literals of each clause. For each literal, we have to remember all the clauses where the literal is watched. In Prolog, this can be implemented efficiently by using coroutines [40]. For this, the set of clauses is traversed once to set up a coroutine for each clause that watches literals. This results in delaying the execution until a watched literal becomes nonvariable. If a watched literal of a clause becomes false and the other watched literal is not true, we search for another unassigned literal to watch in this clause, which effectively is Boolean resolution. A clause is identified as a unit clause if there is no other literal to watch. We watch two literals as was implemented by Howe and King [40]. It should be noted that the watched literals scheme does not guarantee the most amount of simplifications for each clause. If a variable is propagated but not watched in a specific clause, this clause will not be simplified. However, this is not an issue since a clause will be simplified as soon as a variable that has already been propagated is selected to be watched.

5.3.2 Conflict-driven clause learning

The DPLL algorithm decides the value of a selected variable if no unit clause is present. This decision poses a choicepoint and leads to backtracking when finding a conflict. Yet, the last decision might not be the root cause of a conflict. In this case, chronological backtracking leads to unnecessary overhead. Furthermore, a constraint solver should not find the same conflict again in an ongoing search. The idea of conflict-driven clause learning (CDCL) [65, 66] is to analyze the root cause of a conflict clause to learn a formula which prevents this conflict as well as a level in the search tree to backjump to. Learning means to add a clause to the current set of clauses. We deem clause learning to be one of the main improvements compared to ProB’s constraint solver since it uses chronological backtracking and does not learn from conflicts. This often prevents ProB’s constraint solver from disproving formulas, especially when using unbounded domains. In fact, this is a general downside of plain saturation-based solvers.

The cause of a Boolean conflict in the DPLL algorithm can be analyzed by applying Boolean resolution in a certain order or by building and analyzing an implication graph [66]. For both of these techniques, we have to keep track of the sequence of variable assignments, the clause which led to each specific assignment of a variable, the level of each variable propagation, the assigned polarity, and the type of the propagation, which is either a branching decision or a unit propagation. We decided to analyze conflicts by implementing the concept of Boolean resolution, which is more performant since no implication graph has to be built.

Fig. 5
figure 5

Exemplary conflict analysis using Boolean resolution for the formula \((\lnot \textrm{A} \vee \lnot \textrm{B} \vee \lnot \textrm{C} \vee \lnot \textrm{D}) \wedge (\textrm{D} \vee \lnot \textrm{E}) \wedge (\lnot \textrm{A} \vee \textrm{D} \vee \textrm{F}) \wedge (\textrm{E} \vee \lnot \textrm{F}) \wedge (\textrm{C} \vee \lnot \textrm{D})\) with the sequence of variable assignments \(\textrm{A}^{\textrm{d}}, \textrm{B}^{\textrm{d}}, \textrm{C}^{\textrm{d}}, \lnot \textrm{D}, \lnot \textrm{E}\), and \(\textrm{F}\). The clause \((\textrm{E} \vee \lnot \textrm{F})\) is a conflict. The superscript “d” indicates that this variable was assigned by decision. The other variables were assigned by unit propagation. Each step corresponds to a Boolean resolution between two clauses while the variables used for resolution are underlined. The example shows the complete conflict analysis, which can be stopped after deducing \((\lnot \textrm{A} \vee \textrm{D})\)

Full size image

In both techniques, the idea is to trace the antecedent variable assignments that led to a specific unit propagation which is involved in the conflict. For instance, consider the propositional logic formula \((\lnot \textrm{A} \vee \lnot \textrm{B} \vee \lnot \textrm{C} \vee \lnot \textrm{D}) \wedge (\textrm{D} \vee \lnot \textrm{E}) \wedge (\lnot \textrm{A} \vee \textrm{D} \vee \textrm{F}) \wedge (\textrm{E} \vee \lnot \textrm{F}) \wedge (\textrm{C} \vee \lnot \textrm{D})\). Further, assume that the SAT solver made the sequence of assignments \(\textrm{A}^{\textrm{d}}, \textrm{B}^{\textrm{d}}, \textrm{C}^{\textrm{d}}, \lnot \textrm{D}, \lnot \textrm{E}\), and \(\textrm{F}\). A superscript “\(\textrm{d}\)” represents a variable assignment made by decision while all other assignments are caused by unit propagation. The assignment of variables constitutes a contradiction on decision level 2 where \(\textrm{E} \vee \lnot \textrm{F}\) is the conflicting clause. Conflict analysis is performed backwards starting from the conflicting clause. The antecedent assignments of the unit propagation of \(\textrm{F}\) are the decision of \(\textrm{A}\) and the unit propagation of \(\lnot \textrm{D}\) due to the clause \(\lnot \textrm{A} \vee \textrm{D} \vee \textrm{F}\). When performing Boolean resolution with this clause and the conflicting clause, we derive a new clause \(\lnot \textrm{A} \vee \textrm{D} \vee \textrm{E}\) as can be seen in Fig. 5. The analysis can be stopped once a clause has been derived that contains only one variable which has been assigned on the conflict level. Variables assigned by decision are not resolved by Boolean resolution. In the currently derived clause, the variables \(\textrm{D}\) and \(\textrm{E}\) are both assigned on level 2 so that Boolean resolution is continued. For instance, the variable \(\textrm{E}\) can be resolved by the clause \(\textrm{D} \vee \lnot \textrm{E}\) resulting in \(\lnot \textrm{A} \vee \textrm{D}\). This clause contains only the variable \(\textrm{D}\) that has been assigned on the current conflict level. We can thus terminate and learn the derived clause. The level in the search tree to backjump to is the highest decision level in the learned clause other than the conflict level. In our example, we backjump to the decision of \(\textrm{A}\) on level 0. This results in a unit propagation which changes the assignment of the identified root cause of the conflict, i.e., the assignment \(\lnot \textrm{D}\) in our example. One special case is that we always backjump to level 0 when learning a unit clause. This technique guarantees to find the shortest backjump clause by stopping after the first unique implication point (UIP) [74]. A unique implication point is a unit propagated variable assignment which is part of every path between the last variable decision that occurred before the unit propagation and the conflicting assignment. The complete conflict analysis for our example including one more Boolean resolution can be seen in Fig. 5. While the clause \(\lnot \textrm{A} \vee \lnot \textrm{B} \vee \lnot \textrm{C}\) prevents the conflict, the clause learned at the first UIP is more concise. Furthermore, terminating after the first UIP prevents unnecessary computations [74].

5.3.3 Reducing learned clauses

An SMT solver possibly uncovers many conflicts before deciding for satisfiability. While learning clauses from conflicts reduces the search space, the accumulation of too many clauses can slow down the search and can lead to an explosion of consumed memory. It is thus important to forget learned clauses once in a while. Audemard and Simon [8] proposed a technique to forget weak clauses which uses the measure of the literal block distance (LBD) to definitely keep strong clauses that we implement. The literal block distance of a clause is the number of different decision levels in this clause [8]. The authors state that clauses with an LBD of two are most important because they connect two decision levels. In particular, clauses with a small LBD, e.g., between two and five, should not be removed. The half of all other clauses is removed occasionally considering the amount of performed reductions of the set of learned clauses so far. In particular, an SMT solver forgets fewer clauses over time. The LBD score of a clause is computed and stored when it is learned and thus refers to the state of the search tree at that time.

5.3.4 Variable selection heuristics

The selection of the next variable and polarity to assign influences the performance of SAT solving. Many variable selection heuristics have been proposed to date. Moskewicz et al. evaluated different variable selection heuristics during the development of the SAT solver Chaff and proposed an improved heuristic called the variable state independent decaying sum (VSIDS) [58]. The VSIDS heuristic assigns a float value to each variable where a variable with the highest score is assigned next. Initially, all values are set to the corresponding variable’s occurrences among all clauses, which is how we implement it. Alternatively, all values can be initialized with a score of zero to only use knowledge gained during an ongoing search. The main idea of the VSIDS heuristic is to favor variables which took part in recent conflict analyses. In order to do so, the scores of variables that were involved in conflict analyses are increased by a constant value for every \(\textrm{i}\)-th conflict. The parameter \(\textrm{i}\) is usually set to one. Furthermore, all scores are periodically divided by a constant value, e.g., by two, to favor variables that occurred in recent conflict analyses. Note that it is also possible to store values as described above for each variable with a specific polarity. As first tests did not show any performance improvement but rather drawback, we decided to store values for variables only and initially assign decision variables a positive polarity.

Biere proposed an improvement of the VSIDS heuristic called the exponential variable-state independent decaying sum (EVSIDS) [13]. The heuristic adds \(\textrm{f}^{-\textrm{i}}\) to each variable’s score at each \(\textrm{i}\)-th conflict instead of a constant value. Here, \(\textrm{f}\) is a float between zero and one which is usually around 0.9 [13]. This adaption favors variables occurring in recent conflict analyses in the long run and thus does not require worsening scores as is done in the VSIDS heuristic. This is a benefit since it prevents updating heuristic values, which is additional overhead.

While many other heuristics have been built to improve the VSIDS heuristic, Biere and Fröhlich have shown empirically that the EVSIDS heuristic can perform as well as other heuristics in practice [14]. We thus decided to implement the EVSIDS heuristic in our SAT solver. Furthermore, we achieved better results when only increasing the scores of variables occurring in a computed backjump clause instead of all variables that occurred during the conflict analysis.

5.3.5 Restarts with phase saving

The decision for the next variable to assign during SAT solving is guided by a heuristic and thus not necessarily the best decision for all problem instances. In order to recover from bad branching decisions, modern SAT solvers implement restart policies for which the solver backjumps to level 0 in the search tree. Here, the crucial point is to decide how often a search should be restarted to guarantee converging to a solution.

Audemard and Simon [9] proposed a restart policy that includes knowledge gained during a search by using the literal block distance of learned clauses (cf. Sect. 5.3.4). The idea is to restart a search if new learned clauses do not provide much new knowledge. This is implemented by comparing a current short-term average LBD score with a long term average LBD score. In order to prevent restarting right before a solution would have been found, the authors further suggest tracking the size of the stack of variable assignments. The idea is to recognize if a partial assignment is considerably closer to a model than was the case for any prior partial assignment [9].

Pipatsrisawat and Darwiche further observed that frequent restarts can decrease the performance of SAT solving in some cases [62]. To counter this, the authors suggested a partial component caching scheme for SAT solvers [62] which we implement as well. Here, all variable assignments made by decisions are cached. A SAT solver then picks the cached polarity first when deciding to branch on a variable. This guides the search in a similar direction than before and prevents solving components of a formula again. If no polarity is cached for a variable, the SAT solver uses the implemented heuristic that assigns a polarity. We implement phase saving by asserting and retracting facts in Prolog to cache variable assignments made by decision.

5.4 SMT solving

The variables assigned in a (partial) model of a Boolean abstraction are conjoined and translated to first-order logic using the function \(\textrm{B2T}\) defined in Sect. 5.2.1. Afterward, the derived SMT formula is solved by one or more theory solvers.

5.4.1 Early pruning

One bottleneck for performance is to wait for the SAT solver to find a (partial) model before sending formulas to the theory solvers. The implementation spends unnecessary time in the SAT solver in cases where a theory solver can already decide for unsatisfiability using a partial assignment. One important implementation detail is thus to send a constraint to a theory solver as soon as its corresponding Boolean variable is assigned by the SAT solver, this is called early pruning [7]. Theory solvers need to be set up incrementally for early pruning, which is possible with ProB’s constraint solver. We implement early pruning by using coroutines in Prolog for each Boolean variable which abstracts a B formula and use ProB’s constraint solver as the only theory solver by default. Such a coroutine is defined to be triggered if the corresponding Boolean variable is set to either true or false. In this case, the corresponding B formula or its negation is incrementally added to ProB’s constraint solver. We ensure that the effect of coroutines as well as incrementally adding constraints is undone on backtracking, which is simple due to the nature of Prolog being based on backtracking.

One implementation detail is that we connect the SAT variables with the theory solver after possible unit propagations on level 0 of the search tree since these variables can be propagated to the theory solver directly. If we connect the SAT and theory solver before the first unit propagations, we would add the additional overhead of registering predicates in the theory solver for that the solver assumes that they can be either true or false although their truth value is already established.

We refer to the phase of incrementally adding constraints to ProB’s constraint solver as its deterministic propagation phase. Here, the solver is already able to identify theory conflicts but does not ground domains to find an exact solution. It is therefore possible that a conflict is only recognized after grounding the domains of all variables. We enter the grounding phase of ProB’s constraint solver if the SAT solver reports satisfiability for the Boolean abstraction of the input formula. The SMT solver has found a model if the SAT solver and the theory solver report satisfiability. If a contradiction is found by a theory solver (theory conflict), the assignment of SAT variables can be used as a conflict clause for conflict-driven clause learning as described in Sect. 5.3.2.

5.4.2 Unsatisfiable core

When learning from a theory conflict, not necessarily all assigned variables contribute to the actual conflict. In order to learn strong clauses from theory conflicts, it is important to find an unsatisfiable core of a theory conflict before translating it to propositional logic. In particular, a minimal unsatisfiable core is desired. A locally minimal unsatisfiable core of a formula is a subformula which still describes the contradiction but cannot be reduced any further without making it satisfiable. The globally minimal unsatisfiable core of a formula is the smallest formula of all local minima.

One key feature of ProB is that it retains the well-definedness of unsatisfiable cores according to the B language. This is important in the context of clause learning from B formulas since a theory solver would otherwise throw a well-definedness error or would not be able to decide for the satisfiability of a formula when learning a not well-defined clause. For instance, learning a unit clause which corresponds to a theory formula that divides by zero would result in a well-definedness error.

ProB implements a technique to find an unsatisfiable core by gradually removing subformulas from the end of an unsatisfiable formula. Each derived formula is successively checked for satisfiability by ProB’s constraint solver. If a derived formula is satisfiable, we know that the removed subformula is definitely part of the unsatisfiable core. Otherwise, we can remove this subformula from the unsatisfiable core since it does not contribute to the unsatisfiability of the overall formula. If removing a subformula results in a well-definedness error, we know that we have to keep this subformula in order to ensure the well-definedness of the unsatisfiable core. Furthermore, it can be the case that the constraint solver is not able to decide for the satisfiability of a derived formula within a reasonable amount of time. We thus use a small solver timeout (25ms) to decide for the satisfiability of a derived formula to prevent exceeding the predefined solver timeout, and keep a subformula if ProB’s constraint solver cannot decide for the satisfiability in time. In this case, an unsatisfiable core might contain a subformula that does not contribute to the unsatisfiability of the formula.

We deem it to be sufficient for conflict analysis to compute a locally minimal unsatisfiable core instead of a global minimum to save performance.

Another aspect to consider when learning from theory conflicts is the time that a theory conflict is detected. When learning from Boolean conflicts in the SAT solver, the last propagated variable is always part of the actual conflict. Yet, this is not necessarily the case for theory conflicts, especially when using ProB’s constraint solver which has to consider the well-definedness of constraints. We reify Boolean variables with ProB’s constraint solver as explained in Sect. 5.4.1, which is part of the deterministic propagation phase. Here, domains are not necessarily enumerated to prevent exceeding the predefined solver timeout. When propagating a constraint, it can be the case that other constraints are sent to the solver afterwards which allow for a stronger propagation. For instance, consider the propagation of the two constraints \(\textrm{r} \in 1..\textrm{n} \mathbin \rightarrow \mathbb {Z}\) and \(\textrm{x} \in \textrm{dom}(\textrm{r})\). The constraint solver is currently not able to decide for the satisfiability of these constraints since the domain of \(\textrm{r}\) is unknown. After propagating another constraint \(\textrm{n} = 0\), the constraint solver is able to do so.

A conflict may not be detected until the domains of variables are grounded as described in Sect. 5.4.1, especially when constraints entail a well-definedness condition such as a function application. It can thus be the case that the Boolean propagation from the SAT solver that caused the propagation of the conflicting theory constraints was not on the last decision level. For instance, consider the two constraints from above but let \(\textrm{n}\) be an element of the interval 0..2. The constraint solver can now first decide for the satisfiability of all constraints after the variable \(\textrm{n}\) has been grounded. Yet, there can be an arbitrary amount of other propagations in the SAT solver which do not affect these constraints but are necessary to solve the whole Boolean formula. We thus do not necessarily consider the last decision level of the SAT solver as the level where a theory conflict occurred if the conflict is detected in the grounding phase after the SAT solver has found a solution. Instead, we compute the maximum decision level of the variables that are part of the unsatisfiable core of the theory conflict, which is then used for conflict-driven clause learning.

5.4.3 Theory propagation

Until now, the only knowledge passed from the theory solver to the SAT solver is gained by theory conflicts. Yet, a theory solver might deduce formulas which provide new knowledge for the SAT solver as well. Sending such formulas to the SAT solver is called theory propagation [6, 60]. We extend the coroutines which are set up in Prolog for each SAT variable to be triggered if the corresponding SMT formula becomes true as well. For instance, let \(\varPhi := \textrm{x}<0 \wedge \textrm{x}<1\) be a B predicate and \(\textrm{A} \wedge \textrm{B}\) be the corresponding propositional logic formula with \(\textrm{A} \equiv \textrm{x}<0\) and \(\textrm{B} \equiv \textrm{x}<1\). We set up two coroutines for the SAT variables \(\textrm{A}\) and \(\textrm{B}\) that are reified with the corresponding theory formulas. The SAT solver possibly starts with setting A to true which triggers the corresponding coroutine to send the formula \(\textrm{x}<0\) to ProB’s constraint solver. In this case, the solver is able to deduce that the formula \(\textrm{x}<1\) has to be true as well. This triggers the other coroutine which now propagates knowledge from the theory solver to the SAT solver by setting the variable \(\textrm{B}\) to true. Note that one important aspect of theory propagation is to only deduce constraints which already occur in the original formula. Otherwise, new SAT variables would need to be introduced for each new SMT formula. This unnecessarily increases the search space since no new knowledge can be gained by the SAT solver from such formulas. For instance, we do not want to deduce \(\textrm{x}<2\) for the above example.

figure b

The Prolog code that is responsible for the theory propagation of a “less than” comparison in ProB’s constraint solver can be seen in Listing 1. The entry point is the Prolog predicate check_arith_op/4. First, a coroutine check_lt/3 is set up which is suspended as long as the first and second, or the second and third arguments are variables (indicated by the dash in the block declaration). If the third argument is nonvariable, we know the truth value of the integer comparison and enforce that the Prolog variable \(\textrm{X}\) is lower than \(\textrm{Y}\) (line 13) or that \(\textrm{Y}\) is lower than or equal to \(\textrm{X}\) (line 14). Otherwise, both integer variables have concrete values and the integer comparison is checked to set the result variable to either true (line 15) or false (line 16). In line 4 of Listing 1, a CLP(FD) constraint is set up to reify (#\(<=>\)) the integer comparison with a two-valued result variable which is either 0 (false) or 1 (true). Afterward, a coroutine prop_pred_01/2 is set up to be triggered if one of its two arguments becomes nonvariable. The first argument corresponds to the overall result of the integer comparison returned in check_arith_op/4 (line 1) while the second argument corresponds to the reified two-valued variable. Here, the actual theory propagation is implemented which reifies the truth value of the integer comparison in CLP(FD) with the integer comparison’s result in ProB’s constraint solver. In our example above, check_arith_op/4 is called for each integer comparison. After propagating \(\textrm{x}<0\) to ProB’s constraint solver, CLP(FD) enforces the constraint X #< 1, which has been set up in line 4 of Listing 1, to be true as well. This triggers the corresponding two-valued variable to be set to 1 which unblocks the coroutine prop_pred_01/2 that now sets the overall result of the integer comparison \(\textrm{x} < 1\) to true. Thus, this truth value has been propagated by ProB’s constraint solver which now triggers the coroutine that is connected to the SAT variable to set this variable to true.

5.4.4 Explaining theory propagations

It can be the case that a conflict clause contains a SAT variable which has been propagated by a theory solver when using theory propagation with CDCL. In the SAT solver, this propagation is the same as a unit propagation since the theory propagation is a logical consequence of the current assignment of variables. In order to analyze a conflicting assignment, we need to know which clause led to the unit propagation of a variable as explained in Sect. 5.3.2. However, ProB’s constraint solver does not provide an explanation for a theory propagation.

We thus implement a technique to find explanations for B formulas by computing an unsatisfiable core. Let \(\phi \) be an SMT formula which has been propagated by a theory solver, and \(\varPhi \) be the SMT formula corresponding to the current partial assignment without \(\phi \). In order to explain the propagation of \(\phi \), we compute the unsatisfiable core of \(\varPhi \wedge \lnot \phi \). For instance, let \(\varPhi := \textrm{x}<10 \wedge \textrm{x}>1\) and consider the formula \(\textrm{x}<10 \wedge \textrm{x}>1 \wedge \textrm{x}>0\). Furthermore, assume that \(\textrm{x}<10\) and \(\textrm{x}>1\) have been propagated by the SAT solver while \(\phi := \textrm{x}>0\) has been propagated by a theory solver after \(\textrm{x}>1\) has been set. The unsatisfiable core of the formula \(\textrm{x}<10 \wedge \textrm{x}>1 \wedge \lnot \textrm{x}>0\) is \(\textrm{x}>1 \wedge \lnot \textrm{x}>0\). By removing the negated theory propagation, we can conclude that \(\textrm{x}>1\) is the explanation for the theory propagation of \(\textrm{x}>0\). We are then able to add the Boolean abstraction of the negated theory formula \(\lnot \textrm{x}>1 \vee \textrm{x}>0\) to the SAT solver which now enforces a unit propagation corresponding to the theory propagation.

Computing theory explanations by default is too expensive and not necessary in most cases. We thus explain theory propagations lazily to improve performance, i.e., we only explain a theory propagation if conflict-driven clause learning requires an explanation for conflict analysis.

5.4.5 Well-defined SMT solving

The B language has many operators that entail a well-definedness condition. For instance, a well-defined function application requires that the applied element is in the domain of the function. Not well-defined constraints are neither true nor false in ProB’s constraint solver. As explained in Sect. 5.4.1, the SMT solver sends single B predicates to the theory solver via constraint reification. If a predicate is sent to ProB’s constraint solver which is not well-defined, the SMT solver possibly reports unsatisfiability for satisfiable constraints. The reason is that the SAT solver requires a variable to be either satisfiable or unsatisfiable, which is not the case if a reified predicate is not well-defined. For instance, consider the B formula \((0 \in \textrm{dom}(\emptyset ) \wedge (\emptyset (0) = \textrm{a} \Rightarrow \lnot (\emptyset (0) < \textrm{a}))) \vee \textrm{b} = 0\). Note that functions in B are relations, which in turn are sets of pairs. The empty set can thus be considered a function. While the function application in this formula is not well-defined, the whole formula is well-defined since the not well-defined function application is guarded by the corresponding well-definedness condition \(0 \in \textrm{dom}(\emptyset )\). In B, constraints ensuring the well-definedness are placed before the operators that entail the well-definedness condition. Yet, this structure usually gets lost when transforming a B formula to conjunctive normal form as is required for SMT solving. Further, the SAT solver might propagate a predicate that entails a well-definedness condition although the well-definedness is not ensured yet. For instance, the SMT solver might start with propagating the single predicate \(\emptyset (0) = \textrm{a}\). In this case, ProB’s constraint solver would neither confirm the satisfiability nor the unsatisfiability of this predicate since it is not well-defined. This results in finding a spurious counterexample in the SAT solver. For the above example, the solver would report unsatisfiability for the whole formula after evaluating the left-hand side of the disjunction although \(\textrm{b} = 0\) is a solution.

We counter this issue by adding constraints that ensure the well-definedness for each predicate that is reified with a SAT variable and entails a well-definedness condition. This ensures that ProB’s constraint solver is able to decide for the satisfiability of a predicate. For instance, for the above formula we would usually introduce four SAT variables for the unique predicates occurring in the formula, i.e., \(\textrm{A} \equiv 0 \in \textrm{dom}(\emptyset )\), \(\textrm{B} \equiv \emptyset (0) = \textrm{a}\), \(\textrm{C} \equiv \emptyset (0) < \textrm{a}\), and \(\textrm{D} \equiv \textrm{b} = 0\). In order to ensure the well-definedness of each predicate independently of the whole formula, we now adapt the predicates that are reified with ProB’s constraint solver for the second and third predicate to be \(0 \in \textrm{dom}(\emptyset ) \wedge \emptyset (0) = \textrm{a}\) and \(0 \in \textrm{dom}(\emptyset ) \wedge \emptyset (0) < \textrm{a}\).

Additionally, we enforce the well-definedness in the SAT solver by adding an implication for each predicate entailing a well-definedness condition to the conjunctive normal form. This ensures the unit propagation of a well-definedness condition as soon as the predicate entailing the condition is propagated by the SAT solver. For the above example, this results in adding the implications \(\textrm{B} \Rightarrow \textrm{A}\) and \(\textrm{C} \Rightarrow \textrm{A}\). If an input formula is not well-defined, we introduce a new SAT variable for corresponding well-definedness conditions. For instance, the above formula is not well-defined without the predicate \(0 \in \textrm{dom}(\emptyset )\). We then proceed in the same way as described above but introduce a new SAT variable corresponding to the variable \(\textrm{A}\), which is not present in the original formula. ProB’s SMT solver thus always solves well-defined formulas.

6 Additional theory solver

In SMT solving, theory constraints are usually sent to a single dedicated theory solver. Alternatively, constraints can be sent to several solvers which support the same theory to improve performance by using the result of the fastest solver. The only prerequisite is that a theory solver can be used incrementally as described in Sect. 5.4.1.

Empirical results have shown that ProB’s CLP(FD) backend sometimes lacks performance for unsatisfiable constraints over unbounded integer domains. We thus decided to integrate an alternative theory solver for the integer difference logic (IDL) [48, 57] which does not enumerate domains but uses a solver based on graphs and negative cycle detection [70]. We do not have evidence that such constraints often occur in B but see that this alternative technique can improve constraint solving over unbounded integer domains compared to CLP(FD). Moreover, this solver can be used as a fallback in cases where ProB’s constraint solver generates a virtual timeout.

In the following, we describe the theoretical foundation of the implemented constraint solver for IDL constraints and its integration in ProB’s SMT solver.

6.1 Integer difference logic solver

Integer difference logic [48, 57] has shown to be useful, e.g., for reasoning about clocks in timed systems. Atomic IDL constraints are of the form \(\mathrm {v_i} - \mathrm {v_j} \le \textrm{c}\), where \(\mathrm {v_i}\) and \(\mathrm {v_j}\) are integer variables and \(\textrm{c}\) is a constant integer value. Conjunction and negation are the only admitted logical operators.

Many integer constraints can be rewritten to integer difference logic. This might require the introduction of an artificial variable for the constant 0. For instance, the integer constraint \(\textrm{x} < 1\) can be rewritten to \(\textrm{x} - \textrm{zero} \le 0\), where \(\textrm{zero}\) is the artificial variable.

Wang et al. presented a solver for integer difference logic based on weighted directed graphs with an algorithm for incremental negative cycle detection [70].

Each node of a graph represents an integer variable. An edge \((\mathrm {v_j},\mathrm {v_i})\) in a graph with weight \(\textrm{c}\) describes the constraint \(\mathrm {v_i} - \mathrm {v_j} \le \textrm{c}\), while the negated constraint is described by the edge \((\mathrm {v_i},\mathrm {v_j})\) with weight \(- \textrm{c} - 1\). A difference logic constraint system is satisfiable if its corresponding graph does not contain a negative cycle. If this is the case, the shortest path to a variable yields its solution. Otherwise, the conjunction of constraints corresponding to the edges of the negative cycle is an unsatisfiable core. As can be seen, this technique provides an unsatisfiable core for unsatisfiable formulas without further computations. This makes this technique especially suited for conflict-driven clause learning, where unsatisfiable cores have to be computed when a theory conflict occurs (see Sect. 5.4.2).

The authors further propose an incremental decision procedure based on the Bellman–Ford algorithm [12, 33]. The algorithm uses the fact that any created cycle must use the recently added edge [70].

Fig. 6
figure 6

A graph representation of the integer difference logic constraint \(\textrm{x} \in \mathbb {Z} \wedge \textrm{x}>\textrm{y} \wedge \textrm{y}>\textrm{x}\) as suggested by Wang et al. [70]. The graph contains a negative cycle which means that the corresponding constraint is unsatisfiable. The constraints corresponding to the edges of the negative cycle are the unsatisfiable core

Full size image

For instance, consider the B constraint \(\textrm{x} \in \mathbb {Z} \wedge \textrm{x}>\textrm{y} \wedge \textrm{y}>\textrm{x}\). ProB’s constraint solver is not able to solve this constraint with its default CLP(FD) backend since the domains of x and y cannot be narrowed down. The new theory solver first rewrites constraints to integer difference logic if possible. The above constraint is rewritten to \(\textrm{y} - \textrm{x} \le -1~ \wedge ~ \textrm{x} - \textrm{y} \le -1\). Afterward, we create nodes for the variables \(\textrm{x}\) and \(\textrm{y}\) and edges for the two constraints as can be seen in Fig. 6. It can be easily seen that the graph contains a negative cycle between the variables \(\textrm{x}\) and \(\textrm{y}\), i.e., the path \([(\textrm{x},\textrm{y}),(\textrm{y},\textrm{x})]\). This means that the constraint is not satisfiable and the conjunction of constraints corresponding to the edges of the negative cycle are an unsatisfiable core. For our example, the unsatisfiable core is \(\textrm{x}>\textrm{y} \wedge \textrm{y}>\textrm{x}\).

6.2 Theory solver integration

We decided to use the aforementioned theory solver in addition to ProB’s constraint solver, i.e., we send integer difference logic constraints to both theory solvers. For this, we extend the coroutines which are set up for each reification between a SAT variable and theory constraint to check if the constraint can be translated to integer difference logic and distribute constraints accordingly.

We observed severe performance degradation when not all integer constraints can be translated to IDL. For instance, consider the formula \(\textrm{a}-\textrm{b} \le -1 \wedge \textrm{a}*\textrm{b}>10000\). The first conjunct can be sent to both theory solvers while the second one cannot be rewritten to IDL. The graph-based solver for integer difference logic finds the partial model \(\textrm{a}=1 \wedge \textrm{b}=2\) which is not accepted by ProB’s constraint solver because of the constraint \(\textrm{a}*\textrm{b}>10000\). The graph-based solver would now enumerate nearly 10,000 partial models which are refuted by ProB’s constraint solver until finding a solution, e.g., \(\textrm{a}=1 \wedge \textrm{b}=10001\).

To solve this issue, we decided to integrate the integer difference logic solver as follows: IDL constraints are sent to both theory solvers. In case the graph-based solver reports unsatisfiability, the unsatisfiable core is extracted and used as a conflict clause. If the SAT solver and both theory solvers report satisfiability in the deterministic propagation phase, we first propagate the partial model found by the graph-based IDL solver to ProB’s constraint solver. Hereby, we want to prevent a possible (virtual) timeout when grounding domains. SMT solving is finished if this solution is accepted. Otherwise, we do not backtrack in the graph-based solver, but let ProB’s constraint solver enumerate a solution. We fall back to the graph-based solver only if ProB’s constraint solver fails to find a solution because of generating a virtual timeout due to unbounded integer domains.

7 Empirical evaluation

In the following, we present an empirical evaluation of the new integration of Z3 in ProB including the new translation from B to SMT-LIB as well as the direct implementation of SMT solving in ProB.Footnote 3

7.1 Integration of Z3

We split the evaluation of the integration of Z3 in ProB in three categories. First, we focus on the downsides of our employed translation of selected language constructs which we deem to be responsible for a possibly bad performance when solving constraints. Second, we present selected constraints for which the integration of Z3 is superior to ProB’s constraint solver regarding constraint solving to emphasize specific strengths. Third, we evaluate the performance of our translation using a variety of benchmarks from bounded model checking.

7.1.1 Weaknesses of the integration of Z3

The weaknesses of the integration of Z3 are mainly caused by the employed encoding of sets. Most of B’s set theoretic operators are not supported by SMT-LIB such as computing a power set or the cardinality of a set. As discussed in Sects. 3.1 and 4.1, this can lead to involved quantified constraints for which Z3 is not able to find a solution. We thus employ several rewriting rules and a preprocessing phase to prevent sending quantified formulas to Z3 if this is not necessary. The benefit of this preprocessing is discussed in the following.

Finite Sets. The former and new translation from B to SMT-LIB both support infinite sets. It could be shown by Krings and Leuschel [45] that Z3 is able to solve a variety of B constraints over infinite domains which ProB’s constraint solver is not able to solve, especially when a formula is a contradiction. However, the support for infinite domains leads to involved translations for finite set constraints such as the minimum, maximum or the cardinality of a finite set. For instance, the current translation searches for a total bijection mapping sets to their cardinalities to compute the cardinality of a set [45]. A total bijection is rewritten using B quantifiers before the translation to SMT-LIB.

Since Z3 lacks performance when solving quantified formulas, Z3 often fails to find a solution for translated B constraints using set cardinalities. For instance, Z3 is not able to solve the translation of \(\textrm{q} \in 1\mathrel {{.}\,{.}}3 \mathbin \rightarrow 1\mathrel {{.}\,{.}}3 \wedge \textrm{card}(\textrm{ran}(\textrm{q}))=3\). With the use of the rewriting rule for the cardinality of range constraints defined in Sect. 4.1, Z3 is able to solve the constraint in several milliseconds as is ProB’s constraint solver. The rewriting rule replaces the cardinality constraint with \(\textrm{q}(1) \ne \textrm{q}(2) \wedge \textrm{q}(1) \ne \textrm{q}(3) \wedge \textrm{q}(2) \ne \textrm{q}(3)\). Of course, not all cardinality constraints can be replaced by equivalent constraints and remaining quantifiers are still one of the main culprits for a possibly bad performance of the presented translation from B to SMT-LIB. For instance, the integration of Z3 needs around 20 s to find a solution for the predicate \(\textrm{x} \in \mathbb {P}(\mathbb {Z}) \wedge \textrm{card}(\textrm{x})>10\), which can be solved by ProB’s constraint solver in several milliseconds. The reason is that Z3 spends a lot of time to solve the existentially quantified total bijection that is introduced for the translation of the set cardinality constraint as described in Sect. 3.1.

The translation of set constraints to SMT-LIB such as \(\textrm{card}\), \(\max \) or \(\min \) could be improved by focusing on finite sets only, e.g., as presented by Plagge and Leuschel [63] for B by translating to Kodkod [68] or by Konnov et al. [43] for \(\textrm{TLA}^{+}\) [47] by translating to SMT-LIB [10]. Yet, we would then lose the ability to reason over B constraints involving infinite sets.

Contradictions. Translations which result in quantifiers in SMT-LIB can become too involved to be solved by Z3. In some cases, this means that Z3 cannot find contradictions in a translated SMT-LIB formula which are obvious in the corresponding B formula. For instance, Z3 is not able to find the contradiction in the formula . Here, both bijections are translated as quantified formulas in SMT-LIB leading Z3 to report unknown. We are able to detect the contradiction by abstracting the formula to propositional logic and using a SAT solver as described in Sect. 4.2. In particular, we lift negations from B operations before the abstraction which results in \(\textrm{A} \wedge \lnot \textrm{A}\) where . It can be seen that no translation to SMT-LIB is necessary in such cases. Such constraints do often occur in bounded model checking, where invariants are negated to check for counterexamples.

7.1.2 Strengths of the integration of Z3

Weaknesses of the ProB constraint solver are often caused by the use of unbounded integer domains. One motivating example which speaks in favor of the integration of Z3 is the constraint \(\textrm{x}>\textrm{y} \wedge \textrm{y}>\textrm{x}\). ProB’s constraint solver is not able to solve this constraint with its default CLP(FD) backend since the integer domains of \(\textrm{x}\) and \(\textrm{y}\) cannot be narrowed down. Although ProB’s constraint solver is able to solve this constraint by using an additional backend that implements custom constraint handling rules (CHR), the example shows a benefit of using Z3 for unbounded integer domains, in particular for linear integer arithmetic. For example, Z3 is able to solve the constraint \(\forall (\textrm{x},\textrm{y}).(\textrm{x} \in \mathbb {Z} \wedge \textrm{y} \in \mathbb {Z} \Rightarrow \exists \textrm{z}.(\textrm{x} - \textrm{z} = \textrm{y}))\) while ProB’s constraint solver is not. The constraint is taken from the 14th SMT competition for quantified integer difference logic [72]. Another constraint which cannot be disproven by ProB’s constraint solver but using the integration of Z3 is \(\lnot ((\textrm{s2} = \textrm{s} \cup \{0\} \wedge \textrm{s3} = \textrm{s} \cup \{1\} \wedge \textrm{s4} = \textrm{s2} \cup \{1\} \wedge \textrm{s5} = \textrm{s3} \cup \{0\}) \Rightarrow \textrm{s4} = \textrm{s5})\), which stems from a computation that occurred during partial order reduction for B. Again, both constraints contain unbounded sets of the integers which cannot be narrowed down by ProB’s constraint solver. The constraints further indicate that this issue affects model finding as well as the disproving of formulas.

We further observed strengths of Z3 regarding the disproving of constraints involving infinite relations. For instance, the integration of Z3 is able to solve the constraint which cannot be solved by ProB’s constraint solver. Furthermore, this constraint can only be solved when using the new translation from B to SMT-LIB which uses Z3’s lambda functions.

The integration of Z3 is also able to solve several constraints faster than ProB’s constraint solver. Such constraints do not necessarily involve unbounded domains but are related to the enumeration of domains as performed by ProB’s constraint solver. For instance, the integration of Z3 is able to find a model for the constraint \(\textrm{f} = \lambda \textrm{x}.(\textrm{x}\in 1\mathrel {{.}\,{.}}\textrm{n} \mid \textrm{x}+1) \cup \{\textrm{n}+1 \mapsto (\textrm{n}/2)\} \wedge \textrm{x} = \textrm{f}[\textrm{x}] \wedge \textrm{x} \ne \emptyset \wedge \textrm{n} = 20\) in around 0.17 s while ProB’s constraint solver is not able to solve the constraint within 60 s. The reason is that CLP(FD) enumerates many values before finding a solution which does not seem to be the case for Z3. It should be noted that the aforementioned strengths of Z3 are not related to SMT solving but rather to its strong theory solvers, especially for linear integer arithmetic.

Table 1 Bounded model checking (BMC) constraints from \(\textrm{TLA}^{+}\) benchmarks compiled by Konnov et al. [43] as well as classical B and Event-B benchmarks compiled by Krings and Leuschel [44, 46]. BMC uses a bound of 25 and sets up 26 constraints for depth \(0\ldots 25\) for each benchmark. We further state the mean amount of independent components for all constraints of a benchmark
Full size table
Fig. 7
figure 7

An unweighted Venn diagram to visualize and compare the amount of BMC constraints that can be solved by ProB’s constraint solver, the former axiomatic translation from B to SMT-LIB, and the new constructive translation as can be seen in Table 1

Full size image
Fig. 8
figure 8

A visualization of the BMC benchmark results presented in Table 1 showing the amount of constraints that can be solved by a constraint solver within a specific amount of time. We compare ProB’s constraint solver and the four different configurations of the integration of Z3 in ProB. The smallest constraint solver timeout is 1000 ms

Full size image

7.1.3 Bounded model checking

For a more sophisticated performance evaluation, we decided to use constraints from bounded model checking (BMC). In particular, we use the monolithic bounded model checking implementation [46] of ProB which sends a single formula to a selected constraint solving backend. The goal of bounded model checking is to verify a system’s properties symbolically by searching for a counter example considering a maximum amount of successive state changes. For instance, let \(\textrm{I}\) be a B or Event-B machine’s invariant, \(\textrm{v}\) be a machine’s state of variables, \(\textrm{init}(\textrm{v})\) be the machine initialization, and \(\textrm{op}\) be the only machine operation. Further, let \(\textrm{BA}_{\textrm{op}}(\textrm{v}, \mathrm {v'})\) be the before-after predicate applying the operation to the variables in \(\textrm{v}\) and assigning the results to the variables in \(\mathrm {v'}\). This corresponds to a state change in the machine but represented as a predicate using fresh variables \(\mathrm {v'}\). For a bound of 1, we set up the BMC constraint \(\textrm{init}(\textrm{v}) \wedge \textrm{BA}_{\textrm{op}}(\textrm{v}, \mathrm {v'}) \wedge \lnot \mathrm {I'}\), where \(\mathrm {I'}\) is the machine invariant referring to the variables in \(\mathrm {v'}\). If the constraint is satisfiable, its solution corresponds to a machine state that violates the machine invariant and can be reached after a single state change. For our benchmarks, we check the B and Event-B machines from a bound of 0 to 25, i.e., we solve 26 constraints for each machine. We compare the amount of constraints that can be solved by a specific solver as well as the time needed to decide for the satisfiability of all constraints. That means, the presented runtimes are the sum of the times needed to solve all 26 constraints. We use a maximum solver timeout of 2 min for each constraint and compare the ProB constraint solver, its integration of Z3 using the former translation [45], the new translation as described in Sect. 4.1, the parallel integration of Z3 as described in Sect. 4.2, as well as the parallel integration of Z3 that iteratively solves independent components of a constraint as described in Sect. 4.3. We did not investigate the effects of a larger timeout since Z3 rather answers unknown than exceeding the solver timeout.

The evaluated benchmarks can be seen in Table 1. We use four \(\textrm{TLA}^{+}\) [47] benchmarks compiled by Konnov et al. [43]. The authors used the benchmarks to evaluate the performance of their symbolic model checker APALACHE for \(\textrm{TLA}^{+}\) which translates to SMT-LIB. We use the translation from \(\textrm{TLA}^{+}\) to B [36] to load \(\textrm{TLA}^{+}\) models in ProB. Unfortunately, the integration of Z3 is not able to solve many constraints of these benchmarks. We thus only use these four benchmarks which already exhibit this trend. Additionally, we use a set of classical B and Event-B benchmarks compiled by Krings and Leuschel [46]. The benchmarks numbered 8 to 11 are taken from a submission to the ABZ 2016 case study [55] by Hoang et al. [39], the benchmarks 12 to 18 from a submission to the ABZ 2014 landing gear case study [15] by Hansen et al. [35], and the benchmarks 20 to 28 from a model of a pacemaker by Méry and Singh [56]. We deem these models to be suited for a performance evaluation since they represent real-world examples. The classical B and Event-B models are correct according to their specification. Thus, all BMC constraints pose a contradiction. Additionally, we use three classical B machines for which a BMC constraint provides a counter example (benchmarks 5 to 7), i.e., at least one constraint is satisfiable. Besides the amount of solved constraints and runtimes of each solver, we also state the mean amount of independent components for each benchmark. The constraints of all benchmarks have an average amount of 417 unique conjuncts or disjuncts and a median amount of 117. The largest constraint contains 3275 unique conjuncts or disjuncts.

The benchmarks were run on a system with an Intel Core I7-8750H CPU (2.2GHz) and 16 GB of RAM using ProB version 1.11.1, SICStus Prolog version 4.7.0, and Z3 version 4.8.16.

First and foremost, the benchmark’s evaluation shows that the new constructive translation using Z3’s lambda functions improves performance and coverage. Z3 is able to solve many more constraints than is the case for the former axiomatic translation, e.g., for the benchmarks numbered 7 and 19. The 7th benchmark contains constraints that provide a solution while the 19th benchmark does not. This shows that the constructive translation improves performance for model finding as well as the disproving of constraints. Yet, Z3 is also able to solve several constraints only when using the axiomatic translation. For instance, this is the case for the benchmarks numbered 10 and 11. We therefore consider the decision to run two Z3 solvers with both translations in parallel to be justified. Figure 7 shows a Venn diagram to compare the amount of constraints that can be solved by a specific solver. It can be seen that Z3 is able to solve 27 constraints only when using the axiomatic translation and 27 constraints only when using the constructive translation. The parallel integration of Z3 in ProB is able to solve 239 constraints that cannot be solved by ProB’s constraint solver as can be seen in Table 1. Yet, ProB’s constraint solver is also able to solve 47 constraints that cannot be solved by Z3.

A visualization of the benchmark results comparing the amount of constraints that can be solved within a specific amount of time is shown in Fig. 8. It can be seen that all constraint solvers are not able to solve significantly more constraints for a timeout larger than 1 min. We thus deem the selection of a timeout of 2 min to be justified.

Surprisingly, the decomposition of constraints into independent components neither improves the performance of constraint solving nor allows solving any more constraints than is the case for the default parallel integration. Almost all constraints can be decomposed into several independent components as can be seen in the last column of Table 1. As expected, the computation of the independent components and independent Z3 solver calls add some additional overhead. Apparently, the components that pose a contradiction can still not be solved by Z3 as is the case for the whole constraint. We assume that Z3 itself already divides constraints into independent components so that our decomposition does not provide any improvement. The results further show that the fact that Z3 is not able to decide for the satisfiability of a constraint is not necessarily influenced by the size of a constraint but rather by the use of specific operators. This approach is thus probably not worth it to be used in the future.

When comparing the runtimes of the integration of Z3 and ProB’s constraint solver, it can be seen that Z3 is able to solve several constraints better. This does not only affect the performance but more importantly the coverage of constraint solving as can be seen in Fig. 7. For the benchmarks numbered 7, 15 and 17 to 28, the integration of Z3 is able to solve many more constraints than is the case for ProB’s constraint solver. For benchmarks 19 to 28, ProB’s constraint solver is not able to narrow down the domains to find a contradiction for most constraints but exceeds the predefined solver timeout. The machines contain several unbounded domains over the natural numbers and different integer arithmetic constraints. It can be the case that Z3 is able to solve these constraints due to the Boolean abstraction of formulas or due to its strong theory solvers, especially for linear integer arithmetic.

Nonetheless, ProB’s constraint solver is also able to solve several constraints better than the integration of Z3. For the benchmarks numbered 1 to 3, 5, and 8 to 11, ProB’s constraint solver is able to solve many constraints which cannot be solved by Z3.

All in all, it can be seen that the new integration of Z3 and translation from B to SMT-LIB extends the power of ProB’s portfolio of constraint solving backends. Since the decomposition of constraints into independent components does not improve performance for our selected benchmarks, we prefer the plain parallel integration of Z3 in ProB.

7.2 Direct implementation of SMT solving in ProB

Table 2 The same set of BMC benchmarks as used in Table 1 but comparing the different configurations of ProB’s SMT solver with ProB’s constraint solver and the new parallel integration of Z3
Full size table
Fig. 9
figure 9

A visualization of the BMC benchmark results presented in Table 2 showing the amount of constraints that can be solved by a constraint solver within a specific amount of time. We compare ProB’s constraint solver and the four different configurations of ProB’s SMT solver. The smallest constraint solver timeout is 1000 ms

Full size image
Fig. 10
figure 10

A weighted Venn diagram to visualize and compare the amount of BMC constraints that can be solved by ProB’s constraint solver, the parallel integration of Z3 in ProB, and the best performing configuration of ProB’s SMT solver, i.e., using static syntax analysis but no symmetry breaking

Full size image
Table 3 Detailed statistics of the different configurations of ProB’s SMT solver considering all BMC constraints presented in Table 2. Each cell presents two values which are the maximum (top) and mean (bottom) values. The presented mean values have been rounded
Full size table

In the following, we present an empirical evaluation of the direct implementation of SMT solving in ProB. Here, we compare the runtimes of the plain ProB constraint solver, its integration of Z3 [64] (ProB-Z3) running two solvers in parallel without the decomposition of constraints into independent components, the presented SMT solver using ProB’s constraint solver as its only theory solver with and without static syntax analysis as described in Sect. 5.2.3 (SMT, Raw-SMT), in addition to the static syntax analysis using static symmetry breaking (Sym-SMT) as described in Sect. 5.2.2, and using no static syntax analysis but static symmetry breaking (Sym-Raw-SMT). We use a linear domain enumeration order for ProB’s constraint solver in each solver configuration to ensure that the propagation is deterministic. The benchmarks were run on the same settings as used in Sect. 7.1.3.

7.2.1 Bounded model checking

We use the same set of benchmarks as used in Sect. 7.1.3 for bounded model checking. The evaluated benchmarks can be seen in Table 2.

When comparing the results of the SMT and Raw-SMT solver configurations, it can be seen that the static syntax analysis improves the performance of constraint solving for several benchmarks, in particular for the benchmarks numbered 1, 7, 10, 20, 21, 23, 25, and 28. However, for some benchmarks the additional constraints seem to lead the SMT solver in a wrong direction, e.g., for the benchmarks numbered 10 and 11. This can lead to a constellation of theory constraints for which ProB’s constraint solver exceeds the predefined solver timeout or the SAT solver spends a lot of time backtracking between variable decisions. We suppose that the reason is that our decision heuristic is initialized with the occurrences of variables among all clauses as described in Sect. 5.3.4. This initialization changes when adding additional clauses which can lead the SAT solver in a different direction than is the case for the original formula. Table 3 shows more detailed statistics of the different SMT solver configurations. Here, it can be seen that the additional static syntax analysis (SMT, Sym-SMT) reduces the amount of theory propagations by several orders of magnitude compared to the other solver configurations while the amount of Boolean decisions increases slightly. This shows that the deduced constraints successfully pass knowledge from the theory to the SAT solver. Both SMT solver configurations that do not use the static syntax analysis seem to often exceed the predefined timeout in the theory solver, which is probably correlated with the high amount of theory propagations.

Adding symmetry breaking constraints does not improve the performance of constraint solving for the selected benchmarks significantly. Only for the benchmarks numbered 2, 11, and 18, one more constraint can be solved. For the second benchmark, the time needed for constraint solving can be reduced as can be seen when comparing the SMT and Sym-SMT solver configurations in Table 2. We initially expected greater performance improvements of static symmetry breaking, but it should be noted that we do not know how many constraints contain symmetries. Furthermore, a symmetry breaking constraint does not necessarily shift a contradiction to the Boolean level of SMT solving but possibly just supports the theory solver as explained in Sect. 5.2.3. It can thus be the case that the theory solver or the SAT solver still exceeds a predefined solver timeout if the responsible constraints are not affected by symmetry breaking. Unfortunately, in some cases the performance of constraint solving is worse when adding symmetry breaking predicates, e.g., for the benchmarks numbered 7 and 23. Again, we suppose that the additional constraints lead the SMT solver in a wrong direction which results in exceeding the predefined solver timeout due to the enumeration of domains in the theory solver or backtracking between variable decisions in the SAT solver.

We cannot evaluate the usefulness of restarts since the SMT solver configurations do not apply many restarts for the selected benchmarks. Yet, an SMT solver only restarts a search if it recognizes that not much new knowledge can be gained from the current search path as explained in Sect. 5.3.5. It can thus be a good sign that only a few restarts were performed in our empirical evaluation. In Table 3, it can be seen that the mean amount of restarts over all BMC constraints is 0 or 1. The maximum amount of restarts when solving a constraint is 33.

The SMT solver configurations reduce the amount of learned clauses only a few times for the selected benchmarks. In most cases, the total amount of conflicts is less than the threshold defined by the implemented policy as described in Sect. 5.3.3 (cf. Table 3). In particular, we remove half of the learned clauses which have an LBD score higher than 5 after \(4000 + 300 * \textrm{x}\) conflicts, where \(\textrm{x}\) is the amount of reductions performed so far.

The theory solver, i.e., ProB’s constraint solver, is able to deduce many constraints which are propagated to the SAT solver as can be seen in Table 3. We would need to explain such theory propagations if they are necessary for a conflict analysis since ProB’s constraint solver does not provide an explanation by default as described in Sect. 5.4.4. This would add the additional overhead of computing an unsatisfiable core. Yet, the SMT solver configurations do not require a single explanation of a theory propagation for the selected benchmarks.

The results of ProB’s SMT solver for the benchmarks numbered 20 to 28 are not much better than the ones of using only ProB’s constraint solver. The integration of Z3 is still the dominant solver. We suppose that Z3 is able to solve these constraints better than the other solvers not because of conflict-driven clause learning but due to its strong theory solvers for linear integer arithmetic.

Overall, ProB’s SMT solver is able to solve many constraints better than ProB’s constraint solver, e.g., the benchmarks numbered 1, 2, 7, 15, 20, 23, and 28. In Fig. 10, it can be seen that the constraint solver configuration ProB-SMT is able to solve 17 constraints that cannot be solved by Z3 or ProB’s constraint solver, 22 constraints that cannot be solved by Z3, and 86 constraints that can be solved by Z3 but not by ProB’s constraint solver.

In Fig. 9, it can be seen that ProB’s constraint solver is able to solve more constraints than ProB’s SMT solver for a timeout smaller than 40 s. However, for larger timeouts, the SMT solver configuration using static syntax analysis but no symmetry breaking has a better performance than the other constraint solvers. It could thus be beneficial to combine the constraint solvers by first calling ProB’s constraint solver with a timeout of around 20 s and resorting to ProB’s SMT solver if the timeout is exceeded. The results show that CDCL can be beneficial to find contradictions in such large constraints that contain many Boolean decisions as selected from bounded model checking compared to plain saturation-based solving as performed by ProB’s constraint solver. We thus deem this direct implementation of SMT solving in ProB to be of value for constraint solving in B and Event-B, and to further increase the power of ProB’s portfolio of constraint solving backends.

Table 4 A subset of the classical B and Event-B models from Tables 1 and 2, but checking inductivity of the invariant \(\textrm{I}\) for each operation or event \(\textrm{op}\) by solving the constraint \(\textrm{I} \wedge \textrm{BA}_{\textrm{op}}(\textrm{v}, \mathrm {v'}) \wedge \lnot \mathrm {I'}\). The amount of machine operations (events) is equal to the amount of constraints to be solved
Full size table
Table 5 Detailed statistics of the different configurations of ProB’s SMT solver considering all constraints for inductive invariant proofs presented in Table 4. Each cell presents two values which are the maximum (top) and mean (bottom) values. The presented mean values have been rounded
Full size table

7.2.2 Inductive invariant proofs

In order to provide a more diverse performance evaluation, we decided to additionally solve constraints from constraint-based proofs for the inductivity of invariants. The goal is to prove that a classical B machine operation or event in Event-B is not able to reach a state that violates the invariant. For this, a constraint is set up for each machine operation or event which is solved independently. In contrast to bounded model checking, the constraint-based proof for the inductivity of an invariant does not include the machine’s initialization but allows any instantiation. These constraints thus often contain larger or unbounded domains. Further, the constraints are considerably smaller than the ones of bounded model checking since they only consider a single machine operation or event at once. We use a subset of the benchmarks used in Sects. 7.1.3 and 7.2.1 with the same solver settings and compare the runtimes of ProB’s constraint solver, the parallel integration of Z3 (ProB-Z3), as well as all four settings of ProB’s SMT solver (SMT, Raw-SMT, Sym-SMT, Sym-Raw-SMT). We dropped the benchmark SimpleTwoPhase from the evaluation since the B machine only provides a single machine operation for which the constraint to prove the inductivity of the machine invariant is a static contradiction. The benchmarks with the corresponding amount of machine operations or events, i.e., the amount of constraints to be solved, can be seen in Table 4. The constraints of all benchmarks have an average amount of 23 unique conjuncts or disjuncts and a median amount of 56. The largest constraint contains 72 unique conjuncts or disjuncts.

First and foremost, it can be seen that the different configurations of ProB’s SMT solver do not show crucial differences. The additional static syntax analysis and symmetry breaking do not improve but rather drop performance, e.g., for the benchmarks numbered 19, 21, 23, 24, and 26. Only for the 27th benchmark, one more constraint can be solved when using the static syntax analysis. Further, the runtime for the 15th benchmark reduces when using symmetry breaking. For the benchmarks numbered 2, 3, and 18, conflict-driven clause learning improves the coverage compared to ProB’s constraint solver.

The integration of Z3 in ProB shows benefits for the benchmarks numbered 1, 6, and 27, where it is able to solve the maximum amount of constraints. For the 15th benchmark, Z3 is not able to solve 8 constraints which can be solved by the other constraint solvers. These constraints contain several nested functions and set cardinalities which result in quantified formulas in SMT-LIB.

Interestingly, ProB’s constraint solver is the dominant solver for the selected benchmarks regarding performance since it is able to solve the constraints of the benchmarks numbered 15 to 17 and 19 to 26 the fastest. Especially for the benchmarks numbered 19 to 26, it can be seen that ProB’s SMT solver lacks performance while ProB’s constraint solver alone is able to solve the constraints in a short amount of time. Here, the SAT solver again guides the theory solver in an inconvenient direction which results in exceeding the solver timeout as was the case for several benchmarks presented in Sect. 7.2.1. Table 5 shows detailed statistics of the different SMT solver configurations for the benchmarks presented in Table 4. It can be seen that the factor between the amount of Boolean decisions and theory propagations is several orders of magnitude higher than was the case for the benchmarks from bounded model checking. We thus suppose that the advantage of ProB’s constraint solver can be attributed to the constraints’ smaller amount of Boolean decisions compared to the ones of bounded model checking, where conflict-driven clause learning is not necessarily better than setting up all theory constraints at once as is done by ProB’s constraint solver.

7.2.3 Deadlock freedom proofs

In order to further enrich the diversity of the selected benchmarks for our empirical evaluation, we decided to additionally use benchmarks from constraint-based proofs for deadlock freedom. For this, a single constraint is solved for a classical B or an Event-B machine to search for a state which has no successor state, i.e., a deadlock state. We use the same models and settings as in Sect. 7.2.2, but this time we dropped the benchmark R6_lights from the evaluation since the constraint to prove deadlock freedom is a static contradiction. The evaluated benchmarks can be seen in Table 6. A dash indicates that a constraint cannot be solved by a specific constraint solver within the predefined timeout of 2 min. The constraints have a similar size than the ones used for the proofs of the inductivity of invariants but are considerably smaller than the ones of bounded model checking. In particular, the constraints of all benchmarks have an average amount of 25 unique conjuncts or disjuncts and a median amount of 22. The largest constraint contains 48 unique conjuncts or disjuncts.

Table 6 A subset of the classical B and Event-B benchmarks used in Tables 1 and 2 but solving constraints to prove deadlock freedom. One constraint is solved for each benchmark. A dash indicates that a constraint cannot be solved by a specific constraint solver within the predefined timeout of 2 min
Full size table
Table 7 Detailed statistics of the different configurations of ProB’s SMT solver considering all constraints for deadlock freedom proofs presented in Table 6. Each cell presents two values which are the maximum (top) and mean (bottom) values. The presented mean values have been rounded
Full size table

First and foremost, it can be seen that ProB’s constraint solver is the dominant solver for the presented benchmarks. It is able to solve all constraints except for the first and second one. Yet, the other constraint solvers are not able to solve these constraints within the predefined timeout too.

The four configurations of ProB’s SMT solver do not show significant differences in general. Their results are mostly comparable to the results of ProB’s constraint solver. The constraints do not lead to many Boolean decisions as can be seen in Table 7. While conflict-driven clause learning is not necessarily beneficial in such cases, it does not seem to add too much overhead compared to registering all variables at once as is done by ProB’s constraint solver.

The integration of Z3 in ProB is not able to solve 10 constraints in total. Here, Z3 does not exceed the predefined solver timeout but answers unknown in a short amount of time. This shows that Z3’s inability to solve a constraint is not necessarily caused by the size of a constraint but rather by the use of specific operators. We are not sure which operators exactly reduce Z3’s performance, but we suppose that the main reason are quantifiers introduced for the translations of set cardinality constraints and functions.

All in all, the benchmarks selected from proofs of deadlock freedom show that ProB’s constraint solver is superior when it comes to solving constraints with a small amount of Boolean decisions. In such cases, SMT solving usually does not improve performance.

7.2.4 Additional theory solver

The various machines (no. 20–28) of the pacemaker model in Table 2 highlighted some of the drawbacks of ProB’s default and our new SMT solver. Indeed, the pacemaker model contains timing constraints, some over unbounded domains and also has events with an infinite number of parameter values. ProB’s constraint solver was not able to narrow down these domains to a finite interval. We thus decided to combine our new SMT solver with a new additional theory solver for integer difference logic as described in Sect. 6 and evaluate it on the pacemaker constraints from Table 2. We use the same system settings as for the other empirical evaluations and use the additional theory solver for integer difference logic for each configuration of ProB’s SMT solver (columns 6 to 9 in Table 8). It should be noted that the other benchmarks presented in Table 2 do not contain any (or only very few) integer difference logic constraints. The use of the additional theory solver would thus not make any difference.

Table 8 A set of benchmarks from bounded model checking of an Event-B model of a pacemaker by Méry and Singh [56] comparing the different configurations of ProB’s SMT solver using the new theory solver for integer difference logic with ProB’s constraint solver and the new parallel integration of Z3. All constraints contain at least one IDL constraint
Full size table
Fig. 11
figure 11

A weighted Venn diagram to visualize and compare the amount of BMC constraints that can be solved by ProB’s constraint solver, ProB’s SMT solver with static syntax analysis, and the same SMT solver configuration but additionally using the theory solver for integer difference logic (SMT-IDL). Each cell presents two values which are the maximum (top) and mean (bottom) values. The presented mean values have been rounded

Full size image
Table 9 Detailed statistics of the different configurations of ProB’s SMT solver using the additional theory solver for integer difference logic considering all BMC constraints presented in Table 8
Full size table

The evaluated benchmarks are presented in Table 8. It can be seen that the additional theory solver for integer difference logic (SMT-IDL) allows solving 173 more constraints than ProB’s constraint solver and 121 more constraints than ProB’s SMT solver with the default theory solver backend. The SMT solver configurations perform many Boolean decisions as can be seen in Table 9. The additional static syntax analysis improves performance and enables more theory propagations in ProB’s constraint solver, which seem to be beneficial for constraint solving regarding the selected set of benchmarks. Yet, using the additional theory solver prevents solving 7 constraints in total as can be seen in Fig. 11. We assume that the unsatisfiable cores provided by the integer difference logic solver lead the SMT solver in a different and in this case unfavorable direction. Overall, the integration of Z3 is still the superior constraint solver for the selected benchmarks.

While this brief empirical evaluation serves to demonstrate the usefulness of the additional theory solver for ProB’s SMT solver, a more quantitative study is needed to gain more insight on the general strengths of the different constraint solving backends.

8 Related work

In the following, we describe different related work in the area of SMT solving for B and first-order logic in general.

Déharbe et al. [27, 28, 31] presented an integration of an SMT solver for B and Event-B by translating to SMT-LIB. The goal was to support automated theorem provers by disproving single proof-obligations. The authors presented two translations which support a subset of the B language. Sets are translated as uninterpreted characteristic functions. One translation specifically interfaces an SMT solver and uses its lambda expressions, but only basic sets are supported in this case. Our implementation uses Z3’s array theory [25] to translate sets which supports defining nested sets. In the other translation, set operations are axiomatized so that nested sets are supported as well. The axiomatic translation presented by Krings and Leuschel [45] and described in Sect. 3.1 is similar to this translation, but uses Z3’s array theory [25] instead of uninterpreted functions. An empirical evaluation by Déharbe et al. has shown that the amount of proof obligations which can be proven automatically has improved [31]. Krings and Leuschel have shown that their derived high-level translation improves the one by Déharbe et al. regarding constraint solving [45].

The mathematical foundations of \(\textrm{TLA}^{+}\) and B have quite a few similarities, and translations between both formalisms exist [36, 37]. TLC [73] is an explicit state model checker for \(\textrm{TLA}^{+}\) that relies on simple domain enumeration. Konnov et al. [43] presented a translation from \(\textrm{TLA}^{+}\) to SMT-LIB to improve symbolic model checking by interfacing to SMT solvers. The translation only supports finite sets, which avoids many downsides of our translation from B to SMT-LIB. For instance, the authors suggest translating a set membership as a disjunction of equalities, which is feasible for finite sets only. Furthermore, quantifiers are unfolded, e.g., an existential quantification is replaced by a disjunction. In the future, we plan to conduct an empirical comparison with APALACHE’s SMT solver integration [43], which will require a fair translation of \(\textrm{TLA}^{+}\) constraints to B and backwards, and isolating the constraint solving performed by APALACHE from the symbolic verification algorithms.

Davidson et al. [21] presented a portfolio of constraint solving backends for the high-level language Essence Prime. One backend interfaces different SMT solvers including Z3 by translating to SMT-LIB, and supports four different SMT-LIB logics for quantifier-free formulas. The translation uses bit-blasting and only supports finite domains. Besides that the authors’ tool enables to interface different SAT solvers by translating to propositional logic or other constraint solvers using their specific input language. The authors have shown that their SMT solver integration outperforms the baseline approaches for the selected benchmarks. In addition, they also emphasize the need for a portfolio of constraint solving backends to reliably solve various problems.

El Ghazi and Taghdiri [32] presented a translation from Alloy to SMT-LIB. Abbazzi et al. [1] presented an integration of SMT solvers in the Alloy analyzer, as well as an evaluation of different translations from Alloy to SMT-LIB. The Alloy analyzer usually translates Alloy to Kodkod [68] which applies SAT solving. Yet, this eager approach to SMT solving can result in large propositional formulas depending on the size of domains. This possibly leads to bad performance. For instance, sets can be translated as bit vectors where one bit is reserved for each domain element. The authors have shown performance improvements of model finding for Alloy by translating to SMT-LIB. Furthermore, the translation enables reasoning over infinite sets.

Weber [71] presented an SMT solver integration for the HOL4 theorem prover which supports the first-order subset of the language. The translation to SMT-LIB employs an axiomatized style for operators that are not supported by SMT-LIB such as the minimum of a set of integers.

Bride et al. [17] conducted an empirical evaluation and comparison of SMT solving and constraint logic programming for workflow nets. In particular, they interface Z3 and SICStus Prolog as is the case for our implementations. Their results show benefits of SMT solving for unsatisfiable formulas, and benefits of constraint logic programming for satisfiable ones, which fits also with our experience.

9 Future work

In the future, we plan to provide alternative translations for B sequences using lambda functions. Furthermore, the translation of B sequences to SMT-LIB can be improved by translating sequences as finite arrays in SMT-LIB. Yet, this is only possible if sequences interact among other sequences guaranteeing the well-definedness of resulting sequences. This is not necessarily the case since B sequences are relations and might interact with other relations which are not sequences as described in Sect. 3.1. We thus need a static analysis to detect if a translation of sequences as finite arrays in SMT-LIB is applicable for a constraint.

As discussed in Sect. 7.1.1, the support for infinite sets entails several suboptimal translations, e.g., for set cardinality constraints. If only finite sets are used in a formula, we are able to translate sets to a more concise representation, e.g., using a bit vector encoding. Of course, we then have to provide translations for all set operators for this new encoding of finite sets which requires some implementation effort. Yet, this might not be worth it since ProB already provides an interface to Kodkod [63, 68] which has shown to provide good performance on finite set operations [30] and uses a bit vector encoding of sets.

Furthermore, we plan to compile other configurations of the Z3 constraint solver to run in parallel, e.g., using different solver tactics.

Another future work is to use other SMT solvers to solve SMT-LIB models. Currently, the new translation presented in this article uses Z3 specific lambda functions. Once the SMT-LIB standard officially supports lambda functions we should be able to interface to other SMT solvers as well for the new translation. It is worth mentioning that the implementation of an automated translation which interfaces a solver specific programming API is a tedious and error-prone task. Mann et al. [54] presented a solver-agnostic programming API for SMT solving which should be considered for future implementations.

Regarding our direct implementation of SMT solving in ProB  we plan to implement more sophisticated CNF rewriting rules to decrease the number of clauses and their size, e.g., our implementation lacks a heuristic to reduce the introduction of artificial variables [24, 61] as proposed by Tseitin [69]. Besides that the SAT solver’s branching heuristic could use knowledge from theory constraints to improve the ordering (cf. benchmarks 19 to 27 in Table 4). This requires a more detailed analysis of selected constraints to investigate whether we can deduce any rules to improve the branching heuristic. In addition, we want to consider the model-constructing satisfiability calculus (mcSAT) [41] framework in the future to investigate whether we can further improve the overall performance and apply the presented ideas to set theory. Last but not least, there may be some low-hanging fruit in our implementation to improve performance.

10 Conclusion

In conclusion, we have presented a formal description and implementation of a new translation from B to SMT-LIB as well as a parallel integration of the Z3 constraint solver in ProB. Empirical results have shown that the new translation and workflow improves performance and coverage compared to the prior integration in ProB [45] by utilizing Z3’s lambda functions. The integration of Z3 is also able to decide a lot of constraints where ProB’s constraint solver times out (cf. Sect. 7.1.3). In most cases, such constraints contain bounded or unbounded integer domains and function applications. Besides improving the integration of Z3 in ProB  we were able to identify two bugs in Z3 involving lambdas using ProB’s regression tests.

Unfortunately, the integration of Z3 is not effective for constraints involving set cardinality or many quantifiers. We thus also developed a direct implementation of SMT solving in ProB using its constraint solver as a theory solver (cf. Sect. 7.2.1). This new approach was able to solve some constraints that neither ProB nor Z3 were able to solve. The static syntax analysis in Sect. 5.2.3 derives implied constraints and was useful for identifying contradictions. Yet, the additional constraints can also be counter-productive and lead to timeouts. Using a branching heuristic in the underlying SAT solver that considers the style of the actual theory constraints could improve this issue in the future. Adding static symmetry breaking predicates improved the performance for some benchmarks, but not as much as initially expected. The empirical evaluation has shown that the benefit of CDCL compared to plain saturation based solving, as performed by ProB’s constraint solver, is most notable for large constraints with many disjunctions or implications. These occur for example in bounded model checking (Sect. 7.2.1) with a monolithic transition predicate (consisting of a disjunction of the effect of a model’s individual operations).

The use of an additional theory solver for integer difference logic in ProB’s SMT solver has shown to be beneficial for models involving timing constraints (cf. Sect. 7.2.4). This theory solver also provides unsatisfiable cores without requiring further computations.

Generally, the integration of Z3 shows a better performance for most bounded model checking constraints than ProB’s SMT solver. We mainly attribute these differences to the strong theory solvers of Z3, especially for linear integer arithmetic (cf. Sect. 7.1.2). The decomposition of constraints into independent components prior to the translation to SMT-LIB did not improve performance for Z3 (cf. Sect. 7.1.3). Possibly, Z3 is able to infer these components directly or indirectly during the solving process.

Last but not least, ProB’s constraint solver sometimes performs better than the integration of Z3 or the new SMT solver, especially for checking inductivity of invariants and deadlock freedom (cf. Sect. 7.2). These constraints are smaller than the ones of bounded model checking, as there is no repeated inclusion of the transition predicate.

Finally, our empirical evaluation has shown that no constraint solver is the best for all types of constraints. Hence, it is beneficial to have a diverse portfolio of constraint solving backends for the B language. We could either call all available solvers in parallel or iteratively call different constraint solvers.

Our empirical evaluation has shown that it could be useful to first call ProB’s constraint solver with a small timeout and successively resort to the integration of Z3 as well as ProB’s SMT solver if necessary. Further, we could extend the machine learning backend in ProB that is able to predict the best solver for a specific constraint as suggested by Dunkelau et. al [30] (see also Healy et al. [38] for Why3) to combine the strengths of all presented backends into a single constraint solving routine.