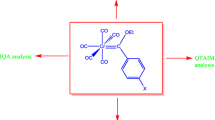
Abstract
An application of the quantum chemical modeling allowed to investigate the nature of the field/inductive substituent effect (SE). For this purpose, series of X-tert-butyl···tert-butane (TTX) complexes (where X = NMe2, NH2, OH, OMe, Me, H, F, Cl, CF3, CN, CHO, COMe, CONH2, COOH, NO2, NO) were studied. A starting distance between central carbon atoms in substituted and unsubstituted fragments of TTX, dC1–C4, was the same as the distance C1–C4 in X-substituted bicyclo[2.2.2]octane (BCO), where the SE acts both via bonds and via space. A strength of interaction between substituted and unsubstituted components of TTX was described by deformation and interaction energies. The substituent effect on electronic structure through the bonds and the space was characterized using charge of the substituent active region (cSAR) approach. The comparison of the SE characteristics obtained for alicyclic BCO and for TTX complexes document a significantly stronger field/inductive effect through bonds than through space.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
Electronic properties of functional groups or substituents are of crucial importance both in organic chemistry and related fields. Numerically, they are most often described by variously defined substituent constants (SC) which are usually modifications of the fundamental concept introduced by Hammett [1,2,3,4]. Already 50 years ago Swain and Lupton [5] mentioned over 20 various SCs. In conclusion, they emphasized that there are only two major factors determining substituent properties: the resonance and field/inductive effects (for review, see also [6,7,8,9,10]). In the first case, in X-R-Y system, the π-electron delocalization and the charge transfer from one (e.g., a donating X) to another part of the molecule (e.g., an attracting Y), leading to a quinoid-like π-electron structure X(+) = C6H4 = Y(−) if the benzene derivative is taken as an example [11,12,13,14], are responsible for the effect. A big problem emerges with an interpretation of the field/inductive effect: whether the interaction is transmitted through the space (the direct electrostatic or field effect) or through the bonds (the inductive effect). The problem arose when Roberts and Moreland [15], following the Hammett procedure, quantitatively estimated the substituent effect directly from acid/base equilibrium constants for 4-substituted bicyclo[2.2.2]octane-1-carboxylic acids. It is a system in which only the abovementioned two types of interactions can work. According to their conclusions, the two abovementioned influences “have to a great extent resisted disentanglement and are very often treated together as a composite effect” [15]. Later, derivatives of 4-substituted quinuclidine [16, 17] and gas-phase acidities of 4-substituted bicycle[2.2.2]octane-1-carboxylic acids [18] have been used for this purpose, leading to the well-correlated data and comparable with the older ones. Several attempts have been undertaken to separate the abovementioned two ways of interactions (components) of the substituent effects in 4-substituted bicyclo[2.2.2]octane-1-carboxylic acids. The electrostatic calculations based on Kirkwood and Westheimer formulas [19, 20] occurred to be not effective [21]. Results of the first quantum chemistry calculations [22, 23] supported the field effect as a main factor for these kinds of interactions. A similar conclusion came from the ab initio calculations of substituent effect parameters estimated for ketenimines, isocyanides, and nitriles [24]. However, the through bond interactions also have followers (for review of these problems, see articles by Galkin, Charton, and Exner [25,26,27]). An application of the molecular electrostatic potential topography [28] reveals that the ratio of through bond/through space effects depends strongly on the kind of a link (alkane, alkene, and alkyne chain) between substituents and the benzene ring. For the alkyl chain, the through bond effect is 20.4%, whereas for unsaturated ones is ~ 55% of all effect. Furthermore, the problem is still open as presented in the detailed review [10].
In the case of π-electron systems, both the resonance and inductive/field effects contribute to the overall observed SE and the problem is in their composition. It is generally accepted that in para-substituted benzene derivatives, there are equal contributions of the resonance (R) and inductive/field (I/F) effects, whereas in the meta ones, the R-effect is around 1/3 of the overall one [29]. This ratio is not always constant, since in many cases correlations of properties measured or computed for meta- and para-substituted benzene derivatives sometimes led to other ratio values [6, 8, 30, 31]. In addition, a linear regression of the original 16 Hammett substituent constants used in this study, σm vs σp, has led to a slope value of 0.488, with the correlation coefficient cc = 0.935, indicating even less than 0.33 contribution of the resonance in the meta position.
In front of the ambiguous interpretations of the nature of the field/inductive effect, we have undertaken quantum chemically based computational model which allows to present a solution of the problem.
Motivation and strategy
Undoubtedly, the substituent effects measured for 4-substituted bicyclo[2.2.2]octane-1-carboxylic acids can be composed of two contributions [15]: the direct electrostatic effect (called often as the field effect) and the through bond electric effect named as the inductive effect. In order to decide about the nature of the composition of the abovementioned interactions, we have undertaken studies on the substituent effect for an isolated system: the substituted tert-butyl interacting through the space with its unsubstituted form, see Scheme 1. Results for this system are compared with the data for mono-substituted bicyclo[2.2.2]octane (BCO) derivatives. For these purposes, X-substituted carbon atoms are denoted as C1 whereas the appropriate carbon atoms in unsubstituted part of BCO and part B of TTX are named as C4. Additionally, for simplicity, positions of CH3 in TTX systems are named as “ortho” and “meta”, and finally for H at C4, as “para”.
The strategy of our research (treatment) is as follows:
- (i)
In the first step, the system consists of monosubstituted tert-butane TX(A) molecule interacting through the space with its unsubstituted form TX(B) in a TTX complex at the fixed distances between the substituted and unsubstituted carbon atoms in tert-butyl- moieties equal to that between C1 and C4 in BCO (dBCO ≈ 2.60 Å).
- (ii)
Then, this distance is increased by ΔdC1–C4, in each step by 0.5 Å, up to ΔdC1–C4 = 3.0 Å (in the first step ΔdC1–C4 = 0).
At each step, for a given distance, there are estimated: interaction energy, Eint, deformation energies of both components of interacting system, Edef,A and Edef,B, and finally cSAR values for X and all CH3, CH2 or CH groups. Additionally, the deformation of both isolated molecules from a typical sp3 geometry for carbon atoms C1 and C4 is determined.
Methods
Series of tert-butyl (TTX) substituted systems (Scheme 1) with 16 substituents were used to investigate the nature of the field/inductive substituent effect. The starting distance between C1 and C4 in TTX was the same as the distance in monosubstituted BCO [32, 33]. In order to reduce the overcrowding effect, the substituted tert-butyl fragment of the TTX systems was twisted around C1–X bonds by 60° in reference to its unsubstituted part. For each studied system, an optimization without any symmetry constraints was performed using the Gaussian09 program [34]. The B3LYP/6-311++G(d,p) method with empirical dispersion D3 correction [35] was used for all calculations. Vibrational frequencies were calculated at the same level of theory to confirm that all calculated systems correspond to the minima on a potential energy surface; energies of the obtained TTX systems are shown in Table S1 (in ESM).
Interaction energy (Eint) between two fragments (A and B) in TTX molecules was calculated with the counterpoise correction method [36, 37], eliminating basis set superposition errors according to the Eq. (1):
where EA(basisA···B; optA···B) and EB(basisA···B; optA···B) are the energies of the A and B molecules, respectively, for its geometries obtained during the optimization of the A···B system and calculated using internal coordinates of the A and B molecules, basisA···B; EA···B(basisA···B; optA···B) means the energy of the optimal A···B complex.
The energy of deformation (Edef) is the amount of energy needed to deform an individual fragment (A and B, Scheme 1) from its optimal (equilibrium) geometry to that obtained in the system A···B. For both fragments, deformation energy is defined by Eqs. (2) and (3):
where EA(basisA;optA···B) and EA(basisA;optA) are the energies of the A molecule for its geometries calculated during the optimization procedure of the A···B complex (optA···B) and the monomer (optA), respectively. The terms in Eq. (3) should be understood in the same way.
The degree of pyramidalization is described by the difference of 360° and the sum of the valence angles at a given carbon atom (C1 and C4); for planar system, it is equal to 0°.
The use of the cSAR approach [38, 39] allows characterizing the nature of interaction between substituted and unsubstituted forms in TTX. The cSAR(X) parameter is defined as a sum of charges all atoms of the substituent X and the charge of the ipso carbon atom. cSAR(CH3) values were calculated as a mean value for CH3 fragments in the ortho and meta positions in TTX. The Hirshfeld method [40] was used to assess atomic charges and then to calculate all cSAR values.
Results and discussion
The obtained results are presented in two subsections devoted to (i) an analysis of interaction and deformation energies of each component of TTX and (ii) a description of their electronic structure in studied systems based on cSAR(X) and cSAR(CHn) as well as their comparison with X-BCO substituted systems.
Influence of a substituent on strength of interactions in TTX systems
Interaction energies and their statistics for TTX series are shown in Table 1 and Table S2. As expected, at shorter distances, interactions are destabilizing, but for the distance dBCO + 2.5 Å (ΔdC1–C4 = 2.5 Å), the system is close to equilibrium state, which is confirmed by the data from Table 1 (details in Table S2 in ESM). This is the case for all substituents (substituted TTX series, Table S1). In addition, systems with ΔdC1–C4 = 2.5 ± 0.1 Å are characterized by higher energy values (less negative), so below systems with ΔdC1–C4 = 2.5 Å are called equilibrium state.
When approaching TX(A) towards TX(B), due to the overcrowding, deformations of both components of the interacting systems appear. Mean values of deformation energies and their statistics for TTX series are presented in Table 2 (details in Table S3 in ESM).
As can be seen from the data in Table 2, averaged deformation energies of A and B parts for TTX equilibrium systems are very small (at the level of 0.01 kcal/mol). Interestingly, these values are larger (by ca 20%) for part B than for A. All these observations are in line with the observed deviation from sp3 geometry of carbon atoms (C1 and C4), described by degree of pyramidalization, shown in Tables 3 and S4 (ESM). A greater deformation from sp3 of the carbon atom for an unsubstituted fragment than that for the substituted one may be understood as a stabilizing effect due to the direct substituent impact on the tert-butyl group. For comparison, the degree of pyramidalization of methane as an ideal trigonal pyramid is 31.7°, while for unsubstituted tert-butyl is 27.0° (Table S4).
The influence of a substituent on electronic structure
The key point of the solution to the main problem of this paper is the analysis of linear relationships between cSAR(CHn) (n = 3, 2 and 1) on cSAR(X) values (collected in Table S5 in ESM) in TTX and BCO, respectively, an example of the equation: cSAR(CH) = a cSAR(X) + b. Table 4 presents slopes and determination coefficients (R2) for these dependences.
The interactions between X and CHn in all BCO positions and in the ortho-position of TTX complex work more via the bonds than through the space [32], whereas they are only through the space for the meta-position of TTX. The comparison of the obtained slope values for the ortho and meta equations reveals the difference in the substituent effect between both types of interactions. Taking into account slopes of cSAR(CH3) on cSAR(X) relations for TTX systems with ΔdC1–C4 = 0 Å, the slope ratio for meta and ortho CH3 group is equal 0.068/0.259 ≈ 0.26. The corresponding slope ratio for BCO [cSAR(CH2) on cSAR(X) relation] is 0.125/0.189 ≈ 0.66. In the first case, there is no bond between the ortho and meta TTX fragments (they belong to substituted and unsubstituted parts of the complex; see Scheme 1). Therefore, assuming that the deformation of the CH3 group of the TTX complex with ΔdC1–C4 = 0 Å does not affect too much its electronic structure, these data reflect relation between the substituent effect acting via the space (TTX) and that working rather through bonds (BCO). This leads to the conclusion that the substituent effect in the TTX system (on the meta position) is almost 3 times weaker than in BCO. As expected, the substituent effect decreases with increasing ΔdC1–C4 distance (documented by the ratios of slopes meta/ortho, Table 4).
Furthermore, for TTX systems, an increase (absolute value) of the slopes (a) for the ortho relation is proportional to its decrease for the meta one, as shown in Fig. 1. For the meta position, the absolute a values are decreasing (with elongation of ΔdC1–C4) since less charge can be transmitted to the B-fragment due to the lack of the through-bond interactions. Thus, more charges are accumulated in the fragment A, what is confirmed by increasing a values for the ortho position. Interestingly, the a-values for the para position for all distances are nearly constant (~ − 0.02, except in the case of ΔdC1–C4 = 0.5 Å), what indicates a very weak influence of the substituent on the para position via the space. Examples of charge-change relationships in the unsubstituted TTX (TB) fragment, for X = NO2 and NH2, as a function of increasing ΔdC1–C4 are shown in Fig. S1 (ESM). It is noteworthy that a greater charge changeability of the unsubstituted TTX fragment (TB part) for the NO2 group than for the NH2 group reflects a stronger attracting power from the TB part by the first substituent than the NH2 donating ability towards electron rich methyl groups.
Relationships between the obtained slope values, a, (Table 4) and ΔdC1–C4 (in Å) for TTX systems
Additionally, for the TTX complexes with ΔdC1–C4 = 0 Å, the changes in the slopes of linear equations cSAR(CHn) vs cSAR(X) are realized at a ratio of approximately 12:3:1 for the ortho, meta, and para positions, whereas for BCO systems the analogous ratio [32] is 3:2:1 (see Fig. S2 in ESM). Thus, it is again confirmed that the transmission step between TX(A) and TX(B) (from ortho to meta CH3 groups) dramatically reduces the substituent effect due to the lack of bonds.
Conclusions
The use of the cSAR concept allows to investigate the nature of the field/inductive substituent effect in monosubstituted BCO and tert-butyl (TTX) systems. For this purpose, the charge flow from substituent X to the rest of the molecule (ortho, meta, and para CHn groups) was compared in the BCO and TTX systems (X-tert-butyl···tert-butane, with a different distance between C1 and C4). In the latter complexes, the starting distance between central carbon atoms in substituted and unsubstituted fragments of TTX was the same as the distance C1–C4, dC1–C4, in BCO (ΔdC1–C4 = 0 Å). In this case, as expected, interactions are destabilizing, while the TTX system with ΔdC1–C4 = 2.5 Å is close to equilibrium state (average values of interaction and deformation energies: − 2.03 and 0.01 kcal/mol, respectively).
A good illustration of the substituent effect in both types of systems is the comparison of charge transfer to ortho and meta CHn groups based on slopes of cSAR(CHn) on cSAR(X) dependences. The slope ratios obtained for ortho and meta CHn group indicate that for TTX systems, the field effect is from almost 3 times (for ΔdC1–C4 = 0 Å) to even more than ~ 10 times weaker (for equilibrium state, ΔdC1–C4 = 2.5 Å) than in the case of monosubstituted BCO.
The estimated values of cSAR(CHn) for methyl groups in the ortho, meta, and para positions of TTX systems with ΔdC1–C4 = 0 Å (dC1–C4 the same as in BCO systems), influenced by substituent X, are attenuated by a ratio of 12:3:1, while for BCO-X system it is 3:2:1. In conclusion, the obtained results confirm again that the field/inductive effect is realized clearly stronger through the bonds than the space.
References
Hammett LP (1937) The effect of structure upon the reactions of organic compounds. Benzene derivatives. J Am Chem Soc 59:96–103
Hammett LP (1938) Linear free energy relationships in rate and equilibrium phenomena. Trans Faraday Soc 34:156–165
Hammett LP (1940) Physical organic chemistry, 1st. McGraw-Hill, New York
Hammett LP (1970) Physical Organic Chemistry, 2nd. McGraw-Hill, New York
Swain CG, Lupton Jr EC (1968) Field and resonance components of substituent effects. J Am Chem Soc 90:4328–4337
Exner O (1972) In: Chapman NB, Shorter J (eds) Advances in linear free energy relationships, Chapter 1. Plenum Press, London, p 1
Shorter J (1991) In: Zalewski RI, Krygowski TM, Shorter J (eds) Similarity models in organic chemistry, biochemistry and related fields, Chpt. 2. Elsevier, Amsterdam, p 77
Hansch C, Leo A, Taft RW (1991) A survey of Hammett substituent constants and resonance and field parameters. Chem Rev 91:165–195
Krygowski TM, Stępień BT (2005) σ- and π-electron delocalization: focus on substituent effects. Chem Rev 105:3482–3512
Exner O, Bohm S (2006) Theory of substituent effects: recent advances. Curr Org Chem 10:763–778
Tsuno Y, Fujio M (1996) Varying resonance demand in carbocationic systems. Chem Soc Rev 25:129–139
Fernandez I, Frenking G (2006) Correlation between Hammett substituent constants and directly calculated π-conjugation strength. J Org Chem 71:2251–2256
Krygowski TM, Palusiak M, Plonka A, Zachara – Horeglad JE (2007) Relationship between substituent effect and aromaticity – Part III: naphthalene as a transmitting moiety for substituent effect. J Phys Org Chem 20:297–306
Ozimiński WP, Dobrowolski JC (2009) σ- and π-electron contributions to the substituent effect: natural population analysis. J Phys Org Chem 22:769–778
Roberts JD, Moreland WT (1953) Electrical effects of substituent groups in saturated systems. Reactivities of 4-substituted bicyclo [2.2.2]octane-1-carboxylic acids. J Am Chem Soc 75:2167–2173
Palecek J, Hlavaty J (1973) Azabicyclo compounds. XII. 4-Substituted ́ quinuclidines as model compounds for the study of polar effects transfer. Collect Czechoslov Chem Commun 38:1985–2002
Grob CA, Schlageter MG (1974) Polar substituent effects on rates and equilibria of 4-substituted quinuclidines. Preliminary communication. Helv Chim Acta 57:509–511
Koppel IA, Mishima M, Stock LM, Taft RW, Topsom RD (1993) Acidities of 4-substituted benzoic, bicyclo[2.2.2]oct-1-yl and bicyclo[2.2.2]oct-2-enyl carboxylic acids. J Phys Org Chem 6:685–689
Kirkwood JG, Westheimer FH (1938) The electrostatic influence of substituents on the dissociation constants of organic acids, I. J Chem Phys 6:506–512
Westheimer FH, Kirkwood JG (1938) The electrostatic influence of substituents on the dissociation constants of organic acids, II. J Chem Phys 6:513–517
Exner O, Böhm S (2002) Inductive effects in isolated molecules: 4-Substituted bicyclo[2.2.2]octane-1-carboxylic Acids. Chem Eur J 8:5147–5152
Marriott S, Topsom RD (1984). J Am Chem Soc 106:7
Exner O, Ingr M, Carsky P (1997) Ab initio calculations of substituent constants: a reinvestigation. J Mol Struct THEOCHEM 397:231–238
Sung K (2002) Ab initio calculations of field substituent parameters and evaluation of substituent parameters through substituent effects on stability of ketenimines, isocyanides, and nitriles. J Soc Chem Perkin 2:1658–1661
Galkin V (1999) Inductive substituent effects. J Phys Org Chem 12:283–288
Charton M (1999) The nature of electrical effect transmission. J Phys Org Chem 12:275–282
Exner O (1999) The inductive effect: theory and quantitative assessment. J Phys Org Chem 12:265–274
Sayyed FB, Suresh CH, Gadre SR (2010) Appraisal of through-bond and through-space substituent effects via molecular electrostatic potential topography. J Phys Chem A 114:12330–12,333
Taft RW (1960) Sigma values from reactivities. J Phys Chem 64:1805–1815
Szatylowicz H, Jezuita A, Ejsmont K, Krygowski TM (2017) Classical and reverse substituent effects in meta- and para-substituted nitrobenzene derivatives. Struct Chem 28:1125–1132
Shahamirian M, Szatylowicz H, Krygowski TM (2017) How OH and O– groups affect electronic structure of meta-substituted and para-substituted phenols and phenolates. Struct Chem 28:1563–1572
Szatylowicz H, Siodla T, Krygowski TM (2017) Inductive or field substituent effect? Quantum chemical modeling of interactions in 1-monosubstituted bicyclooctane derivatives. ACS Omega 2:1746–1749
Szatylowicz H, Jezuita A, Siodla T, Varaksin KS, Domanski MA, Ejsmont K, Krygowski TM (2017) Towards physical interpretation of the inductive and resonance substituent effects. Reexamination based on quantum chemical modeling. ACS Omega 2:7163–7171
Frisch MJ, Trucks GW, Schlegel HB, Scuseria GE, Robb MA, Cheeseman JR, Scalmani G, Barone V, Mennucci B, Petersson GA et al (2013) Gaussian 09, Revision D.01. Gaussian Inc, Wallingford
Grimme S, Antony J, Ehrlich S, Krieg H (2010) A consistent and accurate ab initio parameterization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu. J Chem Phys 132:154104–154118
Boys SF, Bernardi F (1970) The calculation of small molecular interactions by the differences of separate total energies. Some procedures with reduced errors. Mol Phys 19:553–566
Simon S, Duran M, Dannenberg JJ (1996) How does basis set superposition error change the potential surfaces for hydrogen bonded dimers? J Chem Phys 105:11024–11,031
Sadlej-Sosnowska N (2007) On the way to physical interpretation of Hammett constants: how substituent active space impacts on acidity and electron distribution in p-substituted benzoic acid molecules. Pol J Chem 81:1123–1134
Sadlej-Sosnowska N (2007) Substituent active region - a gate for communication of substituent charge with the rest of a molecule: monosubstituted benzenes. Chem Phys Lett 447:192–196
Hirshfeld FL (1977) Bonded-atom fragments for describing molecular charge densities. Theor Chim Acta 44:129–138
Acknowledgments
We gratefully acknowledge the Interdisciplinary Center for Mathematical and Computational Modeling (Warsaw, Poland) and Wrocław Centre for Networking and Supercomputing (http://wcss.pl; grant No. 311) for providing computer time and facilities. This work was financially supported by Warsaw Technical University.
Author information
Authors and Affiliations
Corresponding author
Additional information
Dedicated to Professor Zdzisław Latajka of the Department of Chemistry of the Wrocław University—our friend and outstanding physical chemist on the occasion of his 70 anniversary
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
This paper belongs to the Topical Collection Zdzislaw Latajka 70th Birthday Festschrift
Electronic supplementary material
ESM 1
(PDF 520 kb)
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Szatylowicz, H., Jezuita, A., Ejsmont, K. et al. Most of the field/inductive substituent effect works through the bonds. J Mol Model 25, 350 (2019). https://doi.org/10.1007/s00894-019-4204-3
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s00894-019-4204-3