1 Introduction

Surface nuclear magnetic resonance (SNMR) is an established noninvasive method to examine water distribution and pore parameters in the subsurface [1,2,3]. It utilizes \(^1\)H-NMR in the local Earth’s magnetic field. By transmitting a resonant pulse with an effective current \(I_{\textrm{eff}}\) and a duration \(\tau _p\), the macroscopic magnetization in the subsurface are excited and a free induction decay (FID) can be received. Typically, measurements are performed at multiple pulse moments \(q = I_{\textrm{eff}} \tau _p\) while commonly \(I_{\textrm{eff}}\) is varied. The measured FIDs are a convolution of the subsurface water content depth profile and a kernel function. Consequently, the water content depth profile is obtained from the data by inverse modeling [4, 5] and demands a precise knowledge of the kernel function. Both transmitter (Tx) and receiver (Rx) coils are placed on the surface and have typically diameters ranging from 10 m to 150 m. But coils of these dimensions are limited in their lateral resolution and can be cumbersome to place in the field. Furthermore, SNMR still suffers from a high sensitivity to electromagnetic noise, which can make SNMR measurements time-consuming. In recent years, efforts have been made to address these issues. For example, Grunewald et al. [6] showed that the use of adiabatic pulses can enhance the NMR signal and reduce measurement times. Grombacher et al. [7, 8] propose the use of steady-state sequences to decrease measurement times and restrict the influence of noise on the signal.

Another approach, which will be used in this paper, is the use of prepolarization (PP) to increase the proton magnetization \(M_0(r)\) in the subsurface before the experiment [9, 10]. The resulting increase of the NMR signal enables the use of smaller coils and therefore PP-SNMR measurements become feasible in the unsaturated zone [11] and in underground tunnels [12, 13]. The smaller coils can be fixed to a platform, which makes the use of more complex layouts with intrinsic noise compensation [14] viable. Furthermore, the mapping of soil humidity with a high lateral and vertical resolution can easily be envisioned with such a mobile sensor. Nonetheless, some additional effects need to be considered for the correct modeling of the data obtained with a small scale PP-SNMR sensor. By simulating the magnetization in the subsurface during the switch-off of the prepolarization field, Hiller et al. [15] showed that the shape and timing of the switch-off ramp influences which parts of the enhanced magnetization can be utilized in the experiment.

Another necessary adaption is the so called Bloch–Siegert (BS) effect, which we will address in this paper. While most NMR applications use the rotating wave approximation (RWA) for the excitation pulse, there are numerous applications where the use of this approximation is not suitable [16,17,18]. The RWA originates from the decomposition of the linearly polarized excitation pulse into a sum of the circularly polarized co-rotating and counter-rotating fields. As argued by Bloch and Siegert [19], the counter-rotating field can be neglected as long as its amplitude is sufficiently small compared to the constant field amplitude \(B_0\). While modern laboratory NMR equipment can produce truly circularly polarized pulses [20], in SNMR the generated pulses are always linearly polarized. Additionally, in SNMR the angle between the excitation field and the static magnetic field exhibit arbitrary values depending on the position in the subsurface and, therefore, the excitation field component parallel to \(\varvec{B}_0\) needs to be considered. To the best of our knowledge, the influence of the BS effect on SNMR experiments has only been examined in two papers: In [21], Shushakov and Maryasov use the Magnus expansion up to third order to model the BS effect in SNMR data obtained with a \(100 \, \textrm{m}\) diameter loop on a frozen ice layer over a water reservoir. In a second publication, Shushakov examines the interplay between the BS effect and detuned NMR pulses, as well as the conductivity of the subsurface with a second order Magnus expansion [22].

For SNMR experiments in the unsaturated zone, one can expect a significant influence of the BS effect because of two reasons: firstly, the short relaxation times that can be expected make short excitation pulses of high intensity necessary [23]. Secondly, because the water we would like to detect can be directly beneath the transmitter coil, the excitation field will in some locations of the subsurface surpass the static field \(B_0\) even at medium pulse moments. Therefore, after introducing the relevant concepts and equations in Sect. 2 and a short description of the experimental layout in Sect. 3, we will use the Magnus expansion up to fifth order, as well as the solution of the Bloch equations to examine the significance of the BS effect for the magnetization during the excitation pulses in Sect. 4.1. By calculating the error angle \(\alpha\) between the magnetization vectors obtained with both methods, we show that the Magnus expansion is only valid for a specific range of excitation field magnitudes. In Sect. 4.2, we use a combination of both methods to derive kernel functions that consider the BS effect and compare them to standard SNMR kernels. Section 4.3 presents the results of experiments performed with a small scale PP-SNMR sensor on water containers and demonstrates how the obtained data is influenced by the BS effect.

2 The Bloch–Siegert Effect

2.1 The Oscillating Field

A linearly polarized pulse

$$\begin{aligned} \varvec{B}_{\textrm{lin}}(t) = B_\perp \left( \begin{array}{c} {\textsf{sin}} \left( {\omega _0 t}\right) \\ 0 \\ 0 \end{array} \right) =\varvec{B}_{\textrm{circ}}(t) + \varvec{B}_{\textrm{counter}}(t) \end{aligned}$$
(1)

can be decomposed into a sum of the circularly polarized co-rotating field

$$\begin{aligned} \varvec{B}_{\textrm{circ}}(t) = \frac{1}{2} B_\perp \left( \begin{array}{c} {\textsf{sin}} \left( {\omega _0 t}\right) \\ {\textsf{cos}} \left( {\omega _0 t}\right) \\ 0 \end{array} \right) \end{aligned}$$
(2)

and the counter-rotating field

$$\begin{aligned} \varvec{B}_{\textrm{counter}}(t) = \frac{1}{2} B_\perp \left( \begin{array}{c} {\textsf{sin}} \left( {\omega _0 t}\right) \\ -{\textsf{cos}} \left( {\omega _0 t}\right) \\ 0 \end{array} \right) \, . \end{aligned}$$
(3)

Here \(B_\perp = B_1 {\textsf{sin}} \left( {\Theta }\right)\) is the amplitude of the field component perpendicular to \(\varvec{B}_0\) and \(\omega _0\) is the angular frequency of the resonant NMR pulse.

Since for SNMR the angle \(\Theta\) between \(\varvec{B}_1\) and \(\varvec{B}_0\) is different for each position in the subsurface, we additionally have to consider an oscillating field component parallel to \(\varvec{B}_0\)

$$\begin{aligned} \varvec{B_\parallel } = B_\parallel \left( \begin{array}{c} 0 \\ 0 \\ {\textsf{sin}} \left( {\omega _0 t}\right) \end{array} \right) \end{aligned}$$
(4)

with the amplitude \(B_\parallel = B_1 {\textsf{cos}} \left( {\Theta }\right)\). The complete field of the SNMR pulse is therefore

$$\begin{aligned} \varvec{B}_1(t) = \varvec{B}_{\textrm{circ}}(t) + \varvec{B}_{\textrm{counter}}(t) +\varvec{B}_\parallel (t) \, . \end{aligned}$$
(5)

2.2 Bloch–Siegert Effect in SNMR

The signal recorded in a receiver loop after an SNMR excitation pulse can be calculated with [24]

$$\begin{aligned} U_0&= 2 \omega _{\textrm{L}} \int M_0(\varvec{r}) f(\varvec{r}) M_{\perp } \left( \varvec{B}_1(\varvec{r}) \right) {\textsf{exp}}\left( {\textrm{i} \left( \zeta ^- + \zeta ^+ \right) (\varvec{r})}\right) B^{-}_{\perp } (\varvec{r})\nonumber \\&\quad \left( \varvec{b}^{-}(\varvec{r}) \cdot \varvec{b}^{+}(\varvec{r}) + \textrm{i} \varvec{b}_{0} \cdot \left( \varvec{b}^{-}(\varvec{r}) \times \varvec{b}^{+}(\varvec{r})\right) \right) {\textsf{d}}^{3}r \, , \end{aligned}$$
(6)

where \(M_0(\varvec{r})\) is the magnitude of the local magnetization, f(r) is the water distribution, \(M_{\perp }\left( \varvec{B}_1(\varvec{r})\right)\) is the normalized perpendicular component of the magnetization, \(B^-_\perp (\varvec{r})\) is the virtual perpendicular receive field component, \(\zeta ^\pm\) is the local phase shift of the transmit and the virtual receive field, and \(\varvec{b}^\pm (\varvec{r})\), \(\varvec{b}_0\) are unit vectors along the direction of the respective fields. In the rotating wave approximation, the perpendicular component of the magnetization is calculated with

$$\begin{aligned} M_\perp = {\textsf{sin}} \left( { - \gamma \left| {B_{\textrm{circ}}(\varvec{r})}\right| }\right) \, . \end{aligned}$$
(7)

For large enough \(B_1(r)\) this approximation is no longer valid and the influence of the counter-rotating and the parallel field will result in a different magnetization. In this paper, we will calculate the magnetization by means of an average Hamiltonian, obtained with the Magnus expansion and by solving the Bloch equations for each voxel of the subsurface model.

2.3 The Magnus Expansion

The Magnus expansion is a method that uses the time dependent Hamiltonian H(t) to approximate an average or effective Hamiltonian with a series expansion

$$\begin{aligned} \overline{H}^{[i]} = \overline{H}^{(1)} + \overline{H}^{(2)} + \overline{H}^{(3)} + ... + \overline{H}^{(i)} = \sum _{j=1}^i \overline{H}^{(j)} \, , \end{aligned}$$
(8)

where i is the order of the average Hamiltonian and \(\overline{H}^{(j)}\) is the jth order of the Magnus expansion. The first, second and third order of the Magnus expansions are given by [25]

$$\begin{aligned}&\overline{H}^{(1)} = \frac{1}{T} \int _{0}^{t} {\textsf{d}}{t_1} H(t_1) \,, \end{aligned}$$
(9)
$$\begin{aligned}&\overline{H}^{(2)} = \frac{1}{ 2 {\textsf{i}}T} \int _{0}^{t_1} {\textsf{d}}{t_2} \int _{0}^{t} {\textsf{d}}{t_1} \left[ {H(t_2)}, {H(t_1)}\right] \, , \end{aligned}$$
(10)

and

$$\begin{aligned} \overline{H}^{(3)}&= - \frac{1}{6 T} \int _{0}^{t_2} {\textsf{d}}{t_3} \int _{0}^{t_1} {\textsf{d}}{t_2} \int _{0}^{t} {\textsf{d}}{t_1} \left\{ \left[ {H(t_3)}, {\left[ {H(t_2)}, {H(t_1)}\right] }\right] \right. \nonumber \\&\quad - \left. \left[ {H(t_2)}, {\left[ {H(t_3)}, {H(t_1)}\right] }\right] \right\} \, , \end{aligned}$$
(11)

respectively. A general formula to calculate the Magnus expansion of an arbitrary order can be found in equation 27 of [26].

The Hamiltonian for the SNMR pulse is

$$\begin{aligned} \hat{H} (t) = - \gamma \varvec{\hat{I}} \cdot \varvec{B}_0 -\gamma \varvec{\hat{I}} \cdot \varvec{B}_1 = \hat{H}_0 (t) + \hat{H}_1 (t) \, , \end{aligned}$$
(12)

with the spin operator vector

$$\begin{aligned} \varvec{\hat{I}} =\left( \begin{array}{c} \hat{I}_x \\ \hat{I}_y \\ \hat{I}_z \end{array} \right) \, . \end{aligned}$$
(13)

The Magnus expansion will converge faster in an appropriate interaction frame [25], which in our case is the rotating frame. It enables the calculation of a rotating frame propagator

$$\begin{aligned} \widetilde{U}(t_0,t_0+t) = {\textsf{exp}}\left( { - \textrm{i} t \widetilde{\overline{H}}^{[i]}_1}\right) \end{aligned}$$
(14)

by using the Magnus expansion to average over the interaction frame Hamiltonian of the SNMR pulse

$$\begin{aligned} \hat{\widetilde{H}}_1 (t) = - \gamma \varvec{\hat{I}} \cdot \widetilde{\varvec{B}}_1 \, , \end{aligned}$$
(15)

which can be calculated from the rotating frame magnetic field \(\widetilde{\varvec{B}}_1\). The resulting propagator is then applied to the spin density operator of the system, resulting in the temporal evolution of the spin density operator, from which the macroscopic magnetization can be derived. We would like to emphasize that the method yields only valid results at the end of each period, since it averages the Hamiltonian over full periods \(T = \frac{2 \pi }{\omega _0}\).

The convergence of the Magnus expansion additionally depends on a convergence condition. In [27] such a condition can be found, which for the Hamiltonian under consideration can be written as

$$\begin{aligned} \pi > \int _0^t \left| \left| {H_1(s)}\right| \right| ds = 4 \sqrt{2} \frac{B_1}{B_0} \quad \Rightarrow \quad \frac{B_1}{B_0} < \frac{\pi }{4 \sqrt{2}} \approx 0.56 \, . \end{aligned}$$
(16)

This is a sufficient but not necessary condition, i.e. the Magnus expansion may converge for higher ratios, but is not guaranteed to do so. For a more general description of the Magnus expansion and its application to NMR, we refer the reader to [25].

In this work, we use the general formula for the Magnus expansion from [26] together with the SymPy symbolic math library [28] to obtain the Magnus expansions up to fifth order. The resulting formulas for each order can be found in the appendix.

2.4 Bloch-Simulation

The Bloch equations are a set of differential equations describing the temporal evolution of a two-level system. For the macroscopic nuclear magnetization \(\varvec{M}\) of a spin-\(\frac{1}{2}\) system they read as

$$\begin{aligned} \frac{{\textsf{d}}{\varvec{M}(t)}}{{\textsf{d}}{t}} = \gamma \varvec{M}(t) \times \varvec{B}(t) - \frac{M_x(t)}{T_2}\varvec{e}_x -\frac{M_y(t)}{T_2}\varvec{e}_y - \frac{\left( M_z(t) - M_0 \right) }{T_1} \varvec{e}_z \, , \end{aligned}$$
(17)

where \(\varvec{B}(t) = \varvec{B}_0 + \varvec{B}_1(t)\) is the total magnetic field, and \(T_1\) and \(T_2\) are the longitudinal and transverse relaxation times, respectively. By solving this differential equation, the magnetization \(\varvec{M}(\tau _p)\) at the end of the pulse can be calculated. In our case, we focus on short pulses to avoid the impact of relaxation during the pulse, i.e. the relaxation terms in Eq.  17 can be neglected.

3 Methods

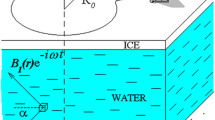
The SNMR experiments were performed with the GMR-Flex (Vista Clara Inc.) device at the Schillerslage test site [29]. The coils were mounted on a wooden board and placed on top of four pallet boxes filled with water as shown in Fig. 1a) and b). The prepolarization field was produced by a current of \(I_{\textrm{PP}} = 31.0 \, \textrm{A}\) running through a coil with a diameter of \(d_{\textrm{PP}} = 1.6\, \textrm{m}\) and \(n_{\textrm{PP}} = 54\) turns. A coil with a diameter of \(d_{\textrm{Tx}} = 1 \, \textrm{m}\) and \(n_{\textrm{Tx}} = 1\) turn was used to transmit short pulses (pulse durations from \(\tau _p = 0.47 \, \textrm{ms}\) to \(\tau _p = 7.57 \, \textrm{ms}\)) at the local Larmor frequency of \(f_{\textrm{L}} = 2115 \, \textrm{Hz}\). Due to the small size of the transmitter loop, the excitation pulse was transmitted in untuned mode. This causes a pulse shape that differs from an ideal sinusoid. A coincident (\(d_{\textrm{Rx}} = 1 \, \textrm{m}\)) receiver coil with \(n_{\textrm{Rx}} = 20\) turns was used to detect the NMR signals. The schematic representation of the layout is presented in Fig. 1c).

Fig. 1
figure 1

Experimental layout: a picture of the pallet boxes filled with water, b pre-polarization, transmitter, and receiver coils mounted on board and placed on top of the boxes, and c schematic top-view of the layout

Full size image

The prepolarization field was applied for \(t_{\textrm{PP}}= 5 \, \textrm{s}\) and switched off with a linear-exponential [15] ramp within \(t_{\textrm{ramp}} = 1 \, \textrm{ms}\). After waiting for \(t_{\textrm{wait}} = 3 \, \textrm{ms}\), the SNMR pulse was applied. To show the influence of the Bloch–Siegert effect we varied the intensity of the pulse as well as the pulse duration (see Sect. 4.3). After a dead time of \(t_{\textrm{dead}} = 2.5 \, \textrm{ms}\) the free induction decay (FID) was recorded for one second. To obtain a higher signal-to-noise ratio, each experiment was repeated eight times and the respective FIDs where stacked together.

The MRSmatlab toolbox [30] was used to process and fit the obtained data and for the calculation of the kernels. We developed an interface with the pyBLOCHUS module of the BLOCHUS software [31] to enable calculations of kernels with the solution of the Bloch equations. The pyBLOCHUS module was further optimized with the help of the numbalsoda library [32] and parallelized to obtain fast solutions of the Bloch equations for each voxel of the subsurface. For the kernel calculations, we neglected the conductivity of the subsurface, because on the small length scales of our experiments no significant phase shift due to conductivity can be expected. We would like to point out that the calculation can easily be adapted to account for subsurface conductivity by incorporating the respective phase shifts into the relevant equations.

4 Results and Discussion

4.1 Evolution of the Nuclear Magnetization

In this paper we will compare three approaches to describe the nuclear magnetization during the SNMR pulse:

  1. 1.

    By solving the Bloch equations (BE). This approach needs relatively long computation times but provides an exact description of the magnetization at every time. This will be used as a benchmark to verify the other approaches.

  2. 2.

    By using the rotating wave approximation (RWA). This is the standard approach used by nearly all SNMR modeling tools. The approximation allows a computational inexpensive calculation of the magnetization after the pulse, but the approximation is only valid if \(B_1 \ll B_0\).

  3. 3.

    By using the average Hamiltonian (AHi) of a specific order i to calculate an average propagator. While this needs slightly longer computation times compared to the second approach, it is still by orders of magnitude faster than the first one. The propagator of the first order average Hamiltonian yields results equivalent to the rotating wave approximation (see Table 1 in appendix A).

Fig. 2
figure 2

Temporal evolution of a, c, and e: the magnetization in the rotating frame during the pulse and b, d, and f: the error angle \(\alpha\) between the magnetization vector obtained with BE and the magnetization vector obtained with the method indicated in the legend. The conditions, given by the parallel and perpendicular field components \(B_\parallel\) and \(B_\perp\) on top of each plot, are equal for each row. The components of the magnetization (first column) are referred to by their color (\(M_x\)—red, \(M_y\)—green, \(M_z\)—blue), while the used approach is referred to by the line style as indicated in the respective legend. The error angle (second column) is only calculated for full periods, the lines serve as a guide to the eye. Please note the different time scales of the two columns

Full size image

In Fig. 2a, c, and e the temporal evolution of the macroscopic magnetization in the rotating frame \(\widetilde{M}(t)\) during four periods of the pulse are shown for three exemplary combinations of the field components \(B_\perp\) and \(B_\parallel\) with respect to \(B_0\). We would like to point out again, that the average Hamiltonian approach is only valid at full periods (vertical black lines). Therefore, the AH approximations can still yield good results even if there are large differences to the BE approach at other times. As a measure for the quality of each approximation, we will use the error angle

$$\begin{aligned} \alpha _{\textrm{AHi}}(nT) = \angle \left( {\varvec{M}_{\textrm{AHi}} (nT)}\, , \, {\varvec{M}_{\textrm{BE}}(nT)}\right) \end{aligned}$$
(18)

between the magnetization vector of the respective approximation and the magnetization vector of the BE-solution after n full periods. The temporal development of this angular difference can be found in Fig. 2b, d, and f.

Figure 2a displays an example where both field components are small compared to \(B_0\). Here, the RWA- and the AH-solutions show no visible differences to the BE-solution in the x and z-component, whereas a slight difference in the y-component for the RWA-approach is visible. This amounts to an error angle (Fig. 2b) of \(\alpha _{\textrm{RWA}} (t=4T) = 0.03 \cdot 180^\circ \approx 7^\circ\), which still might be an acceptable error for the kernel calculation. The error angles for the AH-approach of second order is about one decade smaller for small t and about another decade for the third order AH. All other orders of the AH approximations are omitted because they coincide with the third order, i.e. the approximation converged. At \(t=12 T\) the first order approximation (RWA) results in a smaller error angle than the second order approximation (AH2). This is due to the oscillatory nature of the magnetization components during the pulse, i.e. the first order approximation of the y-component is constant at zero and at this time the y-component obtained by the BE-solution crosses zero.

In Fig. 2c) we show an example with a perpendicular field similar to Fig. 2a but at a significant higher \(B_\parallel\). In contrast to the RWA, where this field is neglected, it results in large oscillations with a period of T in the y-components of the magnetization obtained with the Bloch equations. At full periods (vertical black lines) the amplitude of this oscillation is well represented by the average Hamiltonian approach of fifth order. The respective angular difference \(\alpha\) is shown in Fig. 2d for a larger time frame. As expected, a higher order of the average Hamiltonian leads to a smaller difference to the BE magnetization vector.

The third example is presented in Fig. 2e. Here, the amplitude of the magnetic field is similar to the second example, but the perpendicular component is increased so that it is similar to the parallel component. Due to the higher perpendicular component, we have an increased circularly polarized field, resulting in a faster oscillation of the RWA. Of course, the counter-rotating field is also increased and both, the perpendicular and the parallel field components influence the magnetization. Again, the AH solution of fifth order yields reasonable values at full periods, which results in low angular differences in Fig. 2f for this order.

Fig. 3
figure 3

Angular difference between the magnetization vectors after four periods calculated with the BE approach and the average Hamiltonian of a first (RWA), b third, and c fifth order. The white area represents values smaller than \(\alpha = 0.001 \pi\). The black lines denote lines of equal absolute field strength: \(\left| {\varvec{B}_1}\right| = 0.1 B_0\) continuous line, \(\left| {\varvec{B}_1}\right| = 0.3 B_0\) dotted line, and \(\left| {\varvec{B}_1}\right| = 1.0 B_0\) dashed line. The red dots are the points for which the temporal evolution of the magnetization and \(\alpha\) are shown in Fig. 2

Full size image

In Fig. 3 the angular difference after four periods \(\alpha (4T)\) is shown for three approximations over the relevant part of the \(B_\perp\)-\(B_\parallel\)-space. Figure 3a) displays this error angle for the rotating wave approximation (or first order average Hamiltonian). If one would consider an angular difference of a few degree acceptable, this approximation yields reasonable results for \(\left| {\varvec{B}_1}\right| < 0.1 B_0\), which corresponds to the area below and left of the continuous black line. As we will see later, this threshold can be crossed already for relatively low pulse moments q if the target depth is small and the pulses are short. Figure 3b presents the same parameter for the third order average Hamiltonian (AH3). One can see a clear increase of the area that represents small values of \(\alpha\). For the fifth order average Hamiltonian (Fig. 3c) this area is again increased. This approximation can be considered reasonable up to a field amplitude of \(B_1 = B_0\) (dashed black line). Higher orders might increase this threshold even further, but since the \(B_1\)-\(B_0\)-ratio is already above the sufficient convergence condition given by Eq. 16, the return might be limited. We conclude that above a specific ratio the computational cost for solving the Bloch equations cannot be avoided, but with the average Hamiltonian obtained from the Magnus expansion this threshold can be significantly increased.

For an efficient calculation of the kernels, we propose a mixed approach, in which the Magnus expansion of fifth order is used for voxels in which \(B_1 < B_0\) and the Bloch equations are solved for all other voxels. The difference of the resulting kernels to a kernel calculated completely with the solution of the Bloch equations will be negligible. In the following sections this approach will be used for kernel calculations and the respective kernels will be denominated as BEAH kernels.

4.2 Resulting Kernels

Figure 4 compares the kernel function obtained with the BEAH and RWA approach. The kernels were calculated for a homogeneous resistive half space with pulses of four oscillations at a resonance frequency of \(f_L = 2115 \, \textrm{Hz}\) (pulse duration \(\tau _p = 1.89 \, \textrm{ms})\) and a layout similar to the layout described in Sect. 3. For the real component of the kernels (Fig.  4a and b), there are slight differences visible in magnitude and general behavior at high pulse moments q. While the imaginary part of the RWA-kernel (not depicted) is zero for every depth and q, the BEAH-kernel has an imaginary component (Fig. 4c) of considerable magnitude at high q values. This signal represents the \(M_y\)-component caused by the Bloch–Siegert effect (see Fig. 2).

Fig. 4
figure 4

a and b: real component of the sensitivity kernel obtained with the BEAH approach and with the RWA, respectively. c: imaginary component of the BEAH kernel. The imaginary component of the RWA kernel is zero for all z and q and is, therefore, not shown

Full size image
Fig. 5
figure 5

a presents the signal amplitude of the sounding curves that were obtained by integrating the kernels for the various models (some of which are shown in Fig. 4) over the depth z. In b the respective phase of the signal is shown. The vertical black lines mark values of q at which certain \(B_1\)-levels are reached in the layer \(10\, \textrm{cm}\) from the surface (\(\left| {\varvec{B}_1}\right| = 0.1 B_0\) continuous line, \(\left| {\varvec{B}_1}\right| = 0.3 B_0\) dotted line, and \(\left| {\varvec{B}_1}\right| = 1.0 B_0\) dashed line)

Full size image

By integrating the kernel functions over the depth, one obtains the signal that would be measured over a halfspace filled with water. In Fig. 5 the amplitude and phase of these forward models are shown for the different approaches. From this we can estimate under which condition which approximation is valid and how the signal is influenced by the Bloch–Siegert effect. In the amplitude data shown in Fig. 5a) the predictions of the models start to strongly diverge from each other at \(q=0.05 \, \textrm{As}\). At this q value critical levels of \(\left| {\varvec{B}_1}\right| > B_0\) are already reached in a significant portion of the subsurface. The phase data presented in Fig. 5b) are more sensitive to the Bloch–Siegert effect. Here, differences between the RWA model ignoring the Bloch–Siegert effect and the other models can already be identified if in the first \(10 \, \textrm{cm}\) of the subsurface levels of \(\left| {\varvec{B}_1}\right| > 0.1 B_0\) are reached. The model that uses the fifth order average Hamiltonian (AH5) is in agreement with the BEAH solution up to \(q=0.25 \, \textrm{As}\) in the amplitude data, but only up to \(q=0.05 \, \textrm{As}\) in the phase data. In general, the Bloch–Siegert effect causes significantly increased signal amplitudes at high q values and increased imaginary signal components, i.e. a phase shift, at medium to high q values.

4.3 Experimental Evaluation

Figure 6 presents the amplitudes and phases from SNMR experiments at three different pulse durations and compares them to the predictions of the forward models. The black line represents predictions of a model that ignores the Bloch–Siegert effect, i.e. that uses the rotating wave approximation (RWA). The colored lines represent forward models obtained with the BEAH approach for the respective pulse lengths. The kernel calculation only uses voxels if their center lies within the boundaries of the containers. Compared to a perfect half-space, the amount of water is reduced which results in the lower amplitude compared to Fig. 5. The experiments were performed at different pulse durations, because for shorter pulse duration, high magnetic fields are reached at lower pulse moments q and the sounding curves are, therefore, already influenced by the Bloch–Siegert effect at these lower q values. In general, the amplitude data in Fig. 6a is reasonably well represented by the respective models. The slight differences at higher pulse moments can be attributed to the imperfect pulse shapes and to the more complex geometry of the experiment (compared to a homogeneous half space) caused by the water containers.

Fig. 6
figure 6

a Amplitude and b phase of the SNMR signal as a function of the pulse moment q. The data was obtained at different pulse durations, as indicated by the number of periods in the legend. At the local Larmor frequency of \(f_L = 2115 \, \textrm{Hz}\) one period equals \(T=0.473 \, \textrm{ms}\). The respective forward models obtained from BEAH kernels are presented by the continuous lines. For comparison, a forward model that neglects the Bloch–Siegert effect is shown (black line). Error bars refer to a \(95\%\) confidence interval that results from a mono-exponential fit of the free induction decays of the data

Full size image

In the phase data shown in Fig. 6b), we see the predicted phase shift at high pulse moments for the experimental data as well as for the forward model. While the models and the data are in good agreement at low pulse moments and for the longest pulse (yellow), the phase shift in the experimental data is significantly larger than the prediction of the model at high pulse moments for the shorter pulses. This might be caused by the imperfect pulse shapes of the untuned transmitter. The additional harmonics, that are part of these pulse shapes, and transients after pulse switch-off [18] might influence the phase of the recorded signal, while their influence on the amplitude would likely be small. A short describtion of two exemplary pulse shapes can be found in appendix B. To obtain the correct phase signal, a complete Bloch simulation of the subsurface using the pulse shapes recorded during the experiments (and not with the idealized sinusoidal pulses) might be necessary, but is beyond the scope of this work.

5 Conclusion

Based on simulations of the magnetization during the SNMR pulse, obtained with the solution of the Bloch equations and with the fifth order Magnus expansion, we evaluate the influence of the Bloch–Siegert effect on small scale SNMR experiments. These experiments aim to enable fast and mobile water content measurements in the unsaturated zone. The rotating wave approximation becomes inaccurate at excitation field intensities of \(B_1 = 0.1 B_0\), where the difference to the magnetization obtained with the Bloch equations can already be multiple degrees. Since the solving of the Bloch equations needs relatively long computation times, the Magnus expansion is a valuable tool which allows the fast analytic calculation of the magnetization up to field intensities of \(B_1 = B_0\). For even higher field amplitudes, the solution of the Bloch equations must be used. We demonstrate the effect of the Bloch–Siegert effect on the SNMR kernel functions and corresponding sounding curves. The simulated data is supported by experiments that were performed with a small scale SNMR sensor on water containers. These experiments were conducted with different pulse durations, resulting in different pulse moments at which the Bloch–Siegert effect becomes relevant. While the phase of the measured signal does only agree with the models at low pulse amplitudes, the signal amplitude data is in very good agreement with the forward models.