1 Introduction

Robots are getting better and cheaper—and that means they will play a much larger role in our lives is highlighted by “The Economist” podcast The Rise of Robots.Footnote 1 There is now plenty of evidence of this phenomenon. Taking into account that automation is getting better and widespread, in this paper we address some of the future possible consequences of this process. It is also important to note that very recent evidence has shown the effects of automation on the labor market (e.g., Acemoglu and Restrepo 2020; Bessen et al. 2019; Bogliacino and Lucchese 2016; Bordot 2022). These empirical effects are mixed although pointed for negative effects in employment and wages and to wage polarization. In fact, in a survey of the literature, Barbieri et al. (2019) mentions that studying the effects of automation in labor market features is of major importance.

By devising a Direct Technical Change (DTC) growth model that internalizes the effects of automation considering R &D activities which improve the quality of capital goods (robots or not), it contributes to a more fine-grained discussion of the possible consequences of automation. The model considers two sectors, the routine and non-routine sectors, including the task categorization provided by the task-based model approach of Autor et al. (2003) and Acemoglu and Autor (2011), which uses a “two-by-two matrix” (Frey and Osborne 2017, p. 258): (1) routine versus non-routine tasks; and (2) cognitive versus manual tasks. These papers allow to address the equilibrium ratio between the highest and the medium and between the medium and the lower wages, known as wage polarization (e.g., Autor and Dorn 2013; Goos et al. 2014). The intuitive reason is that medium-income workers tend to be employed in routine tasks that may be automated while both higher income earners and lower income earners tend to be employed in tasks that cannot be automated. However, those papers did not include the possibility of R &D that improve the quality of robots and other capital goods. Acemoglu and Restrepo (2018) introduce the possibility of innovation that eases the replaceability of workers by machines. In particular, R &D increases the number of tasks that can be replaced by machines. Also Irmen (2020) develop a model with tasks and skill-biased technical change although it considers that technical progress (or R &D) is exogenous. We depart from this baseline and consider that endogenous innovation can affect both routine and non-routine sectors by improving the quality of the best variety (e.g., Aghion and Howitt 1992; Afonso 2006). With this in mind, we developed a task-based model with quality ladders in R &D and directed technical change. In this model there is a routine sector and a non-routine sector, each employing inelastically supplied labor classified as human capital or skilled (H), raw labor (L) and medium-skilled (M). In some close approaches (e.g., Afonso et al. 2022) the routine sector may use only a homogeneous type of medium-skilled workers. Our approach is theoretically more flexible (and realistic) as the routine sector may use two types of medium-skilled workers.

Our model allows us to analyze the determinants of the technological-knowledge level, skill premium (or wage inequality), real prices, output, and economic growth. In particular, we focus on three different automation effects. The first assumes that the automation shock increases the production share of the non-routine sector. This may be the outcome of the existence of a set of tasks that is not routinizable at all, as mentioned by, e.g., Feng and Graetz (2020) and/or by the declining trend of prices of robots (e.g., Brinca et al. 2022). The second considers that the automation shock decreases the labor efficiency rate and value-generating ability of workers in the routine sector, due to a higher propensity of routine tasks being replaced by more efficient machines and robots. The third assumes that the automation shock increases the labor efficiency rate and the ability to generate value of workers in the non-routine sector.

We quantitatively address these effects through calibration. Initially, the initial steady-state levels are calculated to target statistics for the US of the key variables. Then, we evaluate the feasibility of the calibration comparing the economic growth rates of the model steady state with the current values for those rates in other technological leading countries than the US. Finally, we quantitatively calculate the effects of shocks caused by increasing the level of automation (measured by the three effects mentioned above) in the balanced growth path. We conclude that (even individually considered) all the changes associated with automation lead to even more wage polarization and a small increase in the economic growth rate. Thus, it is crucial that governments implement policies to help the professional transition of workers with medium qualifications working in the routine sector, in order to promote social cohesion. Overall, this paper adds new knowledge to the academic debate about the potential social and economic effects of automation in wealthy technologically leading nations.

Beginning with this brief Introduction, we present the setup (Sect. 2). In Sect. 3 we solve for the general equilibrium. Finally, in Sect. 4, we calibrate the model for the US, assess its fit to another leading economies and present the quantitative economic effects of potential automation shocks brought about by automation. Section 5 concludes the paper.

2 Model setup

2.1 Consumer’s utility maximization problem

Infinitely-lived households obtain utility from the consumption of the numeraire good, C, and collect income from investments in financial assets (equity) and from labor, which is inelastically supplied by the aforementioned households. Preferences are identical across both non-routine and routine sectors, \(A=\left\{ N,R\right\}\), and workers, \(i=\left\{ L,H,M_{1},M_{2}\right\}\). Thus, the world economy admits a representative household with preferences at time \(t=0\) given by \(U=\int _{0}^{\infty }\left( \frac{C(t)^{1-\theta }-1}{1-\theta }\right) e^{-\rho t}dt\), where \(\rho >0\) is the subjective discount rate, ensuring that U is bounded away from infinity if C were constant over time, and \(\theta >0\) is the inverse of the inter-temporal elasticity of substitution, subject to the flow budget constraint \({\dot{a}}(t)=r(t)\cdot a(t)+w_{N}^{L}(t)\cdot L_{N}+w_{N}^{H}(t)\cdot H_{N}+w_{R}^{M_{1}}(t)\cdot M_{1_{R}}+w_{R}^{M_{2}}(t)\cdot M_{2_{R}}-C(t)\), where \(a(t)=\sum _{i=\left\{ L,H,M_{1},M_{2}\right\} }a_{i}(t)\) denotes household’s real financial assets/wealth holdings (composed of equity of intermediate-good producers, considering the profits seized by the top-quality producers), r is the real interest rate, and \(w_{i}\) is the wage for labor employed that can be \(i=\left\{ L,H,M_{1},M_{2}\right\}\)—where L, H, \(M_{1}\) and \(M_{2}\) represent unskilled, skilled, medium-skilled type 1 and medium-skilled type 2 workers. The initial level of wealth a(0) is given and the non-Ponzi games condition \(\lim {}_{t\rightarrow \infty }e^{-\int _{0}^{t}r(s)ds}a(t)\ge 0\) is imposed. The representative household chooses the path of aggregate consumption \(\left[ C(t)\right] _{t\ge 0}\) to maximize the discounted lifetime utility, resulting in the following optimal consumption path Euler equation. The representative household follows the optimal path of consumption (Euler equation):

$$\begin{aligned} \frac{{\dot{C}}}{C}=\frac{r-\rho }{\theta }, \end{aligned}$$
(1)

where \(\frac{{\dot{C}}}{C}\) is the growth rate of C and the condition \(\lim {}_{t\rightarrow \infty }e^{-\rho t}\cdot a(t)\cdot C(t)^{-\theta }=0\) is standard.

2.2 Produtive activity: outputs, wages, prices and technology

2.2.1 Aggregate and sectoral outputs

Resources, Y(t), that are not absorbed by families as consumption, C(t), are either spent for the production of intermediate goods, X(t), or allocated for R &D activity, Z(t); therefore, the output equilibrium is given by \(Y(t)=C(t)+X(t)+Z(t)\). Aggregate output Y is produced with a CES aggregate production function of competitively produced final goods in sector N and R:

$$\begin{aligned} \begin{array}{ccc} Y(t)&=\left[ \sum \limits _{A=\left\{ N,R\right\} }\gamma _{A}Y_{A}(t)^{\frac{\varepsilon -1}{\varepsilon }}\right] ^{\frac{\varepsilon }{\varepsilon -1}}&,\end{array}\quad \varepsilon \in \left( 0,+\infty \right) , \end{aligned}$$
(2)

where \(Y_{N}\) and \(Y_{R}\) are the total outputs of the N- and the R-sectors, respectively; \(\gamma _{N}\) and \(\gamma _{R}\), with \(\sum _{A=\left\{ N,R\right\} }\gamma _{A}=1\), are the distribution parameters, measuring the relative importance of the sectors; \(\varepsilon \ge 0\) is the elasticity of substitution between the two sectors, where in \(\varepsilon >1\) \(\left( \varepsilon <1\right)\) means that they are gross substitutes (complements) in the production of Y.

Solving the following maximization problem for the producer of Y:

$$\begin{aligned} \underset{Y_{N},Y_{R}}{\max }\Pi _{Y}{} & {} =P_{Y}Y-P_{N}Y_{N}-P_{R}Y_{R}\\ s.t.\; Y{} & {} =\left[ \gamma _{N}Y_{N}^{\frac{\varepsilon -1}{\varepsilon }}+\gamma _{R}Y_{R}^{\frac{\varepsilon -1}{\varepsilon }}\right] ^{\frac{\varepsilon }{\varepsilon -1}}\,and\,\gamma _{N}+\gamma _{R}=1. \end{aligned}$$

From the first order conditions (FOC), we have that

$$\begin{aligned} \frac{\partial \pi }{\partial Y_{A}}=0\Rightarrow \frac{P_{A}}{P_{Y}}=\gamma _{A}\left( \frac{Y_{A}}{Y}\right) ^{-\frac{1}{\epsilon }}. \end{aligned}$$
(3)

Dividing across sectors yields the expression for the demand for the relative output in the non-routine intensive sector:

$$\begin{aligned} \frac{Y_{N}}{Y_{R}}=\left( \frac{\gamma _{N}}{\gamma _{R}}\right) ^{\epsilon }\left( \frac{P_{N}}{P_{R}}\right) ^{-\epsilon }, \end{aligned}$$
(4)

where \(-\frac{\partial \ln \left( \frac{Y_{N}}{Y_{R}}\right) }{\partial \ln \left( \frac{P_{N}}{P_{R}}\right) }=\epsilon\) is the elasticity of substitution. Equation (4) can be interpreted as demand for the relative output in sector N. Higher values for the elasticity of substitution \(\epsilon\) imply that a higher relative price of output of sector N produces a higher decrease in relative output.

Bearing in mind (3) and (2), we have that:

$$\begin{aligned} \left[ \gamma _{R}^{\epsilon }P_{R}^{1-\epsilon }+\gamma _{N}^{\epsilon }P_{N}^{1-\epsilon }\right] ^{\frac{1}{1-\epsilon }}=P_{Y}. \end{aligned}$$
(5)

In turn, from (3), we also have that \(P_{A}Y_{A}=P_{Y}Y^{\frac{1}{\epsilon }}\gamma _{A}Y_{A}^{\frac{\epsilon -1}{\epsilon }}\), which summing across sectors results \(P_{Y}Y=P_{R}Y_{R}+P_{N}Y_{N}\).

2.2.2 Tasks output

Each task producer must pick whether to undertake the productive activity in sector N or R, which means choosing between the Cobb–Douglas production functions below. For sector \(A=\left\{ N,R\right\}\); i.e., non-routine sector N and routine sector R, we consider that:

$$\begin{aligned} Y_{v_{A}}^{i^{*}}(t)= & {} \left[ \int _{0}^{J_{A}}\left( q_{A}^{k(j,t)}{\cdot }x_{v_{A}}^{i^{*}}(k,j,t)\right) ^{1-\alpha _{A}}dj\right] \cdot \left[ \left( 1-v_{A}(t)\right) \cdot s^{*}\cdot i_{v_{A}}^{*}\right] ^{\alpha _{A}} \end{aligned}$$
(6)
$$\begin{aligned} Y_{v_{A}}^{i^{**}}(t)= & {} \left[ \int _{0}^{J_{N}}\left( q_{A}^{k(j,t)}{\cdot }x_{v_{A}}^{i^{**}}(k,j,t)\right) ^{1-\alpha _{N}}dj\right] \cdot \left[ v_{A}(t)\cdot s^{**}\cdot i_{v_{A}}^{**}\right] ^{\alpha _{A}}, \end{aligned}$$
(7)

where \(i^{*}=\left\{ L,M_{1}\right\}\), \(i^{**}=\left\{ H,M_{2}\right\}\), \(s^{*}=\left\{ l,m_{1}\right\}\), \(s^{**}=\left\{ h,m_{2}\right\}\), \(\alpha _{N}>\alpha _{R}\) (i.e., the labor share is higher in the non-routine sector); \(q_{A}\) is size of each quality upgrade; k is the number of quality upgrades; \(s=\left\{ l,h,m_{1},m_{2}\right\}\) is the absolute productivity of each type of labor, assessing its ability to generate value; \(j\in \left[ 0,J_{A}\right]\) is an intermediate good, and \(J_{A}\) is the number of intermediate goods in sector A; \(x_{v_{A}}^{i}(k,j,t)\) is the demand for the top-quality of j from all the producers of the task \(v_{A}\) that use technology complementary with j; \(i_{v_{A}}\), \(i=\left\{ L,H,M_{1},M_{2}\right\}\), is the number of workers performing the task \(v_{i}\) in each sector. Both choices imply different maximization problems, but since they are similar we exemplify for the case when the producer decides to produce in \(A=\left\{ N,R\right\}\), using labor \(i^{*}=\left\{ L,M_{1}\right\}\)—and from now on \(i^{**}=\left\{ H,M_{2}\right\}\)Footnote 2

$$\begin{aligned} \underset{{x_{v_{A}}^{i^{*}}(k,j,t),i_{v_{A}}^{*}(t)}}{\max \,\Pi _{v_{A}}(t)}&=P_{v_{A}}^{i^{*}}(t)\cdot Y_{v_{A}}^{i^{*}}(t)-\int _{0}^{J_{i^{*}}}p^{i^{*}}(k,j,t)\cdot x_{v_{A}}^{i^{*}}(k,j,t)dj-w^{i^{*}}(t)\cdot s\cdot i_{v_{A}}^{*}(t),\nonumber \\ s.t.\; Y_{v_{A}}^{i^{*}}(t)&=\left[ \int _{0}^{J_{i^{*}}}\left( q_{A}^{k(j,t)}{\cdot }x_{v_{A}}^{i^{*}}(k,j,t)\right) ^{1-\alpha _{A}}dj\right] \left[ \left( 1-v_{A}(t)\right) \cdot s\cdot i_{v_{A}}^{*}\right] ^{\alpha _{A}}, \end{aligned}$$
(8)

where \(P_{v_{A}}^{i}(t)\) is the price of a task performed by labor \(i^{*}=\left\{ L,M_{1}\right\}\) in \(A=\left\{ N,R\right\}\) at time t; \(p^{i}(k,j,t)\) denotes the price paid for the intermediate good j by a producer of a task \(v_{A}\); \(w^{i}(t)\) is the wage of each labor unit of type i at t in \(A=\left\{ N,R\right\}\). The FOC with respect to intermediate inputs is the following:

$$\begin{aligned} \frac{\partial \Pi _{n}}{\partial x_{v_{A}}^{i^{*}}(k,j,t)}=0\Leftrightarrow x_{v_{A}}^{i^{*}}(k,j,t)=\left[ \frac{P_{v_{A}}^{i^{*}}(1-\alpha _{A})}{p^{i^{*}}(k,j,t)}\right] ^{\frac{1}{\alpha _{A}}}\left( q_{A}^{k(j,t)}\right) ^{\frac{1-\alpha _{A}}{\alpha _{A}}}\left( 1-v_{A}(t)\right) \cdot s\cdot i_{v_{A}}^{*}. \end{aligned}$$
(9)

Replacing (9) in (8), we have that:

$$\begin{aligned} Y_{v_{A}}^{i^{*}}(t)=\left[ \frac{P_{v_{A}}^{i^{*}}(1-\alpha _{A})}{p^{i^{*}}(k,j,t)}\right] ^{\frac{1-\alpha _{A}}{\alpha _{A}}}\cdot Q_{A}\cdot \left( 1-v_{A}(t)\right) \cdot s\cdot i_{v_{A}}^{*}, \end{aligned}$$
(10)

where \(Q_{A}\) represents the technological-knowledge level of sector A. From the FOC with respect to units of labor, we obtain the expressions for wages in the \(i^{*}\)-sector:

$$\begin{aligned} \frac{\partial \Pi _{v_{A}}}{\partial i_{v_{A}}^{*}}=0\Leftrightarrow P_{v_{A}}^{i^{*}}\frac{\partial Y_{v_{A}}^{i^{*}}}{\partial i_{v_{A}}^{*}}=w^{i^{*}}\Leftrightarrow w^{i^{*}}=\frac{\alpha _{A}P_{v_{A}}^{i^{*}}Y_{v_{A}}^{i^{*}}}{s\cdot i_{v_{A}}^{*}}. \end{aligned}$$
(11)

In turn, replacing \(Y_{v_{A}}^{i}\) by (10) in (11), we have that:

$$\begin{aligned} w^{i^{*}}=\left( P_{v_{A}}^{i^{*}}\right) ^{\frac{1}{\alpha _{A}}}\left[ \frac{(1-\alpha _{A})}{p^{i^{*}}(k,j,t)}\right] ^{\frac{1-\alpha _{A}}{\alpha _{A}}}\cdot Q_{A}\cdot \left( 1-v_{A}(t)\right) \cdot s. \end{aligned}$$
(12)

Hence, from the maximization problem with respect to units of labor, the expressions for wages are: (1) for \(A=N\), \(w^{L}=\left( P_{v_{N}}^{L}\right) ^{\frac{1}{\alpha _{N}}}\left[ \frac{(1-\alpha _{N})}{p^{L}(k,j,t)}\right] ^{\frac{1-\alpha _{N}}{\alpha _{N}}}\cdot Q_{N}\cdot \left( 1-v_{N}(t)\right) \cdot l\) and \(w^{H}=\left( P_{v_{N}}^{H}\right) ^{\frac{1}{\alpha _{N}}}\left[ \frac{(1-\alpha _{N})}{p^{H}(k,j,t)}\right] ^{\frac{1-\alpha _{N}}{\alpha _{N}}}\cdot Q_{N}\cdot v_{N}(t)\cdot h\); (2) for \(A=R\), \(w^{M_{1}}=\left( P_{v_{R}}^{M_{1}}\right) ^{\frac{1}{\alpha _{R}}}\left[ \frac{(1-\alpha _{R})}{p^{M_{1}}(k,j,t)}\right] ^{\frac{1-\alpha _{R}}{\alpha _{R}}}\cdot Q_{R}\cdot \left( 1-v_{R}(t)\right) \cdot m_{1}\) and \(w^{M_{2}}=\left( P_{v_{R}}^{M_{2}}\right) ^{\frac{1}{\alpha _{R}}}\left[ \frac{(1-\alpha _{R})}{p^{M_{2}}(k,j,t)}\right] ^{\frac{1-\alpha _{R}}{\alpha _{R}}}\cdot Q_{R}\cdot v_{R}(t)\cdot m_{2}\).

We define the constants \(\left( P_{v_{N}}^{L}\right) ^{\frac{1}{\alpha _{N}}}\cdot \left( 1-v_{N}(t)\right) \equiv \left( P_{N}^{L}\right) ^{\frac{1}{\alpha _{N}}}\), \(\left( P_{v_{N}}^{H}\right) ^{\frac{1}{\alpha _{N}}}\cdot v_{N}(t)\equiv \left( P_{N}^{H}\right) ^{\frac{1}{\alpha _{N}}}\), \(\left( P_{v_{R}}^{M_{1}}\right) ^{\frac{1}{\alpha _{R}}}\cdot \left( 1-v_{R}(t)\right) \equiv \left( P_{R}^{M_{1}}\right) ^{\frac{1}{\alpha _{R}}}\), \(\left( P_{v_{R}}^{M_{2}}\right) ^{\frac{1}{\alpha _{R}}}\cdot v_{R}(t)\equiv \left( P_{R}^{M_{2}}\right) ^{\frac{1}{\alpha _{R}}}\), which by rearranging in two separate expressions allows us to obtain the relative price in each sector, non-routine and routine, for each task, \(v_{N}\) and \(v_{R}\):

$$\begin{aligned} \frac{P_{v_{A}}^{*}}{P_{v_{A}}^{**}}= & {} \left[ \frac{v_{A}(t)}{1-v_{A}(t)}\right] ^{\alpha _{N}}\cdot \frac{P_{A}^{*}}{P_{A}^{**}},\,i^{*}=\left\{ L,M_{1}\right\} \,and\,i^{**}=\left\{ H,M_{2}\right\} . \end{aligned}$$
(13)

Therefore, the relative prices of each task in both non-routine and routine sectors, \(\frac{P_{v_{A}}^{i^{*}}}{P_{v_{A}}^{i^{**}}},\) can be interpreted as being the result of a relative advantage of producing in \(i^{*}\) specific to each task, represented by the term \(\frac{v_{A}(t)}{1-v_{A}(t)}\), and a relative advantage that is common to all tasks produced in \(i^{*}\), represented by \(\frac{P_{A}^{i^{*}}}{P_{A}^{i^{**}}}\), since a higher \(\frac{P_{A}^{i^{*}}}{P_{A}^{i^{**}}}\) causes the relative prices of all tasks in \(i^{**}\) to be higher.

The product from the profit maximization problems of the producers of output in both non-routine, N, and routine, R, sectors, and task \(v_{A}\), \(P_{v_{A}}Y_{v_{A}}\), allows to conclude that the relative price of each task in A, \(\frac{P_{v_{A}}^{i^{*}}}{P_{v_{A}}^{i^{**}}}\), is a continuous and increasing function of \({\overline{v}}_{A}\), approaching 0 (\(+\infty )\) for values of \(v_{A}\) closer to 0 (1) and being 1 for a threshold task \({\overline{v}}_{A}\). Hence, since perfectly competitive producers choose to produce each task in the sector that provides the lowest price, tasks \(v_{A}<{\overline{v}}_{A}\) (\(v_{A}>{\overline{v}}_{A}\) ) will be produced in \(i^{*}\) (\(i^{**}\)). The expressions of the threshold task and the relative advantage are the following, respectively:

$$\begin{aligned} {\overline{v}}_{A}{} & {} =\left[ 1+\left( \frac{P_{A}^{*}}{P_{A}^{**}}\right) ^{\frac{1}{\alpha _{A}}}\right] ^{-1},\end{aligned}$$
(14)
$$\begin{aligned} \frac{P_{A}^{*}}{P_{A}^{**}}{} & {} =\left( \frac{s^{**}\cdot i^{**}}{s^{*}\cdot i^{*}}\right) ^{\frac{\alpha _{A}}{2}}, \end{aligned}$$
(15)

where \(i^{*}=\left\{ L,M_{1}\right\}\), \(i^{**}=\left\{ H,M_{2}\right\}\), \(s^{*}=\left\{ l,m_{1}\right\}\), and \(s^{**}=\left\{ h,m_{2}\right\}\).

We can now state Proposition 1.

Proposition 1

The threshold task \({\overline{v}}_{A}\) depends negatively on the relative price advantage in \(i^{*}\), \(\frac{P_{A}^{*}}{P_{A}^{**}}\), which, in turn, depends positively on the relative abundance of labor units in \(i^{**}\), \(\frac{i^{**}}{i^{*}}\), and absolute productivity advantage in \(i^{**}\), \(\frac{s^{**}}{s^{*}}\).

Proof

Derive (14) in order to \(\frac{P_{A}^{*}}{P_{A}^{**}}\) and and (15) in order to \(\frac{i^{**}}{i^{*}}\). \(\square\)

2.2.3 Wages, wage differentials and polarization

Intra-sector wage inequality From the expression for wages obtained from the profit maximization problem of the producer of \(Y_{v_{A}}\) and using the definition of price indexes, we have:

$$\begin{aligned} w^{i}=\left( P_{A}^{i}\right) ^{\frac{1}{\alpha _{A}}}\left[ \frac{(1-\alpha _{A})}{p^{i}(k,j,t)}\right] ^{\frac{1-\alpha _{A}}{\alpha _{A}}}\cdot Q_{A}\cdot s,\,i=\left\{ L,H,M_{1},M_{2}\right\} \,and\,s=\left\{ l,h,m_{1},m_{2}\right\} . \end{aligned}$$
(16)

From the expression (16) and replacing \(P_{A}^{i}\) with the price index expressions, we can obtain inter-sector and intra-sector wage gap between proficiencies. The wage differentials for the non-routine and routine sectors are as follows: \(\frac{w_{N}^{H}}{w_{N}^{L}}=\frac{\left( P_{N}^{H}\right) ^{\frac{1}{\alpha _{N}}}\cdot h}{\left( P_{N}^{L}\right) ^{\frac{1}{\alpha _{N}}}\cdot l}=\left( \frac{l}{h}\cdot \frac{H}{L}\right) ^{-\frac{1}{2}}\) and \(\frac{w_{R}^{M_{2}}}{w_{R}^{M_{1}}}=\frac{\left( P_{R}^{M_{2}}\right) ^{\frac{1}{\alpha _{R}}}\cdot m_{2}}{\left( P_{R}^{M_{1}}\right) ^{\frac{1}{\alpha _{R}}}\cdot m_{1}}=\left( \frac{1-{\overline{v}}_{R}}{{\overline{v}}_{R}}\right) ^{-1}=\left( \frac{m_{1}}{m_{2}}\cdot \frac{M_{2}}{M_{1}}\right) ^{-\frac{1}{2}}\), respectively.

The relative advantage wage of \(i^{**}=\left\{ H,M_{2}\right\}\) workers in \(A=\left\{ N,R\right\}\) depends negatively on the relative quantity of the same labor units, \(\left( \frac{i^{**}}{i^{*}}\right) ^{-\frac{1}{2}}\), and depends positively on the relative absolute productivity, \(\left( \frac{s^{**}}{s^{*}}\right) ^{\frac{1}{2}}\). Interestingly intra-sectoral wage gaps do not depend on the technological technological-knowledge level or on technological knowledge bias.

Inter-sector wage inequality and wage polarizationTo obtain the wage gap across sectors, we compared the relative wage advantage of both H and L, components of N sector, against \(M_{1}\) and \(M_{2}\) components of R. For simplicity, from now on, we decided to assume the same value \(\alpha\) for both sectors. Starting with the wage expression 16, we have for the unskilled levels, L and \(M_{1}\), \(\frac{w_{N}^{L}}{w_{R}^{M_{1}}}=\left( \frac{P_{N}^{L}}{P_{R}^{M_{1}}}\right) ^{\frac{1}{\alpha }}\frac{Q_{N}\cdot l}{Q_{R}\cdot m_{1}}\) and for the skilled levels, H and \(M_{2}\), \(\frac{w_{N}^{H}}{w_{R}^{M_{2}}}=\left( \frac{P_{N}^{H}}{P_{R}^{M_{2}}}\right) ^{\frac{1}{\alpha }}\frac{Q_{N}\cdot h}{Q_{R}\cdot m_{2}}\). Using the definition of price indexes written above, we obtain the skill premium of the wage gap which represents the wage polarization in both sectors, as follows:

$$\begin{aligned}{} & {} \frac{w_{N}^{L}}{w_{R}^{M_{1}}}=\left( \frac{P_{N}}{P_{R}}\right) ^{\frac{1}{\alpha }}\left( \frac{{\overline{v}}_{N}}{{\overline{v}}_{R}}\right) ^{-1}{\mathcal {Q}}\frac{l}{m_{1}}, \end{aligned}$$
(17)
$$\begin{aligned}{} & {} \frac{w_{N}^{H}}{w_{R}^{M_{2}}}=\left( \frac{P_{N}}{P_{R}}\right) ^{\frac{1}{\alpha }}\left( \frac{{\overline{v}}_{N}}{{\overline{v}}_{R}}\right) ^{-1}{\mathcal {Q}}\frac{h}{m_{2}}. \end{aligned}$$
(18)

where \({\mathcal {Q}}=\frac{Q_{N}}{Q_{R}}\) is the technological knowledge bias. An increase in the ratios written as (17) and (18) means to obtain wage polarization which can be due more to the increase in the skilled wage gap or more to the decrease in the unskilled wage gap or both. This also mean that intra-sectoral wage inequality and thus wage polarization depend both on the technological knowledge bias.

2.2.4 Sectoral outputs and prices

From the profit maximization problem of the producer of Y and since in each sector, N and R, some part of the tasks are done by L, while others by H in N-sector, whereas in the R-sector some tasks are performed by \(M_{1}\), while others by \(M_{2}\), the final output for each sector is the following:

$$\begin{aligned} P_{A}Y_{A}=\int _{0}^{1}P_{v_{A}}Y_{v_{A}}dv_{A}=\int _{0}^{{\overline{v}}_{A}}P_{v_{A}}^{i^{*}}Y_{v_{A}}^{i^{*}}dv_{A}+\int _{{\overline{v}}_{A}}^{1}P_{v_{A}}^{i^{**}}Y_{v_{A}}^{i^{**}}dv_{A}=P_{A}^{i^{*}}Y_{A}^{i^{*}}+P_{A}^{i^{**}}Y_{A}^{i^{**}}, \end{aligned}$$

where \(i^{*}=\left\{ L,M_{1}\right\}\), \(i^{**}=\left\{ H,M_{2}\right\}\). Taking into account that \(P_{v_{A}}^{i}Y_{v_{A}}\) is constant, the output of each sector generated by each proficiency of labor is given by:

$$\begin{aligned}{} & {} P_{N}^{L}Y_{N}^{L}=\left( P_{v_{N}}^{L}\right) ^{\frac{1}{\alpha }}\left[ \frac{(1-\alpha )}{q}\right] ^{\frac{1-\alpha }{\alpha }}\cdot Q_{N}\cdot \left( 1-v_{N}(t)\right) \cdot l\cdot L, \end{aligned}$$
(19)
$$\begin{aligned}{} & {} P_{N}^{H}Y_{N}^{H}=\left( P_{v_{N}}^{H}\right) ^{\frac{1}{\alpha }}\left[ \frac{(1-\alpha )}{q}\right] ^{\frac{1-\alpha }{\alpha }}\cdot Q_{N}\cdot v_{N}(t)\cdot h\cdot H. \end{aligned}$$
(20)

Therefore, for the A-sector we have that \(P_{A}Y_{A}=Q_{A}\left[ \frac{(1-\alpha )}{q}\right] ^{\frac{1-\alpha }{\alpha }}\cdot \left( P_{A}\right) ^{\frac{1}{\alpha }}\exp \left( -1\right) \cdot {{\textrm{M}}}_{A}\), i.e.,

$$\begin{aligned} P_{A}Y_{A}=Q_{A}\left[ \frac{(1-\alpha )}{q}\right] ^{\frac{1-\alpha }{\alpha }}\cdot \left[ \begin{array}{c} \left( P_{A}\exp \left( -\alpha \right) {\overline{v}}_{A}^{-\alpha }\left( 1-v_{A}\right) ^{-\alpha }\right) ^{\frac{1}{\alpha }}\cdot \left( 1-v_{A}(t)\right) \cdot s^{*}\cdot i^{*}+\\ +\left( P_{A}\exp \left( -\alpha \right) \left( 1-{\overline{v}}_{A}\right) ^{-\alpha }v_{A}^{-\alpha }\right) ^{\frac{1}{\alpha }}\cdot v_{A}(t)\cdot s^{**}\cdot i^{**} \end{array}\right] , \end{aligned}$$
(21)

where \(P_{A}^{i^{*}}=P_{A}\exp \left( -\alpha \right) {\overline{v}}_{A}^{-\alpha }\) and \(P_{A}^{i^{**}}=P_{A}\exp \left( -\alpha \right) \left( 1-{\overline{v}}_{A}\right) ^{-\alpha }\) and, by replacing in 21 we get:

$$\begin{aligned} Y_{A}=Q_{A}\left[ \frac{P_{A}(1-\alpha )}{q}\right] ^{\frac{1-\alpha }{\alpha }}\cdot \exp \left( -1\right) \cdot {{\textrm{M}}}_{A}. \end{aligned}$$
(22)

where \({\textrm{M}}_{A}=\left[ \left( s^{*}\cdot i^{*}\right) ^{\frac{1}{2}}+\left( s^{**}\cdot i^{**}\right) ^{\frac{1}{2}}\right] ^{2}\), \(A=\left\{ N,R\right\}\), is the market size for the producer of intermediate goods complementary to i-type labor. Specifically: \({\textrm{M}}_{N}=\left[ \left( l\cdot L\right) ^{\frac{1}{2}}+\left( h\cdot H\right) ^{\frac{1}{2}}\right] ^{2}\), and \({\textrm{M}}_{R}=\left[ \left( m_{1}\cdot M_{1}\right) ^{\frac{1}{2}}+\left( m_{2}\cdot M_{2}\right) ^{\frac{1}{2}}\right] ^{2}\).

The relative output within the A-sector is determined by dividing across the expressions (19) and (20):

$$\begin{aligned} \frac{P_{A}^{i^{*}}Y_{A}^{i^{*}}}{P_{A}^{i^{**}}Y_{A}^{i^{**}}}=\frac{\left( 1-v_{A}(t)\right) \cdot s^{*}\cdot i^{*}}{v_{A}(t)\cdot s^{**}\cdot i^{**}}=\left( \frac{s^{*}\cdot i^{*}}{s^{**}\cdot i^{**}}\right) ^{\frac{1}{2}}, \end{aligned}$$
(23)

since \(\frac{1-{\overline{v}}_{N}}{{\overline{v}}_{N}}=\left( \frac{h\cdot H}{l\cdot L}\right) ^{\frac{1}{2}}\).

The intra-sector relative prices of the A-sector, \(\frac{P_{A}^{i^{*}}Y_{A}^{i^{*}}}{P_{A}^{i^{**}}Y_{A}^{i^{**}}}\), depend positively on the ratio between absolute labor productivities, \(\frac{s^{*}}{s^{**}}\), and between labor levels, \(\frac{i^{*}}{i^{**}}\).

Since \(P_{A}^{i^{*}}=P_{A}\exp \left( -\alpha \right) {\overline{v}}_{A}^{-\alpha }\), \(P_{A}^{i^{**}}=P_{A}\exp \left( -\alpha \right) \left( 1-{\overline{v}}_{A}\right) ^{-\alpha }\) and \(\frac{1-{\overline{v}}_{A}}{{\overline{v}}_{A}}=\left( \frac{s^{**}\cdot i^{**}}{s^{*}\cdot i^{*}}\right) ^{\frac{1}{2}}\), from (23) we have that:

$$\begin{aligned} \frac{Y_{A}^{i^{*}}}{Y_{A}^{i^{**}}}=\left( \frac{s^{*}\cdot i^{*}}{s^{**}\cdot i^{**}}\right) ^{\frac{1+\alpha }{2}}. \end{aligned}$$
(24)

From 22, dividing across sectors yields \(\frac{Y_{N}}{Y_{R}}=\left( \frac{P_{N}}{P_{R}}\right) ^{\frac{1-\alpha }{\alpha }}\cdot {\mathcal {Q}}\cdot \frac{{\textrm{M}}_{N}}{{\textrm{M}}_{R}}\), which is the relative supply of the output in the N-sector. Bearing in mind (4), it can be written as

$$\begin{aligned} \frac{Y_{N}}{Y_{R}}=\left( \frac{\gamma _{N}}{\gamma _{R}}\right) ^{\left( 1-\alpha \right) \frac{\epsilon }{\sigma }}\cdot \left( {\mathcal {Q}}\cdot \frac{{\textrm{M}}_{N}}{{\textrm{M}}_{R}}\right) ^{\alpha \frac{\epsilon }{\sigma }}, \end{aligned}$$
(25)

where \(1+\frac{1-\alpha }{\epsilon \cdot \alpha }=\frac{\epsilon \alpha +1-\alpha }{\epsilon \alpha }=\frac{1+\alpha \left( \epsilon -1\right) }{\epsilon \alpha }=\frac{\sigma }{\epsilon \alpha }\) where \(\sigma \equiv 1+\alpha \left( \epsilon -1\right)\). Notice that \(\epsilon \gtrless 1\Leftrightarrow \epsilon -1\gtrless 0\Leftrightarrow \alpha \left( \epsilon -1\right) \gtrless 0\Leftrightarrow \sigma \equiv 1+\alpha \left( \epsilon -1\right) \gtrless 1\).Footnote 3

This allows us to write Proposition 2:

Proposition 2

The inter-sector relative output of the non-routine sector, \(\frac{Y_{N}}{Y_{R}}\), depend positively on the relative contribution of each sector to the final good, \(\frac{\gamma _{N}}{\gamma _{R}}\), and relative market size, \(\frac{{\textrm{M}}_{N}}{{\textrm{M}}_{R}}\), and crucially on the technological-knowledge bias, \(Q=\frac{Q_{N}}{Q_{R}}\).

Proof

Derive (25) in order to \(\frac{Y_{N}}{Y_{R}}\), \(\frac{\gamma _{N}}{\gamma _{R}}\), \(\frac{{\textrm{M}}_{N}}{{\textrm{M}}_{R}}\)and Q, respectively. \(\square\)

Moreover, from (4) and (25) we obtain the equilibrium relative prices of output in the N-sector as:

$$\begin{aligned} \frac{P_{N}}{P_{R}}=\left( \frac{\gamma _{N}}{\gamma _{R}}\right) ^{\frac{\alpha }{\sigma }\epsilon }\cdot \left( {\mathcal {Q}}\cdot \frac{{\textrm{M}}_{N}}{{\textrm{M}}_{R}}\right) ^{-\alpha \frac{1}{\sigma }}, \end{aligned}$$
(26)

where \(\sigma \equiv 1+\alpha \left( \epsilon -1\right)\) so that \(\sigma -1+\alpha =\left[ 1+\alpha \left( \epsilon -1\right) \right] -1+\alpha =\alpha \epsilon\). This expression demonstrates how the relative prices of non-routine task intensive sector rely positively on the relative share of production of this sector’s total output and negatively on the technological-knowledge bias, Q, and the relative size of this sector’s market size, \({\textrm{M}}_{N}\).

In turn, from the maximization problem of the producer of Y, the country’s prices definition can be sorted to obtain a specific sector’s price. In this case, for the non-routine sector we have:

$$\begin{aligned} P_{N}=\left( \frac{P_{Y}^{1-\epsilon }-\gamma _{R}^{\epsilon }P_{R}^{1-\epsilon }}{\gamma _{N}^{\epsilon }}\right) ^{\frac{1}{1-\epsilon }}, \end{aligned}$$
(27)

which integrated in the relative price of the N-sector expression (26) gives us the routine sector’s final-good price:

$$\begin{aligned} P_{R}=\left[ \frac{\gamma _{R}^{\alpha /\sigma \epsilon (1-\epsilon )}{\textrm{M}}_{R}^{-\frac{\alpha }{\sigma }(1-\epsilon )}}{\gamma _{N}^{\epsilon +\epsilon (1-\epsilon )\alpha /\sigma }\left[ {\textrm{M}}_{N}{\mathcal {Q}}\right] ^{-\frac{\alpha }{\sigma }(1-\epsilon )}+\gamma _{R}^{\epsilon +\epsilon (1-\epsilon )\alpha /\sigma }{\textrm{M}}_{R}^{-\frac{\alpha }{\sigma }(1-\epsilon )}}\right] ^{\frac{1}{1-\epsilon }}P_{Y}. \end{aligned}$$
(28)

In turn, replacing (28) in the above non-routine sector’s price expression (27), the non-routine sector’s final-good price is:

$$\begin{aligned} P_{N}=\left[ \frac{\gamma _{N}^{\alpha /\sigma \epsilon (1-\epsilon )}\left[ {\textrm{M}}_{N}{\mathcal {Q}}\right] ^{-\frac{\alpha }{\sigma }(1-\epsilon )}}{\gamma _{N}^{\epsilon +\epsilon (1-\epsilon )\alpha /\sigma }\left[ {\textrm{M}}_{N}{\mathcal {Q}}\right] ^{-\frac{\alpha }{\sigma }(1-\epsilon )}+\gamma _{R}^{\epsilon +\epsilon (1-\epsilon )\alpha /\sigma }{\textrm{M}}_{R}^{-\frac{\alpha }{\sigma }(1-\epsilon )}}\right] ^{\frac{1}{1-\epsilon }}P_{Y}. \end{aligned}$$
(29)

Proposition 3

The relative price in the non-routine (routine) sector decreases (increases) with the technological knowledge bias \(Q=\frac{Q_{N}}{Q_{R}}\) towards the non-routine technology; The relative price in the non-routine (routine) sector depend positively on the relative contribution of each sector to the final good, \(\frac{\gamma _{N}}{\gamma _{R}}\), and negatively on the relative market size, \(\frac{{\textrm{M}}_{N}}{{\textrm{M}}_{R}}\); the routine price increases with the technological knowledge bias and the non-routine price decreases with the technological knowledge bias.

Proof

Derive (26), (29) and (28) towards \(\frac{\gamma _{N}}{\gamma _{R}}\), \(\frac{{\textrm{M}}_{N}}{{\textrm{M}}_{R}}\) and Q and also (29) and (28) towards Q. \(\square\)

This is an important proposition because it relates the evolution of prices with the ratio between technological progress in both sectors. So the recent decreasing trend in the prices in the routine sector documented by many authors (e.g. Brinca et al. 2022) may be associated with the high technological development in this sector (\(Q_{R}\)).

2.3 Intermediate-goods sector

In the intermediate goods sector, the production of the top quality k of each j requires a start-up cost of R &D to reach the new design, which can only be recovered if profits at each date are positive for a certain time in the future. This is assured by a system of IPRs that protect the leader firm’s monopoly, while at the same time, disseminating, almost without costs, acquired technological knowledge to other firms. Hence, each firm that holds the patent for the top quality k of j at t supplies all respective tasks in each \(i=\left\{ L,H,M_{1},M_{2}\right\}\). If we consider that each unit of intermediate good \(j\in \left[ 0,J_{A}\right]\) in sector A requires one unit of final output Y, since its price is 1 to 1 and the producer of j gets the following profits:

$$\begin{aligned} \pi _{A}(k,j,t)=[p_{A}(k,j,t)-1]x_{A}(k,j,t), \end{aligned}$$
(30)

where \(x_{A}(k,j,t)\) is the demand for j from all the producers that use technology complementary with j:

$$\begin{aligned} x_{A}(k,j,t)=\int _{0}^{v_{A}}x_{v_{A}}^{i^{*}}(k,j,t)dv_{A}+\int _{v_{A}}^{1}x_{v_{A}}^{i^{**}}(k,j,t)dv_{A}. \end{aligned}$$
(31)

Assuming that the monopolist charges the same price for all these firms, i.e., \(p_{A}(k,j,t)=p(k,j,t)\) we can find the optimal price by replacing \(x_{A}(j,t,k)\) by the demand of the producer of a single task \(v_{A}\), i.e., either by \(x_{v_{A}}^{i^{*}}(k,j,t)\) or by \(x_{v_{A}}^{i^{**}}(k,j,t)\) and then maximizing with respect to \(p_{A}(k,j,t)\):

$$\begin{aligned} \pi _{A}(k,j,t)=\int _{0}^{1}\pi _{v_{A}}(k,j,t)dv_{A}=\int _{0}^{{\overline{v}}_{A}}\pi _{v_{A}}^{i^{*}}(k,j,t)dv_{A}+\int _{{\overline{v}}_{A}}^{1}\pi _{v_{A}}^{i^{**}}(k,j,t)dv_{A}, \end{aligned}$$
(32)

where \(\pi _{v_{A}}^{i^{*}}(k,j,t)\) and \(\pi _{v_{A}}^{i^{**}}(k,j,t)\) are the profits of the producer of j for selling this intermediate good to the producer of task \(v_{A}\). Therefore, we find prices by solving the following maximization problems: \({\mathop {\max }\nolimits _{p(k,j,t)}\,\pi _{A}(t)}=[p(k,j,t)-1]x_{v_{A}}^{i^{*}}(k,j,t)\), \(i^{*}=\{L,M_{1}\}\), \(s.t.x_{v_{A}}^{i^{*}}(k,j,t)=\left[ \frac{P_{v_{A}}^{i^{*}}(1-\alpha )}{p(k,j,t)}\right] ^{\frac{1}{\alpha }}\left( q^{k(j,t)}\right) ^{\frac{1-\alpha }{\alpha }}\left( 1-v_{A}(t)\right) \cdot s\cdot i_{v_{A}}^{*}\), and \({\mathop {\max }\nolimits _{p(k,j,t)}\,\pi _{A}(t)}=[p(k,j,t)-1]x_{v_{A}}^{i^{**}}(k,j,t)\), \(i^{**}=\{H,M_{2}\}\), \(s.t.x_{v_{A}}^{i^{**}}(k,j,t)=\left[ \frac{P_{v_{A}}^{i^{**}}(1-\alpha )}{p(k,j,t)}\right] ^{\frac{1}{\alpha }}\left( q^{k(j,t)}\right) ^{\frac{1-\alpha }{\alpha }}v_{A}(t)\cdot s\cdot i_{v_{A}}^{**}\). Results from this process that the monopoly optimal price is \(p(k,j,t)=p=\frac{1}{1-\alpha }\).

Since only the top quality rung of each intermediate input is used in the production, we generalize and consider that the intermediate input j used by the producer of final good \(v_{A}\) is \({\tilde{x}}_{v_{A}}(k,j,t)=\sum _{0}^{k(j,t)}q_{A}^{k(j,t)}x_{v_{A}}(k,j,t)\); i.e., an input of quality \(k+1\) corresponds to q intermediate inputs of quality k. This implies that the price of an intermediate input of quality k, p(k, j, t), can be at most \(\frac{p(k+1,j,t)}{q}\). Therefore, if the producer of the intermediate input with the top quality adopts a limit pricing strategy and sets the price to \(q-\epsilon\), where \(\epsilon\) is an infinitesimal, than none of the inferior qualities would be able to survive since their profits would be negative. Assuming that the limit pricing strategy is binding we have:

$$\begin{aligned} p(k,j,t)=p=\frac{1}{1-\alpha }=q. \end{aligned}$$
(33)

Therefore, the total demand for j in sector \(A=\left\{ N,R\right\}\) is:

$$\begin{aligned} x_{A}(k,j,t)=\bigg (\frac{(1-\alpha )}{q}\bigg )^{\frac{1}{\alpha }}q^{k(j,t)\frac{1-\alpha }{\alpha }}\cdot \left( \left( P_{A}^{i^{*}}\right) ^{\frac{1}{\alpha }}\cdot s^{*}\cdot i^{*}+\left( P_{A}^{i^{**}}\right) ^{\frac{1}{\alpha }}\cdot s^{**}\cdot i^{**}\right) . \end{aligned}$$
(34)

We can, now, obtain an expression for intermediate goods produced for each sector.

$$\begin{aligned} X_{A}=\int _{0}^{J_{A}}x_{A}(k,j,t)dj=\bigg (\frac{(1-\alpha )}{q}\bigg )^{\frac{1}{\alpha }}Q_{A}\int _{0}^{J_{A}}\left( \left( P_{A}^{i^{*}}\right) ^{\frac{1}{\alpha }}\cdot s^{*}\cdot i^{*}+\left( P_{A}^{i^{**}}\right) ^{\frac{1}{\alpha }}\cdot s^{**}\cdot i^{**}\right) dj. \end{aligned}$$
(35)

2.4 R &D sector

We consider that innovative R &D is performed in both sectors; however, there is no technological-knowledge transfer between sectors. Thus, N has no access to the technological knowledge produced in R, \(Q_{R}^{M_{1}}\) and \(Q_{R}^{M_{2}}\), and vice-versa, R-sector does not have access to \(Q_{N}^{L}\) and \(Q_{N}^{H}\). The value of the leading-edge patent relies on the profit-yields accruing during each time t to the monopolist, and on the duration of the monopoly power. The duration, in turn, depends on the probability of a new innovation, which creatively destroys the current leading-edge design (e.g., Aghion and Howitt 1992, Grossman and Helpman 1991, ch. 12). The probability of successful innovation is, thus, at the heart of the R &D activity. Let \({\mathcal {I}}_{A}(j,t)\) denote the instantaneous probability at time t in \(A=\left\{ N,R\right\}\)—a Poisson arrival rate—of successful innovation in the next higher quality \(\left[ k(j,t)+1\right]\) in intermediate good j,

$$\begin{aligned} {\mathcal {I}}_{A}(k,j,t)=y_{A}(k,j,t)\cdot \beta q^{k(j,t)}\cdot \zeta ^{-1}q^{-\alpha ^{-1}k(j,t)}\cdot M_{A}^{-\xi }, \end{aligned}$$
(36)

where (e.g., Afonso 2012): (1) \(y_{A}(k,j,t)\) is the flow of domestic final-good resources devoted to R &D in j belonging to \(A=\left\{ N,R\right\}\), which defines our framework as a lab-equipment model; (2) \(\beta\) \(q^{k(j,t)}\), \(\beta >0\), is the learning-by-past domestic R &D, as a positive learning effect of public knowledge accumulated from past successful R &D; (3) \(\zeta ^{-1}q^{-\alpha ^{-1}k(j,t)}\), \(\zeta >0\), is the adverse effect—cost of complexity—caused by the increasing complexity of quality improvements;Footnote 4 (4) \(M_{A}^{-\xi }\) is the adverse effect of market size, capturing the idea that the difficulty of introducing new quality intermediate goods and replacing old ones is proportional to the market size measured by effective i-type labor units which are spread in sectors N and R. The parameter \(\xi \ge 0\) determines the degree to which scale benefits on profits can partially (\(0<\xi <1\)), totally (\(\xi =1\)) or over counterbalance (\(\xi >1\)) and thus allows us to remove (explicit) scale effects on the economic growth rate. That is, for reasons of simplicity, we reflect in R &D the costs of scale increasing, due to coordination among agents, processing of ideas, and informational, organizational, and marketing (e.g., Dinopoulos and Thompson 1999).

An innovator that improves the quality of an intermediate good j from k to \(k+1\)will receive monopoly profits during the time in which the patent is valid from time t to \(\tau\). The present value of such profits at time t will be \(V_{A}(k+1,j,t,\tau )=\int _{t}^{\tau }\pi _{A}(k+1,j,v)e^{-\int _{t}^{v}r(w){\textrm{d}}w}{\textrm{d}}v\). The expected Market Value of a patent is a random variable that depends on the uncertainty of the period of the next successful innovation \(\tau\), which then is \(V_{A}(k+1,j,t)\equiv {\mathbb {E}}_{\tau }\left[ V_{A}(k+1,j,t,\tau )\right] =\int _{t}^{+\infty }b(\tau )V_{A}(k+1,j,t,\tau ){\textrm{d}}\tau\), where \(b(\tau )\) is the probability density function of \(\tau\), i.e., the probability that the patent lasts exactly until \(\tau\), which occurs if at that period some entrepreneur is able to obtain a higher quality rung for the intermediate good j. Then \(b(\tau )\) is determined in the following way \(b(\tau )=\left[ 1-B(\tau )\right] \cdot {\mathcal {I}}_{A}(k,j,\tau )\), where \({\mathcal {I}}_{A}(k,j,\tau )\) is the probability of a successful quality upgrade at time \(\tau\) and \(B(\tau )\) is the cumulative density function of \(\tau\). Therefore, the market value of a patent is:

$$\begin{aligned} V_{A}(k+1,j,t)=\frac{\pi _{A}(k+1,j,t)}{r(t)+{\mathcal {I}}_{A}(k,j,\tau )} \end{aligned}$$
(37)

3 General equilibrium

We now move on to characterize the general equilibrium because the sectors’ economic structures have been described for certain technological-knowledge levels represented by the indices \(Q_{A}\). First, it is derived the equilibrium of achieving higher quality rungs, then we derive the aggregate resource constraint of the economy and show that all variables (including consumption) depend on the dynamics of technological indexes—see “Appendix 2” in which we find the R &D equilibrium probability and the aggregate resource constraint. Then, below, we proceed to characterize the transitional dynamics, where we start by deriving the law of motion of each index and the steady-state growth. Throughout this analysis we retain the assumptions that households and firms are rational and solve their problems, that free-entry R &D conditions are met and that markets clear.

3.1 Law of motion of \(Q_{A}\) and transitional dynamics

If a new quality of intermediate good j is introduced the rate of change in the quality index in sector A will be \(\frac{\Delta Q_{A}}{Q_{A}}=\left( q^{\frac{1-\alpha }{\alpha }}-1\right)\). Since the probability of this occurring per unit of time is given by \({\mathcal {I}}_{A}(t)\), we have that \(\frac{{\dot{Q}}_{A}}{Q_{A}}={\mathcal {I}}_{A}\left( t\right) \left( q^{\frac{1-\alpha }{\alpha }}-1\right)\); i.e.,

$$\begin{aligned} \frac{{\dot{Q}}_{A}}{Q_{A}}=\left( \frac{\beta }{\zeta }\cdot \frac{q-1}{q}\cdot \exp \left( -1\right) (1-\alpha )^{\frac{1}{\alpha }}\cdot P_{A}^{\frac{1}{\alpha }}{\textrm{M}}_{A}^{1-\xi }-r(t)\right) \left( q^{\frac{1-\alpha }{\alpha }}-1\right) . \end{aligned}$$
(38)

From the law of motion of each index \(Q_{A}\), we obtain the following expressions for the real interest rate:

$$\begin{aligned} r(t)=\left( \frac{\beta }{\zeta }\cdot \frac{q-1}{q}\cdot \exp \left( -1\right) (1-\alpha )^{\frac{1}{\alpha }}\cdot P_{A}^{\frac{1}{\alpha }}{\textrm{M}}_{A}^{1-\xi }\right) -\frac{1}{q^{\frac{1-\alpha }{\alpha }}-1}\frac{{\dot{Q}}_{A}}{Q_{A}}. \end{aligned}$$
(39)

That is, we obtain two expressions for the real interest rate. Since it is unique and \(\frac{{\dot{\mathcal{Q}}}}{{\mathcal{Q}}}=\frac{{\dot{Q}}_{R}}{Q_{R}}-\frac{{\dot{Q}}_{N}}{Q_{N}}\), we have:

$$\begin{aligned} \frac{{\dot{\mathcal{Q}}}}{{\mathcal{Q}}}=\left[ q^{\frac{1-\alpha }{\alpha }}-1\right] \left[ \frac{\beta }{\zeta }\cdot \frac{q-1}{q}\cdot \exp \left( -1\right) (1-\alpha )^{\frac{1}{\alpha }}\cdot \left( P_{R}^{\frac{1}{\alpha }}{\textrm{M}}_{R}^{1-\xi }-P_{N}^{\frac{1}{\alpha }}{\textrm{M}}_{N}^{1-\xi }\right) \right] . \end{aligned}$$
(40)

3.2 Steady-state equilibrium

Since in steady state \(\frac{{\dot{\mathcal{Q}}}}{{\mathcal{Q}}}=0\) (implying that\(P_{R}^{\frac{1}{\alpha }}{\textrm{M}}_{R}^{1-\xi }-P_{N}^{\frac{1}{\alpha }}{\textrm{M}}_{N}^{1-\xi }=0\)) the long-run equilibrium value for the technological-knowledge bias expression (\({\mathcal{Q}}^{*}\)) is obtained using Eqs. (28) and (29) and yields:

$$\begin{aligned} {\mathcal{Q}}^{*}=\left( \frac{\gamma _{N}}{\gamma _{R}}\right) ^{\epsilon }\left( \frac{{\textrm{M}}_{N}}{{\textrm{M}}_{R}}\right) ^{-1+\sigma \left( 1-\xi \right) }. \end{aligned}$$
(41)

In turn, taking into account the skill-premium expressions (17) and (18) that compare the wage gap between non-routine and routine sectors and replacing \({\overline{v}}_{N}\) and \({\overline{v}}_{R}\) from (14) using (15) and the definitions of \({\textrm{M}}_{N}\) and \({\textrm{M}}_{R}\), replacing \(\frac{P_{N}}{P_{R}}\) from (26) and Q from (41) in the both expressions, we obtain the ratios that measure wage polarization from both sectors:

$$\begin{aligned}{} & {} \left( \frac{w_{N}^{H}}{w_{R}^{M_{2}}}\right) ^{*}=\left( \frac{\gamma _{N}}{\gamma _{R}}\right) ^{\epsilon }\cdot \left( \frac{\mathrm {M_{N}}}{{\textrm{M}}_{R}}\right) ^{(\sigma -1)(1-\zeta )-1/2}\cdot \left( \frac{M_{2}}{H}\right) ^{\frac{1}{2}}\cdot \left( \frac{h}{m_{2}}\right) , \end{aligned}$$
(42)
$$\begin{aligned}{} & {} \left( \frac{w_{N}^{L}}{w_{R}^{M_{1}}}\right) ^{*}=\left( \frac{\gamma _{N}}{\gamma _{R}}\right) ^{\epsilon }\cdot \left( \frac{\mathrm {M_{N}}}{{\textrm{M}}_{R}}\right) ^{(\sigma -1)(1-\zeta )-1/2}\cdot \left( \frac{M_{1}}{L}\right) ^{\frac{1}{2}}\cdot \left( \frac{l}{m_{1}}\right) . \end{aligned}$$
(43)

We expect that both ratios increase due to automation. In this paper we consider that there are three main features or consequences of automation. First, an increase in the production intensity of the non-routine sector, \(\gamma _{N}\) (Frey and Osborne 2017). Second, a decrease of efficiency rate of labor and its capacity to generating value of routine sector workers, \(m_{1}\) and \(m_{2}\), due to a greater risk of routine tasks being replaced by more efficient machines and robots and, consequently, a reduced medium-skilled job demand. Third, an increase of efficiency rate of work and capacity to generate value of non-routine sector workers, l and h, due to the polarizing routine sector workers’ move to both ends of labor proficiency spectrum. Proposition 4 analyze theoretically those three effects.

Proposition 4

An increase in the production intensity of the non-routine sector, \(\gamma _{N}\), a decrease of efficiency rate of medium-skilled labor \(m_{1}\) and \(m_{2}\), and an increase of efficiency rate of raw labor and human capital all lead to wage polarization, i.e. an increase in the skilled and unskilled wages compared with medium skilled wages.

Proof

Derive (42) and (43) in order to \(\gamma _{N}\), (42) in order to \(m_{1}\)and h, respectively and (43) in order to \(m_{2}\)and h, respectively and observe that all the derivatives are negative. \(\square\)

The predictions of Proposition 4 will be quantified in the next section.

Finally, in order to define the steady-state economic growth rate we use (38) and and the fact that in the steady-state \(\frac{{\dot{C}}}{C}=\frac{r^{*}-\rho }{\theta }=g^{*}=g_{R}^{*}=g_{N}^{*}=g_{Q_{A}}^{*}=g_{Q_{B}}^{*}\)we obtain that:

$$\begin{aligned} g^{*}=\frac{\left( \frac{\beta }{\zeta }\cdot \frac{q-1}{q}\cdot \exp \left( -1\right) (1-\alpha )^{\frac{1}{\alpha }}\cdot P_{A}^{\frac{1}{\alpha }}{\textrm{M}}_{A}^{1-\xi }\right) -\rho }{\theta +(q^{\frac{1-\alpha }{\alpha }}-1)^{-1}}, \end{aligned}$$
(44)

where \(A=\left\{ N,R\right\}\), \(P_{N}\) and \(P_{R}\) are given by (28) and (29).

Regarding the determinants of the economic growth rate at the steady-state the positive ones are the spillover effect (\(\beta\)), the markup (\(1/\alpha\)), the intertemporal elasticity of substitution (\(1/\theta\)) and negatively the complexity effect (\(\zeta\)), size of each quality upgrade (q), the discount rate (\(\rho\)). A special note is deserved to the scale effect measured by \({\textrm{M}}_{\textrm{A}}\)and decreases as \(\xi \rightarrow 1\) and the price effect measured by \({\textrm{P}}_{\textrm{A}}\). However the steady-state growth rate can be influenced both by increases in the value of the routine as well as of the non-routine sector as \(A=R,N\) given that in the steady-state \(P_{R}^{\frac{1}{\alpha }}{\textrm{M}}_{R}^{1-\xi }=P_{N}^{\frac{1}{\alpha }}{\textrm{M}}_{N}^{1-\xi }\). Potential effects of automation related with labor productivity or the shares of sectors or production factors in the economy can affect economic growth rates in the transitional dynamics (see Sect. 3.1) but not the long-run economic growth rate.

4 Quantitative results

We will assess the quantitative impact of rising automation through a calibration exercise targeted at the most innovative economies. To that end, first we will quantify the main variables in the steady state of some of the most innovative countries in the world: USA, Germany, France, Italy, Sweden and Finland, as these countries rank high in the 2021 Global Innovation Index Results Report (WIPO 2021).Footnote 5 With this exercise we want to make clear that our model is flexible enough to feature different countries in their long-run equilibrium, approaching their data related to economic growth as well as wage polarization.

4.1 Model calibration and data

To test and validate the theoretical model, we first calibrated several parameters, taking into account the literature. Table 1 summarizes the values, description, and sources for each parameter. According to the model, we are able to determine the value of \(\sigma =1+\alpha \left( \epsilon -1\right)\) and \(q=\frac{1}{1-\alpha }\) (considering \(\epsilon =0.5\) and \(\alpha =0.6\)), meaning that routine and non-routine goods are gross complements. The intensity parameters are set to \(\gamma _{N}=0.6\) and \(\gamma _{R}=0.4\), as the non-routine sector is the human capital intensive sector, hence has a bigger share in the country’s production. As usual in macroeconomic growth models we use \(\theta =2\) and \(\rho =0.01\) (e.g., Strulik 2007; Grossmann et al. 2013).

Table 1 Steady state parameters
Full size table

In line with Afonso (2006), Neves and Sequeira (2018), and Sequeira et al. (2018), we use high values for the learning-for-the-past R &D or spillover effect, \(\beta\), high values of the complexity (\(\zeta\)) and a low scale-effect governed by \(\xi\). However, the specific values for these parameters will be different according to the different countries’ steady state we intend to characterize. In particular we consider that larger countries benefit more from scale effects than smaller countries (\(\xi\) is 0.92 for the US, 0.94 for Germany, France and Italy, 0.96 for Sweden and 1 for Finland); spillovers are higher for more innovative countries (\(\beta\) is 1.6 for Italy, 2.0 for the US, France, Germany, and Finland and 2.5 for Sweden); the complexity effect is higher for countries known to be bigger and thus more complex and with worse institutions (\(\zeta\) is 1.3 for Sweden and Finland, 1.5 for France, and Germany, 1.6 for the US and 1.7 for Italy).

We also search the exogenous parameters of number of workers per proficiency and per sector, in each country analyzed, L, H, \(M_{1}\) and \(M_{2}\). The International Labour Organization (ILOSTAT) provides detailed information on employment in each region and country.Footnote 6 This database compiles data from multiple job surveys and divides it into 11 categories: 10 ISCO-08 (The International Standard Classification of Occupations) classifications and “not classified.” For the purpose of this paper, we ignore the category “not classified” and the ISCO-08 classification 0-Armed Forces Occupations. As for the categories considered for the model, we attributed each ISCO-08 category to a labor proficiency: skilled, H, includes groups 1-Managers, 2-Professionals and 3-Technicians and Associate Professionals; medium-skilled type 2, \(M_{2}\), includes groups 4-Clerical Support Workers, 5-Service and Sales Workers and 6-Skilled Agricultural, Forestry and Fishery Workers; medium-skilled type 1, \(M_{1}\), includes groups 7-Craft and Related Trades Workers and 8-Plant and Machine Operators, and Assemblers; and unskilled, L, includes group 9-Elementary Occupations.

As for s, for unskilled workforce we set a normalization of \(l=1\) is used. Medium-skilled workforce productivities \(m_{1}=1.01\) and \(m_{2}=5\) and \(h=30\) are such that the model steady-state approaches the growth rate of per capita GDP of each country between 2010 and 2019 (Feenstra et al. 2015) as well as the wage ratios. As an example, for the US we were able to replicate the data growth rate of GDP per capita of \(1.51\%\) (Feenstra et al. 2015) as well as the pattern of wage polarization, \(\frac{w_{N}^{H}}{w_{R}^{M_{2}}}=1.65\) and \(\frac{w_{N}^{L}}{w_{R}^{M_{1}}}=0.47\), roughly consistent with the US current values (Timmer et al. 2015).

As a general conclusion it can be said that the model steady state is able to replicate a diversity of country different data characteristics, as the next subsection will show.

4.2 Steady-state results

To determine the economic consequences of the above-mentioned shocks, steady-state values must first be determined. For the analyzed R &D frontier countries, we identify that the average technological-knowledge bias towards the non-routine sector level is, approximately, 0.20, being the Italy that holds the highest value with 0.29 and Sweden the lowest with 0.15. Regarding skill premium of steady-state level wages, we observe a country average of 2.01 on high-skill premia and, 0.75 low-skill premia. Italy shows the largest wage gap in the upper skill premium, 3.05, and in the lower skill premia the largest gap is in the US, 0.47. Regarding the output level, the average for the relative output \(\frac{Y_{N}^{*}}{Y_{R}^{*}}\) is 1.26, being routine sector smaller than the non-routine sector in every country and the largest in Sweden. All countries show positive economic growth in the steady state, with the average being \(0.97\%\) (which compares with \(0.96\%\) in data).

In order to evaluate the fit of the model steady-state for other countries than the US (for which we replicated three variables, growth and wage ratios), we compare the steady-state value of the economic growth rate and the real growth rate from 2010 to 2019, which show a correlation of \(98\%\). This means that even though the calibration was made mostly to fit the data of the US, the outcomes also fit well the most innovative countries per capita real GDP growth. It is worth noting that the model replicates both the minimum (Finland) and the maximum growth rate (US) and the model average is just 1.066 above the data value for this variable. Table 2 summarizes the main steady-state results.

Table 2 Steady-state results
Full size table

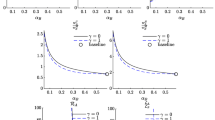
Next, we will assess three different comparative static exercises that are thought to be linked with the expected further automating the production process in the years to come. First due to the decreasing prices of automation and that the increasing routinable tasks (Jungmittag 2021) may have a limit above which some tasks cannot be routinable without huge costs—tasks where sensitive dextricity is essential, where creative and social intelligence are at their core are very difficult to be routinable (Frey and Osborne 2017; Feng and Graetz 2020). This means that the share of the routine sector may decrease in the future as prices decrease and the economy reach the supposedly existing limit above which tasks cannot be routinable. Thus, as a first exercise, we assume that production share \(\gamma _{R}\) may decrease in the future (regardless of some increase in the production of this sector). Second, we assume that automation will impact even further the already existing gap of medium-skilled routine employment and respective flux of medium-skilled workers and, growing polarization with increasing skilled cognitive employment and unskilled manual employment. Therefore, due to an increase in the supply of the non-routine labor markets, a more competitive labor market and lack of experience and capacity to adjust, we predict to lead to a decrease of routine sector workers’ efficiency rate (Goos et al. 2014; Lemieux 2006), \(m_{1}\) and \(m_{2}\). Third, and also according to the previous argument the growing polarization with increasing skilled cognitive employment and unskilled manual employment will imply an increased supply in the non-routine labor markets, a more competitive labor market, and lead to an increase of non-routine sector workers’ efficiency rate, l and h. Figure 1 summarizes all the effects of these shocks which we will detail in the following Sects. 4.2.1 to 4.2.3. The baseline will be the results for the US as these were the country that we were able to better approach the data.

Fig. 1
figure 1

Effects of the shocks performed in Sects. 4.2.1 to 4.2.3

Full size image

4.2.1 Impact of non-routine sector’s production intensity increase

Now, we expect that further automation will lead to an increase in the intensity of the non-routine sector in production (\(\gamma _{N}\)) and, therefore, a decrease in the intensity of the routine sector in production (\(\gamma _{R}\)). As the effects in all countries are qualitatively identical, we focus on the calibration for the US. First, Fig. 1a shows the effects on \(\frac{w_{N}^{H}}{w_{R}^{M_{2}}}\) and \(\frac{w_{N}^{L}}{w_{R}^{M_{1}}}\) and on a ratio of polarization measured by \(\frac{\frac{w_{N}^{H}}{w_{R}^{M_{2}}}}{\frac{w_{R}^{M_{1}}}{w_{N}^{L}}}\) from increasing \(\gamma _{N}\) from 0.6 to 0.8. We can observe that there is an increase in both ratios, but the upper skilled wage inequality rises more and because of that more polarization is expected. The effect on growth of this change is positive but taking the whole possible values for the weights of the routine and the non-routine sectors in production (\(\gamma _{R}\), \(\gamma _{N}\)) we can observe that an initial increase in the non-routine sector share would decrease growth until nearly \(\gamma _{N}=0.45\) and then further increases would contribute to increase economic growth. Thus growth is maximized for small (high) values of \(\gamma _{N}\) (\(\gamma _{R}\)) and for high (small) values of \(\gamma _{N}\) (\(\gamma _{R}\)). This happens because the sectoral shares affect growth mainly through the price effect (as the scale-effect is small)—see the above Eq. (44). Thus observing Eqs. (28) and (29) we note that higher values for either \(\gamma _{N}\) or \(\gamma _{R}\) are relevant.

4.2.2 Impact of routine sector workers’ labor productivity decrease

Now, based on the previous arguments, we observe the effects of decreasing \(m_{1}\) and \(m_{2}\) in Fig. 1b and c, respectively.

A decrease in the productivity of lower productivity workers in the routine sector (\(m_{1}\)) directly implies a increase in \(\frac{w_{N}^{L}}{w_{R}^{M_{1}}}\). However in equilibrium through the negative effect on whole value of the workers in the routine sector together with the fact that \((\sigma -1)(1-\zeta )-\frac{1}{2}<0\) (low elasticity of substitution between routine and non-routine goods in the production of the final good), it also decreases the upper wage inequality ratio \(\frac{w_{N}^{H}}{w_{R}^{M_{2}}}\). As the sub-figure shows, both effects contribute to an increase in wage polarization, measured by \(\frac{\frac{w_{N}^{H}}{w_{R}^{M_{2}}}}{\frac{w_{R}^{M_{1}}}{w_{N}^{L}}}\). On the other hand, a decrease in the productivity of higher productivity workers in the routine sector (\(m_{2}\)) directly implies a increase in \(\frac{w_{N}^{H}}{w_{R}^{M_{2}}}\). However in equilibrium through the negative effect on whole value of the workers in the routine sector together with the fact that \((\sigma -1)(1-\zeta )-\frac{1}{2}<0\) (low elasticity of substitution between routine and non-routine goods in the production of the final good), it also decreases the lower wage inequality ratio \(\frac{w_{N}^{H}}{w_{R}^{M_{2}}}\). As the figure shows, both effects contribute to an increase in wage polarization, measured by \(\frac{\frac{w_{N}^{H}}{w_{R}^{M_{2}}}}{\frac{w_{R}^{M_{1}}}{w_{N}^{L}}}\).

The effects on economic growth are negative but very small: departing from an initial economic growth rate of 1.50 it decreases steadily towards 1.497 (with the change in \(m_{1}\)) and 1.476 (with the change in \(m_{2}\)).

4.2.3 Impact of non-routine sector workers’ labor productivity increase

In this subsection, based on the previous arguments, we increase l and h, which effects can be observed in Fig. 1d and e. An increase in the productivity of unskilled workers employed in the non-routine sector (l) directly implies a increase in \(\frac{w_{N}^{L}}{w_{R}^{M_{1}}}\). However in equilibrium through the positive effect on whole value of the workers in the non-routine sector together with the fact that \((\sigma -1)(1-\zeta )-\frac{1}{2}<0\) (low elasticity of substitution between routine and non-routine goods in the production of the final good), it also decreases the upper wage inequality ratio \(\frac{w_{N}^{H}}{w_{R}^{M_{2}}}\). As the figure shows both effects contribute to an increase in wage polarization, measured by \(\frac{\frac{w_{N}^{H}}{w_{R}^{M_{2}}}}{\frac{w_{R}^{M_{1}}}{w_{N}^{L}}}\). On the other hand, an increase in the productivity of skilled workers in the non-routine sector (h) directly implies an increase in \(\frac{w_{N}^{H}}{w_{R}^{M_{2}}}\). Also, as previously, through the positive effect on whole value of the workers in the non-routine sector together with the fact that \((\sigma -1)(1-\zeta )-\frac{1}{2}<0\) (low elasticity of substitution between routine and non-routine goods in the production of the final good), it also decreases the lower wage inequality ratio \(\frac{w_{N}^{L}}{w_{R}^{M_{1}}}\), contributing again to an increase wage polarization, measured by \(\frac{\frac{w_{N}^{H}}{w_{R}^{M_{2}}}}{\frac{w_{R}^{M_{1}}}{w_{N}^{L}}}\).

The effects on economic growth are positive but again very small: departing from an initial economic growth rate of 1.50 it decreases steadily towards 1.502 (with the change in l) and 1.505 (with the change in h).

5 Conclusions

The rise of automation is a controversial topic that has been discussed in economic fora and scientific literature, with the predicted implications dividing economists. The dominant group of economists claims that the process of innovation has more positive than negative effects (e.g., Acemoglu and Restrepo 2018) meaning that the productivity effects lead by automation overcome the negative substitution effects. However, several have noted that the productivity gains may not be sufficient enough to compensate for the employment losses (e.g., Acemoglu et al. 2020).

In this paper, we examine how automation affects the technological-knowledge progress, production, wage polarization, and economic growth rates. For this purpose, we developed a theoretical model, using a task-based directed technical change setup. Specifically, an increase in the production intensity of the non-routine sector a decrease of efficiency rate of medium-skilled labor, and an increase of efficiency rate of raw labor and human capital all lead to wage polarization, i.e., an increase in the skilled and unskilled wages compared with medium skilled wages. We then proceed with a calibration exercise that intends to fit the relevant growth rate and wage inequality ratios in the US. We extend the exercise for other technologically advanced countries using as inputs specific labor units for each country. We obtain a correlation of \(98\%\) between the model economic growth rate and the data growth rate for these countries. Finally, we study the effects of increasing the production intensity of the non-routine sector, decreasing the efficiency rate of medium-skilled labor, and increasing of efficiency rate of raw labor and human capital quantitatively confirming the theoretical results and identifying the exact sources (upper or lower wage inequality) of wage polarization. We have also quantified the effects of these changes on economic growth, which were very low. In fact, this implication of the model matches the recent literature according to which robotization has low growth effects—as e.g., Acemoglu and Restrepo (2019) and Acemoglu et al. (2020) pointed out about the ‘so-so’ robotic technological improvements, which mainly substitutes labor in the production process without significantly increasing labor productivity.

The most relevant conclusion of this study is that further wage polarization should also be expected, worsening the situation of workers operating in the routine sector, who are assumed to have average skills. Thus, a crucial policy implication of our analysis points to support the occupational transition of medium-skilled workers towards less routinable tasks, through e.g. reskilling and/or re-training.

We believe this paper highlights some ideas for future research through, e.g., the analysis of the transitional dynamics of the model provoked by automation shocks and/or the analysis of possible effects of policies for the reskilling of medium-skilled workers both on economic growth and wage polarization, taking into account a general equilibrium approach with government.