Abstract
We relax two common assumptions in the Hotelling model with third-degree price discrimination: inelastic demand and exogenously assumed price discrimination. Based on the constant elasticity of substitution representative consumer model, we allow firms to endogenously choose whether to acquire consumer information and price discriminate. We find that when the information cost is sufficiently low, there exist two symmetric sub-game perfect Nash equilibria irrespective of the demand elasticity: both firms acquiring information and price discriminating, and neither firm acquiring information and charging a uniform price. This implies that the widely discussed prisoners’ dilemma, in which both firms are exogenously assumed to price discriminate, is not in fact a dilemma. A comparison of social welfare shows that when the demand elasticity is large enough, price discrimination improves social welfare. This is in contrast to the finding—price discrimination harms social welfare—in the existing literature assuming perfect inelastic demand.


Similar content being viewed by others
Notes
Robinson (1933) characterizes the two markets served by a monopolist as “strong” and “weak” markets in a way that its discriminatory prices are higher (lowers) in the strong (weak) market. Such characterization has been extended to oligopoly markets: when firms’ strong markets coincide, it is called best-response symmetry. When one firm’s strong market is the other’s weak market, it is called best-response asymmetry (Corts 1998).
One exception is Liu and Shuai (2013). In a two dimensional model, they find that price discrimination improves firms’ profits.
For example, in Shaffer and Zhang (2000, p. 399), it is concluded that“if both firms can price-discriminate and demand is symmetric, the outcome is a prisoner’s dilemma (as all-out competition ensues)”.
Esteves and Reggiani (2014) find that price discrimination may improve welfare when consumer information is endogenously generated (BBPD). Our results complement their findings by showing that this also holds when consumer information is exogenously given.
In the former case, it could be that firms set a uniform price for all consumers and then send coupons to specific group(s) of consumers. In the latter case, it could be that firms charge different prices to different consumers in one period.
One possible reason is that when the uniform price and discriminatory prices are determined simultaneously, there may exist no pure strategy equilibrium if the segmentation of consumers is improved.
The information in their paper is consumers’ purchasing history, while the information in our paper can be thought of as consumers’ gender, zipcode, etc..
This is consistent with the existing findings that better location information allows for more refined price discrimination, which hurts firms.
Colombo (2011b) assumes linear demand in a unidirectional Hotelling model. Different from the CES demand model in which consumers pay the transportation cost (mill pricing model), he assumes that firms pay the transport cost (delivered pricing model).
A quadratic transport will not affect the determination of the marginal consumers nor firms’ equilibrium prices or profits. But consumer welfare and social welfare will be different due to the difference in transport cost.
We assume Y is sufficiently high such that it is never a binding constraint.
We exclude the possibility of consumer arbitrage when firms price discriminate. See Kosmopoulou et al. (2016) for a discussion of consumer arbitrage.
Following Liu and Shuai (2013), we assume that if a firm acquires information in stage 1, it will use the information to price discriminate in stage 2. In practice, because information collection is costly, a firm will not collect consumers data unless it plans to use it.
Although Caplin and Nalebuff (1991) consider uniform pricing, their existence and uniqueness results still apply in the sub-games with price discrimination because one can consider the firm practicing price discrimination as two sub-firms, one maximizing its profit from the left market while the other maximizing its profit from the right market.
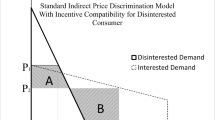
Figure 1 is drawn by assuming that off equilibrium, the marginal consumer is to the right of the middle point (\(p_A>p_B\)). In equilibrium, the marginal consumer will be located at \(\hat{x}=\frac{1}{2}\).
Price discrimination allows firm A to charge a lower price in market 2 and steal some consumers from firm B; in the meanwhile, receives a high profit margin in market 1 at the cost of losing some consumers to firm B.
The marginal consumers in the case of both firms price discriminate are similar.
If the information cost is exactly zero, there may exist a case in which a firm acquires information in the first stage but does not use it in the second stage to price discriminate. We thus assume an infinitely small cost to exclude this case. Alternatively, we can impose an assumption that if a firm has no intention to use the information, it will not acquire it even if the cost is zero. With this assumption, our results hold with zero information cost.
We provide a discussion of \(c>0\) later.
It is worth emphasizing that although the uniform pricing equilibrium dominates price discrimination equilibrium in terms of firms’ profits, both are feasible. This is in accordance with the real world where firms price discriminate in some circumstances and not others.
Although firm B’s poaching behavior intensifies price competition in market 1, our results show that the intensified competition effect is still dominated by the customer poaching effect.
We thank Luis Cabral for pointing this out.
References
Anderson SP, De Palma A (2000) From local to global competition. Eur Econ Rev 44(3):423–448
Bergemann D, Brooks B, Morris S (2015) The limites of price discrimination. Am Econ Rev 105(3):921–957
Bergemann D, Morris S (2018) Information design: a unified perspective. Working paper
Bester H, Petrakis E (1996) Coupons and oligopolistic price discrimination. Int J Ind Organ 14(2):227–242
Caplin A, Nalebuff B (1991) Aggregation and imperfect competition: on the existence of equilibrium. Econometrica 59(1):25–59
Colombo S (2011a) Discriminatory prices and the prisoner dilemma problem. Ann Reg Sci 46(2):397–416
Colombo S (2011b) Spatial price discrimination in the unidirectional Hotelling model with elastic demand. J Econ 102(2):157–169
Corts KS (1998) Third-degree price discrimination in oligopoly: all-out competition and strategic commitment. RAND J Econ 29(2):306–323
Eber N (1997) A note on the strategic choice of spatial price discrimination. Econ Lett 55(3):419–423
Esteves R-B, Reggiani C (2014) Elasticity of demand and behaviour-based price discrimination. Int J Ind Organ 32:46–56
Fudenberg D, Tirole J (2000) Customer poaching and brand switching. RAND J Econ 31:634–657
Gu Y, Wenzel T (2009) A note on the excess entry theorem in spatial models with elastic demand. Int J Ind Organ 27(5):567–571
Gu Y, Wenzel T (2011) Transparency, price-dependent demand and product variety. Econ Lett 110(3):216–219
Jentzsch N, Sapi G, Suleymanova I (2013) Targeted pricing and customer data sharing among rivals. Int J Ind Organ 31(2):131–144
Kosmopoulou G, Liu Q, Shuai J (2016) Customer poaching and coupon trading. J Econ 118(3):219–238
Lien J, Zhang Y, Zheng J (2018) Information, competition, and spatial price discrimination. In: Working paper
Liu Q, Serfes K (2004) Quality of information and oligopolistic price discrimination. J Econ Manag Strategy 13(4):671–702
Liu Q, Shuai J (2013) Multi-dimensional price discrimination. Int J Ind Organ 31(5):417–428
Liu Q, Shuai J (2016) Price discrimination with varying qualities of information. BE J Econ Anal Policy 16(2):1093–1121
Rath KP, Zhao G (2001) Two stage equilibrium and product choice with elastic demand. Int J Ind Organ 19(9):1441–1455
Robinson J (1933) The economics of imperfect competition. Macmillan, London
Shaffer G, Zhang ZJ (1995) Competitive coupon targeting. Mark Sci 14(4):395–416
Shaffer G, Zhang ZJ (2000) Pay to switch or pay to stay: preference-based price discrimination in markets with switching costs. J Econ Manag Strategy 9(3):397–424
Thisse J-F, Vives X (1988) On the strategic choice of spatial price policy. Am Econ Rev 78(1):122–137
Acknowledgements
An earlier version of the paper was circulated under the title “Endogenous Spatial Price Discrimination with Elastic Demand”. We would like to thank the Editor Giacomo Corneo and two anonymous referees whose comments allowed us to improve the paper significantly. We would also like to thank Qihong Liu and participants of the 2017 CES China Conference, the 2nd Asia-Pacific Industrial Organiation Conference and the 11th Conference on Industrial Economics and Economic Theory held at Shandong University for helpful comments. Financial support from the National Science Foundation of China (71603283) and the Planning Projects of Humanities and Social Sciences Foundation of Ministry of Education of China (15XJA790006) is gratefully acknowledged. The usual disclaimers apply.
Author information
Authors and Affiliations
Corresponding author
Appendix
Appendix
Proof of Lemma 1
In this sub-game, each firm charges a uniform price in the second stage. The marginal consumer thus is defined by Eq. (1). Each firm’s profit can be calculated by Eq. (3). The first order conditions are:
Solving the two FOCs, we get the equilibrium prices as follows:
Substitute the prices back into Eq. (2), we get the conditional demands are:
The corresponding profits are,
Consumer surplus and social welfare are respectively
\(\square \)
Proof of Lemma 2
When firm A acquires information and firm B does not, firm A charges \(p_{1A}\) in market 1 and \(p_{2A}\) in market 2, while firm B charges a uniform price \(p_B\) in both markets. By substituting the prices into \(\hat{x}\), we get two marginal consumers \(\hat{x}_1\) and \(\hat{x}_2\) as following.
The profits of firm 1 and firm 2 are
The FOCs are:
Solving the three FOCs, we get the equilibrium prices.
And the conditional demands are:
The corresponding profits are,
Consumer surplus and social welfare are respectively:
\(\square \)
Proof of Lemma 3
When both firms acquire information in the first stage, they each charge different prices in market 1 and 2 in the second period. Due to symmetry, we only need to consider market 1. In that market, the marginal consumer can be calculated as
and firms’ profits are:
The FOCs are:
Solving the two FOCs, we get the equilibrium prices:
The conditional demands are:
The corresponding profits are,
Consumer surplus and social welfare are respectively:
\(\square \)
Proof of Proposition 3
Given the uniform price is \(p_u=(t(1-\varepsilon ))^{\frac{1}{1-\varepsilon }}\), the discriminatory prices are \(p_{d1}=(\frac{2}{3}t(1-\varepsilon ))^{\frac{1}{1-\varepsilon }}\), \(p_{d2}=(\frac{1}{3}t(1-\varepsilon ))^{\frac{1}{1-\varepsilon }}\). The differences between the uniform price and the discriminatory prices are \(\Delta p_1=p_u-p_{d1}=(t(1-\varepsilon ))^{\frac{1}{1-\varepsilon }}-(\frac{2}{3}t(1-\varepsilon ))^{\frac{1}{1-\varepsilon }}\) and \(\Delta p_2=p_u-p_{d2}=(t(1-\varepsilon ))^{\frac{1}{1-\varepsilon }}-(\frac{1}{3}t(1-\varepsilon ))^{\frac{1}{1-\varepsilon }}\). Both \(\Delta p_1\) and \(\Delta p_2\) are positive and decrease with the elasticity of demand. \(\square \)
Proof of Proposition 4
When both firms price discriminate, the consumer surplus for those who buy from a distant firm and those who buy from a close firm are respectively:
When both firms charge uniform price, their consumer surplus are respectively:
The differences between them are
Since both groups of consumers are better with price discrimination, overall consumer surplus is improved. \(\square \)
Proof of Proposition 6
Given information cost c, when both firms price discriminate: \(\pi _A^{I-I}=\pi _B^{I-I}=\frac{5}{18}t(1-\varepsilon )-c\). When firm A price discriminates while firm B does not, the profits are: \(\pi _A^{I-N}=\frac{5}{16}t(1-\varepsilon )-c\), \(\pi _B^{I-N}=\frac{1}{4}t(1-\varepsilon )\). It can be easily shown that when \(c>\frac{1}{36}t(1-\varepsilon )\), \(\pi _B^{I-N}>\pi _B^{I-I}\), such that both firms acquire information and price discriminate is not a SPNE.
Besides, when both firms choose price discrimination, the social welfare is:
when both firms choose uniform price, the social welfare is:
We find that when \(c<\frac{t}{36}(8\varepsilon -1)\), \(W^D>W^U\). Thus, we can draw a conclusion that price discrimination improves social welfare when the demand elasticity is large enough \(\left( \varepsilon >\frac{1}{8}\right) \) and information cost is small enough \(\left( c<\frac{t}{36}(8\varepsilon -1)\right) \). \(\square \)
Rights and permissions
About this article
Cite this article
Zhang, T., Huo, Y., Zhang, X. et al. Endogenous third-degree price discrimination in Hotelling model with elastic demand. J Econ 127, 125–145 (2019). https://doi.org/10.1007/s00712-018-0635-z
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00712-018-0635-z