Smoothed particle hydrodynamics modelling of multiphase flows: an overview

Abstract

Smoothed particle hydrodynamics (SPH) is a meshless, particle-based approach that has been increasingly applied for modelling of various fluid-flow phenomena. Concerning multiphase flow computations, an advantage of the Lagrangian SPH over Eulerian approaches is that the advection step is straightforward. Consequently, the interphasial surface can be explicitly determined from the positions of particles representing different phases; therefore, there is no need for the interface reconstruction step. In this review paper, we briefly recall the basics of the SPH approach, and in particular the physical modelling and numerical implementation issues. We also mention the weaknesses of the approach and some remedies to overcome them. Then, we demonstrate the applicability of SPH to selected interfacial flow cases, including the liquid column break-up, gas–liquid flow regimes in a channel capturing the transitions between them and the wetting phenomena. Concerning the two-fluid modelling, it is illustrated with sediment transport in the presence of surface waves. Various other applications are briefly recalled from the rich and growing literature on the subject, followed by a tentative list of challenges in multiphase SPH.

1 Introduction

Multiphase flows feature rich physics [1], including interphasial momentum and energy couplings, phase changes, surface tension forces, etc. At the level of continuous media, the most detailed description accounts for the dynamics of (generally deformable) interfaces between the immiscible phases, their topological changes due to break-up or coalescence, or interface–wall interactions due to wetting effects. As opposed to these complex (separated or segregated) flows, in disperse flows the entities such as solid particles, droplets or bubbles (all are collectively called particles) and their interactions with a carrier fluid phase are of interest. At this level of description, the coupling between the phases is accounted for in an averaged way (by using semi-empirical formulae for forces and torques). At the next level of averaging, the phases are treated as interpenetrating continua.

Multiphase systems commonly occur in nature, starting from the astrophysical scales, through hydrometeors in the atmosphere, sandstorms, pyroclastic flows, gravity and capillary waves, sediment transport, down to gyrotactic swimmers, red blood cells and submicron particles. From this first look at the bestiary of living and inanimate nature, the wealth and span of scales can be admired. Referring just to the air/water/sand system in environmental hydraulics, they range from the millimetre-sized sand grains that make up a deformable bottom featuring seabed ripples, up to the wind-driven surface waves of hundreds of metres. In the same vein, examples from engineering include spray atomisation, boiling heat transfer, gas and oil transportation systems, and a plethora of other applications. Here again, the length (and time) scales may span a few orders of magnitude. Looked at from the standpoint of phase content, multiphase flows range from dilute systems (cloud droplets), through the collisional regime (fluidised beds), up to the granular/porous medium (saturated soil); different regimes call for different description. Therefore, it is pretty obvious that the diversity of physical phenomena at play, the variability of flow conditions as well as material properties of the various fluids (and solids) that constitute the phases, and a range of time and length scales involved, make it virtually impossible to conceive an “all-inclusive”, yet tractable, model of a multiphase flow.

Generally, corresponding to the above sketch, the physical and mathematical models can roughly be ascribed to two categories: (i) interfacial flow models of gas–liquid or liquid–liquid systems, often in the “one-fluid” formulation [2], and (ii) disperse flow models that may also involve fluid–solid systems. The latter are considered in the present paper as averaged, “two-fluid” models only. However, disperse flows may be efficiently treated in terms of point-particle simulations (Eulerian–Lagrangian, i.e. trajectory approaches) or as particle-resolved simulations. Although they are of less interest in this paper, point-particle models are relatively mature, efficient and in practice the only ones affordable when the carrier phase flow is turbulent; for the sake of completeness, the reader may wish to consult [3,4,5,6] and references therein for the overviews on particles in turbulence, including the direct numerical simulations (DNS), large-eddy simulations (LES), the stochastic approaches, particle deposition, etc. As to the former category, i.e. the interfacial flow models, here the attention is restricted to fully resolved simulations (broadly called DNS), be they of turbulent or laminar flows. The LES of such flows and statistically averaged models (featuring, for example, the interfacial area density), otherwise of keen scientific and practical interest, are not addressed in this review, also because there is no equivalent to them in the smoothed particle hydrodynamics (SPH) approach which will be in focus here.

In line with the developments in general computational fluid mechanics (CFD) since its advent back to the 1960s, say, also the models of interfacial flows have been predominantly conceived in the Eulerian, grid-based approach, with perhaps a notable exception of the marker-and-cell method (MAC) due to Francis Harlow and coworkers at Los Alamos (known as CFD pioneers). In MAC, which is a hybrid Eulerian–Lagrangian method, passive tracers (markers) are applied to track the phase distribution [7]. The MAC method has been a predecessor of the modern front-tracking (FT) approach [2] where the tracer particles (connected marker points) located at the interface enable to follow its evolution. Recently, FT has also been applied to handle three phase systems composed of buoyant bubbles, heavy drops and a carrier liquid (like in the flotation process) [8].

Arguably, the most popular approach nowadays (also in commercial CFD packages) is the volume-of-fluid (VOF) method [9], see also [2] and references therein. The VOF method uses the physical concept of the volume fraction $\alpha$ of a phase ($0\le \alpha \le 1$); from the computational standpoint, it is a marker function simply advected in the flow field and used to reconstruct the actual interface shape in the grid cells where $0< \alpha < 1$. The VOF method conserves mass and may offer high accuracy; however, when this is required, the reconstruction step becomes pretty complex, like the computation of a local curvature necessary to account for the surface tension effects [10]. Another approach where a marker function (here F) is advected is the level set (LS) method. Here, the interface is identified as a particular level set ($F=0$) of the smooth marker function. Including the so-called re-initialisation step [11], the normal vectors to the interface are readily found from $\nabla F$. However, the mass conservation has been an issue in LS; it has been partly overcome at the expense of increased complexity of the method ingredients. One of the options has been to couple VOF and LS into CLSVOF (the acronym is self-explanatory), see [12, 13], to take advantage both of the mass conservation and fast computation of normal vectors to the interface (or to fronts in general, as a “front” is not necessarily a material interface).

Yet another interface capturing approach, increasingly often applied to two-phase systems, is the phase field method (PFM) [14]. Rooted in the physical/thermodynamic description of phase change phenomena and the Cahn–Hilliard equation, the PFM belongs, unlike the previously recalled approaches, to the class of diffuse interface (DI) models where the interface thickness spans a few grid cells [15]. In the macroscopic description, the physical interface is sharp. (Interestingly, in [16] statistical models of the “intermittency region” at the mesoscopic level are advocated.) The PFM has been successfully applied to droplets break-up and coalescence in the flow [17], also surfactant-laden [18], and to bubbles [19]. It has also been compared to the multiphase variant of the lattice Boltzmann method (LBM) [20]; the latter is not addressed here (because of its mesoscopic nature); however, it has proven efficient in multiphase flow computation.

As we will see in the following, some specific features of two-phase flows, such as the presence of steep gradients or even discontinuities in the interfacial region and the effects of surface tension, imply difficulties for numerical solution. Some of them are common for the Eulerian methods briefly recalled above and for the SPH method, basically Lagrangian, that is the main focus of the paper. SPH will be presented in more detail in Sect. 2. An advantage of the Lagrangian description is that the material surfaces (such as the interfaces separating individual, immiscible phases in the absence of phase transitions) are explicitly tracked in the fluid flow. Arguably, another advantageous feature of the Lagrangian approaches, of interest here, is the a priori flexibility to incorporate complex physics into a single system of evolution equations. A relevant example from the area of hydraulic engineering is again a wind–water–sediment system [21, 23] where a comprehensive model would couple, e.g. granular media flow [24], constitutive relationships for the seabed rheology [25], together with two-fluid sediment flow models [26,27,28,29].

Before general SPH is presented in the next section, let us take a moment to look at the work to date regarding SPH for multiphase flows, which is also the main concern of this overview. There have been a few authoritative and comprehensive review papers on free surface flows [30, 31] and on complex fluid flows [32]; there have also been reviews on particular research areas, such as ocean and coastal engineering [33,34,35] or industrial applications [36], including nuclear thermal hydraulics [37]. A valuable overview of SPH for multiphase flows by Wang et al. [38] is considerably more detailed than the present one with respect to the fundamental concepts and technical aspects of one-phase SPH, such as kernel choice, pressure treatment, time integration and boundary conditions. It deals with free-surface and interfacial models of high density ratios. In [38], a number of critical issues in SPH are listed: low accuracy, high (sometimes critically high) computational cost, treatment of boundaries (for two-phase flow systems) and surface tension. In the present review, we revisit some of these issues, hopefully adding new pieces of information as per our own experience. We have also done our best to include (by no means all) relevant references beyond 2015 until mid-2023.

This paper is organised as follows. In Sect. 2, we recall the governing equations of two-phase flows, both with interfaces and at the averaged (mixture) level. We then present the basics of the SPH approach and specific developments for the two-phase flow simulations: density computation, surface tension implementation, micromixing artefacts, etc. Next, we present a selection of SPH applications to interfacial flows (Sect. 3) and the two-fluid modelling of sediment transport (Sect. 4). Challenges in multiphase SPH are discussed at some detail in Sect. 5; conclusions and outlook are given in Sect. 6.

2 Multiphase fluid dynamics and SPH

The title of this section intentionally parallels the title of a comprehensive monograph by Violeau [39] that starts by fundamental concepts of the Lagrangian and Hamiltonian theoretical mechanics, offers the Author’s perspective on fluid dynamics, to smoothly introduce the SPH in action, applying these theoretical concepts. All proportions kept, here we just recall the governing equations of the one-fluid (interfacial) and two-fluid (mixture) models of multiphase fluid dynamics that will then be solved using the SPH machinery.

2.1 Equations to be solved

2.1.1 One-fluid model

Assuming that fluids 1 and 2 separated by an interface are Newtonian and weakly compressible, the multiphase flow dynamics is governed by the continuity and the Navier–Stokes (NS) equations. They are written in the form suitable for SPH discretisation, i.e. with the material derivatives on the LHS:

$$\begin{aligned} \frac{\text {d} \rho }{\text {d}t}&= - \rho \nabla \cdot \textbf{u} \end{aligned}$$

(1)

$$\begin{aligned} \frac{\text {d} \textbf{u}}{\text {d}t}&= -\frac{1}{\rho } \nabla p + \frac{1}{\rho } \nabla \cdot \mu \left( \nabla {\textbf{u}}+\nabla {\textbf{u}}^T - {\tfrac{2}{3}}(\nabla \cdot {\textbf{u}}){\textbf{I}}\right) + {\textbf{g}} + \frac{1}{\rho } {\textbf{f}}_\text {st} \end{aligned}$$

(2)

where $\rho$ is the density, ${\textbf{u}}$ is the velocity, p is the pressure, $\mu$ is a local dynamic viscosity coefficient, and ${\textbf{g}}$ is a body force; ${\textbf{f}}_\text {st}$ stands for the (regularised) surface tension force, further detailed in Sect. 2.3. In the one-phase flow case, the equations remain the same (except that there is no ${\textbf{f}}_\text {st}$ term).

The material parameters, say Q (be it the viscosity or density) may be found from the weighted average of quantities representing the respective phases, $Q_1$ and $Q_2$, using the phase indicator function $\alpha$ often called the colour function (and denoted by c). Let $\alpha \!=\!0$ in the bulk of phase 1 and $\alpha \!=\!1$ in the bulk of phase 2. Then, $Q=(1-\alpha ) Q_1 + \alpha Q_2$; a single field of Q (viscosity, density or other scalar variables where relevant) justifies the name “one-fluid” model. In Eulerian methods of the diffuse interface (DI) type, such as PFM, $\alpha$ changes smoothly across the interfacial region taking intermediate values there. As detailed in Sect. 2.3, an analogous description is used in SPH (although the interface can be seen as sharp when only the particle colours are considered).

In the WC models, the velocity divergence $\nabla \cdot {\textbf{u}}$ in the second RHS term in Eq. (2) is usually neglected because of (approximate) incompressibility. Finally, the system of governing equations, Eqs. (1), (2), is completed by a pressure–density relationship. The Tait equation is often applied for the purpose of WC simulations. It writes

$$\begin{aligned} p = \frac{c_s^2 \rho _0}{\gamma } \left[ \left( \frac{\rho }{\rho _0}\right) ^\gamma -1 \right] \end{aligned}$$

(3)

where $\rho _0$ is a reference density; $c_s$ is a sound speed and $\gamma$ is a constant (often $\gamma =7$ is taken in liquids), chosen to keep the density fluctuations at ${\mathcal {O}}(1\%)$.

2.1.2 Two-fluid model

In the averaged description of two-phase dispersed flows (at the mixture level), the phases are treated as interpenetrating continua, see [1]. In particular, for the material densities of the carrier fluid (f) and the dispersed (d) phases, ${\rho _f}$ and ${\rho _d}$, the respective volume (bulk) densities are ${\hat{\rho }}_f = (1-\theta _d){\rho }_f$ and ${\hat{\rho }}_d = \theta _d {\rho }_d$ where $\theta _d$ is the volume fraction of the dispersed phase. The quantities ${\hat{\rho }}_f$ and ${\hat{\rho }}_d$ obey the standard continuity equations, cf. Eq. (1). The phases interact through the momentum coupling term in the respective momentum equations formulated in terms of the two-fluid model:

$$\begin{aligned} { \frac{\partial \textbf{u}_f}{\partial t} + \left( \textbf{u}_f\cdot \nabla \right) \textbf{u}_f }&= -\frac{\nabla p}{\rho _f} - \frac{K}{{\hat{\rho }}_f} \left( {\textbf{u}}_f -{\textbf{u}}_d \right) + \frac{1}{\rho _f} \left( \nabla \mu \cdot \nabla \right) {\textbf{u}}_f + {\textbf{g}} \end{aligned}$$

(4)

$$\begin{aligned} { \frac{\partial \textbf{u}_d}{\partial t} + \left( \textbf{u}_d\cdot \nabla \right) \textbf{u}_d }&= -\frac{\nabla p}{\rho _d} + \frac{K}{{\hat{\rho }}_d} \left( {\textbf{u}}_f -{\textbf{u}}_d \right) + {\textbf{g}} \end{aligned}$$

(5)

where $\textbf{u}_f$ and $\textbf{u}_d$ stand for the velocities of the respective phases; there is a single pressure field p, though (no collisional effects as the flow regime is not dense/granular). Unlike in Eq. (2), the material derivatives on the LHS of Eqs. (4) and (5) have been expanded to avoid ambiguity in the symbol d/dt and to explicitly distinguish between the two advection velocities; this applies to the continuity equations as well. Then, ${\textbf{g}}$ is the gravity acceleration and $K=K(\text {Re})$ is the interphase drag factor where Re is the Reynolds number based on the local relative velocity of the phases. The volume fractions of the phases and the Stokesian drag formula accounting for a higher-Re correction enter the semi-empirical drag expression for K in the dilute regime. The so-called Gidaspow’s drag formula is a crucial ingredient of the two-fluid model; it becomes more complicated in the dense regime with $\theta _d$ typically larger than 0.2. For variants of the two-fluid model equations, see also [26, 40].

The Eulerian description of two-phase dispersed flows (at the mixture level) using the two-fluid model, although approximate, has proven to be computationally efficient; for an example of computing the sedimentation process, see [41]. The two-fluid model in the SPH implementation is considered in Sect. 2.4.

2.2 Brief presentation of SPH

For an authoritative presentation to the SPH method, the books [39, 42] may be referred to, along with general reviews [32, 43,44,45,46,47] and references therein.

As a brief introduction: SPH is one of the particle-based, meshless approaches in computational mechanics. It originated in astrophysics to deal with large-scale, variable-density systems in unbounded space. Over the years, the (basically) Lagrangian nature of SPH and its conceptual simplicity have attracted attention beyond its native astrophysics. The method has become increasingly popular in the scientific community for the last 20+ years or so. It continues to be developed as an alternative modelling tool for a wide range of problems in the macroscopic mechanics of continua, including multiphase flows, complex fluids and multiphysics phenomena, granular media and solid mechanics [45]; it has also been extended to the mesoscopic level [48, 49]. The word “hydrodynamics” in the SPH acronym refers to the hydrodynamic (continuous medium) level of description, even when referring to dusty gas applications. Actually, the name “Smoothed Particle Applied Mechanics”, proposed in the literature, would much better characterise it but this is unlikely to be changed; this might be due to the misfortunate acronym but, first of all, due to the fact that “SPH” is already well established.

Fig. 1

The SPH discretisation concept; the dash-lined circles show the kernel range for particle–particle interactions. A single-phase case (left picture): SPH averages computed at the location of particle a applying the summation interpolants over neighbouring particles b (red) located within the kernel range. Other particles (grey) do not enter the summation formulae. The two-fluid model (right picture, cf. Sect. 4): two particle sets represent the interpenetrating continua, say water (blue particles denoted as a, b) and sand (black particles denoted as i, j) (Color figure online)

In SPH, the flow continuum is discretised by using particles. The particles, which carry all necessary information about flow variables, can be thought of as Lagrangian fluid elements. They undergo advection in physical space, are assigned a volume, but are not deformable (contrary to the true fluid parcels). The pressure and viscous forces are represented as particles interaction forces (see below). Hence, for such a model of Lagrangian fluid element the problem of distortion (that can become arbitrarily large with time) is avoided.

SPH approach, as its name indicates, makes use of smoothing in space applied to variables related to particles. To explain this idea, consider a function $A(\textbf{x})$; it can be approximated by an integral interpolant $A_{I}(\textbf{x})$

$$\begin{aligned} A_{I}(\textbf{x})= \int A(\textbf{x}') W(\textbf{x}-\textbf{x}',h) \,\text {d}{} \textbf{x}' \end{aligned}$$

(6)

where $A(\textbf{x}')$ are values of the function at points $\textbf{x}'$ and W is a weighting function (a so-called kernel) with a parameter h that can be thought of as a smoothing length. The approximation error is kernel-dependent, with $A_{I}(\textbf{x})-A(\textbf{x}) = {{{\mathcal {O}}}}(h^2 {\nabla }^2 A)$. The kernel is usually chosen as a sufficiently smooth function with compact support to limit the sum to neighbouring particles only. It satisfies the normalisation condition and in the limit of small h tends to the Dirac delta; then, the approximation in Eq. (6) becomes exact. Various proposals have been advanced in the literature: the Gaussian function, regular or spline polynomials (the Wendland kernel is a popular choice [50]).

In particle methods, a fine-grained and differentiable representation of A is introduced. The integral interpolant, Eq. (6), becomes then a discrete, or summation, interpolant $A_{S}(\textbf{x})$ defined by a sum over particles b located in a certain neighbourhood of $\textbf{x}$, with the volume element expressed by the specific volume (the inverse of the particle number density): $d{\textbf{x}}' \rightarrow dm/\rho ({\textbf{x}}')$. The spatial derivatives are computed in a similar way

$$\begin{aligned} A_{S}(\textbf{x})=\sum _{b} m_b\frac{A_{b}}{\rho _{b}} W(\textbf{x}-\textbf{x}_{b},h) , \quad \nabla A_{S}(\textbf{x})=\sum _{b} m_b\frac{A_{b}}{\rho _{b}} \nabla W(\textbf{x}-\textbf{x}_{b},h) \end{aligned}$$

(7)

where the index b denotes the values at the locations $\textbf{x}_{b}$, $m_{b}$ is the particle mass, and $\rho _b$ is fluid density at particle location. The summation is limited to neighbouring particles identified by the range of the kernel function (Fig. 1a). It is a smooth function (hence the method’s name) of compact support whose size, or length scale, roughly determines the spatial resolution of the approach. Another length scale is determined by the mean interparticle distance $\Delta r$. It also affects the method’s accuracy and stability.

In mesh-based finite difference or finite volume spatial discretisations, various algebraic formulae are possible, of direct impact on the properties of the resulting discrete spatial derivative operators. The same applies to SPH: the formula for gradient provided by Eq. (7b) is not unique. As amply discussed in the monographs of the subject, e.g. [39], symmetric and anti-symmetric expressions can be derived for $\nabla A_S$; the starting point is the identity $\nabla A = \nabla \left( (A \rho ^m) (\rho ^{-m}) \right)$, where m is an integer, and the differentiation rule of the product applied to this identity. A convenient discretisation of the pressure gradient term in Eq. (2) is implemented in Eq. (8).

Using the above-presented formalism, the whole set of evolution equations governing the flow are expressed in the SPH approach. In other words, the dynamics of the system results from a certain form of particle interaction. For viscous flows, the momentum equation in the SPH formalism writes

$$\begin{aligned} \frac{\text {d}{} \textbf{u}_{a}}{\text {d}t} = \textbf{g}_a - \sum _{b} \left[ m_b \left( \frac{p_{b}}{\rho _{b}^2} + \frac{p_{a}}{\rho _{a}^2} \right) \nabla _{a} W_{ab} - \Pi _{ab} \right] \end{aligned}$$

(8)

where $\nabla _{a} W_{\text {ab}}=\partial W(\textbf{x}_a-\textbf{x}_b,h)/\partial \textbf{x}_a$, $\textbf{x}_{\text {ab}}= \textbf{x}_a - \textbf{x}_b$, $\textbf{g}_{a}=\textbf{g}(\textbf{x}_{a})$, and $\Pi _{\text {ab}}$ is the viscous term

$$\begin{aligned} \Pi _{ab}= m_b \frac{(\nu _a\rho _a +\nu _b\rho _b) \textbf{x}_{ab} \cdot \nabla _a W_{ab}}{\rho _a \rho _b (\textbf{x}_{ab}^2+{\eta }^2)} (\textbf{u}_a - \textbf{u}_b) \end{aligned}$$

(9)

see Morris et al. [51]. On the RHS of Eq. (8), the external force field and particle interaction forces are distinguished. The system of governing equations includes the advection formula and the SPH-discretised continuity equation, Eq. (1)

$$\begin{aligned} \frac{\text {d} \textbf{x}_a}{\text {d}t}&= \textbf{u}_a \end{aligned}$$

(10)

$$\begin{aligned} \frac{\text {d} \rho _a}{\text {d}t}&= \sum _{b} m_b \left( {\textbf{u}}_a - {\textbf{u}}_b \right) \nabla _{a} W_{ab} \;. \end{aligned}$$

(11)

Another expression of mass conservation in SPH goes through a straightforward density computation applying Eq. (7a):

$$\begin{aligned} \rho _a = \sum _{b} \rho _b \frac{m_b}{\rho _b} W_{ab} = \sum _{b} m_b W_{ab} . \end{aligned}$$

(12)

As pointed out by Vila [52], by differentiating this formula, Eq. (11) is retrieved.

The system of governing equations may be complemented by an equation of state. Even in (nearly) incompressible flows, the weak compressibility (WC) approximation is often applied with Eq. (3) utilised as the equation of state. It was also used (in a modified form) to model natural convection [53].

In incompressible flows, the role of the pressure is purely kinematic, not thermodynamic. So, for truly incompressible approach (ISPH), an elliptic pressure correction equation was proposed [54] to assure the zero-divergence condition of the velocity field. However, in Lagrangian particle methods there is no a priori guarantee that the density field (computed out of particle locations) will remain uniform. Consequently, it was proposed to solve two Poisson equations for pressure corrections in order to preserve both uniform density and solenoidal velocity fields [55]. Incompressible SPH has been amply addressed in [56, 57]. Using the ISPH approach with an appropriate form of particle boundary conditions, viscous incompressible flow cases and flows with internal interfaces have been computed.

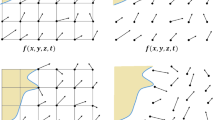
At this point, let us reiterate that the SPH discretisation applies to the fields of relevant variables. Therefore, when analysing the computation results, the “fine-grained” structure of the solution should be understood and interpreted in terms of a (discrete) field. This is illustrated in Fig. 2 (the actual flow case [58] will be introduced and detailed in Sect. 3.2): the deformed liquid column, or filament, should rather be perceived as a smoothed solution (right plot) without bothering too much about nicely rendered particles (left). They are assigned some volume (small spheres visible on the plot) but, actually, they represent interpolation points.

Fig. 2

Multiphase SPH simulation of the Rayleigh–Plateau instability. Left picture: the positions of SPH particles (only the liquid phase is shown). Right picture: the liquid–gas interface location corresponding to the mid-isosurface of the phase indicator ($c=0.5$, interpolated from particles onto a uniform grid). Reproduced from [58]

Following the brief overview of the SPH literature, let us tentatively summarise the more important advantages and drawbacks of the approach. Starting with the single-phase flows: the statement that SPH is self-adaptive, or that “resolution follows matter” in strongly compressible systems, has rather important consequences in astrophysics that go sometimes overlooked: extension to incompressible and weakly compressible flows in bounded domains (for many typical CFD problems) is by far not straightforward despite a conceptual simplicity of the approach. In multiphase flow simulation using Lagrangian SPH, an often reported advantage is no need for interface reconstruction neither any special treatment of topological changes. Concerning the known drawbacks of SPH, they refer to some rather fundamental properties of numerical methods: consistency [59], convergence [60], accuracy of the approach along with its computational complexity as well as the numerical implementation issues, and adaptive particle resolution (APR). In other words: the mesh-free feature of SPH comes at a price of accuracy degradation, particle noise and 0th-order consistency unless remedies are applied; an initially regular particle distribution is sometimes advantageous, sometimes not [61], so a relaxation of particle positions may be required.

Concerning the most computation-greedy part of the SPH algorithm, i.e. the sums involving loops over particles, an efficient identification/sorting of neighbours in particle–particle interaction terms, see Eqs. (8) and (10), (11), (12), is crucial. The structure of so-called linked lists has proven very useful [62]. For recent improvements on neighbour lists for GPU computing, see [63].

Fig. 3

Some variants of boundary conditions formulated in SPH: a using ghost (mirror) particles: the positions of SPH particles ($\bullet$) and ghost ones ($\circ$); b using dummy particles (blue colour) that correspond to a wall (Color figure online)

Boundary conditions (BC) in SPH can be formulated in terms of particles (see Fig. 3 for two of the BC variants): for boundaries limited to plane walls, the so-called mirror (or ghost) particles may be used. The idea is to ascribe respective quantities to such particles so that the imposed boundary condition (in terms of a value or gradient) is approximately satisfied at the wall (when computed from the summation interpolant). In practice, referring to the left panel of Fig. 3, for a no-slip wall moving with velocity ${\textbf{u}}_w$ (in particular, zero), the velocity of each ghost particle is readily determined from $\mathbf {u'}_b=2{\textbf{u}}_w-{\textbf{u}}_b$. Such “ghosts” (see again particles $b'$ in the figure) take part in the summations but are not evolved; as a matter of fact they are not stored in memory but contribute “on the fly” to the computation of the RHS of Eqs. (8)ff. and other sums [54, 55]. This type of BC has recently been applied also to study wetting phenomena [64]. It can be extended to handle right-angled boundaries (corners) [57], or cuboid domains in more general terms, which is sufficient for a number of geometrical setups but definitely not general. A rather universal class of BC, i.e. able to simulate even complex geometries, are expressed through fixed layer of boundary particles (called dummies or again “ghosts” in a number of papers), see particles coloured in blue in the right panel of Fig. 3; the pressure and velocity of these wall particles are suitably set to simulate/respect the imposed boundary condition [51, 65]. Another category are the so-called wall particles: a single layer of them is located exactly on the boundary [39] to exert a repulsive force on the “true” particles that are evolved. A fairly recent implementation of BC in terms of SPH is the so-called unified semi-analytical wall (USAW) boundary conditions that, exploiting the incomplete kernel properties and the resulting relationships, are suitable for boundaries represented by line sections [66]. The USAW type of BC has also been applied to turbulent [67] and multiphase flows [40]. For an SPH implementation of open BC, see [68].

As the bottom line on particle boundary conditions: the meshless nature of SPH is sometimes invoked as advantageous for the treatment of complex geometries; however, the proper BC statement in a general case is not evident. The issue remains open and has been identified as one of the Grand Challenges by the SPH research community [69].

Concerning the adaptive particle refinement (APR), or variable resolution in space, this is another one of the Grand Challenges. SPH is not naturally suited for APR, contrary to the adaptive grid techniques (adaptive mesh refinement) that are well mastered for Eulerian solvers. Over the years, several variants have been proposed. In the astrophysical origins of SPH, with the “resolution follows matter” motto, the kernel size dependence of $h=h(\rho )$ was a natural way to deal with adaptivity. The SPH equations needed to be complemented with terms involving $\nabla h({\textbf{x}})$. With the advent of SPH applications in fluid dynamics, including (nearly) incompressible flows, the ideas appeared of either increased resolution is some predetermined areas or of a truly adaptive (dynamic) one, i.e.: (i) particle splitting (fission) in regions of interest for locally increased accuracy and (ii) their coalescence (fusion) when no longer needed (for the sake of computing time and memory constraints), see [70,71,72,73,74,75,76,77,78]. Generally, the APR involves considerable programming complexity and, in some variants, it is applied on a case-per-case basis. A development of a multilevel APR was recently published in [78]. To complete the picture, we need to mention earlier techniques of remeshing of particle distribution [79] that aimed to reduce the solution errors induced by Lagrangian particle advection, in high-shear zones in particular.

Let us note that another Lagrangian meshless approach, closely related to SPH yet probably less popular, is the so-called moving particle semi-implicit (MPS) method, originally developed for incompressible, free-surface flows. In MPS, gradients are computed using a finite difference formulae representation and the kernels (not the kernel gradients, unlike in SPH). Moreover, kernels are singular at the origin, which helps to preserve particles from clustering. A variety of technical developments for multiphase flows in MPS have been made recently, see for, example, [80,81,82,83,84]. For an overview of MPS, the reader may refer to [85] and bibliography therein; for a selection of recent works on MPS for coastal engineering, see [21, 33, 86].

2.3 SPH model of interfacial flows

In its basic variant considered here, SPH is Lagrangian in nature. As already mentioned, its advantage over Eulerian approaches for multiphase flow computations lies in the fact that free surfaces (or two-phase interfaces) are dealt with in a rather straightforward manner [31]. More precisely, the shape of the interphasial surface can be determined explicitly from positions of the particles of different phases.

Separated two-phase flows may feature considerable differences in the material properties of the phases, such as density or viscosity, across the interface. At the discrete level, steep gradients may result. Generally, high density ratios may be a challenge for multiphase methods (PFM, for example); attention is also needed in SPH [77, 87]. Free-surface flows may not be straightforward to handle either. In particular, referring to the SPH method, Eq. (12) is not suitable for computations of the free-surface flows, as the straightforward summation formula would lead to underestimation of the density in the kernel-range vicinity of the surface. Concerning interfacial flows, this formula would result in the undesired smoothing of density on the interface. To preserve sharp gradients there, Hu and Adams [49] applied the summation formula for density computation in the form

$$\begin{aligned} \rho _a = m_a \sum _{b} W_{ab} . \end{aligned}$$

(13)

Consequently, the density field is represented by the spatial distribution of particles and not by their masses: near the interface, the density computation in one phase is not affected by the density (or respective particle masses) of the other phase. However, this formula is suitable for interfaces and not for a free surface as it is based on a (nearly) uniform distribution of particles within the kernel range.

The pioneering works in multiphase SPH include [49, 88,89,90]. Concerning simplified two-phase flow modelling at the mixture level (no account for the very structure of the phases in terms of interphasial surfaces), the first attempt, again in the context of astrophysics, dates back to Monaghan and Kocharyan [91, 92].

A physically sound account on surface tension forces is of paramount importance in modelling of multiphase flows. At the microscopic level, surface tension results form molecular forces, so the idea appears to propose a representation of particle–particle interactions in the SPH formalism (J.-P. Minier, priv. comm.). A cohesive pressure term to model surface tension effect was advanced by Nugent and Posch [90] and the pairwise force model by Tartakovsky and coworkers [93,94,95,96]. A difficulty with such a meso-scale approach is the calibration of the coefficients in the formulae for repulsive-attractive forces so that they would correspond to a given surface tension coefficient $\sigma$ at the macroscopic level.

The surface tension term appearing in Eq. (2) has been regularised in SPH by Morris [89] who adopted the continuum surface force method (CSF) originally proposed by Brackbill et al. [97]. The surface tension forces ${\textbf{f}}_s$ (per unit area) are converted into a force per unit volume ${\textbf{f}}_{st} = {\textbf{f}}_s \delta _S$ where $\delta _S$ is a suitably chosen surface delta function and ${\textbf{f}}_s = \sigma \kappa \hat{{\textbf{n}}}$ is the surface force, $\hat{{\textbf{n}}}$ is the unit vector normal to the interface, and $\kappa =-\nabla \cdot \hat{{\textbf{n}}}$ is the local curvature of the interface; $\sigma$ is the surface tension coefficient. Using the so-called colour, or phase indicator, function c ($c = 0$ for the first phase and $c = 1$ for the second one), $\hat{{\textbf{n}}}$ is found from

$$\begin{aligned} \hat{{\textbf{n}}}=\frac{{\textbf{n}}}{|{\textbf{n}}|} = \frac{\nabla c}{|\nabla c |} \;. \end{aligned}$$

(14)

In the SPH formalism:

$$\begin{aligned} {\textbf{n}}_a = \sum _b (c_b - c_a) \nabla W_{ab} \Omega _b\; \end{aligned}$$

(15)

and

$$\begin{aligned} \kappa _a = \sum _b (\hat{{\textbf{n}}}_b - \hat{{\textbf{n}}}_a) \nabla W_{ab} \Omega _b \;. \end{aligned}$$

(16)

A macroscopic formulation alternative to CSF exploits the concept of continuous surface stress (CSS) [98].

A simple benchmark to test the implementation of surface tension forces in terms of the CSF model is the spherical droplet (or circle in 2D). The normal vectors and the local curvature can also be computed by using in Eq. (15) a smoothed field ${\tilde{c}}$ of the phase indicator [89]. It is clearly seen from Fig. 4 (left panel) that the procedure of colour smoothing has a direct impact on the velocity magnitude level, in particular at the interface, which manifests itself through the so-called parasitic currents (still of concern in numerical approaches, including in SPH [99]). The pressure profile across the droplet is shown in the same figure (right panel) as rather well represented. The additional smoothing of the colour function naturally makes the interphasial transition region thicker. However, the effect of extra smoothing is not always so beneficial. Considering a system of two neighbouring droplets (Fig. 5): spurious coalescence will set in when the initial distance of two droplets (precisely, the size of the gap between them) becomes smaller than the kernel size or twice this value when the smoothed colour ${\tilde{c}}$ is used in Eq. (15).

Fig. 4

A circular (2D) drop at equilibrium. Velocity magnitude with and without colour function smoothing (left, half/half). Pressure profile over a droplet cross section, normalised by the Young–Laplace jump at the interface (right)

Fig. 5

Two droplets in a side-by-side arrangement: spurious coalescence due to smoothed phase indicator in SPH (left plots), no coalescence (right plots)

Fig. 6

Oscillating droplet, two time instants: impact of the interface correction procedure. Upper plots: no correction (micromixing visible). Lower plots: correction applied

The spurious micromixing, noticed also in Fig. 6 (upper plots), is due to the Lagrangian nature of the SPH approach where particles are not a priori prevented from wandering off into the bulk of the other phase. The spurious fragmentation of the interface was observed in the simulations of bubbles rising in liquids with a low surface tension coefficient. The idea elaborated by Szewc et al. [100] was to introduce a corrective (repulsive) force on the interface which had similar structure to the surface tension force in CSF model:

$$\begin{aligned} \mathbf {\Xi }_{a}= \frac{\epsilon }{m_a} \sum _{\begin{array}{c} b \\ c_b\ne c_a \end{array}} \left( \frac{1}{\theta _a} + \frac{1}{\theta _b}\ \right) \nabla _a W_{ab}(h) \end{aligned}$$

(17)

where $\epsilon =\epsilon (h)$ is the interface correction coefficient; $\epsilon$ was shown in [100] to scale as $h^{-1}$. Please note that the sum in Eq. (17) extends only over the particles of the other phase (not that of particle a). The force term $\mathbf {\Xi }$ is added to the RHS of the discretised momentum equation, along with the surface force term ${\textbf{f}}_s$. As noticed in the benchmark of oscillated droplet, Fig. 6 (lower plots), the computations with the correction applied ($\epsilon =0.1)$ do not exhibit now the artefact of micromixing.

A selection of benchmarks and applications in 2D and 3D have been considered using the multiphase SPH formalism, including the Rayleigh-Taylor instability, rising bubbles (single ones and coalescing pairs) or droplet collisions, see, e.g. [49, 88, 101,102,103,104,105,106,107,108].

A separate category are free-surface flows when the presence of the second, lighter phase (usually gas) can be neglected because of the insignificant influence on the flow dynamics, at the same time reducing the computational effort. In SPH simulations of this flow category, a particular attention is needed close to the free surface to remedy for the incomplete particle sums within the kernel range. The so-called Shepard kernel [109] has been a popular choice. Other specific features of SPH applied to such flows are detection of free surface and surface tension modelling (when necessary) [30, 31, 76, 110,111,112]. Judging on the literature published to date, free-surface flows in the environmental context have been a rich field for SPH applications.

The idea of the so-called $\delta$-SPH model [113, 114] has been to add a numerical diffusion term to the RHS of the continuity equation, Eq. (11). In the simplest form, it writes:

$$\begin{aligned} 2 \delta h c_s \sum _b (\rho _b - \rho _a) \frac{{\textbf{r}}_{ba} \cdot \nabla _a W_{ab}}{r_{ba}^2} \frac{m_b}{\rho _b} \end{aligned}$$

(18)

where $\delta$ is a numerical parameter, often taken as ${\mathcal {O}}(10^{-1})$. It is applied in the WC formulation to alleviate the resulting numerical noise in the pressure field due to the non-uniform distribution of particles (hence, the density); see also Fig. 18 in Sect. 4. The $\delta$-SPH continues to be worked on and applied or extended in many ways, see [115,116,117,118,119,120,121].

The “continuum level equivalent” of the $\delta$-correction, Eq. (18), is the presence in Eq. (1) of the extra term $(\delta h c_s) \nabla ^2 \rho$ where the diffusion coefficient is proportional to $h c_s$. Interestingly, referring to physical description (and not just to numerical remedies), the presence of a diffusion term in the continuity equation has been an issue in the literature and a few attempts have been put forward for variable-density viscous flows, see [122] (and the references therein) for a recent discussion, and a WC model proposal utilising the mass diffusion formulation [123].

2.4 SPH model of dispersed flows (two-fluid approach)

We present the SPH implementation of the two-fluid model where the carrier phase and the dispersed particles are treated as two interpenetrating continua (Sect. 2.1.2). Again, such models appeared first in astrophysics to handle gas–dust systems [92, 124]; more recent works are [125, 126]. The general concept of the present implementation relies on the introduction of two separate sets of SPH particles for the fluid and disperse phases (Fig. 1b); though, in the work of Shi et al. [28] only one set of particles was used. We note in passing that dense suspensions [127, 128] or granular flows [24, 129] call for a different description.

The two-fluid system is governed by the continuity equations formulated in terms of the volume (bulk) densities of the phases, ${\hat{\rho }}_f$ and ${\hat{\rho }}_d$, and the momentum equations coupled due to the drag force interaction terms, Eqs. (4)–(5), limited to fairly dilute suspensions. The equations are suitably discretised in the WC-SPH setting using two particle classes [26, 40, 130]. We keep the original notation of Monaghan and Kocharyan [92]: the particles representing the carrier fluid will be denoted with indices a and b, while i and j will be used for the SPH particles representing the disperse phase. We recall that the latter particles are understood here as parts of a continuum, and not the real physical entities (like single grains of sand). Since free-surface flows are involved here, the SPH formalism proposed by Colagrossi and Landrini [88] is applied

$$\begin{aligned} \frac{\text {d}{\hat{\rho }}_a}{\text {d}t}= & {} -{\hat{\rho }}_a \sum _{b} \frac{m_b}{{\hat{\rho }}_b} \textbf{u}_{ab} \nabla _{a} W_{ab} \end{aligned}$$

(19)

$$\begin{aligned} \frac{\text {d}{\hat{\rho }}_i}{\text {d}t}= & {} -{\hat{\rho }}_i \sum _{j} \frac{m_j}{{\hat{\rho }}_j} \textbf{u}_{\text {ij}} \nabla _{i} W_{ij} \end{aligned}$$

(20)

$$\begin{aligned} \frac{\text {d}{} \textbf{u}_{a}}{\text {d}t}= & {} \textbf{g} + \sum _{b} m_b \left( \frac{\theta _a p_a+\theta _b p_b}{{\hat{\rho }}_a {\hat{\rho }}_b} + \Pi _{ab} \right) \nabla _{a} W_{ab} \nonumber \\{} & {} - \sum _{j} m_j \left( \frac{\theta _j p_a}{{\hat{\rho }}_a {\hat{\rho }}_j} \right) \nabla _{a} W_{aj} - D \sum _{j} m_j \ \frac{K_{aj}}{{\hat{\rho }}_a {\hat{\rho }}_j} \left( \textbf{u}_{aj}\cdot \hat{\textbf{r}}_{aj} \right) \hat{\textbf{r}}_{aj} W_{aj}\end{aligned}$$

(21)

$$\begin{aligned} \frac{\text {d}{} \textbf{u}_{i}}{\text {d}t}= & {} \textbf{g} + \sum _{j} m_j \left( \frac{\theta _i p_i+\theta _j p_j}{{\hat{\rho }}_i {\hat{\rho }}_j} \right) \nabla _{i} W_{ij} \nonumber \\{} & {} - \sum _{b} m_b \left( \frac{\theta _i p_b}{{\hat{\rho }}_i {\hat{\rho }}_b} \right) \nabla _{i} W_{ib} - D \sum _{b} m_b \ \frac{K_{ib}}{{\hat{\rho }}_i {\hat{\rho }}_b} \left( \textbf{u}_{ib}\cdot \hat{\textbf{r}}_{ib} \right) \hat{\textbf{r}}_{ib} W_{ib} \end{aligned}$$

(22)

where $\textbf{u}_{ab}=\textbf{u}_{a}-\textbf{u}_{b}$, etc., and $\hat{\textbf{r}}$ are unit vectors of relative positions; $\Pi$ is the viscous stress tensor of the carrier phase and D (2 or 3) is the dimensionality of the problem. The momentum coupling term is readily identified by the pairs of indices referring to different phases, as in $K_{aj}$ and $K_{ib}$. For the actual form of the drag coupling term, a specific double-hump kernel used to compute the interphase couplings ($W_{aj}$, $W_{ib}$ in the discrete notation), the equation of state applied and further details, see [130]. Please note that Fig. 1b is incomplete for the sake is readability: there is one kernel range centred at particle a of the carrier phase: it involves the sums over (a, b) and (a, j) contributions; there should be another kernel range plotted there, centred at particle i of the disperse phase to involve the sums (i, j) and (i, b).

The system of Eqs. (19)–(22) is supplemented with the respective advection formulae for the two particle classes, a and i, cf. Eq. (10). Unlike in Sect. 2.1.2, in the present Lagrangian approach there is no risk of ambiguity in the symbol $\text {d}/\text {d}t$ as it stands now for the ordinary (time) derivative of particle variables. The quantities of interest are the fields of velocities and the volume fractions of the phases. The discrete equations are solved in the usual way, with an artificial equation of state for the carrier phase.

3 SPH of interfacial flows: selected results

3.1 Interfacial area estimation

To identify and discern among flow regimes, as in a two-phase pipe/channel flow, and also to model them at the averaged level of description, the interfacial area density ($[\text {m}^2/\text {m}^3]$) is a useful quantity. As it transpires from Fig. 7, for the same volume fraction of a phase, the flow structure may differ. Also, a transition from one flow regime to another may occur in the simulation, depending on flow conditions. In particular, the transition from slug to churn flow will occur with the increase of superficial velocities of the phases.

Fig. 7

Gas–liquid flow patterns in a channel, SPH simulation: slug (left), churn (right)

Here, we recall a convenient technique within SPH to follow the evolution of the interface area (in 3D, or interface length in 2D simulations) [131]; it is used next in Sect. 3.3. The interface area S in a domain $\Omega$ can be expressed through the surface delta function $\delta _S({\textbf{x}})$. The formula and its SPH approximation read:

$$\begin{aligned} S = \int _\Omega \delta _S({\textbf{x}}) \text {d}\Omega \;, \quad S\approx \sum _a |{\textbf{n}}_a |\frac{m_a}{\rho _a} \end{aligned}$$

(23)

where the surface delta function has been represented by $|{\textbf{n}} |$, i.e. the length of a normal vector (like used in the CSF model of the surface tension); it attains a maximum at the interface. The expression (23), computed in a SPH code at virtually no extra cost, allows one to estimate the interfacial area S for any topology of the interface.

As an illustration, a simple benchmark case is the deformation of a liquid cube, subject to surface tension forces. In the course of time, the surface of the “droplet” will evolve (not shown, except for the initial and final stages seen in Fig. 8). The process is illustrated in the same figure (right panel). The surface area, suitably normalised, is then checked against the analytical value at the steady state (a sphere) [131, 132]. For $L^3$ being the domain size and a cube of edge $l=0.6L$, the surface of the resulting sphere will be $S=(36\pi )^{1/3}l^2$. It is noticed that the computation error stays at a few-per cent level.

Fig. 8

Cube-to-sphere deformation. Initial configuration (left); final configuration (middle); only SPH particles of liquid are shown. Evolution of the interface relative area (right); three different resolutions, solid line denotes the analytical value [131]

3.2 Liquid column disintegration

The Rayleigh–Plateau (RP) instability is a convenient benchmark case for two-phase flow computations to observe a topological change due to the disintegration of a liquid column. In Lagrangian meshless methods, in particular SPH, the rupture (break-up) or coalescence is dealt with using particles with no specific treatment, unlike in some Eulerian methods where a break-up criterion is imposed beforehand to stop the adaptive grid refinement.

Fig. 9

Multiphase SPH simulation of the Rayleigh–Plateau instability. Evolution of the interface shape: snapshots at $t^+ = 0, 1.49, 3.23, 4.49, 6.49$ (from top to bottom, left plot). The disturbance growth (upper plot, the relative maximum radius of the liquid column): results compared with the VOF of Dai and Schmidt [133]. Reproduced from [58]

The computed evolution of the liquid filament is shown in Fig. 9; multiphase SPH has been applied in 3D [58]. The SPH results are demonstrated to rather correctly predict the time record of the maximum thickness of the filament (right panel of the figure), as well as the time instant of the column disintegration (Fig. 10) in comparison to the VOF reference computation [133]. The very break-up time is estimated from the phase indicator (colour function) profile c(x) computed at the symmetry axis. It is taken as a time instant when the value of c(x) drops to 1/2 at some location. However, a detailed 2D study (not shown) has confirmed the need of a finer resolution, or (even better) the adaptive particle refinement, for the accurate prediction.

Fig. 10

Multiphase SPH simulation of the Rayleigh–Plateau instability: estimating the break-up time. The interface shape at some time instant (left plot) and the phase indicator profile along the symmetry axis of the liquid filament (right plot). Reproduced from [58]

3.3 Gas–liquid flow patterns in channel

Fig. 11

Gas–liquid flow patterns in channel (left panel): slug (top), annular (centre), churn (bottom). Right panel: flow regimes obtained from SPH simulation (symbols) in superficial velocities coordinates. Lines and letters mark the generalised flow map from Berna et al. [135]; B Bubbly, DB Dispersed bubbly, S Slug, C Churn, A Annular. Reproduced from [131]

The analysis of flow structures in internal flows is of importance to predict hydraulic losses (and a necessary pumping power), as well as heat transfer (where relevant). Such studies are of direct interest for transportation systems of crude oil (with presence of water and gas in pipelines); they can also be motivated by thermal–hydraulic problems in nuclear engineering. We obtained first, rather qualitative SPH results [131] for a 2D liquid–gas system (the density ratio of 1000) at coarse resolution using the simplest, periodic boundary conditions at the channel inlet and outlet. Then, another 2D analysis was performed in [134]; it concerned a gravity-affected, two-phase flow (the density ratio was equal to 5) in horizontal pipes with inlet and outlet conditions. In their comprehensive study, the Authors reproduced four different flow regimes (mist, dispersed, intermittent and stratified) as well as the transition processes from one flow pattern to another.

Fig. 12

Liquid phase distribution in SPH simulation of annular flow, the impact of micromixing correction: not applied (top), and with $\epsilon = 0.5$ (bottom); liquid particles are in blue, gas particles omitted for clarity; $\text {Re}_g=100, \text {Re}_l=1000$ (Color figure online)

Using the technique of interface area (or length) tracking in SPH, see Sect. 3.1, we are able to track the changes in flow patterns or regimes in a vertical channel flow (no stratification due to gravity). Also, in the course of SPH simulation we checked whether a statistically steady state was reached for a given flow pattern (slug, annular and churn, see the left part of Fig. 11) without a need to recourse to graphical representation of phase distribution in the flow domain. Finally, this technique has allowed us to plot the flow regime maps out of SPH computations [131]. As seen in Fig. 11 (right panel), the agreement with a reference (experimental) map [135] is quite good for slug and churn regimes, less so for annular flow. The latter discrepancy is probably due to a rather coarse SPH resolution, 2D simulations only, and surface tension model imperfection. A natural development direction for this kind of analysis would be to go for a higher resolution simulations in 3D (computer resources permitting), yet keeping in mind the constraints imposed by the fully resolved simulation.

Fig. 13

SPH simulation of annular flow, droplet entrainment mechanisms: roll wave (left), liquid impingement (right). Liquid droplets in blue, gas particles are omitted for clarity (Color figure online)

Fig. 14

Instantaneous film thickness obtained from 2D SPH simulations of annular flow compared to the experimental correlation of Henstock and Hanratty [137] (black line). The micromixing correction parameters: $\epsilon = 0$ (left graph) and $\epsilon = 0.5$ (right graph)

Following this experience, an additional study was performed of annular flow with a higher gas volume fraction and initial conditions chosen specifically for this regime. The SPH computation resulted in a qualitatively correct prediction of the so-called roll wave and liquid impingement mechanisms [136], leading to entrainment of teared-off droplets into the core of the flow, see Fig. 12 and zoomed-in sequences from the solution, Fig. 13.

To validate the SPH simulations of annular flow against experimental data, the liquid film thickness $\delta$ along the walls (normalised by the plane channel hydraulic diameter D) was computed and compared with some experimental correlation. The one of Henstock and Hanratty [137], in the form $\delta /D=f(\rho _g,\rho _l, \mu _g, \mu _l, \text {Re}_g, \text {Re}_l)$, was established for gas–liquid (g-l) flow in a pipe. The outcome is shown in Fig. 14 and the agreement is, a bit surprisingly, better for the simulation with no micromixing correction. This may suggest that more insight is needed or even some reformulation of the correction.

3.4 Wetting phenomena

To account for the presence of a third phase in interfacial flows, be it another immiscible fluid or a solid surface of predetermined wettability, and the resulting triple points (lines) and contact angles, the surface tension modelling needs to be suitably extended [138,139,140,141]. An SPH model for wetting proposed in [64] bears some similarity to the one developed by Breinlinger et al. [139]; another recent proposal [142] has been successfully implemented in the context of free-surface SPH. However, because of the liquid droplet interaction with a gas flow, we rather opted for a multiphase formulation. The main idea was to apply the CSF model of the surface tension term with a modification in the triple point region.

Fig. 15

Sessile droplet on a solid substrate: shape dependence on the contact angle $\theta _D$. Left panel: hydrophilic cases, right panel: hydrophobic ones

As the first results, the droplet shapes on a surface were reported depending on the contact angle $\theta _D$ that, grosso modo, determines the substrate wettability, see Fig. 15. A quantitative outcome of SPH simulations of sessile droplets is presented in terms of their height H and the size w of contact with the wall (the droplet spreading area in 3D). Both quantities can be analytically determined in function of the initial radius $R_0$ of the semi-spherical droplet placed on the wall, the ratio of the gravitational to capillary forces expressed in terms of the Eötvös number Eö $=\rho g R_{0}^{2}/\sigma$, and the contact angle $\theta _D$. The results are shown in Fig. 16 to agree with the asymptotic limit $H_\infty$ of droplet height in no gravity case and with the analytical solution for w and H, respectively.

The model elaborated in [64] produced accurate results for the shape of a sessile droplet on a horizontal surface for a wide range of imposed contact angles (from $15^\circ$ up to $135^\circ$), both with and without gravity. Some modification of the CSF model, meant to smooth the field of colour gradient, allowed us for a more accurate representation of the normal vectors to the interface in the vicinity of the triple point. Given this encouraging outcome on the one hand, and a rather high computational cost overall on the other hand, SPH may be exploited in microfluidics where wettability effects and free-surface meniscus govern the low-Re flow in minichannels, as in the lab-on-a-chip devices [143].

Fig. 16

Sessile droplet shape: comparison of the SPH results (symbols) with analytical solution (lines), 2D case. Left plot: surface tension and gravity dominated regimes for $\theta _D = 50^\circ$. Right plot: no gravity case (Eö $=0$). Reproduced from [64]

Finally in Fig. 17, results are reported from the multiphase SPH simulation of a gas flow-driven droplet motion on a surface. They illustrate qualitative differences between hydrophilic surfaces (the contact angle $\theta _D=30^{\circ }$) and hydrophobic ones ($\theta _D=120^{\circ }$).

Fig. 17

SPH computation of droplet motion, driven by air flow, on a solid substrate. Left panel: initial configuration (passive tracer stripes added to better illustrate the process). Right panel: zoomed snapshots at a later time instant; smearing out ($\theta _D=30^{\circ }$ hydrophilic case, upper plot) or rolling ($\theta _D=120^{\circ }$ hydrophobic case, lower plot). Reproduced from [64]

4 SPH of dispersed flows

As already discussed in Sects. 2.1.2 and 2.4, dispersed flows are only considered here in the two-fluid approach. As a side remark: basically, the trajectory models could also be coupled to the carrier phase velocity field computed in SPH. However, to the best of our knowledge no simulations of this kind have been reported in the literature, in particular with the two-way momentum coupling. Moreover, there is a priori no clear advantage of such an approach except, perhaps, when point particles of the disperse phase would originate from single SPH particles (or small clusters of them) that left their bulk phase, as in the annular flow case, for example, (Fig. 13, upper graphs); see also discussion in Sect. 5.

The numerical modelling and simulation of sediment transport, often done using the two-fluid models, remains a subject of active research. It is of particular interest in environmental hydraulics and hydro-engineering. A practically important application is the prediction of sand deposition or seabed scour in coastal areas, accounting for the interactions with surface waves. As an alternative to better-established grid-based approaches [144], there have been a number of SPH applications to date [21, 26,27,28,29, 145]; another one [130, 146, 147] is reported here.

The first case studied was a continuous discharge of sediment into a static water tank. The SPH simulation setup was 2D and the initial condition is illustrated in Fig. 18 (the upper left panel); the sediment phase (black) enters at the free surface. At a later time instant, the carrier phase velocity (shown in the upper right panel) features characteristic vortical structures due to the flow entrainment by falling sediment. The disperse phase at the same instant (lower plots) is shown together with the water velocity magnitude, juxtaposed with the pressure distribution; only one-half of the computational domain is shown because of the solution symmetry. Although the first simulation results [130] showed a qualitative agreement with experimental data, some issues of the two-fluid SPH formulation were identified. The biggest one was the stability loss over long periods of time and an excessive numerical noise in the pressure field. It was significantly reduced by utilising the $\delta$-SPH model (Sect. 2) which consists in adding a diffusive term to the continuity equation of the carrier phase [113]. In the improved formulation, the pressure noise effect has been mitigated [146, 147] as seen in Fig. 18 (bottom right panel). Moreover, a reasonable similarity was noticed (not shown) between predicted and observed in experiment vortical structures driven by the falling sand and the water–sand interplay.

Fig. 18

The SPH simulation of sand discharge into a water tank. Upper left panel: the initial condition. Upper right panel: vortical structures of sand-induced water flow. In the left half of the bottom plots, sand particles are coloured in black and water particles are coloured with their velocity magnitude. In the right half of the plots, water particles are coloured with the hydrostatic pressure value assigned to them. Left bottom panel: basic SPH variant, right bottom panel: $\delta$-SPH model applied [146] (Color figure online)

The second problem studied was sediment transport in an oscillatory flow in a wave flume. In the SPH simulation, a generic wave-maker was used, i.e. the moving wall block on the right side of the domain. The flow was generated over a flat and wavy (rippled) bed while sediment was continuously poured through the free surface as in the previous case. The outcome of the two-fluid SPH computation of sediment dispersion driven by the wavy free surface in a water flume is shown in Fig. 19; the sediment is black and the water SPH particles are coloured with their velocity magnitude. For testing purposes, the material density ratio was $\rho _d/\rho _f = 1.1$. Only fairly dilute suspensions were considered ($\theta _d < 2\%$). The intended goal was to compare SPH computational results with experimental findings on sediment concentration, near-bed transport velocities and deposition patterns. The possibility of coupling the two-fluid SPH framework for sediment-laden flows with a suitable model of deformable granular bed [24] remains to be considered.

Fig. 19

SPH simulation of sand dumping into a wave flume. The notional sand particles are coloured in black and the water particles are coloured with the value of their velocity magnitude. Arguably, the increase of the sand settling speed drives the local motion of water; this causes a “necking” effect on the sand column which then widens due to the interaction with the bottom. The green/greenish/blue solid block of SPH particles (in predetermined motion) plays the role of a generic wave-maker (Color figure online)

5 Discussion: challenges in multiphase SPH

Phase changes represent an issue specific for multiphase flows. Basically, numerical approach to it goes through a solution of the energy equation (we have not detailed it here) with the latent heat term. Often, it is formulated in terms of enthalpy that reflects the progress of phase transition (melting, boiling, etc.); the temperature needs to be supplemented by the respective phase fraction variable to uniquely define the state of the process. However, the particle nature of SPH causes a major problem for liquid–vapour (and vice versa) phase change due to considerable change in density, typically for water $\rho _l/\rho _v={\mathcal {O}}(10^3)$. Consequently, the mass or volume of an SPH particle undergoing the phase change would evolve by this factor. The situation is generally better in solid–liquid phase transitions where, typically, $\rho _s/\rho _l={\mathcal {O}}(1)$. Sometimes, the density variation upon solidification or melting may even be neglected. Possible difficulties with this kind of processes come from physics, including the onset of natural convection in liquid upon melting, the formation of mushy zones (in particular for metal alloys), thermodynamic non-equilibrium, mesoscopic-scale phenomena, discontinuity of material properties at the front of phase transition, etc. An early work on freezing in SPH is due to Monaghan et al. [148] (no fluid motion, heat conduction only); Cleary [149] modelled die casting processes; recent applications include drop impact with icing [150, 151]. Some very recent papers on solid–liquid phase transition modelling are [73, 152,153,154,155]. Regarding the liquid–vapour transitions, inherently difficult to handle, recent attempts have been reported for boiling [156, 157] and cavitation [158].

Another challenge for multiphase SPH, already mentioned in the paper (Sect. 2.3), is the spurious fragmentation of the interface. Then, the presence of parasitic (spurious currents) is an issue also in the Eulerian approaches to interfacial flows. In some of those methods (LS, PFM) appears also the problem of phase mass loss. In SPH with predetermined masses of particles belonging to individual phases, there is no such concern. However, in specific flow conditions such as annular flow with droplets being teared-off the wall film (Sec. 3.3, Figs. 11 and 12), the small clusters or even single SPH particles detached from their mother phase are no longer physically meaningful [175]. For violent impact flows such as the dam break benchmark, such particles may appear but are rather insignificant for the overall flow picture. Considering the internal flows, in particular with periodic inlet/outlet, disperse-annular flow regimes may feature many such particles present in the system for a long time. A set of single SPH particles in a 2D pipe flow case has been identified as the mist phase [134], but the authors (rightly) labelled it non-realistic. In our opinion, a physically sound SPH simulation of a disperse-annular flow should rather accommodate the idea of point particles, otherwise well-known in the modelling of turbulent dispersed flows [6]. Such particles would no longer be governed by the SPH-type evolution equations; also, their deposition in the liquid film and re-entrainment into the gas core would call for specific submodels.

Let us continue with some general remarks, not restricted to multiphase flows only. Turbulence modelling and computation still remains a challenge. In the realm of Eulerian approaches, the DNS (fully resolved simulations, no turbulence model) is now well mastered as a tool. From the practical standpoint, the insight offered by DNS remains limited by the problem size and computer resources available. As the numerical methods used for DNS need to be of high order for overall efficiency, the Lagrangian particle methods do not seem to be a good choice here. There have been a few papers reporting turbulence simulations using SPH [30, 67, 121, 159], but in several other works tackling high-Re flows the turbulent regime is not explicitly addressed by a model; instead, rather heuristic numerical diffusion terms are applied for a stable computation. In our opinion, this merits more attention. The computational cost could be reduced by employing the LES approach (see [160] for a rough estimate); however, as shown in [67], LES is problematic within SPH framework. Notwithstanding this caveat, some recent works on LES were reported [161].

On a path to increase computational efficiency, GPU computations and adaptive particle resolution are welcome by practitioners [81, 162, 163]. The latter remains a challenge in SPH although recent progress has been reported; see Sect. 2.2.

Concerning theoretical aspects of the SPH method, Hopkins [164] listed a number of fundamental and general concerns (related to WC-SPH as well): suppression of certain fluid-mixing instabilities, appearance of high numerical viscosity in nominally inviscid flows, introduction of noise in otherwise smooth fields and very slow numerical convergence. He then put forward a new proposal based on a kernel discretisation of volume. Partly following these ideas, Kajzer [165, 166] considered a more general class of particle weighted methods [52, 164] and addressed some inherent limitations of the approach, including the so-called partition noise, in terms of its consistency and accuracy with respect to weakly compressible models.

Recalling the famous statement of John Argyris (and a lecture title, back to 1965): “Computer shapes the theory”, this has also been seen in the development of SPH, one of the reasons being its rather high computational cost. The SPH approach, in particular in the WC variant, readily lends itself to a massive parallelisation because of explicit time advancement, no elliptic problems to be solved, and independent loops over particles. The advent of graphics processing units (GPUs) seemed to promise a breakthrough in this respect. Although very useful, the (multi)GPU architecture faces a major difficulty because of the SPH accuracy needs: many particle–particle interactions are necessary within the kernel range as compared to the stencil size in the Eulerian methods. Inter-thread communication (low-bandwidth memory) is one of the factors behind the SPH simulations still being computationally expensive in general, when judged on the problems that can also be tackled using the Eulerian methods. Moreover, large computational “stencils” are needed for more accurate Lagrangian SPH, so the computations may be poorly scalable in comparison with mesh-based methods.

The following table (Table 1) is intended to synthetically recall the milestones in multiphase SPH formulation, already mentioned in Sect. 2, and to tentatively identify the major challenges specific to such flows. The table is by no means exhaustive (it may even lack proper credits and precedence) and reflects a personal perspective of the authors.

Table 1 SPH of multiphase flows: accomplishments and challenges

Switching to a more optimistic note: over the years, many in-house SPH solvers have been created, some of them as a result of collaborative research work. There are a few that evolved into larger, multipurpose software packages for a broader users’ community. We briefly introduce a selection of them, both open source and commercial. A recent example of the former category is an SPH-based multiphysics and multiresolution library SPHinXsys [167]. Among the first solvers to run entirely on graphic cards with CUDA platform was GPUSPH; many references to papers reporting applications of this software are provided on the website (gpusph.org). Another popular software package, well suited for free-surface flows, is DualSPHysics [168, 169] (website: dual.sphysics.org). PySPH is a recent, Python-based solver (website: pythonhosted.org/PySPH), see [170, 171] and references therein; it is unlike the previous ones that are written in intermediate-level programming languages (such as C or C++). Python is a high level, versatile script language of increasing popularity and PySPH is an open-source framework for SPH that supports parallelisation and dynamic load balancing. A very recent, general-purpose oriented solver using WC-SPH is SPHydro [172]; it has been reported in ocean engineering applications, in particular in the FSI context (wave–structure interaction). As this is a rapidly changing field, other solvers appear. An updated (for some time to come, hopefully), yet a non-exhaustive list, is available on the webpage of the SPHERIC community (www.spheric-sph.org/sph-projects-and-codes).

In the framework of weakly compressible approaches to fluid dynamics, Clausen [173] put forward the entropically damped artificial compressibility (EDAC) method. It consists in solving a suitably formulated pressure evolution equation (featuring a diffusive term that significantly damps the oscillations in the pressure field) instead of finding it from the density through an artificial (and usually stiff) equation of state. Let us note in passing that, unlike in the classical AC methods, where the velocity becomes solenoidal upon convergence at each time step (also in unsteady problems), the velocity field in EDAC is not divergence-free. Therefore, as argued in [174], EDAC (notwithstanding the acronym) belongs in fact to the class of WC methods. The EDAC model has been successfully applied to wall-bounded turbulent flow computation [174]: due to the purely parabolic (non-elliptic) type of the governing equations and explicit integration schemes, it readily lends itself to parallelisation, including on GPUs, resulting in a very good computational efficiency. The EDAC method was adopted in SPH by Ramachandran and Puri [171] and implemented in the PySPH package; promising results were reported as compared to the standard WC-SPH model.

SPH is a particle approach, and hence, the problems appear of non-uniformities of the density field computed out of particle positions (which effectively define the particle volumes). Also the artefact of tensile instability manifests itself, in particular in WC-SPH, and various remedies to it have been put forward, e.g. [117]. Still due to its particle nature, a specific feature of the multiphase SPH is that, close to the interphasial surface, some particles of one phase may migrate into the other phase. This was also observed in simulations of annular flow where the droplets became teared-off from the liquid–gas interface [132]. Single SPH particles do not seem to be physically meaningful [175, 176]. It is a standard practice in SPH to ignore such (small clusters of) particles, which results in a mass loss and inadequate treatment of the flow physics. In our opinion, further work is warranted to possibly model these particles as Lagrangian objects that would move, according to their equation of motion, in the bulk of the other phase. In this context, let us note a recent work on the Eulerian VOF method coupled to the Lagrangian tracking of droplets or bubbles produced from interface break-up, together with a “transition algorithm” to re-integrate those elements into their mother phase [177].

Referring to specific application areas, we are of the opinion that fluid–structure interaction (FSI) problems conveniently lend themselves to modelling that would involve SPH [178] (at least as one part of the solver), in both the context of rigid bodies and deformable ones. As an example of such computation, Ulrich et al. [74] reported a comparison of multiresolution SPH and VOF simulations of a rigid cube plunging into water, so necessarily involving a free surface (Fig. 20). Clearly, there is a reasonable agreement of the two numerical approaches, also with the experimental evidence.

Among diverse application fields of SPH, the environmental, hydraulic and ocean engineering [172] appear to be important, due to the free-surface feature often combined with violent impact flows and dynamic pressure loads, FSI problems and multiphysics aspects. A tentative list includes ship hydrodynamics (ship launching, moonpools, sloshing [179,180,181,182,183], green water on decks [184]), wave patterns, breakwaters [121, 185], wave impact on bodies, water entry dynamics (aircraft digging, projectiles, etc.) [120, 163, 186], devices (hydrokinetic turbines, energy converters [187], spillways [188], soil excavation [189], cavitating flows [158]) and natural phenomena (floods, inundations, tsunami waves [190], ice floe melting [152]). Applications from the area of production and process engineering include additive manufacturing [73], welding [153], gearbox lubrication [191], atomisation [192,193,194] and aerosol mechanics [195], two-phase flow and structures in pipes [134] (see also Sect. 3.1). At last, examples are provided related to biomechanics [47, 196,197,198] and multiphysics phenomena such as electro-coalescence [199], mesoscopic systems, surfactants. Arguably, other multiphysics problems are among the potential applications of particle-based methods, along with a growing world apart: the one of computer animation, e.g. [200].

In the context of the two-fluid approach, sediment transport modelling in environmental flows remains a subject of active research and practical significance, including sediment interaction with surface waves and sea currents, its deposition and the seabed scour. In Sect. 4, we recalled some 2D, coarse-resolution results on sediment dynamics in the bulk of water as a first step towards building a comprehensive model of the phenomena involved. As discussed in [147], this may be attempted by coupling the two-fluid SPH model (a mixture with different velocities of the sand and water phases) for sediment-laden flows with another SPH model of deformable granular bed with a specific rheology [25]. Notwithstanding the caveats recalled earlier in this Section, the idea of building a comprehensive, “all inclusive” physical model of the sediment dynamics remains alluring, even though some aspects of such a model, for example, the account of sediment resuspension, seem challenging. The bed particle entrainment has been reviewed and analysed in detail [201]; some works were published regarding the particle hybrid approaches, such as the SPH or MPS methods coupled to DEM (discrete/distinct element model) [21, 22, 86, 202].

Fig. 20

A cube plunging in a water basin: SPH simulation (left), experiment (centre), VOF simulation (right). Experimental study of M. Kraskowski (CTO Gdańsk, Poland). Reproduced from the work of Ulrich et al. [74]

To conclude this section: because of the limited scope of the present overview, we have not mentioned several significant developments in the methodology of the SPH approach such as (listed in a rather disordered manner): Riemann solvers, transport velocity concept, arbitrary Lagrangian–Eulerian (ALE) formulations, particle shifting techniques or symplectic integrators for time-reversible simulations, see [32, 46, 203,204,205,206,207,208,209,210,211] and references therein.

6 Conclusion

In the present paper, we provided an overview of SPH as an alternative modelling approach for multiphase (also free-surface) flows. The method is definitely less elaborated than the better-established Eulerian approaches: its very first applications to multiphase systems in the fluid-mechanical context date back to the 1990 s. There remain some rather fundamental concerns about SPH referring to its convergence and accuracy; nevertheless, a growing body of literature reports successful applications of the method, within intended or attainable accuracy, to engineering problems involving complex flows or multiphysics problems.

We have briefly recalled the basis of the multiphase SPH formalism, such as the density and pressure computation, the account for surface tension forces, including in the presence of solid walls (wettability effects), and illustrated them with examples of results coming (mostly) from our research group. Some major challenges and difficulties were discussed, as the applicability of SPH has, arguably, its limitations.

Although SPH is not as mature as its Eulerian counterparts, it is worth to note continuous and focused efforts of SPHERIC group (Webpage: spheric.org). The group of dedicated researchers forms a relatively large community which identifies and tackles the most important challenges in SPH as well as environmental and industrial applications. A rather optimistic outlook on further development transpires from their collective, ongoing work.