Abstract
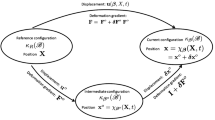
\({\textbf {QR}}\) decomposition-based constitutive relations for hyperelastic materials have attracted great attention from the community of solid mechanics, as hyperelastic models in terms of the distortion tensor \(\varvec{\widetilde{F}}\) have obvious physical meanings. However, there are few works systematically discussing the material parameter identification for \({\textbf {QR}}\) decomposition-based hyperelastic models. In this work, we reformulate the virtual fields method by considering the internal virtual work as the variation of elastic energy caused by virtual displacements. This approach (together with the \({\textbf {QR}}\) decompositions) is more concise and easier to be implemented when compared with the conventional approach, which requires specific stresses, such as Cauchy stress, first or second Piola–Kirchhoff stress, and conjugate virtual strains to calculate the internal virtual work. To validate the reformulated virtual fields method, we derive the Mooney–Rivlin model under the \({\textbf {QR}}\) framework, and then identify its material parameters for incompressible silicone specimens under biaxial tensile tests. The results indicate that the proposed virtual fields method works very well for \({\textbf {QR}}\) decomposition-based models.







Similar content being viewed by others
Notes
The derivation for the IVW of neo-Hookean model is similar (let \(C_{01}=0 \)).
Promma and Grediac used \({\textbf {U}}^{*}\) to denote the virtual displacement, we used \(\delta {\textbf {U}}\) in this section.
References
McLellan, A.: Invariant functions and homogeneous bases of irreducible representations of the crystal point groups, with applications to thermodynamic properties of crystals under strain. J. Phys. C Solid State Phys. 7(18), 3326 (1974)
McLellan, A.: Finite strain coordinates and the stability of solid phases. J. Phys. C Solid State Phys. 9(22), 4083 (1976)
Srinivasa, A.: On the use of the upper triangular (or QR) decomposition for developing constitutive equations for green-elastic materials. Int. J. Eng. Sci. 60, 1–12 (2012)
Ghosh, P., Srinivasa, A.: Development of a finite strain two-network model for shape memory polymers using QR decomposition. Int. J. Eng. Sci. 81, 177–191 (2014)
Freed, A.D., Srinivasa, A.: Logarithmic strain and its material derivative for a QR decomposition of the deformation gradient. Acta Mech. 226(8), 2645–2670 (2015)
Kazerooni, N.A., Srinivasa, A., Freed, A.: Orthotropic-equivalent strain measures and their application to the elastic response of porcine skin. Mech. Res. Commun. 101, 103404 (2019)
Freed, A.D., le Graverend, J.-B., Rajagopal, K.: A decomposition of laplace stretch with applications in inelasticity. Acta Mech. 230(9), 3423–3429 (2019)
Freed, A.D., Zamani, S., Szabó, L., Clayton, J.D.: Laplace stretch: Eulerian and Lagrangian formulations. Z. Angew. Math. Phys. 71, 157 (2020)
Gao, X.-L., Li, Y.: The upper triangular decomposition of the deformation gradient: possible decompositions of the distortion tensor. Acta Mech. 229(5), 1927–1948 (2018)
Li, Y., Gao, X.-L.: Constitutive equations for hyperelastic materials based on the upper triangular decomposition of the deformation gradient. Math. Mech. Solids 24(6), 1785–1799 (2019)
Salamatova, V.Y., Vassilevski, Y.V., Wang, L.: Finite element models of hyperelastic materials based on a new strain measure. Differ. Equ. 54(7), 971–978 (2018)
Annin, B.D., Bagrov, K.V.: Numerical simulation of the hyperelastic material using new strain measure. Acta Mech. 232(5), 1809–1813 (2021)
Freed, A.D., Zamani, S.: On the use of convected coordinate systems in the mechanics of continuous media derived from a QR factorization of F. Int. J. Eng. Sci. 127, 145–161 (2018)
Zamani, S., Paul, S., Kotiya, A.A., Criscione, J.C., Freed, A.D.: Application of QR framework in modeling the constitutive behavior of porcine coronary sinus tissue. Mech. Soft Mater. 3, 7 (2021)
Clayton, J., Freed, A.: A constitutive framework for finite viscoelasticity and damage based on the gram-schmidt decomposition. Acta Mech. 231(8), 3319–3362 (2020)
Clayton, J.D., Freed, A.: A constitutive model for lung mechanics and injury applicable to static, dynamic, and shock loading. Mech. Soft Mater. 2, 3 (2020)
Rivlin, R.S., Saunders, D.: Large elastic deformations of isotropic materials vii experiments on the deformation of rubber. Philos. Trans. R. Soc. Lond. Ser. A Math. Phys. Sci. 243(865), 251–288 (1951)
Ogden, R.W., Saccomandi, G., Sgura, I.: Fitting hyperelastic models to experimental data. Comput. Mech. 34(6), 484–502 (2004)
Kazerooni, N.A., Wang, Z., Srinivasa, A., Criscione, J.: Inferring material parameters from imprecise experiments on soft materials by virtual fields method. Ann. Solid Struct. Mech. 12, 59–72 (2020)
Promma, N., Raka, B., Grediac, M., Toussaint, E., Le Cam, J.-B., Balandraud, X., Hild, F.: Application of the virtual fields method to mechanical characterization of elastomeric materials. Int. J. Solids Struct. 46(3–4), 698–715 (2009)
Tayeb, A., Le Cam, J.B., Grédiac, M., Toussaint, E., Robin, E., Balandraud, X., Canévet, F.: Identifying hyperelastic constitutive parameters with sensitivity-based virtual fields. Strain 57(6), 12397 (2021)
Jiang, M., Wang, Z., Freed, A.D., Moreno, M.R., Erel, V., Dubrowski, A.: Extracting material parameters of silicone elastomers under biaxial tensile tests using virtual fields method and investigating the effect of missing deformation data close to specimen edges on parameter identification. Mech. Adv. Mater. Struct. 29(27), 6421–6435 (2022)
Criscione, J.C., Douglas, A.S., Hunter, W.C.: Physically based strain invariant set for materials exhibiting transversely isotropic behavior. J. Mech. Phys. Solids 49(4), 871–897 (2001)
Criscione, J., Hunter, W.: Kinematics and elasticity framework for materials with two fiber families. Continuum Mech. Thermodyn. 15, 613–628 (2003)
Pierron, F., Grédiac, M.: The Virtual Fields Method: Extracting Constitutive Mechanical Parameters from Full-field Deformation Measurements. Springer, Berlin (2012)
Martins, J., Andrade-Campos, A., Thuillier, S.: Calibration of anisotropic plasticity models using a biaxial test and the virtual fields method. Int. J. Solids Struct. 172, 21–37 (2019)
Marek, A., Davis, F.M., Rossi, M., Pierron, F.: Extension of the sensitivity-based virtual fields to large deformation anisotropic plasticity. Int. J. Mater. Form. 12(3), 457–476 (2019)
Jiang, M., Sridhar, R.L., Robbins, A.B., Freed, A.D., Moreno, M.R.: A versatile biaxial testing platform for soft tissues. J. Mech. Behav. Biomed. Mater. 114, 104144 (2021)
Blaber, J., Adair, B., Antoniou, A.: Ncorr: open-source 2d digital image correlation matlab software. Exp. Mech. 55(6), 1105–1122 (2015)
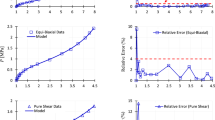
Jiang, M., Dai, J., Dong, G., Wang, Z.: A comparative study of invariant-based hyperelastic models for silicone elastomers under biaxial deformation with the virtual fields method. J. Mech. Behav. Biomed. Mater. 136, 105522 (2022)
Rossi, M., Pierron, F., Štamborská, M.: Application of the virtual fields method to large strain anisotropic plasticity. Int. J. Solids Struct. 97, 322–335 (2016)
Acknowledgements
This work was supported by Anhui Provincial Natural Science Foundation under Grant No. 2108085ME163; the Fundamental Research Funds for the Central Universities under Grant Nos. JZ2020HGQA0183 and JZ2021HGTA0161; Hefei 2021 Innovation and Entrepreneurship Support Plan for Returned Overseas Students; and the Innovation Seed Project Funding and Startup Funding (No. ST2100023) provided by Guangdong Technion - Israel Institute of Technology.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
Appendix A Derivation of IVW based on Promma and Grediac’s approach
Assuming that the material was incompressible and a plane-stress condition, we can have the deformation gradient tensor expressed as
with \(D = F_{11}F_{22}-F_{12}F_{21}\). Therefore, we have
and
According to Eq. 32, Cauchy stress components of Mooney–Rivlin model are
The first Piola–Kirchhoff stress \(\textbf{P}\) is derived from Cauchy stress tensor \(\varvec{\sigma }\) using the following expression:
with \(J=1\) for incompressible materials. We obtain the first Piola–Kirchhoff stress whose components are expressed as below
The derivative of virtual displacementFootnote 2 is written as follows:
The virtual displacement field \(\delta {\textbf {u}}\) is independent of the actual displacement field \({\textbf {u}}\) and can be expressed in terms of spatial coordinates or material coordinates. Therefore, we have \(\delta {\textbf {U}} = \delta {\textbf {u}} \)
Therefore, the IVW for a single mesh element within the body of the specimen is written as follows:
After plugging the components of the first Piola–Kirchhoff stress (Eq. A.6) into the above equation, we can find the formulation of IVW for hyperelastic materials based on the conventional VFM proposed by Promma and Grediac [20] is equivalent to the formulation of IVW in VEE-VFM (Eq. 13).
Appendix B Detailed expression of \(\delta \varvec{\widetilde{F}}\)
with
with
with
with
Appendix C Incompressibility justification
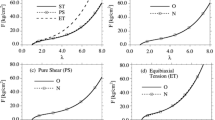
Uniaxial tensile tests were performed on rectangular silicone elastomer. Three specimens were tested up to 60% strain under a strain rate of 1%/s. Ncorr, a Matlab-based digital image correlation software, was used for strain measurement across the surface of the specimens. A rectangular ROI which was far away from the clamps was selected for data analysis. The strain within this region was uniformly distributed. Details about the testing protocol can be found in this paper [28]. The stretch ratio along the stretching direction (\(\lambda _x\)) and stretch ratio across the stretching direction (\(\lambda _y\)) were extracted and averaged over the selected ROI. Since specimens were under uniaxial tension, we assumed that \(\lambda _y = \lambda _z\). Therefore, the ratio of the current volume over the initial volume was calculated as \(\lambda _x*{\lambda _y}^2\). Figure 8 shows that the ratio between the current and initial volumes slightly increases with the stretch ratio. The maximum change of the volume occurred in the last deformation step, which was about 0.46%. This small difference can be considered negligible. Therefore, the material can be assumed to be incompressible.
Appendix D Parameter identification with VEE-VFM for Mooney–Rivlin model under polar decomposition
After extracting the full-field displacement data and forming triangular mesh elements based on nodal positions, the deformation gradient and virtual strain can be calculated respectively. The integral of the IVW for a hyperelastic model under polar decomposition in Eq. 12 can be approximated by a discrete sum as follows
where \(n_e\) represents the total number of mesh elements; and \(A_i\) and \(t_i\) represent the area and the thickness of a specific element under the reference configuration, which do not depend on time; W is the strain energy density function of the hyperelastic material. Note that \(\delta W\) for Mooney–Rivlin model under the polar decomposition is expressed as \(C_{10}\delta I_1 + C_{01}\delta I_2\). \(\delta I_1\) and \(\delta I_2\) can be calculated based on Eq. 15.
For each deformation step k, we can construct one virtual field \({\textbf {U}}^{*}_k\). According to the principle of virtual work, we have
where \(\sum _{i=1}^{n_e} \delta W({\textbf {U}}^{*}_k) \cdot A_it_i \) represents the sum of the IVW of all the mesh elements, and \(\delta W_{ext}({\textbf {U}}^{*}_k)\) represents the EVW. In the case of Mooney–Rivlin model, \(\delta W({\textbf {U}}^{*}_k)\) is expressed as
Therefore, we can have
Note that we constructed three virtual fields in this paper. The rest of the procedure to identify material parameters is the same as that described in Sect. 3.3.
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Jiang, M., Du, X., Srinivasa, A. et al. Reformulation of the virtual fields method using the variation of elastic energy for parameter identification of \({\textbf {QR}}\) decomposition-based hyperelastic models. Acta Mech 234, 4629–4647 (2023). https://doi.org/10.1007/s00707-023-03626-y
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00707-023-03626-y