1 Introduction

This is a continuation of the paper [12], where we studied some mathematical consequences of the constitutive stress–strain relation for hypoplastic granular materials like cohesionless soil or broken rock. The constitutive law is of the rate type, incrementally non-linear, and it is based on the hypoplastic concept proposed by Kolymbas [35]. Compared to other types of nonlinear constitutive equations, e.g. for hyperelastic and hypoelastic material laws, the hypoplastic constitutive relations are not differentiable at zero strain rate. This permits the constitutive modelling of different stiffnesses for loading and unloading typical for inelastic materials. In contrast to the classical elastoplastic concept, the strain in the theory of hypoplasticity is not decomposed into elastic and plastic parts, and there is no need to introduce additional functions to model the transition from elasticity to plasticity on monotone loading or unloading paths. Detailed discussions about physical aspects of hypoplastic models can be found for instance in [25, 37, 43], their response to cycling loading is studied in [14, 38, 47], shear localization in [4, 11, 15, 22, 29], critical states in [5, 7, 53], behaviour under undrained condition in [44], creep and stress relaxation in [6, 9, 40, 46], grain fragmentation in [8, 13], extension to a micropolar continuum in [29, 30], and thermodynamic aspects in [32, 48, 49].

Other typical representatives for incrementally non-linear constitutive equations are for instance the Armstrong-Frederick model [2] as a hypoplastic extension of the von Mises model for plasticity, the endochronic model by Valanis [51], the octolinear model by Darve [20, 21], the CLoE model by Chambon et al. [16], and the barodesy model by Kolymbas [36]. Variational approaches to modelling granular and multiphase media can be found for instance in [1, 33, 39].

There is a large number of investigations devoted to the properties of the stress paths under a monotonic proportional deformation path. Goldscheider [23] formulated two rules saying (a) that a proportional deformation path starting from a nearly stress-free state results in a proportional stress path, and (b) that a proportional deformation path starting from an arbitrary stress state asymptotically converges to the same proportional stress path as the one obtained for the initially stress-free state. These asymptotic properties are an intrinsic feature of frictional granular materials also confirmed by further experiments, e.g., [19, 50], and numerical simulations using the discrete element method, e.g., [31, 41]. This feature can be interpreted by fading memory of the material on the initial state [26]. The asymptotic behaviour of the stress path for proportional deformation has a great importance for constitutive modelling of frictional granular materials. This is, for instance, the basic concept of the framework of barodesy [45] and it is also an intrinsic feature in hypoplasticity [25, 27, 34, 42, 43, 46]. In hypoplasticity, asymptotic properties were numerically investigated by Kolymbas [34] and a mathematical criterion was proposed first by Niemunis [46].

In [12], we have proposed a different strategy by considering the strain–stress law under a given proportional strain trajectory as a nonlinear differential equation for the stress. To this end, a simplified version of the hypoplastic model by Gudehus [24] and Bauer [3] was considered. For the sake of simplicity the pressure dependent properties of granular materials described in [3, 24] were omitted, so that only six material parameters remain in the present model. Note that the same simplified version can also be obtained from the hypoplastic model by von Wolffersdorff [52] as shown in [10]. The solution of the corresponding non-linear problem was found in closed form. In this way we made also a close link to barodesy models [36]. The exact solution provided in [12] made it possible to describe analytically various scenarios of the behaviour of stress paths obtained from monotonic proportional compression, extension, and isochoric deformations. The latter leads to stress limit states or the so-called critical stress states, which can be represented by a conical surface in the space of principal stresses. In particular, we have identified the domain of the constitutive parameters which guarantee that for proportional deformation paths the corresponding stress path starting from an arbitrary initial stress state are asymptotically stable.

The goal of the present paper is to study the phenomenon of ratchetting (that is, the shift of the strain cycles under periodic loading and unloading stress cycles) resulting from the simplified hypoplastic model interpreted as a stress-controlled element test. In its original simplified form [12], the theoretical ratchetting would be infinite, which is not in agreement with experimental observations. This is due to the fact that the influence of the change of the void ratio of the granular material on the incremental stiffness is neglected there. Similarly to the hypoplastic version proposed in [3, 24], we therefore assume here that the non-linear part of the constitutive law contains a multiplier depending on the current void ratio with the property that it vanishes if the void ratio reaches the most condensed admissible state. Herein, the current void ratio, which is defined as the ratio of the volume of the void space to the volume of the solid material, is considered as a state quantity in the constitutive model. In addition, the stress rate obtained from the constitutive equation is scaled by a factor which, for densification of the material, tends to infinity and thus the material becomes asymptotically rigid. For granular materials with incompressible grains the evolution of the void ratio itself can be expressed as a function of the strain rate by virtue of the mass conservation principle. Since we are in the stress-controlled case, the strain rate is the unknown of the problem and has to be found as a solution of a system of differential equations. Unlike in the strain-controlled case, the solution is not found in closed form and has to be computed numerically. On the other hand, we prove that the strain paths subjected to periodic loading-unloading stress cycles converge to an equilibrium independently of whether the proportional stress paths are isotropic or not.

The paper is organized as follows. In Sect. 1, we present the constitutive model used and derive the differential equations which are studied in the sequel. The case of isotropic stress cycles is investigated in detail in Sect. 2. The convergence of the strain trajectory toward the equilibrium when the number of the loading-unloading cycles tends to infinity as well as an estimate of the speed of convergence are proved in Sect. 3. Sect. 4 is devoted to the case of anisotropic stress cycles and we show that the differential equation describing the process has the same asymptotical properties observed in the isotropic case. Some numerical tests are shown in Sect. 5.

2 The constitutive model

In what follows we study the extension of the constitutive model from [12], accounting only for coaxial deformations on the element level, i.e. the case when the direction of principal stresses coincides with the direction of the corresponding principal strains. In this case, the objective stress rate equals the material time derivative of the Cauchy stress, herein denoted by \({\dot{\varvec{\sigma }}}(t)\). Then the constitutive model that we consider to describe the relation between \({\dot{\varvec{\sigma }}}(t)\) and the strain rate tensor \({\dot{\varvec{\varepsilon }}}(t)\) is governed by the following equation

$$\begin{aligned} {\dot{\varvec{\sigma }}}(t) = c_1(t)\left( L(\varvec{\sigma }(t)):{\dot{\varvec{\varepsilon }}}(t) + f(t) N(\varvec{\sigma }(t))\Vert {\dot{\varvec{\varepsilon }}}(t)\Vert \right) , \end{aligned}$$
(1.1)

where \(c_1(t)<0\) and \(f(t)\ge 0\) are given in terms of the current void ratio of the granular material in a sense that will be made more precise below. We further assume that \(L(\varvec{\sigma })\) is a fourth order tensor and \(N(\varvec{\sigma })\) is a second order tensor of the form

$$\begin{aligned} L(\varvec{\sigma })= & {} a^2 \textrm{tr}\,\varvec{\sigma }{\textbf{I}}_4 + \frac{1}{\textrm{tr}\,\varvec{\sigma }}\,\varvec{\sigma }\otimes \varvec{\sigma }, \end{aligned}$$
(1.2)
$$\begin{aligned} N(\varvec{\sigma })= & {} a \left( 2\varvec{\sigma }- \frac{1}{3} \textrm{tr}\,\varvec{\sigma }{\textbf{I}}\right) ,\end{aligned}$$
(1.3)
$$\begin{aligned} {\textbf{I}}= & {} \left( \begin{array}{ccc} {1}&{}\,\,{0}&{}\,\,{0}\\ {0}&{}\,\,{1}&{}\,\,{0}\\ {0}&{}\,\,{0}&{}\,\,{1}\\ \end{array}\right) \end{aligned}$$
(1.4)

under the condition that the trace \(\textrm{tr}\,\varvec{\sigma }\) of \(\varvec{\sigma }\) does not vanish. We denote by \({\textbf{I}}_4\) the unit fourth order tensor, and a is assumed to be a material constant. The incrementally non-linear character of the constitutive equation (1.1) ensures the modelling of inelastic and dissipative material properties. For the case of coaxial deformations, the constitutive equation (1.1) is not restricted to problems of small deformations. Besides, the constitutive equation (1.1) is rate independent and, consequently, invariant with respect to an arbitrary time transformation. Therefore, the variable t need not be necessarily interpreted here as physical time, but rather as an abstract monotonically increasing parameter within an interval \(t \in [b,b+T]\). In our case, as we shall see in (2.6), it will be measured in terms of the stress variation. For our purposes we denote by \(\left\langle \cdot , \cdot \right\rangle \) the canonical scalar product “:” in \({\mathbb {R}}^{3\times 3}\) and, with the help of (1.2)–(1.4), the evolution equation (1.1) can be written in the form

$$\begin{aligned} {\dot{\varvec{\sigma }}} = c_1\left( a^2 \left\langle \varvec{\sigma },{\textbf{I}} \right\rangle {\dot{\varvec{\varepsilon }}} + \left\langle \varvec{\sigma }, {\dot{\varvec{\varepsilon }}} \right\rangle \frac{\varvec{\sigma }}{{\left\langle \varvec{\sigma },{\textbf{I}} \right\rangle }}+a f\Vert {\dot{\varvec{\varepsilon }}}\Vert \left( 2\varvec{\sigma }- \frac{1}{3} \left\langle \varvec{\sigma },{\textbf{I}} \right\rangle {\textbf{I}}\right) \right) , \end{aligned}$$
(1.5)

where, in accordance to [5], f is given as a function of the void ratio e(t) by

$$\begin{aligned} f(t) = f(e(t)):= \left( \frac{e(t) - e_d}{e_c - e_d}\right) ^\alpha , \end{aligned}$$
(1.6)

the function \(c_1\) is assumed to depend on e(t) in the form

$$\begin{aligned} c_1(t) = c_1(e(t)) = -{\bar{c}} \left( e(t) - e_d\right) ^{-\beta }, \end{aligned}$$
(1.7)

and the equations account for six material constants, namely,

$$\begin{aligned} \{a, e_d, e_c, \alpha ,\bar{c}, \beta \}. \end{aligned}$$
(1.8)

Moreover, for granular materials with incompressible particle density the evolution of the void ratio can be computed from the mass balance equation

$$\begin{aligned} \dot{e}(t) = (1+e(t))\left\langle {\dot{\varvec{\varepsilon }}}(t),{\textbf{I}} \right\rangle . \end{aligned}$$
(1.9)

In the density function (1.6) the current value of the void ratio, e(t), is related to the critical void ratio \(e_c\) and minimum void ratio \(e_d\) in such a way that for \(e(t)=e_d\) the value of function f(e(t)) becomes zero. The parameters \(e_c> e_d >0\) and \(\alpha >0\) in (1.6) are assumed to be constant. The idea is to derive from the identities (1.5)–(1.9) a differential equation for the unknown function e(t). We need to check that we have \(e(t) > e_d\) during the whole process to make formulas (1.6) and (1.7) meaningful.

Besides, we assume the constants \({\bar{c}}>0\) and \(\beta > 1\), meaning that the material becomes rigid when e(t) asymptotically converges to \(e_d\).

The stress-controlled proportional loading consists in choosing a fixed tensor

$$\begin{aligned} {\textbf{S}}= \left( \begin{array}{ccc} {S_{11}}&{}\,\,{0}&{}\,\,{0}\\ {0}&{}\,\,{S_{22}}&{}\,\,{0}\\ {0}&{}\,\,{0}&{}\,\,{S_{33}}\\ \end{array}\right) \end{aligned}$$
(1.10)

satisfying the condition \(\textrm{tr}\,{\textbf{S}}< 0\), and assuming \(\varvec{\sigma }(t)\) in the form

$$\begin{aligned} \varvec{\sigma }(t) = \sigma (t) {\textbf{S}}, \end{aligned}$$
(1.11)

where \(\sigma : [b,b+T] \rightarrow (0,\infty )\) is a given monotonic scalar function of the variable \(t\in [b,b+T]\). This is what we call a proportional loading if \(\sigma \) is increasing, and proportional unloading if \(\sigma \) is decreasing. Let us note that for a cohesionless granular material, only negative principal stresses are physically admissible, i.e., all elements in the diagonal of the tensor \({\textbf{S}}\) must be negative. These assumptions ensure that we have \(\dot{\sigma }_{11}<0\), \(\dot{\sigma }_{22}<0\), \(\dot{\sigma }_{33}<0\) for the compression phase and \(\dot{\sigma }_{11}>0\), \(\dot{\sigma }_{22}>0\), \(\dot{\sigma }_{33}>0\) for the extension phase. In view of (1.11), we rewrite Eq. (1.5) as

$$\begin{aligned} {\dot{\sigma }}(t){\textbf{S}}= c_1(t)\sigma (t)\left( a^2 \left\langle {\textbf{S}},{\textbf{I}} \right\rangle {\dot{\varvec{\varepsilon }}}(t) + \frac{1}{\left\langle {\textbf{S}},{\textbf{I}} \right\rangle }\left\langle {\textbf{S}},{\dot{\varvec{\varepsilon }}}(t) \right\rangle {\textbf{S}}+ a f(t) \Vert {\dot{\varvec{\varepsilon }}}(t)\Vert \left( 2{\textbf{S}}- \frac{1}{3} \left\langle {\textbf{S}},{\textbf{I}} \right\rangle {\textbf{I}}\right) \right) . \end{aligned}$$
(1.12)

In Sect. 2 we first consider the isotropic case, while a more general case will be studied in Sect. 4.

3 The case of isotropic stress cycles

Assume for the moment that the condition

$$\begin{aligned} f(t)\ = f(e(t))\ < \frac{1+3a^2}{\sqrt{3}\, a} \end{aligned}$$
(2.1)

holds for all \(t \in [b,b+T]\). The isotropic case is characterized by the choice \({\textbf{S}}= -{\textbf{I}}\); therefore, equation (1.12) corresponds to

$$\begin{aligned} {\dot{\sigma }}(t){\textbf{I}}= c_1(t)\sigma (t)\left( 3 a^2 {\dot{\varvec{\varepsilon }}}(t) + \frac{1}{3}\left\langle {\dot{\varvec{\varepsilon }}}(t),{\textbf{I}} \right\rangle {\textbf{I}}+ a f(t) \Vert {\dot{\varvec{\varepsilon }}}(t)\Vert {\textbf{I}}\right) . \end{aligned}$$
(2.2)

Taking the scalar product with \({\textbf{I}}\) we get

$$\begin{aligned} 3{\dot{\sigma }}(t) = c_1(t)\sigma (t)\left( 3 a^2 \left\langle {\dot{\varvec{\varepsilon }}}(t),{\textbf{I}} \right\rangle + \left\langle {\dot{\varvec{\varepsilon }}}(t),{\textbf{I}} \right\rangle + 3a f(t) \Vert {\dot{\varvec{\varepsilon }}}(t)\Vert \right) , \end{aligned}$$
(2.3)

wherefrom we obtain

$$\begin{aligned} a f(t) \Vert {\dot{\varvec{\varepsilon }}}(t)\Vert = \frac{{\dot{\sigma }}(t)}{c_1(t)\sigma (t)}-\left( a^2+\frac{1}{3}\right) \left\langle {\dot{\varvec{\varepsilon }}}(t),{\textbf{I}} \right\rangle . \end{aligned}$$

Inserting the identity above in (2.2) we can see that

$$\begin{aligned} {\dot{\varvec{\varepsilon }}}(t)=\frac{1}{3}\left\langle {\dot{\varvec{\varepsilon }}}(t),{\textbf{I}} \right\rangle {\textbf{I}},\quad \Vert {\dot{\varvec{\varepsilon }}}(t)\Vert =\pm \frac{1}{\sqrt{3}}\left\langle {\dot{\varvec{\varepsilon }}}(t),{\textbf{I}} \right\rangle . \end{aligned}$$
(2.4)

Recalling that \(c_1(t)<0\), for the loading as \({\dot{\sigma }}(t)>0\), from (2.3) together with (2.4) and (2.1) it follows:

$$\begin{aligned} 3{\dot{\sigma }}(t) =c_1(t) \sigma (t) (3a^2 + 1 - \sqrt{3}a\,f(t)) \left\langle {\dot{\varvec{\varepsilon }}}(t),{\textbf{I}} \right\rangle , \end{aligned}$$

whereas for the unloading as \({\dot{\sigma }}(t)<0\) respectively

$$\begin{aligned} 3{\dot{\sigma }}(t) =c_1(t) \sigma (t) (3a^2 + 1 + \sqrt{3}a\,f(t)) \left\langle {\dot{\varvec{\varepsilon }}}(t),{\textbf{I}} \right\rangle . \end{aligned}$$

Therefore, by using (1.9) for \(\left\langle {\dot{\varvec{\varepsilon }}}(t),{\textbf{I}} \right\rangle \) we obtain the following differential equation for e(t)

$$\begin{aligned} \frac{\dot{e}(t)}{1+e(t)}\, c_1(e(t))(1+3a^2 - \,\textrm{sign}({\dot{\sigma }}(t))\, \sqrt{3}a\,f(e(t)))= \frac{3{\dot{\sigma }}(t)}{\sigma (t)}, \end{aligned}$$
(2.5)

where \(\,\textrm{sign}\) denotes the sign function.

Let us consider now a periodically oscillating function \(\sigma \) between some fixed values \(0<\sigma ^\flat <\sigma ^\sharp \). More specifically, we put \(T= \log (\sigma ^\sharp ) - \log (\sigma ^\flat )\), \(t_k = kT\) for \(k =0,1,2, \dots \), and define

$$\begin{aligned} \sigma (t) = \sigma ^\flat \,\textrm{e}^{t - t_{2j}} \ \text{ for } \ t\in (t_{2j}, t_{2j+1}), \quad \sigma (t) = \sigma ^\sharp \,\textrm{e}^{t_{2j+1} - t} \ \text{ for } \ t\in (t_{2j+1}, t_{2j+2}). \end{aligned}$$
(2.6)

Note that with this choice of a periodic function the right-hand side of (2.5) no longer depends on t which is rather advantageous for the analysis to be carried out in the sequel. Indeed, for \(\sigma \) as in (2.6) we have \(3{\dot{\sigma }}(t)/\sigma (t) =3\) for \(t\in (t_{2j}, t_{2j+1})\), and \(3{\dot{\sigma }}(t)/\sigma (t) =-3\) for \(t\in (t_{2j+1}, t_{2j+2})\) in (2.5) as \(j =0,1,2, \dots \) We define the functions

$$\begin{aligned} h(u)&= -\frac{(1+3a^2) c_1(u+e_d)}{1+e_d+u} = \frac{{\bar{c}}(1+3a^2)}{(1+e_d+u)\,u^\beta }, \end{aligned}$$
(2.7)
$$\begin{aligned} g(u)&= -\frac{\sqrt{3}\,a c_1(u+e_d)\, f(u+e_d)}{1+e_d+u} = \frac{\sqrt{3}\,a {\bar{c}} (e_c - e_d)^{-\alpha }}{(1+e_d+u)\,u^{\beta -\alpha }} \end{aligned}$$
(2.8)

of a new variable \(u = e-e_d > 0\). Then Problem (2.5) consists in integrating for \(j= 0,1,2,\dots \) the system

$$\begin{aligned} \dot{u}(t)(h(u(t)) - g(u(t)))&= -3 \quad \text{ for } \ t \in (t_{2j}, t_{2j+1}), \end{aligned}$$
(2.9)
$$\begin{aligned} \dot{u}(t)(h(u(t)) + g(u(t)))&= 3 \quad \text{ for } \ t\in (t_{2j+1}, t_{2j+2}), \end{aligned}$$
(2.10)

or, equivalently, putting

$$\begin{aligned} G(u) = \int _0^u g(v)\,\textrm{d}v,\quad H(u) = -\int _u^\infty h(v)\,\textrm{d}v\ \text{ for } \ u>0, \end{aligned}$$

problem (2.9) and (2.10) is of the form

$$\begin{aligned} \frac{\,\textrm{d}}{\,\textrm{d}t} \left( H(u(t)) - G(u(t))\right)&= -3 \quad \text{ for } \ t \in (t_{2j}, t_{2j+1}),\end{aligned}$$
(2.11)
$$\begin{aligned} \frac{\,\textrm{d}}{\,\textrm{d}t} \left( H(u(t)) + G(u(t))\right)&= 3\quad \text{ for } \ t\in (t_{2j+1}, t_{2j+2}). \end{aligned}$$
(2.12)

4 Convergence

We first note that, since h in (2.7) and g in (2.8) are positive for \(u>0\), both H and G are increasing in \((0,\infty )\), \(G(0) = 0\), and we have

$$\begin{aligned} \lim _{u\rightarrow 0+} H(u) = -\infty ,\qquad \lim _{u\rightarrow \infty } H(u) = 0. \end{aligned}$$
(3.1)

We shall see below that the convergence is guaranteed as long as the function \(H-G\) is increasing. This is, however, not the case on the whole half-line \((0,\infty )\). Indeed, we have

$$\begin{aligned} \frac{\,\textrm{d}}{\,\textrm{d}u} \left( H - G\right) = h(u) - g(u) = {\bar{c}} \frac{(1+3a^2)u^{-\alpha } -\sqrt{3}\,a (e_c - e_d)^{-\alpha }}{(1+e_d+u)\,u^{\beta -\alpha }}, \end{aligned}$$

which is positive if and only if

$$\begin{aligned} 0< u < U_0:= (e_c - e_d)\left( \frac{1+3a^2}{\sqrt{3}\,a }\right) ^{1/\alpha }. \end{aligned}$$
(3.2)

Put \(u_k = u(t_k)\) for \(k=0,1,\dots \). Integrating (2.11) and (2.12) we get the recurrent relations for \(j=0,1,2,\dots \)

$$\begin{aligned} H(u_{2j+1}) - H(u_{2j}) - \left( G(u_{2j+1}) - G(u_{2j})\right)&= -3T, \end{aligned}$$
(3.3)
$$\begin{aligned} H(u_{2j+2}) - H(u_{2j+1}) + G(u_{2j+2}) - G(u_{2j+1})&= 3T, \end{aligned}$$
(3.4)

with an initial condition \(u_0 > 0\). We prove the following result.

Proposition 31

Let \(u_0 \in (0, U_0)\) be given with \(U_0\) defined by (3.2). Then the sequences \(\{u_{2j+1}\}\) defined by (3.3), and \(\{u_{2j+2}\}\) defined by (3.4) are both decreasing and \(\lim _{j\rightarrow \infty } u_{2j} = 0\), \(\lim _{j\rightarrow \infty } u_{2j+1} = 0\).

Proof Assume that \(u_{2j} \in (0,U_0)\) for some j. The hypotheses ensure that \(\,\textrm{d}(H\pm G)/\,\textrm{d}u>0\) in \((0,U_0)\), thus it follows from (2.11) and (2.12) that u is decreasing in \((t_{2j}, t_{2j+1})\), increasing in \((t_{2j-1}, t_{2j})\), and consequently

$$\begin{aligned} u_{2j}> u_{2j+1}, \quad u_{2j} > u_{2j-1}. \end{aligned}$$
(3.5)

Summing (3.3) and (3.4) we obtain

$$\begin{aligned} H(u_{2j+2}) - H(u_{2j}) + G(u_{2j+2}) - G(u_{2j}) =2\left( G(u_{2j+1}) - G(u_{2j})\right) <0, \end{aligned}$$
(3.6)

therefore

$$\begin{aligned} H(u_{2j+2})+G(u_{2j+2})< H(u_{2j})+G(u_{2j}). \end{aligned}$$

Recalling that \(H+G\) is increasing and \(\lim _{u\rightarrow 0+}(H+G)(u) = -\infty \), we must have \(0< u_{2j+2}<u_{2j}\). The sequence \(\{u_{2j}\}\) is thus decreasing and contained in the interval \((0,U_0)\). There exists therefore \({\bar{u}} \in [0,U_0)\) such that \(\lim _{j\rightarrow \infty } u_{2j} = {\bar{u}}\). We now rewrite (3.4) as

$$\begin{aligned} H(u_{2j}) - H(u_{2j-1}) + G(u_{2j}) - G(u_{2j-1}) = 3T, \end{aligned}$$

and adding this identity to (3.3) yields by virtue of (3.5) that

$$\begin{aligned} H(u_{2j+1}) - H(u_{2j-1}) - (G(u_{2j+1}) - G(u_{2j-1})) =2\left( G(u_{2j-1}) - G(u_{2j})\right) <0. \end{aligned}$$
(3.7)

Since \(H-G\) is increasing in \((0,U_0)\), we have \(0< u_{2j+1}<u_{2j-1}\), in other words, the sequence \(\{u_{2j+1}\}\) is decreasing. Hence, using also (3.5), we see that it converges to some \(0\le {\underline{u}}\le {\bar{u}}\). Assume first that \(\underline{u} > 0\). We can pass to the limit in (3.3) and (3.4) and obtain

$$\begin{aligned} H({\underline{u}}) - H({\bar{u}}) - \left( G({\underline{u}}) - G({\bar{u}})\right)&= -3T, \end{aligned}$$
(3.8)
$$\begin{aligned} H({\bar{u}}) - H({\underline{u}}) + \left( G({\bar{u}}) - G({\underline{u}})\right)&= 3T. \end{aligned}$$
(3.9)

Summing up (3.8) and (3.9) we obtain \(G({\bar{u}}) = G({\underline{u}})\), hence \({\bar{u}} ={\underline{u}}\) and \(H({\bar{u}}) = H({\underline{u}})\), which contradicts (3.9). We thus have \({\underline{u}} = 0\), and from (3.3) and from the boundedness of G it follows that \(H(u_{2j}) \rightarrow -\infty \), hence \({\underline{u}}={\bar{u}}=0\) and the proof is complete. \(\square \)

Recall that the system (3.3)–(3.4) has been derived under the condition (2.1) provided \(u_0 < U_0\). It remains to check a posteriori that its solution satisfies (2.1). Indeed, we have \(0< u(t) < U_0\) during the whole evolution, so that by (1.6) and (3.2) we have

$$\begin{aligned} f(t) = \left( \frac{u(t)}{e_c - e_d}\right) ^\alpha < \left( \frac{U_0}{e_c - e_d}\right) ^\alpha = \frac{1+3a^2}{\sqrt{3} a}, \end{aligned}$$

which is precisely (2.1).

The condition \(u_0 < U_0\) is not a real restriction. It was shown for example in [12] that physically meaningful values of the parameter a are \(1/(2\sqrt{3})< a < 1/\sqrt{3}\). In this range, the function \(\gamma (a) = (1+3a^2)/(\sqrt{3}a)\) is decreasing, hence, \(2=\gamma (1/\sqrt{3})\le \gamma (a)\le \gamma (1/2\sqrt{3}) = 5/2\). In terms of the initial void ratio e(0), this can be interpreted by virtue of (3.2) as

$$\begin{aligned} e(0) - e_d \le \left( \frac{5}{2}\right) ^{1/\alpha }(e_c - e_d). \end{aligned}$$
(3.10)

Typical values of \(\alpha \) for sands lie within the range of \(0.1\le \alpha \le 0.3\), e.g. [3, 28]. Therefore, in practice, the factor on right-hand side of (3.10) can never be exceeded and does not impose a real restriction in the modelling of materials like sand. For other granular materials the relevant range for values of \(\alpha \) may be different depending on particle shape and particle size distribution.

To estimate the convergence rate, we first rewrite (3.3) and (3.4) in the form for \(j=1,2,\dots \)

$$\begin{aligned} H(u_{2j+1}) - H(u_{2j}) - \left( G(u_{2j+1}) - G(u_{2j})\right)&= -3T, \end{aligned}$$
(3.11)
$$\begin{aligned} H(u_{2j}) - H(u_{2j-1}) + G(u_{2j}) - G(u_{2j-1})&= 3T. \end{aligned}$$
(3.12)

Summing up the two equations and using (3.12) we get

$$\begin{aligned} (H-G)(u_{2j+1}) - (H-G)(u_{2j-1})&=2\left( G(u_{2j-1}) - G(u_{2j})\right) \nonumber \\&= \frac{-6T(G(u_{2j-1}) - G(u_{2j}))}{(H+G)(u_{2j-1}) - (H+G)(u_{2j})}\nonumber \\&= \frac{-6T g(u)}{h(u)+g(u)} \end{aligned}$$
(3.13)

where the last equality holds true for some \(u \in [u_{2j-1}, u_{2j}]\) thanks to the Mean Value Theorem. By (2.7), (2.8), and (3.2) we have

$$\begin{aligned} \frac{g(u)}{h(u)+g(u)} = \frac{\sqrt{3}\,a (e_c - e_d)^{-\alpha }}{(1+3a^2)u^{-\alpha } + \sqrt{3}\,a (e_c - e_d)^{-\alpha }} = \frac{u^\alpha }{u^\alpha + U_0^\alpha }. \end{aligned}$$
(3.14)

We can restrict ourselves to the case \(u< U_0\) and obtain from (3.14) the upper bound

$$\begin{aligned} \frac{-6T g(u)}{h(u)+g(u)} \le -M u^\alpha \le -M u_{2j-1}^\alpha \quad \text{ for } \ M = \frac{3T}{U_0^\alpha }. \end{aligned}$$

Let us estimate the decay rate of H(u) as \(u \rightarrow 0+\). By (2.7) we have

$$\begin{aligned} h(u) = \frac{q}{r+u} u^{-\beta } \end{aligned}$$
(3.15)

with \(q = {\bar{c}}(1+3a^2)\), \(r = 1+e_d\). For \(x \in (0,U_0)\) we thus obtain

$$\begin{aligned} H(x) = -\int _x^{U_0} \frac{q}{r+u} u^{-\beta }\,\textrm{d}u - \int _{U_0}^\infty \frac{q}{r+u} u^{-\beta }\,\textrm{d}u. \end{aligned}$$
(3.16)

The two integrals in (3.16) have to be treated separately. For \(u \in (0,U_0)\), we have \(r+u < r+U_0\), while for \(u\ge U_0\) we use the formula \(r+u \le (\frac{r}{U_0} +1)u\). We thus get

$$\begin{aligned} H(x)&\le -\int _x^{U_0} \frac{q}{r+U_0} u^{-\beta }\,\textrm{d}u - \int _{U_0}^\infty \frac{qU_0}{r+U_0} u^{-1-\beta }\,\textrm{d}u\\&= -\frac{q}{r+U_0}\left( \left[ \frac{1}{1-\beta } u^{1-\beta }\right] _x^{U_0} - U_0 \left[ \frac{1}{\beta } u^{-\beta }\right] _{U_0}^\infty \right) \\&= -\frac{q}{r+U_0}\left( \frac{1}{\beta -1} x^{1-\beta } - U_0^{1-\beta } \left( \frac{1}{\beta -1}-\frac{1}{\beta }\right) \right) \\&= -\frac{q}{r+U_0}\left( \frac{1}{\beta } x^{1-\beta } -\left( U_0^{1-\beta } - x^{1-\beta }\right) \left( \frac{1}{\beta -1}-\frac{1}{\beta }\right) \right) \\&\le -\frac{q}{\beta (r+U_0)} x^{1-\beta }. \end{aligned}$$

In particular, for

$$\begin{aligned} \mu := \frac{q}{\beta (r+U_0)} = \frac{{\bar{c}}(1+3a^2)}{\beta (1+e_d+U_0)} \end{aligned}$$
(3.17)

and \(x \in (0,U_0)\) we have

$$\begin{aligned} H(x) \le -\mu x^{1-\beta }. \end{aligned}$$
(3.18)

For \(j \in {\mathbb {N}}\) put

$$\begin{aligned} \xi _j = (H-G)(u_{2j-1}). \end{aligned}$$
(3.19)

Then (3.13) is of the form

$$\begin{aligned} \xi _{j+1} - \xi _j \le -M \big ((H-G)^{-1}(\xi _j)\big )^\alpha . \end{aligned}$$
(3.20)

We now prove for \(x>0\) and \(\xi <0\) the implication

$$\begin{aligned} (H-G)(x)> \xi \ \Longrightarrow \ x > \left( \frac{-\xi }{\mu }\right) ^{1/(1-\beta )}. \end{aligned}$$
(3.21)

The property \(G(x)\ge 0\) implies that if \((H-G)(x) > \xi \), then \(H(x) > \xi \). Inequality (3.18) yields in turn that \(-\mu x^{1-\beta } > \xi \), and (3.21) follows. As a consequence of (3.21), we get for all \(\xi < (H-G)(u_0)\) the inequality

$$\begin{aligned} (H-G)^{-1}(\xi ) \ge \left( \frac{-\xi }{\mu }\right) ^{1/(1-\beta )}. \end{aligned}$$
(3.22)

Indeed, assume that there exists x such that

$$\begin{aligned} (H-G)^{-1}(\xi )< x < \left( \frac{-\xi }{\mu }\right) ^{1/(1-\beta )}. \end{aligned}$$
(3.23)

Then \((H-G)(x) > \xi \), which contradicts the implication (3.21). Using (3.22) we obtain from (3.20) the inequality

$$\begin{aligned} \xi _{j+1} - \xi _j \le -{\bar{M}} \big (-\xi _j\big )^{\alpha /(1-\beta )} \quad \text{ for } \ {\bar{M}} = M \mu ^{-\alpha /(1-\beta )}. \end{aligned}$$
(3.24)

Put \({\hat{\xi }}_j = -\xi _j\), and \(\rho = \frac{\alpha }{\beta -1} > 0\). Then (3.24) is of the form

$$\begin{aligned} {\hat{\xi }}_{j+1} - {\hat{\xi }}_j \ge {\bar{M}} {\hat{\xi }}_j^{-\rho }. \end{aligned}$$
(3.25)

The function

$$\begin{aligned} \Phi ({\hat{\xi }}):= \frac{1}{1+\rho }\,{\hat{\xi }}^{1+\rho } \end{aligned}$$

is increasing and convex on \((0,\infty )\) thanks to the assumption that \(\beta >1\). Hence, \(\Phi ({\hat{\xi }}_{j+1}) - \Phi ({\hat{\xi }}_{j}) \ge \Phi '({\hat{\xi }}_j)({\hat{\xi }}_{j+1} - {\hat{\xi }}_j)\), that is,

$$\begin{aligned} \frac{1}{1+\rho } \left( {\hat{\xi }}_{j+1}^{1+\rho } - \hat{\xi }_j^{1+\rho }\right) \ge {\hat{\xi }}_j^{\rho }\left( {\hat{\xi }}_{j+1} - {\hat{\xi }}_j \right) \ge {\bar{M}} \end{aligned}$$

for every \(j\in {\mathbb {N}}\). We conclude that

$$\begin{aligned} {\hat{\xi }}_{j+1} \ge \left( (1+\rho ){\bar{M}} j + \hat{\xi }_1^{1+\rho }\right) ^{1/(1+\rho )} \ge {\hat{C}} j^{1/(1+\rho )} \end{aligned}$$
(3.26)

for all \(j\in {\mathbb {N}}\) with some constant \({\hat{C}} > 0\). Using (3.19) and (3.26) we thus get

$$\begin{aligned} -(H-G) (u_{2j+1}) = -\xi _{j+1} \ge {\hat{C}} j^{1/(1+\rho )}. \end{aligned}$$

On the other hand, from (3.15) we deduce the following lower bound for H

$$\begin{aligned} H(x) \ge -\int _x^\infty \frac{q}{r} u^{-\beta }\,\textrm{d}u = \frac{{\hat{\mu }}}{ 1-\beta } x^{1-\beta }, \quad {\hat{\mu }} = \frac{{\bar{c}}(1+3a^2)}{(1+e_d)}. \end{aligned}$$
(3.27)

Hence, using the fact that \(G(u_{2j+1}) < G(U_0)\) which is a constant independent of j we obtain that (note that \(\beta >1\) by hypothesis)

$$\begin{aligned} \frac{{\hat{\mu }}}{\beta -1} u_{2j+1}^{1-\beta } \ge -H(u_{2j+1}) \ge {\hat{C}} j^{1/(1+\rho )}-G(U_0). \end{aligned}$$

For \(j\in {\mathbb {N}}\) sufficiently large, we thus deduce the convergence behaviour

$$\begin{aligned} u_{2j+1} \le C j^{-1/((1+\rho )(\beta - 1))} = C j^{-1/(\alpha +\beta - 1)} \end{aligned}$$
(3.28)

with a constant \(C>0\) independent of j. Note that the constant C is related to all material parameters involved in the constitutive equation as well as to the initial void ratio and to the prescribed cyclic stress interval. We see that the number of cycles necessary to reach a given neighborhood of the shakedown state gets large for small values of \(\alpha \) and large values of \(\beta \), see Figs. 5 and 6, respectively.

5 The case of anisotropic stress cycles

In this section we consider the case when the tensor \({\textbf{S}}\) is not necessarily a multiple of the unit tensor, i.e., \(S_{11}\), \(S_{22}\) and \(S_{33}\) can possibly have different (negative) values. This is what characterizes the anisotropy in the stress cycles. Our goal is to show that even in the anisotropic case the problem can be reduced to an equation like (2.5) which exhibits similar asymptotically periodic character as in the isotropic case. The main difference is that in order to obtain an expression for the norm of the strain rate \({\dot{\varvec{\varepsilon }}}\) some further intermediate steps are needed.

Assuming \({\dot{\sigma }}(t) \ne 0\), we introduce the following notation

$$\begin{aligned} {\textbf{X}}(t) = c_1(t)\frac{\sigma (t)}{{\dot{\sigma }}(t)} {\dot{\varvec{\varepsilon }}}(t), \qquad {\textbf{Q}}= \frac{{\textbf{S}}}{\left\langle {\textbf{S}},{\textbf{I}} \right\rangle }. \end{aligned}$$
(4.1)

In the case of loading, that is, \({\dot{\sigma }}(t) > 0\), (1.12) can be rewritten as (note that \(c_1(t)<0\))

$$\begin{aligned} {\textbf{Q}}= a^2 {\textbf{X}}(t) + \left\langle {\textbf{Q}},{\textbf{X}}(t) \right\rangle {\textbf{Q}}- a f(t) \Vert {\textbf{X}}(t)\Vert \left( 2{\textbf{Q}}- \frac{1}{3}{\textbf{I}}\right) . \end{aligned}$$
(4.2)

Similarly, for unloading \({\dot{\sigma }}(t) < 0\) we get

$$\begin{aligned} {\textbf{Q}}= a^2 {\textbf{X}}(t) + \left\langle {\textbf{Q}},{\textbf{X}}(t) \right\rangle {\textbf{Q}}+ a f(t) \Vert {\textbf{X}}(t)\Vert \left( 2{\textbf{Q}}- \frac{1}{3}{\textbf{I}}\right) . \end{aligned}$$
(4.3)

We rewrite (4.2) and (4.3) in a more convenient form. Taking the scalar product of (4.2) and (4.3) with \({\textbf{Q}}\) and noting that \(\left\langle {\textbf{Q}},{\textbf{I}} \right\rangle =1\) yields

$$\begin{aligned} \left\langle {\textbf{Q}},{\textbf{X}}(t) \right\rangle = \frac{\Vert {\textbf{Q}}\Vert ^2}{a^2 + \Vert {\textbf{Q}}\Vert ^2} + \,\textrm{sign}({\dot{\sigma }}(t))\, a f(t) \Vert {\textbf{X}}(t)\Vert \frac{2\Vert {\textbf{Q}}\Vert ^2 - \frac{1}{3}}{a^2 + \Vert {\textbf{Q}}\Vert ^2}, \end{aligned}$$
(4.4)

so that (4.2) and (4.3) can be reformulated as

$$\begin{aligned} \frac{a^2}{a^2 + \Vert {\textbf{Q}}\Vert ^2} {\textbf{Q}}= a^2 {\textbf{X}}(t) - \,\textrm{sign}({\dot{\sigma }}(t))\, a f(t) \Vert {\textbf{X}}(t)\Vert \left( \frac{2a^2 + \frac{1}{3}}{a^2 + \Vert {\textbf{Q}}\Vert ^2} {\textbf{Q}}- \frac{1}{3}{\textbf{I}}\right) . \end{aligned}$$
(4.5)

Putting

$$\begin{aligned} {\textbf{A}}= \frac{{\textbf{Q}}}{a^2 + \Vert {\textbf{Q}}\Vert ^2} \end{aligned}$$
(4.6)

we can simplify (4.5) and get

$$\begin{aligned} {\textbf{A}}= {\textbf{X}}(t) - \,\textrm{sign}({\dot{\sigma }}(t))\, a f(t) \Vert {\textbf{X}}(t)\Vert \left( \left( 2 + \frac{1}{3a^2}\right) {\textbf{A}}- \frac{1}{3a^2}{\textbf{I}}\right) . \end{aligned}$$
(4.7)

In summary, the problem consists in solving the ODEs

$$\begin{aligned} {\textbf{X}}(t) = {\textbf{A}}+ \,\textrm{sign}({\dot{\sigma }}(t))\, a f(t) \Vert {\textbf{X}}(t)\Vert {\textbf{B}}, \end{aligned}$$
(4.8)

with

$$\begin{aligned} {\textbf{B}}= \left( 2 + \frac{1}{3a^2}\right) {\textbf{A}}- \frac{1}{3a^2}{\textbf{I}}. \end{aligned}$$

Note that by (4.1) and (4.6) we have \(\Vert {\textbf{Q}}\Vert ^2 \ge 1/3\) and

$$\begin{aligned} \left\langle {\textbf{A}},{\textbf{B}} \right\rangle = (a^2 + \Vert {\textbf{Q}}\Vert ^2)^{-2} \left( 2\Vert {\textbf{Q}}\Vert ^2 - \frac{1}{3}\right) \ge \frac{1}{3} (a^2 + \Vert {\textbf{Q}}\Vert ^2)^{-2}>0. \end{aligned}$$

The counterpart of condition (2.1) reads here

$$\begin{aligned} f(t) < \frac{1}{a\Vert {\textbf{B}}\Vert }. \end{aligned}$$
(4.9)

Assuming that (4.9) holds we get positiveness for the discriminant of the quadratic equation

$$\begin{aligned} (1-a^2 f^2(t) \Vert {\textbf{B}}\Vert ^2) \Vert {\textbf{X}}(t)\Vert ^2 - \,\textrm{sign}({\dot{\sigma }}(t))\, 2a f(t) \left\langle {\textbf{A}},{\textbf{B}} \right\rangle \Vert {\textbf{X}}(t)\Vert -\Vert {\textbf{A}}\Vert ^2 =0 \end{aligned}$$

following from (4.8), and its positive roots are:

$$\begin{aligned} \Vert {\textbf{X}}(t)\Vert = \frac{af(t)\left\langle {\textbf{A}},{\textbf{B}} \right\rangle + \,\textrm{sign}({\dot{\sigma }}(t))\, \sqrt{\Vert {\textbf{A}}\Vert ^2 - a^2f^2(t) (\Vert {\textbf{A}}\Vert ^2\Vert {\textbf{B}}\Vert ^2 - \left\langle {\textbf{A}},{\textbf{B}} \right\rangle ^2)}}{1- a^2f^2(t) \Vert {\textbf{B}}\Vert ^2}. \end{aligned}$$
(4.10)

Hence,

$$\begin{aligned} {\textbf{X}}(t) = {\textbf{A}}+ af(t) \frac{af(t)\left\langle {\textbf{A}},{\textbf{B}} \right\rangle + \,\textrm{sign}({\dot{\sigma }}(t))\, \sqrt{\Vert {\textbf{A}}\Vert ^2 - a^2f^2(t) (\Vert {\textbf{A}}\Vert ^2\Vert {\textbf{B}}\Vert ^2 - \left\langle {\textbf{A}},{\textbf{B}} \right\rangle ^2)} }{1- a^2f^2(t) \Vert {\textbf{B}}\Vert ^2} {\textbf{B}}. \end{aligned}$$
(4.11)

The reader is invited to verify that in the isotropic case, i.e. \({\textbf{S}}= -{\textbf{I}}\), we have \({\textbf{Q}}= \frac{1}{3} {\textbf{I}}\), \({\textbf{A}}= {\textbf{B}}= \frac{1}{1+3a^2} {\textbf{I}}\), and consequently the identity above yields equation (2.5) studied in Sect. 2. We now rewrite (4.11) in a more concise form

$$\begin{aligned} {\textbf{X}}(t) = {\textbf{A}}+ \phi (f(t)) {\textbf{B}}+ \,\textrm{sign}({\dot{\sigma }}(t))\, \psi (f(t)){\textbf{B}}, \end{aligned}$$
(4.12)

with

$$\begin{aligned} \phi (f)&= \frac{a^2 f^2\left\langle {\textbf{A}},{\textbf{B}} \right\rangle }{1- a^2f^2\Vert {\textbf{B}}\Vert ^2}, \end{aligned}$$
(4.13)
$$\begin{aligned} \psi (f)&= a f \frac{\sqrt{\Vert {\textbf{A}}\Vert ^2 - a^2 f^2 (\Vert {\textbf{A}}\Vert ^2\Vert {\textbf{B}}\Vert ^2 - \left\langle {\textbf{A}},{\textbf{B}} \right\rangle ^2)}}{1- a^2 f^2 \Vert {\textbf{B}}\Vert ^2}. \end{aligned}$$
(4.14)

Then we have

$$\begin{aligned} \left\langle {\textbf{X}}(t),{\textbf{I}} \right\rangle = \left\langle {\textbf{A}},{\textbf{I}} \right\rangle + \phi (f(t)) \left\langle {\textbf{B}},{\textbf{I}} \right\rangle + \,\textrm{sign}({\dot{\sigma }}(t))\, \psi (f(t))\left\langle {\textbf{B}},{\textbf{I}} \right\rangle . \end{aligned}$$
(4.15)

We now use (4.1) and (1.9) to derive the identity

$$\begin{aligned} \left\langle {{\textbf {X}}}(t),{{\textbf {I}}} \right\rangle = \frac{\sigma (t)}{{\dot{\sigma }}(t)}\left\langle {\dot{{\varepsilon }}}(t), {{\textbf {I}}} \right\rangle c_1(e(t)) = \frac{\sigma (t)}{{\dot{\sigma }}(t)}\frac{\dot{e}(t)c_1(e(t))}{1+e(t)}. \end{aligned}$$

Recalling that \(\frac{\sigma (t)}{{\dot{\sigma }}(t)}=1\) for \({\dot{\sigma }}(t) > 0\), and \(\frac{\sigma (t)}{{\dot{\sigma }}(t)}=-1\) for \({\dot{\sigma }}(t) < 0\) and using also (1.6), we obtain differential equations for the unknown function e(t) in the form

$$\begin{aligned} \frac{\dot{e}(t)c_1(e(t))}{(1+e(t))(\left\langle {\textbf{A}},{\textbf{I}} \right\rangle + \phi (f(e(t))) \left\langle {\textbf{B}},{\textbf{I}} \right\rangle + \,\textrm{sign}({\dot{\sigma }}(t))\, \psi (f(e(t)))\left\langle {\textbf{B}},{\textbf{I}} \right\rangle )} = \,\textrm{sign}({\dot{\sigma }}(t)). \end{aligned}$$
(4.16)

Now, let us show that the equation above has the same structure as (2.5). To this end, we rewrite

$$\begin{aligned} \frac{1}{\left\langle {\textbf{A}},{\textbf{I}} \right\rangle + \phi (f) \left\langle {\textbf{B}},{\textbf{I}} \right\rangle + \,\textrm{sign}({\dot{\sigma }}(t))\, \psi (f)\left\langle {\textbf{B}},{\textbf{I}} \right\rangle } = \frac{\left\langle {\textbf{A}},{\textbf{I}} \right\rangle + \phi (f) \left\langle {\textbf{B}},{\textbf{I}} \right\rangle - \,\textrm{sign}({\dot{\sigma }}(t))\, \psi (f)\left\langle {\textbf{B}},{\textbf{I}} \right\rangle }{(\left\langle {\textbf{A}},{\textbf{I}} \right\rangle + \phi (f) \left\langle {\textbf{B}},{\textbf{I}} \right\rangle )^2 - \psi ^2(f)\left\langle {\textbf{B}},{\textbf{I}} \right\rangle ^2},\nonumber \\ \end{aligned}$$
(4.17)

where using the identity \(\phi ^2(f) - \psi ^2(f) =-a^2 f^2 \Vert {\textbf{A}}\Vert ^2(1 - a^2 f^2 \Vert {\textbf{B}}\Vert ^2)^{-1}\) we calculate the denominator

$$\begin{aligned} (\left\langle {\textbf{A}},{\textbf{I}} \right\rangle + \phi (f) \left\langle {\textbf{B}},{\textbf{I}} \right\rangle )^2 - \psi ^2(f)\left\langle {\textbf{B}},{\textbf{I}} \right\rangle ^2 = \frac{\left\langle {\textbf{A}},{\textbf{I}} \right\rangle ^2 - a^2 f^2 \Vert \left\langle {\textbf{A}},{\textbf{I}} \right\rangle {\textbf{B}}- \left\langle {\textbf{B}},{\textbf{I}} \right\rangle {\textbf{A}}\Vert ^2}{1 - a^2 f^2 \Vert {\textbf{B}}\Vert ^2}. \end{aligned}$$

Hence, putting

$$\begin{aligned} {\tilde{h}}(f)&= \frac{\left\langle {\textbf{A}},{\textbf{I}} \right\rangle + a^2 f^2 \big (\left\langle {\textbf{B}},{\textbf{I}} \right\rangle \left\langle {\textbf{A}},{\textbf{B}} \right\rangle - \left\langle {\textbf{A}},{\textbf{I}} \right\rangle \Vert {\textbf{B}}\Vert ^2\big )}{\left\langle {\textbf{A}},{\textbf{I}} \right\rangle ^2 - a^2 f^2 \Vert \left\langle {\textbf{A}},{\textbf{I}} \right\rangle {\textbf{B}}- \left\langle {\textbf{B}},{\textbf{I}} \right\rangle {\textbf{A}}\Vert ^2}, \end{aligned}$$
(4.18)
$$\begin{aligned} {\tilde{g}}(f)&= \frac{af \left\langle {\textbf{B}},{\textbf{I}} \right\rangle \sqrt{\Vert {\textbf{A}}\Vert ^2 - a^2 f^2 (\Vert {\textbf{A}}\Vert ^2\Vert {\textbf{B}}\Vert ^2 - \left\langle {\textbf{A}},{\textbf{B}} \right\rangle ^2)}}{\left\langle {\textbf{A}},{\textbf{I}} \right\rangle ^2 - a^2 f^2 \Vert \left\langle {\textbf{A}},{\textbf{I}} \right\rangle {\textbf{B}}- \left\langle {\textbf{B}},{\textbf{I}} \right\rangle {\textbf{A}}\Vert ^2}, \end{aligned}$$
(4.19)

we see that system (4.16) is of the form

$$\begin{aligned} \frac{\dot{e}(t)c_1(e(t))}{(1+e(t))}\big ({\tilde{h}} (f(e(t))) - \,\textrm{sign}({\dot{\sigma }}(t))\, {\tilde{g}}(f(e(t)))\big ) = \,\textrm{sign}({\dot{\sigma }}(t)), \end{aligned}$$
(4.20)

which is formally the same as (2.5). Indeed, for e(t) close to \(e_d\), the value of the density function \(f(t) =f(e(t))\) is close to 0, hence, \({\tilde{h}}(f)\) behaves asymptotically like the constant \(1/\left\langle {\textbf{A}},{\textbf{I}} \right\rangle \), while \(\tilde{g}(f)\) behaves like the linear function \(g_0 f\) with \(g_0 = a \left\langle {\textbf{B}},{\textbf{I}} \right\rangle \Vert {\textbf{A}}\Vert / \left\langle {\textbf{A}},{\textbf{I}} \right\rangle ^2\), and the convergence proof can be carried out in the same way as in the isotropic case provided that e(0) satisfies the condition (3.10).

6 Numerical tests

The focus of the numerical simulations presented in this section is on the influence of some prescribed quantities on the evolution of the volume change with increasing number of loading cycles. More precisely, the influence of the given non-zero components of the stress direction \(S_{11}\), \(S_{22}\), \(S_{33}\), the initial void ratio e(0), and the value of parameters \(\alpha \) and \(\beta \). The material parameters involved in the present constitutive model, i.e. \(\{a, e_d, e_c, \alpha ,\bar{c}, \beta \}\), have the following meaning: parameter a is related to the intergranular friction angle in a stationary state or the so-called critical state [5, 7, 10]; \(e_d\) and \(e_c\) denote the minimum void ratio and critical void ratio, respectively; parameter \(\alpha \) triggers the amount of the density function f(e) depending on the current void ratio e; parameter \(\bar{c}\) scales the amount of the incremental stiffness (i.e. a higher value of \(\bar{c}\) results in a higher stiffness); and parameter \(\beta >1\) triggers the influence of the state dependent quantity \(u=e-e_d\) on the stiffness factor c.

More details about the physical meaning of the material parameters and the procedure for calibration can be found for instance in [3, 10]. In connection to that, it is worth recalling that for highly non-linear constitutive equations, like the one we investigate here, certain restrictions on the possible range of the parameter values may apply. For the present numerical simulations the material parameters are adapted to experimental data typical for sands, i.e. \(a=0.4\), \(e_c = 0.8\), \(e_d = 0.4\), \({\bar{c}} = 2\), \(\alpha = 0.1\), and assuming \(\beta = 1.03\). For the interval of cyclic loading along the given stress direction, the interval limits of the scalar stress factor in (1.11) are \(\sigma ^\flat = 10\) and \(\sigma ^\sharp = 12\).

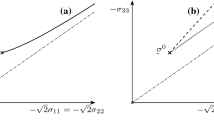
For prescribed isotropic cyclic stress states with \({\textbf{S}}= -\,{\textbf{I}}\), starting from initial conditions at \(t_0 = 0\) chosen as \(e(0) = 0.7\), \(\sigma ^\flat = 10\), \(\varvec{\varepsilon }(0) = 0\cdot {\textbf{I}}\), and for \(n = 25\) cycles the results of the numerical simulation are shown in Fig. 1. From Fig. 1a it is clearly visible that for a full loading-unloading-reloading cycle the compaction, i.e. the decrease of the volumetric strain \(\varepsilon _v= \varepsilon _{11}+\varepsilon _{22}+\varepsilon _{33}\), is more pronounced at the beginning of cyclic loading and becomes smaller with number of stress cycles. This behaviour is in agreement with experimental observations and can be explained by an increase of the incremental stiffness caused by a reduction of the void ratio e. As the number of cycles increases, the void ratio tends towards the minimum void ratio \(e_d\), i.e. the state quantity \(u=e-e_d\) asymptotically approaches zero, as shown in Fig. 1b. It can be noted that experiments with stiff grains usually show after reloading a certain loop of the the stress–strain curve. This is caused by a higher stiffness at the beginning of the reloading path, which is not captured by the present model, but it can be modelled with additional state quantities using more refined hypoplastic material descriptions, e.g. [14, 47]. However, the essential shakedown feature of granular materials can already be simulated with the present simplified model.

Fig. 1
figure 1

Isotropic cyclic stress states: a evolution of the stress \(\sigma \) against the volumetric strain \(\varepsilon _v\); b evolution of \(u=e-e_d\) depending on number of cycles

Full size image
Fig. 2
figure 2

Axisymmetric anisotropic cyclic stress states: a evolution of the strain \(\varepsilon _{22}=\varepsilon _{33}\) against \(\varepsilon _{11}\); b evolution of \(u=e-e_d\) depending on the number of cycles

Full size image

The behaviour under axisymmetric cyclic stress states, i.e. \(S_{11}=-3\), \(S_{22}=-1\), \(S_{33}=-1\), is shown in Fig. 2. From Fig. 2a it can be seen that the components \(\varepsilon _{22} = \varepsilon _{33}\) have a tendency to increase, while the component \(\varepsilon _{11}\) decreases. Within a full stress cycle, the accumulated volumetric strain exhibits compaction, which means a decrease of the void ratio towards the minimum void ratio as shown in Fig. 2b. Numerical simulations show that the sign of the evolution of the individual strain components strongly depends on the degree of stress anisotropy. For instance, for \(S_{11}=-1.5\), \(S_{22}=-1\), \(S_{33}=-1\) the three strain components decrease during the whole evolution.

Fig. 3
figure 3

3-D anisotropic cyclic stress states: a evolution of the strain components; b evolution of \(u=e-e_d\) depending on the number of cycles

Full size image

The results of numerical simulation in the case of triaxial anisotropy with the choice \(S_{11}=-1.5\), \(S_{22}=-0.5\), \(S_{33}=-1\) is shown in Fig. 3. From Fig. 3a it can be seen that the components \(\varepsilon _{11}\) and \(\varepsilon _{33}\) have a tendency to decrease, while the component \(\varepsilon _{22}\) increases. Again the volumetric strain exhibits compaction, which is also related to an decrease of the void ratio towards the minimum void ratio as shown in Fig. 3b. It cannot be expected, however, that in this kind of problems numerical tests would give any useful validation of the convergence rate computed theoretically in Sect. 3. Note that by formula (3.28) the convergence is very slow, therefore any numerical analysis in this matter would require a large number of steps subjected to accumulated numerical error.

Further numerical simulations show that for a full loading-unloading-reloading cycle the changes in the volume depend not only on the number of loading cycles, but also on the material parameters involved in the constitutive model, the given stress direction, the initial void ratio and to the prescribed stress interval. For example, the influence of the initial void ratio \(e(t=0)=e(0)\) on the change of the density factor f(e) is demonstrated in Fig. 4. In particular, Fig. 4a shows the behaviour under isotropic cyclic stress states with \({\textbf{S}}= -\,{\textbf{I}}\), and Fig. 4b shows the behaviour under axisymmetric anisotropic cyclic stress states corresponding to \({\textbf{S}}\) with the components \(S_{11}=-3\), \(S_{22}=-1\), \(S_{33}=-1\). As the density factor f(e) is a function of the current void ratio, a reduction of f(e) means a densification. It is clearly visible that in both cases the cyclic behaviour shows additional compaction with number of cycles. The compaction is more pronounced for the initially higher void ratio, in particular, at the beginning of cyclic loading. After same number of cycles the compaction is higher under isotropic cyclic stress states than for the case of axisymmetric anisotropic cyclic stress states.

Fig. 4
figure 4

Influence of the initial void ratio e(0) on the evolution of the density factor f(e) for: a isotropic cyclic stress states; b axisymmetric anisotropic cyclic stress states

Full size image
Fig. 5
figure 5

Influence of parameter \(\alpha \) on the evolution of the density factor f(e) for: a isotropic cyclic stress states; b axisymmetric anisotropic cyclic stress states

Full size image
Fig. 6
figure 6

Influence of parameter \(\beta \) on the evolution of the density factor f(e) for: a isotropic cyclic stress states; b axisymmetric anisotropic cyclic stress states

Full size image

For an initial void ratio of \(e(0)=0.7\) the influence of parameter \(\alpha \) on the evolution of the density function f(e) is shown in Fig. 5a for the case of isotropic cyclic stress states and in Fig. 5b for the case of axisymmetric anisotropic cyclic stress states (using, in each case, the same components for the tensors \({\textbf{S}}\) as in Fig. 4a and Fig. 4b, respectively). In both cases the evolution of f(e) shows again compaction with an increase in the number of cycles. For same stress cycles and an initial void ratio of \(e(0)=0.7\) the influence of parameter \(\beta \) on the evolution of the density function f(e) is shown in Fig. 6. For a higher value of \(\beta \) the compaction is lower which can be explained by a higher incremental stiffness, i.e., the value of \(c_1\) obtained from (1.7) scales the incremental stiffness and it is higher for a higher value of \(\beta \).

In accordance with the analytical results, the numerical simulations also show that the cyclic behaviour under the particular conditions (1.10) and (1.11) leads to an additional compaction of the material in each loading-unloading-reloading cycle. Independently of the given stress direction and the initial void ratio, the amount of the additional compaction decreases with number of cycles. In this context, it should be noted that in the present constitutive model compaction is not an inherent property of formula (1.6) for the density factor f(e). Indeed, it is shown in [3] that an increase of the volume can be observed for the same choice of density function (1.6) under stress cycles different from (1.10) and (1.11).

7 Conclusion

We study a special case of the extended hypoplastic constitutive model for granular materials subjected to proportional periodically oscillating stresses under the assumption that the evolution of the strain components depends on the prescribed stress interval and the current void ratio, which is defined as the ratio of the volume of the void space to the volume of the solid material. For a prescribed stress cycle a part of the corresponding deformations is irreversible, indicating to the dissipative property of the incrementally non-linear constitutive model used. In the analysis it is proved that within each full stress cycle the resulting volumetric strain exhibits a compaction, i.e., a reduction of the void ratio. The amount of additional compaction reduces non-linearly with the number of cycles in both isotropic and anisotropic loading scenarios. Under technical assumptions on the parameters of the model, we find an upper bound for the initial void ratio which guarantees that the current void ratio converges asymptotically to its minimum value, which corresponds to the full compaction of the material. Numerical results indicate that the ratchetting trajectories very strongly depend on the degree of stress anisotropy. This question, however, deserves to be studied in more detail in a future work.