Exact solutions for the buckling and postbuckling of a shear-deformable cantilever subjected to a follower force

Abstract

The buckling and postbuckling of a shear-deformable cantilever is studied using Reissner’s geometrically exact relations for the planar deformation of beams. The cantilever is subjected to a compressive follower force whose line of action passes through a spatially fixed point. To study the buckling behavior, a consistent linearization of equilibrium and kinematic relations is introduced. The influence of shear deformation and extensibility on the critical loads is studied. The buckling behavior turns out to crucially depend on the ratio between the shear stiffness and the extensional stiffness of the structure. Closed-form solutions in terms of elliptic integrals for buckled configurations of the cantilever are derived in the present paper.

1 Introduction

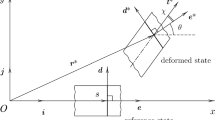
The buckling of beams subjected to compressive forces is one of the classical problems in structural mechanics and stability. For centuries, scientists have studied critical loads at which structures become unstable and sought for methodologies to determine these loads. We mention Euler’s pioneering work in the appendix of his monograph [13], in which he determined the critical load of a column subjected to a compressive force and studied the buckled shapes. The treatise of Timoshenko and Gere [29] gives a detailed account of diverse stability problems of rods under different end restraints and loadings. Besides the four classical buckling problems with combinations of clamped, pinned and free ends, which have found their way into every mechanics textbook, they also present the buckling problem that is studied in the present paper. In the problem they refer to as “Column with Load through a Fixed Point,” which is illustrated in Fig. 1a, the line of action of the compressive force P is assumed to pass through the spatially fixed point C. Unlike classical buckling problems, in which the direction of the loading remains constant, the orientation of the force depends on the buckled configuration of the structure, which is why it can be regarded as one kind of a follower load. Still, the described problem is conservative which allows us to study the stability using static considerations only. By contrast, a follower load whose direction is determined by the orientation of the tangent to the beam’s axis at the point of application requires dynamics to be accounted for. This specific buckling problem is appealing from an experimental point of view, since the force can be realized by tensioning a cable that is mounted to the free tip of the beam and runs through the fixed point C. Exemplarily, such a setup was used in investigations to increase the critical loads of slender beams by means of piezoelectric transducers and feedback control [31, 32].

The main focus of the present paper is twofold: As a first important aspect, we study the influence of shear and extensibility on the critical loads at which the beam buckles. Euler’s beam theory, which is often referred to as elastica, only admits flexural deformation but no shearing or stretching. For moderately thick structures, Timoshenko [27, 28] required that cross sections of the beam remain plane and undistorted in the course of deformation, but he no longer assumed that cross sections had to remain perpendicular to the beam’s axis. Timoshenko’s linear theory was generalized to arbitrarily large deformations by Reissner [25] and Antman [1]. For the three-dimensional relations governing the spatial deformation of beams, we refer to Eliseev [10, 11]. Engesser [12] and Haringx [17] obtained differing results for the critical loads of shear-deformable beams under a compressive force. The discrepancy was later resolved by Bažant [7, 8], who showed that Engesser’s and Haringx’ results do coincide once consistent tangent stiffnesses corresponding to the respective strain measures are used. Antman and Rosenfeld [2] studied the buckling of beams for general types of nonlinearly elastic material behavior and boundary conditions. The effects of shear deformation and extensibility on the buckling behavior of the classical problems, in particular, the statically indeterminate cases of clamped-hinged and clamped-clamped beams, were investigated by Humer [19].

Fig. 1

Undeformed and deformed configurations of a cantilever subjected to a follower force P (a); kinematics and stress resultants of a shear-deformable beam (b)

The second focus of the paper lies on the construction of closed-form relations for the buckled configuration of shear-deformable beams. For the classical elastica, Kirchhoff noted the close resemblance between the equilibrium relations of a beam subjected to concentrated loads at its ends and the equations of motion of a pendulum [20]. Based on what is referred to as Kirchhoff’s kinetic analogue [21], Saalschütz presented closed-form solutions in terms of elliptic integrals [26]. We also mention the work of Frisch-Fay [14], who derived the elliptic integral relations describing the buckled configuration of a simply supported beam. Results for the clamped-hinged beam were presented in [9, 23]. For the extensible elastica, which has a finite extensional stiffness but is rigid with respect to shear, elliptic integral solutions were presented, e.g., by Pflüger [24] and Humer [18]. Magnusson et al. [22] studied the postbuckling behavior of a simply supported extensible elastica in detail. Elliptic integral solutions accounting for shear deformation were presented by Goto et al. [15]. The contribution by Humer [19] on the four classical buckling problems, in which he derived solutions for the buckled configurations of beams based on Reissner’s geometrically nonlinear theory, provides the groundwork for the present paper. An additional transformation enables closed-form solutions in terms of elliptic integrals also for the generalized elastica which exhibits both stretching and shear deformation. The family of Jacobi-elliptic functions can be regarded as inverse functions to elliptic integrals. Batista presented solutions in terms of Jacobi-elliptic functions for both the classical elastica [4, 5] and shear-deformable beams [3, 6]. The problem of a classical elastica whose tip is pulled by a cable [4] is closely related to the present problem. However, shear deformation and extensibility were neglected and the stability problem was not addressed.

We also want to mention that a large number of contributions seek for approximate solutions to equilibrium configurations of largely deformed beams in general and buckled configurations in particular. With the focus lying on analytical solutions, however, we do not further go into details here.

The present paper is organized as follows: In Sect. 2, we introduce the kinematics of shear-deformable beams and derive the equilibrium relations for the present problem of a cantilever subjected to a follower load. For the sake of generality, a non-dimensional setting is adopted subsequently. In Sect. 3, a consistent linearization of the geometrically nonlinear relations is performed. We obtain a transcendental equation whose roots determine the critical loads at which the trivial solution of a compressed beam becomes unstable. We provide both qualitative and quantitative results for the buckling behavior. By a series of transformations, closed-form relations for both the rotation of cross sections and the axial displacement and the transverse deflection in terms of elliptic integrals are derived in Sect. 4. Exemplarily, we illustrate several buckled configurations for different geometries.

2 Governing equations

In the present paper, we focus on the planar buckling and postbuckling of beams. In what follows, the beam’s axis is assumed to be straight in the undeformed reference configuration. The axis coincides with the x-axis of a global Cartesian frame $\left\{ \varvec{e}_x, \varvec{e}_y, \varvec{e}_z\right\}$; the beam deforms in the (x, y)-plane of the global frame.

2.1 Geometrically exact beam theory

The present investigations are based on the geometrically exact theory for shear-deformable beams which was proposed by Reissner [25] and Antman [1]. By introducing appropriate strain-generalized measures, the beam theory translates Timoshenko’s kinematic hypothesis [27, 28] on the deformation of cross sections to large deformations. Accordingly, cross sections initially plane and perpendicular to the beam’s axis remain plane and undistorted but not necessarily perpendicular to the axis in the deformed configuration, see Fig. 1b. The beam’s cross section spans the local frame $\left( \varvec{t}_1, \varvec{t}_2\right)$, which is rotated by the angle $\phi$ about the z-axis relative to the global frame,

$$\begin{aligned} \varvec{t}_1= \cos \phi \, \varvec{e}_x+ \sin \phi \, \varvec{e}_y, \qquad \varvec{t}_2= - \sin \phi \, \varvec{e}_x+ \cos \phi \, \varvec{e}_y. \end{aligned}$$

(1)

According to Timoshenko’s hypothesis, the current position of the beam’s axis $\varvec{r}_0$ and the rotation of the cross section $\phi$ fully determine the deformed configuration of the beam. The current position vector $\varvec{r}$ of a material point that was originally located at $\varvec{X}= X\varvec{e}_x+ Y\varvec{e}_y+ Z\varvec{e}_z$ in the undeformed configuration is given by

$$\begin{aligned} \varvec{r}= \varvec{r}_0 + Y\, \varvec{t}_2+ Z\, \varvec{e}_z= \left( X+ u- Y\sin \phi \right) \varvec{e}_x+ \left( w+ Y\cos \phi \right) \varvec{e}_y+ Z\varvec{e}_z, \end{aligned}$$

(2)

where the displacement vector of the axis and its components relative to the global frame $\varvec{u}= \varvec{r}_0 - X\, \varvec{e}_x= u\, \varvec{e}_x+ w\, \varvec{e}_y$ have been introduced. The derivative of the axis’ position vector with respect to the axial material coordinate gives a vector that is tangential to the beam’s axis,

$$\begin{aligned} \frac{\partial \varvec{r}_0}{\partial X} = \varLambda \left( \cos \vartheta \, \varvec{t}_1+ \sin \vartheta \, \varvec{t}_2\right) . \end{aligned}$$

(3)

The length of the above vector corresponds to the axial stretch, i.e., the length ratio of a material line element in the deformed and the undeformed configuration. Further, the so-called shear angle, which is enclosed by the beam’s axis and the normal to the cross section, is denoted by $\vartheta$. As the positive direction of rotation is counterclockwise, $\vartheta < 0$ holds for the situation illustrated in Fig. 1b. The components of the axial position gradient in the global frame follow from (1) and (3) as

$$\begin{aligned} \frac{\partial \varvec{r}_0}{\partial X}\cdot \varvec{e}_x= 1 + \frac{\partial u}{\partial X} = \varLambda \cos (\phi + \vartheta ) \end{aligned}$$

(4)

in the x-direction, and

$$\begin{aligned} \frac{\partial \varvec{r}_0}{\partial X}\cdot \varvec{e}_y= \frac{\partial w}{\partial X} = \varLambda \sin (\phi + \vartheta ) \end{aligned}$$

(5)

in the y-direction. The geometrically exact beam theory requires strain measures that can account for large deformations and are invariant to arbitrary rigid-body rotations. Based on variational arguments, Reissner introduced generalized strains for stretching, i.e., the axial force strain

$$\begin{aligned} \varepsilon = \frac{\partial \varvec{r}_0}{\partial X}\cdot \varvec{t}_1- 1= \varLambda \cos \vartheta - 1, \end{aligned}$$

(6)

the shear strain

$$\begin{aligned} \gamma = \frac{\partial \varvec{r}_0}{\partial X}\cdot \varvec{t}_2= \varLambda \sin \vartheta , \end{aligned}$$

(7)

and the bending strain

$$\begin{aligned} \kappa = \frac{\partial \phi }{\partial X}. \end{aligned}$$

(8)

The generalized strains are conjugate to the components of the stress resultants with respect to the local frame of the deformed cross section, i.e., the resultant force $\varvec{f}$

$$\begin{aligned} \varvec{f}= N \, \varvec{t}_1+ Q \, \varvec{t}_2, \end{aligned}$$

(9)

where N denotes the normal forces and Q the shear forces, and the resultant moment M about the z-axis, which we simply refer to as bending moment (Fig. 1b). In our studies on buckling and postbuckling, we adopt the conventional linear material behavior of structural mechanics. Assuming that no physical nonlinearities are present and that the shape of the cross section allows a decoupling of the strains, the constitutive equations read

$$\begin{aligned} N = D\, \varepsilon , \, \qquad Q = S\, \gamma , \, \qquad M = B\, \kappa . \end{aligned}$$

(10)

In the above equations, $D$ denotes the extensional stiffness, $S$ is the shear stiffness, and $B$ is referred to as bending stiffness. For simple cross sections, the effective stiffnesses can be related to the elastic moduli from elasticity,

$$\begin{aligned} D= E\!A, \qquad S= kG\!A , \qquad B= EI, \end{aligned}$$

(11)

where E and G denote Young’s modules and the shear modulus, respectively, and k is the shear correction factor that accounts for the non-uniform distribution of shear stresses over the cross section. The cross-sectional area and moment of inertia about the z-axis are denoted by A and I.

2.2 Equilibrium relations

To derive the equilibrium relations, we consider the free-body diagram illustrated in Fig. 2, in which the stress resultants N, Q and M are introduced in the local frame, which is aligned with the deformed cross section and rotated by the angle $\phi$ about the z-axis. At the base of the cantilever, we find the horizontal and vertical components of the applied force P, where the angle $\alpha$ depends on the position of the beam’s free tip in the deformed configuration, see Fig. 1a. The reaction moment at the clamping is denoted by $M_0$. Although the orientation of the applied force “follows” the deformation of the beam, we can find a potential V, whose derivative with respect to the tip displacement gives the force. Let $\varvec{v}$ denote the vector from the beam’s tip to the point C (cf. Fig. 1a),

$$\begin{aligned} \varvec{v}= -\, c \, \varvec{e}_x- \varvec{u}(l). \end{aligned}$$

(12)

we choose the product of the force intensity P and the length $c - \Vert \varvec{v}\Vert$ as potential V:

$$\begin{aligned} V = P \left( c - \Vert \varvec{v}\Vert \right) . \end{aligned}$$

(13)

By direct computation, we can convince ourselves that the derivative with respect to the tip displacement gives the force vector,

$$\begin{aligned} \frac{\partial V}{\partial \varvec{u}(l)} = P \, \varvec{e}_P, \qquad \varvec{e}_P= \frac{\varvec{v}}{\Vert \varvec{v}\Vert }, \end{aligned}$$

(14)

where we have introduced the unit vector $\varvec{e}_P$ along the force’s line of action. By including the constant c in the potential V, we obtain an intuitive interpretation: We assume that the load is imposed by pulling an (inextensible) rope that is attached to the beam’s tip and passes through C. At the point C, we can further assume the rope to be deflected into some constant direction. The distance $c - \Vert \varvec{v}\Vert$ then represents the displacement of the rope’s end at which the force P is applied. The potential V therefore corresponds to the work performed by P, which is the product of the force intensity and the displaced length.

Fig. 2

Free-body diagram of a beam subjected to a follower load. At the clamped end, reaction forces

Summing up the forces in x-direction, we obtain the equilibrium relation

$$\begin{aligned} P \cos \alpha + N \cos \phi - Q \sin \phi = 0. \end{aligned}$$

(15)

Equilibrating the forces in y-direction gives

$$\begin{aligned} P \sin \alpha + N \sin \phi + Q \cos \phi = 0. \end{aligned}$$

(16)

For the balance of moments, we use the cross section $X$ as point of reference when forming the resultant torque,

$$\begin{aligned} M - M_0 + w \, P \cos \alpha - (X + u) P \sin \alpha = 0, \end{aligned}$$

(17)

in which the components of the axis’ position vector $X+ u$ and $w$ occur. Taking the derivative with respect to (material) coordinate $X$ of the beam’s axis, the (constant) reaction moment at the clamping vanishes, and we obtain the relation

$$\begin{aligned} \frac{\partial M}{\partial X} + \frac{\partial w}{\partial X}\, P \cos \alpha - \left( 1 + \frac{\partial u}{\partial X}\right) P \sin \alpha = 0. \end{aligned}$$

(18)

In the above equation, we want to express the components of the position gradient of the axis in terms of the generalized strain measures. For this purpose, we expand the trigonometric functions in (4) and (5) and introduce the definitions of the axial strain (6) and the shear strain (7), i.e.,

$$\begin{aligned}&1 + \dfrac{\partial u}{\partial X} = \varLambda \left( \cos \phi \cos \vartheta - \sin \phi \sin \vartheta \right) = (1 + \varepsilon ) \cos \phi - \gamma \sin \phi , \end{aligned}$$

(19)

$$\begin{aligned}&\dfrac{\partial u}{\partial X} = \varLambda \left( \sin \phi \cos \vartheta + \cos \phi \sin \vartheta \right) = ( 1 + \varepsilon ) \sin \phi + \gamma \cos \phi . \end{aligned}$$

(20)

Substituting the components of the position gradient into the equilibrium relation (18) gives

$$\begin{aligned} \frac{\partial M}{\partial X}+ (1 + \varepsilon ) P \left( \sin \phi \cos \alpha - \cos \phi \sin \alpha \right) + \gamma \, P \left( \cos \phi \cos \alpha + \sin \phi \sin \alpha \right) = 0. \end{aligned}$$

(21)

Note that we recover Timoshenko’s relations for the classical elastica if both the axial strain and shear strain vanish, i.e., $\varepsilon = 0$, $\gamma = 0$. The generalized strains, in turn, can be expressed from the force equilibrium (15)–(16) and the constitutive equations (10) in terms of the external force and the material parameters as

$$\begin{aligned} \varepsilon = - \,\frac{P}{D} \left( \cos \alpha \cos \phi + \sin \alpha \sin \phi \right) , \qquad \gamma = -\, \frac{P}{S} \left( \sin \alpha \cos \phi - \cos \alpha \sin \phi \right) . \end{aligned}$$

(22)

Along with the constitutive equation for the bending moment, we eventually obtain the equilibrium relation

$$\begin{aligned} B \, \frac{\partial ^2 \phi }{\partial X^2}+ P \left( \sin \phi \cos \alpha - \cos \phi \sin \alpha \right) \left\{ 1 - \left( \frac{1}{D} - \frac{1}{S} \right) P \left( \cos \phi \cos \alpha + \sin \phi \sin \alpha \right) \right\} = 0, \end{aligned}$$

(23)

which is the starting point for our investigations on buckling and postbuckling. Before we proceed, however, we want to introduce a non-dimensional setting for the sake of generality. To this end, we relate the axial coordinate X, the distance c as well as the components of the displacement vector u and w to the length l of beam in the reference configuration,

$$\begin{aligned} \bar{X}= \frac{X}{l} , \qquad \bar{u}= \frac{u}{l} , \qquad \bar{w}= \frac{w}{l} , \qquad \bar{c}= \frac{c}{l}. \end{aligned}$$

(24)

Further, we introduce the ratio $\nu$ between the extensional stiffness D and the shear stiffness S and the non-dimensional slenderness parameter $\lambda$, which relates the extensional stiffness and the bending stiffness,

$$\begin{aligned} \nu = \frac{D}{S}, \qquad \lambda = l^2 \frac{D}{B}. \end{aligned}$$

(25)

The motivation for our particular choice of non-dimensional parameters is twofold: The stiffness ratio $\nu$ turns out to play an essential role in buckling. The slenderness is inspired by Timoshenko and Gere [29], who introduced the slenderness of homogeneous rods as the ratio l / r, where the radius of gyration is obtained from the cross-sectional area A and its second moment of area I as $r = \sqrt{I / A}$. For notational simplicity, we introduce the square in our definition of the slenderness (25).

The external force is made non-dimensional using the bending stiffness B. Alternatively, we can also introduce Euler’s load $P_\mathrm{e}$, i.e., the (first) critical load, at which a simply supported beam buckles under a concentrated compressive force,

$$\begin{aligned} P_\mathrm{e}= \frac{\pi ^2 B}{l^2} , \qquad \chi = \frac{l^2 P}{B} = \frac{\pi ^2 P}{P_\mathrm{e}}. \end{aligned}$$

(26)

With the aid of these definitions, the non-dimensional equilibrium relation is obtained from (23) as

$$\begin{aligned} \frac{\partial ^2 \phi }{\partial \bar{X}^2}+ \chi \left( \sin \phi \cos \alpha - \cos \phi \sin \alpha \right) \left\{ 1 - (1 - \nu ) \frac{\chi }{\lambda } \left( \cos \phi \cos \alpha + \sin \phi \sin \alpha \right) \right\} = 0 . \end{aligned}$$

(27)

Assuming that the external loading $\chi$ is given, the solution to the equation is governed by the two non-dimensional similarity parameters $\nu$ and $\lambda$ only. For rectangularly shaped homogeneous cross sections, the slenderness parameter is related to the square of the length-to-height ratio, i.e., $\lambda = 12 \, l^2 / h^2$.

We can recover the equilibrium relation of the so-called extensible elastica as the limiting case of an infinite shear stiffness, i.e., $S \rightarrow \infty \Rightarrow \nu = 0$,

$$\begin{aligned} \frac{\partial ^2 \phi }{\partial \bar{X}^2}+ \chi \left( \sin \phi \cos \alpha - \cos \phi \sin \alpha \right) \left\{ 1 - \frac{\chi }{\lambda } \left( \cos \phi \cos \alpha + \sin \phi \sin \alpha \right) \right\} = 0. \end{aligned}$$

(28)

If we further let the extensional stiffness become infinitely large, $D \rightarrow \infty \Rightarrow \lambda \rightarrow \infty$, we obtain Euler’s classical elastica, for which the equilibrium relation simplifies to

$$\begin{aligned} \frac{\partial ^2 \phi }{\partial \bar{X}^2}+ \chi \left( \sin \phi \cos \alpha - \cos \phi \sin \alpha \right) = 0. \end{aligned}$$

(29)

Note that, fully aware of the abuse of the notation, we omit the over-bars for the sake of simplicity in our subsequent derivations. Unless otherwise stated, we refer to the non-dimensional setting in what follows.

3 Linearized problem

To determine the critical loads, at which the trivial solution of a straight rod becomes unstable, we need to linearize the geometrically exact equilibrium relation (27). For this purpose, we take the directional derivatives with respect to the $\phi$ and $\alpha$, i.e., we substitute $\phi$ with $\phi _0 + s \, \phi$ and $\alpha$ with $\alpha _0 + s \, \alpha$, take the derivative with respect to s and evaluate the limit $s \rightarrow 0$, by which we obtain

$$\begin{aligned} \frac{\partial ^2 \phi }{\partial X^2} + \left\{ 1 - (1 - \nu ) \frac{\chi }{\lambda } \right\} \chi \left( \phi - \alpha \right) = 0 . \end{aligned}$$

(30)

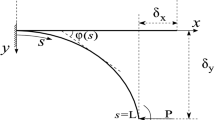
To express the angle $\alpha$ in terms of $\phi$, we need to consider the tip displacement of the beam, whose axial and transversal components are related through

$$\begin{aligned} \tan \alpha = \frac{w(1)}{c + u(1)}, \end{aligned}$$

(31)

see Fig. 1a. Linearizing the geometric relation above about the trivial solution, in which the deflection must vanish, $w_0(1) = w(1) = 0$, we obtain

$$\begin{aligned} \alpha = \frac{w(1)}{c + u_0(1)}. \end{aligned}$$

(32)

Note that the axial displacement u does not vanish in the trivial (unbuckled) solution, since the extensional stiffness is finite. The corresponding axial displacement of the beam’s free tip in the pre-compressed state is denoted by $u_0(1)$.

The components of the tip displacement, in turn, can be rewritten as integrals over the components of gradient vector $\partial \varvec{r}_0/ \partial X$ (19)–(20),

$$\begin{aligned} 1 + u(1) = \int _0^1 \left\{ (1 + \varepsilon ) \cos \phi - \gamma \sin \phi \right\} \mathrm dX, \qquad w(1) = \int _0^1 \left\{ ( 1 + \varepsilon ) \sin \phi + \gamma \cos \phi \right\} \mathrm dX, \end{aligned}$$

(33)

where $u(0) = w(0) = 0$ has been used. Once again, we express the axial strain and the shear strain in terms of the external forces (22), which gives

$$\begin{aligned} 1 + u(1) = \int _0^1 \left\{ 1 - \frac{\chi }{\lambda } \left( \cos \phi \cos \alpha + \sin \phi \sin \alpha \right) \right\} \cos \phi \, \mathrm dX+ \int _0^1 \nu \, \frac{\chi }{\lambda } \left( \cos \phi \sin \alpha - \sin \phi \cos \alpha \right) \sin \phi \, \mathrm dX, \end{aligned}$$

(34)

for the x-position of the beam’s tip, and

$$\begin{aligned} w(1) = \int _0^1 \left\{ 1 - \frac{\chi }{\lambda } \left( \cos \phi \cos \alpha + \sin \phi \sin \alpha \right) \right\} \sin \phi \, \mathrm dX- \int _0^1 \nu \, \frac{\chi }{\lambda } \left( \cos \phi \sin \alpha - \sin \phi \cos \alpha \right) \cos \phi \, \mathrm dX\end{aligned}$$

(35)

for its transverse deflection. The linearization of the axial tip displacement of the unbuckled but compressed rod follows as

$$\begin{aligned} u_0(1) = -\, \frac{\chi }{\lambda }. \end{aligned}$$

(36)

The linearization of the tip deflection about the unbuckled solution gives

$$\begin{aligned} w(1) = \int _0^1 \left( 1 - \frac{\chi }{\lambda } \right) \phi + \nu \, \frac{\chi }{\lambda } \left( \phi - \alpha \right) \mathrm dX= -\, \nu \, \frac{\chi }{\lambda } \, \alpha + \int _0^1 \left\{ 1 - \left( 1 - \nu \right) \frac{\chi }{\lambda } \right\} \phi \, \mathrm dX. \end{aligned}$$

(37)

Inserting the above result and the axial displacement (36) into (32), we obtain the following linearized relation for the angle $\alpha$:

$$\begin{aligned} \alpha = \left\{ c - \left( 1 - \nu \right) \frac{\chi }{\lambda } \right\} ^{-1} \left\{ 1 - \left( 1 - \nu \right) \frac{\chi }{\lambda } \right\} \int _0^1 \phi \, \mathrm dX. \end{aligned}$$

(38)

Substituting the result for $\alpha$, the non-homogeneous eigenvalue problem, from which the critical load is to be determined subsequently, follows from (30) as

$$\begin{aligned} \frac{\partial ^2 \phi }{\partial X^2} + a^2 \phi = a^4 \left\{ \left( c - e \right) \chi \right\} ^{-1} \int _0^1 \phi \, \mathrm dX, \qquad a^2 = \left( 1 - e \right) \chi , \qquad e = (1 - \nu ) \frac{\chi }{\lambda }, \end{aligned}$$

(39)

where the abbreviations a and e have been introduced for notational simplicity. The solution for the homogeneous problem of the linearized equation reads

$$\begin{aligned} \phi = C_1 \sin (a \, X) + C_2 \cos (a \, X), \end{aligned}$$

(40)

with constants $C_1$ and $C_2$. Any solution of the inhomogeneous problem therefore has to satisfy

$$\begin{aligned} \phi = C_1 \sin (a \, X) + C_2 \cos (a \, X) + a^2 \left\{ \left( c - e \right) \chi \right\} ^{-1} \int _0^1 \phi \, \mathrm dX. \end{aligned}$$

(41)

To determine the integral of $\phi$, we integrate the above equation over the beam’s axis, i.e.,

$$\begin{aligned} \int _0^1 \phi \, \mathrm dX= \frac{C_1 (1 - \cos a) + C_2 \sin a}{a} + a^2 \left\{ \left( c - e \right) \chi \right\} ^{-1} \int _0^1 \phi \, \mathrm dX, \end{aligned}$$

(42)

by which we obtain the relation

$$\begin{aligned} a^2 \left\{ \left( c - e \right) \chi \right\} ^{-1} \int _0^1 \phi \, \mathrm dX= a^2 \left\{ \left( c - e \right) \chi - a^2 \right\} ^{-1} \frac{C_1 (1 - \cos a) + C_2 \sin a}{a}. \end{aligned}$$

(43)

The solution of the linearized equilibrium equation (30) is therefore found as

$$\begin{aligned} \phi = C_1 \sin (a \, X) + C_2 \cos (a \, X) + a \left\{ \left( c - e \right) \chi - a^2 \right\} ^{-1} \left\{ C_1 (1 - \cos a) + C_2 \sin a \right\} , \end{aligned}$$

(44)

where the integration constants remain to be adjusted to the boundary conditions. In the present problem of a clamped cantilever, the angle of rotation must vanish at the clamping. At the opposing end, the bending moment $M= B \, \partial \phi / \partial X$ is zero. In our non-dimensional setting, these conditions translate into

$$\begin{aligned} \phi (0) = 0, \qquad \left. \frac{\partial \phi }{\partial X} \right| _{X=1} = 0. \end{aligned}$$

(45)

From the latter, we immediately find the relation

$$\begin{aligned} C_1 = C_2 \tan a, \end{aligned}$$

(46)

which, substituted into the first condition, yields

$$\begin{aligned} C_2 \left( 1 + a \left\{ \left( c - e \right) \chi - a^2 \right\} ^{-1} \tan a \right) = 0. \end{aligned}$$

(47)

Upon buckling, we require the existence of a non-trivial solution, $C_2 \ne 0$. As a consequence, the solutions of the eigenvalue problem (39), i.e., the critical loads at which the trivial solution is no longer unique, are the roots of the transcendental equation

$$\begin{aligned} \frac{\tan a}{a} = 1 - \left( c - e \right) \frac{\chi }{a^2}. \end{aligned}$$

(48)

Recalling the definitions (39) of a and e, we realize that the roots of the transcendental equation are hyper-surfaces in the four-dimensional space spanned by the non-dimensional geometry parameter c, the slenderness $\lambda$, the stiffness ratio $\nu$ and the force factor $\chi$. For the case $c = 1$, i.e., a force whose line of action runs through the base of the cantilever, the surfaces corresponding to the lowest four critical loads are exemplarily illustrated in Fig. 3. In Fig. 3, the critical loads of Euler’s classical elastica are indicated as light-gray planes parallel to the ($\nu$, $\lambda$)-plane. From (48), we recover the corresponding critical loads of the classical elastica as the limiting case $\nu \rightarrow 0$, $\lambda \rightarrow \infty$, which results in Timoshenko’s relation

$$\begin{aligned} \tan \sqrt{\chi } = \sqrt{\chi } \left( 1 - c \right) . \end{aligned}$$

(49)

Note that we also obtain the relation of the classical elastica if the shear stiffness and extensional stiffness coincide, i.e., $\nu = 1$, though all stiffnesses remain finite and axial deformation takes place. Interestingly, the critical loads no longer depend on the slenderness $\lambda$ is this case.

Fig. 3

For the case $c = 1$, the first four critical loads $\chi _\mathrm{crit}/ \pi ^2$ are illustrated as (orange) surfaces in the three-dimensional parameter space spanned by the stiffness ratio $\nu$, the slenderness $\lambda$ and the force $\chi$. The light-gray surfaces parallel to the ($\nu$, $\lambda$)-plane represent the corresponding critical loads of the classical elastica, where intersections with the surfaces of the shear-deformable beam are highlighted in red (colour figure online)

Fig. 4

Critical loads $\chi _\mathrm{crit}/ \pi ^2$ as function of the slenderness $\lambda$ for $c=1/2$. Dotted lines represent the critical loads of the classical elastica. The dashed line marks the limiting case of a beam compressed to zero length

Fig. 5

Critical loads $\chi _\mathrm{crit}/ \pi ^2$ as function of the slenderness $\lambda$ for $c=1$. Dotted lines represent the critical loads of the classical elastica. The dashed line marks the limiting case of a beam compressed to zero length

Fig. 6

Critical loads $\chi _\mathrm{crit}/ \pi ^2$ as function of the slenderness $\lambda$ for $c=2$. Dotted lines represent the critical loads of the classical elastica. The dashed line marks the limiting case of a beam compressed to zero length

To provide a deeper insight, we illustrate (up to) four critical loads as function of the slenderness $\lambda$ for different values of the stiffness ratio $\nu$ and for the three cases $c = 1 / 2$, $c = 1$ and $c = 2$ in Figs. 4, 5 and 6. The dotted lines in the figures represent the critical loads of the classical elastica. Dashed lines delimit the admissible region of deformation and correspond to the limiting case of a beam being compressed to zero length, i.e., $\varepsilon = -\,1$, which occurs for a load of $\chi = \lambda$. The results in Figs. 4a–d show that the buckling behavior crucially depends on the stiffness ratio $\nu$. In cases where the extensional stiffness is greater than the shear stiffness, i.e., $\nu > 1$, the critical loads of the shear-deformable beam are smaller than the corresponding loads in the classical elastica. The critical loads increase with increasing slenderness $\lambda$, and we obtain the critical loads of the classical elastica in the limit $\lambda \rightarrow \infty$. We further note that, for a given slenderness $\lambda$, the critical loads decrease if the shear stiffness is decreased compared to the extensional stiffness.

Similar as in the classical buckling problems [19], the picture changes completely, if the shear stiffness becomes greater than the extensional stiffness, i.e., $\nu < 1$. In this case, the critical loads at which the beam buckles are greater than in Euler’s classical elastica and approach that latter from above in the limit of an infinite slenderness, i.e., $\lambda \rightarrow \infty$. Regarding the number of critical loads and the corresponding buckling modes, we can make the following observations: The classical elastica has an infinite number of critical loads and corresponding buckling modes. If the extensional stiffness is equal or greater than the shear stiffness, i.e., $\nu \ge 1$, the number of buckling modes is restricted by the requirement $\chi \le \lambda$ and therefore depends on the slenderness $\lambda$. The dependence on $\lambda$ is distinct if the shear stiffness is greater than the extensional stiffness, i.e., $\nu < 1$. We note that a second critical load exists for each buckling mode, which lies, at least partially, within the admissible region. For each buckling mode, however, we can determine a slenderness, for which the two roots of the transcendental equation (48) and below which no critical load exists. In fact, the region enclosed by the dashed line and first critical load includes configurations of strongly compressed beams, in which the unbuckled equilibrium state is stable. Table 1 provides the critical loads $\chi _\mathrm{crit}/ \pi ^2$ corresponding to the first three buckling modes ($N=1,2,3$) for two values of the slenderness $\lambda$. In case two critical loads exist, we only provide the lower one; dashes indicate parameter combinations for which no critical load is found.

Increasing the distance c, the qualitative behavior remains unchanged. In Figs. 5 and 6, the critical loads are plotted as functions of the slenderness $\lambda$ for the cases $c=1$ and $c=2$. The case $c=1$, i.e., the line of action of the compressive force runs through the base of the cantilever has the same critical loads as a simply supported beam under a compressive force. Moving the point C further away from the base, we observe that the critical loads decrease. The limiting case $c \rightarrow \infty$ corresponds to a clamped cantilever subjected to a compressive force that does not change its direction, i.e., the angle $\alpha$ vanishes identically. Quantitative results for the critical loads are provided in Tables 2 and 3, where different values of $\nu$ and $\lambda$ have been considered.

4 Postbuckling solution

Having determined the critical loads at which trivial solutions of axially compressed beams bifurcate, we return to the nonlinear problem to construct the shapes of beams once buckling has already occurred. Note that the attribute trivial refers to the angle of rotation $\phi$ only, since the compressed state generally exhibits an axial deformation in view of its finite stiffness. In a first step, we introduce a first transformation, which shifts the angle $\phi$ by the (spatially) constant $\alpha$,

$$\begin{aligned} \beta = \phi - \alpha , \end{aligned}$$

(50)

Table 1 Critical loads $\chi _\mathrm{crit}/ \pi ^2$ for $c = 1/2$

Table 2 Critical loads $\chi _\mathrm{crit}/ \pi ^2$ for $c = 1$

Table 3 Critical loads $\chi _\mathrm{crit}/ \pi ^2$ for $c = 2$

which allows us to rewrite the equilibrium relation (27) using the definition (39) of e as

$$\begin{aligned} \frac{\partial ^2 \beta }{\partial X^2}+ \chi \sin \beta \left( 1 - e \cos \beta \right) = 0. \end{aligned}$$

(51)

Pulling out a spatial derivative and subsequent integration over the beam’s (non-dimensional) length gives

$$\begin{aligned} \frac{1}{2} \left( \frac{\partial \beta }{\partial X}\right) ^2 - \chi \cos \beta + e \, \frac{\chi }{2} \cos ^2 \beta = C, \end{aligned}$$

(52)

where C denotes a constant of integration. We can determine this constant of integration by considering the boundary conditions at the free end $X=1$, which, in terms of $\beta$, read

$$\begin{aligned} \beta _1= \beta (1) = \phi (1) - \alpha , \qquad \left. \frac{\partial \beta }{\partial X} \right| _{X=1} = \left. \frac{\partial \phi }{\partial X} \right| _{X=1} = 0. \end{aligned}$$

(53)

Evaluating the first integral (52) at the free end yields

$$\begin{aligned} - \,\chi \cos \beta _1+ e \, \frac{\chi }{2} \cos ^2 \beta _1= C. \end{aligned}$$

(54)

Once we substitute the above relation into (52), we obtain the relation

$$\begin{aligned} \left( \frac{\partial \beta }{\partial X}\right) ^2 = 2 \, \chi \left( \cos \beta - \cos \beta _1\right) - e \, \chi \left( \cos ^2 \beta - \cos ^2 \beta _1\right) . \end{aligned}$$

(55)

Though the above result has a relatively simple structure, we cannot relate the individual terms immediately to elliptic integrals in their canonical form. To identify the right-hand side of (55) as integrands of elliptic integrals, we need introduce several transformations in what follows. As a next step, we make use of the trigonometric identities

$$\begin{aligned} \cos \beta = 1 - 2 \sin ^2 \frac{\beta }{2} , \qquad \cos ^2 \beta = 1 - 4 \sin ^2 \frac{\beta }{2} + 4 \sin ^4\frac{\beta }{2}, \end{aligned}$$

(56)

which allows us to rewrite (55) as

$$\begin{aligned} \left( \frac{\partial \beta }{\partial X}\right) ^2 = 4 \chi \left\{ \left( 1 - e \right) \left( \sin ^2 \frac{\beta _1}{2} - \sin ^2 \frac{\beta }{2} \right) + e \left( \sin ^4\frac{\beta _1}{2} - \sin ^4\frac{\beta }{2} \right) \right\} . \end{aligned}$$

(57)

By means of a second transformation, we introduce the angle $\theta$, which is related to $\beta$ through the nonlinear equation

$$\begin{aligned} \sin \frac{\beta }{2} = -\, q \sin \theta , \qquad q = \sin \frac{\beta _1}{2}. \end{aligned}$$

(58)

The local relation between $\beta$ and $\theta$,

$$\begin{aligned} \frac{\partial \beta }{\partial \theta } = -\, 2 \, q \, \cos \theta \left( 1 - q^2 \sin ^2 \theta \right) ^{-1/2}, \end{aligned}$$

(59)

along with the chain rule of differential calculus allows us to substitute $\theta$ for $\beta$ in (57), i.e.,

$$\begin{aligned} \left( \frac{\partial \theta }{\partial X}\right) ^2 = \left( \frac{\partial \beta }{\partial X}\right) ^2 \left( \frac{\partial \beta }{\partial \theta } \right) ^{-2} = \chi \left( 1 - q^2 \sin ^2 \theta \right) \left\{ 1 - e + q^2 e \left( 1 + \sin ^2 \theta \right) \right\} . \end{aligned}$$

(60)

By means of a third transformation, we want to eliminate the product on the right-hand side of the above equation. For this purpose, consider the angle $\psi$, which is related to $\theta$ through

$$\begin{aligned} \sin \psi = \left\{ 1 - e + q^2 e \left( 1 + \sin ^2 \theta \right) \right\} ^{-\frac{1}{2}} \sqrt{1 - e + 2 \, q^2 e} \sin \theta . \end{aligned}$$

(61)

Again, we use the local relationship among the variables, i.e.,

$$\begin{aligned} \left( \frac{\partial \theta }{\partial \psi } \right) ^2 = \left( 1 - e + q^2 e \right) \left( 1 - e + 2 \, q^2 e \right) \left( 1 - e + 2 \, q^2 e - q^2 e \sin ^2 \psi \right) ^{-2}, \end{aligned}$$

(62)

to rewrite (60) in terms of $\psi$

$$\begin{aligned} \left( \frac{\partial \psi }{\partial X}\right) ^2 = \left( \frac{\partial \theta }{\partial X}\right) ^2 \left( \frac{\partial \theta }{\partial \psi } \right) ^{-2} = \chi \left\{ 1 - e + 2 \, q^2 e - q^2 \left( 1 + q^2 e \right) \sin ^2 \psi \right\} . \end{aligned}$$

(63)

Note that $\theta$ and $\psi$ coincide if the parameter e vanishes, which is the case if the shear stiffness and the extensional stiffness are identical ($\nu = 1$), and for Euler’s classical elastica ($\nu = 0$ and $\lambda \rightarrow \infty$).

Before we proceed, we want to briefly discuss the respective boundary conditions in terms of the variables $\beta$, $\theta$ and $\psi$. At the clamped end, the cross-sectional angle of rotation vanishes, cf. (45), whereas the rotation at the free end $\phi (1)$ remains to be determined from the equilibrium state. As $\beta$ is merely offset from $\phi$ by the constant angle $\alpha$, we immediately find the equivalent relations

$$\begin{aligned} \beta _0 = \beta (0) = -\, \alpha , \qquad \beta _1 = \beta (1) = \phi (1) - \alpha . \end{aligned}$$

(64)

From the transformation relation between $\beta$ and $\theta$, which is explicitly given by

$$\begin{aligned} \theta = \arcsin \left( -\, \frac{1}{q} \sin \frac{\beta }{2} \right) = \arcsin \left\{ -\, \left( \sin \frac{\beta _1}{2} \right) ^{-1} \sin \frac{\beta }{2} \right\} , \end{aligned}$$

(65)

we obtain the terminal values of $\theta$ as

$$\begin{aligned} \theta _0 = \theta (0) = \arcsin \left\{ \left( \sin \frac{\beta _1}{2} \right) ^{-1} \sin \frac{\alpha }{2} \right\} , \qquad \theta _1 = \theta (1) = \arcsin (-\,1) = -\, \frac{\pi }{2}. \end{aligned}$$

(66)

The relation (61) between the angles $\theta$ and $\psi$ gives

$$\begin{aligned} \psi _0 = \psi (0) = \arcsin \left( \left\{ 1 - e + q^2 e \left( 1 + \sin ^2 \theta _0 \right) \right\} ^{-\frac{1}{2}} \sqrt{1 - e + 2 \, q^2 e} \sin \theta _0 \right) , \qquad \psi _1 = \psi (1) = -\, \frac{\pi }{2}, \end{aligned}$$

(67)

which implies that $\theta$ and $\psi$ have the same sign. We have already noted that the bending moment vanishes at the free end of the beam, cf. (45). According to the constitutive equation of the bending moment (10), the bending strain $\kappa$, which can be regarded as a material measure of curvature, is therefore zero at the free end, i.e., $\kappa (1) = 0$. The material curvature $\kappa$ and the geometric curvature $\varkappa$ of the axis are related by the axial stretch $\varLambda$,

$$\begin{aligned} \kappa = \frac{\partial \phi }{\partial X} = \varLambda \, \frac{\partial \phi }{\partial x} = \varLambda \, \varkappa . \end{aligned}$$

(68)

For this reason, the geometric curvature $\varkappa$ must vanish at those material points where the bending strain $\kappa$ vanishes, i.e., the inflection points of the beam’s axis in the buckled configuration. Due to the shift by $\alpha$, the angle $\beta$ is introduced such that the relations $\beta = \pm \,\beta _1$ and, consequently, $\theta = \psi = \pm \, \pi /2$ hold at all inflections point of the axis. The number of inflection points depends on the buckling mode on the one hand, and on the value of c on the other hand. For $c > 1$, the number of inflection points along the axis is N, where N denotes the corresponding buckling mode, whereas the axis shows $N+1$ inflection points for $c \le 1$. Note that inflection points at end points of the beam are included in the numbers above. Exemplarily, we consider the first buckling mode ($N=1$), for which we find a single inflection point at the free tip if $c > 1$, whereas an additional inflection point occurs along the axis if $c \le 1$. To avoid a cumbersome case-by-case analysis regarding the change of signs, we exploit the periodicity of trigonometric functions, which allows $\psi$ to be taken as a monotonically increasing function ranging from $\psi _0 > 0$ at the clamped end to $\psi _1 = N \pi + \pi / 2$ at the free end; under this assumption, we can distinguish the three different cases with respect to $\psi _0$: For $c < 1$, we obtain the interval $0< \psi _0 < \pi /2$; we find $\psi _0 = \pi / 2$ for $c = 1$, and for $c > 1$, the angle must lie in the range of $\pi / 2< \psi _0 < \pi$.

The ordinary differential equation (63) allows a separation of variables, and subsequent integration over the domains of the axial coordinate X and the angle $\psi$ yields

$$\begin{aligned} \sqrt{\chi }= \left( 1 - e + 2 \, q^2 e \right) ^{-\frac{1}{2}} \int _{\psi _0}^{N \pi + \pi /2}\frac{\mathrm d \psi }{\sqrt{1 - m \sin ^2 \psi }} , \qquad m = q^2 \frac{1 + q^2 e}{1 - e + 2 \, q^2 e}, \end{aligned}$$

(69)

which can be briefly written as

$$\begin{aligned} \sqrt{\chi }\sqrt{1 - e + 2 \, q^2 e} = \left( 2 \, N + 1\right) F(m) - F(\psi _0, m), \end{aligned}$$

(70)

where F(m) and $F(m, \psi _0)$ denote the complete and incomplete elliptic integrals of the first kind. We want to emphasize that the notation of elliptic integrals is not consistent in the literature. In what follows, we adopt the notation that is used in the symbolic software Mathematica [30]. The above result relates the compressive force to the angle $\psi _0$ and, through the transformations (61), (58), (50), to the rotation $\phi _1 = \phi (1)$ at the tip of the cantilever. As a second unknown, relation (70) also contains the angle $\alpha$, which depends on the equilibrium configuration of the buckled beam. We can establish a further equation by considering the reaction moment at the clamped end of the beam, whose non-dimensional representation is given by

$$\begin{aligned} \left. \frac{\partial \phi }{\partial X}\right| _{X = 0} = ( c - 1 ) \, \chi \sin \alpha . \end{aligned}$$

(71)

Evaluating the integral (55) of the balance relation formulated in $\beta$ at the clamped end $X = 0$, we obtain the transcendental equation

$$\begin{aligned} \chi ( c - 1 )^2 \sin ^2 \alpha = 2 \left( \cos \alpha - \cos \beta _1\right) - e \left( \cos ^2 \alpha - \cos ^2 \beta _1\right) , \end{aligned}$$

(72)

where (64) has been substituted. The set of nonlinear equations (70) and (72) can be solved for the unknowns $\phi _1$ and $\alpha$, e.g., by means of Newton’s method. Once $\phi _1$ and $\alpha$ have been determined, we can establish a relationship between X and the corresponding angle $\psi (X)$ if we integrate (63) only over a part of the beam rather than the whole structure,

$$\begin{aligned} \sqrt{\chi }\sqrt{1 - e + 2 \, q^2 e} \, X = F(\psi , m) - F(\psi _0, m). \end{aligned}$$

(73)

With the rotation of the beam’s cross section being determined in closed form, we can compute the position of the its axis. For this purpose, we introduce the definitions (50), (39) of the angle $\beta$ and the constant parameter e in the integrands of (34)–(35), which gives the relation

$$\begin{aligned} 1 + \frac{\partial u}{\partial X}= -\, \frac{\nu }{1 - \nu } \, e \cos \alpha + \cos \beta \cos \alpha - \sin \beta \sin \alpha - e \cos ^2 \beta \cos \alpha + e \sin \beta \cos \beta \sin \alpha \end{aligned}$$

(74)

for the axial component of the position gradient, whereas the transverse component is given by

$$\begin{aligned} \frac{\partial w}{\partial X}= -\, \frac{\nu }{1 - \nu } \, e \sin \alpha + \sin \beta \cos \alpha + \cos \beta \sin \alpha - e \cos ^2 \beta \sin \alpha - e \cos \beta \sin \beta \cos \alpha . \end{aligned}$$

(75)

We follow the same procedure as with the rotation of the cross section, i.e., with the aid of the identities (56) and the transformation (58), we can express the components of the axis’ position gradient in terms of the angle $\theta$ as

$$\begin{aligned} 1 + \frac{\partial u}{\partial X}= & {} -\, \cos \alpha - \frac{\nu }{1 - \nu } \, e \cos \alpha + 2 \left( 1 - q^2 \sin ^2 \theta \right) \cos \alpha \nonumber \\&-\, 2 \, q \sin \theta \sqrt{1 - q^2 \sin ^2 \theta } \left( 1 - e + 2 \, q^2 e \sin ^2 \theta \right) \sin \alpha \nonumber \\&-\, e \left\{ 1 - 4 \left( 1 - q^2 \sin ^2 \theta \right) + 4 \left( 1 - q^2 \sin ^2 \theta \right) ^2 \right\} \cos \alpha \end{aligned}$$

(76)

as well as

$$\begin{aligned} \frac{\partial w}{\partial X}= & {} -\, \sin \alpha - \frac{\nu }{1 - \nu } \, e \sin \alpha + 2 \left( 1 - q^2 \sin ^2 \theta \right) \sin \alpha \nonumber \\&+\, 2 \, q \sin \theta \sqrt{1 - q^2 \sin ^2 \theta } \left( 1 - e + 2 \, q^2 e \sin ^2 \theta \right) \cos \alpha \nonumber \\&-\, e \left\{ 1 - 4 \left( 1 - q^2 \sin ^2 \theta \right) + 4 \left( 1 - q^2 \sin ^2 \theta \right) ^2 \right\} \sin \alpha . \end{aligned}$$

(77)

Substituting the definition (61) of the angle $\psi$, the spatial derivatives are formulated as

$$\begin{aligned} 1 + \frac{\partial u}{\partial X}= & {} -\, \cos \alpha - \frac{\nu }{1 - \nu } \, e \cos \alpha + 2 \, \frac{1 - m \sin ^2 \psi }{1 - n \sin ^2 \psi } \cos \alpha - e \left( 2 \, \frac{1 - m \sin ^2 \psi }{1 - n \sin ^2 \psi } - 1 \right) ^2 \cos \alpha \nonumber \\&-\, 2 \, q \, \frac{\sqrt{1 - e + q^2 e} \sqrt{1 - m \sin ^2 \psi } \sqrt{1 - e + 2 \, q^2 e} \left( 1 - e + q^2 e \sin ^2 \psi \right) \sin \psi }{\left( 1 - e + 2 \, q^2 e \right) \left( 1 - n \sin ^2 \psi \right) ^2} \sin \alpha \end{aligned}$$

(78)

as well as

$$\begin{aligned} \frac{\partial w}{\partial X}= & {} - \,\sin \alpha - \frac{\nu }{1 - \nu } \, e \sin \alpha + 2 \, \frac{1 - m \sin ^2 \psi }{1 - n \sin ^2 \psi } \sin \alpha - e \left( 2 \, \frac{1 - m \sin ^2 \psi }{1 - n \sin ^2 \psi } - 1 \right) ^2 \sin \alpha \nonumber \\&+\, 2 \, q \, \frac{\sqrt{1 - e + q^2 e} \sqrt{1 - m \sin ^2 \psi } \sqrt{1 - e + 2 \, q^2 e} \left( 1 - e + q^2 e \sin ^2 \psi \right) \sin \psi }{\left( 1 - e + 2 \, q^2 e \right) \left( 1 - n \sin ^2 \psi \right) ^2} \cos \alpha . \end{aligned}$$

(79)

The chain rule of differential calculus allows us to express the spatial derivatives in terms of derivatives with respect to $\psi$, i.e.,

$$\begin{aligned} \frac{\partial u}{\partial \psi }= \frac{\partial u}{\partial X}\left( \frac{\partial \psi }{\partial X}\right) ^{-1} = \frac{\partial u}{\partial X}\left( \sqrt{\chi }\sqrt{ 1 - e + 2 \, q^2 e} \sqrt{1 - m \sin ^2 \psi } \right) ^{-1}, \end{aligned}$$

(80)

where the square root of relation (63) has been utilized. The starting point for the construction of an elliptic integral solution is therefore obtained as

$$\begin{aligned}&\sqrt{\chi }\sqrt{ 1 - e + 2 \, q^2 e} \left\{ \left( \frac{\partial \psi }{\partial X}\right) ^{-1} + \frac{\partial u}{\partial \psi }\right\} = \left( - \cos \alpha - e \cos \alpha - \frac{\nu }{1 - \nu } \, e \cos \alpha \right) \frac{1}{\sqrt{1 - m \sin ^2 \psi }} \nonumber \\&\quad +\, 2 \, \frac{\sqrt{1 - m \sin ^2 \psi }}{1 - n \sin ^2 \psi } \cos \alpha + 4 \, e \, \left\{ \frac{\sqrt{1 - m \sin ^2 \psi }}{1 - n \sin ^2 \psi } - \frac{\left( 1 - m \sin ^2 \psi \right) ^2}{\sqrt{1 - m \sin ^2 \psi } \left( 1 - n \sin ^2 \psi \right) ^2} \right\} \cos \alpha \nonumber \\&\quad -\, 2 \, q \, \frac{\sqrt{1 - e + q^2 e} \sqrt{ 1 - e + 2 \, q^2 e} \left( 1 - e + q^2 e \sin ^2 \psi \right) \sin \psi }{\left( 1 - e + 2 \, q^2 e \right) \left( 1 - n \sin ^2 \psi \right) ^2} \sin \alpha , \end{aligned}$$

(81)

where we have kept the positive root only. For the transverse deflection, the corresponding relation reads

$$\begin{aligned}&\sqrt{\chi }\sqrt{ 1 - e + 2 \, q^2 e} \, \frac{\partial w}{\partial \psi }= \left( -\, \sin \alpha - e \sin \alpha - \frac{\nu }{1 - \nu } \, e \sin \alpha \right) \frac{1}{\sqrt{1 - m \sin ^2 \psi }} \nonumber \\&\quad +\, 2 \, \frac{\sqrt{1 - m \sin ^2 \psi }}{1 - n \sin ^2 \psi } \sin \alpha + 4 \, e \, \left\{ \frac{\sqrt{1 - m \sin ^2 \psi }}{1 - n \sin ^2 \psi } - \frac{\left( 1 - m \sin ^2 \psi \right) ^2}{\sqrt{1 - m \sin ^2 \psi } \left( 1 - n \sin ^2 \psi \right) ^2} \right\} \sin \alpha \nonumber \\&\quad +\, 2 \, q \, \frac{\sqrt{1 - e + q^2 e} \sqrt{ 1 - e + 2 \, q^2 e} \left( 1 - e + q^2 e \sin ^2 \psi \right) \sin \psi }{\left( 1 - e + 2 \, q^2 e \right) \left( 1 - n \sin ^2 \psi \right) ^2} \cos \alpha . \end{aligned}$$

(82)

Though the beam can buckle in both directions, we have also dropped the negative sign for the transverse deflection, since the signs of $\psi (1)$ and $\alpha$ determine the direction into which the beam deflects in the buckled configuration. After a separation of variables, we can integrate the above relations from $X = 0$, $u(0) = 0$, $w(0) = 0$ and $\psi (0) = \psi _0$, respectively, to some point X, at which the displacements u, w and the angle $\psi$ occur. In addition to the elliptic integral of the first kind, which has already emerged in the solution of the rotation (73), further, more complicated terms emerge, which we want to briefly discuss in what follows. For further details, we refer to the table of integrals by Gröbner and Hofreiter [16]. We start with the integral of the second term on the right-hand side of the above equations, which evaluates to

$$\begin{aligned} \begin{aligned} \int \frac{\sqrt{1 - m \sin ^2 \psi }}{1 - n \sin ^2 \psi } \, \mathrm d \psi&= \int \left( \frac{m}{n} \frac{1}{\sqrt{1 - m \sin ^2 \psi }} + \frac{n - m}{n} \frac{1}{\sqrt{1 - m \sin ^2 \psi } \left( 1 - n \sin ^2 \psi \right) } \right) \mathrm d \psi \\&= \frac{m}{n} \, F (\psi , m) + \frac{n - m}{n} \, \varPi (n, \psi , m) + C. \end{aligned} \end{aligned}$$

(83)

In the above relation, $\varPi (n, \psi , m)$ denotes the (incomplete) elliptic integral of the third kind, whose second parameter n is also referred to as the characteristic, and C is some constant of integration. The integral of the second term in the curly braces on the right-hand side of (81) and (82) gives

$$\begin{aligned}&\int \frac{\left( 1 - m \sin ^2 \psi \right) ^2}{\sqrt{1 - m \sin ^2 \psi } \left( 1 - n \sin ^2 \psi \right) ^2} \, \mathrm d \psi \nonumber \\&\quad = \int \frac{1}{\sqrt{1 - m \sin ^2 \psi }} \left\{ \frac{m^2}{n^2} - 2 \, \frac{m(m-n)}{n^2} \frac{1}{1 - n \sin ^2 \psi } + \frac{(m - n)^2}{n^2} \frac{1}{\left( 1 - n \sin ^2 \right) ^2 \psi } \right\} \mathrm d \psi \nonumber \\&\quad = \frac{m^2}{n^2} \, F(\psi , m) - 2 \, \frac{m(m-n)}{n^2} \, \varPi (n, \psi , m) \nonumber \\&\quad \quad +\, \frac{m - n}{2 (1-n)} \left\{ \frac{\sin \psi \cos \psi \sqrt{1 - m \sin ^2 \psi }}{1 - n \sin ^2 \psi } - \frac{m - n}{n^2} \, F(\psi , m) - \frac{1}{n} \, E(\psi , m)\right. \nonumber \\&\quad \quad \left. + \,\frac{n^2 - 2 m n - 2 n + 3 m}{n^2} \, \varPi (n, \psi , m) \right\} + C, \end{aligned}$$

(84)

where $E(\psi , m)$ denotes the (incomplete) elliptic integral of the second kind. The integral of the last term on the right-hand side of (81) and (82) is obtained as

$$\begin{aligned} \int \frac{\left( 1 - e + q^2 e \sin ^2 \psi \right) \sin \psi }{\left( 1 - n \sin ^2 \psi \right) ^2} \, \mathrm d \psi = - \frac{ \left( 1 - e + 2 \, q^2 e \right) ^2 \cos \psi }{1 - e + 2 \, q^2 e - q^2 e \sin ^2 \psi } + C. \end{aligned}$$

(85)

Once we put the individual terms together, we arrive the following closed-form expression for the axial displacement,

$$\begin{aligned} \left( X + u \right) \sqrt{\chi }+ C_u= & {} -\, \frac{F ( \psi , m )}{\sqrt{ 1 - e + 2 \, q^2 e}} \frac{\nu \, e}{1 - \nu } \cos \alpha - \sqrt{ 1 - e + 2 \, q^2 e} \cos \alpha \left( F(\psi , m) - 2 \, E (\psi , m) \right) \nonumber \\&-\, \frac{2 \, q \, \cos \psi }{1 - n \sin ^2 \psi } \left( \sqrt{1 - e + q^2 e} \sin \alpha + \frac{q \, e \sqrt{1 - m \sin ^2 \psi } \sin \psi }{\sqrt{1 - e + 2 \, q^2 e}} \cos \alpha \right) , \end{aligned}$$

(86)

where we note that elliptic integrals of the third kind have canceled. The constant of integration follows from the boundary conditions at the clamping $X = 0$, where the axial displacement vanishes, i.e., $u(0) = 0$,

$$\begin{aligned} C_u= & {} -\, \frac{F ( \psi _0, m )}{\sqrt{ 1 - e + 2 \, q^2 e}} \frac{\nu \, e}{1 - \nu } \cos \alpha - \sqrt{ 1 - e + 2 \, q^2 e} \cos \alpha \left( F(\psi _0, m) - 2 \, E (\psi _0, m) \right) \nonumber \\&-\, \frac{2 \, q \, \cos \psi _0}{1 - n \sin ^2 \psi _0} \left( \sqrt{1 - e + q^2 e} \sin \alpha + \frac{q \, e \sqrt{1 - m \sin ^2 \psi _0} \sin \psi _0}{\sqrt{1 - e + 2 \, q^2 e}} \cos \alpha \right) . \end{aligned}$$

(87)

For the transverse displacement, we obtain the result

$$\begin{aligned} w \sqrt{\chi }+ C_w&= -\, \frac{F ( \psi , m )}{\sqrt{ 1 - e + 2 \, q^2 e}} \frac{\nu \, e}{1 - \nu } \sin \alpha - \sqrt{ 1 - e + 2 \, q^2 e} \sin \alpha \left( F(\psi , m) - 2 \, E (\psi , m) \right) \nonumber \\&\quad +\, \frac{2 \, q \, \cos \psi }{1 - n \sin ^2 \psi } \left( \sqrt{1 - e + q^2 e} \cos \alpha - \frac{q \, e \sqrt{1 - m \sin ^2 \psi } \sin \psi }{\sqrt{1 - e + 2 \, q^2 e}} \sin \alpha \right) , \end{aligned}$$

(88)

where the boundary condition at the clamping $w(0) = 0$ gives

$$\begin{aligned} C_w= & {} -\, \frac{F ( \psi _0, m )}{\sqrt{ 1 - e + 2 \, q^2 e}} \frac{\nu \, e}{1 - \nu } \sin \alpha - \sqrt{ 1 - e + 2 \, q^2 e} \sin \alpha \left( F(\psi _0, m) - 2 \, E (\psi _0, m) \right) \nonumber \\&+\, \frac{2 \, q \, \cos \psi _0}{1 - n \sin ^2 \psi _0} \left( \sqrt{1 - e + q^2 e} \cos \alpha - \frac{q \, e \sqrt{1 - m \sin ^2 \psi _0} \sin \psi _0}{\sqrt{1 - e + 2 \, q^2 e}} \sin \alpha \right) . \end{aligned}$$

(89)

With the constants of integration being determined, we arrive at a closed-form relationship between the axial position X, the angle of rotation $\psi$, the axial displacement u and the transverse deflection w by means of the results (73), (86) and (88). To construct the buckled shapes, we first have to solve the nonlinear relations (70)–(72) for $\phi _1$ and $\alpha$ and compute the corresponding $\psi _0$ to subsequently evaluate the elliptic integral solutions within the range $\psi \in \left[ \psi _0, N \, \pi + \pi / 2 \right]$.

Fig. 7

Buckled shapes corresponding to the first three buckling modes for $c = 1/2$

Fig. 8

Buckled shapes corresponding to the first three buckling modes for $c = 1$

Fig. 9

Buckled shapes corresponding to the first three buckling modes for $c = 2$

In Figs. 7, 8 and 9, several buckled configurations are illustrated for the cases $c = 1/2$, $c = 1$ and $c = 2$, where the respective load intensities are provided in the figures. The illustrated shapes correspond to the first three buckling modes of the cantilever.

As for the critical loads, we obtain the solutions of the extensible elastica as the limiting case $\nu = 0$. If we further let $\lambda \rightarrow \infty$, the corresponding relations of Euler’s classical elastica are recovered from the above results.

5 Conclusion

In the present paper, we have discussed the buckling and postbuckling of a cantilever subjected to a follower load. Adopting Reissner’s theory for large deformations of beams, we have included the effects of shear deformation and extensibility of the beam’s axis. Linearizing the governing equations about the unbuckled configuration, we have obtained an inhomogeneous eigenvalue problem, from which the critical loads at which the trivial solution becomes unstable have been determined. The critical loads depend on both the slenderness of the structure and, more importantly, on the ratio between the shear stiffness and the extensional stiffness. While the buckling behavior of a shear-deformable beam qualitatively follows the classical elastica if the shear stiffness is smaller than the extensional stiffness, we find a different behavior if the shear stiffness exceeds the extensional stiffness. In the latter case, up to two bifurcation points exist per buckling mode. Moreover, we have observed admissible regions of the slenderness, in which no critical loads are found, i.e., buckling does not occur. Subsequently, we have determined exact solutions for buckled configurations of the beam in terms of elliptic integrals. An additional nonlinear equation related to the orientation of the force has to be solved before the closed-form relations for the rotation of the cross sections and the displacement of the beam’s axis can be evaluated. We have presented examples of buckled shapes for several locations of the fixed point, through which the follower force passes.