1 Introduction

Near-surface air temperature is one of the most important climatological variables. In its roughest traits, it defines climate zones, reflects altitude, and summarizes climatic evolution. To a great extent, it also determines humans’ and other living beings’ way of life. Information on its statistical characteristics is essential in a wide range of fields. To cite only a few, environmental research and planning such as agriculture (e.g., Wheeler et al. 2000; Asseng et al. 2011), health (Pascual et al. 2006; Kjellstrom et al. 2009), and climate impact research in general require knowledge of its seasonal and interannual variability (e.g., Legates and Willmott 1990; Luterbacher et al. 2004), past and future evolution (Easterling et al. 1997; IPCC 2013), extremes (Kharin and Zwiers 2005), and other characteristics. Depending on the application, near-surface air temperature can often be modeled quite satisfactorily with a normal distribution. Yet, based on station observations, Harmel et al. (2002) and Ruff and Neelin (2012) provide evidence that the distribution of daily temperature data is skewed and that the skewness depends on the season. Perron and Sura (2013) examine reanalysis data and show that not only skewness but also kurtosis should be considered, that differs in summer and winter. Evin et al. (2019) successfully modeled surface air temperature in Switzerland for a weather generator using a distribution with seasonally dependent location, variance, skewness, and kurtosis.

The seasonal cycle is of course not the only non-stationarity of air temperature that needs to be addressed. Air temperature in Switzerland has increased strongly over the last decades, with a more pronounced increase in later decades (Brönnimann et al. 2014; Begert and Frei 2018; Isotta et al. 2019). This temperature increase varies from one season to the other; as for instance, higher temperature trends are observed in summer and spring than in winter and fall in recent decades (Rebetez and Reinhard 2008; Brönnimann et al. 2014; Begert and Frei 2018; Isotta et al. 2019). Thus, we can expect modeling daily surface air temperature at a particular location, in a region with complex terrain such as Switzerland, to require a model with at least four parameters to describe higher-order behavior with some accuracy. These should be dependent on the year on the one hand to represent long-term climatic change and depend on the Julian day on the other hand. Thereby, we accommodate seasonal variations not only of the parameters themselves but also of the long-term trend.

Informing the public about extreme climatic events is an important task of the national meteorological and hydrological services (NMHS). In particular, they must provide some quantitative measure for the degree to which they are extreme. This is generally formulated as a return period T, the event’s recurrence probability in the long-term average, given an assumed climate. In earlier years, MeteoSwiss, for instance, relied on an empirical estimator, Weibull’s formula (Table 18.3.1 of Stedinger et al. 1993), which is based on the rank of observation with respect to the period of observation. This method is simple and yields acceptable results for events that are sufficiently frequent, but becomes inadequate for events that occur on average only a few times in the period considered or less often. Using the framework of extreme value statistics has become more common, as it allows an estimation of the frequency of events beyond the range of observation if sufficiently long periods of observation are available. The most common estimation procedures (Coles 2001) are either to divide the data into blocks of equal size and fit the generalized extreme value (GEV) distribution to the block maxima (BM) or define a threshold and fit the generalized Pareto distribution (GPD) to threshold excesses (Peaks-over-Threshold, or POT). A return period is then simply the inverse of the probability that a value will be exceeded. In their basic form, both methods are only meaningful in a stationary climate.

However, the climate is known to undergo long-term changes (IPCC 2013 and references therein), with higher temperatures in the current climate than in the past. Indeed, hot spells have occurred more frequently in recent years (e.g., Schär et al. 2004; Klein Tank and Können 2003; Furrer et al. 2010; Perkins et al. 2012), and new temperature records have emerged. In a transient climate, the classification of temperature extremes (e.g., Wigley 2009; Katz 2013; Cooley 2013) must be addressed differently. Rusticucci and Tencer (2008) and Kharin et al. (2013), for instance, chose to fit the GEV over different periods and compare the respective return periods. Another approach consists of introducing yearly varying parameters in the GEV distribution (e.g., Kharin and Zwiers 2005; Kharin et al. 2013; Wang et al. 2014; Cheng et al. 2014). Since these studies aim at quantifying long-term changes in climatic characteristics, they only consider the annual maxima of a temperature variable of interest.

Considering only the yearly maxima distorts the estimation of return periods and ignores deviations from the usual seasonal cycle that may have heavy socio-economic consequences. Unusually high temperatures in mid-summer tend to attract attention because they challenge known temperature records. Yet, the same relative increase in temperature occurring at another time of the year, while resulting in an unimpressive absolute temperature, may be just as relevant. For instance, it is known that unusually high temperatures at the beginning of summer can have a greater effect on human well-being and mortality rates than later in the season (e.g., Hajat et al. 2002; Gasparrini et al. 2016; Ragettli et al. 2017), even if the temperature is, in effect, less high. Furthermore, unusually high temperatures in winter affect snow coverage (Beniston 2005), the economy of ski tourism, especially at the more vulnerable low-lying ski locations (Steiger 2011), water availability in spring and summer (Beniston and Stoffel 2014), or can result in a welcome reduction in traffic accidents (Norrman et al. 2000) and road maintenance costs (Lorentzen 2020). During the transition seasons, high temperatures can lead to early plant and pollen development (Gehrig and Clot 2021), while extremely cold conditions in late spring as they occurred in April 2017 in Switzerland (Vitasse and Rebetez 2018) can have devastating effects on the crops in their developing phase. For the estimation of return periods, seasonal non-stationarity has often been addressed by considering summer and winter months separately (Nogaj et al. 2006; Abaurrea et al. 2007) or by using a threshold that follows temperature’s seasonal variation in the POT approach (Coelho et al. 2008).

None of these studies, however, address the convergence properties of the maxima of the Gaussian variables. Fisher and Tippett (1928) mention that “From the normal distribution, the limiting distribution is approached with extreme slowness.” In other words, for the maxima to converge towards a GEV, the blocks must contain a very large number of observations. Hall (1979) quantifies the rate of convergence, finding it to be bounded by \(3/\mathrm{ln}(n)\), while Davis (1982) indicates and Gasull et al. (2015) show that this upper bound of the convergence rate can be reduced to \(1/\mathrm{ln}(n)\). For temperature observations, this problem is compounded by the strong serial correlation, which further limits the number of independent values in a block. Thus, we can assume a large systematic error in the estimation of the GEV that cannot be quantified. In principle, it is possible to pool consecutive years into larger blocks in the hope of ensuring asymptotic behavior, but this reduces the number of blocks available and increases the estimation uncertainty. Also, the number of years necessary in a block to ensure asymptotic behavior is unknown.

In this study, we take a novel approach to classifying daily air temperatures that take into account both long-term changes and the seasonal cycle. We first model temperature’s inherent complexity, allowing for four time-varying parameters, then transform the observations to a standard normal distribution. To avoid uncertainties due to convergence issues, rather than estimating a GEV with the now stationary yearly maxima, we classify unusually warm or cold standardized temperatures by means of their empirical quantile. This approach dissociates “extremeness” from seasonal and long-term variations and allows us to compare the severity of events in their local intensity and spatial extension from season to season and year to year. Thus, we provide.

  • a detailed probabilistic description of the daily temperature distribution as a function of the year and of the day in the year, and

  • a method to classify individual events in their prevailing climate at a given time (for each day of the year and each year) and thereby estimate recurrence values.

As a case study area, we consider meteorological observations from Switzerland, a mid-latitude region where the temperature is subject to a pronounced seasonal cycle, high variability in space due to dominating alpine topographic features, and a strong anthropogenic warming signal in recent decades.

The paper is structured as follows. Section 2 gives a brief description of the study area and the data, while the temperature model and the classification method are detailed in Section 3. The model is validated in Section 4.1, and the seasonal cycle of the model parameters is examined in Section 4.2. Section 4.3 presents the results of a Switzerland-wide classification of warm and cold events and illustrates how it brings to light the relative extremeness with respect to the seasons or the change of the prevailing climate between the beginning and the end of the analyzed period. Finally, the way events are distributed over seasons and years since 1965 is discussed in Sections 4.4 and 4.5. The results are discussed in Section 5, and finally, some conclusions are drawn in Section 6.

2 Study area and data

2.1 Study area

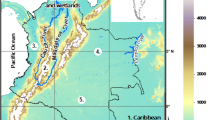
Switzerland is a small country in Central Europe, and approximately 60% of its area is part of the European Alps (Fig. 1). With their high peaks (some exceeding 4000 m a.s.l.) and deep valleys (some below 1000 m a.s.l.), the Alps separate the hilly Swiss Plateau and the Jura mountains (peaks up to 1600 m a.s.l.) in the north from the Ticino and other regions in the south. The Plateau and Jura are mainly exposed to air masses from the Atlantic Ocean and, to a lesser extent, to continental air masses from Eastern Europe. The climate south of the main divide is predominantly influenced by Mediterranean air masses (CH2018 2018). The interaction of the atmospheric flow with the complex topography can lead to small-scale horizontal temperature contrasts, which deviate considerably from a simple linear vertical dependence (Frei 2014; Scherrer et al. 2021). In particular, this can result in cold-air pools that form frequently in mountain valleys (Whiteman 1982; Barry 2008) and on the Swiss Plateau in the winter half-year, often in conjunction with fog situations (Salzmann et al. 2015; Scherrer and Appenzeller 2014; Wanner and Kunz 1983). In summer, considerable thermal contrasts can develop between the mountainous foreland and the inner Alpine valleys (Steinacker 1984; Whiteman 1990). In addition, regional wind systems can influence the spatial temperature structure considerably. For example, the foehn, a warm downslope wind, can lead to complex temperature patterns, sometimes penetrating into the adjacent flatland (Hoinka 1985; Gutermann et al. 2012).

Fig. 1
figure 1

Map of Switzerland with the location of the analyzed stations (black crosses and dots) and five main climatological regions (Jura, Plateau, Prealps, Alps, and South). The colored dots indicate eleven stations representing typical flavors of the Swiss temperature climate. For these stations, detailed analyses of the parameter distribution are shown in Fig. 5

Full size image

2.2 Data

The data used for this study stems from the MeteoSwiss observational network. Three daily temperature variables measured at 2 m from the ground are available for many decades: the daily maximum, daily minimum, and daily mean temperature, henceforth denominated by \({T}_{\mathrm{min}}\), \({T}_{\mathrm{max}}\), and \({T}_{\mathrm{mean}}\). When not further specified, “daily temperature” denotes any of these three temperatures. Temperature aggregates over several days can be of particular interest for classifying prolonged cold or warm periods. In agreement with the literature (Wehner et al. 2018), we analyze 3-, 5-, 7-, 10-, and 15-day means of \({T}_{\mathrm{min}}\), \({T}_{\mathrm{max}}\), and \({T}_{\mathrm{mean}}\). The procedures described in Section 3 are applied separately, at each station, to each of the three daily temperature variables, and to each of the temporal aggregates.

To avoid artificial trends and shifts in the data due to changes in instrument or location, only homogenized temperature data is used for estimating the temperature distribution (Begert et al. 2003; 2005). The number of stations available in a given year depends on the temperature variable. The period of the analysis is 1965 to 2020, as it was found to yield the largest number of available stations: 38 stations for \({T}_{\mathrm{max}}\), 41 for \({T}_{\mathrm{min}}\), and 56 for \({T}_{\mathrm{mean}}\) (crosses and circles in Fig. 1). The selected stations cover the entire study area and range from elevations of 203 m a.s.l. in Cadenazzo close to Bellinzona in southern Switzerland to 3571 m a.s.l. at Jungfraujoch. Eleven stations (colored dots in Fig. 1), which were previously found to be highly representative of the Swiss temperature climatology (Begert 2008), are analyzed in more detail in Section 4.1.

The annual average northern hemispheric temperature anomaly over land areas from the CRUTEM4 dataset by MetOffice (Jones et al. 2012) is used as a predictor variable to model the long-term temperature changes in Switzerland. It is based on station records, many of them homogenized. The anomaly was smoothed using a locally weighted polynomial regression implemented in the lowess R-function with default settings (Becker et al. 1988; Cleveland 1979, 1981). This smoothed yearly northern hemispheric temperature anomaly is denoted by \({T}_{\mathrm{CRU},y}\), with \(y\) denoting the year. The temperature anomaly \({T}_{\mathrm{CRU}, 2018}\) in the year 2018 was set to zero, and the other values adapted accordingly.

3 Methods

The classification procedure adopted in this study is to first transform the temperature data to a standard normal distribution and then determine the return periods as empirical quantiles. These estimates will only have some degree of reliability if the distribution chosen to model temperature is sufficiently accurate. The complex behavior of surface air temperature in a mountainous area requires a distribution with four parameters and the flexibility to model non-stationarities explicitly. The skewed generalized error distribution (SGED) lends itself well to this task. Developed in the context of financial applications (Nelson 1991; Fernández and Steel 1998; Theodossiou 2015), it was successfully used by Evin et al. (2019) to model temperature. Note that the distribution is also known as the skew exponential power (SEP) distribution. The explicit modeling of the daily temperature distribution under consideration of seasonality and climate change is described in Section 3.1. The conversion of the data to standard normal and the subsequent classification can be found in Section 3.2.

3.1 Temperature model

As mentioned above, there is evidence that surface air temperature cannot be modeled with a normal distribution and that not only its mean and variance but also its higher-order moments have a seasonal cycle. Long-term changes, on the other hand, only seem to affect the mean behavior of temperature. Indeed, Scherrer et al. (2005) found temporal trends in the variance of daily temperatures from 1961 to 2004 to be mostly insignificant. A preliminary analysis of our selected data confirmed this: the estimated linear trends in standard deviation turned out to be both weakly positive and negative, depending on the station. Therefore, a statistical model for surface air temperature needs not to include a year-to-year variation of the standard deviation or of the parameters that describe the behavior of higher moments.

To model daily surface air temperature, we use the skewed generalized error distribution (SGED), which has the four parameters, location, scale, skewness, and kurtosis, with the following features:

  1. (a)

    location, scale, skewness, and kurtosis have a seasonal cycle and thus change from day to day,

  2. (b)

    the seasonal behavior of scale, skewness, and kurtosis is the same for all years, and

  3. (c)

    the location parameter is expressed as a linear function of \({T}_{\mathrm{CRU},y}\) with seasonally dependent coefficients.

Let \({X}_{d,{T}_{\mathrm{CRU},y}}\) refers to the temperature on day \(d\) of year \(y\), (i.e., daily maximum, minimum, or mean temperature or aggregates thereof). Then,

$${X}_{d,{T}_{CRU,y} } \sim SGED\left({\mu }_{d,{T}_{CRU,y}}, {\sigma }_{d}, {\lambda }_{d}, {p}_{d}\right)$$
(1)

The location parameter is denoted by \({\mu }_{d,{T}_{\mathrm{CRU},y}}\); \({\sigma }_{d}>0\) is the scale parameter, \({\lambda }_{d}\) describes the skewness, and \({p}_{d}\) the kurtosis, with values depending on the day of the year \(d\) as illustrated in Eq. (3) below. The SGED is a parametric distribution function that presents similarities with a normal distribution but allows modeling moderate discrepancies therefrom, including skewness and short-/long-tail behavior (see Fig. 2 for a simple graphic representation of the role played by skewness and kurtosis). The expected value of the distribution is \(\mu\) and its variance is \({\sigma }^{2}\). Note that the skewness and kurtosis parameters are non-dimensional. Here, positive values of \(\lambda\) result in right-skewed and negative values in a left-skewed distribution, while a kurtosis parameter \(p>2\) results in a short-tailed (platykurtic), and \(p<2\) in a long-tailed (leptokurtic) distribution.

Fig. 2
figure 2

Probability densities of the skewed generalized error distribution (SGED) for different parameter values \(\lambda\) and \(p\). The location and scale parameters are kept fixed at \(\mu =0\) and \(\sigma =1\)

Full size image

Rather than explicitly modeling the dependence of the location parameter both on the year (long-term trend) and on the day of the year (seasonal cycle), we make use of CRUTEM4’s northern hemispheric mean temperature anomaly over land, i.e., \({T}_{\mathrm{CRU},y}\). We express the long-term dependence of the location parameter as a linear function of \({T}_{\mathrm{CRU},y}\), the coefficients of which are day-dependent. In this way, the dependence on the year is implicit, while the seasonal cycle of this dependence is explicit.

$${\mu }_{{d,T}_{CRU,y}}:=\mu \left({T}_{CRU,y},d\right)={\mu }_{0}\left(d\right)+{\mu }_{1}\left(d\right)\bullet {T}_{CRU,y}$$
(2)

As mentioned in Section 2.2, \({T}_{\mathrm{CRU}, 2018}=0\) and thus \({\mu }_{0}(d)=\mu \left({T}_{\mathrm{CRU},2018},d\right)\) is the location parameter in the year 2018. A residual analysis (not shown) indicated that the assumption of normal and i.i.d. residuals is satisfied.

The seasonality in the parameters \({\mu }_{0,d}\), \({\mu }_{1,d}\), \({\sigma }_{d}\), \({\lambda }_{d}\), and \({p}_{d}\) is modeled as a 2nd-order harmonic function of the day of the year \(d\). As the same approach is applied for all parameters, the model is only shown for the scale parameter \({\sigma }_{d}\):

$${\sigma }_{d}:=\sigma \left(d\right)= {b}_{0}+ \sum_{j=1}^{2}[{b}_{1,j}\mathrm{cos}(\frac{2\pi j}{n}\bullet d)+ {b}_{2,j}\mathrm{sin}(\frac{2\pi j}{n}\bullet d)]$$
(3)

where \(d=1, \dots , n=366\) refers to the calendar day including February 29th and \({b}_{i,j}\) are the Fourier coefficients. The Fourier transforms ensure continuity between the last day of 1 year and the first day of the next. In accordance with the assumptions in the previous section, the three parameters \(\sigma\), \(\lambda ,\) and \(p\) vary only from day to day, and not from year to year. Thus, for example, the estimated scale parameter on 3 February 1981 is the same as on 3 February 2017 but differs from that on 3 July 1981.

All the Fourier coefficients were simultaneously estimated using maximum likelihood estimation (MLE) by applying the R-function optim (R Core Team 2018). The estimation of the Fourier coefficients was done at each station and for each variable and temporal aggregate independently. The start values for optimization were obtained in a two-step approach. In the first step, daily estimates of the linear trend and the SGED parameters were determined independently from each other. The daily temperature data was separated into long-term time series for each day of the year. These daily long-term time series were subsequently used to obtain, for each day of the year, the trend parameters on the one hand, by regressing them on \({T}_{\mathrm{CRU},y}\), and the SGED parameters on the other hand, by applying the R-function sgedFit from R-package fGarch (Wuertz et al. 2019). In the second step, for each parameter, a Fourier transformation was applied to the resulting series of daily estimates. Then, the Fourier coefficients were randomly disturbed to generate 30 differing sets of start coefficients for optimization. The best optimization, in terms of maximizing the likelihood function, determined the final Fourier coefficients for the model parameters as described in Eq. (3).

The modeling was done univariately and at each station separately. The upper plot in Fig. 3 shows the estimated temperature distribution at Zürich/Fluntern (SMA) for the daily mean temperature for 1966 and 2016. The upward shift between the two curves illustrates a temperature change of approximately 2 °C in 50 years. Evidently, the long-term changes are stronger in summer than in winter and result in a slight change in the seasonal cycle of the location parameter from 1966 to 2016. The higher variance in winter than in summer leads to a wider distribution in winter. For both years, unusually cold or warm temperatures can be distinguished visually, lying outside the 1–99% quantiles of the SGED.

Fig. 3
figure 3

In the upper panel, the crosses indicate the mean daily temperature observations in the years 2016 (blue) and 1966 (brown) at station Zürich/Fluntern (SMA). The lines show the expected value (or location) \(\mu\). Shaded areas of the corresponding hue highlight the respective swaths between the 1% and 99% quantiles of the fitted SGED. In the lower figure, the crosses show the same temperature observations, transformed into standardized anomalies. By construction, the observations in either year should now approximately follow a standard normal distribution. The shaded area between + 2.33 and − 2.33 represents the swath between the 1% and 99% quantiles of the standard normal distribution

Full size image

3.2 Assessment of events

The modeling described above is used to standardize the temperature data in order to make temperatures comparable within a year and between years. The standardization is done by first applying the probability integral transform of model (1) to convert \(X\) to a standard uniform random variable called \(Y\). Subsequently,\(Y\) is transformed into a stationary standard normal distributed random variable referred to as \(Z\). Note that the random variable \(Z\) is hereafter called standardized temperature anomaly, or standardized anomaly for short. The annual maxima of the standardized temperature anomalies \(Z\) are then used to classify the extreme temperature anomalies. Since the annual maxima are determined from the standardized anomalies, they can occur on any day of the year, and they have been stripped of the influence of the long-term trend. Thus, using their ordered distribution as a scale allows a “fair” comparison between temperatures across seasons and years.

The return period of a standardized temperature anomaly is determined by means of the empirical quantile with respect to the aforementioned annual maximum standardized anomaly. For instance, if the standardized anomaly of an event corresponds to the 90% quantile of the yearly maxima, the probability that such a temperature anomaly is reached or exceeded in a given year is 0.1. In other words, such an anomaly occurs or is exceeded on average once in 10 years. Note that an anomaly can refer to both directions, i.e., warm or cold anomalies. For cold anomalies, the ordered yearly minima of the standardized anomalies are used to determine the quantiles.

The lower plot in Fig. 3 shows the standardized anomalies corresponding to the observations in 1966 and 2016. Since these are stationary, individual data points are comparable, both within each year and between the 2 years. Both datasets now have the same location and scale (and, if the model were perfect, they would have neither skewness nor kurtosis), all year round. In particular, the data points huddled about their mean in summer in the upper plot are now stretched further apart and have thereby acquired a lower relative frequency of occurrence. Temperatures that are unusually warm and cold for the time of year stand out on either side of the 1–99%-quantile swath. For instance, the warmest anomalies took place on October 3rd, 1966 (17.6 °C) and August 28th, 2016 (24.6 °C), and the coldest on January 16th, 1966 (-13.6 °C) and July 14th, 2016 (11.1 °C). Note that these are the yearly maxima/minima in 1966 and 2016 used for the assessment of the extreme temperature anomalies as described above.

4 Results

The described approach allows for various potentially insightful analyses of the characteristics of daily temperatures in Switzerland. We validate model (1) in Section 4.1 and illustrate the seasonal behavior of the estimated parameters at eleven representative stations in Switzerland (Section 4.2). Then, Section 4.3 analyzes the influence of seasonality and climate change on the estimated return periods. Finally, some pronounced past warm and cold anomalies that have occurred since 1965 are illustrated in Sections 4.4 and 4.5.

4.1 Model validation

Should the model describe the temperature distribution accurately, the transformed variable \(Z\) (the standardized anomalies) would be normally distributed. The Gaussian QQ-plots before (detrended daily temperature) and after transformation (standardized anomalies) are shown in Fig. 4 at four selected stations. The upper row brings to light the inadequacy of the normal distribution to describe the behavior of surface air temperature. Daily \({T}_{\mathrm{mean}}\) in January in Davos (DAV) are left-skewed (Fig. 4a), while the opposite is the case for \({T}_{\mathrm{max}}\) in Altdorf (ALT) in December (Fig. 4b). Due to the foehn phenomenon, warm \({T}_{\mathrm{min}}\) are more likely to occur in Altdorf in October than a normal distribution would suggest, as illustrated by the long tail on the right side of the distribution (Fig. 4c). In contrast, the distribution of \({T}_{\mathrm{max}}\) at La Chaux-de-Fonds (CDF) in June is clearly short-tailed (Fig. 4d).

Fig. 4
figure 4

Selected Gaussian QQ-plots of detrended daily minimum, mean, or maximum temperature data \(T\) for four selected months at different stations (top figures). The bottom figures illustrate the Gaussian QQ-plots of the corresponding transformed standardized anomalies \(Z\)

Full size image

The QQ-plots of the standardized anomalies \(Z\) in the lower row of Fig. 4, on the contrary, show that the assumption that the standardized anomalies follow a standard normal distribution holds reasonably well, supporting the choice of model (1) to describe surface air temperature. Generally, deviations from the diagonal are small for all quantiles. To formally test the validity of the normality assumption, we stratified the data by the month of the year and applied the Shapiro-Wilk test to the daily temperature month by month for each month between 1965 and 2020 at a confidence level of 1%. Analyzed for all three daily temperature variables, all stations, and each month separately, we find the normality assumption is rejected for 77–90% of the station months before the transformation. After transformation, the normality assumption is rejected in less than 15% of the station months. Differences exist, however, both between variables and regions. Generally, the model fits \({T}_{\mathrm{max}}\) and \({T}_{\mathrm{mean}}\) slightly better than \({T}_{\mathrm{min}}\), which is very likely due to the stronger influence of localized microclimates on \({T}_{\mathrm{min}}\). Regionally, while in the Jura and the Plateau, the transformation works very well for \({T}_{\mathrm{min}}\), the normality assumption is rejected in almost 50% of the months in spring and fall at the prealpine and southern stations. This is likely due to the effect of foehn, with its extremely high minimum temperatures resulting in heavy tails at the right side of the distribution (cf. Altdorf, Fig. 4c). Applying model (2) generally leads to less heavy tails, but the problem is still recognizable (cf. Figure 4g). No effort was made to further address such particular behavior explicitly, as it would require a model that accounts for bimodality in the data, a complexity that is beyond the scope of this study.

In summary, the deviation from the normality of the original distribution is strongly reduced, and the presented model works reasonably well to describe daily temperatures. This is even more the case for temperature aggregates because the more the data are aggregated, the closer they are to the normal distribution. Nevertheless, we should keep in mind that at stations affected by foehn, we will tend to overestimate the return period and thereby classify the events as rarer than they truly are.

4.2 Characteristics of daily temperatures

At eleven representative Swiss stations (Fig. 1), we illustrate the seasonal cycle of the estimated SGED parameters (i.e., mean, scale, skewness, and kurtosis) as well as the long-term changes in the mean (Fig. 5).

Fig. 5
figure 5

Seasonal behavior of the estimated SGED parameters, i.e., the location \(\mu = {\mu }_{0}+{\mu }_{1}\bullet {T}_{\mathrm{CRU}}\), the scale σ, the skewness λ, and the kurtosis p (from top to bottom) for the three variables \({T}_{\mathrm{min}}\), \({T}_{\mathrm{mean}}\), and \({T}_{\mathrm{max}}\)(from left to right). The first two rows show the intercept \({\mu }_{0}\) and the slope \({\mu }_{1}\) of the location parameter. The colors indicate the eleven stations representing the temperature climate of Switzerland ordered by elevation (OTL is the lowest, JUN the highest; see also Fig. 1)

Full size image

4.2.1 Location parameter \({\varvec{\mu}}\)

The location parameter is modeled as a linear function of the smoothed northern hemisphere land temperature anomaly determined from the CRUTEM dataset, which is denoted by \({T}_{\mathrm{CRU},y}\), i.e., \(\mu \left(d,{T}_{\mathrm{CRU},y}\right)={\mu }_{0}\left(d\right)+{\mu }_{1}\left(d\right)\bullet {T}_{\mathrm{CRU},y}\). We discuss the seasonal behavior of the intercept µ0 (Fig. 5a–c) and slope µ1 separately (Fig. 5d–f). The intercept \({\mu }_{0}\) is given in degrees Celsius and shows the expected temperature in the year 2018. The slope \({\mu }_{1}\) denotes a temperature trend at a station in °C per °C temperature change in \({T}_{\mathrm{CRU},y}\).

4.2.2 Intercept \({{\varvec{\mu}}}_{0}\)

The expected daily temperature \({\mu }_{0}\) in Switzerland undergoes a pronounced seasonal cycle (Fig. 5a–c). It has an amplitude (defined as half the difference between the minimum and the maximum) ranging between 7.2 and 11.2 °C, depending on the station and temperature variable. The smaller amplitudes are found at stations influenced by the free atmosphere (high mountain peaks), while higher amplitudes occur in the boundary layer. The date of the yearly minimum \({\mu }_{0}\) shifts towards later dates at higher elevations. For instance, the yearly minima occur between the 5th and 18th of January at low-elevation stations and at the beginning of February at high-elevation stations. Annual maxima all occur in late July regardless of elevation. As might be expected, the yearly average \({\mu }_{0}\) decreases with altitude, here roughly by 5 °C/km for \({T}_{\mathrm{min}}\) and 6.2 °C/km for \({T}_{\mathrm{max}}\).

4.2.3 Slope \({{\varvec{\mu}}}_{1}\)

The slope parameter denotes the temperature increase (i.e., the climate trend) at a station in °C per °C temperature increase of \({T}_{\mathrm{CRU},y}\). Thus, a slope of 2 °C/°C indicates a temperature increase twice as large as the increase in \({T}_{\mathrm{CRU}}\). For instance, in Basel, each increase of 0.1 °C of \({T}_{\mathrm{CRU},y}\) results in an average increase of 0.26 °C from 1965 to 2018. For the vast majority of variables, months, and stations, the local increases are larger than those of \({T}_{\mathrm{CRU}}\), but there is a large variability. The trends are generally strongest in spring and summer, and weaker in autumn and winter (Fig. 5d and e). For example, in Basel, the change in \({T}_{\mathrm{min}}\) over the last 54 years is equivalent to the change in \({T}_{\mathrm{CRU}}\) in February, but is 3.5 times as large in June. In Geneva and in Altdorf, the winter changes in \({T}_{\mathrm{min}}\) are even weaker than \({T}_{\mathrm{CRU}}\) trends. Furthermore, especially at the high-elevation stations, the slopes are higher for \({T}_{\mathrm{max}}\) than for \({T}_{\mathrm{min}}\) in spring confirming the findings by Matiu et al. (2016) and Scherrer and Begert (2019).

4.2.4 Scale parameter \({\varvec{\sigma}}\)

For the daily mean temperature, the scale \(\sigma\) (and accordingly the variance) and location parameters have essentially opposed seasonal patterns. The scale is largest in winter and smallest in summer (Fig. 5g and h), as already shown in Fig. 3. It is mostly driven by \({T}_{\mathrm{min}}\), while \({T}_{\mathrm{max}}\) appears to behave according to the local circumstances, with a general tendency to increase in spring and decrease in autumn. For \({T}_{\mathrm{min}}\), \(\sigma\) undergoes a clear seasonal cycle at all stations except for the station Locarno-Monti (OTL) in southern Switzerland. The highest variances occur in winter at high-elevation stations, which are directly exposed to the large-scale flow of the free atmosphere. Stations prone to the formation of cold-air pools (e.g., La Chaux-de-Fonds, CDF) have a very high variance in winter. In spring, \(\sigma\) increases at stations with high foehn frequency (e.g., Locarno-Monti and Altdorf). \({T}_{\mathrm{max}}\) offers quite a different picture: the seasonal cycle is much less contrasted than for \({T}_{\mathrm{min}}\), and on average, the variance is approximately 0.8 °C higher. Again, Locarno-Monti (OTL) stands out with a particularly low variance, except in spring. Evidently, the processes that give \({T}_{\mathrm{min}}\) its form dominates the behavior of \({T}_{\mathrm{mean}}\).

4.2.5 Skewness parameter \({\varvec{\lambda}}\)

Most high-elevation stations show a pronounced left skew (\(\lambda <0\), i.e., a surplus of very cold events compared to very warm events) during the whole year for both \({T}_{\mathrm{min}}\) and \({T}_{\mathrm{max}}\) (Fig. 5j and l). An interesting case is Altdorf where \({T}_{\mathrm{min}}\) shows two distinct peaks of right skew in spring and fall—periods with a high frequency of foehn (cf. Gutermann et al. 2012). A similar pattern can also be found in the Ticino in winter, potentially related to northern foehn. In the lowlands, the skew is mostly weak.

4.2.6 Kurtosis parameter \({\varvec{p}}\)

Most stations except for some high-elevation stations show a bimodal behavior of the kurtosis parameter \(p\) over the year. For these stations, the temperature distribution is platykurtic (“flat”;\(p>2\)) in spring (primary maximum) and fall (secondary maximum). This bimodal behavior is most pronounced for \({T}_{\mathrm{max}}\).

4.3 Examples of event assessment

The proposed classification approach offers the possibility not only of comparing the return periods of events at one selected station in different seasons and different years but also, since we use the same period for all stations, it yields a spatial “signature” of the event, bringing to light the relative rarity between one station and another. We first focus on the influence of seasonality using the example of two heat waves that occurred in 2019 and then consider the influence of long-term changes using the example of cold nighttime temperatures in 2017.

In the summer of 2019, two heat waves of comparable intensity and duration struck Switzerland: the first from June 25 to July 1 and the second from July 20 to 26. We will refer to them as the June and July heat waves, respectively. While both heat waves had the same duration, they differed slightly in magnitude and regional distribution. In particular, maximum temperatures during the July heat wave were approximately 1 °C warmer (colder) in western (eastern) Switzerland than maximum temperatures during the June heat wave but were similar in the northern and southern parts of the country (MeteoSchweiz 2019a). Despite these small differences, these 2019 heat waves are particularly useful for comparing our newly proposed classification approach with the traditional one, as they took place during the same summer, thus leaving out differences due to the long-term temperature trend. The variable considered here is the 7-day mean temperature\({T}_{\mathrm{mean}, 7}\), and its standardized anomaly \({Z}_{\mathrm{mean},7}\). The June heat wave’s standardized anomaly \({Z}_{\mathrm{mean},7}\) yields empirical return periods ranging between 1.1 and 5 years around Lake Geneva and in the Ticino, for instance, and up to 10–25 years at a number of high alpine stations (Fig. 6, a1). In contrast, the anomalies incurred during the July heat wave occur at least once a year at more than 60% of the stations and barely reach a return period of 1.1–3 years at a third of the stations (Fig. 6, b1). Thus, the explicit modeling of the seasonal cycle allows a fair comparison between the two heat waves and shows that the June heat wave was far more exceptional than the July heat wave, despite similar absolute values.

Fig. 6
figure 6

Classification of the averaged 7-day mean temperatures observed during the two heat waves in summer 2019 lasting from June 25 to July 1 (left figures, denoted by a)) and from July 21–26 (right figures, denoted by b)). The first row (a1 and b1) illustrates the classification of the standardized anomalies as proposed in this publication. The second row (a2 and b2) shows the classification of the averaged 7-day mean daily temperatures with a traditional block maximum approach

Full size image

To complement the previous analysis, we also classified the two events in the traditional manner by determining their return periods empirically based on an annual block maximum approach of the absolute 7-day mean temperatures \({T}_{\mathrm{mean}, 7}\). The estimated return periods of the absolute temperatures of the June heat wave (Fig. 6, a2) are comparable to those of the standardized anomalies (Fig. 6, a1). For the July heat wave, on the other hand, the absolute temperatures (Fig. 6, b2) are classified as rarer than the standardized anomalies (Fig. 6, b1). The return periods range between 1.1 and 3 years and 5 and 8 years in the Ticino and around Lake Neuchâtel. By construction, the difference in return periods between the two analyses results from the fact that the second analysis accounts neither for seasonality nor for long-term changes in air temperature. Both factors play a role. The warming trend implies that hot events are more frequent at the end of the period under consideration since it results in higher absolute values. Thus, the traditional approach to classifying the observed temperatures assigns too large return periods to events at the end of the time series, such as the 2019 event, for both the June and July heat waves. Similarly, since temperatures are higher on average in July than in June, classifying the absolute values will obviously yield higher return periods in July.

Cold events can be analyzed in the same way. In the spring of 2017, a devastating frost event with particularly cold night temperatures between April 19 and 21 severely affected the development of crops, especially grapes (Vitasse and Rebetez 2018). We examine the effect of climatic change on the estimated return periods for this event by comparing the results with those obtained from a fictitious frost event of the same amplitude exactly 40 years earlier. We choose to represent the frost event with the minimum temperature averaged over three days, \({T}_{\mathrm{mean}, 3}\), and its standardized anomaly, \({Z}_{\mathrm{mean}, 3}\). Again, since we standardize the values of air temperature, the obtained cold extremes (large negative anomalies) are not dominated by the coldest values in winter and are mitigated or magnified by climate change. For the climate of 2017, the standardized anomaly corresponding to the 3-day mean minimum temperature during the event certainly does not occur every year at more than 85% of the investigated stations (Fig. 7a). At some, the return period is between 2 and 15 years, and in Arosa, where the 3-day mean minimum temperature goes down to − 11 °C, it reaches 10–20 years. Should exactly the same frost event have occurred 40 years earlier between April 19 and 21 in 1977, it would be classified as an anomaly that occurs yearly or more frequently at 80% of the stations, while at the remaining 20% of the stations, the anomaly is classified as a 1.1–3 year’s event (Fig. 7b). In other words, in 1977, the same event would have been nothing exceptional.

Fig. 7
figure 7

The left map (a) shows the empirically estimated return periods of the standardized anomalies corresponding to a three-day cold spell (minimum temperatures) from April 19 to 21 in 2017. The right map (b) shows the hypothetical return periods if this event had occurred 40 years ago, i.e., between April 19 and 21 in 1977

Full size image

4.4 Catalogue of unusually warm events since 1965

In this section, the temporal distribution of all 1-day warm minimum and maximum temperature anomalies since 1965 classified with a return period of 1.1 years or higher is illustrated at five stations representing different climates in Switzerland. Figure 8 clearly shows that the detected high-temperature anomalies are evenly distributed over the years and over all seasons since 1965. For instance, the largest dots (i.e., the largest standardized anomalies) are not always in the season one would expect them to be (i.e., in summer) as it would be the case if one had classified absolute temperatures. They are also not all at the end of the analyzed period, as one could expect under climate change. This is because the method highlights temperature episodes that are unusual with respect to the season and year during which they occurred and show that the time-dependent SGED captures the essential features of the temperature variables, including climate change.

Fig. 8
figure 8

Return periods (RP) of warm anomalies of daily minimum (left column) and maximum (right column) temperatures at five stations in Switzerland, namely, la Chaux-de-Fonds (CDF), Zürich/Fluntern (SMA), Altdorf (ALT), Jungfraujoch (JUN), and Locarno-Monti (OTL). Each station is representative of a region, i.e., CDF for the Jura, SMA for the Plateau, ALT for the Prealps, JUN for the Alps, and OTL for southern Switzerland. The x-axis denotes the years, and the y-axis the months of the year. Each dot represents a temperature anomaly with an empirical return period that is strictly larger than 1 year. The size of the dots increases with the return period, i.e., the bigger the dot, the rarer the anomaly. The color of each dot corresponds to the absolute mean daily temperature measured at the time of the event. The five numbers indicate the standardized anomalies of the five events with the highest median daily temperature over the region the station belongs to (see Table 1)

Full size image

For each of the stations and variables in Fig. 8, the circled numbers highlight five events (see also Table 1) selected for their regional extension within the regions mentioned above. For each region, they correspond to the 5 days in the last 55 years with the largest median of the temperature anomalies in the region. This procedure was chosen in order to analyze events of regional relevance. For example, we observe that the 26th of June 2019, i.e., a day within the 2019 June heat wave discussed above, appears as one of the five most extreme regional 1-day events in the Alpine region (Fig. 8i and j, number 3). Note that the standardized anomalies appearing in Table 1 are those at the representative station on the day of that regional event, and may, therefore, not be the most exceptional ones at that station. For instance, the dot for 7 July 2015 on Fig. 8f represents a maximum temperature of 34.6 °C recorded at Zürich/Fluntern (SMA). This value is among the 10 highest maximum temperatures reached at SMA and is classified as a 1.1–3 year’s event, as can be seen from the size of the dot and in Table 1. On that day, Geneva was hitting a new record of 39.7 °C. As by the median, this event is accounted for as the third most extreme event in the Plateau. On 31 July 1983, on the other hand, the maximum temperature at SMA was 35.8 °C, but the event only classifies as the 5th on record regarding the Plateau.

Table 1 «Top-five» anomalies referred to by the date of occurrence for daily minimum and maximum temperatures ranked over all stations within each region Jura, Plateau, Prealps, Alps, and South. The ranking is meant to reflect regional extremes. It is based on the median over all stations in a region of the standardized anomalies on a given day (corresponding to the temperatures observed on that day). Thus, the more stations with high anomalies within a region, the higher the ranking. Each of the five regions is represented by a station: CDF represents the Jura, SMA represents the Plateau, ALT represents the Prealps, JUN represents the Alps, and OTL represents the southern part of Switzerland. Note that for a given event, the representative station may not be the one with the highest anomaly in the region. For each station, the date of the event is given, followed by the minimum resp. maximum temperature (T) observed on that day at the station. The next two columns show the corresponding return period (RP) and the expected temperature (ET), defined as the value of the location parameter on that day
Full size table

On the Plateau, the top-ranking anomaly for the regional \({T}_{\mathrm{max}}\) was observed during the very hot summer of 2003 on August 13. Temperatures reached 36 °C in Zürich/Fluntern (SMA), the highest in situ \({T}_{\mathrm{max}}\) on record for SMA, corresponding to a deviation of 12.3 °C from the expected absolute temperature (defined as the value of the location parameter on that day). This regional event was highly anomalous on the Plateau, the Prealps, and the Jura. In contrast, at Alpine stations such as Jungfraujoch, the deviation from the expected value reached only 4 °C. On the Plateau, the 2003 event is followed by a warm anomaly that occurred in April 1968 with a \({T}_{\mathrm{max}}\) of 26.5 °C in Zürich/Fluntern (SMA) that corresponds to a deviation of 13.1 °C from the expected temperature. This event affected large parts of Switzerland and was due to an Eastern European high-pressure system extending to Central Europe (MeteoSchweiz 1968). In the Jura, the top regional event occurred on 31 July 1983, registering 33.8 °C in La Chaux-de-Fonds, a deviation of 12.8 °C from the expected temperature on that day, followed by an extremely warm December day in 1989 with a deviation from the expected value of 15.3°. In the Prealps, the top event occurred in mid-May 1969 in Altdorf, where the daily \({T}_{\mathrm{max}}\) went up to 31.1 °C during a very sunny period caused by a shallow high over Central and Southern Europe (MeteoSchweiz 1969). In the Alps, the strongest anomalies are 31 July 1983, 13 and 14 May 1969, and the last day of the heat wave in mid-July 2019 described in Section 4.3 and Fig. 6. These events resulted in the strongest anomalies at high altitudes for both \({T}_{\mathrm{max}}\) and \({T}_{\mathrm{min}}\). In Ticino, the top regional event occurred on 24 October 2018 at 30.5 °C in Lugano. It was attributed to the north foehn and was the first hot day (Tmax ≥ 30 °C) ever recorded in Switzerland in October (MeteoSchweiz 2019b).

Similar analyses can be performed for warm \({T}_{\mathrm{min}}\) (Table 1). For instance, we observe that the five most pronounced regional warm \({T}_{\mathrm{min}}\) events occurred during south foehn in Altdorf.Footnote 1 The warmest night anomalies in the Ticino, such as 6 January 2013, are related to foehn, illustrating its importance with regard to warm \({T}_{\mathrm{min}}\) at foehn locations (MeteoSchweiz 2014).

4.5 Catalogue of unusually cold events since 1965

Cold anomalies since 1965 with return periods of 1.1 years or higher are depicted in Fig. 9. As for the warm anomalies, they are evenly distributed across seasons and years. Figure 9 and Table 1 show that the cold anomalies occurring on 6 March 1971, 3 December 1973, 5–9 January 1985, 10 February 1986, and 12 January 1987 affected all regions, even if not always with the same ranking. On 6 March 1971 for instance, \({T}_{\mathrm{min}}\) went down to − 36.6 °C at Jungfraujoch, corresponding to a deviation of − 20.1 °C from the expected \({T}_{\mathrm{min}}\), and down to − 15 °C in Basel, and − 6.8 °C in Lugano. On 3 December 1973, \({T}_{\mathrm{min}}\) in Basel and Altdorf went below − 15 °C, and reached − 6.5 °C in Lugano, and − 28.1 °C at Jungfraujoch. From 5 to 9 January 1985, a strong Bise led to a 5-day cold anomaly affecting all of Switzerland, with \({T}_{\mathrm{max}}\) of − 14.7 °C on 8 January in Zürich/Fluntern and − 4.3 °C in Locarno-Monti, and \({T}_{\mathrm{min}}\) of − 19.6 °C on 9 January in Zürich/Fluntern and of − 29.5 °C at La Chaux-de-Fonds. In contrast to the warmest events and with a few exceptions, the most severe cold events occurred in wintertime and are spatially consistent over all regions.

Fig. 9
figure 9

Same as Fig. 8 but for anomalously low minimum and maximum temperatures. The five numbers indicate the standardized anomalies of the five events with the lowest median daily temperature over the region the station belongs to

Full size image

5 Discussion

The results bring to light the complexity of the daily temperature distribution, regardless of whether mean, minimum, or maximum. Seasonality not only affects all parameters of the distribution in a given year, but also the long-term shifts in the location parameter. The pronounced seasonal cycle of temperatures in mid-latitudes is well represented by the location parameter with amplitudes ranging from 7 to 11 °C. Differences in the estimated location parameter \(\mu\) between individual stations mainly stem from altitude, resulting in lapse rates of 5 °C/km (\({T}_{\mathrm{min}}\)) to 6.2 °C/km (\({T}_{\mathrm{max}}\)) on average. The observed weaker lapse rates for \({T}_{\mathrm{min}}\) can be linked to cold-air pooling and fog situations in winter (c.f., Scherrer and Appenzeller 2014), affecting \({T}_{\mathrm{min}}\) rather than \({T}_{\mathrm{max}}\). These can also lead to weaker temperature decreases with elevation in winter than in summer (e.g., Kunz et al. 2007), as observed here. With regard to trends in the location parameter \(\mu\), they are known to be stronger in summer than in winter (e.g.,Rebetez and Reinhard 2008; Ceppi et al. 2012).

Unlike the location, the scale (variance) is largest in the cold season, as already noted by Evin et al. (2019), with the greatest amplitudes at higher elevations, where the stations are exposed to the large-scale flow. The temperature is predominantly left-skewed. This means that unusually cold events happen more often than would be expected for a normal distribution (e.g., Underwood 2013). Stations affected by foehn are an exception: the temperature is right-skewed in spring and fall for \({T}_{\mathrm{min}}\) and \({T}_{\mathrm{max}}\), and from September to February for \({T}_{\mathrm{max}}\). Geographically, Southern Switzerland stands out as a region with a different temperature regime characterized by distinctly warmer temperatures and a small variance reaching its maximum in spring.

The results have shown that the explicit modeling of seasonality in the temperature distribution parameters is critical to compare the severity of temperature anomalies regardless of the season or year in which they occurred. As we have seen, not only the location parameter, but also the higher-order parameters display a pronounced seasonal cycle (Fig. 5). Thus, we argue that the presented approach is more accurate than classifying “ordinary” temperature anomalies, defined as the difference from the expected value, or adopting a semi-annual approach (e.g., Nogaj et al. 2006; Abaurrea et al. 2007). Because of the seasonal cycle in the higher moments, ordinary temperature anomalies are not comparable across or even within individual seasons. To give a specific example, the variance of \({T}_{\mathrm{min}}\) is almost twice as high in winter than in summer at high-elevation stations, resulting in larger ordinary temperature anomalies in winter. Thus, only winter events would be classified as exceptional when classifying ordinary temperature anomalies. Furthermore, the scale parameter can change significantly even within one season. At Locarno-Monti, for instance, the scale parameter of the \({T}_{\mathrm{max}}\) distribution decreases by around one-third from April to August. Neglecting seasonality in the distributions’ parameters can thus lead to an “unfair” comparison of events and a misleading classification.

By explicitly modeling the temperature trend, the presented approach accounts for climate change. Indeed, we show that cold events are classified as more unusual today than if they had occurred a few decades ago, while the reverse is the case for hot events. The catalogue of unusually cold and warm events over the entire period since 1965 indicates that these unusual events are evenly distributed, indicating that the presented method works well with respect to its intended purpose, i.e., the comparability of temperatures within the year and between years. Nevertheless, the five most anomalous and spatially consistent cold events all occurred during the winter and during the first 22 years of analysis (e.g., in 1971 1973 1985 1986 1987). Whether this is systematically related to the chosen approach remains, however, an open question because the inherent rarity makes it difficult to analyze the statistical behavior of the largest anomalies. In addition, small temperature differences can lead to significant changes in the estimated return periods due to the negative shape of the temperature maxima distribution (e.g., Cooley 2009; Kharin and Zwiers 2005).

Similar modeling approaches have been implemented in a few previous studies. For instance, Evin et al. (2019) aimed at stochastically generating temperature series at 26 stations in Switzerland. In contrast to the present study, they separately estimate the linear temperature trend, the monthly mean, and the standard deviation (which are smoothed in a second step), and finally model the residuals based on the SGED. A visual comparison of the results of the two studies reveals high agreement between the estimated parameters. A benefit of the present study is the simultaneous estimation of all parameters, potentially reducing biases and uncertainties. Furthermore, Underwood (2013) analyzed the summary statistics characterizing the daily temperature at de Bilt, Holland, for two periods 1904–1984 and 1985–2009 based on a GEV-distribution with seasonally smoothed parameters. They find that the moments of the distribution change slightly from one period to the other, a finding that could put in question the assumption of constant (with regard to different years) higher-order moments adopted here.

6 Conclusion

This study presents a novel approach to modeling daily air temperatures and classifying unusually warm or cold events. The skewed generalized error distribution (SGED) selected for this purpose can model skewness and long/short tails. By letting parameters vary daily and assuming a linear dependence of the location parameter on the smoothed northern hemisphere land temperature, non-Gaussianity, seasonality, and global warming can be accounted for all in one. The daily variation of all model parameters is modeled as second-order Fourier series that are estimated simultaneously. Analyses of the yearly cycle and the long-term changes of the model parameters both provide new insights and confirm well-known characteristics of daily air temperatures in Switzerland, supporting the appropriateness of the applied model.

Once the SGED parameters are estimated, they are used to transform the temperature observations into standardized temperature anomalies. These are stationary, i.e., comparable within a year and between years. Yearly return periods are then determined empirically from the annual maxima of the standardized anomalies. Through standardization, each event is classified in terms of the climate prevalent in the year and the day of the year on which it occurred. The proposed method works well, as shown by the cataloging of past extreme events, which are evenly distributed across years and months. For instance, a heat wave in early summer is classified as less frequent than a heat wave of comparable intensity in mid-summer. This is appropriate because lower temperatures are expected in early summer than in mid-summer. In addition, the approach classifies unusually warm events as more frequent in recent years than a few decades ago, while the opposite is the case for cold anomalies. The approach can thus be used to illustrate differences in the frequency of extremes due to both seasonality and climate change. It is further capable of identifying the largest cold and warm anomalies.

We conclude that the presented approach is appropriate to accurately model daily air temperatures to gain insights into diverse climatological characteristics, including the classification of extreme temperatures. Considering the complex topography in which the approach has been tested, it should be applicable worldwide, requiring solely a daily time series of high-quality temperature observations.