Abstract
In this paper, a stochastic model for the analysis of the daily maximum temperature is proposed. First, a deseasonalization procedure based on the truncated Fourier expansion is adopted. Then, the Johnson transformation functions were applied for the data normalization. Finally, the fractionally autoregressive integrated moving average model was used to reproduce both short- and long-memory behavior of the temperature series. The model was applied to the data of the Cosenza gauge (Calabria region) and verified on other four gauges of southern Italy. Through a Monte Carlo simulation procedure based on the proposed model, 105 years of daily maximum temperature have been generated. Among the possible applications of the model, the occurrence probabilities of the annual maximum values have been evaluated. Moreover, the procedure was applied for the estimation of the return periods of long sequences of days with maximum temperature above prefixed thresholds.









Similar content being viewed by others
References
Akaike H (1974) Maximum likelihood identification of Gaussian autoregressive moving average models. Biometrika 60:255–265
Alonso AM, Peña D, Romo J (2002) Forecasting time series with sieve bootstrap. J Stat Plan Infer 100:1–11
Alonso AM, Peña D, Romo J (2003) On sieve bootstrap prediction intervals. Statist Probab Lett 65:13–20
Anderson TW, Darling DA (1952) Asymptotic theory of certain “goodness-of-fit” criteria based on stochastic processes. Ann Math Stat 23:193–212
Anderson TW, Olkin I (1985) Maximum-likelihood estimation of the parameters of a multivariate normal distribution. Linear Algebra Appl 70:147–171
Baillie RT, Chung S (2002) Modeling and forecasting from trend-stationary long memory models with applications to climatology. Int J Forecasting 18:215–226
Bechini L, Bocchi S, Maggiore T, Confalonieri R (2006) Parameterization of a crop growth and development simulation model at sub-model components level. An example for winter wheat (Triticum aestivum L.). Environ Model Softw 21:1042–1054
Bisaglia L, Grigoletto M (2001) Prediction intervals for FARIMA processes by bootstrap methods. J Stat Comput Simul 68:185–201
Box GEP, Jenkins GM (1976) Time series analysis forecasting and control. Holden-Day
Burnham KP, Anderson DR (2002) Model selection and multimodel inference: a practical information-theoretic approach. Springer, New York
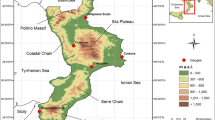
Buttafuoco G, Caloiero T, Coscarelli R (2015) Analyses of drought events in Calabria (southern Italy) using standardized precipitation index. Water Resour Manag 29:557–573
Caballero R, Jewson S, Brix A (2002) Long memory in surface air temperature: detection, modeling, and application to weather derivative valuation. Clim Res 21:127–140
Caldiz DO, Gaspari FJ, Haverkort AJ, Struik PC (2001) Agro-ecological zoning and potential yield of single or double cropping of potato in Argentina. Agric For Meteorol 109:311–320
Caloiero T, Coscarelli R, Ferrari E, Sirangelo B (2015a) Analysis of dry spells in southern Italy (Calabria). Water 7:3009–3023
Caloiero T, Buttafuoco G, Coscarelli R, Ferrari E (2015b) Spatial and temporal characterization of climate at regional scale using homogeneous monthly precipitation and air temperature data: an application in Calabria (southern Italy). Hydrol Res 46:629–646
Caloiero T, Callegari G, Cantasano N, Coletta V, Pellicone G, Veltri A (2015c) Bioclimatic analysis in a region of southern Italy (Calabria). Plant Biosystems, in press, doi:10.1080/11263504.2015.1037814
Campbell SD, Diebold FX (2005) Weather forecasting for weather derivatives. J Am Stat Assoc 100:6–16
Chen SS, Gopinath RA (2000) Gaussianization. Adv Neural Comput Syst 13:423–429
Coscarelli R, Caloiero T (2012) Analysis of daily and monthly rainfall concentration in southern Italy (Calabria region). J Hydrol 416–417:145–156
Curriero FC, Heiner KS, Samet JM, Zeger SL, Strug L, Patz JA (2002) Temperature and mortality in 11 cities of the eastern United States. Am J Epidemiol 155:80–87
Doukhan P, Oppenheim G, Taqqu MS (2003) Theory and application of long-range dependence. Birkhäuser, Boston
Ehsanzadeh E, Adamowski K (2010) Trends in timing of low stream flows in Canada: impact of autocorrelation and long-term persistence. Hydrol Process 24:970–980
Ferrari E, Caloiero T, Coscarelli R (2013) Influence of the North Atlantic oscillation on winter rainfall in Calabria (southern Italy). Theor Appl Climatol 114:479–494
Granger CWJ, Joyeux R (1980) An introduction to long-range time series models and fractional differencing. J Time Ser Anal 1:15–30
Grimaldi S (2004) Linear parametric models applied on daily hydrological series. J Hydrolog Eng 9:383–391
Grimaldi S, Serinaldi F, Tallerini C (2005) Multivariate linear parametric models applied to daily rainfall time series. Adv Geosc 2:87–92
Hajat S, Kovats RS, Atkinson RW, Haines A (2002) Impact of hot temperatures on death in London: a time series approach. J Epidemiol Community Health 56:367–372
Hólm E, Andersson E, Beljaars A, Lopez P, Mahfouf JF, Simmons AJ, Thépaut JN (2002) Assimilation and modelling of the hydrological cycle: ECMWF’s status and plans. ECMWF Tech Memo 383, Reading
Hosking JRM (1981) Fractional differencing. Biometrika 68:165–176
Hosking JRM (1984) Modeling persistence in hydrological time series using fractional differencing. Water Resour Res 20:1898–1908
Hurst HE (1951) Long-term storage capacity of reservoirs. Trans Am Soc Civil Eng 116:770–799
Jewson S, Caballero R (2003) Seasonality in the statistics of surface air temperature and the pricing of weather derivatives. Meteorol Appl 10:367–376
Johnson NL (1949) Systems of frequency curves generated by methods of translation. Biometrika 36:149–176
Keellings D, Waylen P (2012) The stochastic properties of high daily maximum temperatures applying crossing theory to modeling high-temperature event variables. Theor Appl Climatol 108:579–590
Kendall MG (1962) Rank correlation methods. Hafner Publishing Company, New York
Koscielny-Bunde E, Kantelhardt JW, Braun P, Bunde A, Havlin S (2006) Long-term persistence and multifractality of river runoff records: detrended fluctuation studies. J Hydrol 322:120–137
Koutsoyiannis D (2002) The Hurst phenomenon and fractional Gaussian noise made easy. Hydrolog Sci J 47:573–595
Kunst AE, Looman CWN, Mackenbach JP (1993) Outdoor air temperature and mortality in the Netherlands: a time-series analysis. Am J Epidemiol 137:331–341
Lee T (2015) Stochastic simulation of precipitation data for preserving key statistics in their original domain and application to climate change analysis. Theor Appl Climatol. doi:10.1007/s00704-015-1395-0
Lohre M, Sibbertsen P, Könning T (2003) Modeling water flow of the Rhine River using seasonal long memory. Water Resour Res 39:1132
Lye LM, Lin Y (1994) Long-term dependence in annual peak flows of Canadian rivers. J Hydrol 160:89–103
Mann HB (1945) Nonparametric tests against trend. Econometrica 13:245–259
Montanari A, Rosso R, Taqqu MS (1997) Fractionally differenced ARIMA models applied to hydrologic time series: identification, estimation, and simulation. Water Resour Res 33:1035–1044
Montanari A, Rosso R, Taqqu MS (2000) A seasonal fractional ARIMA model applied to the Nile River monthly flows at Aswan. Water Resour Res 36:1249–1259
Pelletier JD, Turcotte DL (1997) Long-range persistence in climatological and hydrological time series: analysis, modeling and application to drought hazard assessment. J Hydrol 203:198–208
Prass TS, Bravo JM, Clarke RT, Collischonn W, Lopes SRC (2012) Comparison of forecasts of mean monthly water level in the Paraguay River, Brazil, from two fractionally differenced models. Water Resour Res 48:W05502
Richardson CW (1981) Stochastic simulation of daily precipitation, temperature, and solar radiation. Water Resour Res 17:182–190
Rupasinghe M, Mukhopadhyayb P, Samaranayakec VA (2014) Obtaining prediction intervals for FARIMA processes using the sieve bootstrap. J Stat Comput Sim 84:2044–2058
Rupasinghe M, Samaranayake VA (2012) Asymptotic properties of sieve bootstrap prediction intervals for FARIMA processes. Statist Probab Lett 82:2108–2114
Servidio S, Greco A, Matthaeus WH, Osman KT, Dmitruk P (2011) Statistical association of discontinuities and reconnection in magnetohydrodynamic turbulence. J Geophys Res 116:A09102
Sheng H, Chen YQ (2011) FARIMA with stable innovations model of Great Salt Lake elevation time series. Signal Process 91:553–561
Smith RL (1993) Long-range dependence and global warming. In: Barnett V, Turkerman KF (eds) Statistics for the environment. Wiley, New York, pp. 141–146
Snedecor GW, Cochran WG (1989) Statistical methods, 8th edn. Iowa State University Press, Iowa City
Sugiura N (1978) Further analysis of the data by Akaike’s information criterion and the finite corrections. Commun Stat A-Theor 7:13–26
Tuenter HJH (2001) An algorithm to determine the parameters of the S U -curves in the Johnson system of probability distributions by moment matching. J Stat Comput Sim 70:325–347
Verdoodt A, Van Ranst E, Ye L (2004) Daily simulation of potential dry matter production of annual field crops in tropical environments. Agron J 96:1739–1753
Yang G, Bowling LC (2014) Detection of changes in hydrologic system memory associated with urbanization in the Great Lakes region. Water Resour Res 50:3750–3763
Ye L, Tang H, Zhu J, Verdoodt A, Van Ranst E (2008) Spatial patterns and effects of soil organic carbon on grain productivity assessment in China. Soil Use Manage 24:80–91
Ye L, Van Ranst E (2002) Population carrying capacity and sustainable agricultural use of land resources in Caoxian County (North China). J Sustain Agr 19:75–94
Ye L, Van Ranst E (2009) Production scenarios and the effect of soil degradation on long-term food security in China. Global Environ Chang 19:464–481
Ye L, Xiong W, Li Z, Yang P, Wu W, Yang G, Fu Y, Zou J, Chen Z, Van Ranst E, Tang H (2013) Climate change impact on China food security in 2050. Agron Sustain Dev 33:363–374
Yevjevich V (1972) Structural analysis of hydrologic time series. Hydrol Pap 56, Colorado State University, Fort Collins (CO)
Acknowledgments
The authors thank the reviewer Salvatore Grimaldi for providing the constructive comments which have contributed to the improvement of the paper.
Author information
Authors and Affiliations
Corresponding author
Appendices
Appendix 1: Estimation of the number of harmonics
The hypothesis, H 0 , μ : μ Y , 1 = μ Y , 2 = … = μ Y , M = μ Y , can be verified by using the statistics
with
where \( {s}_{Y,m}^2 \) is the sample variance of the data referred to the m th class, m Y , m is the sample mean of the data referred to the m th class, and m Y is the mean of the whole sample \( y\left({i}_{k_{*}}\right) \). The statistics \( {S}_V^2 \) is approximately distributed according to a Fisher variance-ratio law v 2(f 1, f 2) with f 1 = M − 1 and f 2 = K * − M degrees of freedom. For a significance level α SL, the null hypothesis cannot be refused if \( {S}_V^2<{v}_{1-{\alpha}_{SL}}^2\left({f}_1,{f}_2\right) \), where \( {v}_{1-{\alpha}_{SL}}^2\left({f}_1,{f}_2\right) \) is the 1 − α SL percentile of the ν2 distribution.
The hypothesis \( {H}_{0,{\sigma}^2}\kern0.5em :\kern0.5em {\sigma}_{Y,1}^2={\sigma}_{Y,2}^2=\dots ={\sigma}_{Y,M}^2={\sigma}_Y^2 \) can be verified through the Bartlett’s test (Snedecor and Cochran 1989), based on the statistics
where
The statistics \( {S}_B^2 \) is approximately distributed according to a χ 2(f 1) law, with f 1 = M − 1 degree of freedom. With a significance level equal to α SL, the hypothesis cannot be rejected if \( {S}_B^2<{\chi}_{1-{\alpha}_{SL}}^2\left({f}_1\right) \), where \( {\chi}_{1-{\alpha}_{SL}}^2\left({f}_1\right) \) is the 1 − α SL percentile of the χ 2distribution.
The smallest values of n h , μ and \( {n}_{h,{\sigma}^2} \), for which both the hypotheses H 0 , μ and \( {H}_{0,{\sigma}^2} \) cannot be rejected, detect the number of harmonics \( {\widehat{n}}_{h,\mu } \) and \( {\widehat{n}}_{h,{\sigma}^2} \) to be used in the truncated Fourier expansion for the functions μ T (i) and \( {\sigma}_T^2(i) \).
Appendix 2: Monte Carlo procedure
The Monte Carlo simulation procedure, used in this work to generate the daily maximum temperature t max (i) series, can be schematized as follows:
-
1.
By using L’Ecuyer random generator, a sequence υ(i), with i = 1 , 2 , . . . , L s , of random number uniformly distributed on the interval (0,1) is created.
-
2.
The sequence υ(i) is transformed into a sequence ε(i) of random numbers, distributed according to a normal law, with zero mean and variance \( {\sigma}_{\varepsilon}^2 \), through the Box and Müller technique.
-
3.
According to an \( \mathrm{ARMA}\;\left(\widehat{p},\widehat{q}\right) \) model, initialized with u(i) = 0 and ε(i) = 0 for i ≤ 0, a sequence of numbers is generated,
$$ \begin{array}{cc}\hfill u(i)={\displaystyle \sum_{k_p=1}^{\widehat{p}}{\widehat{\varphi}}_{k_p}}u\left(i-{k}_p\right)+{\displaystyle \sum_{k_q=0}^{\widehat{q}}{\widehat{\psi}}_{k_q}}\varepsilon \left(i-{k}_q\right)\hfill & \hfill i=1,2,\dots, {L}_s\hfill \end{array} $$(B1) -
4.
By using the series development of the \( {\left(1-B\right)}^{-\widehat{d}} \) operator, the sequence u(i) is transformed into a number sequence z(i) corresponding to the \( \mathrm{FARIMA}\kern0.5em \left(\widehat{p},\widehat{d},\widehat{q}\right) \) model with zero mean and unit variance
$$ \begin{array}{cc}\hfill z(i)=\frac{1}{\varGamma \left(\widehat{d}\right)}{\displaystyle \sum_{s=0}^{s_{\max }}\frac{\varGamma \left(\widehat{d}+s\right)}{s!}}u\left(i-s\right)\hfill & \hfill i={s}_{\max }+1,\dots, {L}_s\hfill \end{array} $$(B2)where
s max is fixed so that \( \varGamma \left(\widehat{d}+{s}_{\max }+1\right)/\left({s}_{\max }+1\right)\kern0.5em !<\xi {\displaystyle {\sum}_{s=0}^{s_{\max }}\varGamma \left(\widehat{d}+s\right)/s!} \), with ξ = 10−4.
The value of the variance \( {\sigma}_{\varepsilon}^2 \) is fixed in order to obtain \( {\sigma}_Z^2=1 \). If a \( \mathrm{FARIMA}\kern0.5em \left(1,\widehat{d},0\right) \) model is employed, the value for \( {\sigma}_{\varepsilon}^2 \) is
$$ {\sigma}_{\varepsilon}^2=\frac{\varGamma^2\left(1-\widehat{d}\right)}{\varGamma \left(1-2\widehat{d}\right)}\cdot \frac{1+{\widehat{\varphi}}_1}{{}_2F_1\left(1,1+\widehat{d},1-\widehat{d};{\widehat{\varphi}}_1\right)} $$(B3)where Γ (.) and 2 F 1(.) indicate the complete gamma function and the hypergeometric function, respectively.
-
5.
The sequence z(i) = s max + 1 , . . . , L s is transformed into the sequence y(i) = s max + 1 , . . . , L s , by using the inverse function of the unbounded Johnson transformation
$$ \begin{array}{cc}\hfill y(i)=\widehat{\alpha}+\widehat{\beta} \sinh \left[\frac{z(i)-\widehat{\eta}}{\widehat{\theta}}\right]\hfill & \hfill i={s}_{\max }+1,\dots, {L}_s\hfill \end{array} $$(B4)or the inverse function of the bounded Johnson transformation
$$ \begin{array}{cc}\hfill y(i)=\frac{\widehat{\alpha}+\left(\widehat{\alpha}+\widehat{\beta}\right) \exp \left[\frac{z(i)-\widehat{\eta}}{\widehat{\theta}}\right]}{1+ \exp \left[\frac{z(i)-\widehat{\eta}}{\widehat{\theta}}\right]}\hfill & \hfill i={s}_{\max }+1,\dots, {L}_s\hfill \end{array} $$(B5) -
6.
The sequence of daily maximum temperature t max(i) = s max + 1 , . . . , L s is obtained as
$$ \begin{array}{cc}\hfill {t}_{\max }(i)={\mu}_T(i)+{\sigma}_T(i)y(i)\hfill & \hfill i={s}_{\max }+1,\dots, {L}_s\hfill \end{array} $$(B6)where
$$ {\mu}_T(i)=\frac{1}{2}{\widehat{a}}_{\mu, 0}+{\displaystyle \sum_{j=1}^{n_{h,\mu }}\left[{\widehat{a}}_{\mu, j} \cos \left(\frac{2\pi \kern0.5em j}{D}i\right)+{\widehat{b}}_{\mu, j} \sin \left(\frac{2\pi \kern0.5em j}{D}i\right)\right]} $$(B7)$$ {\sigma}_T(i)={\left\{\frac{1}{2}{\widehat{a}}_{\sigma^2,0}+{\displaystyle \sum_{j=1}^{n_{h,{\sigma}^2}}\left[{\widehat{a}}_{\sigma^2,j} \cos \left(\frac{2\pi \kern0.5em j}{D}i\right)+{\widehat{b}}_{\sigma^2,j} \sin \left(\frac{2\pi \kern0.5em j}{D}i\right)\right]}\right\}}^{1/2} $$(B8)
Rights and permissions
About this article
Cite this article
Sirangelo, B., Caloiero, T., Coscarelli, R. et al. A stochastic model for the analysis of maximum daily temperature. Theor Appl Climatol 130, 275–289 (2017). https://doi.org/10.1007/s00704-016-1879-6
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00704-016-1879-6