1 Introduction

Poincaré type inequalities bound the \(L^q\)-norm of a function f on a domain \(\varOmega \subset \mathbb {R}^d\) in terms of the \(L^p\)-norm of its gradient, i.e.,

$$\begin{aligned} \left\| f\right\| _{L^q(\varOmega ,w)} \le C ~\left\| \nabla f\right\| _{L^p(\varOmega ,w)} \quad \text {for all } f \in \mathcal {C}, \end{aligned}$$
(2)

where \(\mathcal {C}\) is a suitable vector space of differentiable (at least in a weak sense) functions on \(\varOmega \). The constant C in (2) may depend on \(\varOmega , w, p, q\) and \(\mathcal {C}\) but cannot depend on f.

For Eq. (2) to hold obviously \(\mathcal {C}\) cannot contain any constant function besides \(f\equiv 0\). Typical choices for \(\mathcal {C}\) are either

  1. (i)

    Dirichlet boundary conditions, i.e., \(\mathcal {C}\) consisting of functions vanishing on the boundary \(\partial \varOmega \) or

  2. (ii)

    vanishing mean, i.e.,

    $$\begin{aligned} \int _\varOmega f w = 0\quad \text {for all } f\in \mathcal {C}. \end{aligned}$$

We will only discuss the second case, which amounts to considering the inequality

$$\begin{aligned} \left\| f-\left( \int _\varOmega w\right) ^{-1} \cdot \int _\varOmega f w\right\| _{L^q(\varOmega ,w)} \le C ~\left\| \nabla f\right\| _{L^p(\varOmega ,w)}. \end{aligned}$$
(3)

Depending on p, q and d, in the literature Poincaré inequalities are also linked to the names of Wirtinger (\(p=q=2\) and \(d=1\)) and Sobolev (\(p<d\) and \(q=dp/(d-p)\)).

Due to its importance in the theory of partial differential equations a vast amount of work and effort has been put in the study of Poincaré type inequalities. The following overview is by far not a complete collection of the available research on this topic.

In case of a constant weight a Poincaré inequality (3) is known to hold provided \(\varOmega \) is a bounded Lipschitz domain and

  • \(p=q\): in this case the Poincaré inequality is covered by the Lemma of Deny-Lions, see [11, 15].

  • \(p<d\) and \(q\le dp/(d-p)\), see [6, 20].

A well studied class of weights supporting Poincaré equations are the so called Muckenhoupt weights as introduced in [21], compare [12, 17]. For certain weight functions, \(q=p\) and arbitrary bounded domains a sufficient condition for a Poincaré to hold is provided in [3, 14]. However—depending on w—these criteria may be very difficult to verify.

Explicit bounds for the constant C in (3) are known only under very specific restrictions on the parameters d, p, q, the geometry of the domain \(\varOmega \) and the weight w: In case w is constant, \(p=q\) and \(\varOmega \) is convex and bounded it is known that

$$\begin{aligned} C\le \left\{ \begin{array}{ll} {{\,\mathrm{diam}\,}}(\varOmega )/2, &{}\quad p=q=1,\\ {{\,\mathrm{diam}\,}}(\varOmega )/\pi _p, &{}\quad p=q\ge 2, \end{array}\right. \end{aligned}$$
(4)

where

$$\begin{aligned} \pi _p:=2\pi \frac{(p-1)^{1/p}}{p\cdot \sin (\pi /p)}. \end{aligned}$$

The bound for \(p=q=2\) was first established in [22], see also [4]. Generalizations of the proof for the cases \(p=q=1\) and \(p=q\ge 2\) are due to [1, 16].

For star shaped domains—again under the assumptions that w is constant and \(p=q\)—an explicit bound on the Poincaré constant is given in [18].

In the onedimensional situation [9] provides a bound on the Poincaré constant for arbitrary p, q and w, which in certain cases is sharp in some sense. Computing the bound amounts to determining the supremum of a possibly complicated expression and therefore—depending on w—may not be feasible. In [10] the same authors give explicit bounds on the Poincaré constant when \(q\le p\), \(\varOmega \) is bounded and convex and w is a positive power of a concave function.

Gaussian or more generally so called log-concave weights on the full space \(\varOmega =\mathbb {R}^d\) are considered in [5, 7] for the case \(p=q=2\).

For arbitrary weight w and domain \(\varOmega \) the Poincaré constant can be estimated from above in terms of the so called Cheeger constant—a well studied concept in Riemannian geometry—see [8] and [19, Appendix]. Again computation of the Cheeger constant may not be feasible depending on w.

Explicit bounds for the constant in weighted Poincaré inequalities are only known in very specific scenarios. The main result of this paper shows that the Poincaré constant w.r.t. a weight w can be controlled in terms of the Poincaré constants w.r.t. the constant weight 1 on the superlevel sets of w. Combined with knowledge of Poincaré constants for the unweighted case this yields a powerful tool for estimating the Poincaré constant on a general domain equipped with a weight whose superlevel sets only have to be connected. The key ideas are inspired by the work of Dyda and Kassmann in [13], where radially symmetric weights were considered. As we will see a similar approach can be taken in a much more general setting.

2 Preliminaries

In the following \(\varOmega \) will be called a domain in \(\mathbb {R}^d\), if \(\varOmega \) is a nonempty, open and connected subset of \(\mathbb {R}^d\). We call a function \(w:\varOmega \rightarrow \mathbb {R}\) a weight on \(\varOmega \subset \mathbb {R}^d\) if w is measurable and nonnegative.

For \(p\in [1,\infty )\) the space \(L^p(\varOmega ,w)\) consists of all measurable functions \(f:\varOmega \rightarrow \mathbb {R}\) such that \(\left\| f\right\| _{L^p(\varOmega ,w)} < \infty \), where

$$\begin{aligned} \left\| f\right\| _{L^p(\varOmega ,w)} := \left( \int _\varOmega \left| f(x) \right| ^p w(x) ~dx \right) ^{1/p}. \end{aligned}$$

In the unweighted case, i.e. \(w\equiv 1\) we will drop the reference to the weight and write \(L^p(\varOmega )\). For a set \(A\subset \mathbb {R}^d\) the d-dimensional Lebesgue measure of A will be denoted by \(\left| A \right| \). For \(v\in \mathbb {R}^d\) we write \(\left| v \right| \) for the euclidean length of v.

The space of Lipschitz functions on \(\varOmega \), i.e. the set of functions that are Lipschitz continuous on every compact subset of \(\varOmega \) will be denoted by \(Lip(\varOmega )\). For \(q\in [1,\infty )\) we define

$$\begin{aligned} Lip^q(\varOmega ,w):=Lip(\varOmega )\cap L^q(\varOmega ,w). \end{aligned}$$
(5)

Again, in the unweighted case we will use the notation \(Lip^q(\varOmega )\).

Let \(D\subset \varOmega \). We will occasionally abuse the notation and write

$$\begin{aligned} w(D):=\int _D w(x)~dx. \end{aligned}$$

For \(f:\varOmega \rightarrow \mathbb {R}\) measurable the weighted mean of f on D is denoted by

$$\begin{aligned} f_D^w:=\frac{1}{w(D)}\int _D f(x)w(x)~dx. \end{aligned}$$
(6)

Remark 1

Suppose w is integrable on \(\varOmega \), \(D\subset \varOmega \) and that \(f\in L^p(\varOmega ,w)\) for \(p\ge 1\). Using Hölder’s inequality for \(\frac{1}{p}+\frac{1}{p'}=1\) we obtain

$$\begin{aligned} \left\| f\right\| _{L^1(D,w)}= & {} \left\| f\cdot w\right\| _{L^1(D)} = \left\| f w^{1/p} \cdot w^{1-1/p}\right\| _{L^1(D)} \\\le & {} \left\| f w^{1/p}\right\| _{L^p(D)} \cdot \left\| w^{1/p'}\right\| _{L^{p'}(D)} =\left\| f\right\| _{L^p(D,w)} \cdot \left\| w\right\| _{L^1(D)}^{1/p'} < \infty . \end{aligned}$$

Therefore—provided \(w(D)>0\)—in this case \(f_D^w\) as defined in (6) is a well defined real number.

The central topic of this work are so called Poincaré inequalities:

Definition 1

Let \(\varOmega \) be a domain in \(\mathbb {R}^d\), w an integrable weight on \(\varOmega \), \(\rho \) a weight on \(\varOmega \) and let \(p,q\in [1,\infty )\). Then a weighted (q, p)-Poincaré inequality holds if there exists a finite constant C such that

$$\begin{aligned} \left\| f-f_\varOmega ^w\right\| _{L^q(\varOmega ,w)} \le C \left\| \nabla f\right\| _{L^p(\varOmega ,\rho )} \quad \text {for all } f\in Lip^q(\varOmega ,w). \end{aligned}$$
(7)

The smallest possible C in (7) is called Poincaré constant and denoted by \(C_q^p(\varOmega ,w,\rho )\).

Another important object will be the so called superlevel sets defined by

$$\begin{aligned} \varOmega _t^w:=\left\{ x\in \varOmega : w(x)>t\right\} \quad \text {for } t\ge 0. \end{aligned}$$

3 Main theorem

In the literature one can often find Poincaré inequalities defined by

$$\begin{aligned} \inf _{c\in \mathbb {R}} \left\| f-c\right\| _{L^q(\varOmega ,w)} \le C \left\| \nabla f\right\| _{L^p(\varOmega ,\rho )} \quad \text {for all } f, \end{aligned}$$
(8)

instead of our definition, cf. (7). The next lemma tells us that the two concepts are essentially the same. A proof can be found in [13].

Lemma 1

Let \(\varOmega \subset \mathbb {R}^d\), let w be an integrable weight on \(\varOmega \) and \(p\in [1,\infty )\). Then for any \(f\in L^p(\varOmega ,w)\) it holds that

$$\begin{aligned} \inf _{c\in \mathbb {R}} \left\| f-c\right\| _{L^p(\varOmega ,w)} \le \left\| f-f_\varOmega ^w\right\| _{L^p(\varOmega ,w)} \le 2 \inf _{c\in \mathbb {R}} \left\| f-c\right\| _{L^p(\varOmega ,w)}. \end{aligned}$$

The following lemma provides a formula on how to write a weighted integral as a double integral.

Lemma 2

Let \(\varOmega \subset \mathbb {R}^d\), let w be an integrable weight on \(\varOmega \) and let \(g\in L^1(\varOmega ,w)\) then

$$\begin{aligned} \int _\varOmega g(x)w(x)~dx = \int _0^{\infty } \int _{\varOmega _t^w} g(x) ~dx ~dt \end{aligned}$$

Proof

For a set A let \(\chi _A\) denote the characteristic function of A, then

$$\begin{aligned} \int _\varOmega g(x)w(x)~dx = \int _\varOmega g(x) \int _0^{w(x)} dt~dx = \int _\varOmega \int _0^\infty g(x) \chi _{[0,w(x))}(t) ~dt~dx. \end{aligned}$$
(9)

Obviously Eq. (9) still holds true when g is replaced by \(\left| g \right| \). Since \(g\in L^1(\varOmega ,w)\) we can apply Fubini’s theorem and change order of integration. Using \(\chi _{[0,w(x))}(t)=\chi _{\varOmega _t^w}(x)\) we obtain

$$\begin{aligned} \int _\varOmega \int _0^\infty g(x) \chi _{[0,w(x))}(t) ~dt~dx= & {} \int _0^\infty \int _\varOmega g(x) \chi _{\varOmega _t^w}(x) ~dx~dt\\= & {} \int _0^\infty \int _{\varOmega _t^w} g(x)~dx~dt. \end{aligned}$$

\(\square \)

Next we show a simple relation between Lipschitz function spaces as defined in (5).

Lemma 3

Let w be a weight on a domain \(\varOmega \) and \(q\ge 1\). Then for any \(t>0\)

$$\begin{aligned} Lip^q(\varOmega ,w)\subset Lip^q(\varOmega _t^w). \end{aligned}$$

Proof

Let \(f\in Lip^q(\varOmega ,w)\). Then f is a Lipschitz function on \(\varOmega _t:=\varOmega _t^w\) for arbitrary \(t>0\). We can now estimate

$$\begin{aligned} \left\| f\right\| _{L^q(\varOmega _t)}^q = \int _{\varOmega _t} \left| f(x) \right| ^q~dx \le \int _{\varOmega _t} \left| f(x) \right| ^q \frac{w(x)}{t}~dx\le \frac{1}{t} \left\| f\right\| _{L^q(\varOmega ,w)}^q <\infty . \end{aligned}$$

Therefore \(f\in Lip^q(\varOmega _t)\). \(\square \)

We are set to state the main result:

Theorem 1

Let w be a bounded and integrable weight on a domain \(\varOmega \subset \mathbb {R}^d\), let \(\rho \) be a weight on \(\varOmega \) and let \(1\le q\le p\). Then

$$\begin{aligned} \begin{aligned} C_q^p(\varOmega ,w,w\rho )&\le 8 \cdot \inf _{\begin{array}{c} 0\le \tau \le \left\| w\right\| _{L^\infty (\varOmega )} \\ q\le s \le p \end{array}} \left( \frac{\left\| w\right\| _{L^\infty (\varOmega )}}{\tau } \cdot \frac{\left| \varOmega \right| }{\left| \varOmega _\tau ^w \right| } \right) ^{1/q} \cdot w\rho (\varOmega )^{\frac{1}{q}-\frac{s}{pq}} \\&\quad \cdot \left\| t\mapsto C_q^s(\varOmega _t^w,1,\rho )\right\| _{L^{\frac{sq}{s-q}}([0,\tau ])} \end{aligned} \end{aligned}$$
(10)

Assuming that there is a number \(\tau \) such that the quantity

$$\begin{aligned} \left( \frac{\left\| w\right\| _{L^\infty (\varOmega )}}{\tau } \cdot \frac{\left| \varOmega \right| }{\left| \varOmega _\tau ^w \right| }\right) ^{1/q} \end{aligned}$$

is of moderate size, Theorem 1 reveals—by choosing \(\rho \equiv 1\)—that the weighted Poincaré constant \(C_q^p(\varOmega ,w,w)\) can be essentially controlled by the norm of \( t\mapsto C_q^s(\varOmega _t^w,1,1). \) The Poincaré constant \(C_q^s(\varOmega _t^w,1,1)\) is infinite whenever the underlying domain consists of more than one connected component. Thus application of Theorem 1 only makes sense if all the superlevel sets \(\varOmega _t^w\) are connected (at least for \(t\in [0,\tau ]\)).

As already mentioned in the introduction Poincaré constants can also be estimated using the concept of the Cheeger constant. This means that—loosely speaking—the Poincaré constant is rather large in the presence of a bottleneckFootnote 1 since this is precisely what the Cheeger constant captures - and vice versa. In this spirit Theorem 1 can be qualitatively read as follows:

  1. 1.

    If none of the superlevel sets \(\varOmega _t^w\) possesses a bottleneck w.r.t. to the constant weight 1 then neither will \(\varOmega \) w.r.t. w. In that case \(C_q^p(\varOmega ,w,w)\) is small.

  2. 2.

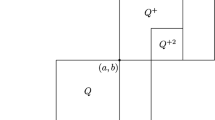
    However if \(C_q^p(\varOmega ,w,w)\) is large then some of the superlevel sets \(\varOmega _t^w\) will have large Poincaré constants w.r.t. the constant weight 1 and therefore a bottleneck, see Fig. 1.

Fig. 1
figure 1

The left figure shows a typical example of a bottlenecked weight on a plane domain. The two main parts of its superlevel sets—as sketched on the right—are connected by a thin bridge and therefore we observe the presence of a bottleneck

Full size image

Proof of Theorem 1

For \(\tau \in [0,\left\| w\right\| _{L^\infty (\varOmega )}]\) let \(w_\tau \) be the weight w cut off at level \(\tau \), i.e.,

$$\begin{aligned} w_\tau (x):=\min \{w(x),\tau \}. \end{aligned}$$

Then obviously

$$\begin{aligned} w_\tau \le w \le \frac{\left\| w\right\| _{L^\infty (\varOmega )}}{\tau } w_\tau \end{aligned}$$
(11)

and therefore by Lemma 1 we obtain for any \(f\in L^q(\varOmega ,w)\)

$$\begin{aligned} \begin{aligned} \left\| f-f_\varOmega ^w\right\| _{L^q(\varOmega ,w)}^q&\le 2^q \inf _{c\in \mathbb {R}} \left\| f-c\right\| _{L^q(\varOmega ,w)}^q \\&\le 2^q \frac{\left\| w\right\| _{L^\infty (\varOmega )}}{\tau } \inf _{c\in \mathbb {R}} \left\| f-c\right\| _{L^q(\varOmega ,w_\tau )}^q\\&\le 2^q \frac{\left\| w\right\| _{L^\infty (\varOmega )}}{\tau } \left\| f-f_\varOmega ^{w_\tau }\right\| _{L^q(\varOmega ,w_\tau )}^q \end{aligned} \end{aligned}$$
(12)

We set \(g:=f-f_\varOmega ^{w_\tau }\). Since \(\varOmega _t^{w_\tau }\) coincides with \(\varOmega _t:=\varOmega _t^w\) for \(t\le \tau \) and is empty for \(t>\tau \), using Lemma 2 we obtain that

$$\begin{aligned} 0=\int _\varOmega g \cdot w_\tau ~dx= & {} \int _0^\infty \int _{\varOmega _t^{w_\tau }} g(x) ~dx~dt\\= & {} \int _0^\tau \int _{\varOmega _t} g(x)~dx~dt\\= & {} \int _0^\tau g_{\varOmega _t}^1 \cdot \left| \varOmega _t \right| ~dt \end{aligned}$$

and observe that

$$\begin{aligned} t\mapsto g_{\varOmega _t}^1=:g_{\varOmega _t} \text { has integral mean } 0 \text { w.r.t. to the measure } \left| \varOmega _t \right| dt \text { on } [0,\tau ]. \end{aligned}$$
(13)

Since for any real numbers a, b the inequality \(\left| a+b \right| ^q\le 2^{q-1} \left( \left| a \right| ^q+\left| b \right| ^q\right) \) holds we estimate

$$\begin{aligned} \begin{aligned} \left\| g\right\| _{L^q(\varOmega ,w_\tau )}^q&= \int _0^\tau \int _{\varOmega _t} \left| g(x) \right| ^q~dx~dt \\&\le 2^{q-1} \int _0^\tau \int _{\varOmega _t} \left( \left| g(x)-g_{\varOmega _t} \right| ^q+\left| g_{\varOmega _t} \right| ^q\right) ~dx~dt =: 2^{q-1} \cdot \left( \hbox {I}+\hbox {II} \right) . \end{aligned} \end{aligned}$$
(14)

The inner integral of \(\hbox {I}\) is already set up to apply Poincaré’s inequality. The key trick lies in how to bound \(\hbox {II}\) in terms of \(\hbox {I}\). First \(\hbox {II}\) can be rewritten in the following way:

$$\begin{aligned} \hbox {II}= \int _0^\tau \left| g_{\varOmega _t} \right| ^q \cdot \left| \varOmega _t \right| ~dt = \left| \varOmega _\tau \right| ^{-1} \int _{\varOmega _\tau } \int _0^\tau \left| g_{\varOmega _t} \right| ^q \cdot \left| \varOmega _t \right| ~dt~dx. \end{aligned}$$
(15)

Using observation (13) together with Lemma 1 guarantees that the inner integral of the right hand side is bounded by

$$\begin{aligned} 2^q\int _0^\tau \left| g_{\varOmega _t}-c \right| ^q \cdot \left| \varOmega _t \right| ~dt, \end{aligned}$$

where c is an arbitrary real number. The choice \(c=g(x)\) yields

$$\begin{aligned} \hbox {II} \le \left| \varOmega _\tau \right| ^{-1}\cdot 2^q \int _{\varOmega _\tau } \int _0^\tau \left| g_{\varOmega _t}-g(x) \right| ^q \cdot \left| \varOmega _t \right| ~dt~dx \end{aligned}$$
(16)

Changing order of integration and since for \(t\in [0,\tau ]\) the inclusions \(\varOmega _\tau \subset \varOmega _t \subset \varOmega \) hold we arrive at

$$\begin{aligned} \hbox {II}\le 2^q \frac{\left| \varOmega \right| }{\left| \varOmega _\tau \right| } \cdot \hbox {I}. \end{aligned}$$
(17)

Collecting the estimates from (12), (14) and (17) gives

$$\begin{aligned} \left\| f-f_\varOmega ^w\right\| _{L^q(\varOmega ,w)}^q \le 2^{3q} \cdot \frac{\left\| w\right\| _{L^\infty (\varOmega )}}{\tau } \cdot \frac{\left| \varOmega \right| }{\left| \varOmega _\tau \right| } \cdot \hbox {I}. \end{aligned}$$
(18)

We proceed with bounding the expression \(\hbox {I}\) by applying Poincaré’s inequality on each of the superlevel sets \(\varOmega _t\). Let \(s\in [q,p]\) and set \(r:=s/q\) and \(1/r+1/r'=1\), then

$$\begin{aligned} \begin{aligned} \hbox {I}&= \int _0^\tau \int _{\varOmega _t} \left| g(x)-g_{\varOmega _t} \right| ^q~dx~dt\\&\le \int _0^\tau C_q^s(\varOmega _t,1,\rho )^q \cdot \left( \int _{\varOmega _t} \left| \nabla g(x) \right| ^s \rho (x)~dx\right) ^{q/s}~dt\\&\le \left\| t\mapsto C_q^s(\varOmega _t,1,\rho )^q\right\| _{L^{r'}([0,\tau ])} \cdot \left( \int _0^\tau \int _{\varOmega _t} \left| \nabla g(x) \right| ^s \rho (x)~dx~dt\right) ^{1/r}\\&=\left\| t\mapsto C_q^s(\varOmega _t,1,\rho )\right\| _{L^{\frac{sq}{s-q}}([0,\tau ])}^q \cdot \left\| \nabla g\right\| _{L^s(\varOmega ,w\rho )}^q \end{aligned} \end{aligned}$$
(19)

Again making use of Hölder’s inequality we can estimate the last term in the following way

$$\begin{aligned} \left\| \nabla g\right\| _{L^s(\varOmega ,w\rho )} \le \left\| \nabla g\right\| _{L^p(\varOmega ,w\rho )} \cdot w\rho (\varOmega )^{1-\frac{s}{p}}. \end{aligned}$$
(20)

Since \(\nabla g=\nabla f\) we obtain by combining (18), (19) and (20) that

$$\begin{aligned} \begin{aligned} \left\| f-f_\varOmega ^w\right\| _{L^q(\varOmega ,w)}&\le 8 \left( \frac{\left\| w\right\| _{L^\infty (\varOmega )}}{\tau } \cdot \frac{\left| \varOmega \right| }{\left| \varOmega _\tau \right| } \right) ^{1/q} \cdot w\rho (\varOmega )^{\frac{1}{q}-\frac{s}{pq}}\\&\quad \cdot \left\| t\mapsto C_q^s(\varOmega _t,1)\right\| _{L^{\frac{sq}{s-q}}([0,\tau ])} \cdot \left\| \nabla f\right\| _{L^p(\varOmega ,w\rho )} \end{aligned} \end{aligned}$$

Since this holds for arbitrary \(\tau \in [0,\left\| w\right\| _{L^{\infty }(\varOmega )}]\) and \(s\in [q,p]\) we can conclude that (10) holds true. \(\square \)

Finally we consider a concrete example. Our aim here is not to find the smallest possible bound on the Poincaré constant but rather to indicate how the result of Theorem 1 can be applied in practice. We choose a weight that is neither a power of a concave function nor log-concave in order to emphasize that our method yields results in situations where existing techniques are not applicable.

Example 1

Let \(\varOmega \) be the unit ball in \(\mathbb {R}^2\) equipped with the radially symmetric weight

$$\begin{aligned} w(x):=1-\left| 2\left| x \right| -1 \right| . \end{aligned}$$

Since w vanishes at the origin and on the boundary of the domain, w is not equivalent to a constant weight. Thus we can not resort to results for the unweighted case in order to find a bound for the Poincaré constant.

For \(0<r<R\) let the annulus centered at the origin be defined by \( A_{r,R}:=B_R{\setminus } \overline{B_r}\). The superlevel sets of w are given by

$$\begin{aligned} \varOmega _t^w = A_{\frac{t}{2},1-\frac{t}{2}}=:A(t). \end{aligned}$$

The Poincaré constant for annuli have been studied in [2, Theorem 2.3], where they considered the existence of a finite number \(\gamma \) such that

$$\begin{aligned} C_2^2(A_{r,R},1,1)\le \gamma R. \end{aligned}$$
(21)

for all \(r<R\). Note that one could explicitly find a \(\gamma \) such that (21) holds true by exploiting Cheeger’s inequality.

Next we apply Theorem 1 with \(\tau =1/2, s=2\) and \(\rho \equiv 1\). Thus we obtain for any \(p\ge 2\) that

$$\begin{aligned} C_2^p(\varOmega ,w,w) \le 8 \cdot \left( 2 \frac{\left| \varOmega \right| }{\left| A(1/2) \right| }\right) ^{1/2} \cdot w(\varOmega )^{\frac{1}{2}-\frac{1}{p}}\cdot \gamma . \end{aligned}$$

Elementary computations yield that

$$\begin{aligned} \left| A(t) \right| =\pi (1-t) \quad \text {and} \quad w(\varOmega )=\frac{\pi }{2}. \end{aligned}$$

Therefore we arrive at \( C_2^p(\varOmega ,w,w) \le 16 \cdot \frac{\pi }{2}^{\frac{1}{2}-\frac{1}{p}} \cdot \gamma . \)