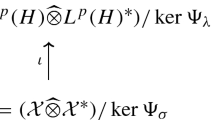A Wiener Lemma for the discrete Heisenberg group

Abstract

This article contains a Wiener Lemma for the convolution algebra $\ell ^1({{\mathrm{\mathbb {H}}}},{{\mathrm{\mathbb {C}}}})$ and group $C^*$-algebra $C^*({{\mathrm{\mathbb {H}}}})$ of the discrete Heisenberg group ${{\mathrm{\mathbb {H}}}}$. At first, a short review of Wiener’s Lemma in its classical form and general results about invertibility in group algebras of nilpotent groups will be presented. The known literature on this topic suggests that invertibility investigations in the group algebras of ${{\mathrm{\mathbb {H}}}}$ rely on the complete knowledge of $\widehat{{{\mathrm{\mathbb {H}}}}}$—the dual of ${{\mathrm{\mathbb {H}}}}$, i.e., the space of unitary equivalence classes of irreducible unitary representations. We will describe the dual of ${{{\mathrm{\mathbb {H}}}}}$ explicitly and discuss its structure. Wiener’s Lemma provides a convenient condition to verify invertibility in $\ell ^1({{\mathrm{\mathbb {H}}}},{{\mathrm{\mathbb {C}}}})$ and $C^*({{\mathrm{\mathbb {H}}}})$ which bypasses $\widehat{{{\mathrm{\mathbb {H}}}}}$. The proof of Wiener’s Lemma for ${{\mathrm{\mathbb {H}}}}$ relies on local principles and can be generalised to countable nilpotent groups. As our analysis shows, the main representation theoretical objects to study invertibility in group algebras of nilpotent groups are the corresponding primitive ideal spaces. Wiener’s Lemma for ${{\mathrm{\mathbb {H}}}}$ has interesting applications in algebraic dynamics and time-frequency analysis which will be presented in this article as well.

1 Motivation

Let $\varGamma$ be a countably infinite discrete group. The aim of this article is to find a verifiable criterion—a Wiener Lemma—for invertibility in the group algebra

$$\begin{aligned} \ell ^1(\varGamma ,{{\mathrm{\mathbb {C}}}}) := \biggl \{ (f_\gamma )_{\gamma \in \varGamma }\,:\, \sum _{\gamma \in \varGamma } |f_\gamma | < \infty \biggr \}, \end{aligned}$$

in particular for the case where $\varGamma$ is the discrete Heisenberg group ${{\mathrm{\mathbb {H}}}}$.

Our main motivation to study this problem is an application in the field of algebraic dynamics which we introduce first. An algebraic $\varGamma$ -action is a homomorphism $\alpha : \varGamma \longrightarrow \,\text {Aut}\, (X)$ from $\varGamma$ to the group of automorphisms of a compact metrisable abelian group X [33].

We are especially interested in principal actions which are defined as follows. Let f be an element in the integer group ring ${{\mathrm{\mathbb {Z}}}}[\varGamma ]$, i.e., the ring of functions $\varGamma \longrightarrow {{\mathrm{\mathbb {Z}}}}$ with finite support. The Pontryagin dual of the discrete abelian group ${{\mathrm{\mathbb {Z}}}}[\varGamma ]/{{\mathrm{\mathbb {Z}}}}[\varGamma ]f$ will be denoted by $X_f \subseteq {{\mathrm{\mathbb {T}}}}^{\varGamma }$, where ${{\mathrm{\mathbb {T}}}}=\mathbb {R}/\mathbb {Z}$ (which will be identified with the unit interval (0, 1]). Pontryagin’s duality theory of locally compact abelian groups tells us that $X_f$ can be identified with the annihilator of the principal left ideal ${{\mathrm{\mathbb {Z}}}}[\varGamma ]f$, i.e.,

$$\begin{aligned} X_f = ({{\mathrm{\mathbb {Z}}}}[\varGamma ]f)^\perp =\biggl \{x\in {{\mathrm{\mathbb {T}}}}^{\varGamma }\,:\, \sum _{\gamma \in \varGamma } f_\gamma x_{\gamma '\gamma } =0 \,\,\text {for every}\,\gamma '\in \varGamma \biggr \}. \end{aligned}$$

(1)

The left shift-action $\lambda$ on ${{\mathrm{\mathbb {T}}}}^\varGamma$ is defined by $(\lambda ^\gamma x)_{\gamma '} = x_{\gamma ^{-1}\gamma '}$ for every $x \in {{\mathrm{\mathbb {T}}}}^\varGamma$ and $\gamma ,\gamma ' \in \varGamma$. Denote by $\alpha _f$ the restriction of $\lambda$ on ${{\mathrm{\mathbb {T}}}}^{\varGamma }$ to $X_f$. The pair $(X_f,\alpha _f)$ forms an algebraic dynamical system which we call principal $\varGamma$ -action—because it is defined by a principal ideal [cf. (1)].

Since a principal $\varGamma$-action $(X_f,\alpha _f)$ is completely determined by an element $f\in \mathbb {Z}[ \varGamma ]$, one should be able to express its dynamical properties in terms of properties of f. Expansiveness is such a dynamical property which allows a nice algebraic interpretation. Let $(X,\alpha )$ be an algebraic dynamical system and d a translation invariant metric on X. The $\varGamma$-action $\alpha$ is expansive if there exists a constant $\varepsilon >0$ such that

$$\begin{aligned} \sup _{\gamma \in \varGamma } d(\alpha ^{\gamma } x, \alpha ^{\gamma } y) > \varepsilon , \end{aligned}$$

for all pairs of distinct elements $x,y\in X$. We know from [8, Theorem 3.2] that $(X_f,\alpha _f)$ is expansive if and only if f is invertible in $\ell ^1(\varGamma ,{{\mathrm{\mathbb {R}}}})$. This result was proved already in the special cases $\varGamma ={{\mathrm{\mathbb {Z}}}}^d$ and for groups $\varGamma$ which are nilpotent in [33] and in [9], respectively. Although, this result is a complete characterisation of expansiveness, it is in general hard to check whether f is invertible in $\ell ^1(\varGamma ,{{\mathrm{\mathbb {R}}}})$ or not.

1.1 Outline of the article

In Sect. 2 we will recall known criteria for invertibility in symmetric unital Banach algebras $\mathcal A$. The most important result links invertibility investigations in $\mathcal A$ to the representation theory of $\mathcal A$. More precisely, the existence of an inverse $a^{-1}$ of $a \in \mathcal A$ is equivalent to the invertibility of the operators $\pi (a)$ for every irreducible unitary representation $\pi$ of $\mathcal A$. The representation theory of ${{\mathrm{\mathbb {H}}}}$ is unmanageable as we will demonstrate in Sect. 3.

Theorem 11—Wiener’s Lemma for the discrete Heisenberg group—is the main result of this paper and allows one to restrict the attention to certain ‘nice’ and canonical irreducible representations for questions concerning invertibility in the group algebra of the discrete Heisenberg group ${{\mathrm{\mathbb {H}}}}$. The proof of Theorem 11 can be found in Sect. 4. Moreover, as will be shown in Sect. 4 as well, invertibility of $f\in {{\mathrm{\mathbb {Z}}}}[{{\mathrm{\mathbb {H}}}}]$ in $\ell ^1({{\mathrm{\mathbb {H}}}},{{\mathrm{\mathbb {R}}}})$ can be verified with the help of the finite-dimensional irreducible unitary representations of ${{\mathrm{\mathbb {H}}}}$.

In Sect. 5 we generalise Theorem 11 to countable discrete nilpotent groups $\varGamma$. This result says that an element a in $C^*(\varGamma )$ is invertible if and only if for every primitive ideal $\mathtt I$ of $C^*(\varGamma )$ the projection of a onto the quotient space $C^*(\varGamma )/\mathtt I$ is invertible. As we will see, the primitive ideal space is more accessible than the space of irreducible representations and easy to determine. Moreover, this Wiener Lemma for nilpotent groups can be converted to a statement about invertibility of evaluations of irreducible monomial representations.

In Sect. 6 we will explore a connection to time-frequency analysis. Allan’s local principle (cf. Sect. 4) directly links localisations of ${{\mathrm{\ell ^1(\mathbb {H},\mathbb {C})}}}$ to twisted convolution algebras and hence, the representations of ${{\mathrm{\mathbb {H}}}}$ and the relevant representation theory in the field of time-frequency analysis coincide. In order to highlight this connection even more, time-frequency analysis might be interpreted as the Fourier theory on the discrete Heisenberg group ${{\mathrm{\mathbb {H}}}}$; due to the striking similarities to the Fourier analysis of the additive group ${{\mathrm{\mathbb {Z}}}}$ and its group algebras. Moreover, we give an alternative proof of Wiener’s Lemma for twisted convolution algebras, which only uses the representation theory of ${{\mathrm{\mathbb {H}}}}$. Theorem 22—which is based on a result of Linnell (cf. [25])—gives a full description of the spectrum of the operators $\pi (f)$ acting on $L^2({{\mathrm{\mathbb {R}}}},{{\mathrm{\mathbb {C}}}})$, where $\pi$ is a Stone-von Neumann representation [cf. (23] for a definition) and $f\in {{\mathrm{\mathbb {Z}}}}[{{\mathrm{\mathbb {H}}}}]$.

Section 7 contains applications of Theorem 11 and Wiener’s Lemma for twisted convolution algebras, in particular, conditions for non-invertibility for ‘linear’ elements in $f\in {{\mathrm{\mathbb {Z}}}}[{{\mathrm{\mathbb {H}}}}]$.

2 Invertibility in group algebras and Wiener’s Lemma: a review

In this section we review known conditions for invertibility in group algebras of nilpotent groups $\varGamma$. First of all we refer to the article [14] by Gröchenig for a modern survey of Wiener’s Lemma and its variations. Gröchenig’s survey focuses on two main topics, namely on invertibility of convolution operators on $\ell ^p$-spaces (cf. Sect. 2.2 and in particular Theorem 7) and inverse-closedness. Moreover, Gröchenig explains how these topics are related to questions on invertibility in time-frequency analysis and invertibility in group algebras. Although, Wiener’s Lemma for convolution operators is stated here as well it will play an insignificant role in the rest of the paper. However, we would like to bring the reader’s attention to Theorem 8 which is yet another result which relates invertibility in $\ell ^1(\varGamma ,{{\mathrm{\mathbb {C}}}})$ to invertibility of convolution operators. This result is completely independent of Theorem 7 and holds in much greater generality.

In this review we will explain why a detailed understanding of the space of irreducible representations of a nilpotent group $\varGamma$ is of importance for invertibility investigations in the group algebras of $\varGamma$. Furthermore, we will present Gelfand’s results on invertibility in commutative Banach algebras in the form of local principles; which will be discussed in greater detail in later sections of this article.

We start the discussion with Wiener’s Lemma in its classical form. Let us denote by $\mathcal A ({{\mathrm{\mathbb {T}}}})$ the Banach algebra of functions with absolutely convergent Fourier series on ${{\mathrm{\mathbb {T}}}}$.

Theorem 1

(Wiener’s Lemma) An element $F\in \mathcal A ({{\mathrm{\mathbb {T}}}})$ is invertible, i.e. $1/F \in \mathcal A ({{\mathrm{\mathbb {T}}}})$, if and only if $F(s)\not = 0$ for all $s \in {{\mathrm{\mathbb {T}}}}$.

Before we start our review of more general results let us mention the concept of inverse-closedness which originates from Wiener’s Lemma as well. The convolution algebra $\ell ^1({{\mathrm{\mathbb {Z}}}},{{\mathrm{\mathbb {C}}}})$ is isomorphic to $\mathcal A ({{\mathrm{\mathbb {T}}}})$ and hence $\ell ^1({{\mathrm{\mathbb {Z}}}},{{\mathrm{\mathbb {C}}}})$ can be embedded in the larger Banach algebra of continuous functions $C({{\mathrm{\mathbb {T}}}},{{\mathrm{\mathbb {C}}}})$ in a natural way. The fact that $F\in \mathcal A ({{\mathrm{\mathbb {T}}}})$ is invertible in $\mathcal A ({{\mathrm{\mathbb {T}}}})$ if and only if F is invertible in $C({{\mathrm{\mathbb {T}}}},{{\mathrm{\mathbb {C}}}})$ leads to the question: for which pairs of nested unital Banach algebras $\mathcal A ,\mathcal B$ with $\mathcal A \subseteq \mathcal B$ and with the same multiplicative identity element does the following implication hold:

$$\begin{aligned} a\in \mathcal A \quad \text {and}\quad a^{-1}\in \mathcal B \,\,\Longrightarrow \,\, a^{-1}\in \mathcal A. \end{aligned}$$

(2)

In the literature a pair of Banach algebras which fulfils (2) is called a Wiener pair.

Wiener’s Lemma was the starting point of Gelfand’s study of invertibility in commutative Banach algebras. Gelfand’s theory links the question of invertibility in a commutative Banach algebra $\mathcal A$ to the study of its irreducible representations and the compact space of maximal ideals $\text {Max} (\mathcal A)$. We collect in the following theorem several criteria for invertibility in unital commutative Banach algebras.

Theorem 2

(cf. [11]) Suppose $\mathcal A$ is a unital commutative Banach algebra. The set of irreducible representations of $\mathcal A$ is isomorphic to the compact space of maximal ideals $\text {Max} (\mathcal A)$. Furthermore, the following statements are equivalent

• 1. $a \in \mathcal A$ is invertible;

• 2. $a \not \in m$ for all $m \in \, \text {Max}\, (\mathcal A)$;

• 3. $\varPhi _m(a)$ is invertible in $\mathcal A /m$ for all $m \in \text {Max} (\mathcal A)$, where $\varPhi _m: \mathcal A \longrightarrow \mathcal A /m \cong {{\mathrm{\mathbb {C}}}}$ is the canonical projection map;

• 4. $\varPhi _m(a) \not = 0$ for all $m \in \text {Max} (\mathcal A)$;

• 5. $\pi (a)v \not = 0$ for every one-dimensional irreducible unitary representation $\pi$ of $\mathcal A$ and $v\in {{\mathrm{\mathbb {C}}}}{\backslash } \{ 0\}$ (definitions can be found in Sect. 2.1).

The main goal of this article is to prove that similar results hold for group algebras of nilpotent groups and, in particular, for the discrete Heisenberg group.

In this article we concentrate on the harmonic analysis of rings associated with a countably infinite group $\varGamma$ furnished with the discrete topology. Beside ${{\mathrm{\mathbb {Z}}}}[\varGamma ]$ and $\ell ^1(\varGamma ,{{\mathrm{\mathbb {C}}}})$ we are interested in $C^*(\varGamma )$, the group- $C^*$ -algebra of $\varGamma$, i.e., the enveloping $C^*$-algebra of $\ell ^1(\varGamma ,{{\mathrm{\mathbb {C}}}})$.

Let $\ell ^\infty (\varGamma ,\mathbb {C})$ be the space of bounded complex-valued maps. We write a typical element $f \in \ell ^\infty (\varGamma ,{{\mathrm{\mathbb {C}}}})$ as a formal sum $\sum _{\gamma \in \varGamma } f_\gamma \cdot \gamma$, where $f_\gamma = f(\gamma )$. The involution $f\mapsto f^*$ is defined by $f^*=\sum _{\gamma \in \varGamma } \bar{f}_{\gamma ^{-1}} \cdot \gamma$. The product of $f\in \ell ^1(\varGamma ,{{\mathrm{\mathbb {C}}}})$ and $g\in \ell ^\infty (\varGamma ,{{\mathrm{\mathbb {C}}}})$ is given by convolution

$$\begin{aligned} fg=\sum _{\gamma ,\gamma '\in \varGamma }f_\gamma g_{\gamma '}\cdot \gamma \gamma ' =\sum _{\gamma ,\gamma '\in \varGamma }f_\gamma g_{\gamma ^{-1}\gamma '}\cdot \gamma '\,. \end{aligned}$$

(3)

For $1\le p <\infty$ we set

$$\begin{aligned} \ell ^p(\varGamma ,\mathbb {C})=\left\{ f=(f_\gamma )\in \ell ^\infty (\varGamma ,\mathbb {C}) \,: \,\Vert f\Vert _p=\left( \sum _{\gamma \in \varGamma }|f_\gamma |^p\right) ^{1/p}<\infty \right\} . \end{aligned}$$

2.1 Representation theory

We recall at this point some relevant definitions and results from representation theory, which will be used later. Moreover, we will state results for symmetric Banach-$^*$-algebras which are in the spirit of Wiener’s Lemma.

2.1.1 Unitary representations

Let $\mathcal {H}$ be a complex Hilbert space with inner product $\langle \cdot ,\cdot \rangle$. We denote by $\mathcal {B}(\mathcal {H})$ the algebra of bounded linear operators on $\mathcal {H}$, furnished with the strong operator topology. Further, denote by $\mathcal {U}(\mathcal {H})\subset \mathcal {B}(\mathcal {H})$ the group of unitary operators on $\mathcal {H}$. If $\varGamma$ is a countable group, a unitary representation $\pi$ of $\varGamma$ is a homomorphism $\gamma \mapsto \pi (\gamma )$ from $\varGamma$ into $\mathcal {U}(\mathcal {H})$ for some complex Hilbert space $\mathcal {H}$. Every unitary representation $\pi$ of $\varGamma$ extends to a $^*$-representation of $\ell ^1(\varGamma ,\mathbb {C})$, which is again denoted by $\pi$, and which is given by the formula $\pi (f)=\sum _{\gamma \in \varGamma }f_\gamma \pi (\gamma )$ for $f=\sum _{\gamma \in \varGamma }f_\gamma \cdot \gamma \in \ell ^1(\varGamma ,\mathbb {C})$. Clearly, $\pi (f^*)=\pi (f)^*$. The following theorem was probably first published in [12] but we refer to [30, Theorem 12.4.1].

Theorem 3

Let $\varGamma$ be a discrete group. Then there are bijections between

• the class of unitary representations of $\varGamma$;

• the class of non-degenerate¹ $^*$-representations of $\ell ^1(\varGamma ,{{\mathrm{\mathbb {C}}}})$;

• the class of non-degenerate $^*$-representations of $C^*(\varGamma )$.

Moreover, these bijections respect unitary equivalence and irreducibility.

Hence the representation theories of $\varGamma$, $\ell ^1(\varGamma ,{{\mathrm{\mathbb {C}}}})$ and $C^*(\varGamma )$ coincide. In consideration of this result we will use the same symbol for a unitary representation of $\varGamma$ and its corresponding $^*$-representations of the group algebras $\ell ^1(\varGamma ,{{\mathrm{\mathbb {C}}}})$ and $C^*(\varGamma )$.

2.1.2 States and the GNS construction

Suppose that $\mathcal A$ is a unital $C^*$-algebra. A positive linear functional $\phi : \mathcal A \longrightarrow {{\mathrm{\mathbb {C}}}}$ is a state if $\phi (1_{\mathcal A})=1$. We denote by $\mathcal S (\mathcal A )$ the space of states of $\mathcal A$, which is a weak$^*$-compact convex subset of the dual space of $\mathcal A$. The extreme points of $\mathcal S (\mathcal A)$ are called pure states.

A representation $\pi$ of $\mathcal A$ is cyclic if there exists a vector $v \in \mathcal H _\pi$ such that the set $\{ \pi (a)v \,:\,a\in \mathcal A\}$ is dense in $\mathcal H _\pi$, in which case v is called a cyclic vector. The Gelfand–Naimark–Segal (GNS) construction links the cyclic representations of $\mathcal A$ and the states of $\mathcal A$ in the following way. If $\pi$ is a cyclic representation with a cyclic unit vector v, then $\phi _{\pi ,v}$, defined by

$$\begin{aligned} \phi _{\pi ,v}(a)= \langle \pi (a)v,v\rangle \end{aligned}$$

for every $a \in \mathcal A$, is a state of $\mathcal A$. If $\pi$ is irreducible, then $\phi _{\pi ,v}$ is a pure state. Moreover, for every state $\phi$ of $\mathcal A$ there is a cyclic representation $(\pi _\phi ,\mathcal H _\phi )$ and a cyclic unit vector $v_\phi \in \mathcal H _\phi$ such that $\phi (a)=\langle \pi _\phi (a)v_\phi ,v_\phi \rangle$ for every $a\in \mathcal A$. The pure states of $\mathcal A$ correspond to irreducible representations of $\mathcal A$ (up to unitary equivalence) via the GNS construction.

2.1.3 Type I groups

Let $\mathcal H$ be a Hilbert space. The commutant of a subset N of $\mathcal B (\mathcal H )$ is the set

$$\begin{aligned} N^{'}:= \{\text {A} \in \mathcal B (\mathcal H)\,:\, \text {A}S =\text {S}A \,\,\text {for all}\,\, \text {S} \in N\}\,. \end{aligned}$$

A von Neumann algebra $\mathcal N$ is a $^*$-subalgebra of bounded operators on some Hilbert space $\mathcal H$ which fulfils $\mathcal N = (\mathcal N^{'})^{'}$. The von Neumann algebra $\mathcal N _\pi$ generated by a unitary representation $\pi$ of a group $\varGamma$, is the smallest von Neumann algebra which contains $\pi (\varGamma )$.

We call a representation $\pi$ a factor if $\mathcal N _\pi \cap \mathcal N^{'} _\pi = {{\mathrm{\mathbb {C}}}}\cdot 1_{\mathcal B (\mathcal H _\pi )}$. A group is of Type I if every factor representation is a direct sum of copies of an irreducible representation.

2.1.4 Induced and monomial representations

Let H be a subgroup of a countably infinite group $\varGamma$. Suppose $\sigma$ is a unitary representation of H with representation space $\mathcal H _\sigma$. A natural way to extend the representation $\sigma$ of H to a representation of $\varGamma$ is as follows: consider the Hilbert space $\mathcal H_\sigma ^{\varGamma }$ consisting of all maps $F\in L^2 (\varGamma ,\mathcal H _\sigma )$ which satisfy

$$\begin{aligned} F( \gamma \delta )= \sigma (\delta )F(\gamma )\quad \text {for every}\, \delta \in H\, \text {and}\, \gamma \in \varGamma . \end{aligned}$$

The induced representation $\text {Ind}^\varGamma _H(\sigma ) : \varGamma \ni \gamma \mapsto \text {Ind}^\varGamma _H(\sigma )(\gamma )\in \mathcal B( \mathcal H_\sigma ^{\varGamma })$ is then defined by

$$\begin{aligned} \text {Ind}^\varGamma _H(\sigma )(\gamma ) F(\gamma ') = F(\gamma '\gamma ) \quad \forall \gamma '\in \varGamma . \end{aligned}$$

Hence, $\text {Ind}_H^\varGamma (\sigma )$ can be viewed as the right regular representation of $\varGamma$ acting on the Hilbert space $\mathcal H_\sigma ^\varGamma$.

This construction will become more transparent when we discuss specific examples below.

A representation of $\varGamma$ is called monomial if it is unitarily equivalent to a representation induced from a one-dimensional representation of a subgroup of $\varGamma$.

Theorem 4

([16]) If $\varGamma$ is a nilpotent group of Type I, then all its irreducible representations are monomial.

2.2 Symmetric Banach-$^*$-algebras

Let $\mathcal A$ be a Banach algebra with multiplicative identity element $1_{\mathcal A}$. The spectrum of $a\in \mathcal A$ is the set of elements $c\in {{\mathrm{\mathbb {C}}}}$ such that $a-c 1_{\mathcal A}$ is not invertible in $\mathcal A$ and will be denoted by $\sigma (a)$.

In order to study invertibility in $\ell ^1(\varGamma ,{{\mathrm{\mathbb {C}}}})$ and $C^*(\varGamma )$ in the non-abelian setting we will try to find criteria similar to those described in Theorem 2. For this purpose the following definition will play a key role.

Definition 1

A unital Banach-$^*$-algebra $\mathcal A$ is symmetric if for every element $a\in \mathcal A$ the spectrum of $a^*a$ is non-negative, i.e., $\sigma (a^*a) \subseteq [0,\infty )$.

Typical examples of symmetric Banach-*-algebras are $C^*$-algebras.

We turn to the study of nilpotent groups and their associated group algebras.

Theorem 5

([19]) Let $\varGamma$ be a countably infinite discrete nilpotent group. Then the Banach-$^*$-algebra $\ell ^1(\varGamma ,{{\mathrm{\mathbb {C}}}})$ is symmetric.

The reason why it is convenient to restrict to the study of invertibility in symmetric unital Banach-$^*$-algebra is demonstrated by the following theorems, which show similarities to Wiener’s Lemma and Theorem 2, respectively.

For the class of symmetric group algebras one has the following important result on inverse-closedness.

Theorem 6

([26], see also [30, Theorem 11.4.1 and Corollary 12.4.5]) If $\ell ^1(\varGamma ,{{\mathrm{\mathbb {C}}}})$ is a symmetric Banach-$^*$-algebra, then

• 1. $\ell ^1(\varGamma ,{{\mathrm{\mathbb {C}}}})$ is semisimple, i.e., the intersection of the kernels of all the irreducible representations of $\ell ^1(\varGamma ,{{\mathrm{\mathbb {C}}}})$ is trivial.

• 2. $\ell ^1(\varGamma ,{{\mathrm{\mathbb {C}}}})$ and its enveloping $C^*$-algebra $C^*(\varGamma )$ form a Wiener pair.

Next we are discussing spectral invariance of convolution operators. It is a well known fact (cf. [14]) that invertibility of $f\in \ell ^1({{\mathrm{\mathbb {Z}}}},{{\mathrm{\mathbb {C}}}})$ can be validated by studying invertibility of the convolution operator $\text {C}_f$ acting on the Hilbert space $\ell ^2({{\mathrm{\mathbb {Z}}}},{{\mathrm{\mathbb {C}}}})$. Moreover, the spectrum of $\text {C}_f$ is independent of the domain, i.e., the spectrum of the operator $\text {C}_f: \ell ^p({{\mathrm{\mathbb {Z}}}},{{\mathrm{\mathbb {C}}}})\longrightarrow \ell ^p({{\mathrm{\mathbb {Z}}}},{{\mathrm{\mathbb {C}}}})$ is the same for all $p\in [1,\infty ]$. As the following theorem shows, this result is true for a large class of groups, in particular, for all finitely generated nilpotent groups.

Theorem 7

([3]) Let $f\in \ell ^1(\varGamma ,{{\mathrm{\mathbb {C}}}})$ and $\text {C}_f$ the associated convolution operator on $\ell ^p(\varGamma ,{{\mathrm{\mathbb {C}}}})$. For all $1\le p \le \infty$ one has $\sigma _{\mathcal B (\ell ^p(\varGamma ,{{\mathrm{\mathbb {C}}}}))}(\text {C}_f)=\sigma _{\mathcal B (\ell ^2(\varGamma ,{{\mathrm{\mathbb {C}}}}))}(\text {C}_f)$ if and only if $\varGamma$ is amenable and $\ell ^1(\varGamma ,{{\mathrm{\mathbb {C}}}})$ is a symmetric Banach-$^*$-algebra.

In particular, for a nilpotent group $\varGamma$, $f\in \ell ^1(\varGamma ,{{\mathrm{\mathbb {C}}}})$ is invertible in $\ell ^1(\varGamma ,{{\mathrm{\mathbb {C}}}})$ if and only if $0 \notin \sigma _{\mathcal B (\ell ^p(\varGamma ,{{\mathrm{\mathbb {C}}}}))}(\text {C}_f)$ for any $p\in [1,\infty ]$.

Let us now give a condition for invertibility of an element $\ell ^1(\varGamma ,{{\mathrm{\mathbb {C}}}})$, where $\varGamma$ is an arbitrary discrete countably infinite group, in terms of the point spectrum of the corresponding convolution operator.

Theorem 8

([8, Theorem 3.2]) An element $f\in \ell ^1(\varGamma ,{{\mathrm{\mathbb {C}}}})$ is invertible in $\ell ^1(\varGamma ,{{\mathrm{\mathbb {C}}}})$ if and only if

$$\begin{aligned} K_\infty (f):= \{ g\in \ell ^\infty (\varGamma ,{{\mathrm{\mathbb {C}}}})\,:\, \text {C}_f g=0 \}=\{0\}. \end{aligned}$$

This theorem says that it is enough to check if 0 is an eigenvalue of the left convolution operator $\text {C}_f: \ell ^\infty (\varGamma ,{{\mathrm{\mathbb {C}}}})\longrightarrow \ell ^\infty (\varGamma ,{{\mathrm{\mathbb {C}}}})$ in order to determine whether f is invertible or not [cf. (3)].

Finally, we present a condition for invertibility in a symmetric unital Banach-$^*$-algebra $\mathcal A$ which links invertibility in $\mathcal A$ to its representation theory.

Theorem 9

([28]) An element a in a symmetric unital Banach-$^*$-algebra $\mathcal A$ is not left invertible in $\mathcal A$ if and only if there exists a pure state $\phi$ with $\phi (a^*a)=0$. Equivalently, a is not left invertible if and only if there exists an irreducible representation $\pi$ of $\mathcal A$ and a unit vector $u \in \mathcal H _\pi$ such that $\pi (a)u=0$.

This result should be compared with Gelfand’s theory for commutative Banach algebras. Wiener’s Lemma for $\ell ^1({{\mathrm{\mathbb {Z}}}},{{\mathrm{\mathbb {C}}}})$ says that an element $f \in \ell ^1({{\mathrm{\mathbb {Z}}}},{{\mathrm{\mathbb {C}}}})$ is invertible if and only if the Fourier-transform of f does not vanish on $\mathbb {T}$, i.e., $(\mathcal F f) (s) \not = 0$ for all $s\in \mathbb {T}$.² The Fourier-transform of f, evaluated at the point $\theta \in \mathbb {T}$, can be viewed as the evaluation of the one-dimensional irreducible unitary representation $\pi _\theta : n\mapsto e^{2\pi in\theta }$ of ${{\mathrm{\mathbb {Z}}}}$ at f, i.e.,

$$\begin{aligned} (\mathcal F f) (\theta )= \Bigl (\sum \nolimits _{n\in {{\mathrm{\mathbb {Z}}}}} f_n \pi _\theta (n)\Bigr )1 = \pi _\theta (f)1. \end{aligned}$$

We will explain in the next section that it is not feasible to describe explicitly the space of unitary equivalence classes of irreducible representations of a non-Type I group. Hence, Theorem 9 seems to be of limited use for investigating invertibility of an element $f \in \ell ^1(\varGamma ,{{\mathrm{\mathbb {C}}}})$ for a non-Type I nilpotent group $\varGamma$. However, as we will see later, it is one of the key results for obtaining a Wiener Lemma for $\ell ^1(\varGamma ,{{\mathrm{\mathbb {C}}}})$.

3 The dual of the discrete Heisenberg group and a Wiener Lemma

In this section we explain how results from ergodic theory give insight into the space of irreducible representations of the discrete Heisenberg group, but that this space has no reasonable parametrisation and is therefore not useful for determining invertibility in the corresponding group algebras (cf. Theorem 9). At the end of this section, we will state our main result—a Wiener Lemma for the discrete Heisenberg group ${{\mathrm{\mathbb {H}}}}$—which allows one to restrict the attention to certain canonical representations of ${{\mathrm{\mathbb {H}}}}$ which can be parametrised effectively and used for solving the invertibility problem.

3.1 The dual of a discrete group

Let $\varGamma$ be a countable discrete group. Denote by $\widehat{\varGamma }$ the dual of $\varGamma$, i.e., the set of all unitary equivalence classes of irreducible unitary representations of $\varGamma$.

Definition 2

Let $\mathcal A$ be a $C^*$-algebra. A closed two-sided ideal $\mathtt I$ of $\mathcal A$ is primitive if there exists an irreducible representation $\pi$ of $\mathcal A$ such that $\ker (\pi )=\mathtt I$. The set of primitive ideals of $\mathcal A$ is denoted by $\text {Prim}(\mathcal A)$.

Suppose that the group $\varGamma$ is not of Type I. Then certain pathologies arise:

• The map $\widehat{\varGamma } \longrightarrow \text {Prim}(C^*(\varGamma ))$ given by $\pi \mapsto \ker (\pi )$ is not injective. In other words, if $\pi _1, \pi _2 \in \widehat{\varGamma }$, then $\ker (\pi _1 )=\ker (\pi _2 )$ does not necessarily imply that $\pi _1$ and $\pi _2$ are unitarily equivalent.

• $\widehat{\varGamma }$ is not behaving nicely neither as a topological space nor as a measurable space in its natural topology or Borel structure, respectively (cf. [11, Chapter 7] for an overview).

Furthermore, there are examples where the direct integral decomposition of a representation is not unique, in the sense that there are disjoint measures $\mu ,\nu$ on $\widehat{\varGamma }$ such that $\int _{\widehat{\varGamma }}^\oplus \pi d\mu$ and $\int _{\widehat{\varGamma }}^\oplus \pi d\nu$ are unitarily equivalent. Moreover, we cannot assume that all irreducible representations are induced from one-dimensional representations of finite-index subgroups, as is the case for nilpotent groups of Type I by Theorem 4.

3.2 The discrete Heisenberg group and its dual

The discrete Heisenberg group ${{\mathrm{\mathbb {H}}}}$ is generated by $S=\{x,x^{-1},y,y^{-1}\}$, where

$$\begin{aligned} x = \left( \begin{array}{l@{\quad }l@{\quad }l} 1 &{} 1 &{} 0 \\ 0 &{} 1 &{} 0 \\ 0 &{} 0 &{} 1 \end{array} \right) , \quad y = \left( \begin{array}{l@{\quad }l@{\quad }l} 1 &{} 0 &{} 0 \\ 0 &{} 1 &{} 1 \\ 0 &{} 0 &{} 1 \end{array} \right) . \end{aligned}$$

The centre of ${{\mathrm{\mathbb {H}}}}$ is generated by

$$\begin{aligned} {z= xyx^{-1}y^{-1}= \left( \begin{array}{l@{\quad }l@{\quad }l} 1 &{} 0 &{} 1 \\ 0 &{} 1 &{} 0 \\ 0 &{} 0 &{} 1 \end{array} \right) .} \end{aligned}$$

The elements x, y, z satisfy the following commutation relations

$$\begin{aligned} xz=zx,yz=zy,x^ky^l=y^lx^kz^{kl},k,l\in \mathbb {Z}. \end{aligned}$$

(4)

The discrete Heisenberg group is nilpotent and hence amenable.

Since ${{\mathrm{\mathbb {H}}}}$ does not possess an abelian normal subgroup of finite index it is not a group of Type I (cf. [34]), and hence the space of irreducible representations does not have any nice structure as discussed above. As we will show below, one can construct uncountably many unitarily inequivalent irreducible representations of ${{\mathrm{\mathbb {H}}}}$ for every irrational $\theta \in \mathbb {T}$. These representations arise from certain singular measures on ${{\mathrm{\mathbb {T}}}}$. This fact is well-known to specialists, but details are not easily accessible in the literature. Since these results are important for our understanding of invertibility, we present this construction in some detail for the convenience of the reader. We would like to mention first that Moran announced in [27] a construction of unitary representations of ${{\mathrm{\mathbb {H}}}}$ using the same approach as presented here. These results were not published as far as we know. Moreover, Brown [6] gave examples of unitary irreducible representations of the discrete Heisenberg group which are not monomial.

Let $(X,\mathfrak {B},\mu )$ be a measure space, where X is a compact metric space, $\mathfrak {B}$ is a Borel $\sigma$-algebra, and $\mu$ a finite measure.

Definition 3

A probability measure $\mu$ is quasi-invariant with respect to a homeomorphism $\phi : X\longrightarrow X$ if $\mu (B)=0$ if and only if $\mu (\phi B)=0$, for $B \in \mathfrak {B}$. A quasi-invariant measure $\mu$ is ergodic if

$$\begin{aligned} B \in \mathfrak {B}\quad \text {and}\quad \phi B= B \implies \mu (B) \in \{0,1\} . \end{aligned}$$

In [23] uncountably many inequivalent ergodic quasi-invariant measures for every irrational rotation of the circle were constructed. Later it was shown in [22] that a homeomorphism $\phi$ on a compact metric space X has uncountably many inequivalent non-atomic ergodic quasi-invariant measures if and only if $\phi$ has a recurrent point x, i.e., $\phi ^n (x)$ returns infinitely often to any punctured neighbourhood of x.

Let ${{\mathrm{\mathbb {Z}}}}$ act on ${{\mathrm{\mathbb {T}}}}$ via rotation

$$\begin{aligned} \text {R}_\theta : t \mapsto t +\theta \mod 1 \end{aligned}$$

(5)

by an irrational angle $\theta \in {{\mathrm{\mathbb {T}}}}$.

Theorem 10

For each irrational $\theta \in {{\mathrm{\mathbb {T}}}}$ there is a bijection between the set of ergodic $\text {R}_\theta$-quasi-invariant probability measures on ${{\mathrm{\mathbb {T}}}}$ and the set of irreducible representations $\pi$ of ${{\mathrm{\mathbb {H}}}}$ with $\pi (z)=e^{2\pi i \theta }$.

We use the measures found in [23] to construct unitary irreducible representations of ${{\mathrm{\mathbb {H}}}}$. Suppose $\mu$ is an ergodic $\text {R}_\theta$-quasi-invariant probability measure on ${{\mathrm{\mathbb {T}}}}$. Let $\text {T}_{\theta ,\mu }: L^2({{\mathrm{\mathbb {T}}}},\mu ) \longrightarrow L^2({{\mathrm{\mathbb {T}}}},\mu )$ be the unitary operator defined by

$$\begin{aligned} (\text {T}_{\theta ,\mu }F)(t) = \sqrt{\frac{d\mu (t+\theta )}{d\mu (t)}} F(t+\theta ) = \sqrt{\frac{d\mu (\text {R}_{\theta } t)}{d\mu (t)}} F(\text {R}_{\theta } t), \end{aligned}$$

(6)

for every $F \in L^2({{\mathrm{\mathbb {T}}}},\mu )$ and $t \in {{\mathrm{\mathbb {T}}}}$. The operator $\text {T}_{\theta ,\mu }$ is well-defined because of the quasi-invariance of $\mu$. Consider also the unitary operator $\text {M}_\mu$ defined by

$$\begin{aligned} (\text {M}_\mu F)(t) = e^{2 \pi i t} F(t) \,, \end{aligned}$$

(7)

for every $F \in L^2({{\mathrm{\mathbb {T}}}},\mu )$ and $t \in {{\mathrm{\mathbb {T}}}}$.

We will show that the representation $\pi _{\theta ,\mu }$ of ${{\mathrm{\mathbb {H}}}}$ defined by

$$\begin{aligned} \pi _{\theta ,\mu }(x):= \text {T}_{\theta ,\mu },\quad \quad \pi _{\theta ,\mu }(y):= \text {M}_\mu \quad \text {and}\quad \pi _{\theta ,\mu }(z):= e^{2\pi i \theta } \end{aligned}$$

(8)

is irreducible. Obviously, $\text {T}_{\theta ,\mu } \text {M}_\mu = e^{2 \pi i \theta } \text {M}_\mu \text {T}_{\theta ,\mu } = \pi _{\theta ,\mu } (z) \text {M}_\mu \text {T}_{\theta ,\mu }$.

Lemma 1

The unitary representation $\pi _{\theta ,\mu }$ of ${{\mathrm{\mathbb {H}}}}$ given by (8) is irreducible.

Proof

Every element in $L^2({{\mathrm{\mathbb {T}}}},\mu )$ can be approximated by linear combinations of elements in the set

$$\begin{aligned} \{\text {M}_\mu ^n1\,:\,n\in {{\mathrm{\mathbb {Z}}}}\}=\{t \mapsto e^{2 \pi i n t}\,:\,n\in {{\mathrm{\mathbb {Z}}}}\}\,. \end{aligned}$$

A bounded linear operator $\text {O}$ on $L^2({{\mathrm{\mathbb {T}}}},\mu )$, which commutes with all operators of the form $\text {M}_\mu ^n$, $n \in {{\mathrm{\mathbb {Z}}}}$, and hence with multiplication with any $L^\infty$-function, must be a multiplication operator, i.e., $\text {O} F(t)= G(t)\cdot F(t)$ for some $G \in L^\infty ({{\mathrm{\mathbb {T}}}},\mu )$. Indeed, if $\text {O}$ commutes with multiplication by $H \in L^\infty ({{\mathrm{\mathbb {T}}}},\mu )$, then

$$\begin{aligned} \text {O} H=H\cdot \text {O}1=HG, \end{aligned}$$

say. Denote by $\Vert \cdot \Vert _{op}$ the operator norm, then

$$\begin{aligned} \Vert HG\Vert _{L^2({{\mathrm{\mathbb {T}}}},\mu )} = \Vert \text {O} H\Vert _{L^2({{\mathrm{\mathbb {T}}}},\mu )} \le \Vert \text {O}\Vert _{op}\Vert H\Vert _{L^2({{\mathrm{\mathbb {T}}}}\mu )}, \end{aligned}$$

(9)

which implies that $G \in L^\infty ({{\mathrm{\mathbb {T}}}},\mu )$ [otherwise one would be able to find a measurable set B with positive measure on which G is strictly larger than $\Vert \text {O}\Vert _{op}$, and the indicator function $1_B$ would lead to a contradiction with (9)].

The ergodicity of $\mu$ with respect to $\text {R}_\theta$ implies that only constant functions in $L^\infty ({{\mathrm{\mathbb {T}}}},\mu )$ are $\text {R}_\theta$-invariant $\mu$-a.e.. Hence, if $\text {O}$ commutes with $\text {T}_{\theta ,\mu }$ as well, then we can conclude that $\text {O}$ is multiplication by a constant $c\in {{\mathrm{\mathbb {C}}}}$. By Schur’s Lemma, the operators $\text {T}_{\theta ,\mu },\text {M}_\mu \in \mathcal B (L^2({{\mathrm{\mathbb {T}}}},\mu ))$ define an irreducible representation $\pi _{\theta ,\mu }$ of ${{\mathrm{\mathbb {H}}}}$.   $\square$

Suppose that $\theta \in {{\mathrm{\mathbb {T}}}}$ is irrational, and that $\mu$ and $\nu$ are two ergodic $\text {R}_\theta$-quasi-invariant measures on ${{\mathrm{\mathbb {T}}}}$. Let $\pi _{\theta ,\mu }$ and $\pi _{\theta ,\nu }$ be the corresponding irreducible unitary representations constructed above.

Lemma 2

The representations $\pi _{\theta ,\mu }$ and $\pi _{\theta ,\nu }$ are unitarily equivalent if and only if $\mu$ and $\nu$ are equivalent.

Proof

Assume $\pi _{\theta ,\mu }$ and $\pi _{\theta ,\nu }$ are unitarily equivalent. Then there exists a unitary operator $\text {U}: L^2({{\mathrm{\mathbb {T}}}},\mu ) \longrightarrow L^2({{\mathrm{\mathbb {T}}}},\nu )$ such that

$$\begin{aligned} \text {U} \pi _{\theta ,\mu }(\gamma )= \pi _{\theta ,\nu }(\gamma )\text {U} \end{aligned}$$

(10)

for every $\gamma \in {{\mathrm{\mathbb {H}}}}$.

Denote multiplication by a function $H\in C(\mathbb {T},\mathbb {C})$ by $\text {O}_H$. The set of trigonometric polynomials, which is spanned by $\{\text {M}_\mu ^n 1\,:\,n\in {{\mathrm{\mathbb {Z}}}}\}$, is dense in $C({{\mathrm{\mathbb {T}}}},{{\mathrm{\mathbb {C}}}})$. This implies that (10) holds for all $H\in C({{\mathrm{\mathbb {T}}}},{{\mathrm{\mathbb {C}}}})$, i.e., that $\text {U} O _H = \text {O}_H \text {U}$ for any $H \in C({{\mathrm{\mathbb {T}}}},{{\mathrm{\mathbb {C}}}})$.

Since $\text {U}$ is an isometry we get that

$$\begin{aligned} \int |H|^2 1^2 d\mu&= \langle \text {O}_H 1 , \text {O}_H 1 \rangle _\mu \end{aligned}$$

(11)

$$\begin{aligned}&= \langle \text {O}_H \text {U}(1) , \text {O}_H \text {U}(1) \rangle _\nu \end{aligned}$$

(12)

$$\begin{aligned}&= \int |H|^2 |\text {U}(1)|^2 d\nu \,, \end{aligned}$$

(13)

where $\langle \cdot ,\cdot \rangle _\sigma$ is the standard inner product on the Hilbert space $L^2 ({{\mathrm{\mathbb {T}}}},\sigma )$. Using the same argument for $\text {U}^{-1}$ we get, for every $H\in C(\mathbb {T},\mathbb {C})$,

$$\begin{aligned} \int |H|^2 1^2 d\nu = \int |H|^2 |\text {U}^{-1}(1)|^2 d\mu \,. \end{aligned}$$

(14)

Define, for every positive finite measure $\sigma$ on ${{\mathrm{\mathbb {T}}}}$, a linear functional

$$\begin{aligned} I_\sigma : C({{\mathrm{\mathbb {T}}}},{{\mathrm{\mathbb {C}}}})\longrightarrow {{\mathrm{\mathbb {C}}}}\quad \text {by}\quad I_\sigma (H)=\int H \,d\sigma \,. \end{aligned}$$

Since $I_\mu (H)=I_{|\text {U}(1)|^2\nu }(H)$ and $I_\nu (H)=I_{|\text {U}^{-1}(1)|^2\mu }(H)$ for all positive continuous functions H by (11)–(14), we conclude from the Riesz representation theorem that $\mu$ and $\nu$ are equivalent.

Conversely, if $\mu$ and $\nu$ are equivalent, then the linear operator

$$\begin{aligned} \text {U}: {L^{2}}({\mathbb {T}},{\mu } )\longrightarrow {L^{2}}({\mathbb {T}},{\nu } ) \quad \text {given by} \quad \text {U}F={\sqrt{\frac{d\mu }{d\nu }}}F \end{aligned}$$

for every $F\in L^2(\mathbb {T},\mu )$, is unitary and satisfies that $\text {U}\pi _{\theta ,\mu } (\gamma )=\pi _{\theta ,\nu } (\gamma )\text {U}$ for every $\gamma \in {{\mathrm{\mathbb {H}}}}$. $\square$

In this way one obtains uncountably many inequivalent irreducible unitary representation of ${{\mathrm{\mathbb {H}}}}$ for a given irrational rotation number $\theta \in \mathbb {T}$.

In fact, every irreducible unitary representation $\pi$ of ${{\mathrm{\mathbb {H}}}}$ with $\pi (z)=e^{2\pi i \theta }$, $\theta$ irrational, is unitarily equivalent to $\pi _{\theta ,\mu }$ for some probability measure $\mu$ on $\mathbb {T}$ which is quasi-invariant and ergodic with respect to an irrational circle rotation. For convenience of the reader we sketch a proof of this fact based on elementary spectral theory of unitary operators.

Let $\pi$ be an irreducible unitary representation of ${{\mathrm{\mathbb {H}}}}$ with representation space $\mathcal H_\pi$ such that $\pi (x)\pi (y)=e^{2 \pi i \theta }\pi (y)\pi (x)$. Let $v\in \mathcal H_\pi$ be a normalised cyclic vector, put $\text {U}=\pi (y)$ and denote by $\mathcal H _v$ the closure of the subspace generated by $\{\text{ U } ^n v \,: \, n\in {{\mathrm{\mathbb {Z}}}}\}$. The GNS-construction tells us that $a_n=\langle \text {U}^n v,v\rangle _{\mathcal H _\pi }$, $n\in {{\mathrm{\mathbb {Z}}}}$, forms a positive-definite sequence. Due to Herglotz’ (or, more generally, Bochner’s) representation theorem there exists a probability measure $\mu _v$ on $\widehat{{\mathrm{\mathbb {Z}}}}\simeq {{\mathrm{\mathbb {T}}}}$ whose Fourier-Stieltjes transform $\widehat{\mu _v}$ fulfils

$$\begin{aligned} \widehat{\mu _v}(n)= \int _{{{\mathrm{\mathbb {T}}}}} e^{- 2 \pi i n t} d \mu _v (t) = a_n \quad \text {for every}\, n \in {{\mathrm{\mathbb {Z}}}}. \end{aligned}$$

One easily verifies that there exists an isometric isomorphism $\phi : \mathcal H _v \longrightarrow L^2 ({{\mathrm{\mathbb {T}}}},\mu _v)$ which intertwines the restriction $\text {U}_v$ of $\text {U}$ to $\mathcal H_v$ with the modulation operator $\text {M}_v$ on $L^2 ({{\mathrm{\mathbb {T}}}},\mu _v)$ consisting of multiplication by $e^{ 2 \pi i t}$. In other words, the unitary operators $\text {U}_v$ and $\text {M}_v$ are unitarily equivalent.

Put $\text {S} =\pi (x)$ and consider the cyclic normalised vector $w=\text {S} v$ of the representation $\pi$. By replacing v by w in the construction above one can define the corresponding objects $\mathcal H _w, \text {U}_w, \mu _w, L^2 ({{\mathrm{\mathbb {T}}}},\mu _w), \text {M}_w$.

Lemma 3

The measures $\mu _v$ and $\mu _w$ are equivalent.

Proof

First note that $\text {U}_v$ and $\text {U}_w$ are unitarily equivalent. From this fact and the discussion preceding the lemma one concludes that $\text {M} _v$ and $\text {M}_w$ are unitarily equivalent as well, i.e., that there exists a unitary operator $\text {O}: L^2 ({{\mathrm{\mathbb {T}}}},\mu _v) \longrightarrow L^2 ({{\mathrm{\mathbb {T}}}},\mu _w)$ such that $\text {O} \text {M} _v = \text {M} _w \text {O}$. By arguing as in the first part of the proof of Lemma 2 one gets that $\text {O}$ is a multiplication operator. Put $G=\text {O} 1_{ L^2 ({{\mathrm{\mathbb {T}}}},\mu _v)}$. Since $\text {O}$ is an isometry one gets for all $\mu _v$-measurable sets B

$$\begin{aligned} \mu _v(B)= \int _{{{\mathrm{\mathbb {T}}}}} |1_B|^2 d \mu _v = \int _{{{\mathrm{\mathbb {T}}}}} |G|^2|1_B|^2 d \mu _w \,. \end{aligned}$$

By repeating these arguments with v and w interchanged one concludes that $\mu _v$ and $\mu _w$ are equivalent. $\square$

Lemma 4

The measure $\mu _v$ is $\text {R} _\theta$-quasi-invariant.

Proof

Note that $\widehat{\mu _w}(n)=\langle \text {S} ^{-1}\text {U} ^n \text{ S } v,v\rangle _{\mathcal H _\pi } = e^{-2 \pi i \theta n} \widehat{\mu _v}(n)$ for every $n\in \mathbb {Z}$. As one can easily verify, for every probability measure $\mu$ on ${{\mathrm{\mathbb {T}}}}$, multiplying $\widehat{\mu }$ with a character $e^{-2 \pi i \theta n}$ is the same as the Fourier-Stieltjes transform of $\mu \circ \text {R} _\theta$. Hence, we obtain that $\mu _w=\mu _v \circ \text {R} _\theta$. As $\mu _v$ and $\mu _w$ are equivalent, $\mu _v$ is a $\text {R} _\theta$-quasi-invariant probability measure on ${{\mathrm{\mathbb {T}}}}$. $\square$

Proof

(Completion of the proof of Theorem 10) The preceding discussion allows us to define an irreducible representation $\pi _v$ of ${{\mathrm{\mathbb {H}}}}$ acting on $L^2 ({{\mathrm{\mathbb {T}}}},\mu _v)$ which is unitarily equivalent to $\pi$. The evaluation of $\pi _v$ at y is given by $\text {M}_v$ and $\text {T}_v= \pi _v(x)$ acts as composition of a translation operator by an angle $\theta$ and multiplication by some function $D_v\in L^\infty ({{\mathrm{\mathbb {T}}}},\mu _v)$. Due to the fact that $\text {T}_v$ has to be a unitary (and hence, an isometric) operator on $L^2 ({{\mathrm{\mathbb {T}}}},\mu _v)$ the form of $D_v$ is fully determined (cf. the definition of $\text {T} _{\theta ,\mu }$ in (6) for a $\text {R} _\theta$-quasi-invariant measure $\mu$). Since $\pi _v$ is irreducible only those multiplication operators in $\mathcal B ( L^2 ({{\mathrm{\mathbb {T}}}},\mu _v))$ which act via multiplication by a constant function $c\in {{\mathrm{\mathbb {C}}}}$ will commute with multiples of the modified translation operator $\text {T}_v$. This implies the ergodicity of $\mu _v$ and completes the proof of the theorem. $\square$

3.3 Wiener’s Lemma for the discrete Heisenberg group

Theorem 9 states that in order to decide on invertibility of $f \in \ell ^1 ({{\mathrm{\mathbb {H}}}},{{\mathrm{\mathbb {C}}}})$, one has to check invertibility of $\pi (f)$ for every irreducible representations $\pi$ of ${{\mathrm{\mathbb {H}}}}$, and hence for every $\pi _{\theta ,\mu }$ as above, where $\mu$ is a probability measure on $\mathbb {T}$ on $\mathbb {T}$ which is quasi-invariant and ergodic with respect to a circle rotation $R_\theta$.

The problem of deciding on invertibility of $f\in {{\mathrm{\ell ^1(\mathbb {H},\mathbb {C})}}}$ via Theorem 9 becomes much more straightforward if one is able to restrict oneself to unitary representations arising from rotation invariant probability measures. This is exactly our main result.

Before formulating this result we write down the relevant representations explicitly. Take $\theta \in \mathbb T$, and consider the corresponding rotation $\text {R}_\theta : {{\mathrm{\mathbb {T}}}}\longrightarrow {{\mathrm{\mathbb {T}}}}$ given by (5). If $\theta$ is irrational, the Lebesgue measure $\lambda =\lambda _\mathbb {T}$ on $\mathbb {T}$ is the unique $\text {R}_\theta$-invariant probability measure, and the representation $\pi _{\theta ,\lambda }$ on $L^2(\mathbb {T},\lambda )$ defined in (8) is irreducible. One can modify this representation by setting, for every $s,t\in \mathbb {T}$,

$$\begin{aligned} \pi _{\theta }^{(s,t)}(x) = e^{2\pi is}\pi _{\theta ,\lambda }(x),\quad \pi _{\theta }^{(s,t)}(y) =e^{2\pi it}\pi _{\theta ,\lambda }(y), \quad \pi _{\theta }^{(s,t)}(z)=e^{2\pi i\theta }. \end{aligned}$$

(15)

Then $\pi _{\theta }^{(s,t)}$ is obviously again an irreducible unitary representation of ${{\mathrm{\mathbb {H}}}}$ on $\mathcal H_{\pi ^{(s,t)}_\theta }= L^2(\mathbb {T},\lambda )$.

If $\theta$ is rational we write it as $\theta =p/q$ where p, q are integers with the properties $0\le p <q$ and $\gcd (p,q)=1$ and consider the unitary representation $\pi _\theta ^{(s,t)}$ of ${{\mathrm{\mathbb {H}}}}$ on $\mathcal H_{\pi ^{(s,t)}_\theta }=\mathbb {C}^q$ given by

$$\begin{aligned} \pi _\theta ^{(s,t)}(x)&= e^{2\pi i s} \left( \begin{array}{ll} 0 &{}\quad I_{q-1} \\ 1 &{}\quad 0 \end{array}\right) \,, \end{aligned}$$

(16)

$$\begin{aligned} \pi _\theta ^{(s,t)}(y)&= e^{2\pi i t} \left( {\begin{matrix} 1 &{}\quad 0 &{}\quad \ldots &{}\quad 0&{}\quad 0 \\ 0 &{}\quad e^{2\pi i\theta }&{}\quad \ldots &{}\quad 0 &{}\quad 0 \\ \vdots &{}\quad \vdots &{}\quad \ddots &{}\quad \vdots &{}\quad \vdots \\ 0 &{}\quad 0&{}\quad \ldots &{}\quad e^{2\pi i(q-2)\theta }&{}\quad 0\\ 0 &{}\quad 0&{}\quad \ldots &{}\quad 0 &{}\quad e^{2\pi i(q-1)\theta } \end{matrix}}\right) \quad \text {and} \quad \pi ^{(s,t)}_\theta (z)= e^{2 \pi i \theta }I_q\,, \end{aligned}$$

(17)

with $s,t\in \mathbb {T}$, where $I_{q-1}$ is the $(q-1)\times (q-1)$ identity matrix. Every $\text {R}_\theta$-invariant and ergodic probability measure $\mu$ on $\mathbb {T}$ is uniformly distributed on the set $\{t,1/q+t,\ldots ,t+(q-1)/q\}\subset \mathbb {T}$ for some $t\in \mathbb {T}$; if we denote this measure by $\mu _t$ then $\mu _t=\mu _{t+k/q}$ for every $k=0,\ldots ,q-1$.

With this notation at hand we can state our main result, the proof of which will be given in Sect. 4.

Theorem 11

An element $f\in \ell ^1({{\mathrm{\mathbb {H}}}},{{\mathrm{\mathbb {C}}}})$ is invertible if and only if the linear operators $\pi _{\theta }^{(s,t)}(f)$ are invertible on the corresponding Hilbert spaces $\mathcal {H}_{\pi _{\theta }^{(s,t)}}$ for every $\theta ,s,t\in {{\mathrm{\mathbb {T}}}}$.

The main advantage of Theorem 11 over Theorem 9 is that it is not necessary to check invertibility of $\pi (f)$ for every irreducible representation of ${{\mathrm{\mathbb {H}}}}$, but that one can restrict oneself for this purpose to the ‘nice’ part of the dual of the non-Type I group ${{\mathrm{\mathbb {H}}}}$. As we shall see later, one can make a further reduction if $\theta$ is irrational: in this case one only has to check invertibility of $\pi _{\theta }(f)= \pi _{\theta }^{(1,1)}(f)$ on $L^2(\mathbb {T},\lambda )$.

4 Wiener’s Lemma for the discrete Heisenberg group: a proof and a first application

In this section we will present one possible proof of Wiener’s Lemma for $\ell ^1({{\mathrm{\mathbb {H}}}}, {{\mathrm{\mathbb {C}}}})$ and $C^*({{\mathrm{\mathbb {H}}}})$. This proof has two main ingredients, namely:

• Allan’s local principle, which reduces the problem of verifying invertibility in $\ell ^1({{\mathrm{\mathbb {H}}}}, {{\mathrm{\mathbb {C}}}})$ and $C^*({{\mathrm{\mathbb {H}}}})$ to the study of invertibility in rotation algebras.

• The fact that irrational rotation algebras are simple will eliminate the ‘non-Type I problem’ for questions about invertibility in $\ell ^1({{\mathrm{\mathbb {H}}}}, {{\mathrm{\mathbb {C}}}})$ and $C^*({{\mathrm{\mathbb {H}}}})$ discussed in the previous section.

These results will be generalised in Sect. 5 to group algebras of nilpotent groups.

4.1 Local principles

Let $\mathcal {A}$ be a unital Banach algebra and $a \in \mathcal A$. Local principles are based on the following idea: one checks invertibility of projections of a onto certain quotient algebras of $\mathcal A$ in order to conclude from this information whether a is invertible or not. Therefore, the main task is to find a sufficient family $\mathfrak J$ of ideals of $\mathcal A$ such that one can deduce the invertibility of a from the invertibility of the projections of a on $\mathcal A/\mathtt I$ for all $\mathtt I \in \mathfrak J$.

Allan’s local principle provides us with such a sufficient family of ideals in case the centre of $\mathcal A$ is large enough. We have used Allan’s local principle already in [13] to study invertibility in $\ell ^1({{\mathrm{\mathbb {H}}}},{{\mathrm{\mathbb {C}}}})$. However, in that paper we were not able to prove Theorem 11 with this approach.

Suppose $\mathcal {A}$ is a unital Banach algebra with non-trivial centre

$$\begin{aligned} \mathcal C (\mathcal {A}) := \bigl \{c \in \mathcal A \,:\, cb=bc \,\,\,\text {for all }b \in \mathcal A\bigr \}\,. \end{aligned}$$

The commutative Banach subalgebra $\mathcal C (\mathcal {A})$ is closed and contains the identity $1_{\mathcal A}$. For every $m \in \text {Max} (\mathcal C(\mathcal {A}))$ (the space of maximal ideals of $\mathcal {C}(\mathcal {A})$) we denote by $\mathtt {J}_m$ the smallest closed two-sided ideal of $\mathcal {A}$ which contains m and denote by $\varPhi _m: a\mapsto \varPhi _m(a)$ the canonical projection of an element $a\in \mathcal {A}$ to the quotient algebra $\mathcal {A}/\mathtt {J}_m$. The algebra $\mathcal {A}/\mathtt {J}_m$, furnished with the quotient norm

$$\begin{aligned} \Vert \varPhi _m (a)\Vert := \inf _{b\in \mathtt J_m} \Vert a + b\Vert _{\mathcal A} \, \end{aligned}$$

(18)

becomes then a unital Banach algebra.

Theorem 12

([1] Allan’s local principle) An element $a \in \mathcal {A}$ is invertible in $\mathcal {A}$ if and only if $\varPhi _m(a)$ is invertible in $\mathcal {A}/\mathtt {J}_m$ for every $m\in \text {Max} (\mathcal C(\mathcal {A}))$.

We would like to mention already here that in Sect. 7 Allan’s local principle will appear a second time and will link invertibility of $f\in {{\mathrm{\ell ^1(\mathbb {H},\mathbb {C})}}}$ to the invertibility of the evaluations of Stone-von Neumann representations at f.

Let us now prove our main theorem.

4.2 Proof of Wiener’s Lemma

We apply the general observations made in the previous subsection to explore invertibility in ${{\mathrm{\ell ^1(\mathbb {H},\mathbb {C})}}}$ and $C^*({{\mathrm{\mathbb {H}}}})$. Since ${{\mathrm{\ell ^1(\mathbb {H},\mathbb {C})}}}$ is inverse-closed in $C^*({{\mathrm{\mathbb {H}}}})$ we can focus on the study of invertibility in $C^*({{\mathrm{\mathbb {H}}}})$.

Due to Allan’s local principle we have to check invertibility only in $\mathcal Q_\theta =C^*({{\mathrm{\mathbb {H}}}})/\mathtt J_\theta$ for all $\theta \in \mathbb {T}$, where ${\mathtt J} _\theta =\overline{(z-e^{2\pi i\theta })C^*({{\mathrm{\mathbb {H}}}})}$. Indeed, $\mathcal C (C^*({{\mathrm{\mathbb {H}}}})) \simeq C({{\mathrm{\mathbb {T}}}},{{\mathrm{\mathbb {C}}}})$, and the maximal ideals of $C({{\mathrm{\mathbb {T}}}},{{\mathrm{\mathbb {C}}}})$ are given by the sets

$$\begin{aligned} m_\theta := \{F\in C({{\mathrm{\mathbb {T}}}},{{\mathrm{\mathbb {C}}}}) \,:\, F(\theta )=0 \}\, \end{aligned}$$

and $\mathtt {J}_{m_\theta } = \mathtt J _\theta$.

Since ${\mathtt J} _\theta =\overline{(z-e^{2\pi i\theta })C^*({{\mathrm{\mathbb {H}}}})}$ is a two-sided closed ideal we know that the quotient $\mathcal Q_\theta$ is a $C^*$-algebra and hence symmetric for each $\theta \in {{\mathrm{\mathbb {T}}}}$.

By Schur’s Lemma, if $\pi$ is an irreducible unitary representation of ${{\mathrm{\mathbb {H}}}}$, then $\pi (z)= e^{2\pi i\theta }1_{\mathcal B (\mathcal H _\pi )}$ for some $\theta \in \mathbb {T}$. Hence, $\mathtt J_\theta$ is a subset of $\ker (\pi )$ for every irreducible unitary representation $\pi$ of ${{\mathrm{\mathbb {H}}}}$ with $\pi (z)= e^{2\pi i\theta }1_{\mathcal B (\mathcal H _\pi )}$.

If $\theta$ is rational the irreducible unitary representations of ${{\mathrm{\mathbb {H}}}}$ vanishing on $\mathtt J _\theta$ are given by (16)–(17) and were determined in [5]. Due to the fact that $\mathcal Q_\theta$ is symmetric we can apply Theorem 9 in order to study invertibility in $\mathcal Q_\theta$ via the representations (16)–(17).

Now suppose $\theta$ is irrational. In order to study the representation theory of the $C^*$-algebra $\mathcal Q_\theta$ we have to understand the link to one of the most studied non-commutative $C^*$-algebras—the irrational rotation algebras.

We call a $C^*$-algebra an irrational rotation algebra if it is generated by two unitaries $\text {U},\text {V}$ which fulfil the commutation relation

$$\begin{aligned} \text {U}\text {V}=e^{2\pi i\theta }\text {V}\text {U} \,, \end{aligned}$$

(19)

for some irrational $\theta \in \mathbb {T}$. We already saw examples of irrational rotation algebras above, namely, the $C^*$-subalgebras of $\mathcal B (L^2({{\mathrm{\mathbb {T}}}},\mu ))$ which are generated by $\text {M}_\mu$ and $\text {T}_{\theta ,\mu }$, where $\mu$ is a $\text {R}_\theta$-quasi-invariant and ergodic measure. The reason why we call all $C^*$-algebras which fulfil (19) irrational rotation algebras with parameter $\theta$ is the following striking result which can be found in [7, Theorem VI.1.4] (and which was already proved in the 1960s, cf. [32] for a list of references).

Theorem 13

If $\theta \in \mathbb {T}$ is irrational, then all $C^*$-algebras which are generated by two unitaries $\text {U},\text {V}$ satisfying (19), are $^*$-isomorphic.

We will denote the irrational rotation algebra with parameter $\theta$ by $\mathcal R _\theta$ and will not distinguish between the different realisations of $\mathcal R _\theta$ because of the universal property described in Theorem 13. Let us further note that the proof of Theorem 13 is deduced from the simplicity of the universal irrational rotation algebra.

The $C^*$-algebra $\mathcal Q_\theta$ is clearly a rotation algebra with parameter $\theta$. The simplicity of $\mathcal R _\theta$ implies that $\mathtt J _\theta$ is a maximal two-sided ideal of $C^*({{\mathrm{\mathbb {H}}}})$. Hence, there exists an irreducible representation $\pi$ of ${{\mathrm{\mathbb {H}}}}$ such that $\ker (\pi )=\mathtt J _\theta$, since every two-sided maximal ideal is primitive (cf. [29, Theorem 4.1.9]). Moreover, all the irreducible representations $\pi$ vanishing on $\mathtt J _\theta$ have the same kernel: otherwise we would get a violation of the maximality of $\mathtt J _\theta$. These representations are not all in the same unitary equivalence class (as we saw in Sect. 3), which is an indication of the fact that ${{\mathrm{\mathbb {H}}}}$ is not of Type I.

Proof

(Proof of Theorem 11) First of all recall that ${{\mathrm{\ell ^1(\mathbb {H},\mathbb {C})}}}$ is inverse-closed in $C^*({{\mathrm{\mathbb {H}}}})$. By applying Allan’s local principle for $C^*({{\mathrm{\mathbb {H}}}})$ the problem of verifying invertibility in ${{\mathrm{\ell ^1(\mathbb {H},\mathbb {C})}}}$ and $C^*({{\mathrm{\mathbb {H}}}})$ reduces to the study of invertibility in the $C^*$-algebras $\mathcal Q_\theta$, with $\theta \in {{\mathrm{\mathbb {T}}}}$.

The rational case is trivial and was already treated at the beginning of the discussion.

If $\theta$ is irrational, any irreducible representation $\pi$ of ${{\mathrm{\mathbb {H}}}}$ which vanishes on $\mathtt J_\theta$ can be used to check invertibility in $\mathcal Q_\theta$. Indeed, since for an arbitrary unital $C^*$-algebra $\mathcal A$ and an irreducible representation $\pi$ of $\mathcal A$, the $C^*$-algebras $\pi (\mathcal A)$ and $\mathcal A /\ker ( \pi )$ are isomorphic one gets

$$\begin{aligned} \pi (C^*({{\mathrm{\mathbb {H}}}})) \simeq C^*({{\mathrm{\mathbb {H}}}}) / \ker (\pi ) = C^*({{\mathrm{\mathbb {H}}}}) / \mathtt J _\theta = \mathcal Q _\theta \end{aligned}$$

due to Theorem 13. In particular we may use the representations $\pi _{\theta }^{(1,1)}$ as in (15). $\square$

Remark 1

We should note here that for all realisations of the irrational rotation algebra the spectrum of $a \in \mathcal R_\theta$ is the same as a set. But this does not imply that an eigenvalue (or an element of the continuous spectrum) of a in one realisation is an eigenvalue (or an element of the continuous spectrum) of a in all the other realisations.

4.3 Finite-dimensional approximation

The following proposition follows from Theorem 11 and might be useful for checking invertibility of $f\in {{\mathrm{\mathbb {Z}}}}[{{\mathrm{\mathbb {H}}}}]$ via numerical simulations.

Proposition 1

Let $f\in {{\mathrm{\mathbb {Z}}}}[{{\mathrm{\mathbb {H}}}}]$. Then $\alpha _f$ is expansive if and only if there exists a constant $c>0$ such that $\pi (f)$ is invertible and $\Vert \pi (f)^{-1}\Vert \le c$ for every finite-dimensional irreducible representation $\pi$ of ${{\mathrm{\mathbb {H}}}}$.

For the proof of the Proposition we work with the representations $\pi _{\theta }^{(1,1)}$ in (15). For irrational $\theta$,

$$\begin{aligned} (\pi _{\theta }^{(1,1)}(x) H)(t)=H(t+\theta ), \quad (\pi _{\theta }^{(1,1)}(y) H)(t)=e^{2\pi i t}H(t), \end{aligned}$$

(20)

for every $H \in L^2(\mathbb {T},\lambda _\mathbb {T})$ and $t\in {{\mathrm{\mathbb {T}}}}$. For rational $\theta$ of the form $\theta =p/q$ with $(p,q)=1$ we replace the Lebesgue measure $\lambda =\lambda _\mathbb {T}$ in (20) by the uniform probability measure $\nu _q$ concentrated on the cyclic group $\{1/q,\ldots ,(q-1)/q,1\}\subset \mathbb {T}$.

Proof

One direction is obvious. For the converse, assume that $\alpha _f$ is non-expansive, but that there exists a constant $c>0$ such that $\pi (f)$ is invertible and $\Vert \pi (f)^{-1}\Vert \le c$ for every finite-dimensional irreducible representation $\pi$ of ${{\mathrm{\mathbb {H}}}}$.

Since $\alpha _f$ is non-expansive, there exists an irrational $\theta$ (by our assumption) such that the operator $\pi _{\theta }^{(1,1)}(f)$ has no bounded inverse due to Theorem 11 and its proof. Therefore, $\pi _{\theta }^{(1,1)}(f)$ is either not bounded from below or its range is not dense in the representation space or both.

We consider first the case where $\pi _{\theta }^{(1,1)}(f)$ is not bounded from below. Then there exists, for every $\varepsilon >0$, an element $H_\varepsilon \in L^2(\mathbb {T},\lambda _\mathbb {T})$ with $\Vert H_\varepsilon \Vert _2 =1$ and $\Vert \pi _{\theta }^{(1,1)}(f)H_\varepsilon \Vert _2 < \varepsilon$. By approximating the $H_\varepsilon$ by continuous functions we may obviously assume that each $H_\varepsilon$ is continuous.

Let q be a rational prime, and let p satisfy $|\theta -p/q|<1/q$. Then

$$\begin{aligned} \int |H_\varepsilon |^2 d\nu _q \quad \text {and} \quad \int |\pi _{\theta }^{(1,1)}(f) H_\varepsilon |^2 d\nu _q \end{aligned}$$

are Riemann approximations to the corresponding integrals with respect to $\lambda$. Hence,

$$\begin{aligned} \lim _{q \rightarrow \infty } \int |H_\varepsilon |^2 d\nu _q =1 \quad \text {and} \quad \lim _{q \rightarrow \infty } \int |\pi _{\theta }^{(1,1)}(f) H_\varepsilon |^2 d\nu _q \le \varepsilon ^2\,. \end{aligned}$$

Furthermore, as $q\rightarrow \infty$, $\pi _{p/q}^{(1,1)}(f) H_\varepsilon$ converges uniformly to $\pi _{\theta }^{(1,1)}(f) H_\varepsilon$. From this we deduce that

$$\begin{aligned} \limsup _{q \rightarrow \infty } \int |\pi _{p/q}^{(1,1)}(f) H_\varepsilon |^2 d\nu _q \le \varepsilon ^2. \end{aligned}$$

This clearly violates the hypothesis that $\pi _{p/q}^{(1,1)}(f)$, q prime, have uniformly bounded inverses.

Finally, assume that $\pi _{\theta }^{(1,1)}(f)$ has no dense image in $L^2({{\mathrm{\mathbb {T}}}},\lambda )$. In that case the adjoint operator $(\pi _{\theta }^{(1,1)}(f))^*=\pi _{\theta }^{(1,1)}(f^*)$ is not injective.³ Furthermore, by our assumptions, $\Vert \pi (f^*)^{-1}\Vert \le c$ for every finite-dimensional irreducible representation $\pi$ of ${{\mathrm{\mathbb {H}}}}$. The same arguments as in the first part of the proof lead to a contradiction. $\square$

5 Invertibility in group algebras of discrete nilpotent groups

In this section we aim to find more evident conditions for invertibility in group algebras for discrete countable nilpotent groups than the one given in Theorem 9. The main objects of our investigations are the primitive ideal space and the class of irreducible monomial representations of the group.

5.1 Wiener’s Lemma for nilpotent groups

Let $\varGamma$ be a countable discrete nilpotent group. As we have seen earlier, $\ell ^1(\varGamma ,{{\mathrm{\mathbb {C}}}})$ is inverse-closed in $C^*(\varGamma )$. Hence we concentrate on the group $C^*$-algebra $C^*(\varGamma )$.

In order to establish a Wiener Lemma in this more general setting we are first going to reinterpret Wiener’s Lemma for the discrete Heisenberg group. From the discussion in Sect. 4.2 one can easily see that the irreducible unitary representations $\pi _\theta ^{(s,t)}$, $\theta ,s,t\in {{\mathrm{\mathbb {T}}}}$, those representations which correspond to ergodic $\text {R}_\theta$-invariant measures on ${{\mathrm{\mathbb {T}}}}$, generate the primitive ideal space $\text {Prim}(C^*({{\mathrm{\mathbb {H}}}}))$. Moreover, since $\pi (C^*({{\mathrm{\mathbb {H}}}})) \simeq C^*({{\mathrm{\mathbb {H}}}}) / \ker (\pi )$ for every $\pi \in \widehat{{\mathrm{\mathbb {H}}}}$ the study of invertibility is directly linked to invertibility of projections onto the primitive ideals. We may interpret this as a localisation principle.

Before formulating a Wiener Lemma for an arbitrary discrete nilpotent group let us fix some notation. Let $\mathcal A$ be a unital $C^*$-algebra. For every two-sided closed ideal $\mathtt J$ of $\mathcal A$, denote by $\varPhi _{\mathtt J}$ the canonical projection from $\mathcal A$ onto the $C^*$-algebra $\mathcal A/ \mathtt J$.

Theorem 14

(Wiener’s Lemma for nilpotent groups) If $\varGamma$ is a discrete nilpotent group, then $a \in C^*(\varGamma )$ is invertible if and only if $\varPhi _\mathtt {I}(a)$ is invertible for every $\mathtt I \in \text {Prim}(C^*(\varGamma ))$.

This theorem links questions about invertibility in $\ell ^1(\varGamma ,{{\mathrm{\mathbb {C}}}})$ and $C^*(\varGamma )$ to their representation theory and, to be more specific, to the primitive ideal space $\text {Prim}(C^*(\varGamma ))$. At the same time this result provides us with a sufficient family of ideals in order to study invertibility and hence, Wiener’s Lemma for nilpotent groups describes a localisation principle. We will learn in the next subsection that for discrete nilpotent groups $\varGamma$ the class of irreducible representation which are induced by one-dimensional representations of subgroups of $\varGamma$ provide us with an effective tool to generate $\text {Prim}(C^*(\varGamma ))$. In other words, it is a feasible task to determine the primitive ideal space $\text {Prim}(C^*(\varGamma ))$.

Theorem 14 can be generalised to all unital $C^*$-algebras. Moreover, we provide a sufficient condition for a family of ideals in order to check invertibility via localisations.

Suppose $\mathfrak I$ is a collection of ideals of a $C^*$-algebra $\mathcal A$, such that

• (i) every $\mathtt I\in \mathfrak I$ is closed and two-sided,

• (ii) for any primitive ideal $\mathtt J\in \text {Prim}(\mathcal A)$ there exists $\mathtt I\in \mathfrak I$ such that $\mathtt I\subseteq \mathtt J$.

Theorem 15

Let $\mathcal A$ be a unital $C^*$-algebra. Suppose $\mathfrak I$ satisfies conditions (i) and (ii) above. Then an element a in $\mathcal A$ is invertible if and only if for every $\mathtt I\in \mathfrak I$ the projection of a on $\mathcal A/\mathtt I$ is invertible.

By setting $\mathfrak I=\text {Prim}(C^*(\varGamma ))$, Theorem 14 just becomes a particular case of Theorem 15.

Proof

If $a \in \mathcal A$ is not invertible, then by Theorem 9 there exists an irreducible unitary representation $\pi$ of $\mathcal A$ such that $\pi (a)v=0$ for some non-zero vector $v\in \mathcal H_ \pi$. Moreover, for every two-sided closed ideal $\mathtt I \subseteq \ker (\pi )$ of $\mathcal A$ the representation $\pi$ induces a well-defined irreducible representation $\pi _{\mathtt I}$ of the $C^*$-algebra $\mathcal A/ \mathtt I$, i.e.,

$$\begin{aligned} \pi _{\mathtt I}(\varPhi _{\mathtt I}(a))=\pi (a) \,. \end{aligned}$$

Hence, for every two-sided closed ideal $\mathtt I \subseteq \ker (\pi )$ of $C^*({{\mathrm{\mathbb {H}}}})$, the element $\varPhi _{\mathtt I}(a)$ is not invertible in $\mathcal A/ \mathtt I$, since the operator $\pi _{\mathtt I}(\varPhi _{\mathtt I}(a))$ has a non-trivial kernel in $\mathcal H_\pi$.

Let us assume now that $\varPhi _{\mathtt I}(a)$ is not invertible in the $C^*$-algebra $\mathcal A/ \mathtt I$ for some $\mathtt I\in \mathfrak I$. Hence, there exists an irreducible representation $\rho$ of $\mathcal A/ \mathtt I$ such that

$$\begin{aligned} \rho (\varPhi _{\mathtt I}(a)) v =0 \end{aligned}$$

for some vector $v\in \mathcal H _\rho$. The irreducible representation $\rho$ can be extended to an irreducible representation $\tilde{\rho }$ of $\mathcal A$ which vanishes on $\mathtt I$ and which is given by $\tilde{\rho }= \rho \circ \varPhi _{\mathtt I}$. Therefore, a is not invertible in $\mathcal A$. $\square$

From the proof of Theorem 15 we get the following corollary.

Corollary 1

If $\pi (a)$ is not invertible for an irreducible representation $\pi$, then for every two-sided closed ideal $\mathtt I \subseteq \ker (\pi )$ of $C^*({{\mathrm{\mathbb {H}}}})$, the element $\varPhi _{\mathtt I}(a)$ is non-invertible in $\mathcal A/ \mathtt I$.

Example 1

Denote by $\mathtt J_\theta$, with $\theta \in {{\mathrm{\mathbb {T}}}}$, the localisation ideals of $C^*({{\mathrm{\mathbb {H}}}})$ as defined in Sect. 4 and set

$$\begin{aligned} \mathfrak J_{{{\mathrm{\mathbb {H}}}}} := \{\mathtt J _\theta \,: \,\theta \in {{\mathrm{\mathbb {T}}}}\}. \end{aligned}$$

Obviously, the restriction $r: \text {Prim}(C^*({{\mathrm{\mathbb {H}}}})) \longrightarrow \mathfrak J_{{{\mathrm{\mathbb {H}}}}}$ given by $\mathtt I \mapsto r(\mathtt I)=\mathtt I \cap \mathcal C (C^*({{\mathrm{\mathbb {H}}}}))$ for every primitive ideal $\mathtt I$ of $C^*({{\mathrm{\mathbb {H}}}})$, defines a surjective map. Hence, Theorem 15 provides a proof of Allan’s local principle for $C^*({{\mathrm{\mathbb {H}}}})$. Moreover, Allan’s local principle can be viewed as the most effective way to apply Theorem 15 in order to check invertibility.

5.2 Monomial representations

5.2.1 The Heisenberg group

Denote by $\text {Ind}^{{{\mathrm{\mathbb {H}}}}}_N(\sigma _{\theta ,s})$ the representation of ${{\mathrm{\mathbb {H}}}}$ induced from the normal subgroup

$$\begin{aligned} N:= \left\{ \left( \begin{array}{l@{\quad }l@{\quad }l} 1 &{} a &{} b \\ 0 &{} 1 &{} 0 \\ 0 &{} 0 &{} 1 \end{array} \right) \,:\, a,b \in {{\mathrm{\mathbb {Z}}}}\right\} \end{aligned}$$

and the character $\sigma _{\theta ,s}$ which is defined by

$$\begin{aligned} \sigma _{\theta ,s}(z)=e^{2 \pi i \theta } \quad \text {and} \quad \sigma _{\theta ,s}(x)=e^{-2 \pi i s}. \end{aligned}$$

For the convenience of the reader we will write down $\text {Ind}^{{{\mathrm{\mathbb {H}}}}}_N ( \sigma _{\theta ,s} )$ for every $\theta , s \in {{\mathrm{\mathbb {T}}}}$ explicitly

$$\begin{aligned} \left( \text {Ind}^{{{\mathrm{\mathbb {H}}}}}_N ( \sigma _{\theta ,s}) (x^k y^l z^m)F \right) (n) = e^{2 \pi i (m \theta - k(n\theta +s) )} F(n+l) \end{aligned}$$

(21)

for all $k,l,m,n\in {{\mathrm{\mathbb {Z}}}}$ and $F\in \ell ^2({{\mathrm{\mathbb {Z}}}},{{\mathrm{\mathbb {C}}}})$.

The representations $\text {Ind}^{{{\mathrm{\mathbb {H}}}}}_N(\sigma _{\theta ,s})$ play a special role since they can be extended to the Stone-von Neumann representations of the real Heisenberg group ${{\mathrm{\mathbb {H}}}}_{{{\mathrm{\mathbb {R}}}}}$ consisting of all unipotent upper triangular matrices in $\text {SL}(3,\mathbb {R})$. The Stone-von Neumann representations of ${{\mathrm{\mathbb {H}}}}_{{{\mathrm{\mathbb {R}}}}}$ are obtained from Mackey’s induction procedure from the real analogue of N, i.e.,

$$\begin{aligned} N_{{{\mathrm{\mathbb {R}}}}} := \left\{ \left( \begin{array}{l@{\quad }l@{\quad }l} 1 &{} a &{} b \\ 0 &{} 1 &{} 0 \\ 0 &{} 0 &{} 1 \end{array} \right) \,:\, a,b \in {{\mathrm{\mathbb {R}}}}\right\} \end{aligned}$$

and its characters. The Stone-von Neumann representations are defined by modulation and translation operators on $L^2({{\mathrm{\mathbb {R}}}},{{\mathrm{\mathbb {C}}}})$.

It is easy to see that for irrational $\theta$ the representation $\pi _{\theta }^{(1,1)}$ in (15) is unitarily equivalent (via Fourier transformation) to the representation $\text {Ind}^{{{\mathrm{\mathbb {H}}}}}_N(\sigma _{\theta ,1})$. Moreover, every irreducible finite dimensional representation of a nilpotent group $\varGamma$ is induced from a one dimensional representation of a subgroup of $\varGamma$ (cf. [6, Lemma 1]).

Therefore, the monomial representations contain all representations involved in validating invertibility via Theorem 11.

The natural question arises, whether one can always restrict oneself to the class of monomial representations of $\varGamma$ when analysing invertibility in the corresponding group algebras, in case $\varGamma$ is a countable discrete nilpotent group. We will show that the answer is positive.

5.2.2 The general case

Let $\varGamma$ be a countable discrete nilpotent group. Define an equivalence relation on $\widehat{\varGamma }$ as follows:

$$\begin{aligned} \pi _1 \sim \pi _2 \iff \ker (\pi _1 ) = \ker (\pi _2 )\,, \end{aligned}$$

where $\pi _1,\pi _2$ are irreducible unitary representations of $\varGamma$. This equivalence relation is the same as the notion of weak equivalence according to [10].

The next theorem was established by Howe in [17, Proposition 5].

Theorem 16

Suppose that $\varGamma$ is a countable discrete nilpotent group. Then every irreducible unitary representation is weakly equivalent to an irreducible monomial representation of $\varGamma$.

In other words the map from the subclass of irreducible monomial representations to the primitive ideal space is surjective and as a conclusion the monomial representations generate the primitive ideal space. It is therefore not surprising that the class of irreducible monomial representations contains all the information which is necessary in order to study invertibility in the group algebras. As we will show, combining Theorem 16 with Theorem 9 leads to another Wiener Lemma:

Theorem 17

An element $a\in C^*(\varGamma )$ is non-invertible if and only if there exists an irreducible monomial representation $\pi$ such that $\pi (a)$ has no bounded inverse.

For convenience of the reader we explain the ideas once more.

Proof

If a is not invertible, then there exists an irreducible unitary representation $\pi$ and a non-zero vector $v\in \mathcal H _\pi$ such that $\pi (a)v=0$. This implies that $\varPhi _{\ker (\pi )}(a)$ is not invertible in $C^*(\varGamma )/\ker (\pi )$. Moreover, there exists an irreducible monomial representation $\rho$ with $\ker (\rho )=\ker ( \pi )$ (cf. Theorem 16) and hence

$$\begin{aligned} \pi ( C^*(\varGamma ) ) \simeq C^*(\varGamma ) / \ker (\pi )= C^*(\varGamma ) / \ker (\rho ) \simeq \rho (C^*(\varGamma ) ) \,. \end{aligned}$$

Therefore, $\varPhi _{\ker (\rho )}(a)$ and $\rho (a)$ are not invertible.

On the other hand, if $\pi (a)$ is not invertible for an irreducible monomial representation $\pi$, then $\varPhi _{\ker (\pi ) }(a)$ is not invertible in the $C^*$-algebra $C^*(\varGamma ) / \ker (\pi )$. Hence there exists an irreducible representation $\rho$ of $C^*(\varGamma ) / \ker (\pi )$ such that $\rho (\varPhi _{\ker (\pi )}(a))$ has a non-trivial kernel. Moreover, $\rho$ can be extended to a representation $\tilde{\rho }$ of $C^*(\varGamma )$ vanishing on $\ker (\pi )$. Therefore, a is not invertible. $\square$

5.3 Maximality of primitive ideals

In the previous subsection we saw that we can restrict our attention to irreducible monomial representations for questions about invertibility. Unfortunately, this subclass of irreducible representations might still be quite big. We will use another general result about the structure of $\text {Prim}(C^*(\varGamma ))$ to make the analysis of invertibility in $C^*(\varGamma )$ easier.

Theorem 18

([31]) Let $\varGamma$ be a discrete nilpotent group. Then

$$\begin{aligned} \text {Prim}(C^*(\varGamma ))=\text {Max}(C^*(\varGamma )), \end{aligned}$$

i.e., every primitive ideal of $C^*(\varGamma )$ is maximal.

The simplification in the study of invertibility in $C^*({{\mathrm{\mathbb {H}}}})$ was due to the simplicity of the irrational rotation algebras $\mathcal R _\theta$, which is equivalent to the maximality of the two-sided closed ideal $\mathtt J _\theta$. We should note here that Theorem 13 is usually proved by the construction of a unique trace on $\mathcal R _\theta$, which is rather complicated. Alternatively, let $\theta \in {{\mathrm{\mathbb {T}}}}$ be irrational. Then it easily follows from Theorem 18 and the fact that $\pi _{\theta }^{(s,t)}$ is an irreducible representation (cf. Lemma 1) with $\ker (\pi _{\theta }^{(s,t)}) = \mathtt J_\theta$ that $\mathtt J_\theta$ is maximal. This is exactly the statement of Theorem 13. In the next subsection we will see applications of Theorem 18. It turns out that this representation theoretical result will eliminate the ‘non-Type I issues’ exactly as the simplicity of irrational rotation algebras did for the group algebras of the discrete Heisenberg group.

5.4 Examples

The first example shows how to establish a Wiener Lemma for ${{\mathrm{\mathbb {H}}}}$ from the general observation made in this section.

Example 2

Consider the monomial representations $\text {Ind}_N^{{{\mathrm{\mathbb {H}}}}}(\sigma _{\theta , s})$ of ${{\mathrm{\mathbb {H}}}}$ as defined in (21) for irrational $\theta$ and arbitrary $s\in {{\mathrm{\mathbb {T}}}}$. Obviously, one has for every $s\in {{\mathrm{\mathbb {T}}}}$ that $\ker (\text {Ind}_N^{{{\mathrm{\mathbb {H}}}}}(\sigma _{\theta , s})) =\mathtt J_\theta$.

We will show that there is no bounded operator on $\ell ^2({{\mathrm{\mathbb {Z}}}},{{\mathrm{\mathbb {C}}}})$ which commutes with the operators $\text {Ind}_N^{{{\mathrm{\mathbb {H}}}}}(\sigma _{\theta , s})(x)$ and $\text {Ind}_N^{{{\mathrm{\mathbb {H}}}}}(\sigma _{\theta , s})(y)$ except multiples of the identity operator. Let $\{\delta _k \,:\, k \in {{\mathrm{\mathbb {Z}}}}\}$ be the standard basis of $\ell ^2({{\mathrm{\mathbb {Z}}}},{{\mathrm{\mathbb {C}}}})$ and $\text {C} = (c_{n,k})_{n,k\in {{\mathrm{\mathbb {Z}}}}}$ an operator which commutes with $\text {Ind}_N^{{{\mathrm{\mathbb {H}}}}}(\sigma _{\theta , s})(x)$ and $\text {Ind}_N^{{{\mathrm{\mathbb {H}}}}}(\sigma _{\theta , s})(y)$. From the equations

$$\begin{aligned} e^{-2 \pi i s}\sum _{n \in {{\mathrm{\mathbb {Z}}}}} c_{n,k} e^{-2 \pi i \theta n} \delta _n&=\text {C} \left( \text {Ind}_N^{{{\mathrm{\mathbb {H}}}}}(\sigma _{\theta , s})(x) \delta _k \right) \\&=\text {Ind}_N^{{{\mathrm{\mathbb {H}}}}}(\sigma _{\theta , s})(x) (\text{ C } \delta _k)\\&= e^{-2 \pi i s}e^{-2 \pi i \theta k}\sum _{n \in {{\mathrm{\mathbb {Z}}}}} c_{n,k} \delta _n \end{aligned}$$

and the fact that $\theta$ is irrational we can conclude that $c_{n,k}= 0$ for all $n, k \in {{\mathrm{\mathbb {Z}}}}$ with $n \not = k$. On the other hand, for $k\in {{\mathrm{\mathbb {Z}}}}$

$$\begin{aligned} c_{k,k} \delta _{k+1}&=\text {Ind}_N^{{{\mathrm{\mathbb {H}}}}}(\sigma _{\theta , s})(y)(\text {C} \delta _k) \\&= \text {C} \left( \text {Ind}_N^{{{\mathrm{\mathbb {H}}}}}(\sigma _{\theta , s}) (y) \delta _k\right) \\&= c_{k+1,k+1} \delta _{k+1} \,. \end{aligned}$$

Therefore, the only operators in the commutant of $\text {Ind}_N^{{{\mathrm{\mathbb {H}}}}}(\sigma _{\theta , s}) ({{\mathrm{\mathbb {H}}}})$ are scalar multiples of the identity, which is equivalent to the irreducibility of the representation $\text {Ind}_N^{{{\mathrm{\mathbb {H}}}}}(\sigma _{\theta , s})$ by Schur’s Lemma. Hence, the kernel of the irreducible monomial representation $\text {Ind}_N^{{{\mathrm{\mathbb {H}}}}}(\sigma _{\theta , s})$ is a maximal two-sided ideal (cf. Theorem 18) given by $\mathtt J _\theta$.

For every irreducible representation $\pi$ of ${{\mathrm{\mathbb {H}}}}$ with $\mathtt J _\theta \subseteq \ker (\pi )$ one has $\ker (\pi ) =\mathtt J _\theta$ due to the maximality of $\mathtt J _\theta$ which we deduce from the irreducibility of $\text {Ind}_N^{{{\mathrm{\mathbb {H}}}}}(\sigma _{\theta , s})$.

Consider $\theta =\frac{n}{d}$ with relatively prime $n,d \in {{\mathrm{\mathbb {N}}}}$. We note that analysing invertibility in $\mathcal Q _\theta$ reduces to the study of monomial representations as well. Set

$$\begin{aligned} {{\mathrm{\mathbb {H}}}}/ Z(d) := \left\{ \left( \begin{array}{l@{\quad }l@{\quad }l} 1 &{} a &{} \bar{b} \\ 0 &{} 1 &{} c \\ 0 &{} 0 &{} 1 \end{array}\right) , \quad a,c \in {{\mathrm{\mathbb {Z}}}}\,\text {and}\, \bar{b} \in {{\mathrm{\mathbb {Z}}}}/d{{\mathrm{\mathbb {Z}}}}\right\} , \quad d\in {{\mathrm{\mathbb {N}}}}, \end{aligned}$$

and note the isomorphism $\mathcal Q _\theta \cong C^*({{\mathrm{\mathbb {H}}}}/ Z(d))$. The nilpotent group ${{\mathrm{\mathbb {H}}}}/ Z(d)$ is of Type I since ${{\mathrm{\mathbb {H}}}}/ Z(d)$ has normal abelian subgroups of finite index, e.g.,

$$\begin{aligned} \left\{ \left( \begin{array}{l@{\quad }l@{\quad }l} 1 &{} a d &{} \bar{b} \\ 0 &{} 1 &{} c \\ 0 &{} 0 &{} 1 \end{array}\right) , \quad a,c \in {{\mathrm{\mathbb {Z}}}}\,\text {and}\, \bar{b} \in {{\mathrm{\mathbb {Z}}}}/d{{\mathrm{\mathbb {Z}}}}\right\} . \end{aligned}$$

Hence, all irreducible representations are monomial by Theorem 4.

A Wiener Lemma can now be deduced from Theorem 18.

Note that in the general study of invertibility in this example we have not used Allan’s local principle or any results from Sect. 4 explicitly.

We give another example of a group where Theorem 18 simplifies the analysis.

Example 3

Let us denote by $\mathbb G$ the multiplicative group given by

$$\begin{aligned} \left\{ \left( \begin{array}{l@{\quad }l@{\quad }l@{\quad }l} 1 &{} a &{} c &{} f \\ 0 &{} 1 &{} b &{} e \\ 0 &{} 0 &{} 1 &{} d \\ 0 &{} 0 &{} 0 &{} 1 \end{array} \right) \,:\, a,b,c,d,e,f \in {{\mathrm{\mathbb {Z}}}}\right\} . \end{aligned}$$

One can easily verify that the centre of this group is given by

$$\begin{aligned} \left\{ \left( \begin{array}{l@{\quad }l@{\quad }l@{\quad }l} 1 &{} 0 &{} 0 &{} f \\ 0 &{} 1 &{} 0 &{} 0 \\ 0 &{} 0 &{} 1 &{} 0 \\ 0 &{} 0 &{} 0 &{} 1 \end{array} \right) \,:\, f \in {{\mathrm{\mathbb {Z}}}}\right\} \simeq {{\mathrm{\mathbb {Z}}}}, \end{aligned}$$

and hence the corresponding central sub-algebra $\ell ^1({{\mathrm{\mathbb {Z}}}})$ is exactly the same as it was in the case of the discrete Heisenberg group. It is therefore not surprising that the invertibility problem can be addressed in a similar fashion.

Let us construct monomial representations, which will be sufficient to check global invertibility (cf. Theorem 17).

First note that $\mathbb G$ can be identified with the semi-direct product $G_1\rtimes G_2$ of the normal abelian subgroup

$$\begin{aligned} G_1:= \left\{ \left( \begin{array}{l@{\quad }l@{\quad }l@{\quad }l} 1 &{} 0 &{} c &{} f \\ 0 &{} 1 &{} b &{} e \\ 0 &{} 0 &{} 1 &{} 0 \\ 0 &{} 0 &{} 0 &{} 1 \end{array} \right) \,:\, b,c,e,f \in {{\mathrm{\mathbb {Z}}}}\right\} \simeq {{\mathrm{\mathbb {Z}}}}^4 \end{aligned}$$

and the abelian subgroup

$$\begin{aligned} G_2 := \left\{ \left( \begin{array}{l@{\quad }l@{\quad }l@{\quad }l} 1 &{} a &{} 0 &{} 0 \\ 0 &{} 1 &{} 0 &{} 0 \\ 0 &{} 0 &{} 1 &{} d \\ 0 &{} 0 &{} 0 &{} 1 \end{array} \right) \,:\, a,d \in {{\mathrm{\mathbb {Z}}}}\right\} \simeq {{\mathrm{\mathbb {Z}}}}^2\,. \end{aligned}$$

In such a situation the construction of induced representations becomes very easy. We refer to [21, Section 2.4] for all the details. Now let $\sigma _{\theta _b,\theta _c,\theta _e,\theta _f}$ be the one-dimensional representation of $G_1$ given by

$$\begin{aligned} \sigma _{\theta _b,\theta _c,\theta _e,\theta _f} \left( \left( \begin{array}{l@{\quad }l@{\quad }l@{\quad }l} 1 &{} 0 &{} c &{} f \\ 0 &{} 1 &{} b &{} e \\ 0 &{} 0 &{} 1 &{} 0 \\ 0 &{} 0 &{} 0 &{} 1 \end{array} \right) \right) = e^{2 \pi i \theta _b b}e^{2 \pi i \theta _c c}e^{2 \pi i \theta _e e }e^{2 \pi i \theta _f f }\,. \end{aligned}$$

The inclusion map from $G_2$ to $\mathbb G$ will serve as a cross-section. The induced representation $\text {Ind}_{G_1}^{\mathbb G}(\sigma _{\theta _b,\theta _c,\theta _e,\theta _f})$ (is unitarily equivalent to a representation which) acts on the Hilbert space $\ell ^2({{\mathrm{\mathbb {Z}}}}^2,{{\mathrm{\mathbb {C}}}})$ and is given by

$$\begin{aligned}&\left( \text {Ind}_{G_1}^{\mathbb G}(\sigma _{\theta _b,\theta _c,\theta _e,\theta _f})\left( \left( \begin{array}{l@{\quad }l@{\quad }l@{\quad }l} 1 &{} 0 &{} c &{} f \\ 0 &{} 1 &{} b &{} e \\ 0 &{} 0 &{} 1 &{} 0 \\ 0 &{} 0 &{} 0 &{} 1 \end{array} \right) \left( \begin{array}{l@{\quad }l@{\quad }l@{\quad }l} 1 &{} a &{} 0 &{} 0 \\ 0 &{} 1 &{} 0 &{} 0 \\ 0 &{} 0 &{} 1 &{} d \\ 0 &{} 0 &{} 0 &{} 1 \end{array} \right) \right) F\right) (k,l)\\&\qquad \quad \quad = e^{2 \pi i \theta _b b} e^{2 \pi i \theta _c (c-kb)}e^{2 \pi i \theta _e (e+lb) }e^{2 \pi i \theta _f (f+lc-ke-klb) } F(k-a,l-d),\nonumber \end{aligned}$$

(22)

for every $a,b,c,d,e,f,k,l \in {{\mathrm{\mathbb {Z}}}}$ and $F\in \ell ^2({{\mathrm{\mathbb {Z}}}}^2,{{\mathrm{\mathbb {C}}}})$.

The localisation fibres are indexed by $\theta _f$. It is clear that for every irrational $\theta _f$ and arbitrary $\theta _b, \theta _c, \theta _e$,

$$\begin{aligned} \ker \left( \text {Ind}_{G_1}^{\mathbb G}(\sigma _{\theta _b,\theta _c,\theta _e,\theta _f})\right) = \mathtt J_{\theta _f}\,. \end{aligned}$$

In the case of irrational $\theta _f$, the commutant of $\text {Ind}_{G_1}^{\mathbb G}(\sigma _{\theta _b,\theta _c,\theta _e,\theta _f})(\mathbb G)$ in $\mathcal B(\ell ^2({{\mathrm{\mathbb {Z}}}}^2,{{\mathrm{\mathbb {C}}}}))$ is trivial which is equivalent to irreducibility by Schur’s Lemma. Hence, for irrational $\theta _f$ the two-sided closed ideal $\mathtt J_{\theta _f}$ is maximal by Theorem 18 and one has to consider only a single representation, e.g., the one given in (22) for fixed parameters $\theta _b,\theta _c,\theta _e$, to study invertibility on these fibres.

5.5 A kernel condition and finite-dimensional representations

The proof of Proposition 1 provides an approximation argument which allows restricting oneself to finite-dimensional representations for the purpose of proving invertibility. This result can be reinterpreted as a density argument. The finite-dimensional irreducible representations of ${{\mathrm{\mathbb {H}}}}$ correspond to ‘rational’ points in the dual of ${{\mathrm{\mathbb {H}}}}$. We know that the intersection of all irreducible representations $\pi$ with $\pi (z)=e^{2\pi i \theta }$ coincides with $\mathtt J _\theta$. In the same way as one shows that no non-zero element in $C({{\mathrm{\mathbb {T}}}})$ (which is isomorphic to $C^*({{\mathrm{\mathbb {Z}}}})$) vanishes at all rational points, one can prove that

$$\begin{aligned} \bigcap _{\text {rational} \,\theta \in {{\mathrm{\mathbb {T}}}}} \mathtt J_\theta = \{0\}\,. \end{aligned}$$

We will show that this empty-intersection condition actually implies that for checking invertibility of $a\in C^*({{\mathrm{\mathbb {H}}}})$ it is enough to check the invertibility of the evaluations $\pi (a)$ for all finite-dimensional irreducible representations of $C^*({{\mathrm{\mathbb {H}}}})$ provided that the inverses $\pi (a)^{-1}$ of these elements are uniformly bounded in norm.

Let $\mathcal A$ and $\mathcal B _t$, for all $t\in I$ for some index set I, be $C^*$-algebras. Let us denote by $\mathfrak F$ a family of $^*$-morphisms $\phi _t : \mathcal A \longrightarrow \mathcal B_t$, $t\in I$, which fulfils

• for all $t\in I$ one has $\mathtt J_t = \ker (\phi _t )$ is a two-sided closed ideal of $\mathcal A$, hence $\mathcal A _t= \mathcal A / \mathtt J_t$ is a $C^*$-algebra with quotient norm $\Vert \cdot \Vert _t$;

• $\bigcap _{t \in I} \mathtt J _t = \{0\}$.

Furthermore, let us denote by $\mathcal A_I$ the set of elements $a=(a_t)_{t\in I} \in \prod _{t\in I} \mathcal A_t$ with $\Vert a\Vert _I := \sup _{t\in I}\Vert a_t \Vert _t< \infty$; $\mathcal A_I$ together with the norm $\Vert \cdot \Vert _I$ forms a $C^*$-algebra. Let $\varPhi : \mathcal A \longrightarrow \mathcal A_I$ be defined by $a\mapsto (\phi _t(a))_{t\in I}$. Since

$$\begin{aligned} \bigcap _{t\in I } \mathtt J_t = \{0\}, \end{aligned}$$

one has that $\varPhi$ is a bijective map from $\mathcal A$ to $\varPhi (\mathcal A)$. The $C^*$-algebras $\varPhi (\mathcal A)$ and $\mathcal A_I$ form a Wiener pair. Hence, $a\in \mathcal A$ is invertible if and only if $\phi _t (a)$ is invertible for all $t\in I$ and $\Vert \phi _t (a) ^{-1} \Vert _t$ is uniformly bounded in t.

Example 4

We apply these ideas to $C^*({{\mathrm{\mathbb {H}}}})$ and set

$$\begin{aligned} \mathfrak F _{{{\mathrm{\mathbb {H}}}}}= \{ \pi \in \widehat{{{\mathrm{\mathbb {H}}}}} \,: \, \pi \text {a finite dimensional representation}\} \end{aligned}$$

in order to get an algebraic interpretation of Proposition 1.

Example 5

Definitions and results that are used in this example can be found in [18] by Howe. Consider a finitely-generated nilpotent torsion-free group $\varGamma$. The set of kernels of finite-dimensional representations forms a dense subset of $\text {Prim}(C^*(\varGamma ))$ with respect to the hull-kernel topology. Since all $C^*$-algebras are semi-simple one gets that for every dense subset $\mathfrak J \subseteq \text {Prim}(C^*(\varGamma ))$ the following holds

$$\begin{aligned} \bigcap _{\mathtt J \in \mathfrak J}\mathtt J = \bigcap _{\mathtt J \in \overline{\mathfrak J}}\mathtt J= \bigcap _{\mathtt J \in \text {Prim}(C^*(\varGamma ))}\mathtt J =\{0\}\,. \end{aligned}$$

Hence, for verifying invertibility in $C^*(\varGamma )$, the study of the evaluations of the finite-dimensional representations—combined with a boundedness condition—is sufficient.

Suppose that $\varGamma$ is also elementarily-exponentiable—Howe labels such groups to have a well-defined ‘Lie-algebra’, say $\mathcal L$. Then the finite dimensional representations correspond to finite quasi-orbits of a canonical action of $\varGamma$ on $\mathcal L$ and the representation theory of $\varGamma$ is closely related to the one of its Mal’cev completion.

A systematic treatment of group-$C^*$-algebras $C^*(\varGamma )$ whose finite-dimensional representations separate points of $C^*(\varGamma )$ can be found in Section 4 of [4].

6 A connection to time-frequency-analysis via localisations

In this section we formulate yet another Wiener Lemma for $\ell ^1({{\mathrm{\mathbb {H}}}},{{\mathrm{\mathbb {C}}}})$ which involves Stone-von Neumann representations. These unitary representations of the discrete Heisenberg group are highly reducible and therefore, not the first choice for invertibility investigations (cf. Theorem 9). However, by exploring a connection from localisations of $\ell ^1({{\mathrm{\mathbb {H}}}},{{\mathrm{\mathbb {C}}}})$ to twisted convolution algebras we establish a link to Time-Frequency-Analysis. In this discipline of mathematics Stone-von Neumann representations are of great importance.

6.1 Localisations and twisted convolution algebras

In [13] we determined the explicit form of the localisation ideals $\mathtt J _m$ in order to formulate Allan’s local principle for the group algebra $\ell ^1({{\mathrm{\mathbb {H}}}},{{\mathrm{\mathbb {C}}}})$ of the discrete Heisenberg group. Let us recall this result.

We write a typical element $f\in \ell ^1({{\mathrm{\mathbb {H}}}},{{\mathrm{\mathbb {C}}}})$ in the form:

$$\begin{aligned} f=\sum _{(k,l,m)\in {{\mathrm{\mathbb {Z}}}}^3} f_{(k,l,m)}x^k y^l z^m , \end{aligned}$$

with $f_{(k,l,m)}\in {{\mathrm{\mathbb {C}}}}$ and $\sum _{(k,l,m)\in {{\mathrm{\mathbb {Z}}}}^3} |f_{(k,l,m)}| < \infty$. We identify the centre of ${{\mathrm{\ell ^1(\mathbb {H},\mathbb {C})}}}$ with $\ell ^1({{\mathrm{\mathbb {Z}}}},{{\mathrm{\mathbb {C}}}})$ since the centre of the group ${{\mathrm{\mathbb {H}}}}$ is generated by powers of z. The maximal ideal space $\text {Max}(\ell ^1({{\mathrm{\mathbb {Z}}}},{{\mathrm{\mathbb {C}}}}))$ is canonically homeomorphic to $\widehat{{{\mathrm{\mathbb {Z}}}}}\cong {{\mathrm{\mathbb {T}}}}$. The smallest closed two-sided ideal in $\ell ^1({{\mathrm{\mathbb {H}}}},{{\mathrm{\mathbb {C}}}})$ containing $m_\theta \in \text {Max}(\ell ^1({{\mathrm{\mathbb {Z}}}},{{\mathrm{\mathbb {C}}}}))$, $\theta \in \mathbb {T}$, is given by the subset $\mathtt J _\theta \subset \ell ^1({{\mathrm{\mathbb {H}}}},{{\mathrm{\mathbb {C}}}})$ which consists of all elements $f \in \ell ^1({{\mathrm{\mathbb {H}}}},{{\mathrm{\mathbb {C}}}})$ such that

$$\begin{aligned} f^\theta := \sum _{(k,l,m)\in {{\mathrm{\mathbb {Z}}}}^3} f_{(k,l,m)} x^k y^l e^{2\pi im\theta } = 0_{\ell ^1({{\mathrm{\mathbb {H}}}},{{\mathrm{\mathbb {C}}}})}. \end{aligned}$$

The next definition plays an important role in the field of time-frequency-analysis. Fix $\theta \in {{\mathrm{\mathbb {T}}}}$. The twisted convolution $\natural _\theta$ on $\ell ^1({{\mathrm{\mathbb {Z}}}}^2,{{\mathrm{\mathbb {C}}}})$ is defined as follows. Let $f,g \in \ell ^1 ({{\mathrm{\mathbb {Z}}}}^2,{{\mathrm{\mathbb {C}}}})$, then

$$\begin{aligned} (f \natural _\theta g)_{m,n} = \sum _{k,l \in {{\mathrm{\mathbb {Z}}}}} f_{k,l}g_{m-k,n-l} e^{2\pi i(m-k)l \theta }. \end{aligned}$$

Moreover, define the involution $f^*_{k,l}=\overline{f_{-k,-l}} e^{2\pi ikl\theta }$ for every $f \in \ell ^1({{\mathrm{\mathbb {Z}}}}^2,{{\mathrm{\mathbb {C}}}})$. The triple $(\ell ^1 ({{\mathrm{\mathbb {Z}}}}^2,{{\mathrm{\mathbb {C}}}}),\natural _{\theta },^*)$ forms a Banach-$^*$-algebra—the so called twisted convolution algebra.

The Banach-algebras $\mathcal Q_\theta := \ell ^1({{\mathrm{\mathbb {H}}}},{{\mathrm{\mathbb {C}}}})/\mathtt J _\theta$ and $(\ell ^1 ({{\mathrm{\mathbb {Z}}}}^2,{{\mathrm{\mathbb {C}}}}),\natural _{\theta },^*)$ are connected by the $^*$-isomorphism $\kappa : \mathcal Q _\theta \longrightarrow (\ell ^1 ({{\mathrm{\mathbb {Z}}}}^2,{{\mathrm{\mathbb {C}}}}),\natural _{\theta },^*)$ defined by

$$\begin{aligned} \kappa (\varPhi _\theta (f))= f^\theta . \end{aligned}$$

6.2 Wiener’s Lemma for twisted convolution algebras

Principal results were obtained by Janssen [20] and Gröchenig and Leinert [15]. Let $\alpha , \beta$ be strictly positive real parameters and let $\theta = \alpha \beta$. On the Hilbert space $L^2({{\mathrm{\mathbb {R}}}},{{\mathrm{\mathbb {C}}}})$ define the translation operator $\text {T}_\alpha$ and the modulation operator $\text {M}_\beta$ as follows:

$$\begin{aligned} (\text {T}_\alpha F)(t) = F(t+\alpha ) \quad \text {and} \quad (\text {M}_\beta F)(t)= e^{2 \pi i \beta t} F(t) \end{aligned}$$

(23)

where $F\in L^2({{\mathrm{\mathbb {R}}}},{{\mathrm{\mathbb {C}}}})$ and $t\in {{\mathrm{\mathbb {R}}}}$. The representation $\pi _{\alpha ,\beta }$ of $(\ell ^1 ({{\mathrm{\mathbb {Z}}}}^2,{{\mathrm{\mathbb {C}}}}),\natural _{\theta },^*)$ on $L^2({{\mathrm{\mathbb {R}}}},{{\mathrm{\mathbb {C}}}})$ is defined as follows: for each $f\in \ell ^1({{\mathrm{\mathbb {Z}}}}^2,{{\mathrm{\mathbb {C}}}})$, let

$$\begin{aligned} \pi _{\alpha ,\beta } (f) =\sum _{k,l\in {{\mathrm{\mathbb {Z}}}}} f_{k,l} \text {T}_\alpha ^k \text {M}_\beta ^l . \end{aligned}$$

Gröchenig and Leinert established the following Wiener Lemma for twisted convolution algebras.

Theorem 19

([15, Lemma 3.3]) Suppose that $\theta \in {{\mathrm{\mathbb {T}}}}$, $\alpha \beta =\theta \mod 1$, and that $f\in \ell ^1 ({{\mathrm{\mathbb {Z}}}}^2,{{\mathrm{\mathbb {C}}}})$ and $\pi _{\alpha ,\beta }(f)$ is invertible on $L^2({{\mathrm{\mathbb {R}}}},{{\mathrm{\mathbb {C}}}})$. Then f is invertible in $(\ell ^1 ({{\mathrm{\mathbb {Z}}}}^2,{{\mathrm{\mathbb {C}}}}),\natural _{\theta },^*)$.

The representation $\pi _{\alpha ,\beta }$ of $(\ell ^1 ({{\mathrm{\mathbb {Z}}}}^2,{{\mathrm{\mathbb {C}}}}),\natural _{\theta },^*)$ induces a representation of ${{\mathrm{\mathbb {H}}}}$, $\ell ^1({{\mathrm{\mathbb {H}}}},{{\mathrm{\mathbb {C}}}})$ and $\mathcal Q _\theta$ on $L^2({{\mathrm{\mathbb {R}}}},{{\mathrm{\mathbb {C}}}})$ in a canonical way:

$$\begin{aligned} \pi _{\alpha ,\beta } (x)= \text {T}_\alpha ,\quad \pi _{\alpha ,\beta } (y)=\text {M}_\beta , \quad \text {and}\quad \pi _{\alpha ,\beta } (z)= e^{2 \pi i \theta } \,. \end{aligned}$$

The representations $\pi _{\alpha ,\beta }$ appear in the literature under various names: Stone-von Neumann, Weyl-Heisenberg or Schrödinger representations.

As an immediate corollary of Theorem 19 one obtains the following Wiener Lemma for the discrete Heisenberg group.

Theorem 20

Let $f\in {{\mathrm{\ell ^1(\mathbb {H},\mathbb {C})}}}$, then f is invertible if and only if $\pi _{\alpha ,\beta }(f)$ is invertible for each non-zero pair $\alpha ,\beta \in {{\mathrm{\mathbb {R}}}}$.

Proof

The result follows by combining Allan’s local principle with Wiener’s Lemma for twisted convolution algebras. $\square$

Finally, we give an alternative proof of Wiener’s Lemma for the twisted convolution algebra which relies on the representation theory of ${{\mathrm{\mathbb {H}}}}$ only. We start with the following lemmas.

Lemma 5

The twisted convolution algebra $(\ell ^1 ({{\mathrm{\mathbb {Z}}}}^2,{{\mathrm{\mathbb {C}}}}),\natural _{\theta },^*)$ is symmetric.

Proof

First, recall that the Banach algebras $(\ell ^1 ({{\mathrm{\mathbb {Z}}}}^2,{{\mathrm{\mathbb {C}}}}),\natural _{\theta },^*)$ and $\mathcal Q_\theta$ are $^*$-isomorphic. For every $f\in \ell ^1({{\mathrm{\mathbb {H}}}},{{\mathrm{\mathbb {C}}}})$ the following holds: if $\varPhi _\theta (f) \in \mathcal Q _\theta$ is not invertible, then f is not invertible in ${{\mathrm{\ell ^1(\mathbb {H},\mathbb {C})}}}$ by Allan’s local principle. Hence, $\sigma _{\mathcal Q _\theta }(\varPhi _\theta (f)) \subseteq \sigma _{{{\mathrm{\ell ^1(\mathbb {H},\mathbb {C})}}}}(f)$ for every $f\in \ell ^1({{\mathrm{\mathbb {H}}}},{{\mathrm{\mathbb {C}}}})$. In particular, for every $f\in {{\mathrm{\ell ^1(\mathbb {H},\mathbb {C})}}}$,

$$\begin{aligned} \sigma _{\mathcal Q _\theta }(\varPhi _\theta (f^*f)) \subseteq \sigma _{{{\mathrm{\ell ^1(\mathbb {H},\mathbb {C})}}}}(f^*f)\subseteq [0,\infty ) \end{aligned}$$

by the symmetry of ${{\mathrm{\ell ^1(\mathbb {H},\mathbb {C})}}}$. $\square$

Lemma 6

Consider an irrational $\theta \in {{\mathrm{\mathbb {T}}}}$. Then $f \in (\ell ^1 ({{\mathrm{\mathbb {Z}}}}^2,{{\mathrm{\mathbb {C}}}}),\natural _{\theta },^*)$ is invertible if and only if $\pi _{\alpha ,\beta }(f)$ has a bounded inverse, where $\alpha \beta =\theta \mod 1$.

Proof

Let $\theta$ be irrational and suppose $a \in \mathcal Q _\theta \simeq (\ell ^1 ({{\mathrm{\mathbb {Z}}}}^2,{{\mathrm{\mathbb {C}}}}),\natural _{\theta },^*)$ is not invertible. We just have to show that the non-invertibility of the element a implies that a is not invertible in the irrational rotation algebra $\mathcal R_\theta$ and, in particular, not in its realisation $\pi _{\alpha ,\beta }(C^*({{\mathrm{\mathbb {H}}}}))$ with $\alpha \beta =\theta \mod 1$. Since $\mathcal Q_\theta$ is symmetric (cf. Lemma 5), there exists an irreducible unitary representation $\pi$ of ${{\mathrm{\mathbb {H}}}}$ such that $\pi$ vanishes on $\mathtt J_\theta$ and $\pi (\varPhi _\theta (a))v =0$ for some non-zero vector $v\in \mathcal H _\pi$. This implies that a is not invertible in $\mathcal R_\theta$. $\square$

The proof of Lemma 6 basically says that for irrational $\theta$ the Banach algebra $\mathcal Q _\theta$ is inverse-closed in $\mathcal R_\theta$.

We will show that Lemma 6 holds for rational $\theta$ as well. The representation $\pi _{\alpha ,\beta }$ of ${{\mathrm{\mathbb {H}}}}$ can be decomposed in the following way (cf. [2]). Let $\nu$ be the Haar measure on $(0,\theta ]$, where $\theta \in {{\mathrm{\mathbb {T}}}}$ with $\theta = \alpha \beta \mod 1$. There exists a unitary operator

$$\begin{aligned} \text {U} : L^2({{\mathrm{\mathbb {R}}}}) \longrightarrow \int _{(0,\theta ]}^{\oplus } [\ell ^2({{\mathrm{\mathbb {Z}}}},{{\mathrm{\mathbb {C}}}})]_t \,d \nu (t) \end{aligned}$$

and a family of representations $\{ \text {Ind}^{{{\mathrm{\mathbb {H}}}}}_N (\sigma _{\theta ,s}) \,:\,s\in (0,\theta ]\}$ such that $\pi _{\alpha ,\beta }$ is unitarily equivalent via $\text {U}$ to the direct integral

$$\begin{aligned} \int _{(0,\theta ]}^{\oplus } \text {Ind}^{{{\mathrm{\mathbb {H}}}}}_N (\sigma _{\theta ,t}) \, d \nu (t)\,. \end{aligned}$$

(24)

Since unitary equivalence of two representations implies weak equivalence one gets that

$$\begin{aligned} \ker (\pi _{\alpha ,\beta })=\ker \left( \int _{(0,\theta ]}^{\oplus } \text {Ind}^{{{\mathrm{\mathbb {H}}}}}_N (\sigma _{\theta ,t}) \, d \nu (t)\right) = \bigcap _{t\in (0,\theta ]} \ker \left( \text {Ind}^{{{\mathrm{\mathbb {H}}}}}_N (\sigma _{\theta ,t}) \right) = \mathtt J _{\theta } \end{aligned}$$

and hence that $\pi _{\alpha ,\beta }(\ell ^1({{\mathrm{\mathbb {H}}}},{{\mathrm{\mathbb {C}}}}))\simeq \ell ^1({{\mathrm{\mathbb {H}}}},{{\mathrm{\mathbb {C}}}}) / \mathtt J _\theta = \mathcal Q _{\theta }$. From this observation we get the following lemma.

Lemma 7

Let $\theta \in {{\mathrm{\mathbb {T}}}}$ be rational. Then $a\in \mathcal Q _\theta$ is invertible if and only if $\pi _{\alpha ,\beta }(a)$ is invertible in $\mathcal B (L^2({{\mathrm{\mathbb {R}}}},{{\mathrm{\mathbb {C}}}}))$.

Proof

(Proof of Theorem 19) Combine Lemmas 6 and 7. $\square$

Remark 2

The decomposition (24) of $\pi _{\alpha ,\beta }$ depends only on the product $\alpha \beta =\theta \mod 1$ and is thus independent of the particular choice of $\alpha$ and $\beta$. Hence, in Theorems 19 and 20 one has to consider, e.g., $\alpha =\theta$ and $\beta =1$ only.

6.3 An application to algebraic dynamical systems

As already mentioned in the first section of this article the problem of deciding on the invertibility in $\ell ^1({{\mathrm{\mathbb {H}}}},{{\mathrm{\mathbb {C}}}})$ has an application in algebraic dynamics. The following result is important to check invertibility for $f \in {{\mathrm{\mathbb {Z}}}}[{{\mathrm{\mathbb {H}}}}]$ in the group algebra $\ell ^1({{\mathrm{\mathbb {H}}}},{{\mathrm{\mathbb {C}}}})$ because it tells us that $\pi _{\alpha ,\beta }(f)$ has a trivial kernel in $L^2({{\mathrm{\mathbb {R}}}},{{\mathrm{\mathbb {C}}}})$ for $\alpha ,\beta \not = 0$.

Theorem 21

([25]) Let G be a non-zero element in $L^2({{\mathrm{\mathbb {R}}}},{{\mathrm{\mathbb {C}}}})$, then for every finite set $A \subseteq {{\mathrm{\mathbb {Z}}}}^2$ the set $\{\text {T}_\alpha ^k\text {M}_\beta ^l G \,:\, (k,l)\in A\}$ is linear independent over ${{\mathrm{\mathbb {C}}}}$.

The following result is a reformulation of Theorem 21 and gives an exact description of the spectrum of an operator $\pi _{\alpha ,\beta }(f)$, for $\alpha ,\beta \in {{\mathrm{\mathbb {R}}}}{\backslash }\{0\}$ and $f\in {{\mathrm{\mathbb {C}}}}[{{\mathrm{\mathbb {H}}}}]$, where ${{\mathrm{\mathbb {C}}}}[{{\mathrm{\mathbb {H}}}}]$ is the ring of functions ${{\mathrm{\mathbb {H}}}}\longrightarrow {{\mathrm{\mathbb {C}}}}$ with finite support.

Theorem 22

Let $f \in {{\mathrm{\mathbb {C}}}}[{{\mathrm{\mathbb {H}}}}]$ with $f^\theta \not = 0$ for $\theta =\alpha \beta \not = 0$, $\alpha ,\beta \in {{\mathrm{\mathbb {R}}}}$, then for all $c\in \sigma (\pi _{\alpha ,\beta }(f))$ the operators $\pi _{\alpha ,\beta }(c -f)$ are injective and have dense range in $L^2({{\mathrm{\mathbb {R}}}},{{\mathrm{\mathbb {C}}}})$ but are not bounded from below.

Proof

Suppose $f\in {{\mathrm{\mathbb {C}}}}[{{\mathrm{\mathbb {H}}}}]$ is such that $\pi _{\alpha ,\beta }(f) \not = 0$ and $c\in \sigma (\pi _{\alpha ,\beta }(f))$. By Theorem 21, for every non-zero $G\in L^2({{\mathrm{\mathbb {R}}}},{{\mathrm{\mathbb {C}}}})$ the finite linear combination

$$\begin{aligned} (c - \pi _{\alpha ,\beta }(f))G = \left( c - \sum _{(k,l,m)\in {{\mathrm{\mathbb {Z}}}}^3} f_{(k,l,m)}\text {T}_{\alpha }^k \text {M}_\beta ^l e^{2 \pi i \theta m} \right) G \not = 0 \,. \end{aligned}$$

This is equivalent to the injectivity of $c - (\pi _{\alpha ,\beta }(f))$.

Suppose that the range of $c - \pi _{\alpha ,\beta }(f)$ is not dense in $L^2({{\mathrm{\mathbb {R}}}},{{\mathrm{\mathbb {C}}}})$. Then

$$\begin{aligned} (\pi _{\alpha ,\beta }(c-f))^*=\pi _{\alpha ,\beta }((c-f)^*) \end{aligned}$$

is not injective (cf. the footnote on page 19) which is a contradiction to Theorem 21 because $(c -f)^*\in {{\mathrm{\mathbb {C}}}}[{{\mathrm{\mathbb {H}}}}]$. Hence, $c - \pi _{\alpha ,\beta }(f)$ not being invertible on $L^2({{\mathrm{\mathbb {R}}}},{{\mathrm{\mathbb {C}}}})$ is equivalent to $c - \pi _{\alpha ,\beta }(f)$ not being bounded from below. $\square$

Therefore, non-expansiveness of $\alpha _f$ can be checked via two different approaches:

• The dual of ${{\mathrm{\mathbb {H}}}}$: there is an irreducible representation $\pi$ of ${{\mathrm{\mathbb {H}}}}$ such that 0 is an eigenvalue of $\pi (f)$.

• Stone-von Neumann representations: For all Stone-von Neumann representations $\pi _{\alpha ,\beta }$, 0 is an eigenvalue of $\pi _{\alpha ,\beta }(f)$ if and only if $\pi _{\alpha ,\beta }(f)=0$; and $\pi _{\alpha ,\beta }(f)$ is not invertible if and only if $\pi _{\alpha ,\beta }(f)$ is not bounded from below.

Remark 3

The authors are not aware whether the approach based on Theorem 9 and the construction of the dual of ${{\mathrm{\mathbb {H}}}}$ via ergodic quasi-invariant measures are well-known results in the field of Time-Frequency Analysis. It would be interesting to investigate whether this eigenvalue approach would simplify the problem of deciding on invertibility—at least—for some examples $f \in \ell ^1({{\mathrm{\mathbb {H}}}},{{\mathrm{\mathbb {C}}}}) {\backslash } {{\mathrm{\mathbb {C}}}}[{{\mathrm{\mathbb {H}}}}]$.

7 Examples

We now demonstrate how to apply Wiener’s Lemma to obtain easily verifiable sufficient conditions for non-expansivity of a principal algebraic action.

Let $f\in {{\mathrm{\mathbb {Z}}}}[{{\mathrm{\mathbb {H}}}}]$ be of the form

$$\begin{aligned} f=g_1(y,z)x-g_0(y,z) \end{aligned}$$

(25)

with $g_1(y,z),g_0(y,z) \in {{\mathrm{\mathbb {Z}}}}[y,z]\simeq {{\mathrm{\mathbb {Z}}}}[{{\mathrm{\mathbb {Z}}}}^2]$.

We set

$$\begin{aligned} \mathsf {U}(g_i) = \{(\zeta ,\chi )\in {{\mathrm{\mathbb {S}}}}^2\,:\, g_i(\zeta ,\chi )=0\}, \, i=0,1. \end{aligned}$$

Moreover, for a polynomial $h\in {{\mathrm{\mathbb {C}}}}[{{\mathrm{\mathbb {Z}}}}^d]$ define the logarithmic Mahler measure $\mathfrak m(h)$ by the integral

$$\begin{aligned} \mathfrak m(h) =\int _{{{\mathrm{\mathbb {T}}}}^d} \log |h(e^{2\pi i\theta _1}, \ldots , e^{2\pi i\theta _d})| \, d\theta _1\ldots d\theta _d. \end{aligned}$$

In [24] (cf. [13, Theorem 2.6] for a proof) the following result was established: for linear $f\in {{\mathrm{\mathbb {Z}}}}[{{\mathrm{\mathbb {H}}}}]$ of the form (25) with $\mathsf {U}(g_i)=\varnothing$ for $i=0,1$, the action $\alpha _f$ is expansive if and only if

$$\begin{aligned} \mathfrak m(g_0)\ne \mathfrak m(g_1)\,. \end{aligned}$$

In this section we use results on invertibility to derive criteria for non-expansiveness of principal actions of elements f in ${{\mathrm{\mathbb {Z}}}}[{{\mathrm{\mathbb {H}}}}]$ of the form $f=g_1(y,z)x-g_0(y,z)$ in cases when the unitary varieties $\mathsf {U}(g_0)$ and $\mathsf {U}(g_1)$ are not necessarily empty.

For every $\chi \in {{\mathrm{\mathbb {S}}}}$, consider the rational function $\psi _\chi$ on ${{\mathrm{\mathbb {S}}}}$:

$$\begin{aligned} \psi _\chi (\zeta )=\frac{g_0(\zeta ,\chi )}{g_1(\zeta \chi ^{-1},\chi )}\, \end{aligned}$$

and consider the map $\psi : {{\mathrm{\mathbb {N}}}}\times {{\mathrm{\mathbb {S}}}}\longrightarrow {{\mathrm{\mathbb {C}}}}$ given by

$$\begin{aligned} \psi _{\chi }(n,\zeta )= {\left\{ \begin{array}{ll} 1 &{}\quad \text{ if } n = 0 \\ \prod _{j=0}^{n-1}\psi _\chi (\zeta \chi ^{-j}) &{}\quad \text{ if } n\ge 1. \end{array}\right. } \end{aligned}$$

7.1 Either $\mathsf {U}(g_0)$ or $\mathsf {U}(g_1)$ is a non-empty set

We fix the following notation. For every $\chi \in {{\mathrm{\mathbb {S}}}}$ and $i=0,1$, put

$$\begin{aligned} \mathsf {U}_\chi (g_i)=\{\zeta \in {{\mathrm{\mathbb {S}}}}\,:\,g_i(\zeta ,\chi )=0\}\,, \end{aligned}$$

and

$$\begin{aligned} g_{i,\chi }(y) =g_i(y,\chi )\,, \end{aligned}$$

which we will view as a Laurent polynomial in y with complex coefficients, i.e., $g_{i,\chi }\in {{\mathrm{\mathbb {C}}}}[{{\mathrm{\mathbb {Z}}}}]$ for every $\chi$ and $i=0,1$. Note also that the set $\mathsf {U}_\chi (g_i)$ is infinite if and only if $g_{i,\chi }$ is the zero polynomial.

For notational convenience we put

$$\begin{aligned} \phi _\chi (\zeta )=\log |\psi _\chi (\zeta ) | \quad \text {and}\quad \phi _\chi (n,\zeta )=\log |\psi _\chi (n,\zeta ) |\,, \end{aligned}$$

for every $\zeta \in {{\mathrm{\mathbb {S}}}}$ and $n\ge 0$.

Theorem 23

Let $f\in {{\mathrm{\mathbb {Z}}}}[{{\mathrm{\mathbb {H}}}}]$ be of the form $f=g_1(y,z)x-g_0(y,z)$. Suppose there exists an element $\chi \in {{\mathrm{\mathbb {S}}}}$ of infinite order which satisfies either of the following conditions.

• (i) $\mathsf {U}_\chi (g_0)=\varnothing$, $\mathsf {U}_\chi (g_1)\not =\varnothing$ and $\int \phi _\chi d\lambda _{{{\mathrm{\mathbb {S}}}}} <0$.

• (ii) $\mathsf {U}_\chi (g_0)\not =\varnothing$, $\mathsf {U}_\chi (g_1)=\varnothing$ and $\int \phi _\chi d\lambda _{{{\mathrm{\mathbb {S}}}}} >0$.

Then $\alpha _f$ is non-expansive.

Proof

We will prove only the first case, the second case can be proved similarly.

Suppose f is such that $(X_f,\alpha _f)$ is expansive and the conditions in (i) are satisfied. We will now show that certain consequences of expansivity of $\alpha _f$ are inconsistent with the conditions in (i). Hence, by arriving to a contradiction, we will prove that under (i) $\alpha _f$ is not expansive.

We know that $(X_f,\alpha _f)$ is expansive if and only if f is invertible in ${{\mathrm{\ell ^1(\mathbb {H},\mathbb {C})}}}$. Hence $(X_f,\alpha _f)$ is expansive if and only if there exists a $w\in {{\mathrm{\ell ^1(\mathbb {H},\mathbb {C})}}}$,

$$\begin{aligned} w = \sum _{k,l,m} w_{k,l,m} y^l x^k z^m, \end{aligned}$$

such that

$$\begin{aligned} f\cdot w = w\cdot f = 1_{{{\mathrm{\ell ^1(\mathbb {H},\mathbb {C})}}}}. \end{aligned}$$

Suppose $\theta \in (0,1]$ is irrational and that $\chi =e^{2\pi i\theta }\in \mathbb S$ satisfies condition (i). Consider the following representation $\pi _{1,\theta }$ of $\ell ^1({{\mathrm{\mathbb {H}}}},{{\mathrm{\mathbb {C}}}})$ on $L^2(\mathbb R,{{\mathrm{\mathbb {C}}}})$, defined by

$$\begin{aligned} (\pi _{1,\theta }(x) F)(t)= \text {T}_1F(t) = F(t+1)&, \quad (\pi _{1,\theta }(y) F)(t) = \text {M}_\theta F(t)= e^{2\pi i\theta t} F(t),\\ \text {and}\quad&\ (\pi _{1,\theta }(z) F)(t) = e^{2\pi i\theta } F(t)\,. \end{aligned}$$

If

$$\begin{aligned} f= g_1(y,z)x-g_0(y,z) \quad \text {and} \quad w=f^{-1} = \sum _{k,l,m} w_{k,l,m} y^k x^l z^m\,, \end{aligned}$$

then

$$\begin{aligned} \pi _{1,\theta }(f) = g_1(e^{2\pi i\theta t},e^{2\pi i\theta })\text {T}_1 -g_0(e^{2\pi i\theta t},e^{2\pi i\theta }) \end{aligned}$$

and

$$\begin{aligned} \pi _{1,\theta }(w)= & {} \sum _{(k,l,m)\in {{\mathrm{\mathbb {Z}}}}^3} w_{k,l,m} \text {M}^k_\theta \text {T}_1^l {\chi }^m\\= & {} \sum _{l\in {{\mathrm{\mathbb {Z}}}}} \Bigl [ \sum _{(k,m)\in {{\mathrm{\mathbb {Z}}}}^2} w_{(k,l,m)}e^{2\pi i\theta t k} e^{2\pi i\theta m} \Bigr ] \text {T}_1^l. \end{aligned}$$

Set

$$\begin{aligned} P_{l,\theta }(t):= \sum _{(k,m)\in {{\mathrm{\mathbb {Z}}}}^2} w_{(k,l,m)}e^{2\pi i\theta t k} e^{2\pi i\theta m}\,, \end{aligned}$$

then $\pi _{1,\theta }(w)=\sum _{l\in {{\mathrm{\mathbb {Z}}}}} P_{l,\theta }(t) \text {T}_1^l$.

The functions $P_{l,\theta }(\cdot ): {{\mathrm{\mathbb {R}}}}\longrightarrow {{\mathrm{\mathbb {C}}}}$, $l\in {{\mathrm{\mathbb {Z}}}}$, are bounded and continuous. Indeed, for any $l\in {{\mathrm{\mathbb {Z}}}}$

$$\begin{aligned} P_{l,\theta }(t)=\sum _{(k,m)\in {{\mathrm{\mathbb {Z}}}}^2} w_{(k,l,m)}e^{2\pi i\theta t k} e^{2\pi i\theta m} \end{aligned}$$

is a Fourier series with absolutely convergent coefficients:

$$\begin{aligned} \sum _{k\in {{\mathrm{\mathbb {Z}}}}} \Bigl |\sum _{m\in {{\mathrm{\mathbb {Z}}}}} w_{(k,l,m)} e^{2\pi i\theta m}\Bigr |&\le \sum _{k\in {{\mathrm{\mathbb {Z}}}}} \sum _{m\in {{\mathrm{\mathbb {Z}}}}} | w_{(k,l,m)} | \\ {}&\le \Vert w\Vert _{\ell ^1({{\mathrm{\mathbb {H}}}},{{\mathrm{\mathbb {C}}}})}<\infty \,. \end{aligned}$$

For similar reasons,

$$\begin{aligned} \sum _{l\in {{\mathrm{\mathbb {Z}}}}} \sup _{t\in {{\mathrm{\mathbb {R}}}}}| P_{l,\theta }(t)|&\le \sum _{l\in {{\mathrm{\mathbb {Z}}}}} \Bigl [ \sum _{k,m} |w_{k,l,m}|\Bigr ]\end{aligned}$$

(26)

$$\begin{aligned}&=\Vert w\Vert _{\ell ^1({{\mathrm{\mathbb {H}}}},{{\mathrm{\mathbb {C}}}})} <\infty \,. \end{aligned}$$

(27)

Since $w\cdot f = 1_{{{\mathrm{\ell ^1(\mathbb {H},\mathbb {C})}}}}$ and $\pi _{1,\theta }(1_{{{\mathrm{\ell ^1(\mathbb {H},\mathbb {C})}}}}) = 1_{\mathcal B (L^2({{\mathrm{\mathbb {R}}}},{{\mathrm{\mathbb {C}}}}))}$ – the identity operator on $L^2({{\mathrm{\mathbb {R}}}},{{\mathrm{\mathbb {C}}}})$, one has

$$\begin{aligned} 1_{\mathcal B (L^2({{\mathrm{\mathbb {R}}}},{{\mathrm{\mathbb {C}}}}))}= & {} \pi _{1,\theta }(w)\pi _{1,\theta }(f)\\= & {} \Bigl [ \sum _{l\in {{\mathrm{\mathbb {Z}}}}} P_{l,\theta }(t) \text {T}_1^l\Bigr ] \cdot \Bigl [ g_1(e^{2\pi i \theta t},e^{2\pi i \theta })\text {T}_1 - g_0(e^{2\pi i \theta t},e^{2\pi i \theta })\Bigr ] \\= & {} \Bigl [ \sum _{l\in {{\mathrm{\mathbb {Z}}}}} P_{l,\theta }(t) \text {T}_1^l\Bigr ] \cdot \Bigl [ g_{1,\chi }(e^{2\pi i \theta t})\text {T}_1 - g_{0,\chi }(e^{2\pi i \theta t})\Bigr ] \\= & {} \sum _{l\in {{\mathrm{\mathbb {Z}}}}} \Bigl [ P_{l-1,\theta }(t) g_{1,\chi }(e^{2\pi i\theta (t+l-1)})- P_{l,\theta }(t) g_{0,\chi }(e^{2\pi i\theta (t+l)}) \Bigr ] \text {T}_1^l . \end{aligned}$$

Set

$$\begin{aligned} Q_{l,\theta }(t)=P_{l-1,\theta }(t) g_{1,\chi }(e^{2\pi i\theta (t+l-1)})- P_{l,\theta }(t) g_{0,\chi }(e^{2\pi i\theta (t+l)})\,. \end{aligned}$$

(28)

Since $\{Q_{l,\theta }(\cdot )|\, l\in {{\mathrm{\mathbb {Z}}}}\}$ are again bounded continuous functions, one concludes that

$$\begin{aligned} Q_{0,\theta }(t)\equiv 1 \quad \text {and}\quad Q_{l,\theta }(t)\equiv 0,\quad \text {for every}\,\ l\ne 0. \end{aligned}$$

Hence, for every $t\in \mathbb R$, one has

$$\begin{aligned} Q_{0,\theta }(t)= P_{-1,\theta }(t) g_{1,\chi }(e^{2\pi i\theta (t-1)})- P_{0,\theta }(t) g_{0,\chi }(e^{2\pi i\theta t}) =1\,, \end{aligned}$$

(29)

and for every $l\ge 1$

$$\begin{aligned} Q_{l,\theta }(t) = P_{l-1,\theta }(t) g_{1,\chi }(e^{2\pi i\theta (t+l-1)})- P_{l,\theta }(t) g_{0,\chi }(e^{2\pi i\theta (t+l)})=0\,. \end{aligned}$$

(30)

Since $\mathsf {U}_\chi (g_0)=\varnothing$, Eq. (30) imply that

$$\begin{aligned} P_{l,\theta }(t)=P_{l-1,\theta }(t)\cdot \frac{g_{1,\chi }(e^{2\pi i\theta (t+l-1)})}{g_{0,\chi }(e^{2\pi i\theta (t+l)})} \end{aligned}$$

for every t, and hence for each $l\ge 1$ and every $t\in {{\mathrm{\mathbb {R}}}}$, one has

$$\begin{aligned} P_{l,\theta }(t) = P_{0,\theta }(t) \cdot \frac{g_{1,\chi }(e^{2\pi i\theta t})}{g_{0,\chi }(e^{2\pi i\theta (t+1)})}\ldots \frac{g_{1,\chi }(e^{2\pi i\theta (t+l-1)})}{g_{0,\chi }(e^{2\pi i\theta (t+l)})}\,, \end{aligned}$$

or

$$\begin{aligned} P_{l,\theta }(t) = P_{0,\theta }(t) \frac{1}{\psi _{\chi ^{-1}}(l,\zeta _t \chi )}\, \end{aligned}$$

where $\zeta _t = e^{2\pi i\theta t}$.

Then since $\mathsf {U}_\chi (g_0)=\varnothing$, the logarithmic Mahler measure $\mathfrak m(g_{0,\chi })$ is finite, and hence $\mathfrak m(g_{1,\chi })>-\infty$. Therefore, $g_{1,\chi }(\eta )$ is not identically 0 on $\mathbb S^1$, and since $g_{1,\chi }$ is a polynomial, we can conclude that $\mathsf {U}_\chi (g_1)$ is finite. Therefore, the set of points

$$\begin{aligned} B_1=\Bigl \{ \zeta \in \mathbb S^1: \zeta e^{2\pi i \theta k}\in \mathsf {U}_\chi (g_1)\quad \text {for some }k\in {{\mathrm{\mathbb {Z}}}}\Bigr \} =\bigcup _{k\in {{\mathrm{\mathbb {Z}}}}} \text {R}_\theta ^k( \mathsf {U}_\chi (g_1)) \end{aligned}$$

is at most countable, and hence has Lebesgue measure 0.

Both functions $\log |g_{0,\chi }(\cdot )|$ and $\log |g_{1,\chi }(\cdot )|$ are integrable. Moreover, the irrational rotation $\text {R}_\theta : {{\mathrm{\mathbb {T}}}}\longrightarrow {{\mathrm{\mathbb {T}}}}$ is an ergodic transformation. By Birkhoff’s ergodic theorem there exists a set $B_2\subset \mathbb S^1$ of full Lebesgue measure such that for any $\zeta \in B_2$

$$\begin{aligned} \frac{1}{n} \sum _{k=1}^{n} \log&|g_{0,\chi }(\zeta e^{2\pi i\theta k})|\rightarrow \mathfrak m( g_{0,\chi })\,,\\ \frac{1}{n} \sum _{k=0}^{n-1} \log&|g_{1,\chi }(\zeta e^{2\pi i\theta k})|\rightarrow \mathfrak m( g_{1,\chi })\,. \end{aligned}$$

Therefore, since $\mathfrak m( g_{1,\chi })>\mathfrak m( g_{0,\chi })$, on the set of full measure $B_1^c\cap B_2$

$$\begin{aligned} \varPsi _n(\zeta ) = \frac{1}{\psi _{\chi ^{-1}}(n,\zeta \chi )} \ne 0 \quad \forall n\ge 1, \end{aligned}$$

(31)

and

$$\begin{aligned} \lim _{n\rightarrow \infty } \varPsi _n(\zeta )= +\infty . \end{aligned}$$

(32)

Since $\theta \ne 0$, the set of points

$$\begin{aligned} C=\Bigl \{t\in \mathbb R\,:\, e^{2\pi i t\theta } \not \in B_1^c\cap B_2\Bigr \} \end{aligned}$$

has full measure, and for every $t\in C$, one has that the sum

$$\begin{aligned} \sum _{l\ge 0} |P_{l,\theta }(t)| =|P_{0,\theta }(t)| +|P_{0,\theta }(t)|\varPsi _1(e^{2\pi i t\theta })+ \cdots + |P_{0,\theta }(t)|\varPsi _l(e^{2\pi i t\theta })+\cdots \nonumber \\ \end{aligned}$$

(33)

is finite if and only if $|P_{0,\theta }(t)|=0$. Combining this fact with the uniform bound (26), (27), we are able to conclude that

$$\begin{aligned} P_{0,\theta }(t) =0 \end{aligned}$$

(34)

on a set of full measure in ${{\mathrm{\mathbb {R}}}}$. The function $P_{0,\theta }(t)$ is continuous and therefore, $P_{0,\theta }$ must be the identically zero function on ${{\mathrm{\mathbb {R}}}}$.

Finally, consider the remaining Eq. (29) for $Q_{0,\theta }(t)$. Since $P_{0,\theta }(t)\equiv 0$, one has that there exists a continuous bounded function $P_{-1,\theta }$ such that

$$\begin{aligned} P_{-1,\theta }(t) g_{1,\chi }(e^{2\pi i\theta (t-1)}) = 1 \,, \end{aligned}$$

(35)

for every $t\in {{\mathrm{\mathbb {R}}}}$. However, since the unitary variety $\mathsf {U}_{\chi }(g_1)$ is not empty, one can find $t\in {{\mathrm{\mathbb {R}}}}$ such that

$$\begin{aligned} g_{1,\chi }(e^{2\pi i\theta (t-1)})=0, \end{aligned}$$

and hence, (35) cannot be satisfied. Therefore, we arrived to a contradiction with the earlier assumption that $\alpha _f$ is expansive. $\square$

The assumption that $\int \phi _\chi d\lambda _{{{\mathrm{\mathbb {S}}}}} < 0$ cannot be dropped in (i) of Theorem 23 as the following simple minded example shows.

Example 6

Suppose $\chi$ is not a root of unity and $\mathsf {U}_\chi (g_1)\not =\varnothing$. Set $g_0(y,z)\equiv K$, where we pick $K \in {{\mathrm{\mathbb {N}}}}$ such that

• 1. $K> \Vert g_1(y,z)\Vert _{\ell ^1({{\mathrm{\mathbb {H}}}},{{\mathrm{\mathbb {C}}}})}$;

• 2. $\int \phi _\chi d\lambda _{{{\mathrm{\mathbb {S}}}}} > 0$.

Then $f=g_1(y,z)x-K$ is invertible since

$$\begin{aligned} f= K \left( \frac{g_1(y,z)x}{K} - 1 \right) \quad \text {and}\quad \left\| \frac{g_1(y,z)x}{K}\right\| _{\ell ^1({{\mathrm{\mathbb {H}}}},{{\mathrm{\mathbb {C}}}})} < 1. \end{aligned}$$

7.2 The sets $\mathsf {U}(g_0)$ and $\mathsf {U}(g_1)$ are both non-empty

Let us denote by

$$\begin{aligned} \text {Orb}_{\chi }(\zeta ) =\{\zeta \chi ^{n} \,:\, n\in {{\mathrm{\mathbb {Z}}}}\} \end{aligned}$$

the orbit of $\zeta$ under the circle rotation $\text {R}_\chi : {{\mathrm{\mathbb {S}}}}\longrightarrow {{\mathrm{\mathbb {S}}}}$ with $\zeta \mapsto \zeta \chi$, for every $\zeta \in {{\mathrm{\mathbb {S}}}}$. We consider first linear elements $f=g_1(y,z) x-g_0(y,z)$ for which

• 1. $\mathsf {U}(g_0) \not = \varnothing$ and $\mathsf {U}(g_1) \not = \varnothing$;

• 2. and there exists an element $(\zeta ,\chi ) \in \mathsf {U}(g_0)$ with

  $$\begin{aligned} \{ (\eta ,\chi )\in {{\mathrm{\mathbb {S}}}}^2\,:\, \eta \in \text {Orb}_{\chi }(\zeta )\} \cap \mathsf {U}(g_1) \not = \varnothing . \end{aligned}$$

Theorem 24

If f is of the form (25) and for some $m\in {{\mathrm{\mathbb {Z}}}}$

$$\begin{aligned} \mathsf {U}(g_1) \cap \left\{ ( \xi \chi ^m ,\chi )\in {{\mathrm{\mathbb {S}}}}^2\,:\, (\xi ,\chi )\in \mathsf {U}(g_0)\right\} \not = \varnothing , \end{aligned}$$

then $\alpha _f$ is non-expansive.

Although this result could be proved with the help of Stone-von Neumann representations as well, it is more suitable to use monomial representations. For the following discussion it is convenient to work with slightly modified versions of the monomial representations defined in (21). For every $\zeta ,\chi \in {{\mathrm{\mathbb {S}}}}$ let $\pi ^{(\zeta ,\chi )}$ be the representation of ${{\mathrm{\mathbb {H}}}}$ acting on $\ell ^2({{\mathrm{\mathbb {Z}}}},{{\mathrm{\mathbb {C}}}})$ which fulfils

$$\begin{aligned} (\pi ^{(\zeta ,\chi )}(x)F)(n)&=F(n+1), \quad (\pi ^{(\zeta ,\chi )}(y)F)(n)=\zeta \chi ^n F(n) \quad \text {and} \end{aligned}$$

(36)

$$\begin{aligned} (\pi ^{(\zeta ,\chi )}(z)F)(n)&=\chi F(n) \end{aligned}$$

(37)

for each $F\in \ell ^2({{\mathrm{\mathbb {Z}}}},{{\mathrm{\mathbb {C}}}})$ and $n\in {{\mathrm{\mathbb {Z}}}}$.

Proof

Consider the case $m \ge 0$ first. Suppose f is invertible and hence $\pi (f)$ is invertible for every unitary representations of ${{\mathrm{\mathbb {H}}}}$ and in particular, $\pi ^{(\zeta ,\chi )}(f)$ is invertible for every pair $(\zeta ,\chi ) \in {{\mathrm{\mathbb {S}}}}^2$. By the assumptions of the theorem there exists a pair $(\xi ,\chi ) \in {{\mathrm{\mathbb {S}}}}^2$ such that

$$\begin{aligned} g_1( \xi \chi ^m,\chi )=0 \quad \text {and}\quad g_0(\xi ,\chi )=0\,. \end{aligned}$$

(38)

Without loss of generality we may assume that m is the minimal power such that (38) is satisfied, i.e., $g_1( \xi \chi ^l,\chi )\not =0$ for each $l\in {{\mathrm{\mathbb {Z}}}}$ with $0\le l\le m-1$.

Suppose $G\in \ell ^2({{\mathrm{\mathbb {Z}}}},{{\mathrm{\mathbb {C}}}})$ is in the image of $\pi ^{(\xi ,\chi )}(f)$, then there exists an $F\in \ell ^2({{\mathrm{\mathbb {Z}}}},{{\mathrm{\mathbb {C}}}})$ such that

$$\begin{aligned} G(n)=g_1(\xi \chi ^n,\chi )F(n+1)-g_0(\xi \chi ^n,\chi )F(n) \end{aligned}$$

(39)

holds for every $n\in {{\mathrm{\mathbb {Z}}}}$. Given the choice of $(\xi ,\chi )$ [cf. (38)], one immediately concludes that

$$\begin{aligned} G(0)=g_1(\xi ,\chi )F(1). \end{aligned}$$

If $m=0$, then $G(0)=0$, and we arrive to a contradiction with the assumption that $\pi ^{(\xi ,\chi )}(f)$ is invertible, and hence has a dense range in $\ell ^2({{\mathrm{\mathbb {Z}}}},{{\mathrm{\mathbb {C}}}})$: Indeed, for every $F\in \ell ^2({{\mathrm{\mathbb {Z}}}},{{\mathrm{\mathbb {C}}}})$ one has that

$$\begin{aligned} (\pi ^{(\xi ,\chi )}(f)F)(0)=0\, \end{aligned}$$

and hence, the range of $\pi ^{(\xi ,\chi )}(f)$ is not dense.

If $m >0$, then F must satisfy the following system of linear equations

$$\begin{aligned} G(0)&=g_1(\xi ,\chi )F(1) \end{aligned}$$

(40)

$$\begin{aligned} G(l)&=g_1(\xi \chi ^l,\chi )F(l+1)-g_0(\xi \chi ^l,\chi )F(l), \quad 1 \le l \le m-1 \end{aligned}$$

(41)

$$\begin{aligned} G(m)&=-g_0(\xi \chi ^m,\chi )F(m)\,. \end{aligned}$$

(42)

We can eliminate $F(1),F(2),\ldots ,F(m)$ in (40)–(42) to obtain an expression for G(m) in terms of $G(0),G(1),\ldots ,G(m-1)$. Indeed, one can easily verify that, for each $0\le l \le m-1$, $F(l+1)$ can be written as

$$\begin{aligned} F(l+1)&=\frac{G(l)}{g_1(\xi \chi ^l,\chi )}+ \frac{ g_0(\xi \chi ^l,\chi )}{g_1(\xi \chi ^l,\chi )}F(l)=\cdots \end{aligned}$$

(43)

$$\begin{aligned}&= \sum _{i=0}^l\frac{G(l-i)}{g_1(\xi \chi ^{l},\chi )}\prod _{n=0}^{i-1}\frac{g_0(\xi \chi ^{l-n},\chi )}{g_1(\xi \chi ^{l-n-1},\chi )} \end{aligned}$$

(44)

$$\begin{aligned}&=\sum _{i=0}^l\frac{G(l-i)}{g_1(\xi \chi ^{l},\chi )} \psi _\chi (i,\xi \chi ^l) \end{aligned}$$

(45)

(we use the convention that the empty product $\prod _{\varnothing }$ is equal to 1). Due to our choice of m, $F(l+1)$ in (43) is well-defined. Moreover, since $G(m)=g_0(\xi \chi ^m,\chi )F(m)$, one gets

$$\begin{aligned} G(m)&=-g_0(\xi \chi ^{m},\chi ) F(m)\\&= -\sum _{i=0}^{m-1}G(m-1-i) \psi _\chi (i+1,\xi \chi ^{m-1})\,. \end{aligned}$$

Hence, G(m) depends continuously on the values $G(0),G(1),\ldots ,G(m-1)$. Again, this is a contradiction with our hypothesis that $\pi ^{(\xi ,\chi )}(f)$ has dense range in $\ell ^2({{\mathrm{\mathbb {Z}}}},{{\mathrm{\mathbb {C}}}})$.

If $m<0$, then we choose $\pi$ such that

$$\begin{aligned} (\pi (x)F)(n)=F(n-1) \quad \text {and} \quad (\pi (y)F)(n)=\xi \chi ^{-n} F(n) \end{aligned}$$

for each $F\in \ell ^2({{\mathrm{\mathbb {Z}}}},{{\mathrm{\mathbb {C}}}})$ and $n\in {{\mathrm{\mathbb {Z}}}}$. Exactly the same arguments as in the case $m \ge 0$ can be used to get a contradiction to the invertibility of $\pi (f)$. $\square$

Corollary 2

Let f be of the form (25) which satisfies the conditions of Theorem 24. Then $\alpha _{f^\diamond }$ defined by $f^\diamond =g_0(y,z)x-g_1(y,z)$ is non-expansive.

Proof

Since

$$\begin{aligned} \mathsf {U}(g_1) \cap \left\{ ( \xi \chi ^m ,\chi )\in {{\mathrm{\mathbb {S}}}}^2\,:\, (\xi ,\chi )\in \mathsf {U}(g_0)\right\} \not = \varnothing \,, \end{aligned}$$

there exists a $k\in {{\mathrm{\mathbb {Z}}}}$ such that

$$\begin{aligned} \mathsf {U}(g_0) \cap \left\{ ( \xi \chi ^k ,\chi )\in {{\mathrm{\mathbb {S}}}}^2\,:\, (\xi ,\chi )\in \mathsf {U}(g_1)\right\} \end{aligned}$$

is non-empty as well. Hence, Theorem 24 guarantees the non-expansiveness of $\alpha _{f^\diamond }$. $\square$

Example 7

Consider

$$\begin{aligned} g_1(y,z)=1-y-y^{-1}-z-z^{-1} \quad \text {and} \quad g_0(y,z)=3-y-y^{-1}-z-z^{-1}\,. \end{aligned}$$

We will show that the dynamical systems $(X_f,\alpha _f)$ and $(X_{f^\diamond },\alpha _{f^\diamond })$, with $f=g_1(y,z)x -g_0(y,z)$ and $f^\diamond =g_0(y,z)x -g_1(y,z)$, are non-expansive.

For this purpose we introduce, for $m\in {{\mathrm{\mathbb {Z}}}}$, the ‘m-sheared version’ of $g_0(y,z)$ given by

$$\begin{aligned} g_0^{(m)}(y,z)=g_0(yz^m,z)= 3- y z^m-y^{-1} z^{-m}- z-z^{-1}\,; \end{aligned}$$

and note that

$$\begin{aligned} \mathsf {U}(g_1) \cap \left\{ ( \xi \chi ^m ,\chi )\in {{\mathrm{\mathbb {S}}}}^2\,:\, (\xi ,\chi )\in \mathsf {U}(g_0)\right\} \not = \varnothing \iff \mathsf {U}(g_1) \cap \mathsf {U}(g_0^{(m)})\not = \varnothing \,. \end{aligned}$$

The Fourier transforms of $g_1(y,z)$ and $g^{(m)}_0(y,z)$ are given by the functions

$$\begin{aligned} (\mathcal F g_1)(s,t)&= 1-2 \cos (2 \pi s) - 2 \cos (2 \pi t) \quad \text {and}\\ \left( \mathcal F g_0^{(m)} \right) (s,t)&= 3- 2 \cos (2 \pi (s+mt))-2 \cos (2 \pi t), \end{aligned}$$

respectively.

Fig. 1

In this figure the curves corresponding to the solution sets K (thick line) and K[2] (thin line) are plotted

Let

$$\begin{aligned} K&= \left\{ (s,t)\in {{\mathrm{\mathbb {T}}}}^2 \,:\, (\mathcal F g_1)(s,t)=0\right\} \quad \text {and}\\ K[m]&=\left\{ (s,t)\in {{\mathrm{\mathbb {T}}}}^2 \,:\, \left( \mathcal F g_0^{(m)} \right) (s,t)=0\right\} \,. \end{aligned}$$

Fix $m\in {{\mathrm{\mathbb {Z}}}}$. By solving the equations

$$\begin{aligned} (\mathcal F g_1)(s,t)=0 \quad \text {and} \quad \left( \mathcal F g_0^{(m)} \right) (s',t')=0 \end{aligned}$$

for s and $s'$ we get curves s(t) and $s'(t')$ corresponding to the solution sets K and K[m]. If these curves intersect, then K and K[m] have a non-empty intersection. It is clear that $(s,t) \in K$ if and only if $(e^{2 \pi i s},e^{2 \pi i t})\in \mathsf {U}(g_1)$. For every $m\in {{\mathrm{\mathbb {Z}}}}$ the sets K[m] and $\mathsf {U}(g_0^{(m)})$ are related in the same way. The sets K and K[2] have a non-empty intersection as Fig. 1 shows; while $K \cap K[0] = \varnothing$ and $K \cap K[1] = \varnothing$.

Since the conditions of Theorem 24 and Corollary 2 are satisfied, f and $f^\diamond$ are not invertible.

The next result can be easily deduced from the proof of Theorem 23.

Theorem 25

Let $f\in {{\mathrm{\mathbb {Z}}}}[{{\mathrm{\mathbb {H}}}}]$ be of the form (25). Suppose there exists an element $\chi \in {{\mathrm{\mathbb {S}}}}$ of infinite order such that the following conditions are satisfied

$$\begin{aligned} \mathsf {U}_\chi (g_0)\not =\varnothing \quad \text {and} \quad \mathsf {U}_\chi (g_1)\not =\varnothing \,, \end{aligned}$$

(46)

and

$$\begin{aligned} \mathfrak {m} (g_{0,\chi }) \not = \mathfrak {m} (g_{1,\chi })\,. \end{aligned}$$

Then $\alpha _f$ is non-expansive.

Proof

Suppose (46) holds. Let us first treat the trivial cases.

If $g_{0,\chi }(y)$ is the zero-element in ${{\mathrm{\mathbb {C}}}}[{{\mathrm{\mathbb {Z}}}}]$, then for every $\zeta \in {{\mathrm{\mathbb {S}}}}$

$$\begin{aligned} \pi ^{(\zeta ,\chi )}(f)= \pi ^{(\zeta ,\chi )}(g_1(y,z)x). \end{aligned}$$

Fix $\xi \in \mathsf {U}_\chi (g_1)$, which is a non-empty set by the assumptions of the theorem. Since one has $(\pi ^{(\xi ,\chi )}(f)F)(0)$ is equal to 0 for every $F\in \ell ^2({{\mathrm{\mathbb {Z}}}},{{\mathrm{\mathbb {C}}}})$, 0 is an element of $\sigma (\pi ^{(\xi ,\chi )}(f))$ and hence f is not invertible. The same conclusions can be drawn for the cases $g_{1,\chi }= 0_{{{\mathrm{\mathbb {C}}}}[{{\mathrm{\mathbb {Z}}}}]}$ and $g_{0,\chi }= g_{1,\chi }= 0_{{{\mathrm{\mathbb {C}}}}[{{\mathrm{\mathbb {Z}}}}]}$.

Next consider the case where $g_{0,\chi }$ and $g_{1,\chi }$ are not the zero elements in ${{\mathrm{\mathbb {C}}}}[{{\mathrm{\mathbb {Z}}}}]$, which implies that $\mathfrak {m} (g_{0,\chi })$ and $\mathfrak {m} (g_{1,\chi })$ are finite and moreover $\mathsf {U}_\chi (g_0)$ and $\mathsf {U}_\chi (g_1)$ are finite sets. Suppose that $\mathfrak {m} (g_{0,\chi })< \mathfrak {m} (g_{1,\chi })$. We follow the line of arguments in the proof of Theorem 23. The only adaption one has to make is to take the countable set

$$\begin{aligned} B=\Bigl \{ t\in {{\mathrm{\mathbb {R}}}}\,:\, e^{2 \pi i t} \chi ^{k}\in \mathsf {U}_\chi (g_0)\,\,\text {for some }k\in {{\mathrm{\mathbb {Z}}}}\Bigr \} \end{aligned}$$

into consideration, i.e., to exclude points in $\mathcal B$ in the Eqs. (31)–(34).

The case $\mathfrak {m} (g_{0,\chi }) > \mathfrak {m} (g_{1,\chi })$ can be proved analogously. $\square$