Creep Versus Consolidation in Tunnelling through Squeezing Ground—Part B: Transferability of Experience

Abstract

This paper investigates potential differences between creep and consolidation in mechanised tunnelling through squeezing ground, placing focus on the practical question of using experiences gained from existing tunnels about the required thrust force as a reference for tunnels of different diameter or adjacent tunnels. The investigations focus on two aspects. First, the effect of the tunnel diameter on the risk of shield jamming is examined. The paper demonstrates that larger-diameter tunnels are more favourable in poor-quality ground, while the opposite holds in better-quality ground, as well as in the case of pronouncedly time-dependent ground behaviour due to consolidation or creep. Second, the effect of a tunnel on the required thrust force in a neighbouring tunnel built later is examined. The paper shows that this interaction effect is particularly important in water-bearing ground of low permeability, where the drainage action of the first tunnel induces pore pressure relief and ground consolidation in an extensive area, leading to a remarkable reduction of the thrust force in the second tunnel. Conversely, in the case of creep the interaction is negligible even under extremely squeezing conditions, due to the fundamentally different nature of the purely mechanical rheological processes from coupled hydromechanical processes. The presented investigations into the transferability of experiences are valuable for tunnelling practice, in cases of twin tunnels as well as in situations where a smaller-diameter tunnel is constructed prior to the main tunnel (e.g. a pilot tunnel for exploration, advance drainage or ground improvement), or also the opposite (e.g. upgrade of a road tunnel by later construction of a safety tunnel with a smaller diameter).

Highlights

• The rate of ground deformations is independent of diameter in the case of creep, but extremely increases with decreasing diameter in the case of consolidation.

• The risk of shield jamming is lower in larger-diameter tunnels crossing poor-quality ground without pronounced time-dependent behaviour.

• The risk of shield jamming is lower in smaller-diameter tunnels crossing ground of higher quality or exhibiting pronounced time-dependent behaviour.

• The effect of adjacent tunnel on shield jamming risk is generally minor in the case of creep, even for extreme squeezing conditions and large overcuts.

• The effect of adjacent tunnel on shield jamming risk is remarkable in the case of consolidation, leading to a substantial reduction of the thrust force.

1 Introduction

In the companion paper (Leone et al. 2024), the authors examined fundamental similarities and differences between creep and consolidation in mechanised tunnelling through squeezing ground, placing focus on the evolution of rock deformations and stresses, as well as—associated with the latter—the required thrust force and the risk of shield jamming. In this paper, the comparison between creep and consolidation is extended by investigating whether experiences gained from previously constructed tunnels about the required thrust force can be transferred to tunnels of different diameter or to adjacent tunnels of the same diameter built under the same geotechnical conditions (rock properties, pore pressure, overburden, etc.). The investigations into experience transferability are valuable in practical situations where a smaller-diameter pilot tunnel is constructed prior to the main tunnel for exploration, advance drainage or ground improvement, or also the opposite (e.g. upgrading of a road tunnel by later construction of a safety tunnel with a smaller diameter), as well as in cases of sequentially excavated twin tunnels.

Within this backdrop, the paper addresses two key aspects: (i), the effect of the tunnel diameter on the risk of shield jamming (“scale effect”) and, (ii), the effect of a tunnel on the required thrust force in an adjacent, later excavated tunnel (“interaction”). There is a significant volume of literature on creep and consolidation in tunnelling in general, as well as specifically on the problem of shield jamming in mechanised tunnelling through squeezing ground (see Leone et al. 2023, 2024 for recent reviews); however, the aforementioned interaction effect has not been studied so far, while the scale effect has only been investigated by Ramoni and Anagnostou (2011) for the case of consolidation. Therefore, there is sufficient scope for a systematic investigation of both aspects in the present work.

1.1 Scale Effect

Besides the practical question of experience transferability, the investigation into the scale effect is also motivated by a theoretical consideration—the well-known finding of consolidation theory that consolidation time increases with the second power of the drainage path length, e.g. the thickness of a low-permeability layer. Based on this, squeezing would develop slower in a larger-diameter tunnel, as the drainage paths around it are longer in relation to a tunnel of smaller diameter. In turn, this should also affect the rock pressure acting on the advancing shield and thus the force required to overcome shield skin friction and the risk of shield jamming. As this scale effect is related to the specific process of transient seepage flow and excess pore pressure dissipation, it is expected that there may be significant differences in scale effects between consolidation and creep—the other principal mechanism of the time dependency of squeezing.

Although the aforementioned theoretical considerations are valid concerning the rate of development of squeezing deformations, the effect of the tunnel diameter on the risk of shield jamming is much more complex to assess, due to three reasons. First, depending on the tunnel diameter, there are different technical limitations for certain parameters of the tunnel boring machine (TBM), including the overcut, shield length, shield and lining stiffnesses and maximum installable thrust force, which also have mutually competing effects on the rock pressure that develops on the shield. Second, the tunnel diameter also poses limitations on certain operational parameters, specifically the TBM advance rate and the duration of construction standstills, which must also be considered in cases of time-dependent ground behaviour due to creep or consolidation. Third, a larger cross section is associated with a higher potential of encountering adverse conditions (e.g. weak zones, water inflows, etc.; Kovári 1979; Schneider 2002); however, as squeezing ground is often weak even at the small scale of a specimen, the differences in the ground properties between different diameter tunnels is of secondary importance in relation to the above.

Considering all limitations discussed above, Ramoni and Anagnostou’s investigations (2011) showed that a smaller diameter is consistently less prone to shield jamming than a larger one in the case of consolidation; however, the differences between them decrease in weaker ground. Based on these findings, two questions arise: Is the scale effect the same in the case of creep? Is it possible that a larger diameter is more favourable than a smaller one in weaker ground? These questions are addressed in Sect. 2, which examines the effect of the tunnel diameter both on the rock deformations and on the risk of shield jamming during advance or after a standstill of the TBM, based on exemplary, transient numerical simulations that incorporate the limitations discussed above. The specifications of the employed numerical models and all relevant computational assumptions are discussed in detail in the companion paper (see Sect. 2 of Leone et al. 2024).

1.2 Interaction

Tunnelling through heavily squeezing ground can cause stress redistribution and deformations in an extended area, in turn affecting other existing or planned underground structures. In the case of a twin tunnel, the excavation of the first tube may affect the stress field at the location of the second tube and thus the construction and support of the latter significantly; and vice versa, the construction of the second tube may have a relevant effect on the lining of the first tube. Besides the spacing between the tunnels, the interaction effects may be more or less pronounced depending on the construction method. They are expected to be more pronounced in the case of conventional tunnelling with a yielding support, and less pronounced in the case of a construction method that limits ground deformations by foreseeing a stiff support close to the tunnel face (resistance principle). Shield tunnelling is closer to the second case, as the available space is very limited due to the construction equipment, with ground deformations therefore being small in general.

A special situation arises in the case of saturated, water-bearing ground, where the drainage action of a tunnel results in pore pressure relief over a very extended area (Arn 1989). In the case of a twin tunnel, pore pressure relief due to the first tube has a favourable influence on the subsequently excavated second tube, which is analogous to that of advance drainage (Anagnostou and Zingg 2013): it results in higher effective stresses, hence in a higher undrained shear strength of the ground, and thus in lower short-term deformations during excavation. This experience has often been reported in tunnelling practice. Prominent examples are the Simplon railway tunnel and the Gotthard motorway tunnel in Switzerland (Lombardi 1976; Steiner 1996; Anagnostou 2009); in the latter case, noteworthy is the influence of consolidation up to ca. ten diameters around the first tube, which was also much smaller than the second tube.

On the one hand, due to the aforementioned large-scale pore pressure relief and consolidation in the case of low-permeability water-bearing ground and, on the other hand, due to the limited excavation-induced stress redistribution in the case of shield tunnelling through creeping but not water-bearing ground, it is expected that time-dependent interaction effects will be more pronounced in the case of consolidation than in the case of creep. Section 3 numerically investigates this hypothesis considering the problem of shield jamming in a twin tunnel with variable spacing between its two tubes. It shows that the required thrust force in the second tube is significantly lower than in the first tube in the case of consolidation, even for large spacings of the two tunnels, whereas in the case of creep the first tube has a negligible effect on the construction of the second tube. The methods adopted in the numerical simulations are discussed in the same section and are based on the model specifications and computational assumptions described in detail in the companion paper (see Sect. 2 of Leone et al. 2024).

Other potentially important interactions, such as the effect of the first tube on the lining of the second tube and vice versa, are beyond the scope of this paper, which focuses solely on differences/similarities between creep and consolidation with respect to TBM–ground interaction.

2 Scale Effect

To obtain a basic insight into the effect of the tunnel diameter, our investigations start with a simple plane-strain problem—the time-development of tunnel convergences in a cross section far behind the face (Sect. 2.1). Subsequently, they continue with the core subject of this paper, the scale effect with respect to the risk of shield jamming (Sect. 2.2).

2.1 Time-Dependent Contraction of a Deep Tunnel

2.1.1 Homogeneous Ground

Analogously to the companion paper (see Sect. 3 in Leone et al. 2024), the problem is analysed based on the classic, rotationally symmetric, plane-strain model of a cylindrical and uniformly supported tunnel located deep below the ground surface and the water table. The radial displacement of the tunnel boundary u_R can then be expressed as a function of the significant problem parameters as

$$\frac{u_R }{R} = f\left( {\frac{E}{\sigma_0 },\;\nu ,\;\frac{f_c }{{\sigma_0 }},\;\phi ,\;\psi ,\;\frac{tE}{\eta }} \right)$$

(1)

in the case of creep, and as

$$\frac{u_R }{R} = f\left( {\frac{E}{\sigma_0 },\;\nu ,\;\frac{f_c }{{\sigma_0 }},\;\phi ,\;\psi ,\;\frac{p_0 }{{\sigma_0 }},\;\frac{R_p }{R},\;\frac{tkE}{{\gamma_w R^2 }}} \right)$$

(2)

in the case of consolidation (Leone et al. 2024). In these equations, R is the tunnel radius, R_p is the far-field radius of the seepage flow domain considered in the numerical model—taken to be equal to the depth of the tunnel under the water table (Ramoni and Anagnostou 2011)—σ₀ and p₀ are, respectively, the in situ stress and pore pressure at the depth of the tunnel axis, γ_w is the unit weight of the pore water and t the time that has elapsed upon excavation. The rock is assumed to obey a linear elastic and perfectly plastic constitutive model with a Mohr–Coulomb yield condition and a non-associated plastic flow rule, defined by five parameters: the Young’s modulus, E, the Poisson’s ratio, v, the uniaxial compressive strength, f_c, the angle of internal friction, ϕ, and the angle of dilation, ψ. The rheological ground behaviour due to creep is modelled as purely viscoplastic based on Perzyna’s overstress theory (Perzyna 1966), according to which the rate of viscoplastic deformations is governed solely by the ground viscosity η (for a detailed description of the model formulation and numerical implementation see Leone et al. 2023). Seepage flow in water-bearing ground is modelled according to Darcy’s law, considering a constant ground permeability k.

The expression of the dimensionless time parameter in Eq. (2) is identical to that in Terzaghi’s 1D consolidation theory (Terzaghi 1925), the only difference being that the drainage path length is replaced by the tunnel radius R, which is the characteristic length in the present problem. Based on this expression, one can directly infer that the time required to attain a given percentage of the displacement increment during the consolidation process, e.g. 95% (denoted as t₉₅ henceforth), is proportional to R² for given ground parameters, initial stress and pore pressure. Such a dependency does not exist in the case of creep, as R does not appear in the r.h.s. parameter list of Eq. (1). In practical terms, this means that, e.g. if the tunnel diameter was 4 times larger, then the displacements would develop at the same rate in the case of creep, but 16 times slower in the case of consolidation. The same delay in the displacement evolution would be observed if the permeability of the ground was lower by a factor of 16 in the smaller-diameter tunnel.

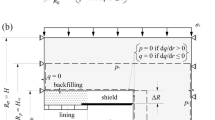
The above quadratic dependency holds as long as the tunnel lies deep under the water table (R_p > > R), which fixes the influence of the penultimate term in Eq. (2) and renders R the only relevant geometric parameter. However, problems also exist that are characterised by more than one significant geometric parameters, for example, the case of tunnelling in a low-permeability layer (aquitard) embedded between two aquifers (Fig. 1a). In this case the aquitard thickness induces an additional, non-trivial scale effect, which is examined in the next subsection.

Fig. 1

Plane-strain scale problem: a geotechnical situation for tunnelling through a horizontal aquitard and, b, simplified rotationally symmetric computational model

2.1.2 Confined Aquitard

In the case of an aquitard confined between permeable layers, the in situ pore pressure p₀ practically acts at the layer interfaces and the hydraulic head difference between the aquifer and tunnel is dissipated practically only within the aquitard, along a drainage path whose length corresponds to half the aquitard thickness (d/2 in Fig. 1a). This constraint may give rise to a secondary, non-trivial scale effect, which becomes relevant when the ratio of the aquitard thickness to the tunnel diameter d/D is small, as this generates two competing effects: on the one hand, the drainage path becomes shorter, which accelerates the consolidation process, but on the other hand the hydraulic gradients and thus the seepage forces are higher, which induces more extensive ground plastification and thereby decelerates the consolidation process.

The scale effects related to the tunnel diameter and the size of the seepage flow domain are demonstrated on the example of a deep geological repository for radioactive waste, which is planned to be constructed in Switzerland over the next years (for a detailed description see Nagra 2023; SFOE 2008). Circular drifts of diameter D = 3.5 m will be used for the disposal of high-level waste (Nordas et al. 2023b), while low/intermediate-level waste will be stored in caverns with four times larger average diameter D = 14 m (Morosoli et al. 2023). The repository will be embedded at a maximum depth of 900 m, within a practically horizontal, ca. 100 m-thick layer of Opalinus clay, a claystone with several favourable properties for waste containment, mainly its extremely low permeability. The Opalinus clay layer is interspersed between substantially more permeable layers of marls; hence, the in situ pore pressure p₀ = 9 MPa can be considered to act at its boundaries. The problem layout is shown in Fig. 1a.

For simplicity, variations in the geodetic height are ignored and the low/intermediate-level waste caverns are idealised as circular; this enables analysing the problem under the assumption of rotational symmetry, using the plane-strain model shown in Fig. 1b, which has been developed in Abaqus^® (Dassault Systèmes 2018). Apart from the ground heterogeneity, the model specifications are identical to those described in Sects. 2.1 and 2.2 of the companion paper (Leone et al. 2024), as given in Table 1. Parametric numerical simulations are conducted considering variable distance of the tunnel axis from the drainage boundary (R_p in Eq. 2) of 30–60 m, which in this case represents the half-thickness d/2 of the Opalinus clay layer wherein seepage flow occurs. The equivalent isotropic material constants for the Opalinus clay given in Table 1 are based on the anisotropic parameters determined from experimental results by Nordas et al. (2023a), and consider low, intermediate, and high values of the uniaxial compressive strength f_c = 7, 9 and 17 MPa, respectively, to account for the strength anisotropy and brittle softening that the Opalinus clay has been shown to exhibit.

Table 1 Parameters adopted in the numerical investigations into the problem of tunnelling through a horizontal aquitard (Sect. 2)

Figure 2 shows the ratio t₉₅ (D = 14 m) /t₉₅ (D = 3.5 m) between caverns and drifts (Fig. 2a), along with the corresponding plastic radii ρ (Fig. 2b) and normalised displacements u/R (Fig. 2c) at steady-state conditions (i.e. upon completion of the consolidation process), as functions of the distance of the tunnel axis from the drainage boundary d/2 for the three values of f_c.

Fig. 2

Scale effect associated with the hydromechanical coupling in the problem of tunnelling through a horizontal aquitard (Fig. 1): a ratio of the consolidation time t₉₅ in a 14 m diameter tunnel to the consolidation time t₉₅ in a 3.5 m diameter tunnel, b, steady-state radius of the plastic zone ρ and, c, steady-state displacement of the tunnel boundary u/R, as functions of the distance of the aquifer from the tunnel axis d/2 (parameters: Table 1)

Considering first the lowest f_c (7 MPa), one can observe that in the case of an aquitard thickness d of 120 m, only the basic scale effect is relevant: consolidation in the caverns takes place at a rate that is lower than in the drifts by a factor of 16, according to the ratio of the squares of their diameters, i.e. t₉₅ (D = 14 m) /t₉₅ (D = 3.5 m) = (14 / 3.5)² (Fig. 2a). The non-trivial scale effect starts to immediately become relevant for smaller d-values, where the ratio of t₉₅ can be seen to increase rapidly and monotonically towards very high values (Fig. 2a).

The monotonic increase indicates that in the case of the caverns (D = 14 m), where d/D (or, equivalently, R_p/R in Eq. 2) is smaller, the acceleration of the consolidation process due to the shorter drainage path is negligible compared to the deceleration imposed by the more extensive ground plastification due to the higher seepage forces. The dominant effect of plastification becomes evident by the increase in the steady-state radius of the plastic zone (Fig. 2b) and normalised displacement (Fig. 2c) for the caverns; for a lower aquitard thickness d of 60 m, the plastic zone even approaches the boundary of the seepage flow domain, indicating an almost complete plastification of the Opalinus clay layer. Conversely, for the drifts (D = 3.5 m) where d/D is higher, both the plastic radii and displacement remain constant. The non-trivial scale effect is qualitatively similar, but less pronounced for f_c = 9 MPa and can be seen to vanish completely for f_c = 17 MPa, which indicates that it is only relevant in weaker ground.

For the actual thickness of the Opalinus clay layer of ca. 100 m at the repository sites, consolidation around the caverns is expected to take place 16–20 times slower than around the drifts; it can thus be considered to obey the quadratic rule of consolidation theory that holds for deep tunnels in homogeneous ground, with some small deviations. The key takeaway from these results, however, is that in confined aquitards the consolidation rate may deviate dramatically from the quadratic rule of consolidation theory—and, this is even more so the case for lower aquitard thickness and weaker ground—indicating that ground deformations may continue to develop for a very long time after excavation. This may prove critical in respect of serviceability requirements or the structural safety of the final lining, as rock pressures will continue developing on it long after its installation.

2.2 Risk of Shield Jamming

The effect of the tunnel diameter on the risk of shield jamming will be investigated only for homogeneous ground, considering the rotationally symmetric, plane-strain model of a cylindrical and uniformly supported tunnel located deep below the ground surface and the water table, analogously to the companion paper (see Sect. 4 of Leone et al. 2024). In this case, the average rock pressure that develops on the shield $\overline{\sigma}_{\text{R}}$ can be

$$\frac{{\overline{\sigma }_R }}{\sigma_0 } = f\left( {\frac{E}{\sigma_0 }\frac{\Delta R}{R},\nu,\frac{f_c }{{\sigma_0 }},\phi ,\psi ,\frac{L}{R},\frac{K_s R}{E},\frac{K_l R}{E},\frac{\text{v}}{R}\frac{\eta }{E},t\frac{E}{\eta }} \right)$$

(3)

expressed as a function of the significant problem parameters asin the case of creep, and

$$\frac{{\overline{\sigma }_R }}{\sigma_0 } = f\left( {\frac{E}{\sigma_0 }\frac{\Delta R}{R},\nu ,\frac{f_c }{{\sigma_0 }},\phi ,\psi ,\frac{L}{R},\frac{K_s R}{E},\frac{K_l R}{E},\frac{p_0 }{{\sigma_0 }},\frac{R_p }{R},\text{v}\frac{\gamma_w R}{{kE}},t\frac{kE}{{\gamma_w R^2 }}} \right)$$

(4)

in the case of consolidation, where L is the shield length, ΔR is the radial overcut around the shield, K_s and K_l are the radial stiffnesses of the shield and lining, respectively, v is the average advance rate of the TBM during regular operation, and t is the standstill duration (Leone et al. 2024).

Due to technical limitations, the TBM parameters (overcut ΔR, shield length L and shield and lining stiffnesses K_s and K_l) that can be materialised in practice vary within a specific range independently of the tunnel diameter, while the advance rate v decreases with increasing diameter. Consequently, the nondimensional parameters EΔR/(σ₀R), L/R, K_sR/E, K_lR/E, (vη)/(ER) and (v γ_w R²)/(kE) in general cannot take the same values for different diameter tunnels, which gives rise to a scale effect with respect to the risk of shield jamming (Ramoni and Anagnostou 2011). The strength and stiffness of the ground may also tentatively decrease with increasing representative volume, and thus tunnel diameter; however, as squeezing ground is often weak even at the small scale of a specimen, the differences with respect to ground parameters in the large scale, between two tunnels of different diameter, are secondary in relation to the above and will be neglected.

Assessing the scale effect qualitatively is cumbersome even in the case of time-independent ground behaviour, since many TBM parameters have mutually competing effects on the rock pressure. Note, for example, that with increasing tunnel diameter both the normalised shield length L/R and the normalised overcut ΔR/R decrease (Ramoni and Anagnostou 2010); however, the former is favourable concerning the risk of shield jamming, while the latter is unfavourable (see also Ramoni and Anagnostou 2011). The problem becomes even more complex in the case of time-dependent ground behaviour due to creep or consolidation, where the additional influence of the advance rate v and the standstill duration t must be considered. Therefore, resorting to numerical simulations is necessitated for the assessment of the scale effect.

The section starts with some basic theoretical considerations concerning the influence of the advance rate v and the standstill duration t on the rock pressure in Sects. 2.2.1 and 2.2.2, based upon simplified and realistic assumptions, respectively (the influence of the other TBM parameters is discussed in Ramoni and Anagnostou 2010). Subsequently, it proceeds with investigating numerically the scale effect, based on exemplary computations with realistic specifications for all parameters. First, for the case of time-independent ground behaviour (Sect. 2.2.3), where only the influence of the TBM parameters is relevant, and then for the case of time-dependent behaviour due to creep or consolidation, considering the operational stages during TBM advance (Sect. 2.2.4) and restart after a standstill (Sect. 2.2.5).

2.2.1 Simplified Theoretical Analysis

The influence of the last two parameters in Eqs. (3) and (4) on the rock pressure is analysed considering an idealised situation where all other ground and TBM parameters are fixed regardless of R.

It is more convenient to start our analysis considering the conditions during restart after a standstill. As rock pressure may already develop during the advance phase, its value in this case depends not only on the standstill duration (last term), but also on the advance rate (penultimate term) (Leone et al. 2023). To eliminate the influence of the advance rate, a case where the excavation occurs rapidly (v η or v/k → ∞) is assumed, where the penultimate term is infinite regardless of R and only the last term is relevant. The latter is identical to the time parameter in the plane-strain problem (last term in Eqs. 1, 2), therefore the time development of the rock pressure in this case will be analogous to that of tunnel contraction in Sect. 2.1.1 in the case of creep, the pressure develops at a rate that is independent of R, while in the case of consolidation the pressure develops at a rate inversely proportional to R², and thus slower in a larger-diameter tunnel (effect equivalent to lower permeability).

Next, the conditions during the advance phase are examined. The rock pressure in this case depends only on the penultimate term (the last term is irrelevant). In the case of creep, R appears in the denominator, which means that for a given v the advance will occur slower in a larger-diameter tunnel (equivalent effect to lower viscosity), and hence a higher rock pressure will develop (alternatively, to achieve a given rock pressure the advance rate must be higher in the larger-diameter tunnel). In the case of consolidation, R appears in the numerator and the effect is exactly the opposite.

At this point, it is important to note that in order to compare the rock pressure in different diameter tunnels, v alone is not the most suitable measure of the rate of advance. Specifically, when the shield reaches any given tunnel cross section, it remains exposed to pressure at that section for as long as it is required for its entire length L to pass through it. Therefore, the shield pressure ultimately depends on the time required for the TBM to advance by one shield length, that is, L/v (= (L/R)/(v/R)), which is only a function of v/R since L/R is considered as being fixed. The ratio v/R, which expresses how fast the TBM excavates the length of one radius R, is thus a more suitable measure to compare the rate of advance in different diameter tunnels, since a fixed v/R means that the TBM takes the same time to advance by one shield length L regardless of R.

For a given v/R, in the case of creep the normalised advance rate (v/R) (η/Ε) is constant, which means that the pressure develops at the same rate regardless of R; in the case of consolidation, the normalised advance rate can be expressed as (v/R) (γ_w R²)/(kE) and is proportional to R², which means that the pressure develops at a rate inversely proportional to R², and thus slower in a larger-diameter tunnel. The effect of the tunnel diameter therefore becomes the same here as in the case of the standstill examined previously and analogous to the tunnel contraction in Sect. 2.1.1. Conclusively, both during advance and for restart after a standstill of the TBM, in the case of creep there will be no scale effect for tunnels excavated at the same rate v/R, while in the case of consolidation the well-known dependency of consolidation time on the square of the characteristic length—here R—holds.

2.2.2 Theoretical Analysis Under Realistic Assumptions Concerning the Advance Rate

The assumption adopted in the preceding section that v/R can be the same for the two tunnels (i.e., v is proportional to R) is purely theoretical, since in practice it is well known that the larger the boring diameter, the slower the TBM advances, i.e. v decreases with increasing R. In fact, v can be assumed to be inversely proportional to R, as in Ramoni and Anagnostou (2011), which then makes v/R inversely proportional to R². This is explained hereafter.

The operations during mechanised excavation with a TBM can be idealised as a “stop-and-go” process, where intervals of continuous TBM propulsion (ΔT₁) over the length of one prefabricated segmental lining ring (L_T) regularly alternate with intervals where the TBM remains at standstill (ΔT₂) for the installation of the corresponding ring. The net advance rate of the TBM during the continuous propulsion intervals can be expressed as v_N = L_T/ΔT₁, while the average advance rate over the entire “stop-and-go” process adopted in the present work (Eqs. 3, 4) can be expressed as v = L_T/(ΔT₁ + ΔT₂) (Leone et al. 2023). The net advance rate is defined as v_N = ROP * RPM, where ROP is the rate of penetration and RPM the number of rotations of the TBM cutterhead per minute (or, more generally, per unit time). It is reasonable to assume that ROP is the same for tunnels under identical ground conditions (strictly speaking, this is valid as long as the installed thrust force is higher in the larger TBM, as is common in practice). It is also reasonable to assume that RPM is inversely proportional to R, considering that an upper limit of 150–200 m/min is imposed on the linear velocity of the gauge cutters to avoid overheating, irrespective of the TBM diameter (Rispoli et al. 2020; Hamburger and Weber 1992). Under these assumptions, v_N can be considered inversely proportional to R. Assuming that the prefabricated lining rings have the same length L_T irrespective of R, ΔT₁ can be considered proportional to R. Based on this, it is also reasonable to consider ΔT₂ to be proportional to R (cf., among others, Tahernia & Rostami 2021; Farokh 2013, 2020), which then makes v inversely proportional to R, as is v_N.

Under the realistic assumption of inverse proportionality between v and R, the situation differs from the simplified one discussed in Sect. 2.2.1: in the case of creep the normalised advance rate (v/R) (η/Ε) becomes inversely proportional to R², which means that the pressure develops faster in a larger tunnel (effect equivalent to lower viscosity); in the case of consolidation, the normalised advance rate (v/R) (γ_w R²)/(kE) becomes independent of R, and hence the shield pressure develops at the same rate in both tunnels (the favourable effect of a faster advance in the case of a smaller-diameter tunnel outweighs the unfavourable effect of faster developing convergences).

The assumption concerning the advance rate does not influence the conditions during a standstill preceded by a rapid advance (v η or v/k → ∞), and the conclusions of Sect. 2.2.1 for this case remain valid. Regardless, as the tunnel diameter influences each stage differently, the scale effect already becomes cumbersome to assess qualitatively for general cases of a standstill preceded by an excavation at a normal advance rate. This is even more so the case when additionally considering the effect of the other TBM parameters, hence a numerical investigation is necessitated. This is conducted in Sects. 2.2.4 and 2.2.5, based on an example that considers practically relevant parameters. Previously, however, the case of time-independent ground behaviour is examined in Sect. 2.2.3, which offers a better understanding of the influence of the TBM parameters isolated from that of the advance rate and standstill time.

2.2.3 Time-Independent Ground Behaviour

The theoretical analysis of the previous sections assumed that the first eight dimensionless parameters on the r.h.s. of Eqs. (3) and (4) do not depend on the tunnel radius, when in fact the dimensionless TBM parameters in general cannot take the same values for a large and a small tunnel. This generates a scale effect, even without time-dependent ground behaviour.

The scale effect related to the TBM parameters is assessed herein by comparing two tunnels with diameters of 12 m and 4 m excavated under identical ground conditions, disregarding creep and consolidation (the scale effect in the case of time-dependent ground behaviour will be analysed in Sects. 2.2.4 and 2.2.5). For the numerical simulations, the computational model of the advancing tunnel heading developed in Abaqus^® (Dassault Systèmes 2018) and introduced in Sect. 2.3 of the companion paper (Leone et al. 2024) is employed, which is also shown in Fig. 3.

The assumed parameter values are given in Table 2. The common overcut ΔR = 5 cm and shield length L = 10 m adopted for both tunnels are realistic, considering that the corresponding normalised values (ΔR/R_, L/R) (= (2.5%, 5) and (0.8%, 1.7) for D = 4 m and 12 m, respectively) are typical (cf. Figure 6 in Ramoni and Anagnostou 2010). The thicknesses d_s of the shield and d_l of the lining are assumed proportional to the radius R, which is reasonable and makes the normalised radial stiffnesses, K_sR/E = (E_s/E) d_s/R and K_lR/E = (E_l/E) d_l/R, identical for the two tunnels and dependent only on the Young’s moduli E_s, E_c and E of steel, concrete and the ground, respectively.

Fig. 3

Axisymmetric computational model for determining the shield loading during TBM advance and standstills

Table 2 Parameters adopted in the numerical investigations into the effect of tunnel diameter on thrust force utilisation (Sect. 2)

When evaluating potential scale effects with respect to the risk of shield jamming, it is not sufficient to consider only the shield loading or the required thrust force F_r (which depend on the parameters in Eqs. 3 and 4), but also the installed or installable thrust force F_i. The latter increases with the tunnel diameter, which also introduces a scale effect to be considered. The comparison between the two tunnels is thus based on the ratio F_r /F_i, which expresses the percentage of the F_i utilised by F_r and will be hereafter referred to as thrust utilisation factor (TUF). The required thrust force F_r is computed as μ 2πR L µ $\overline{\sigma}_{\text{R}}$, where μ denotes the static friction coefficient; this expression holds for the conditions during TBM restart, which is the relevant operational stage in most cases (see Ramoni and Anagnostou 2010). The installed TBM thrust force is assumed to increase proportionally to the cross-sectional area, and thus to R², according to the expression F_i = 5 R² MN/m², which provides values in the high end of the range of technical data collected from various TBMs (cf. Figure 7 in Ramoni and Anagnostou 2010; Ates et al. 2014).

Figure 4 shows the thrust utilisation factors of the two tunnels as functions of the rock quality, expressed by its uniaxial compressive strength f_c. The intuitive perception that the smaller-diameter tunnel is less vulnerable than the larger-diameter one is unconditionally true for other potential hazards (e.g. an instability of the tunnel face) but not for the risk of shield jamming, where it is true only in better-quality ground (f_c > 3.2 MPa in the example of Fig. 4). The opposite holds in weaker ground and, interestingly enough, this has been shown to be generally true for any two tunnels with different radii, by means of a more extensive parametric study considering a wide range of practically relevant in situ stresses, boring radii, ground and TBM parameters (Nordas et al. 2024). The general validity of this result also confirms that it is sufficient to consider only two diameters to demonstrate the scale effect, as conducted herein.

Fig. 4

Scale effect in the absence of time-dependency (no creep, no consolidation): Thrust force required to overcome shield skin friction, normalised by the installed thrust force (“thrust utilisation factor”, TUF), as a function of the uniaxial compressive strength of the ground f_c for a 12 m diameter tunnel and for a 4 m diameter tunnel (parameters: Table 2)

For the parameters adopted herein, the TUF in the larger-diameter tunnel is less sensitive to variations of rock quality (expressed by f_c) than in the smaller-diameter tunnel, and also consistently lower than unity, indicating that its excavation is feasible irrespective of the ground conditions. The small tunnel excavation, on the other hand, is only feasible in better-quality ground with f_c > ca. 2.7 MPa.

The TUFs are equal for f_c = ca. 3.2 MPa, which means that the competing effects of the TBM parameters outweigh one other. This situation is thus suitable for investigating the scale effect that results purely from the time dependency of the ground behaviour due to creep or consolidation in the next sections.

2.2.4 Time-Dependent Ground Behaviour: TBM Advance

The scale effect during TBM advance in the case of creep and consolidation is examined under the same assumptions as in the previous section (Table 2), setting f_c = 3.2 MPa to eliminate the influence of the TBM parameters. Based upon Sect. 2.2.2, advance rates of 90 and 30 m/day (average values during the stop-and-go operation) are considered for the 4 m and for the 12 m diameter tunnel, respectively.

Figure 5 shows the thrust utilisation factor as a function of the viscosity (creep case, red lines) and of the permeability (consolidation case, blue lines) for the smaller diameter (solid lines) and for the larger diameter (dashed lines). With the exception of high viscosities or low permeabilities, a scale effect clearly exists with respect to the risk of shield jamming (expressed by the TUF) both in creep and consolidation: an increase in diameter results in a higher utilisation of the thrust force (the red dashed line is above the red solid line and the blue dashed line is above the blue solid line), which means that due to the time dependency the situation is more favourable for the smaller diameter. This is consistent with the results of the last section shown in Fig. 4: time dependency delays squeezing, the rock thus responds to tunnel excavation as if it were of a higher quality, and an increase in rock quality renders a smaller diameter more favourable, as shown in the last section. The scale effect is negligible if the viscosity is sufficiently high or the permeability sufficiently low; in this case, the convergences around the advancing shield area are nonetheless small regardless of the tunnel diameter, as the rock behaviour is practically elastic (creep case) or undrained (consolidation case).

Fig. 5

Scale effect in the case of time-dependent ground behaviour: Thrust force required to overcome shield skin friction during TBM advance, normalised by the installed thrust force (“thrust utilisation factor”, TUF), as a function of the viscosity η in the case of creep and the permeability k in the case of consolidation (f_c = 3.2 MPa; other parameters: Table 2)

The vertical distance between the two red lines reflects the scale effect in the case of creep. As it is slightly greater than the vertical distance between the two blue lines, the scale effect is slightly more pronounced in the case of creep than in the case of consolidation.

In the example of Fig. 5, TUF < 1 over the entire viscosity and permeability ranges, which means that the thrust force would be sufficient also for the larger-diameter tunnel in the cases of both creep and consolidation. Nevertheless, the assumed values of the installed thrust forces (F_i = 5 R² MN/m²) are very high for rock TBMs (20 MN for a 4 m diameter tunnel and 180 MN for a 12 m diameter tunnel). With a moderate assumption (e.g. F_i = 3 R² MN/m², which gives 12 and 108 MN for the 4 m and 12 m diameter tunnels, respectively), the larger TBM might experience jamming, while the smaller TBM would still be safe; this would happen in the range of η = ca. 10–100 MPa^.d and k = 10^–9–10^–8 m/s.

The scale effect can be demonstrated also in another way. Assume that the 4 m diameter tunnel was constructed first (a pilot tunnel) and that the force actually applied was equal to 20% of the installed one (TUF = 0.2). Assuming that the strength and stiffness parameters of the rock are known and correspond to the ones underlying Fig. 5, the observed (rather low) required thrust force could be explained on the basis of the convergence delay due to creep or to consolidation (points A in Fig. 5). What could one expect for the main, larger-diameter tunnel? For the thrust utilisation factor to remain the same, the viscosity η would have to be higher by a factor of about 50 in the case of creep (red point B vs. red point A), while in the case of consolidation the permeability k would have to be lower by a factor of about 20 (blue point B vs. blue point A). Alternatively, for the given η and k (as in points A), the advance rate in the main tunnel would have to be about 50 (creep) or 20 (consolidation) times higher than assumed (note the dimensionless expressions in Eqs. 3 and 4); this is, of course, impossible, but provides an alternative view on the scale effect and its magnitude in the case of creep and consolidation.

2.2.5 Time-Dependent Ground Behaviour: Standstill

The same conclusions can essentially be drawn for the thrust force needed for restart after a standstill. Figure 6 shows the TUF as a function of the standstill duration. The computations have been performed considering the same parameters as before (Table 2), as well as a high viscosity (η = 10,000 MPa d) and low permeability (k = 10^–10 m/s), which ensure that the behaviour during advance is elastic (in the case of creep) or undrained (in the case of consolidation) and hence relevant shield loading develops only during the standstill (cf. TUFs in Fig. 5 for η = 10,000 MPa d and k = 10^–10 m/s). This enables examining as far as possible the isolated influence of the standstill duration t, analogously to the theoretical case of rapid advance considered in Sects. 2.2.1 and 2.2.2.

Fig. 6

Scale effect in the case of time-dependent ground behaviour: thrust force required for TBM restart after a standstill, normalised by the installed thrust force (“thrust utilisation factor”, TUF), as a function of the standstill duration t (f_c = 3.2 MPa; η = 10⁴ MPa^.d, k = 10^–10 m/s; other parameters: Table 2)

The distances between the dashed and solid lines in Fig. 6 clearly indicate the existence of a scale effect with respect to the TUF. The width of the band defined by the two red lines reflects the effect of tunnel radius in the case of creep. As it is wider than the band defined by the two blue lines in the case of consolidation, one may say that the scale effect is more pronounced in the case of creep.

3 Interaction

The hypothesis that interaction is significant in the case of consolidation but negligible in the case of creep (Sect. 1) is tested herein, considering the problem of shield jamming in a twin tunnel (Fig. 7) and comparing the thrust forces required to overcome shield skin friction during construction of its two tubes (Tunnels 1, 2) for variable spacing e/D = 1, 2.5 and 5 between them. The construction of Tunnel 2 is assumed to take place long after the completion of Tunnel 1, such that steady state conditions have been re-established when it passes through any cross section A–A (Fig. 7). The adopted parameters are given in Table 3.

Fig. 7

Interaction problem: geotechnical situation during the advance of the second tunnel, long after construction of the first tunnel (plan view x–y)

Table 3 Parameters adopted in the numerical analyses for the interaction problem (Sect. 3)

To validate the hypothesis made, it is sufficient to consider and compare only two limit cases: the case of minimum interaction in consolidation versus the case of maximum interaction in creep.

In the case of consolidation, the effect of Tunnel 1 on Tunnel 2 is, first, due to the stress redistribution associated with the deformations of the ground ahead of the advancing face and around the TBM shield, and, second, the long-term large-scale pore pressure relief and increase in the undrained shear strength (Sect. 1). This effect is minimum when the excavation-induced deformations are as small as possible, which is the case when the ground permeability is very low and its response to excavation practically undrained.

In the case of creep, the effect of Tunnel 1 on Tunnel 2 is solely due to the aforementioned stress redistribution, as rheological processes are of purely mechanical nature. This effect is maximum if the deformations of the ground ahead of the advancing face and around the shield of Tunnel 1 are as large as possible, which is the case when the advance is very slow and all viscoplastic deformations due to creep occur practically simultaneously with the progress of the excavation (practically time-independent response with instantaneous manifestation of squeezing).

Based on the above, consideration is given in the sequel to the cases of a water-bearing ground of extremely low permeability that exhibits an undrained response during shield advance (“consolidation case”), and an extremely slow excavation through a non-water-bearing ground (“creep case”).

Instead of resorting to more complex, 3D, transient numerical simulations, the problem will be analysed in a simplified manner using sequentially two models: (i) an axisymmetric model of the advancing tunnel heading, which simulates the TBM advance and lining installation step by step (Fig. 3; computational assumptions discussed in Sect. 2 of the companion paper by Leone et al. 2024) and, (ii), a plane-strain, twin-tunnel model of a cross section A–A (cf. Figure 7) far behind the face of both tubes (Fig. 8; besides the inclusion of gravity effects, the model specifications are identical to those discussed in Sect. 2 of the companion paper by Leone et al. 2024). To facilitate the connection of the input and output parameters of the models, adequate and well-founded assumptions are adopted. Both models have been developed in Abaqus^® (Dassault Systèmes 2018).

Fig. 8

Interaction problem: plane-strain model (cross section A–A of Fig. 7) in the computational stage that simulates the excavation of the first tunnel

The consolidation case will be examined first. Initially, the short-term shield–lining–ground interaction in Tunnel 1 will be analysed and the thrust force required to overcome shield skin friction will be determined, using the axisymmetric model (Fig. 3). This model will be used for the calculation of the required thrust force in Tunnel 2, as well, although it will consider different initial conditions that reflect the stress redistribution, pore pressure relief and ground consolidation induced by Tunnel 1. The alteration of the initial stress and pore pressure fields will be quantified using the plane-strain model (Fig. 8). The latter will also be used to show that it is adequate to consider uniform and isotropic initial stress and pore pressure fields for simulating the construction of Tunnel 2, thereby verifying the adequacy of the axisymmetric model (Fig. 3) for this purpose. Based on these analyses, it will be shown that the required thrust force in Tunnel 2 is significantly lower than in Tunnel 1, even if the tunnel spacing is as large as ten diameters.

The analysis for the creep case essentially follows the same approach and will show that the interaction is negligible for tunnel spacings for which it is substantial in the consolidation case. This is because the construction of Tunnel 1 has a negligible effect on the stresses in the location of Tunnel 2, which will be shown to be true even under extreme squeezing conditions, and even considering an unusually large annular gap around the shield.

3.1 Results for the Consolidation Case

Figure 9 shows the longitudinal distribution of the rock pressure that develops in the short term upon the shield and the lining of Tunnel 1, along with the corresponding equilibrium point of the rock (2.3 MPa, 0.10 m), as determined using the axisymmetric model (Fig. 3).

Fig. 9

Interaction problem, consolidation case: Radial rock pressure distribution along the shield and lining of Tunnel 1 during rapid excavation (determined based on axisymmetric computation with σ₀ = 10 MPa, p₀ = 4 MPa and other parameters after Table 3)

The excavation of Tunnel 1 is also simulated as an undrained plane-strain problem using the plane-strain model (Fig. 8), by instantaneously reducing the tractions along its boundary from the in situ values. Figure 10 shows the numerically computed change in diameter horizontally and vertically (ΔD_h,v) as a function of the deconfinement factor λ (Panet 1995), along with the equilibrium point resulting from the axisymmetric analysis of Fig. 9 (2.3 MPa, 0.10 m; point A in Fig. 10). The small deviation of the actual equilibrium point from the plane-strain curve is due to the different stress paths of the ground in the two models (Cantieni and Anagnostou 2009). As it is impossible to exactly reproduce both the displacement and the rock pressure with the plane-strain model, a simplified assumption must be adopted to determine the conditions prevailing in the short-term, immediately upon excavation of Tunnel 1, considering unloading either down to point B₁ or to point B₂. Here, point B₂ is considered.

Fig. 10

Interaction problem, consolidation case: relationship between change in diameter ΔD_h,v and deconfinement factor λ during excavation of Tunnel 1 (determined based on plane-strain computation with σ₀ = 10 MPa, p₀ = 4 MPa and other parameters after Table 3)

Starting from the state at point B₂, beam elements representing the Tunnel 1 lining are activated in the plane-strain model, the boundary is completely unloaded, and a transient consolidation analysis is performed to determine the steady state prevailing long after the construction of Tunnel 1 and before construction of Tunnel 2. Figure 11 shows the pore pressure, effective stress, and total stress distributions along the horizontal y-axis, which allow drawing the following conclusions: The drainage action of Tunnel 1 is evident in an extended zone and induces a significant pore pressure relief even at long distances (note the decrease to 50% at a distance of 50 m from Tunnel 1). The total stresses decrease in general only slightly, except for the immediate vicinity of Tunnel 1 where the ground yields plastically (left of point P in Fig. 11). Due to the combination of the above, the effective stresses increase, which—as explained in Sect. 1.2—is expected to have a favourable effect since it increases the undrained shear strength.

Fig. 11

Interaction problem, consolidation case: stress and pore pressure distribution along the y-axis, long after construction of Tunnel 1 (steady state) but before construction of Tunnel 2 (determined based on plane-strain computation with σ₀ = 10 MPa, p₀ = 4 MPa and other parameters after Table 3)

The stress fields are neither uniform nor hydrostatic, which raises the question of whether an axisymmetric model (Fig. 3) is adequate for simulating the Tunnel 2 excavation. To check the applicability of such a model, an additional computational step with the plane-strain model (Fig. 8) is performed: starting from the state of Fig. 11, the excavation of Tunnel 2 is simulated as an undrained cavity unloading problem. The black lines in Fig. 12a show the numerically computed change in diameter horizontally and vertically (ΔD_h,v) as a function of the deconfinement factor λ for a tunnel spacing of e = 2.5D. The two lines almost coincide, which shows that the response nearly obeys rotational symmetry in spite of the non-uniformity and anisotropy of the stress field prevailing before the Tunnel 2 excavation. The red line is the ground response curve (GRC; computed after Anagnostou and Kovári 1993) in the case of uniform and isotropic initial pore pressure and stress fields with magnitude equal to that prevailing at the centre of Tunnel 2 just before its excavation. The high level of concordance with the numerical response curves justifies the use of the axisymmetric model of Fig. 3 (with the same initial values as the red curve) to determine the thrust force for Tunnel 2. (Of course, the adequacy of this simplification would be questionable for smaller spacings between the tunnels, where the differences among the aforementioned curves increase; Fig. 12b).

Fig. 12

Interaction problem, consolidation case: relationship between convergence ΔD_h,v and deconfinement factor λ during excavation of Tunnel 2  for tunnel spacing, a, e/D = 2.5 or, b, e/D = 1 (determined based on plane-strain computations with σ₀ = 10 MPa, p₀ = 4 MPa and other parameters after Table 3)

The use of the axisymmetric model (Fig. 3), with the initial conditions described above, provides the rock pressure distribution along the shield and, finally, the thrust force required to overcome shield skin friction in Tunnel 2. Figure 13 shows the rock pressure distribution in Tunnel 1 (according to Fig. 9) as well as in Tunnel 2 for various spacings e. The comparison of the rock pressure in the two tunnels reflects the very favourable effect of the drainage-induced consolidation in the vicinity of Tunnel 2. This is also reflected in the pronouncedly reduced thrust force of Tunnel 2 compared to Tunnel 1, as shown in Fig. 14; it is remarkable that the Tunnel 2 thrust force is about 65% less even if the spacing of the tunnels is as wide as five diameters.

Fig. 13

Interaction problem, consolidation case: radial rock pressure distribution along the shield in Tunnels 1 and 2 during rapid excavation (determined based on axisymmetric computations with homogeneous and isotropic initial stress and pore pressure fields; Tunnel 1: in-situ values σ₀ = 10 MPa, p₀ = 4 MPa; Tunnel 2: values prevailing at its center according to the results in  Fig. 11; other parameters: Table 3)

Fig. 14

Interaction problem, consolidation case: required thrust force in Tunnels 1 and 2 during rapid excavation as a function of the tunnel spacing (determined based on axisymmetric computations with homogeneous and isotropic initial stress and pore pressure fields; Tunnel 1: in-situ values; Tunnel 2: values prevailing at the its center according to the results in Fig. 11; other parameters: Table 3)

3.2 Results for the Creep Case

Same as in the consolidation case, the computations start with the axisymmetric analysis of Tunnel 1, which provides the longitudinal stress distributions on the shield and lining, as well as and the equilibrium point of the rock. This is shown in Fig. 15 for the reference case (σ₀ = 10 MPa and ΔR = 0.05 m; black lines), as well as for an extreme squeezing case with large overcut (σ₀ = 40 MPa and ΔR = 0.15 m; red lines); the latter is considered to demonstrate later that the effect of Tunnel 1 on Tunnel 2 is negligible even under such extremely unfavourable conditions.

Fig. 15

Interaction problem, creep case: radial rock pressure distribution along the shield and lining in Tunnel 1 during extremely slow excavation, allowing steady state to be reached practically simultaneously with the advance of the TBM (determined based on axisymmetric computations; parameters: Table 3)

Figure 16 shows, analogously to Fig. 10, the results of the simulation of the Tunnel 1 excavation with the plane-strain model (Fig. 8), along with the equilibrium points resulting from the axisymmetric analysis (points A). The deviations of the equilibrium points from the respective plane-strain curves are due to the stress-path dependency of the ground response, as mentioned above; they are expectedly greater in this case than in Fig. 10, due to the more pronounced ground plastification. The Tunnel 1 excavation is again simulated considering an unloading of its boundary down to point B₂ followed by an installation of the lining.

Fig. 16

Interaction problem, creep case: relationship between convergence ΔD_h,v and deconfinement factor λ during excavation of Tunnel 1 (determined based on plane-strain computations; parameters: Table 3)

As the response is effectively time independent in this case, the stresses at the state corresponding to point B₂ are also those prevailing prior to excavation of Tunnel 2. Figure 17 shows the stress distributions along the horizontal y-axis. Again, a significant drop in the stresses can be observed only inside the plastic zone, which is limited—even in the extreme squeezing and large overcut case—to the close vicinity of Tunnel 1 (left of the points P₁ and P₂ in Fig. 17). As is well known (Kirsch 1898), outside the plastic zone the mean stress remains constant and equal to the in situ stress σ₀, while the anisotropy of the stress field decreases with increasing distance from Tunnel 1. This non-uniform, anisotropic stress state is the initial state to be considered in the analysis of the Tunnel 2 excavation.

Fig. 17

Interaction problem, creep case: stress distribution along the y-axis, after construction of Tunnel 1 but before construction of Tunnel 2 (determined based on plane-strain computations; parameters: Table 3)

The adequacy of an axisymmetric model (Fig. 3) for this purpose is assessed again by simulating the Tunnel 2 cavity unloading using the plane-strain model (Fig. 8). Figure 18a shows the numerically computed changes in diameter horizontally and vertically (ΔD_h,v) as a function of the deconfinement factor λ (black lines), as well as the analytically determined GRC (red lines); the latter assumes rotational symmetry and considers the average stress at the Tunnel 2 centre as initial condition, which is the in situ stress σ₀. The numerically computed curves and the GRC almost coincide, which means that the cavity response is practically rotationally symmetric in spite of the anisotropy and non-uniformity of the stress field. Therefore, the thrust force of Tunnel 2 can be computed with the axisymmetric model (Fig. 3); as the initial stress to be considered is equal to the in situ stress, the Tunnel 2 thrust force is equal to that of Tunnel 1.

Fig. 18

Interaction problem, creep case: relationship between convergence ΔD_h,v and deconfinement factor λ during excavation of Tunnel 2 (determined based on plane-strain computations; parameters: Table 3)

In conclusion, the construction of Tunnel 1 does not have a relevant effect on the Tunnel 2 thrust force for the considered spacing of e = 2.5 D, and this lack of relevant interaction can be observed also in the extreme squeezing and large overcut case (Fig. 18b). The difference to the consolidation case is remarkable—at a spacing of 2.5D or even greater, the interaction in the consolidation case leads to a reduction of the Tunnel 2 thrust force by 65–90% (Fig. 14).

4 Conclusions

The present paper constitutes the second of two companion papers comparing the time-dependent effects due to transient creep and consolidation processes in shield tunnelling through the squeezing ground. The paper addressed two practical aspects relevant in tunnel construction, related to the effect of the tunnel diameter (scale effect) and the interaction between adjacent, consecutively excavated tunnels, placing specific focus on the risk of shield jamming. These investigations are valuable in relation to the transferability of experiences in analogous situations arising in practice.

The investigations into the scale effect examined first the time development of the convergences of an unsupported opening. It was shown that these are independent of the tunnel diameter in the case of creep, while in the case of consolidation the convergence rate is inversely proportional to the square of the tunnel diameter, which means that convergences develop slower in larger tunnels. The latter is directly analogous to the well-known quadratic dependency between consolidation time and length of the drainage path in Terzaghi’s 1D consolidation theory, but it holds only if there is only one significant geometric parameter, the tunnel diameter. Otherwise, e.g. when tunnelling through a confined aquitard whose thickness defines the size of the seepage flow domain and is thus also a significant geometric parameter, the consolidation rate may be much lower than indicated by consolidation theory.

Subsequently, the more complex problem of rock, TBM and tunnel support interaction was examined, with focus on the risk of shield jamming during advance and during restart after a construction standstill. The mechanisms underlying the scale effect in this case have been shown to be far more complex than indicated by consolidation theory, due to the different influence of the technical limitations posed on several TBM parameters. The investigations demonstrated that a larger diameter is more favourable than a smaller one in poor-quality ground with time-independent behaviour, while the opposite is true in the case of better-quality ground, creep or consolidation. This scale effect is slightly more pronounced in the case of creep than in the case of consolidation.

The investigations into the tunnel interaction demonstrated vastly different effects in creep and consolidation, resulting from the fundamentally different nature of the purely mechanical rheological and the coupled hydromechanical consolidation processes.

In the case of creep, the interaction is solely governed by the stress redistributions and plastic yielding caused by the excavation of the first tunnel, which are limited within a narrow zone since the construction equipment in mechanised tunnelling does not allow for large ground deformations to occur. The interaction has therefore been shown to be generally minor, even under extreme squeezing conditions and for an unusually large overcut.

In the case of consolidation, the drainage action of the first tunnel causes pore pressures relief and an increase in the effective stresses and undrained shear strength in the surrounding ground; this influence is analogous to that of advanced drainage and generates substantially more favourable conditions for the second tunnel, while it has also been shown to extend over a much larger zone compared to creep. This favourable influence of consolidation results in a remarkably reduced thrust force, a prominent difference in relation to creep.