1 Introduction

Rock is a naturally occurring solid material, formed by various geological processes. As such, the physical and mechanical properties vary very rapidly even within the same deposit and from outcrop to another (e.g., Aladejare 2016; Guan et al. 2021). The determination of these properties remains one of the research questions in rock mechanics and mining engineering (e.g., Heidari et al. 2012; Wang and Aladejare 2015; Aliyu et al. 2019; Aladejare 2020, 2021; Aladejare et al. 2021). It is a common practice in mining engineering to relate a rock property to others. In literature, mechanical properties like uniaxial compressive strength, tensile strength, Young’s modulus among other have been related to other properties of rock (e.g., Jaeger et al. 2009; Singh et al. 2012; Karakul and Ulusay 2013; Sharma et al. 2017; Heidari et al. 2018; Aliyu et al. 2019). These empirical relationships among rock properties have helped mining engineers and practitioners to bypass the difficulty often associated with the determination of any rock properties. Among the rock properties that have emerged very important for decision making and design analysis in mining engineering is rock characteristics impedance. In shock waves, the characteristic impedance of a material was defined as the product of the density and the shock wave velocity of the material (e.g., Cooper 1996). The concept of characteristic impedance of rock can be used to resolve many issues involving shock wave transmission and dissipation in rockmass. Zhang et al. (2020) explained that shock waves change as they travel from low-impedance material to high-impedance one. The shock pressure in the former is smaller than that in the latter. This is logical because from the definition of characteristic impedance, the higher the wave velocity, the higher the corresponding impedance and vice versa. As the characteristic impedance of rock depends on density and shock wave velocity which change within the same formation themselves, the impedance of rock is also a variable parameter and not a constant.

Zhang et al. (2020) explained that characteristic impedance can be used to classify rocks, because it is well related to the mechanical properties of rocks. The popular methods of classifying and characterizing rocks include rock quality designation (RQD) (Deere 1967), tunnelling quality index (Q) (Barton et al. 1974), rock mass rating system (RMR) (Bieniawski 1973), geological strength index (GSI) (Hoek et al. 1995; Wang and Aladejare 2016a), rock mass index (RMi) (Palmström 1996). The classification methods have played an important role in rock mechanics and rock engineering, ranging from depicting the type and strength of rocks, to obtaining input parameters for mining engineering design and analysis. However, the classification methods have drawbacks which includes little to no quantitative information on mechanical behaviour of rocks during GSI estimation (Hoek et al. 2002; Wang and Aladejare 2016b), and extensive field and laboratory testing of rock behaviour required in Q, RMR, RMi and RQD estimations. To resolve the bottlenecks and drawbacks associated with rock classifications, Zhang (2016) suggested using characteristic impedance of rock to evaluate a rock mass and classify rocks. This suggestion was because the characteristic impedance of rock could provide an approximate depiction of the geological structures of the rock mass, e.g., joints, faults, bedding, and mineral composition. With the recent study by Zhang et al. (2020), the characteristic impedance of rocks can be related to some physical and mechanical properties of rock. The study by Zhang et al. (2020) developed simple regressions between characteristic impedance and different rock mechanical properties. However, the inherent variabilities in rock properties are not considered in regression models. In addition, the study pointed the possibility of relating physical properties to the characteristic impedance of rock but did not explore this possibility. The results of the regression analyses from Zhang et al. (2020) showed satisfactory correlations between characteristic impedance to other rock properties like uniaxial compressive strength (UCS), tensile strength etc. However, no study has been undertaken to systematically combine test results of more than one property of rock for the estimation of characteristic impedance of rock.

With the recent gain in the application of characteristic impedance in rock mechanics and mining engineering, there is need to improve the method for estimation of characteristic impedance of rock. Therefore, this study aims to develop more reliable and robust models to predict characteristic impedance of rocks from Jaali, in northern Finland using soft computing analyses. The study makes use of artificial neural network (ANN) and adaptive neuro-fuzzy inference system (ANFIS) based on laboratory test results to eliminate the need for time-consuming and energy demanding experimental analysis. Soft computing models such as ANFIS and ANN are becoming increasingly popular in rock mechanics, as they have been used in rock property estimation (e.g., Gokceoglu and Zorlu 2004; Yilmaz and Yuksek 2009; Armaghani et al. 2016; Aladejare et al. 2020; Lawal et al. 2021a). Laboratory tests were conducted to determine UCS, wave velocity, density, and water absorption of the rock samples. The results of the density and wave velocity tests will be used to estimate the characteristic impedance of the rocks, and they are taken as measured characteristic impedance in this study since they are obtained in the laboratory. The UCS and water absorption (WA) test results will be used as the input parameters in the proposed models and the characteristic impedance will be the targeted output. Multiple linear regression (MLR) model will be developed to compare with ANN and ANFIS models. The predicted results of the ANFIS and ANN as well as MLR will be compared with the measured characteristic impedance. The model with the best fit/performance from the coefficient of determination, average absolute error, average biased error and mean the absolute error will be proposed for predicting the characteristic impedance of rock from UCS and WA test results.

2 Geography and Geology of Study Area

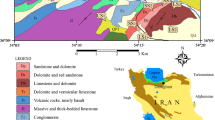
The sample materials for this study were recovered from an exposed section along Ouluntie road, close to Jaali. This location is about 15 km northeast of Oulu and about 106 km southeast of Kemi, a mining town in Northern Finland. The study area is part of the Karelia province of Finland (Fig. 1). The Karelia province comprise five major Archaean blocks namely Central Lapland nappe complex, Northern Karelia nappe complex, Northern Ostrobothnia nappe complex, Northern Savo nappe complex and Kainuu nappe complex (GTK 2017). The Karelia province experienced several tectonic events, some of which significantly modified the province. The Northern Ostrobothnia nappe which represents a lithologic unit that was thrust against the Pudasjärvi block during early Svecofennian orogeny. This, amongst several orogenic events have led to the formation of deep seated fault lines with NE–SW and NNE–SSW trends as well as zones of mineral enrichment in the study area (Fig. 1). The Pudasjärvi Granulite Belt (PGB) is a north–south trending belt located about 70 km northeast of Oulu (Fig. 1). The Pudasjärvi Granulite Belt are characterized by bimodal magmatism forming both felsic rocks [e.g., the tonalite–trondhjemite–granodiorite (TTG) group] and mafic rocks (e.g., pyribolites and basalt) (Mutanen and Huhma 2003). In this study area, lithologic units were cored from the basaltic section of the Pudasjärvi complex. Cored lithologic units were mafic with aphanitic texture, suggesting abundance of mafic minerals and relatively fast cooling paleo-environmental conditions.

Fig. 1
figure 1

Geologic map showing location of the Karelia province in Finland (modified from GTK 2017). Inset: tectonostratigraphic units of Kainuu and Northern Ostrobothnia according to Finstrati (GTK 2017). Rk Rimpikangas klippe, Ik Itämäki klippe. Lithodemic units in the Archaean basement blocks are LeC Lentua complex, IsC Iisalmi complex, PuC Pudasjärvi complex, MaC Manansala complex, KaC Kalpio complex, KjC Kalhamajärvi complex

Full size image

3 Sample Preparation and Testing

Test specimens which are basalts were sampled in situ using NX core drill bits. Each of the recovered samples was cut into sizes suitable for uniaxial compression and wave velocity tests. Lengths of the prepared test specimens followed the recommendation of International Society for Rock Mechanics (ISRM 2007). Care was taken to ensure parallelism and smoothness of the specimen end faces by using relatively low cutting speed and sandpapering using 220 and 320 grit sandpaper. In addition, some rock fragments were also obtained from each core sample for determination of physical properties. All specimens were air-dried to constant mass.

Instron compression machine was used to perform uniaxial compression tests. The test procedure followed was in accordance with ISRM (2007), in which prepared specimens were loaded at a constant rate of 1 MPa/s. The core surfaces were kept parallel to avoid surface irregularities.

A PunditLab digital ultrasonic tester (transit time range: from 1 to 9999 μs; EHT voltage: 500 V; pulse mode: continuous; measuring resolution: 0.1 μs) with two 250 kHz transducers was used to measure P-wave velocity (Vp) of the specimens prepared for the uniaxial compression test. A thin film of coupling gel was applied uniformly to the specimen end faces to increase precision of the test. Direct pitch-catch transmission technique was employed for ultrasonic testing with the coaxial arrangement of the specimen and the transducers at a constant coupling pressure. P-wave velocities (Vp) were determined by the tester by processing the arrival times of the waves from the transmitter to the receiver.

To measure water absorption, rock specimens were placed in an oven and dried at a constant temperature of 105 °C for 24 h to remove all absorbed fluids in its natural state. The specimen dimensions were more than ten times the maximum grain size to ensure that the specimen are representatives of the rock mass in accordance with the ISRM (2007) recommendation. The specimens were then placed in a desiccator for 30 min to cool after which the weight in air (i.e., weight of dry rock) was measured as (W1). The specimens were then soaked in distilled water for 24 h, after which the surface was cleaned and air-dried to eliminate surface moisture. The weight of the saturated specimen was then measured (W2). The water absorption of specimen was then estimated using Eq. (1).

$$\text{Water absorption} \; \left(\text{WA}\right)=\frac{{W}_{2}-{W}_{1}}{{W}_{1}}\times 100\%.$$
(1)

The density of the specimens is expressed as the ratio of specimen mass (kg) in air to its volume. The volume of the specimen is calculated using the dimensions of the core samples. Therefore, density is calculated as expressed in (Eq. 2).

$$\text{Density} \; (\rho )= \frac{{W}_{1}}{V}.$$
(2)

For the characteristic impedance (Z) of rocks, no laboratory testing was done. The study adopted the relationship explained by Zhang et al. (2020) that characteristic impedance of rock is a product of its density and wave velocity as expressed in Eq. (3).

$$\mathrm{Z}=\rho {V}_{\mathrm{p}}.$$
(3)

Hence the characteristic impedance from laboratory is determined based on this relationship and treated as measured characteristic impedance of rock in this study.

4 Artificial Neural Network (ANN)

ANN has been used successfully in previous research studies to estimate rock properties (Yılmaz and Yuksek 2008; Miah et al. 2020). An ANN model is developed for predicting the characteristic impedance of the igneous rock in this study using the data presented in Appendix 1. The number of samples upon which various tests were carried out are 100 samples. However, many of these samples fail during the compression test and as a result the P-wave velocity and UCS could not be obtained for the failed samples. Hence, about 38 datasets are used in developing the proposed model. The number of datasets adopted is enough to give a reasonable ANN model since there is no rule established in literature that specified the minimum or maximum number of datasets required for ANN model and many previous researchers have used less than the number of datasets adopted in this study to develop reliable models. For instance, Monjezi et al. (2013) used 20 datasets to predict the blast induced ground vibration. Dehghan et al. (2010) used 30 datasets to predict both the uniaxial compressive strength and Young modulus of rock. Ebrahimi et al. (2015) used 34 datasets to predict rock fragmentation size. All the above-mentioned authors used ANN approach in developing their models and their models have been well adopted.

The datasets are first pre-processed by normalizing them within the range compatible with the adopted transfer functions using Eq. (4) (Lawal and Idris 2019).

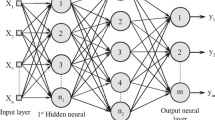
$${X}_{\mathrm{norm}}=\frac{({S}_{\mathrm{max}}-{S}_{\mathrm{min}})(X-{X}_{\mathrm{min}})}{{X}_{\mathrm{max}}-{X}_{\mathrm{min}}}+{S}_{\mathrm{min}}$$
(4)

where Xnorm is the required normalized data, Smin and Smax are the maximum and minimum normalization range, X is the actual data while Xmin and Xmax are the minimum and maximum values of X. Afterwards, the model parameters such as the water absorption, UCS, and the characteristic impedance which is the only targeted output are loaded into the MATLAB. The model parameters are then divided into three datasets which are 70% for the training, 15% for the testing and 15% for the validation respectively. The transfer functions for the hidden and output layers are then defined to be hyperbolic tangent (f1) and purelin (f2) respectively. The number of hidden neurons is varied between 1 and 5 to obtain a model that is of practical interest. The optimum ANN architecture selected is 2–2–1 based on the best validation performances of different networks tried as shown in Fig. 2 and the correlation coefficients obtained as presented in Table 1. The convergence of the curves of the networks tried are as presented in Fig. 2. All the tried networks convergence curves indicated a successful ANN model although some variations in the trend of curves are noticed in 2–4–1 and 2–5–1 architectures. The 2–2–1 network has the lowest best validation performance error and consequently, the best R-values for the training, testing and validation datasets. Therefore, 2–2–1 network (Fig. 3) is selected in this study for further transformation into the mathematical form (Eq. (5)).

$$Z = 5720.043(x_{1} + x_{2} ) + 13785.228.$$
(5)

where x1 and x2 are given as in Eq. (6)

$$x_{1} = - 1.74701\tanh ( - 0.02025WA - 0.03624UCS + 1.3225)$$
(6a)
$$x_{2} = 0.15382\tanh (0.3289WA + 0.1781UCS - 12.3108)$$
(6b)
Fig. 2
figure 2

Best validation performances of the tried ANN structures for a 2–1–1, b 2–2–1, c 2–3–1, d 2–4–1, and e 2–5–1

Full size image
Table 1 Different ANN architecture tried
Full size table
Fig. 3
figure 3

2–2–1 ANN architecture selected

Full size image

5 Adaptive Neuro Fuzzy Inference System (ANFIS)

An adaptive network-based fuzzy inference system (ANFIS) is a variant of ANN that is centred on the Takagi–Sugeno fuzzy inference system. The origin of the ANFIS can be traced back to 1990s and it has been widely used in various fields including engineering due to its potential to capture the advantage of both the ANN and fuzzy logic principles (Jang 1991, 1993; Lawal and Kwon 2020). It utilizes the If–then rule inference system which has the learning capability to approximate nonlinear functions (Abraham 2005). Therefore, it is said to be a universal estimator (Jang 1997). Considering the architecture, ANFIS has five layers. The first layer serving as the input layer and determination of the membership functions belonging to the input variables (fuzzification layer). The second layer is known as rule layer where the firing strength for the rules is generated. The third layer normalize the computed firing strengths by using the overall firing strength to divide each value. The fourth layer receives the output of the third layer and the consequence parameter set and then returned the defuzzificated values which are then passed to the fifth layer for the final output (Karaboga and Kaya 2018; Lawal et al. 2020, 2021b).

The ANFIS model is developed in this study to enable the comparison of its prediction with that of the ANN model. The same number of parameters used in developing the ANN is also used in this case. However, the data pre-processing is slightly different in that the datasets are normalized within the range of 0 and 1 (Eq. (5)). Although, the same number of experimental datasets used for training, testing and validation is also used but it was ensured that the data belonging to the training phase contains the minimum and maximum values of the model parameters.

The dataset for the training is loaded to the ANFIS toolbox in MATLAB, then the triangular membership type/function is selected for the input while the constant membership type/function is selected for the output. The linguistic variable used for both the WA and UCS are low (L), high (H) and very high (VH) as shown in Fig. 4a and b. The number of epoch is set to 100 and the training is performed. The obtained ANFIS structure is given as in Fig. 5. The plot showing the relationship between the models’ inputs together with the 9 rules used in predicting the characteristics impedance are also shown in Fig. 6.

Fig. 4
figure 4

a Membership function for UCS. b Membership function for WA

Full size image
Fig. 5
figure 5

The ANFIS structure

Full size image
Fig. 6
figure 6

Fuzzy rules

Full size image

6 Results and Discussion

6.1 Model Performance

The performances of the proposed models are evaluated firstly by comparing the predictions at various stages of the models with the ideal prediction. The ideal fit line is also associated with the ± 5% error bar as shown in Fig. 7. For the ANFIS model, all the predicted training and testing data points fall within the error bar while one of the points under the validation falls closely outside the positive error bar, indicating that the prediction of the ANFIS model is close to the ideal prediction (Fig. 7a). On the other hand, the predictions for the training, testing and validation data points using the ANN model are also presented in Fig. 7b. It can be seen that some of the datasets fall outside the error bar. However, the data points are largely within the ± 5% error bar. This is an indication that ANN model can also give a reasonable prediction of the characteristic impedance (Z).

Fig. 7
figure 7

Performances of the models at various stages for a ANFIS and b ANN

Full size image

The performances of the proposed models are further evaluated using some statistical indices such as mean absolute percentage error and coefficient of determination (R2) as presented in Eqs. (7) and (8).

$${\text{MAPE}} = \frac{1}{n}\left( {\frac{{\left| {y_{{{\text{m}}_{i} }} - y_{{{\text{es}}_{i} }} } \right|}}{{y_{{{\text{m}}_{i} }} }} \times 100\% } \right),$$
(7)
$$R^{2} = \left[ {\frac{{\sum\nolimits_{i = 1}^{n} {(y_{{{\text{m}}_{i} }} - \overline{y}_{{\text{m}}} )(y_{{{\text{es}}_{i} }} - \overline{y}_{{{\text{es}}}} )} }}{{\sqrt {\sum\nolimits_{i = 1}^{n} {(y_{{{\text{m}}_{i} }} - \overline{y}_{{\text{m}}} )^{2} } } \sqrt {\sum\nolimits_{i = 1}^{n} {(y_{{{\text{es}}_{i} }} - \overline{y}_{{{\text{es}}}} )^{2} } } }}} \right]^{2} ,$$
(8)

where ym is the measured value, yes is the model estimated value and n is the number of datasets. The ym and yesi with bar symbol indicated their mean values. The obtained evaluation is presented in Table 2 for the training, testing and validation datasets. The MAPE values obtained using ANFIS for the training, testing and validation are 0.665, 1.177 and 1.894 while their respective R2 values are 0.9987, 0.9995 and 0.998. For the proposed ANN model, the MAPE values obtained are 0.777, 0.977, and 0.372 for the respective training, testing and validation while their respective R2 values are 0.9984, 0.9989, and 0.9999. Even though the predicted R2 values of ANFIS are better than the ANN for the training and testing, the MAPE values of ANFIS are higher than the ANN for the testing and validation cases. This also agrees with Fig. 7 where all the predicted data points fall within the ± 5% error bar in the case of both ANFIS and ANN but that of ANN seems to be closer to an ideal fit line.

Table 2 Performance evaluation with statistical indicators
Full size table

6.2 Model Comparison

The proposed models are further compared using the overall dataset used in developing the models to evaluate how close the model predictions to the measured values are. To ensure logical comparison and to further validate the reliability of the developed models, a multiple linear regression is developed to compare with the ANFIS, and ANN models developed in this study. The MLR technique in this study aims at determining the values of characteristic impedance for a function that causes the function to best fit an available set of measured WA and UCS data. MLR technique has been used in many rock mechanics studies to develop models for engineering applications (Khandelwal and Armaghani 2016; Aladejare et al. 2020; Mahmoodzadeh et al. 2021). The MLR developed to predict the characteristic impedance of igneous rock is presented in Eqs. (9).

$$Z=47.3681-66.9977\mathrm{WA}+257.0982\mathrm{UCS}.$$
(9)

The prediction model for Z in Eq. (9) is logical, because the dependent variable (Z) increases with decreasing independent variable WA and increasing independent variable UCS. Since characteristic impedance increases with UCS, a strength parameter, it is logical for characteristic impedance to decrease with increasing WA. The study of Zhang et al. (2020) also indicates that the characteristic impedance increases with increasing uniaxial compressive strength. In addition, increasing water absorption leads to decreasing uniaxial compressive strength (Ündül and Tuğrul 2012; Tang et al. 2018). Therefore, it is reasonable that characteristic impedance will increase with increasing uniaxial compressive strength and decreasing water absorption, and vice versa. This is because there is an inverse correlation between uniaxial compressive strength and water absorption, and this propagate to their relationship with characteristic impedance.

The outcome of the comparison is presented in Figs. 8, 9 and 10. The ANN model’s predicted data points are the closest to the measured characteristic impedance, followed by the ANFIS model’s predicted data points and the MLR model’s predicted data points in that order (see Figs. 8a, 9a and 10a). Their respective R2 values which are 0.997 for ANFIS (Fig. 8b), 0.999 for ANN (Fig. 9b) and 0.991 for MLR (Fig. 10b) also indicate that ANN model predictions are slightly better than those of ANFIS and MLR. Although, both soft computing models as well as the MLR model can give reasonable predictions of the rock characteristics impedance. The proposed models will help mining engineers and practitioners when there is need to estimate characteristic impedance of rocks. Although efforts have been made previously to develop models to enhance rock properties estimation, like the generic transformation models developed by Ching et al. (2018). However, they did not develop models for estimation of characteristic impedance and did not use soft computing approaches in their study. Interestingly, no study is reported in literature to have developed soft computing-based models for estimation of characteristic impedance. Therefore, mining practitioners will find the proposed models useful when there is data of uniaxial compressive strength and water absorption at project sites and there is a need to estimate characteristic impedance of rock for such project sites.

Fig. 8
figure 8

Comparison of the ANFIS model predictions with measured values

Full size image
Fig. 9
figure 9

Comparison of the ANN model predictions with measured values

Full size image
Fig. 10
figure 10

Comparison of the MLR model predictions with measured values

Full size image

7 Conclusion

Based on the experimental data obtained and models of ANN, ANFIS and MLR developed in this study, the following conclusions can be drawn:

  1. 1.

    The characteristic impedance of rock is related to both physical and mechanical properties of rock. Therefore, the characteristic impedance can be estimated using combination of data of physical and mechanics properties of rock.

  2. 2.

    The Pearson's correlation coefficients of the models show that ANN has the highest R2, followed by ANFIS and lastly MLR. This indicates that the soft computing models (i.e., ANN and ANFIS) have high reliability in estimating characteristic impedance of rock.

  3. 3.

    The ANN model gives a lower RMSE than ANFIS model, indicating that it produces low error when used to estimate characteristic impedance of rock.

  4. 4.

    The performances of the proposed soft computing models are promising with the ANN being the best of the models developed.

  5. 5.

    Both ANN and ANFIS models as well as the MLR model can be used to estimate the characteristic impedance of rock when there are results of physical and mechanical tests (i.e., data of water absorption and uniaxial compressive strength) for a rock site/deposit.

  6. 6.

    It is possible to estimate characteristic impedance of rocks using the proposed models. However, the reliability of such estimates depends on the quality and quantity of rock data available and the rock type at a project site. Rock properties are site-specific; therefore, the models may have varying performance levels across different rock types because of geological features and lithology of different rock types. For instance, the models in the study are developed from data of igneous rocks and may perform better in estimation of characteristic impedance of igneous rocks than other rock types.