Poroelasticity of the Callovo–Oxfordian Claystone

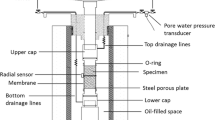
Abstract

This work is devoted to an experimental investigation of the poroelastic behavior of the Callovo–Oxfordian claystone, a potential host rock for the deep underground repository of high-level radioactive waste in France. Drained, undrained, pore pressure loading and unjacketed tests were carried out in a specially designed isotropic compression cell to determine the poroelastic parameters of fully saturated specimens. Great care was devoted to the saturation procedure, and small loading rates were used to ensure full drainage conditions in drained and pore pressure tests (0.5 kPa/min) and in the unjacketed test (2 kPa/min). High-precision strain measurements were performed by ensuring direct contact between the LVDT stems and the specimen. An analysis in the framework of transverse isotropic poroelasticity provided the Biot effective stress coefficients b ₁ (perpendicular to bedding) between 0.85 and 0.87 and b ₂ (parallel to bedding) between 0.90 and 0.98 under different stress conditions (pore pressure 4 MPa, total isotropic stresses of 14 and 12 MPa, respectively). A set of equivalent isotropic poroelastic parameters was also determined and a very good compatibility between the results of different tests was found, giving confidence in the parameters determined. The unjacketed test provided a directly reliable measurement of the unjacketed modulus (K _s = 21.7 GPa) that was afterward confirmed by an indirect evaluation that showed the non-dependency of K _s with respect to the stress level. These parameters were obtained for specimens cored and trimmed in the laboratory. A parametric study was then conducted so as to provide an estimation of the parameters in situ, i.e., not submitted to the damage supported by laboratory specimens. A minimal value b = 0.77 seems to be a reasonable lower bound for the equivalent isotropic Biot parameter.

Appendices

Appendix 1: Loading Rates

In all the tests performed with controlled pore water pressure (drained test, pore pressure loading and unjacketed test), the pore water pressure field should be homogeneous within the samples. A drained compression test should be performed with no excess pore pressure (Gibson and Henkel 1954), but, as recalled by the calculations conducted by Monfared et al. (2011a), a low level of excess pore pressure may be observed even at very slow loading rate. The drained condition is considered satisfactory if the excess pore pressure is negligible with respect to the applied confining pressure.

Commonly, a rate of 0.5 kPa/min is used in drained isotropic compression test on stiff clays (e.g., Sultan et al. 2000). The calculations run by Monfared et al. (2011a) confirmed the validity of this rate in a hollow triaxial cell with a drainage length of 10 mm, equal to that adopted here. To confirm Monfared et al. (2011a) calculations, a numerical resolution of the coupled hydromechanical equations of poroelasticity was performed using the finite element method with the 2D FreeFem++ code considering an axisymmetric calculation (Hecht 2012). In a purpose of simplicity, the calculations are performed considering an isotropic material. The governing equations are recalled below:

$$\nabla \cdot \sigma + f = 0$$

(23)

$$\nabla \cdot q + \frac{{\partial m_{f} }}{\partial t} = 0$$

(24)

$$q = - \rho_{f} \, \frac{k}{{\mu_{f} }}\nabla \cdot p_{f}$$

(25)

$$\underline{{{\text{d}}\varepsilon }} = \underline{\underline{S}} \left( {\underline{{{\text{d}}\sigma }} - b\underline{{{\text{d}}u}} } \right)$$

(26)

with

$$\underline{\underline{S}} = \left( {\begin{array}{*{20}c} {\frac{1}{E}} & {\frac{ - \nu }{E}} & {\frac{ - \nu }{E}} \\ {\frac{ - \nu }{E}} & {\frac{1}{E}} & {\frac{ - \nu }{E}} \\ {\frac{ - \nu }{E}} & {\frac{ - \nu }{E}} & {\frac{1}{E}} \\ \end{array} } \right)$$

(27)

$${\text{d}}\phi = - b{\text{d}}\varepsilon_{v} + \frac{1}{N}{\text{ d}}u,\frac{1}{N} = \frac{{b - \phi_{0} }}{{K_{\text{s}} }}$$

(28)

The Young modulus E and Poisson ratio $\nu$ were taken equal to 4000 MPa and 0.3, respectively (Gens et al. 2007), providing a drained bulk modulus K _d of 3333 MPa. The unjacketed bulk modulus K _s was taken equal to 21.7 GPa (Sect. 4.1), resulting in a Biot coefficient b of 0.84 (Eq. 14). A permeability coefficient k of 20⁻²⁰ m² was adopted, with a porosity ϕ of 14%, a bulk water compression modulus K _w = 2237 MPa and a water viscosity at 25 °C μ _w = 8.9 × 10⁻¹⁰ MPa.s at 25 °C (Spang 2002).

The effects of changes in loading rates of total stress v _σ  = dσ/dt (drained isotropic compression test and unjacketed test) and pore pressure v _u = du/dt (unjacketed test and pore pressure loading test) were considered in the simulations. The drained isotropic compression test was started from a confining stress of 12 MPa and a pore water pressure of 4 MPa with an applied increase in confining pressure Δσ = 1 MPa. The pore pressure test started from the same conditions with an applied increase in pore water pressure Δu = 1 MPa. In the unjacketed test, values of Δσ = Δu = 2 MPa were adopted. The principle of the calculations conducted and boundary conditions are presented in Fig. 10.

Fig. 10

Initial and boundary conditions for the different tests. a Drained test. b Pore pressure test. c Unjacketed test

1.1 Drained Compression Test

The result of the simulations is presented, for all the considered loading rates (0.5, 1 and 2 kPa/min) in terms of excess pore pressure at z = 10 mm (the farthest point from the drainage porous disk) in Fig. 11a, and in terms of pore pressure profile in Fig. 11b. It is observed that, unsurprisingly, the lowest excess pore pressure calculated at z = 10 mm is obtained at the lowest rate of 0.5 kPa/min with a value of 9 kPa (obtained once the confining stress reaches 12.05 MPa), negligible with respect to the value of 4 MPa imposed at the bottom boundary. Note, however, that the value of 38 kPa obtained at 2 kPa/min is not critical and that a rate of 1 kPa/min (19 kPa excess pore pressure, with the steady state reached when the confining stress is equal to 12.10 MPa) could be satisfactory. The pore pressure profiles have a shape typical of a consolidation problem.

Fig. 11

Calculated pore water pressure in a drained isotropic compression test: a pore pressure versus confining pressure at Z = 10 mm, b calculated pore pressure along the sample at the end of loading

1.2 Pore Pressure Loading Test

Unsurprisingly, the conclusions drawn from the data of the simulations of pore pressure loading tests at all rates (0.5, 1 and 2 kPa/min, pore pressure profiles in Fig. 12) lead to the same conclusions as for the drained state, with an maximum excess pore pressure of 11 kPa at z = 10 mm at 0.5 kPa/min. Here also, the excess pore pressure at 2 kPa/min is smaller than 50 kPa, and it seems that tests could have been run at 1 kPa/min, with a maximum excess pore pressure of 23 kPa.

Fig. 12

Calculated excess pore pressure profile in a pore pressure test

1.3 Unjacketed Compression Test

The unjacketed test was carried out by maintaining Δσ = Δu, starting from σ _i = 12 MPa and u _i = 4 MPa and increased up to 14 and 6 MPa, respectively. There are less water exchanges involved during unjacketed tests compared to the previous drained tests because only the compression of the solid phase is involved, with K _s larger than K _d, resulting in less sample volume changes involved.

Figure 13 shows the changes in pore pressure at z = 10 mm for rates of 2, 5 and 10 kPa/min. The negligible difference in pore pressure computed at 2 kPa/min at z = 10 mm (5.991 MPa instead of 6 MPa) shows that the pore pressure field is satisfactorily homogeneous. A difference of 20 kPa (around 0.3%) is observed at 5 kPa/min, showing that this rate could also have been adopted.

Fig. 13

Evolution of pore pressure at z = 10 mm with respect to confining pressure

Appendix 2: Correction of the Effect of the Drainage System in Undrained Tests

The expression of the corrected Skempton coefficient (B ^cor) with respect to the measured one (B ^mes) is given below (Monfared et al. (2011a), following Bishop (1976)). For the sake of simplicity, the equations are written in terms of compressibility c _i = 1/K _i.

$$B^{{\text{cor}}} = \frac{{B^{{\text{mes}}} }}{{1 + \frac{1}{{V\left( {c_{\text{d}} + c_{\text{s}} } \right)}}\left( {V_{\text{p}} c_{{\text{dp}}} + V_{\text{g}} c_{{\text{dg}}} - B^{{\text{mes}}} \left( {V_{\text{p}} \left( {c_{{\text{dp}}} + \phi c_{\text{w}} } \right) + V_{\text{g}} c_{{\text{dg}}} + V_{\text{L}} \left( {c_{\text{w}} + c_{\text{L}} } \right)} \right)} \right)}}$$

(29)

The corrected undrained compressibility (c ^cor_u ) is then written as:

$$c_{\text{u}}^{{\text{cor}}} = \frac{{c_{\text{d}} - c_{\text{u}}^{{\text{mes}}} }}{{1 + \frac{1}{{V\left( {c_{\text{d}} + c_{\text{s}} } \right)}}\left[ {V_{\text{p}} c_{{\text{dp}}} + V_{\text{g}} c_{{\text{dg}}} - \frac{{V_{\text{p}} \left( {c_{{\text{dp}}} + \phi_{\text{p}} c_{\text{w}} } \right) + V_{\text{g}} c_{{\text{dg}}} + V_{\text{L}} \left( {c_{\text{w}} + c_{\text{L}} } \right)}}{{\left( {c_{\text{d}} - c_{\text{s}} } \right)}}\left( {c_{\text{d}} - c_{\text{u}}^{{\text{mes}}} } \right)} \right]}}$$

(30)

where V _p, V _g and V _L are the volumes of the porous disk, geotextile and connecting lines, respectively, and c _dp , c _dg and c _L their drained compressibilities. ϕ and ϕ _p are the porosities of the sample and the porous disk, respectively. V, c _d, c _u, and B are the volume, the drained compressibility, the undrained compressibility and the Skempton coefficient of the sample. c _s is the unjacketed compressibility.

The volume of samples EST31912c and EST31912e are V = 11795 mm³ and V = 13847 mm³, respectively. The volume of the connecting lines, porous disk and geotextile are V _L = 2412 mm³ , V _p = 2268 mm³ and V _g = 113 mm³, respectively. Monfared et al. (2011a) performed a calibration test on a dummy metal sample and found a drained compressibility of the connecting lines c _L = 0.32 GPa⁻¹, a drained compressibility of the porous disk c _dp = 1.02 GPa⁻¹ and a drained compressibility of the geotextile c _dg = 9.33 GPa⁻¹. The porosity of the porous disk was ϕ _p = 0.22. The water compressibility at 25 °C is c _w = 0.447 GPa⁻¹ (Spang 2002). The corrected undrained bulk modulus and Skempton coefficient presented in Sect. 4.4 are calculated using these parameters.

2.1 Parametric Study on the Induced Errors

A parametric study is presented here to better clarify the influence of various material and drainage system properties on the induced errors on different undrained parameters. The error on a quantity Q is evaluated as (Q _measured–Q _corrected)/Q _corrected. The most influent parameters on the error are the drained compressibility c _d, the porosity ϕ and the ratio of the volume of the drainage system to the volume of the tested sample V _L /V. Three values of the drained compressibility c _d in the range of that of the COx claystone (0.1, 0.3 and 0.6 GPa⁻¹) and c _s = 0.05 GPa⁻¹. The volume ratio V _L /V was taken equal to 0.21 which corresponds to our experiment, and to further analyze the effect of the dead volume, a second ratio of 0.05 is also taken. The porosity is varied from 0.03 to 0.45.

Figure 14 shows the error on the measurement of the Skempton coefficient. When the rock is relatively highly compressible (c _d = 0.5 and c _d = 0.3 GPa⁻¹), the range of error does not vary a lot between small and high porosities. A greater volume of the drainage system underestimates the Skempton coefficient (B). The measured Skempton coefficient juggles between a slight underestimating and a slight overestimating when a geotextile is used. But with a lower compressibility, the error varies a lot as a function of the porosity. In fact, we can observe that for a volume ratio of 0.21 the Skempton coefficient is underestimated with an error of 44% in case of geotextile for 0.03 porosity and it is overestimated with an error of 35% for 0.45 porosity. When a porous disk is used, the Skempton coefficient is always underestimated (from 65 to 22%) for the same volume ratio. The error is more important and B is highly overestimated if the volume ratio is smaller on the use of geotextile and a high-porosity material.

Fig. 14

Parametric study of the error on Skempton coefficient (B). a Geotextile. b Porous disk

The error made on the measurement of the undrained bulk modulus (K _u) is shown in Fig. 15. Unlike for the Skempton coefficient, the error is more important for higher compressibilities. The effect of the volume ratio is more significant in the error on the measurement of K _u, as a large difference is shown between the two volume ratios. Once more, the error induced by the use of a porous disk is slightly more important than the geotextile.

Fig. 15

Parametric study of the error on the undrained modulus (K _u)