On scale-dependent vibration of circular cylindrical nanoporous metal foam shells

Abstract

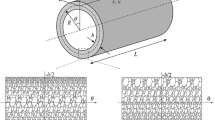
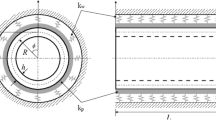
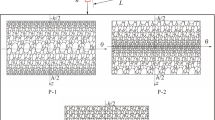
In this paper, free vibrations of cylindrical nanoshells made of nanoporous metal foam are investigated for the first time. Based on the modified couple stress theory and Love’s thin shell theory, the governing equations of the present system are derived by using Hamilton’s principle. Two types of nanoporosity distribution are considered in the construction of the nanoporous shells. Then, the Navier method and Galerkin method are utilized to solve natural frequencies of the nanoporous shells under different boundary conditions. Afterwards, a detailed parametric study is conducted. Results show that the nanoporosity type, the material length scale parameter, the porosity coefficient, the length-to-radius ratio, and the radius-to-thickness ratio play important role on the free vibrations of nanoporous shells. To check the validity of the present analysis, the results are compared with those in previous studies for the special cases.

Appendix

The elements in the matrix of Eq. (53) are given by (porosity distribution 1):

$$\begin{aligned} q_{11} & = \frac{{hE_{1} \left( { - 2e_{0} + \pi } \right)\left\{ { - 8k_{m}^{2} R^{4} + n^{4} l^{2} \left( { - 1 + \nu } \right) + n^{2} \left[ {4R^{2} + l^{2} \left( {4 + k_{m}^{2} R^{2} } \right)} \right]\left( { - 1 + \nu } \right)} \right\}}}{{8\pi R^{4} \left( { - 1 + \nu^{2} } \right)}} \\ & \quad \frac{{ - h\left( { - 2e_{m} + \pi } \right)\rho_{1} \omega^{2} }}{\pi }; \\ q_{12} & = \frac{{E_{1} hk_{m} n\left( { - 2e_{0} + \pi } \right)\left\{ {n^{2} l^{2} \left( { - 1 + \nu } \right) + R^{2} \left[ {k_{m}^{2} l^{2} \left( { - 1 + \nu } \right) + 4\left( {1 + \nu } \right)} \right]} \right\}}}{{8\pi R^{3} \left( { - 1 + \nu^{2} } \right)}}; \\ q_{13} & = \frac{{E_{1} hk_{m} \left( { - 2e_{0} + \pi } \right)\left[ {3n^{2} l^{2} \left( { - 1 + \nu } \right) + 4R^{2} \nu } \right]}}{{4\pi R^{3} \left( { - 1 + \nu^{2} } \right)}}; \\ q_{21} & = q_{12} ; \\ q_{22} & = \frac{1}{{8\pi R^{4} \left( { - 1 + \nu^{2} } \right)}}h\left\{ { - 2e_{0} E_{1} \left[ {n^{2} \left( { - 8R^{2} + l^{2} \left( {4 + k_{m}^{2} R^{2} } \right)\left( { - 1 + \nu } \right)} \right)} \right.} \right. \\ & \left. {\quad + k_{m}^{2} R^{2} \left( {4R^{2} + l^{2} \left( {12 + k_{m}^{2} R^{2} } \right)} \right)\left( { - 1 + \nu } \right)} \right] \\ & \quad + E_{1} \pi \left[ {n^{2} \left( { - 8R^{2} + l^{2} \left( {4 + k_{m}^{2} R^{2} } \right)\left( { - 1 + \nu } \right)} \right) + k_{m}^{2} R^{2} \left( {4R^{2} + l^{2} \left( {12 + k_{m}^{2} R^{2} } \right)} \right)\left( { - 1 + \nu } \right)} \right] \\ & \quad \left. { - 8\left( { - 2e_{m} + \pi } \right)R^{4} \left( { - 1 + \nu^{2} } \right)\rho_{1} \omega^{2} } \right\}; \\ q_{23} & = \frac{{E_{1} hn\left( { - 2e_{0} + \pi } \right)\left[ { - 4R^{2} + l^{2} \left( {2n^{2} + 5k_{m}^{2} R^{2} } \right)\left( { - 1 + \nu } \right)} \right]}}{{4\pi R^{4} \left( { - 1 + \nu^{2} } \right)}}; \\ q_{31} & = q_{13} ; \\ q_{32} & = q_{23} ; \\ q_{33} & = - \frac{1}{{24\pi^{3} R^{4} \left( { - 1 + \nu^{2} } \right)}}h\left\{ {E_{1} \pi^{3} \left[ {24R^{2} + h^{2} \left( {2n^{4} + 2k_{m}^{4} R^{4} + k_{m}^{2} n^{2} \left( {4R^{2} - l^{2} \left( { - 1 + \nu } \right)} \right)} \right)} \right.} \right. \\ & \left. {\quad - 12l^{2} \left( {k_{m}^{2} R^{2} + \left( {n^{2} + k_{m}^{2} R^{2} } \right)^{2} } \right)\left( { - 1 + \nu } \right)} \right] - 6e_{0} E_{1} \left[ {4\pi^{2} \left[ {2R^{2} - l^{2} \left( {k_{m}^{2} R^{2} + \left( {n^{2} + k_{m}^{2} R^{2} } \right)^{2} } \right)} \right.} \right. \\ & \quad \left. {\left. { \times \left( { - 1 + \nu } \right)} \right] + h^{2} \left( { - 8 + \pi^{2} } \right)\left( {2n^{4} + 2k_{m}^{4} R^{4} + k_{m}^{2} n^{2} \left( {l^{2} + 4R^{2} - l^{2} \nu } \right)} \right)} \right] \\ & \quad + 2R^{2} \left[ {\pi^{3} \left( {12R^{2} + h^{2} \left( {n^{2} + k_{m}^{2} R^{2} } \right)} \right) - 6e_{m} \left( {4\pi^{2} R^{2} + h^{2} \left( { - 8 + \pi^{2} } \right)\left( {n^{2} + k_{m}^{2} R^{2} } \right)} \right)} \right] \\ & \left. {\quad \times {\kern 1pt} \left( { - 1 + \nu^{2} } \right)\rho_{1} \omega^{2} } \right\}.{\kern 1pt} \\ \end{aligned}$$

(59)

where $k_{m} = \frac{m\pi }{L}$.

The elements in the matrix of Eq. (53) are given by (porosity distribution 2):

$$\begin{aligned} q_{11} & = \frac{{hE_{1} \left( { - 2e_{0} + \pi } \right)\left\{ { - 8k_{m}^{2} R^{4} + n^{4} l^{2} \left( { - 1 + \nu } \right) + n^{2} \left[ {4R^{2} + l^{2} \left( {4 + k_{m}^{2} R^{2} } \right)} \right]\left( { - 1 + \nu } \right)} \right\}}}{{8\pi R^{4} \left( { - 1 + \nu^{2} } \right)}} \\ & \quad \frac{{ - h\left( { - 2e_{m} + \pi } \right)\rho_{1} \omega^{2} }}{\pi }; \\ q_{12} & = \frac{{E_{1} hk_{m} n\left( { - 2e_{0} + \pi } \right)\left\{ {n^{2} l^{2} \left( { - 1 + \nu } \right) + R^{2} \left[ {k_{m}^{2} l^{2} \left( { - 1 + \nu } \right) + 4\left( {1 + \nu } \right)} \right]} \right\}}}{{8\pi R^{3} \left( { - 1 + \nu^{2} } \right)}}; \\ q_{13} & = \frac{1}{{4\pi^{2} R^{4} \left( { - 1 + \nu^{2} } \right)}}hk_{m} \left\{ {E_{1} \pi^{2} R\left( {3n^{2} l^{2} \left( { - 1 + \nu } \right) + 4R^{2} \nu } \right) + 2e_{0} E_{1} \left[ {h\left( { - 4 + \pi } \right)} \right.} \right. \\ & \left. {\quad k_{m}^{2} R^{4} + n^{2} \left( { - 2R^{2} + l^{2} \left( { - 1 + \nu } \right)} \right) + \pi R\left( { - 3n^{2} l^{2} \left( { - 1 + \nu } \right) - 4R^{2} \nu } \right)} \right] \\ & \quad \left. { - 4e_{m} h\left( { - 4 + \pi } \right)R^{4} \left( { - 1 + \nu^{2} } \right)\rho_{1} \omega^{2} } \right\}; \\ q_{21} & = q_{12} ; \\ q_{22} & = \frac{1}{{8\pi R^{4} \left( { - 1 + \nu^{2} } \right)}}h\left\{ { - 2e_{0} E_{1} \left[ {n^{2} \left( { - 8R^{2} + l^{2} \left( {4 + k_{m}^{2} R^{2} } \right)\left( { - 1 + \nu } \right)} \right)} \right.} \right. \\ & \left. {\quad + k_{m}^{2} R^{2} \left( {4R^{2} + l^{2} \left( {12 + k_{m}^{2} R^{2} } \right)} \right)\left( { - 1 + \nu } \right)} \right] \\ & \quad + E_{1} \pi \left[ {n^{2} \left( { - 8R^{2} + l^{2} \left( {4 + k_{m}^{2} R^{2} } \right)\left( { - 1 + \nu } \right)} \right) + k_{m}^{2} R^{2} \left( {4R^{2} + l^{2} \left( {12 + k_{m}^{2} R^{2} } \right)} \right)\left( { - 1 + \nu } \right)} \right] \\ & \quad \left. { - 8\left( { - 2e_{m} + \pi } \right)R^{4} \left( { - 1 + \nu^{2} } \right)\rho_{1} \omega^{2} } \right\}; \\ q_{23} & = \frac{1}{{4\pi^{2} R^{4} \left( { - 1 + \nu^{2} } \right)}}hn\left\{ {E_{1} \pi^{2} \left( { - 4R^{2} + l^{2} \left( {2n^{2} + 5k_{m}^{2} R^{2} } \right)\left( { - 1 + \nu } \right)} \right)} \right. \\ & \quad + 2e_{0} E_{1} \left[ {R\left( {\pi R\left( {4 - 5k_{m}^{2} l^{2} \left( { - 1 + \nu } \right)} \right) + hk_{m}^{2} \left( { - 4 + \pi } \right)\left( {l^{2} + 2R^{2} - l^{2} \nu } \right)} \right)} \right. \\ & \left. {\left. {\quad + 2n^{2} \left( {h\left( { - 4 + \pi } \right)R + l^{2} \left( {\pi - \pi \nu } \right)} \right)} \right] + 4e_{m} h\left( { - 4 + \pi } \right)R^{3} \left( { - 1 + \nu^{2} } \right)\rho_{1} \omega^{2} } \right\}; \\ q_{31} & = q_{13} ; \\ q_{32} & = q_{23} ; \\ q_{33} & = - \frac{1}{{24\pi^{3} R^{4} \left( { - 1 + \nu^{2} } \right)}}h\left\{ {E_{1} \pi^{3} \left[ {24R^{2} + h^{2} \left( {2n^{4} + 2k_{m}^{4} R^{4} + k_{m}^{2} n^{2} \left( {4R^{2} - l^{2} \left( { - 1 + \nu } \right)} \right)} \right)} \right.} \right. \\ & \left. {\quad - 12l^{2} \left( {k_{m}^{2} R^{2} + \left( {n^{2} + k_{m}^{2} R^{2} } \right)^{2} } \right)\left( { - 1 + \nu } \right)} \right] - 6e_{0} E_{1} \left[ {4\pi^{2} \left[ {2R^{2} - l^{2} \left( {k_{m}^{2} R^{2} + \left( {n^{2} + k_{m}^{2} R^{2} } \right)^{2} } \right)} \right.} \right. \\ & \quad \left. { \times \left( { - 1 + \nu } \right)} \right] + 8h\left( { - 4 + \pi } \right)\pi R\left( {n^{2} + k_{m}^{2} R^{2} \nu } \right) + h^{2} \left( { - 32 + \pi \left( {8 + \pi } \right)} \right) \\ & \quad \times \left. {\left( {2n^{4} + 2k_{m}^{4} R^{4} + k_{m}^{2} n^{2} \left( {l^{2} + 4R^{2} - l^{2} \nu } \right)} \right)} \right] + 2R^{2} \left[ {\pi^{3} \left( {12R^{2} + h^{2} \left( {n^{2} + k_{m}^{2} R^{2} } \right)} \right)} \right. \\ & \quad \left. {\left. { - 6e_{m} \left( {4\pi^{2} R^{2} + h^{2} \left( { - 32 + \pi \left( {8 + \pi } \right)} \right)\left( {n^{2} + k_{m}^{2} R^{2} } \right)} \right)} \right]\left( { - 1 + \nu^{2} } \right)\rho_{1} \omega^{2} } \right\}.{\kern 1pt} {\kern 1pt} \\ \end{aligned}$$

(60)