$\ell$-convex Legendre curves and geometric inequalities

Abstract

In this paper we consider $\ell$-convex Legendre curves, which are natural generalizations of strictly convex curves. We generalize various optimal geometric inequalities, isoperimetric inequality, Bonnesen’s inequality and Green–Osher inequality, for strictly convex curves to ones for $\ell$-convex Legendre curves. Moreover we generalize the inverse curvature curve flow for this class of Legendre curves and prove that it always converges to a compact soliton after rescaling. Unlike in the class of regular curves, there are infinitely many compact solitons, which include circles and astroids.

1 Introduction

In this paper we are interested in Legendre curves, which are in general not regular, but have a smooth unit normal vector field. Such a curve is also called frontal, especially in the theory of singularities. Precisely, a curve (or one dimensional map) $\gamma :I\rightarrow \mathbb {R}^2$ is a Legendre curve, if there exists a unit vector field $\nu :I\rightarrow {\mathbb {S}^{1}}$ such that

$$\begin{aligned} \langle \gamma '(\theta ), \nu (\theta ) \rangle =0, \quad \hbox { for any } \theta \in I, \end{aligned}$$

(1.1)

where $\gamma '(\theta )=\frac{d\gamma }{d\theta }$. It is easy to see that this condition is equivalent to the one that $(\gamma , \nu ): I\rightarrow \mathbb {R}^2\times {\mathbb {S}^{1}}$ is a Legendre curve w.r.t. the canonical contact structure of $\mathbb {R}^2\times {\mathbb {S}^{1}}$. Let J be the standard complex structure and define $\mu := J\nu$. Then one can define a curvature pair for $\gamma$:

$$\begin{aligned} \ell :=\langle \nu ', \mu \rangle , \quad \quad \beta := \langle \gamma ', \mu \rangle .\end{aligned}$$

(1.2)

See for example [4, 17]. It is clear that a Legendre curve is regular if and only if $\beta$ never vanishes. In this case $\gamma$ has the usual curvature $\kappa$ and it is easy to see that $\kappa =\ell /|\beta |$. In general $\beta$ has zeros, and hence $\kappa$ could not be defined or is infinite.

In our paper we focus on a special class of Legendre curves, which have positive $\ell$. We call such a curve an $\ell$-convex curve. An $\ell$-convex curve is in general not convex, see [5]. Our first observation is that any closed $\ell$-convex Legendre curve can be reparametrized as a map

$$\begin{aligned} \gamma (\theta ) =p(\theta ) (\cos \theta , \sin \theta ) +p'(\theta ) (-\sin \theta , \cos \theta ),\end{aligned}$$

(1.3)

for a smooth function $p:{\mathbb {S}^{1}}\rightarrow \mathbb {R}$, which will be called a support function for the $\ell$-positive Legendre curve. It is well-known that a closed, strictly convex curve can be represented by (1.3) with $p>0$ and $p+p''>0$ and p is the Minkowski support function. Hence the class of $\ell$-convex Legendre curves is much larger than the one of strictly convex curves. The study of this class goes back at least to the work of Geppert [9], where the author called such a curve stützbar (supportable). Such a curve is also called hedgehog. For the recent study on such curves see [14]. A map with form (1.3) is clearly a Legendre curve with

$$\begin{aligned} \ell =1, \qquad \beta =p+p''. \end{aligned}$$

For a strictly convex curve it is clear that $\beta$ is the principal radius, i.e., $\beta =1 /\kappa .$ Hence with the terminology of the curvature pair $(\ell , \beta )$ for Legendre curves we have a very natural generalization of the concept of principal radius, which in general now could be zero or even negative.

The paper consists of three parts. The first part of this paper is to generalize isoperimetric inequalities (isoperimetric type inequalities) for convex curves to ones for $\ell$-convex curves. One of inequalities we obtain is

Theorem 1.1

For any $\ell$-convex Legendre curve, there holds

$$\begin{aligned} 0\le \left( \int _{\mathbb {S}^{1}}\beta ^2 d\theta -2A\right) - 8\left( \frac{L^2}{4\pi }-A \right) \le \frac{1}{12} \int _{\mathbb {S}^{1}}\beta '^2 d\theta - 2\left( \frac{L^2}{4\pi }-A \right) . \end{aligned}$$

(1.4)

Moreover, equality in the first inequality holds if and only if $\gamma$ is generated by

$$\begin{aligned} p= a_0+ a_1 \cos \theta + b_1\sin \theta + a_2 \cos 2 \theta + b_2\sin 2\theta \end{aligned}$$

(1.5)

and equality in the second inequality holds if and only if

$$\begin{aligned} p= a_0+ a_1 \cos \theta + b_1\sin \theta + a_2 \cos 2\theta + b_2\sin 2\theta + a_3 \cos 3 \theta + b_3\sin 3\theta . \end{aligned}$$

(1.6)

Here L and A are the algebraic length and the algebraic area of an $\ell$-convex Legendre curve, which are natural generalizations of the length and the enclosed area of a regular planar curve. See Definition 3.4 below. We remark that L and A could be zero or negative. Indeed the class of Legendre curves with $L=0$ (which implies $A<0$ by Theorem 1.1) is an important one which we are interested in. When $\gamma$ is a regular convex curve, the first inequality was proved in [13], while the second in a very recent work [11]. There are a series of optimal inequalities in the latter paper by using a higher order Wirtinger inequality for regular convex curves. When $L=0$, an $\ell$-convex Legendre curve is nerve a regular curve. As a direct consequence we have a characterization of astroid in the class of $\ell$-convex Legendre curves with $L=0$.

Corollary 1.2

If $\gamma$ is an $\ell$-convex Legendre curve with $L=0$, then

$$\begin{aligned} \int _{\mathbb {S}^{1}}\beta ^2 d\theta \ge -6A=6|A| \end{aligned}$$

with equality if and only if $\gamma$ is an astroid, i.e.,

$$\begin{aligned} p= a_1 \cos \theta + b_1\sin \theta + a_2 \cos 2 \theta + b_2\sin 2\theta . \end{aligned}$$

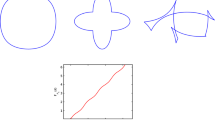
For a figure of an astroid centered at the origin, see Fig. 1 below. For further discussion see below.

Another consequence (1.4) is a

$$\begin{aligned} \int _{\mathbb {S}^{1}}\beta ^2 d\theta \ge 2A. \end{aligned}$$

(1.7)

Moreover equality holds iff $\gamma$ is a circle. When $\gamma$ is a regular, (1.7) is equivalent to

$$\begin{aligned} \int _{\gamma } \frac{1}{\kappa }ds \ge 2 A, \end{aligned}$$

where s is the arc-length element and $\kappa$ the curvature of $\gamma$. In this case, it is a known inequality. Its higher dimensional analogue is the Heintze-Karcher-Ros inequality.

In the second part we prove Bonnesen’s inequality and Green–Osher’s inequality [8] for $\ell$-convex curves.

Theorem 1.3

(Bonnesen’s inequality) If $\gamma$ is an $\ell$-convex and not a circle, then

$$\begin{aligned}{} & {} \pi t^2-tL+A < 0, \quad t\in [r_{in}, r_{out}],\end{aligned}$$

(1.8)

$$\begin{aligned}{} & {} \quad L^2-4\pi A> \pi ^2(r_{out}-r_{in})^2. \end{aligned}$$

(1.9)

Here $r_{in}$ and $r_{out}$ are the generalization of the ordinary inradius $r_{in}$ and outradius $r_{out}$ for regular curves. See Definition 5.1 below. We emphasize that $r_{in}$ and $r_{out}$ are not necessarily positive. Example 5.1 shows that our Bonnesen’s inequality is sharper than ordinary Bonnesen’s inequality for $\ell$-convex curves.

Theorem 1.4

[Green–Osher inequality] Let F be a positive convex function on $\mathbb {R}$, i.e. $F''(x)\ge 0$, for any $x\in \mathbb {R}$. Then

$$\begin{aligned} \frac{1}{2\pi }\int _{{\mathbb {S}^{1}}} F(\beta ) d\theta \ge \frac{1}{2}(F(-t_1)+F(-t_2)), \end{aligned}$$

(1.10)

where

$$\begin{aligned} t_1=-\frac{L}{2\pi }+\frac{\sqrt{L^2-4\pi A}}{2\pi }, \quad t_2=-\frac{L}{2\pi }-\frac{\sqrt{L^2-4\pi A}}{2\pi }. \end{aligned}$$

It is easy to see that (1.7) follows also from (1.10) by choosing $F(x)=x^2$. We prove this result following closely the method given in [8], while generalizing certain geometric concepts to $\ell$-convex curves. In fact, we use the support function p to replace the curve itself and use analytic properties of p to replace the geometric properties of the curve. It seems that this way is more flexible.

In the third part of this paper we observe that the inverse curvature curve flow is well-defined for $\ell$-convex curves and prove the global convergence.

Theorem 1.5

The inverse curvature flow has a global convergence for any initial $\ell$-convex curve with algebraic length $L_0$. Moreover we have

• (1) If $L_0 >0$, the flow expands exponentially and the evolving curve becomes convex after a certain time. After a suitable rescaling, the flow converges to a circle.

• (2) If $L_0=0$, then the flow shrinks and after a suitable rescaling it converges to a Legendre curve with a form

  $$\begin{aligned} a_1\cos \theta + b_1 \sin \theta + a_k \cos k\theta + b_k \sin k\theta \end{aligned}$$

  (1.11)

  for some integer $k\ge 2$. The curves given by (1.11), together with circles, are all closed solitons of the inverse curvature flow.

Here $L_0$ is the algebraic length of the initial curve, which we may always assume $L_0\ge 0$. See Definition 3.4 and the following remark.

Though the proof is elementary, the phenomenon that Theorem 1.5 shows is rather interesting. For the convex regular curves, it is well-known that the inverse curvature curve flow expands and admits only circles as its compact solitons [1]. Now for $\ell$-convex curves we have two cases: when $L_0>0$, the inverse curvature flow first evolves to a regular convex curve and then expands as in the case of regular curves; when $L_0=0$ then the flow shrinks to a point and converses to a curve with form (1.11) after rescaling. The curves given by (1.11) are compact solitons. Therefore the inverse curvature flow admits infinitely many compact solitons. For non-closed solitons see [2]. In (1.11) in Theorem 1.5 (2), $a_k$ and $b_k$ could be both zero. In this case the flow starts from a constant curve (i.e. a point) and keeps fixed. We remark that a point $(a_1, b_1)\in \mathbb {R}^2$ is also a Legendre curve with support function $p= a_1\cos \theta +b_1\sin \theta$. See Sect. 3.

It would be interesting to ask if one can generalize these results to higher dimensional non-regular hypersurfaces. We will consider this problem later.

The curves with support function in form (1.11) play an important role in this paper. They are called astroids for $k=2$ and deltoids for $k=3$. See Figs. 1 and 2. Actually one of main aims of this paper is to show these curves play a very similar role for Legendre curves as the circles for regular planar curves.

The paper is organized: In Sect. 2 we recall notions of frontals, fronts and Legendre curves and their fundamental theorems. In Sect. 3 we introduce $\ell$-convex curves. The isoperimetric inequalities for $\ell$-convex curves are presented in Sect. 4, while Bonnesen’s inequality and Green–Osher’s inequality are proved in Sect. 5. We study the inverse curvature curve flow in Sect. 6.

2 Fronts and Legendre curves

As defined in the Introduction, a Legendre curve is a one dimensional map $\gamma :I\rightarrow \mathbb {R}^2$, together with a unit vector field $\nu :I\rightarrow {\mathbb {S}^{1}}$, satisfying

$$\begin{aligned} \langle \gamma '(\theta ), \nu (\theta ) \rangle =0, \quad \hbox { for any } \theta \in I. \end{aligned}$$

(2.1)

It is also called a frontal. If $|\gamma '(\theta )|^2+ | \nu '(\theta )|^2 \not =0$, $\forall \theta \in I$, then it is called a front.

For frontals and fronts, there is a complete equivalent definition by using the language of Legendre curves on the contact manifold $T_1\mathbb {R}^2$, the unit circle bundle of $\mathbb {R}^2$. To describe the structure of interest here, we first review the geometry of tangent bundle $\pi _0: T\mathbb {R}^2 \rightarrow \mathbb {R}^2$ of $\mathbb {R}^2$, that is $T\mathbb {R}^2$ is the tangential bundle of $\mathbb {R}^2$, which is equivalent to $\mathbb {R}^2\times \mathbb {R}^2$. If $(x_1, x_2)$ are local coordinates on $\mathbb {R}^2$, then $(x_1, x_2)$ together with the fibre coordinates $(y_1, y_2)$ form local coordinates on $T\mathbb {R}^2$, which is Kählerian with the standard inner product $g_0$, the integrable complex structure $J_0$ and the Liouville form $\eta _0$:

$$\begin{aligned} g_0=\sum \nolimits _{i=1}^2(dx_i\otimes dx_i+dy_i\otimes dy_i), \quad J_0\frac{\partial }{\partial x_i}=\frac{\partial }{\partial y_i}, \quad J_0\frac{\partial }{\partial y_i}=-\frac{\partial }{\partial x_i}, \quad \eta _0=\sum \nolimits _{i=1}^2y_idx_i. \end{aligned}$$

The unit circle bundle, $\pi : T_1\mathbb {R}^2=\mathbb {R}^2\times {\mathbb {S}^{1}}\rightarrow \mathbb {R}^2$, is the hypersurface of $T\mathbb {R}^2$ defined by

$$\begin{aligned} \sum _{i=1}^2y_i^2=1. \end{aligned}$$

The vector field $\sum \nolimits _{i=1}^2y_i\frac{\partial }{\partial y_i}$ is a unit normal as well as the position vector for points in $T_1\mathbb {R}^2$. $T_1\mathbb {R}^2$ is a contact manifold with a contact metric structure $(g, \phi , \eta , \xi )$ that is given by

$$\begin{aligned} \eta =\eta _0|_{T_1\mathbb {R}^2}, \quad \xi =y_i\frac{\partial }{\partial x_i}\Big |_{T_1\mathbb {R}^2}, \quad g=g_0|_{T_1\mathbb {R}^2}, \quad \phi X=J_0X-\eta _0(X)(y_i\frac{\partial }{\partial y_i}). \end{aligned}$$

We remark that $T_1\mathbb {R}^2$ is not Sasakian, since one can check that $\xi$ is not a Killing vector field. See also Remark 2.2.

Definition 2.1

Let I be an interval or $\mathbb {R}$. A curve $\Gamma : I \rightarrow T_1 \mathbb {R}^2$ is called a Legendre curve, if

$$\begin{aligned} \Gamma ^* (\eta )= 0, \quad \text{ on } I. \end{aligned}$$

That is, the pull-back of the canonical contact form $\eta$ vanishes everywhere on I. If it is immersion, then it is called Legendre immersion.

For a Legendre curve $\Gamma : I \rightarrow T_1\mathbb {R}^2=\mathbb {R}^2\times {\mathbb {S}^{1}}$, one can decompose it into

$$\begin{aligned} \Gamma =(\gamma , \nu ). \end{aligned}$$

It is easy to see that

$$\begin{aligned} \Gamma ^*(\eta )=\langle \gamma ', \nu \rangle . \end{aligned}$$

Hence, $\Gamma$ is a Legendre curve if and only if $\gamma$, together with $\nu$, is a frontal. Moreover, if $\Gamma$ is an immersion, then $\gamma$ is a front.

As a curve in a 3-dimensional manifold, we have the ordinary definition of its second fundamental form. We present them in terms of $\ell$, $\beta$ and their derivatives. Along a Legendre immersion $\Gamma =(\gamma , \nu ): I \rightarrow T_1\mathbb {R}^2$, we choose a unit orthogonal adapted frames

$$\begin{aligned} \left\{ \begin{array}{l} e_1= \frac{1}{\sqrt{\ell ^2+\beta ^2}}(\gamma ', \nu ')=\frac{1}{\sqrt{\ell ^2+\beta ^2}}(\beta \mu , \ell \mu ), \\ e_2=\phi e_1=\frac{1}{\sqrt{\ell ^2+\beta ^2}}(-\nu ', \gamma ')=\frac{1}{\sqrt{\ell ^2+\beta ^2}}(-\ell \mu , \beta \mu ), \\ e_3=(\nu , 0)=\xi . \end{array}\right. \end{aligned}$$

(2.2)

Hence

$$\begin{aligned} \Gamma '=\sqrt{\ell ^2+\beta ^2}e_1, \quad \Gamma ''\Big |_{T_1\mathbb {R}^2}=\frac{\ell \ell '+\beta \beta '}{\sqrt{\ell ^2+\beta ^2}}e_1 +(\ell ^2+\beta ^2)(h^2_{11}e_2 + h^3_{11}e_3), \end{aligned}$$

where

$$\begin{aligned} h^2_{11}=\frac{\ell '\beta -\ell \beta '}{(\sqrt{\ell ^2+\beta ^2})^3}, \quad h^3_{11}=-\frac{\ell \beta }{\ell ^2+\beta ^2} \end{aligned}$$

are coefficients of the second fundamental form of the Legendre curve $\Gamma$ in $T_1\mathbb {R}^2$.

Remark 2.2

A Legendrian surface (or curve) in a Sasakain manifolds has a property that its second fundamental form with respect to the Reeb field $\xi$ vanishes, since $\xi$ is Killing. The above computation shows that $T_1\mathbb {R}^2$ is not Sasakian.

We now give an example of Legendre curves. For more examples see Sect. 3 below.

Example 2.1

Let m, n be two natural numbers with $k=n-m\ge 1$. Then $\Gamma =(\gamma , \nu ):\mathbb {R}\rightarrow T_1\mathbb {R}^2$ defined by

$$\begin{aligned} \gamma (\theta ) =\left( \frac{1}{m} {\theta }^m, \frac{1}{n} {\theta }^n\right) , \quad \nu ( \theta )=\frac{1}{\sqrt{ {\theta }^{2k}+1}}(- {\theta }^k,1) \end{aligned}$$

is a Legendre curve. It is a Legendre immersion if and only if $m=1$ or $k=1$. Such a curve is called a curve of type (m, n), which is important in the theory of singularities. It is easy to check that

$$\begin{aligned} \ell (\theta )=\frac{k {\theta }^{k-1}}{{\theta }^{2k}+1}, \quad \beta (\theta ) =- {\theta }^{m-1}\sqrt{{\theta }^{2k}+1}. \end{aligned}$$

It is clear that when $k=1$ then $\ell (\theta )= \frac{1}{{\theta }^2+1}>0$, while $\beta$ changes sign near 0, if m is even. Hence the curve is not convex, by [5]. One can easily show that the curve is convex for odd m.

3 $\ell$-convex Legendre curves

First we generalize convex curves to $\ell$-convex curves.

Definition 3.1

A Legendre curve is called $\ell$-convex if $\ell >0$.

It was proved in [5] that a Legendre curve is convex if and only if both $\ell$ and $\beta$ do not change sign. By changing the orientation, it is equivalent to $\ell \ge 0$ and either $\beta \ge 0$ or $\beta \le 0$. In this paper we consider the set of $\ell$-convex Legendre curves, which is much more larger than the set of strictly convex regular curves. This can be seen clearly in the following Lemmas.

Lemma 3.2

If a front $\gamma : I=[a,b] \rightarrow \mathbb {R}^2$ is $\ell$-convex, then there exists a parametrization $\varphi : J \rightarrow I$ such that $\tilde{\gamma }=\gamma \circ \varphi$ satisfies $\tilde{\ell }=1$.

Proof

Let $\psi (t) =\int _a^t 1/\ell (s) ds$ and $\varphi :J\rightarrow I$ its inverse. Here $J=[0, \int _a^b \frac{1}{\ell (s)} ds]$. Set

$$\begin{aligned} \tilde{\gamma }(t):= \gamma \circ \varphi , \quad \tilde{\nu }=\nu \circ \varphi . \end{aligned}$$

It is clear that $(\tilde{\gamma }, \tilde{\nu })$ is a Legendre curve with $\tilde{\mu }= \mu \circ \varphi .$ Moreover

$$\begin{aligned} \tilde{\ell }= \langle \tilde{\nu }', \tilde{\mu }\rangle = \varphi ' \ell \circ \varphi =1. \end{aligned}$$

$\square$

We call the parametrization founded in Lemma 3.2canonical parametrization for $\ell$-convex curves. For $\ell$-convex curves we always use the canonical parametrization and hence consider only Legendre curves with $\ell =1$.

Lemma 3.3

If a closed Legendre curve $\gamma : {\mathbb {S}^{1}}\rightarrow \mathbb {R}^2$ has $\ell (\theta )=1$ for any $\theta \in {\mathbb {S}^{1}}$, then there exists a function $p: {\mathbb {S}^{1}}\rightarrow \mathbb {R}$ and $\theta _0 \in {\mathbb {S}^{1}}$ such that

$$\begin{aligned} \gamma (\theta +\theta _0)=p(\theta )(\cos \theta , \sin \theta )+p'(\theta )(-\sin \theta , \cos \theta ). \end{aligned}$$

Proof

Let $f(\theta )$ be the angle function of $\nu$, i.e., $\nu (\theta )=(\cos f(\theta ), \sin f(\theta ))$. It is clear that $\mu (\theta )=(-\sin f(\theta ), \cos f(\theta )).$ We can represent $\gamma$ by

$$\begin{aligned} \gamma (\theta )=p(\theta )\nu (\theta )+q(\theta )\mu (\theta ). \end{aligned}$$

Since $\langle \gamma ', \nu \rangle = p'-q,$ the Legendrian condition (2.1) is equivalent to $q= p'$. The condition $\ell =1$ is equivalent to

$$\begin{aligned} 1=\ell (\theta )=\langle \nu ', \mu \rangle =f', \end{aligned}$$

i.e., $f(\theta )= \theta -\theta _0$, for some $\theta _0\in {\mathbb {S}^{1}}$. Therefore we have

$$\begin{aligned} \gamma (\theta )=p(\theta -\theta _0)(\cos (\theta -\theta _0), \sin (\theta -\theta _0))+p'(\theta -\theta _0)(-\sin (\theta -\theta _0), \cos (\theta -\theta _0)). \end{aligned}$$

$\square$

Moreover, it is clear that a map with the following form

$$\begin{aligned} \gamma (\theta )=p(\theta )(\cos \theta , \sin \theta )+p'(\theta )(-\sin \theta , \cos \theta )\end{aligned}$$

(3.1)

is a Legendre curve with $\nu (\theta ) =(\cos \theta ,\sin \theta )$ and $\ell =1$. Hence to consider $\ell$-convex Legendre curves we only need to consider curves with form (3.1). For a convex regular curve the associated function p is the so-called Minkowski support function. Therefore, we call the function p in (3.1) support function of $\gamma$. From now on all curves we consider are closed Legendre curves with form (3.1).

Definition 3.4

Let $\gamma$ be a closed Legendre curve with support function p. We define its (algebraic) length L and (algebraic) enclosed area A by

$$\begin{aligned} L=\int _{{\mathbb {S}^{1}}}(p+p'') d\theta =\int _{{\mathbb {S}^{1}}} p d\theta ,\qquad A=\frac{1}{2}\int _{{\mathbb {S}^{1}}}p(p+p'') d\theta . \end{aligned}$$

We emphasize that the length and the area of a Legendre curve could be zero or even negative. By replacing p to $-p$ we can change the sign of L and keep the sign of A. Hence we only need to consider $\ell$-convex curves with $L\ge 0$ in this paper. If a curve $\gamma$ is strictly convex, then it is well-known that p can be chosen such that

$$\begin{aligned} p(\theta )>0, \quad p(\theta )+p''(\theta )> 0, \quad \theta \in {\mathbb {S}^{1}}. \end{aligned}$$

Remark 3.5

An $\ell$-convex curve with support p has

$$\begin{aligned} \beta =p+p''. \end{aligned}$$

(3.2)

One can easily check that $\beta$ satisfies

$$\begin{aligned} \int _{\mathbb {S}^{1}}\beta (\theta ) \cos \theta d \theta = \int _{\mathbb {S}^{1}}\beta (\theta )\sin \theta d\theta =0. \end{aligned}$$

(3.3)

It follows from $\gamma ' (\theta )= \beta (\theta ) \mu (\theta )$. Vice versa, if a function $\beta :{\mathbb {S}^{1}}\rightarrow \mathbb {R}$ satisfies (3.3), then there exists an $\ell$-convex curve with support function p such that its $\beta$-curvature satisfies (3.2).

Now we give examples of $\ell$-convex Legendre curves $\gamma$ with support function p.

Example 3.1

(Points) The first example is the most trivial one, points. A point $(a_1, b_1)\in \mathbb {R}^2$ can be represented by an $\ell$-convex curve with support function $p=a_1\cos \theta +b_1 \sin \theta .$

Example 3.2

(Circles) Any constant $a_0\in \mathbb {R}$ defines an $\ell$-convex Legendre curve with support $p=a_0$. Its corresponding curve $\gamma$ is $\gamma (\theta )=a_0(\cos \theta , \sin \theta )$. If $a_0>0$, then it is the circle of radius $a_0$ centered at the origin. If $a_0<0$, we view it as a circle of negative radius $a_0$. If $a_0=0$, we also see it as a circle of zero radius. Certainly in this case, i.e., $p=0$, it can also be seen as a point, the origin.

For any two $\ell$-convex curves with support functions $p_1$ and $p_2$, we define their Minkowski sum, the curve with support function $p=p_1+p_2$. For strictly convex regular it is well-known that the Minkowski sum of two curves has this property. For the definition of Minkowski sum and its properties, we refer to the classical book [18]. With the Minkowski sum a circle of radius $a_0$ centered at $(a_1, b_1)$ can also be seen as a Minkowski sum of a circle and a point, with the support function $a_0 + a_1\cos \theta +b_1 \sin \theta .$

For a Legendre curve $(\gamma , \nu )$ one can define parallel curves by

$$\begin{aligned} \gamma _\lambda := \gamma +\lambda \nu , \end{aligned}$$

for $\lambda \in \mathbb {R}$. When this curve is an $\ell$-convex curve with support function p, then it is easy to check that the support functions of its parallel curves are

$$\begin{aligned} p_\lambda =p+\lambda . \end{aligned}$$

Example 3.3

(Astroid) Except circles, i.e., the curves with $p=a_0 +a_1 \cos \theta + b_1 \sin \theta$, we are also interested in astroids, which are $\ell$-convex curves with support function

$$\begin{aligned} a_2\cos 2\theta + b_2 \sin 2 \theta . \end{aligned}$$

See Fig. 1. It is a superellipse, i.e., it satisfies

$$\begin{aligned} x^{2/3} +y^{2/3}=a^{2/3}, \end{aligned}$$

for certain constant a.

Fig. 1

Astroid with $p=\sin 2\theta$

Astroids have $\beta$-curvature

$$\begin{aligned} -3 (a_2 \cos 2\theta +b_2 \sin 2\theta ). \end{aligned}$$

Since the $\beta$-curvature changes sign, it is not convex. Moreover, it has 4 singular points. An $\ell$-convex curve with support function

$$\begin{aligned} a_0 +a_1\cos \theta + b_1 \sin \theta +a_2 \cos 2\theta + b_2 \sin 2 \theta \end{aligned}$$

is a parallel curve of an astroid centered at $(a_1, b_1)$. It has $\beta$-curvature

$$\begin{aligned} a_0-3 (a_2 \cos 2\theta +b_2 \sin 2\theta ). \end{aligned}$$

Hence, if $a_0>0$ is large enough, it is a strictly convex regular curve.

In general, for any $k\in \mathbb {N}$, a curve with support function

$$\begin{aligned} p=a_k\cos k\theta + b_k \sin k\theta \end{aligned}$$

is an interesting figure. See [12]. For $k=3$ the corresponding curve is called deltoid. See Fig. 2.

Fig. 2

Left $p=\cos 3\theta$,       right $p=\sin 3\theta$

We remark that the deltoid has in fact 6 singularities. It runs twice as $\theta$ goes from 0 to $2\pi$.

In Sect. 4 we will be interested in isoperimetric type inequalities and geometric problems, in which astroids or deltoid achieve optimality.

4 Isoperimetric inequalities for $\ell$-convex Legendre curves

We start this section with the isoperimetric inequality.

Theorem 4.1

Suppose that $\gamma$ is $\ell$-convex. Then

$$\begin{aligned} \Delta _1:=\frac{L^2}{4\pi } -A\ge 0, \end{aligned}$$

with equality if and only if $\gamma$ is a circle.

Its proof is standard by using the Fourier series, which was first used by Hurwitz [10]. It is well known that this classical inequality is true even under a very weaker condition. We remark that |L| is less than or equals to the length of $\gamma$, $\int _{{\mathbb {S}^{1}}} |\gamma ' | d\theta$. There has been a lot of work on the isoperimetric inequality. Here we just refer to one nice survey by Osserman [16] and a recent work [15].

Moreover, L could be zero. When $L=0$, then A must be negative. Indeed, Theorem 4.1 implies that in this case $A\le 0$. If $A=0$, i.e., $\Delta _1=0$, then again from Theorem 4.1$\gamma$ is a circle, which is a contradiction. Here, $\Delta _1$ is called deficit of the isoperimetric inequality.

With the concept of curvature pair $(\ell , \beta )$ we have another simple inequality.

Proposition 4.2

A closed, $\ell$-convex front $\gamma$ in the plane satisfies

$$\begin{aligned} \Delta _2:=\int _{{\mathbb {S}^{1}}} \beta ^2 d\theta -2A \ge 0, \end{aligned}$$

(4.1)

equality holds if and only if $\gamma$ is a circle.

Proof

A direct computation gives

$$\begin{aligned} \begin{array}{rcl} \displaystyle \int _{{\mathbb {S}^{1}}} \beta ^2 d\theta &{} =&{} \displaystyle \int _{{\mathbb {S}^{1}}} (p+ p'')^2 d\theta = \displaystyle 2A+ \int _{{\mathbb {S}^{1}}} p''(p+p'') d\theta \\ &{}=&{} 2A+ \displaystyle \int _{{\mathbb {S}^{1}}} \left( p''^2-p'^2 \right) d\theta . \end{array} \end{aligned}$$

Since $\int _{{\mathbb {S}^{1}}} p' d\theta =0$, the Proposition follows from the Wirtinger inequality. $\square$

If $\gamma$ is a convex regular curve with curvature $\kappa$, then the above inequality has the following equivalent form

$$\begin{aligned} \int _{{\mathbb {S}^{1}}} \frac{1}{\kappa } ds \ge 2A, \end{aligned}$$

(4.2)

where s is the arc-length element and $ds=(p+p'')d\theta$. In this case, it is a known inequality and follows from the isoperimetric inequality

$$\begin{aligned} \int _{{\mathbb {S}^{1}}} \frac{1}{\kappa } ds =\frac{1}{2\pi } \int _{\mathbb {S}^{1}}\frac{1}{\kappa }ds \cdot \int _{\mathbb {S}^{1}}\kappa ds \ge \frac{1}{2\pi } L^2 \ge 2A. \end{aligned}$$

Its higher dimensional analogue is the Heintze-Karcher-Ros inequality. When the algebraic area is non-positive, (4.1) is trivial. We can improve this proposition in the following stronger form.

Theorem 4.3

For any $\ell$-convex Legendre curve, there holds

$$\begin{aligned} 0\le \Delta _3:= \left( \int _{\mathbb {S}^{1}}\beta ^2 d\theta -2A\right) - 8\left( \frac{L^2}{4\pi }-A \right) \le \frac{1}{12} \int _{\mathbb {S}^{1}}\beta '^2 d\theta - 2\left( \frac{L^2}{4\pi }-A \right) =: \Delta _4.\nonumber \\ \end{aligned}$$

(4.3)

Moreover equality in the first inequality holds, i.e., $\Delta _3=0$, iff $\gamma$ is generated by

$$\begin{aligned} p=a_0+a_1\cos \theta +b_1\sin \theta + a_2 \cos 2\theta + b_2\sin 2\theta , \end{aligned}$$

(4.4)

and equality in the second inequality holds, i.e., $\Delta _4=\Delta _3,$ iff

$$\begin{aligned} p=a_0+a_1\cos \theta +b_1\sin \theta + a_2 \cos 2\theta + b_2\sin 2\theta + a_3\cos 3\theta +b_3\sin 3\theta . \end{aligned}$$

(4.5)

Proof

Let $p=a_0 +\sum _{k=1}^\infty (a_k\cos k \theta + b_k \sin k\theta )$. An elementary computation yields

$$\begin{aligned} L= & {} 2\pi a_0, \\ A= & {} \pi a^2_0+\frac{1}{2} \pi \sum _{k\ge 2} (1-k^2) (a_k^2 +b_k^2),\\ \int _{\mathbb {S}^{1}}\beta ^2 d\theta= & {} 2\pi a^2_0 + \pi \sum _{k\ge 2} (k^2-1)^2 (a_k^2+b_k^2),\\ \Delta _1= & {} \frac{L^2}{4\pi }-A=\frac{1}{2} \pi \sum _{k\ge 2} (k^2-1) (a_k^2 +b_k^2),\\ \Delta _2= & {} \int _{\mathbb {S}^{1}}\beta ^2 d\theta -2A=\pi \sum _{k\ge 2} (k^2-1) k^2 (a_k^2+b_k^2), \\ \Delta _3= & {} \left( \int _{\mathbb {S}^{1}}\beta ^2 d\theta -2A\right) -8 \left( \frac{L^2}{4\pi }-A \right) \\ {}= & {} \pi \sum _{k\ge 3} (k^2-1) (k^2-4) (a_k^2+b_k^2)\ge 0. \end{aligned}$$

In the last line equality holds if and only if p has form (4.4). Recall that $\beta =p+p''$, thus

$$\begin{aligned} \beta =a_0 + \sum _{k\ge 2} (1-k^2) (a_k\cos k\theta + b_k \sin k\theta )\end{aligned}$$

(4.6)

and

$$\begin{aligned} \int _{\mathbb {S}^{1}}\beta '^2 d\theta =\pi \sum _{k\ge 2} (k^2-1)^2 k^2 ( a_k^2 +b_k^2).\end{aligned}$$

(4.7)

It follows

$$\begin{aligned}{} & {} \Delta _4=\frac{1}{12}\int _{\mathbb {S}^{1}}\beta '^2 d\theta -2\left( \frac{L^2}{4\pi }-A\right) =\frac{\pi }{12} \sum _{k\ge 3} (k^2-1)(k^4-k^2-12) (a_k^2+b_k^2)\ge 0, \end{aligned}$$

and

$$\begin{aligned}{} & {} \frac{1}{12}\int _{\mathbb {S}^{1}}\beta '^2 d\theta - 2\left( \frac{L^2}{4\pi }-A\right) - \left( \int _{\mathbb {S}^{1}}\beta ^2 d\theta -2A\right) +8\left( \frac{L^2}{4\pi }-A \right) \\{} & {} \quad =\frac{\pi }{12} \sum _{k\ge 4} (k^2-1) (k^2-4)(k^2-9) (a_k^2 +b_k^2)\ge 0, \end{aligned}$$

and equality holds if and only if its support function has form (4.5). $\square$

From (4.6) and (4.7), we get

$$\begin{aligned} \beta ''=\sum _{k\ge 2}k^2(k^2-1)(a_k \cos k\theta +b_k \sin k\theta ) \end{aligned}$$

and thus

$$\begin{aligned} \int _{\mathbb {S}^{1}}\beta ''^2 d\theta =\pi \sum _{k\ge 2}k^4(k^2-1)^2(a_k^2+b_k^2). \end{aligned}$$

Now we can estimate further

$$\begin{aligned} \int _{\mathbb {S}^{1}}\beta ''^2 d\theta \ge 4\int _{\mathbb {S}^{1}}\beta '^2 d\theta +72\Delta _4,\end{aligned}$$

(4.8)

where

$$\begin{aligned}{} & {} \int _{\mathbb {S}^{1}}\beta ''^2 d\theta - 4\int _{\mathbb {S}^{1}}\beta '^2 d\theta -72\Delta _4-216(\Delta _4-\Delta _3)\\= & {} \pi \sum _{k\ge 5}(k^2-1)(k^2-4)(k^2-9)(k^2-16)(a_k^2+b_k^2). \end{aligned}$$

When $\gamma$ is a regular convex curve, the first inequality in Theorem 4.3 was proved in [13], while the second in a very recent work [11]. There is a series of sharp geometric inequalities for closed curves in the latter paper by using a higher order Wirtinger inequality.

Remark 4.4

All terms in (4.3) have geometric meaning. We explain the geometric meaning of $\int _{\mathbb {S}^{1}}\beta '^2 d \theta .$ It was observed in [6] that the concept of evolute of a convex curve can be naturally generalized to $\ell$-convex curves:

$$\begin{aligned} \gamma _E:=\gamma - \frac{\beta }{\ell }\nu =\gamma -\beta \nu . \end{aligned}$$

Due to $\beta =p+p''$ there holds

$$\begin{aligned} \gamma _E (\theta )= & {} p(\theta )(\cos \theta , \sin \theta ) +p' (\theta )(-\sin \theta , \cos \theta ) - (p(\theta )+p''(\theta ) ) (\cos \theta , \sin \theta )\\= & {} -p''(\theta )(\cos \theta , \sin \theta ) +p' (\theta )(-\sin \theta , \cos \theta ) \\= & {} p'(\theta )(\cos (\theta +\frac{\pi }{2}), \sin (\theta +\frac{\pi }{2}) ) +p'' (\theta )(-\sin (\theta +\frac{\pi }{2}), \cos ( \theta +\frac{\pi }{2})). \end{aligned}$$

Hence $\gamma _E (\theta -\frac{\pi }{2})$ is an $\ell$-convex curve with support function $p'(\theta -\frac{\pi }{2})$, and the associated $\beta$-curvature satisfies $\beta _{\gamma _E}=\beta '(\theta -\frac{\pi }{2})$. Thus

$$\begin{aligned} \int _{\mathbb {S}^{1}}\beta '^2 d\theta =\int _{\mathbb {S}^{1}}\beta _{\gamma _E}^2 d \theta . \end{aligned}$$

Moreover one can easily check that the algebraic area $A_{E}$ of $\gamma _E$ has the following relation to $\int _{\mathbb {S}^{1}}\beta ^2 d\theta$

$$\begin{aligned} -2A_E=- \int _{\mathbb {S}^{1}}(p'^2-p''^2) d\theta = \frac{1}{2} \int _{\mathbb {S}^{1}}\beta ^2 d\theta -2A. \end{aligned}$$

Together with Bonnesen’s inequality proved in the next Section we have

Corollary 4.5

For any $\ell$-convex Legendre curve, there holds

$$\begin{aligned} \int _{\mathbb {S}^{1}}\beta ^2 d\theta -2A \ge 8 \left( \frac{L^2}{4\pi }-A\right) \ge 2\pi (r_{out}-r_{in})^2. \end{aligned}$$

(4.9)

For the definition of $r_{out}$ and $r_{in}$ see the next Section. Hence if the deficit of inequality (4.1), $\int _{\mathbb {S}^{1}}\beta ^2 d\theta -2A$, is small, then the curve is close to a circle. This is a stability result for inequality (4.1).

Problem 1

It would be interesting to ask the stability of (4.3): when $\frac{1}{12}\int _{\mathbb {S}^{1}}\beta '^2 d\theta -2(\frac{L^2}{4\pi }-A)$ is close to zero, is $\gamma$ close to a parallel curve of an astroid?

Corollary 4.6

If $\gamma$ is an $\ell$-convex Legendre curve with $L=0$, then

$$\begin{aligned} \int _{\mathbb {S}^{1}}\beta ^2 d\theta \ge -6A=6|A| \end{aligned}$$

with equality holding iff $\gamma$ is an astroid.

It would also be interesting to ask if Theorem 4.3 is true for higher dimensions.

Conjecture 1

(Improved Heintze-Karcher-Ros inequality). Let $\Sigma \subset \mathbb {R}^{n+1}$ be a closed hypersurface with positive mean curvature $H>0$ and $\Omega$ its enclosed domain. There exists a positive constant $C_n$ depending only on n such that

$$\begin{aligned} \int _\Sigma \frac{n}{H} \ge (n+1)|\Omega | + C_n \left( \frac{1}{ (n+1)\omega _n^{\frac{1}{n}}} |\Sigma |^{\frac{n+1}{n}} - |\Omega |\right) , \end{aligned}$$

(4.10)

where $\omega _n$ is the area of the unit n-sphere, $|\Sigma |$ the area of $\Sigma$ and $|\Omega |$ the volume of $\Omega$. Here the mean curvature H is defined by the sum of all principal curvatures.

The classical isoperimetric inequality is

$$\begin{aligned} \frac{1}{ (n+1)\omega _n^{\frac{1}{n}}} |\Sigma |^{\frac{n+1}{n}} - |\Omega | \ge 0. \end{aligned}$$

Hence (4.10) is an improved inequality. If it is true, (4.10), together with a work of Figalli-Maggi-Pratelli [3], implys a stability result of the Heintze-Karcher-Ros inequality.

5 Bonnesen’s inequality and Green–Osher’s inequality

In this section we generalize Bonnesen’s inequality and Green–Osher’s inequality [8] for convex curves to $\ell$-convex Legendre curves. The proof is very close to the one given in [8]. The main modification is that we use the analytic properties of the support function to replace the geometric ones of the corresponding curve, which could be different. See Example 5.1 below.

Let A(t) denote the area of closed fronts $\gamma (t,\theta )$ under the following constant speed flow

$$\begin{aligned} \gamma (t, \theta )=\gamma (\theta )+t\nu (\theta ).\end{aligned}$$

(5.1)

If the initial curve $\gamma _0$ has $\ell _0=1$, then for any t,

$$\begin{aligned} \gamma '(t, \theta )=\gamma '(\theta )+t\nu '(\theta )=(\beta (\theta )+t)\mu (\theta ), \end{aligned}$$

which implies (5.1) preserves the Legendrian condition (2.1) and

$$\begin{aligned} \nu (t,\theta )=\nu (\theta ), \quad \ell (t, \theta )=1. \end{aligned}$$

Therefore under flow (5.1)

$$\begin{aligned} p(t, \theta )=\langle \gamma (t, \theta ), \nu (t, \theta ) \rangle =p(\theta )+t. \end{aligned}$$

Following Definition 3.4

$$\begin{aligned}A(t)&=\frac{1}{2}\int _{{\mathbb {S}^{1}}}p(t, \theta )(p(t, \theta )+p''(t, \theta )) d\theta \nonumber =\frac{1}{2}\int _{{\mathbb {S}^{1}}}(p(\theta )+t)(p(\theta )+t+p''(\theta )) d\theta \nonumber \\ {}&= \frac{1}{2}\int _{{\mathbb {S}^{1}}}p(\theta )(p(\theta )+p''(\theta )) d\theta +\frac{t}{2}\int _{{\mathbb {S}^{1}}}(2p(\theta )+p''(\theta )) d\theta +\frac{t^2}{2}\int _{{\mathbb {S}^{1}}} d\theta \\ {}&= A+tL+\pi t^2, \end{aligned}$$

which can be rewritten as

$$\begin{aligned} A(t)=\pi (t+\frac{L}{2\pi })^2+A-\frac{L^2}{4\pi }. \end{aligned}$$

Let $t_1\ge t_2$ be the roots of A(t), that is

$$\begin{aligned} t_1=-\frac{L}{2\pi }+\frac{\sqrt{L^2-4\pi A}}{2\pi }, \quad t_2=-\frac{L}{2\pi }-\frac{\sqrt{L^2-4\pi A}}{2\pi }. \end{aligned}$$

For a convex curve one can define inradius $r_{in}$ and outradius $r_{out}$. In this case $r_{in}$ and $r_{out}$ are defined by the radii of the largest inscribed and smallest circumscribed circles of the domain of $\gamma$ respectively. See for example [8]. The same definition can be used for any Jordon curves. For our $\ell$-convex Legendre curves we need to generalize these concepts for $\ell$-convex Legendre curves by using the support function. Let $r\in \mathbb {R}$ and $z=(a_1, b_1) \in \mathbb {R}^2=\mathbb {C}$ and define

$$\begin{aligned} c_{(z,r)} (\theta ) =r + a_1 \cos \theta +b_1\sin \theta . \end{aligned}$$

If there is no confusion, we denote the Legendre curve with support function $c_{(z,r)}$ also by $c_{(z,r)}$. If $r>0$, $c_{(z,r)}$ is the circle of radius r centered at z. For $r\le 0$ we view $c_{(z,r)}$ as a circle of radius $r\le 0$ centered at z, as mentioned above. For any $\ell$-convex Legendre curve $\gamma$ with potential p we call $c_{(z,r)}$ an inscribed circle of $\gamma$ if

$$\begin{aligned} c_{(z,r)} (\theta ) \le p(\theta ), \quad \forall \theta \in {\mathbb {S}^{1}}. \end{aligned}$$

A circumscribed circle of $\gamma$ can be defined similarly. Now we define the inradius $r_{in}$ and outradius $r_{out}$ for $\ell$-convex curves.

Definition 5.1

Let $\gamma$ be an $\ell$-convex curve with support function p. The inradius $r_{in}$ and outradius $r_{out}$ of $\gamma$ are defined by

$$\begin{aligned} r_{in} = \max \{ r\in \mathbb {R}\, |\, c_{(z,r)} (\theta ) \le p(\theta ), \forall \theta \in {\mathbb {S}^{1}}\} \end{aligned}$$

and

$$\begin{aligned} r_{out } = \min \{ r\in \mathbb {R}\, |\, c_{(z,r)} (\theta ) \ge p(\theta ), \forall \theta \in {\mathbb {S}^{1}}\} \end{aligned}$$

respectively.

It is easy to prove that there exists a maximal inscribed circle $c_{z,r}$ such that $r=r_{in}$. An inscribed circle $c_{(z,r)}$ of $\gamma$ is called tangent to $\gamma$ at $\gamma (\theta _0)$ if $c_{(z,r)} (\theta _0)=p(\theta _0)$. One can consider circumscribed circles analogously. We remark that $r_{in}$ could be negative. It is easy to see that if $\gamma$ is a regular convex curve then the definitions of $r_{in}$ and $r_{out}$ are the same as the ordinary ones. However in general it could be quite different. See Example 5.1 below.

With these notations we can generalize Bonnesen’s inequality for $\ell$-convex Legendre curves.

Theorem 5.2

If $\gamma$ is an $\ell$-convex and not a circle, then

$$\begin{aligned} \pi t^2-tL+A < 0, \quad t\in [r_{in}, r_{out}],\end{aligned}$$

(5.2)

$$\begin{aligned} L^2-4\pi A> \pi ^2(r_{out}-r_{in})^2. \end{aligned}$$

(5.3)

As in [8] we need the following Lemma

Lemma 5.3

Let $c_{(z,r)}$ be either a maximal inscribed or minimal circumscribed circle for an $\ell$-convex Legendre curve. Then for any $\theta _0$ there exists $\tilde{\theta }\in [\theta _0, \theta _0+\pi ]$ such that $c_{(z,r)}$ is tangent to $\gamma$ at $\gamma (\tilde{\theta })$.

Proof

We follow the proof given in [8], with a different setting, and consider also only the case of the inscribed circle. The case of circumscribed circle is the same. By a translation we may assume $z=0$. Assume, by contradiction, that there exists $\theta _0$ such that $c_{(z,r)}$ is not tangent to $\gamma$ at $\gamma (\theta )$ for any $\theta \in [\theta _0, \theta _0+\pi ]$. Wlog, we may assume that $\theta _0=0$. Hence we have $r<p(\theta )$ for any $\theta \in [0,\pi ]$. Since $[0,\pi ]$ is compact, there exist $\epsilon >0$ such that $r+2\epsilon < p(\theta )$ for $\theta \in [0,\pi ]$. Consider a new circle with the radius r defined by the support function $r+ \epsilon \sin \theta$. Since $r+\epsilon \sin \theta < r \le p(\theta )$ for any $\theta \in (\pi , 2\pi )$, we have

$$\begin{aligned} r+\epsilon \sin \theta < p(\theta ), \qquad \forall \theta \in [0,2\pi ]. \end{aligned}$$

This contradicts the maximality of r. $\square$

Now we prove Theorem 5.2.

Proof of Theorem 5.2

Choosing points of tangency $\theta _1, \theta _2,..., \theta _N$ on $[0, 2\pi ]$ so we get

$$\begin{aligned} \theta _{i+1}- \theta _i\le \pi , \quad p(\theta _i)=r_{in}, \ i=1,2,...,N. \end{aligned}$$

Then integration by parts implies

$$\begin{aligned}A(-r_{in})&=\frac{1}{2}\int _{{\mathbb {S}^{1}}} (p-r_{in})(p+ p''-r_{in}) d\theta \\&=\frac{1}{2}\int _{{\mathbb {S}^{1}}} [(p-r_{in})^2- p'^2] d\theta \\&= \frac{1}{2}\sum _{i=1}^N\int _{\theta _i}^{\theta _{i+1}} [(p-r_{in})^2-p'^2] d\theta \le 0. \end{aligned}$$

In the last inequality we have used the Wirtinger inequality. The same argument works for $r_{out}$. Hence we have finised the proof of (5.2). (5.2) and the isoperimetric inequality means that

$$\begin{aligned} t_2<-r_{out}< -\frac{L}{2\pi }< -r_{in} < t_1. \end{aligned}$$

It implies

$$\begin{aligned} r_{out}-r_{in} < t_1-t_2 = \frac{1}{\pi }\sqrt{L^2-4\pi A}, \end{aligned}$$

and hence (5.3), which completes the proof. $\square$

The Bonnesen inequality holds for a general regular simple curve. Though our inequalities (5.2) and (5.3) have the same form as the classical Bonnesen inequality, the definitions of $r_{in}$ and $r_{out}$ are not the same for non-convex $\ell$-convex Legendre curves. Our inequalities are stronger for non-convex curves. This is showed in the following example.

Example 5.1

Let $\gamma$ with $p=\sin 2\theta$, namely $\gamma$ is an astroid. Then it is easy to see that its algebraic length and area are $L=0$, $A=-\frac{3}{2}\pi$. Moreover, it is easy to see that $r_{in}=-1$ and $r_{out}=1$. Hence we have

$$\begin{aligned} L^2-4\pi A = 6\pi ^2, \quad \pi ^2(r_{out}-r_{in})^2= 4\pi ^2. \end{aligned}$$

(5.4)

The curve is given by

$$\begin{aligned} (x,y):=(2\sin ^3 \theta , 2\cos ^3\theta ). \end{aligned}$$

We have

$$\begin{aligned} x^{\frac{2}{3}} + y^{\frac{2}{3}} =2^{\frac{2}{3}}. \end{aligned}$$

Its absolute length is ${\bar{L}}= 12$ and the absolute (or enclosed) area ${\bar{A}}=\frac{3}{2} \pi$. This curve is a Jordan curve and one can define the inradius ${\bar{r}}_{in}$ and outradius ${\bar{r}}_{out}$ by a usual way. Now one can easily check that ${\bar{r}}_{in}=1$ and ${\bar{r}}_{out}=2$. Hence

$$\begin{aligned} \begin{array}{rcl} \bar{L}^2-4\pi \bar{A} = 144- 6\pi ^2=6\pi ^2 + 12(12-\pi ^2), \quad \pi ^2({\bar{r}}_{out}-{\bar{r}}_{in})^2 = \pi ^2. \end{array} \end{aligned}$$

It is now clear to see that the usual Bonnesen inequality ${\bar{L}}^2-4\pi \bar{A} \ge \pi ^2({\bar{r}}_{out}-{\bar{r}}_{in})^2$ is less precise than our inequality $L^2-4\pi A \ge \pi ^2( r_{out}- r_{in})^2$, for

$$\begin{aligned} {\bar{L}}^2-4\pi \bar{A}> L ^2-4\pi A> \pi ^2(r_{out}-r_{in})^2> \pi ^2({\bar{r}}_{out}-{\bar{r}}_{in})^2. \end{aligned}$$

Problem 2

From Example 5.1 it would be interesting to ask: is there an improved Bonnesen’s inequality for $\ell$-convex curves with $L=0$ such that the above example is an optimal one, namely an improved Bonnesen’s inequality with equality iff it is an astroid. For example, is

$$\begin{aligned} L^2-4\pi A \ge \frac{3}{2} \pi ^2(r_{out}-r_{in})^2 \end{aligned}$$

true? (5.4) shows that the astroid achieves equality.

Now we prove the Green–Osher inequality for $\ell$-convex curves.

Theorem 5.4

Let $F(\theta )$ be a convex function on $\mathbb {R}$, i.e. $F''(\theta )\ge 0$. Then

$$\begin{aligned} \frac{1}{2\pi }\int _{{\mathbb {S}^{1}}} F(\beta ) d\theta \ge \frac{1}{2}[F(-t_1)+F(-t_2)]. \end{aligned}$$

To prove this theorem, we make the following definition and notation: Consider

$$\begin{aligned} \sup \left\{ \int _I\beta (\theta )d\theta \, |\, I\subset {\mathbb {S}^{1}}, \int _I d\theta =\pi \right\} . \end{aligned}$$

Let $I_1$ denote a subset of ${\mathbb {S}^{1}}$ of measure $\pi$ realizing this bound, and let $I_2$ be its complement. There exists a real number a such that

$$\begin{aligned} I_1\subseteq \{\theta , \beta (\theta )\ge a\}, \quad I_2\subseteq \{\theta , \beta (\theta )\le a\}. \end{aligned}$$

Set

$$\begin{aligned} \beta _1=\frac{1}{\pi }\int _{I_1} \beta (\theta ) d\theta , \quad \beta _2=\frac{1}{\pi }\int _{I_2} \beta (\theta ) d\theta . \end{aligned}$$

Note that

$$\begin{aligned} \beta _1+\beta _2=\frac{L}{\pi }, \quad \beta _1\ge \beta _2, \end{aligned}$$

and we may write

$$\begin{aligned} \beta _1=\frac{L}{2\pi }+b, \quad \beta _2=\frac{L}{2\pi }-b \end{aligned}$$

for some $b\ge 0$.

$\gamma$ is called symmetric if $p(\theta )=p(\theta +\pi )$ for all $\theta \in {\mathbb {S}^{1}}$.

Proposition 5.5

Let $\gamma$ be symmetric, then

$$\begin{aligned} \beta _1\ge -t_2. \end{aligned}$$

Proof

Since $\gamma$ is symmetric, then for any given $\theta _0$, we get

$$\begin{aligned} A(-p(\theta _0))&=\frac{1}{2}\int _{{\mathbb {S}^{1}}} (p-p(\theta _0))(p+p''-p(\theta _0)) d\theta \\&=\frac{1}{2}\int _{{\mathbb {S}^{1}}} [(p-p(\theta _0))^2-p'^2] d\theta \\&= \frac{1}{2}\int _{\theta _0}^{\theta _{0}+\pi } [(p-p(\theta _0))^2- p'^2] d\theta + \frac{1}{2}\int _{\theta _0+\pi }^{\theta _{0}+2\pi } [(p-p(\theta _0))^2- p'^2] d\theta \\&\le 0, \end{aligned}$$

which means for all $\theta$,

$$\begin{aligned} -t_1\le p(\theta ) \le -t_2. \end{aligned}$$

In other words

$$\begin{aligned} -u\le p(\theta )-\frac{L}{2\pi }\le u, \end{aligned}$$

where $u=\frac{\sqrt{L^2-4\pi A}}{2\pi }$. The inequality we are trying to prove is equivalent to

$$\begin{aligned} b\ge u. \end{aligned}$$

On $I_1$, it follows from $\beta (\theta )-a\ge 0$ that

$$\begin{aligned} -\left( p(\theta )-\frac{L}{2\pi }\right) (\beta (\theta )-a)\le u(\beta (\theta )-a). \end{aligned}$$

Integrating, we have

$$\begin{aligned} -\frac{1}{\pi }\int _{I_1} \left( p(\theta )-\frac{L}{2\pi }\right) (\beta (\theta )-a) d\theta \le u(\beta _1-a).\end{aligned}$$

(5.5)

On $I_2$, since $\beta (\theta )-a\le 0$,

$$\begin{aligned} -\left( p(\theta )-\frac{L}{2\pi }\right) (\beta (\theta )-a)\le -u(\beta (\theta )-a). \end{aligned}$$

Integrating, we have

$$\begin{aligned} -\frac{1}{\pi }\int _{I_2} \left( p(\theta )-\frac{L}{2\pi }\right) (\beta (\theta )-a) d\theta \le -u(\beta _2-a).\end{aligned}$$

(5.6)

Adding (5.5) and (5.6) gives

$$\begin{aligned} -\frac{1}{\pi }\int _{{\mathbb {S}^{1}}}\left( p(\theta )-\frac{L}{2\pi }\right) (\beta (\theta )-a) d\theta \le u(\beta _1-\beta _2). \end{aligned}$$

The left-hand side simplifies to

$$\begin{aligned} \frac{1}{2\pi ^2}(L^2-4\pi A)=2u^2. \end{aligned}$$

The right-hand side is 2ub, and thus $u\le b$ as desired. $\square$

For the symmetrization we can follow their idea again, but in our setting. Given $\theta _0$, let us want to do for the half curve $\gamma : [\theta _0,\theta _0+\pi ]$ as in their proof by rotating this half curve by the line connecting $\gamma (\theta _0)$ and $\gamma (\theta _0+\pi )$ with respect to their middle point. In term of the support function, one can show that the translated curve $\tilde{\gamma }$ has a support function

$$\begin{aligned} {\tilde{p}}(\theta )=p(\theta )-\frac{p(\theta _0)-p(\theta _0+\pi )}{2} \cos (\theta -\theta _0) - \frac{p'(\theta _0)-p'(\theta _0+\pi ) }{2} \sin (\theta -\theta _0). \end{aligned}$$

It is clear that $\tilde{\gamma }$ admits the same $\beta$, length L and area A with $\gamma$ on interval $[0, 2\pi ]$, and

$$\begin{aligned} {\tilde{p}}(\theta _0)={\tilde{p}}(\theta _0+\pi )=\frac{1}{2} (p(\theta _0)+p(\theta _0+\pi )), \quad {\tilde{p}}'(\theta _0)=\frac{1}{2} (p'(\theta _0)+p'(\theta _0+\pi )). \end{aligned}$$

Proposition 5.6

If $\gamma$ is an $\ell$-convex curve with $\ell =1$, then

$$\begin{aligned} \beta _1\ge -t_2. \end{aligned}$$

Proof

We proceed by a symmetrization argument as in [8]. For any $\theta$, $\gamma$ can be divided into two curves by joining the points on $\gamma$ corresponding to $\theta , \theta +\pi$ by a straight line. Let $L_1$ and $L_2$ be the lengths of the two pieces of $\gamma$, and denote

$$\begin{aligned} A_1=\frac{1}{2}\int _{\theta }^{\theta +\pi } p(p+p'') d\theta , \ A_2=\frac{1}{2}\int _{\theta +\pi }^{\theta +2\pi } p(p+p'') d\theta , \end{aligned}$$

then

$$\begin{aligned} L=L_1+L_2, \ A=A_1+A_2. \end{aligned}$$

Choose $\theta _0$ such that

$$\begin{aligned} L_1^2-2\pi A_1=L_2^2-2\pi A_2. \end{aligned}$$

We assume $\gamma$ satisfies

$$\begin{aligned} p(\theta _0 +\pi )=p(\theta _0). \end{aligned}$$

Otherwise we can translate it via ${\tilde{p}}$, which owns the same $\beta$, length L and area A with $\gamma$.

Let $\gamma _1$ and $\gamma _2$ be two symmetric curves that have support functions

$$\begin{aligned} p_1 (\theta )={\left\{ \begin{array}{ll} p(\theta ), \quad \quad \quad \theta \in [\theta _0,\theta _0+\pi ],\\ p (\theta -\pi ), \ \quad \theta \in [\theta _0+\pi , \theta _0+2\pi ] \end{array}\right. } \end{aligned}$$

and

$$\begin{aligned} p_2 (\theta )={\left\{ \begin{array}{ll} p(\theta +\pi ), \quad \theta \in [\theta _0,\theta _0+\pi ],\\ p (\theta ), \quad \quad \quad \theta \in [\theta _0+\pi , \theta _0+2\pi ] \end{array}\right. } \end{aligned}$$

respectively. It is clear that $\gamma _i$ has perimeter $2L_i$, area $2A_i$, and $p_i(\theta +\pi )=p_i(\theta )$ for any $\theta$, $i=1, 2$.

Of importance we notice, for symmetric curves $\gamma _1$ and $\gamma _1$, their subsets $I_1(\gamma _1)$ and $I_1(\gamma _2)$ are both symmetric. Since $\int _I\beta (\theta ) d\theta$ is maximized by $I_1$ among all subsets of measure $\pi$, it follows that

$$\begin{aligned} \beta _1\ge \frac{1}{2}\left( \int _{I_1(\gamma _1)}\beta (\theta ) d\theta + \int _{I_1(\gamma _2)}\beta (\theta ) d\theta \right) =\frac{1}{2}(\beta _1(\gamma _1)+\beta _1(\gamma _2)). \end{aligned}$$

By Proposition 5.5,

$$\begin{aligned} \beta _1(\gamma _1)\ge \frac{2L_1}{2\pi }+\frac{\sqrt{(2L_1)^2-8\pi A_1}}{2\pi }, \quad \beta _1(\gamma _2)\ge \frac{2L_2}{2\pi }+\frac{\sqrt{(2L_2)^2-8\pi A_2}}{2\pi }. \end{aligned}$$

Taking the average

$$\begin{aligned} \beta _1\ge \frac{L_1+L_2}{2\pi }+\frac{\sqrt{(2L_1)^2-8\pi A_1}+\sqrt{(2L_2)^2-8\pi A_2}}{4\pi } =\frac{L}{2\pi }+\frac{\sqrt{(2L_1)^2-8\pi A_1}}{2\pi }. \end{aligned}$$

The inequality we want is

$$\begin{aligned} \beta _1\ge \frac{L}{2\pi }+\frac{\sqrt{L^2-4\pi A}}{2\pi } =\frac{L}{2\pi }+\frac{\sqrt{(L_1+L_2)^2-4\pi (A_1+A_2)}}{2\pi }, \end{aligned}$$

which holds since

$$\begin{aligned} (2L_1)^2-8\pi A_1{} & {} =2L_1^2-4\pi A_1+2L_2^2-4\pi A_2 \\{} & {} =(L_1+L_2)^2+(L_1-L_2)^2-4\pi (A_1+A_2). \end{aligned}$$

This proves the proposition. $\square$

To prove Theorem 5.4, we need the elementary lemma:

Lemma 5.7

If $F(\theta )$ is convex, then if $b\ge a\ge 0$ and c arbitrary, then

$$\begin{aligned} F(c-a)+F(c+a)\le F(c-b)+F(c+b). \end{aligned}$$

Proof of Theorem 5.4

By Jensen’s inequality, applied to $I_i$, we have

$$\begin{aligned} \frac{1}{\pi }\int _{I_i}F(\beta (\theta ))d\theta \ge F\left( \frac{1}{\pi }\int _{I_i}\beta (\theta )d\theta \right) =F(\beta _i), \ i=1, 2. \end{aligned}$$

Taking the average of these two inequalities for $i=1, 2$ gives

$$\begin{aligned} \frac{1}{2\pi }\int _{{\mathbb {S}^{1}}}F(\beta (\theta ))d\theta \ge \frac{1}{2}(F(\beta _1)+F(\beta _2)). \end{aligned}$$

By Lemma 5.7,

$$\begin{aligned} F(\beta _1)+F(\beta _2)\ge F(-t_1)+F(-t_2). \end{aligned}$$

The Theorem then holds. $\square$

When F is strictly convex, one can show that equality in Green–Osher’s inequality implies that the curve is a circle. This follows from [7]. It would be interesting to ask if one can find an optimal Green–Osher type inequalities in the class of $\ell$-convex curves with $L=0$, which include Corollary 4.6 as a special case. Moreover equality in such an inequality holds iff the curve is an astroid.

6 An inverse curve flow for $\ell$-convex curves

In this section we consider an inverse curve flow for $\ell$-convex curves, which preserves the Legendrian condition, namely (2.1). In order to construct such a flow, instead of $\gamma$ it would be better to consider the pair $(\gamma ,\nu )$ as a curve into the contact manifold $\mathbb {R}^2\times {\mathbb {S}^{1}}$. In our recent paper we propose a general approach to consider curvature flows for Legendre curves. It was proved that a suitable flow with a normal velocity, which means keeping the Legendrian condition (2.1), must have the following form

$$\begin{aligned} {\left\{ \begin{array}{ll} \displaystyle \frac{\partial \gamma (t, \theta )}{\partial t}= \frac{\ell f' }{{\ell ^2+\beta ^2}}\mu +f\nu , \\ \displaystyle \frac{\partial \nu (t, \theta )}{\partial t}=- \frac{\beta f'}{{\ell ^2+\beta ^2}}\mu , \end{array}\right. } \end{aligned}$$

(6.1)

where f is some smooth function defined on the evolving Legendre curve, for example the curvature. Since adding a tangential vector field does not change the flow, we can normalize (6.1) by adding $(\frac{\beta h}{\sqrt{\ell ^2+\beta ^2}}\mu , \frac{\ell h}{\sqrt{\ell ^2+\beta ^2}} \mu )$, which is a tangential vector field in view of (2.2), to (6.1) for any h

$$\begin{aligned} \left\{ \begin{array}{rcl} \displaystyle \partial _t\gamma &{}=&{} \displaystyle \frac{\beta h}{\sqrt{\ell ^2+\beta ^2}}\mu + \frac{\ell f'}{\ell ^2+\beta ^2}\mu +f\nu , \\ \displaystyle \partial _t\nu &{}=&{} \displaystyle \frac{\ell h}{\sqrt{\ell ^2+\beta ^2}} \mu -\frac{\beta f'}{\ell ^2+\beta ^2} \mu . \end{array} \right. \end{aligned}$$

(6.2)

When $\ell >0$, we can choose h satisfying

$$\begin{aligned} h=\frac{\beta }{\ell }\frac{f'}{\sqrt{\ell ^2+\beta ^2}}, \end{aligned}$$

and obtain a simpler flow

$$\begin{aligned} \left\{ \begin{array}{rcl} \displaystyle \partial _t\gamma &{}=&{} \displaystyle \quad \frac{f'}{\ell }\mu +f\nu , \\ \displaystyle \partial _t\nu &{}=&{} 0. \end{array} \right. \end{aligned}$$

(6.3)

It follows that

$$\begin{aligned} \partial _t\mu =0, \quad \partial _t\ell =0, \quad \partial _t\beta =\left( \frac{f'}{\ell }\right) '+fl. \end{aligned}$$

Lemma 6.1

If the initial curve is $\ell$-convex, then flow (6.3) preserves the normal field $\nu$, and hence $\mu$. Moreover if the initial curve $\gamma _0$ has $\ell _0=1$, then for any t, $\ell (t, \theta )=1$ and $\gamma (t, \theta )$ has form (3.1) with support function $p(t, \theta )$.

Now we consider an inverse curvature type Legendrian flow for $\ell$-convex curves by choosing

$$\begin{aligned} f= \frac{\beta }{\ell }. \end{aligned}$$

(6.4)

Remember that for regular curves it is the reciprocal of the curvature $\kappa$. Therefore, the corresponding flow is a natural generalization of the inverse curvature flow. By Lemma 6.1 we can consider $f=\beta$ for the initial curves with $\ell _0=1$. By Lemma 6.1 again we can write the flow by using support functions.

Lemma 6.2

If the initial curve $\gamma _0$ has form (3.1) with support function $p_0$, then flow (6.3) with velocity (6.4) is equivalent to

$$\begin{aligned} \partial _t p =p+p'' \end{aligned}$$

(6.5)

with $p(0)=p_0$.

Proof

The proof is now obvious with

$$\begin{aligned} \partial _t p=\partial _t\langle \gamma , \nu \rangle =\langle \partial _t\gamma , \nu \rangle +\langle \gamma , \partial _t\nu \rangle =\beta =p+p''. \end{aligned}$$

$\square$

This is a very simple parabolic equation. Now we compute the evolution equation for various geometric quantities under this flow.

$$\begin{aligned} \frac{dL}{dt}=\int _{{\mathbb {S}^{1}}}\frac{\partial p}{\partial t}d\theta =\int _{{\mathbb {S}^{1}}}\beta d\theta = \int _{{\mathbb {S}^{1}}} p d\theta =L.\end{aligned}$$

(6.6)

Since the area function is

$$\begin{aligned} A=\frac{1}{2}\int _{{\mathbb {S}^{1}}}p(p+p'') d\theta =\frac{1}{2}\int _{{\mathbb {S}^{1}}}(p^2-p'^2) d\theta , \end{aligned}$$

then

$$\begin{aligned}\frac{dA}{dt}&= \int _{{\mathbb {S}^{1}}} \left( p\partial _t p- p'\frac{\partial ^2 p}{\partial \theta \partial t}\right) d\theta \\&= \int _{{\mathbb {S}^{1}}} p(p+ p'') d\theta - \int _{{\mathbb {S}^{1}}} p' d(p+ p'') \\&= \int _{{\mathbb {S}^{1}}} \beta ^2 d\theta . \end{aligned}$$

The evolution equation for $\beta$ is

$$\begin{aligned} \partial _t\beta =\beta +\beta ''.\end{aligned}$$

(6.7)

Hence,

$$\begin{aligned} \frac{d}{dt} \int _{\mathbb {S}^{1}}\beta ^2 d\theta = 2\int _{\mathbb {S}^{1}}(\beta ^2-\beta '^2) d\theta . \end{aligned}$$

If $L_0=0$, i.e, $\int _{\mathbb {S}^{1}}\beta _0 d\theta =0$, we have $\int _{\mathbb {S}^{1}}\beta d\theta =L(t)=0$. Moreover we have

$$\begin{aligned} \int _{\mathbb {S}^{1}}\beta \cos \theta d\theta = \int _{\mathbb {S}^{1}}\beta \sin \theta d\theta =0. \end{aligned}$$

Hence for such a $\beta$ we know that

$$\begin{aligned} 4\int _{\mathbb {S}^{1}}\beta ^2 d\theta \le \int _{\mathbb {S}^{1}}\beta '^2 d\theta . \end{aligned}$$

It follows that

$$\begin{aligned} \frac{d}{dt}\left( \int _{\mathbb {S}^{1}}\beta ^2d\theta +6A \right) = 2\int _{\mathbb {S}^{1}}\left( 4\beta ^2-\beta '^2 \right) d\theta \le 0. \end{aligned}$$

Theorem 6.3

The inverse curvature flow has a global convergence for any initial $\ell$-convex curve. Moreover we have

(1) If $L_0 >0$, the flow expands exponentially and after a certain time the evolving curve becomes convex. After a suitable rescaling, the flow converges to a circle.

(2) If $L_0=0$, then the flow shrinks and after a suitable rescaling it converges to a Legendre curve with a form

$$\begin{aligned} a_1 \cos \theta +b_1 \sin \theta + a_k \cos k\theta +b_k \sin k\theta \end{aligned}$$

(6.8)

for a certain $k\ge 2$, which is determined by $\gamma _0$.

The curves given by (6.8), together with circles, are all closed solitons of the inverse curvature flow.

Proof

If one expand p(t) into the Fourier series

$$\begin{aligned} p(t)=a_0(t) +\sum _k a_k(t) \cos k \theta + b_k (t) \sin k\theta , \end{aligned}$$

then it is easy to see that along the flow

$$\begin{aligned} \frac{d}{dt}a_0(t)= & {} a_0(t) \\ \frac{d}{dt}a_1(t)= & {} 0\\ \frac{d}{dt}a_k(t)= & {} (1-k^2) a_k, \quad \forall k\ge 2, \end{aligned}$$

and the same equations for $b_k$. Hence

$$\begin{aligned} p(t)=a_0 e^t+ a_1(0)\cos \theta + b_ 1(0) \sin \theta +\sum _{k=2}^\infty e^{-(k^2-1)t}(a_k(0)\cos k \theta + b_k (0) \sin k\theta ) \end{aligned}$$

is the solution of the inverse curvature flow. Consider

$$\begin{aligned} {\tilde{p}}(t):= p(t)- a_1(0)\cos \theta - b_1(0) \sin \theta . \end{aligned}$$

Then it is easy to see that after a suitable rescaling one can prove (1) and (2).

One can prove that a homothetic soliton of the flow is a solution of

$$\begin{aligned} p+p''=cp, \end{aligned}$$

for some constant c. It is easy to see that $c=0$ or $c=k$ for some positive integer $k\ge 2$. $c=0$ corresponds to a circle, while $c =k$ a solution in form (6.8). $\square$

Under the inverse curvature flow for $\ell$-convex Legendre curves we have a monotone property for isoperimetric quantities.

Theorem 6.4

The isoperimetric ratio $\frac{L^2}{A}$, $\Delta _1, \Delta _2, \Delta _3$ and $\Delta _4$, which are defined in Section 4, are all exponentially decreasing under the inverse curvature flow. Moreover $\Delta _1, \Delta _2, \Delta _3$ and $\Delta _4$ converges to zero as the time t goes to infinity.

Proof

With the help of the evolution equations for L and A, we compute

$$\begin{aligned} \frac{d}{d t}\left( \frac{L^2}{A}\right) =\frac{2L}{A}\frac{d L}{d t}-\frac{L^2}{A^2}\frac{d A}{d t}=\frac{L^2}{A^2}\left( 2A-\frac{dA}{dt}\right) =\frac{L^2}{A^2}\left( 2A-\int _{{\mathbb {S}^{1}}} \beta ^2 d\theta \right) \le 0. \end{aligned}$$

According to (4.3), there holds

$$\begin{aligned} \frac{d \Delta _1}{d t}= & {} \frac{L^2}{2\pi }-\int _{{\mathbb {S}^{1}}} \beta ^2 d\theta =\frac{L^2}{2\pi }-2A-\left( \int _{{\mathbb {S}^{1}}} \beta ^2 d\theta -2A\right) \\= & {} 2\Delta _1-\Delta _2=-6\Delta _1-\Delta _3\le -6\Delta _1. \end{aligned}$$

Now we use (6.7) to deduce

$$\begin{aligned} \frac{d \Delta _2}{d t}=2\int _{{\mathbb {S}^{1}}} \beta \frac{\partial \beta }{\partial t} d\theta -2\frac{d A}{dt}=2\int _{{\mathbb {S}^{1}}} \beta (\beta +\beta '') d\theta -2\int _{{\mathbb {S}^{1}}} \beta ^2 d\theta =-2\int _{{\mathbb {S}^{1}}} \beta '^2 d\theta . \end{aligned}$$

By (4.3), it suffices

$$\begin{aligned} \frac{d \Delta _2}{d t}=-24\Delta _4-48\Delta _1=-6\Delta _2-18\Delta _3+24(\Delta _3-\Delta _4)\le -6\Delta _2. \end{aligned}$$

When comes to $\Delta _3$, we have

$$\begin{aligned} \frac{d \Delta _3}{d t}=\frac{d \Delta _2}{d t}-8\frac{d \Delta _1}{d t}=-24\Delta _4-48\Delta _1-8(-6\Delta _1-\Delta _3)=-24\Delta _4+8\Delta _3\le -16\Delta _3. \end{aligned}$$

Since

$$\begin{aligned} \frac{d}{d t}\int _{{\mathbb {S}^{1}}} \beta '^2 d\theta =2\int _{{\mathbb {S}^{1}}} \beta '\frac{\partial \beta }{\partial \theta \partial t} d\theta =2\int _{{\mathbb {S}^{1}}} \beta '(\beta +\beta '')' d\theta =2\int _{{\mathbb {S}^{1}}} (\beta '^2-\beta ''^2) d\theta , \end{aligned}$$

due to (4.8) there holds

$$\begin{aligned} \frac{d}{d t}\int _{{\mathbb {S}^{1}}} \beta '^2 d\theta \le -6\int _{{\mathbb {S}^{1}}} \beta '^2 d\theta -144\Delta _4=-72(2\Delta _1+3\Delta _4), \end{aligned}$$

and hence

$$\begin{aligned} \frac{d \Delta _4}{d t}\le -6(2\Delta _1+3\Delta _4)-2(-6\Delta _1-\Delta _3)=-18\Delta _4+2\Delta _3\le -16\Delta _4. \end{aligned}$$

Integrating $\frac{d\Delta _i}{d t}\le -n_i\Delta _i$ with $n_1=n_2=6, n_3=n_4=16$ yields

$$\begin{aligned} \Delta _i(t)\le \Delta _i(0)e^{-n_i t}, \end{aligned}$$

which means that $\Delta _i, i=1, 2, 3, 4$ of the evolving curve converges to zero as t goes to infinity. $\square$

Theorem 6.4 indicates that all inequalities given in Sect. 4 are stable, at least under the inverse curvature flow.