1 Introduction

Feedback linearization of nonlinear control systems is a widely known control method applied to continuous-time nonlinear plants that satisfy certain conditions such as involutivity and being transformable into special canonical forms like Brunovsky or normal form [1,2,3,4]. The feedback linearization method is developed for discrete-time nonlinear systems too, both for affine [5] and non-affine systems [6]. By means of applying the artificial neural network (ANN) approach to the feedback linearization domain, ANN-based feedback linearization control methods have been proposed as powerful strategies for the control of the nonlinear systems in order to provide the ability of learning and generalization from the real data [6,7,8,9,10,11,12,13,14]. An approximate feedback linearization was developed by means of multilayer perceptron (MLP) based on a nonlinear state transformation providing local diffeomorphism conditions [8]. ANN-based control methods generally construct nonlinear auto-regressive moving-average (NARMA) plant models learned from the plant’s input and output and design NARMA-based neuro controllers [6,7,8,9,10]. ANN-based feedback linearization methods usually implement two separate ANN blocks, each of which defines a nonlinear function to make the overall feedback system with the newly defined input as linear [6, 8, 9, 12]. The direct adaptive neural control scheme of [11] can also be considered as a kind of implementation of feedback linearization but with a radial basis function neural network for an affine nonlinear multi–input–multi–output system. The so-called Learning Feedback Linearization (LFL) method proposed in [12] employs an ANN-based NARMA model implementing input-to-state feedback linearization blocks and then uses the conventional PID controller for the overall feedback-linearized control system.

On the other hand, several adaptive control methods have been used in the literature [15,16,17,18,19,20,21] for controlling nonlinear systems. The adaptive control method in [15] uses ANN-based prediction of a reference trajectory and the model-free adaptive controller simultaneously via the feedback-linearized model of the nonlinear dynamics [15]. An inverse system-based adaptive nonlinear controller employing ANN is developed in [16]. A model reference adaptive control and its extension version are used together for guaranteeing adaptive control parameters converge [17]. The work in [18] introduces an adaptive ANN-based control method having adaptation laws obtained from input–output data for the control of inverted pendulum. An output feedback-based adaptive ANN controller scheme is developed in [19] for tracking control of switched non-strict-feedback nonlinear systems. The proposed adaptive control scheme is applied to the interconnected nonlinear system with the global stability condition [20]. A kind of inverse system approach is applied for an adaptive nonlinear controller design [22]. This study employs a Wiener-type nonlinear controller model and a Hammerstein-type nonlinear plant model such that the overall closed-loop system becomes a linear system to which the online learning ARMA controller design method of [23] is applied.

The study presented in this paper proposes a new LFL method that applies online learning NARMA controller design methodology, originally developed in [23] for linear SISO plants, to the input–output feedback-linearized nonlinear affine SISO systems. The online learning NARMA controller design provides a Schur stable robust adaptive control scheme that is formulated in this work as a data-dependent robust solution to a system identification problem of a partially known system, i.e., the closed system. Herein, the known part is the data-dependent LFL-based identified plant model, whereas the unknown part is the controller to be adjusted online. The scheme firstly achieves the input–output feedback linearization of the nonlinear plant via LFL, and then, the plant model is identified as the combination of feedback linearization block and nonlinear plant. The overall linearized plant model parameters are computed by minimizing the plant identification error. The determination of the ARMA controller parameters is then performed by minimizing the tracking error, which is considered as the closed-loop system identification error, under Schur stability conditions. Both error terms are defined as regularized ε-insensitive loss functions that provide robustness property against to noise and disturbances, where the regularization is used for the penalization of generalization error [23,24,25].

The main contributions of the developed control scheme by which it differs from the related works existing in the literature are listed as follows.

  1. (i)

    The proposed control scheme relies on formulating both the plant identification and adaptive controller design as supervised learning problems. So, the proposed controller design gets benefit of the data-dependent online learning by which the closed-loop stability, adaptiveness, robustness, and generalization ability can be embedded in controller design process.

  2. (ii)

    As one of the most distinguished features of the proposed method, the controller design for tracking control purposes is described as an identification problem of a partially known system where the controller is the unknown part and the already identified plant model is the known part. From this point of view, the introduced supervised learning scheme for the controller design is applied in a direct way with no need to apply any preprocessing such as finding an inverse system for the plant. By means of this closed-loop system identification framework, the closed-loop system stability is ensured by imposing Schur conditions as linear inequality constraints in tracking error minimization. In the tracking error minimization procedure, which is implemented by pattern/batch mode minimization algorithms, the error is chosen as regularized ε-insensitive loss functions \({{\ell}}_{1,\varepsilon }\left(\cdot ,\cdot \right)\). Herein, being absolute for the error measures, i.e., \({{\ell}}_{1}\)’ness, provides robustness against disturbances and other outliers. The ε-insensitiveness provides robustness against noise, and immunization for the model errors originated from the ANN-based LFL approximation to the nonlinear plant. The regularization term added to the loss functions makes the controller model possess higher generalization abilities. The regularize \({{\ell}}_{1,\varepsilon }\left(\cdot ,\cdot \right)\) norm is used also in the plant identification phase as the identification error measure for building up a robust neural network model of the plant with high generalization ability.

  3. (iii)

    The proposed method provides the possibility of exploiting a linear ARMA controller for nonlinear plants by means of deriving a linear (augmented) plant model as a cascade of the LFL block and the nonlinear plant via input–output feedback linearization. The obtained linear closed-loop system model allows for exploitation of the online ARMA controller design method of [23] that is developed for linear plants. In the method of this paper, both the LFL block and linear ARMA controller are determined in a data-dependent way by using input–output data pairs measured from the nonlinear plant and the closed-loop system. It should be noted that the data-dependent LFL scheme of the proposed controller design method, which yields an ANN-based LFL approximation, does not require a known nonlinear plant model satisfying certain technical conditions such as involutivity to which the standard procedure of feedback linearization method valid for continuous-time systems [1, 2, 26] is applied. With the underlying learning abilities of ANN-based LFL approximation, the proposed data-dependent feedback linearization learns an approximate but acceptable linearized closed-loop system model. Herein, the approximation error is indeed defined in terms of the tracking and plant identification errors to be minimized. The learning feedback linearization scheme applied here is similar to the linearization method of [12]. Both are data-dependent feedback linearization. It means that the feedback-linearized (augmented) plant model is designed by learning in a supervised way. The main differences between them are the following. The method proposed in this paper is based on input–output linearization, while the study in [12] employs input-state linearization. On the other hand, the method in [12] employs a conventional PID whose parameters are learned by learning, so it does not have the adaptiveness, robustness, generalization ability and the guarantee for the closed-loop stability described in (i)–(ii). In contrast, the method proposed in this paper has all these features that are important, especially for nonlinear control systems.

The most decisive aspect of this article's main contributions, which are described above, in terms of system identification and control applications of artificial neural networks is the definition of model identification and controller design problems as supervised learning that runs online. With the “learning of feedback linearization” proposed in this article, the study given in [23], which is based on linear (ARMA) system identification and online learning of ARMA controller parameters, has been extended to the method of supervised learning of linear ARMA-based closed-loop system identification. This is achieved by employing a learned feedback-linearized model of the nonlinear plant. Thus, linear ARMA-based system identification, which is a widely studied method not only in control area but also in time-series analysis, has been extended to the identification and control of nonlinear systems, where both system identification and controller design have been defined as supervised learning schemes that run online. In this sense, the paper has contributed to the use of artificial neural networks and machine learning in the field of system identification and control.

In short, the proposed controller design scheme is the extension of the method of online learning ARMA controllers developed in [23] for linear plants to nonlinear affine plant cases with exploiting the method of learning feedback linearization introduced in [12]. Preliminary results of this study are partially published in the conference paper [27]. The method can be called in two ways: stable robust adaptive ARMA controller for feedback-linearized nonlinear plants or stable robust adaptive NARMA controller for nonlinear plants. In the former case, LFL block is considered as the front side block of the linearized (augmented) plant model. In the latter, LFL block is considered as the backside block coming after the linear ARMA controller to constitute a NARMA controller. Since the LFL block is not a part of the plant such that it is just used to transform the plant to a linear one by a linearization feedback control, the LFL block is appropriate to be considered as a part of the controller so the developed controller in this paper is preferred to be named as the NARMA controller that consists of a linear ARMA block cascaded by the LFL block. In the application part of this study, to show its superiority, the developed LFL-based stable robust adaptive NARMA controller is compared to the linear quadratic regulator (LQR) of [28] and the coupled sliding mode controller (SMC) [29, 30] in terms of their tracking performances. As the nonlinear plant, the ROTary inverted PENdulum (ROTPEN) is chosen. The experiments are conducted in two different modes: ROTPEN model is implemented in the software-in-the-loop mode first, that is, the computer simulation. Then, the developed method is applied for controlling a real ROTPEN plant in prototyping real-time simulation mode [31].

This paper is organized as follows. In Sect. 2, the developed LFL-based stable robust adaptive control scheme is explained. In Sect. 3, the performances of the proposed adaptive controller and the other controllers considered are compared to each other for the ROTPEN simulation model and a real ROTPEN plant. The conclusion and the possible future directions are provided in Sect. 4.

2 Proposed LFL-based stable robust adaptive control scheme

The proposed stable robust adaptive controller scheme, which is shown in Fig. 1, is implemented in three stages as follows. (1) A feedback-linearized plant model is constructed by an LFL block implemented with ANN that is cascaded by the nonlinear plant. The cascade combination of LFL block and the plant is identified as a linear ARMA plant model by minimizing the augmented plant identification error in (9). (2) The overall linear closed-loop system model that provides Schur stability is identified as an ARMA system model by minimizing the closed-loop system identification error in (12). (3) The linear ARMA controller parameters are calculated from the ARMA parameters of the closed-loop system found in 2) by using the augmented plant’s ARMA model parameters found in 1). These three stages might be followed from Fig. 1 in identifying the operation in the 1st stage that yields \({\left\{{a}_{n}\right\}}_{n=1}^{N}\) and \({\left\{{b}_{n}\right\}}_{n=1}^{M}\) as the plant ARMA model parameters, the operation in the 2nd stage that yields \({\left\{{\alpha }_{n}\right\}}_{n=1}^{\widehat{N}}\) and \({\left\{{\beta }_{n}\right\}}_{n=1}^{\widehat{M}}\) as the closed-loop system ARMA model parameters, and the operation in the 3rd stage that yields \({\left\{{f}_{m}\right\}}_{m=1}^{P}\), \({\left\{{c}_{m}\right\}}_{m=1}^{R}\) and \({\left\{{d}_{m}\right\}}_{m=1}^{Q}\) as the controller ARMA model parameters.

Fig. 1
figure 1

The proposed LFL-based adaptive control scheme (Color figure online)

Full size image

2.1 LFL for the nonlinear plant

This subsection presents the rationale behind the augmented plant model, which is the cascade of the LFL nonlinear block and the SISO plant together with a state-feedback architecture, by a linear ARMA model. For this purpose, let us give a brief explanation of the input–output feedback linearization method for time-invariant discrete-time Single-Input Single-Output (SISO) affine plants [5]. Assume that the plant is defined in the following input–output form.

$$\begin{aligned} y^{k + 1} = & f_{n} \left( {y^{k} , \ldots ,y^{k - n + 1} ; u^{k - d} , \ldots ,u^{k - d - m + 1} } \right) \\ & \; + g_{n} \left( {y^{k} , \ldots ,y^{k - n + 1} ; u^{k - d} , \ldots ,u^{k - d - m + 1} } \right) u^{k - d + 1} \\ \end{aligned}$$
(1)

Herein \(f_{n} \left( \bullet \right): {\varvec{R}}^{n} \times {\varvec{R}}^{m} \to R\;{\text{and}}\;g_{n} \left( \bullet \right): {\varvec{R}}^{n} \times {\varvec{R}}^{m} \to R\) are infinitely many differentiable functions such that \(g_{n} \left( \bullet \right)\) has a multiplicative inverse. \(u^{k} \in {\varvec{R}}\) is the control input, and \(y^{k} \in {\varvec{R}}\) is the output of the SISO system. \(m \le n\) and \(d\) stand for the relative degree of the system.

Defining a set of state variables as \(x_{i}^{k} = y^{k - i + 1}\) with \(i \in \left\{ {1, 2, \ldots ,n} \right\}\) and \(x_{n + i}^{k} = y^{k - m - d + i}\) with \(i \in \left\{ {1, 2, \ldots ,m + d - 1} \right\}\), the following state form is obtained for the system defined in (1).

$$\begin{aligned} x_{i}^{k + 1} &= x_{i + 1}^{k} \;{\text{with}}\;i \in \left\{ {1, 2, \ldots ,n} \right\} \\ x_{n}^{k + 1} &= f_{n} \left( {x^{k} } \right) + g_{n} \left( {x^{k} } \right) x_{n + m}^{k} \\ x_{n + i}^{k + 1} &= x_{n + i + 1}^{k} \;{\text{with}}\;i \in \left\{ {1, 2, \ldots ,m + d - 2} \right\} \\ x_{n + m + d - 1}^{k + 1} &= u^{k} \\ y^{k} &= x_{n}^{k} \\ \end{aligned}$$
(2)

For a system with relative degree one, i.e., \(d = 1\), we get

$$x_{n}^{k + 1} = f_{n} \left( {{\varvec{x}}^{k} } \right) + g_{n} \left( {{\varvec{x}}^{k} } \right) u^{k} .$$
(3)

So, the linearizing control input is obtained as

$$u^{k} = \frac{{ - f_{n} \left( {{\varvec{x}}^{k} } \right) + v^{k} }}{{g_{n} \left( {{\varvec{x}}^{k} } \right)}}$$
(4)

where \({v}^{k}\) represents the reference, namely the desired output at time \(k+1\).

For a system with the relative degree \(d>1\), the linearizing control can be derived [5] as follows.

$$u^{k} = \frac{{ - f_{n} \left( {{\varvec{T}}^{ - 1} \left[ {{\varvec{z}}^{k} } \right]} \right) + v^{k} }}{{g_{n} \left( {{\varvec{T}}^{ - 1} \left[ {{\varvec{z}}^{k} } \right]} \right)}}$$
(5)

where the invertible transformation \({\varvec{z}}^{k} = {\varvec{T}}\left[ {{\varvec{x}}^{k} } \right]\) is defined below.

$$\begin{aligned} z^{k} = & \left[ {z_{11}^{k} \ldots z_{1n}^{k} z_{1,n + 1}^{k} \ldots z_{1,n + d - 1}^{k} z_{21}^{k} \ldots z_{2m}^{k} } \right]^{T} \\ & \; = \left[ {x_{1}^{k} \ldots x_{n}^{k} x_{n}^{k + 1} \ldots x_{n}^{k + d - 1} x_{n + 1}^{k} \ldots x_{n + m}^{k} } \right]^{T} \\ \end{aligned}$$
(6)

So, for an arbitrary relative degree \(d\), the linearizing feedback control is defined in terms of \({\varvec{x}}\) and \(v\) as:

$$u=\gamma \left({\varvec{x}},v\right)$$
(7)

In this paper, the LFL block that is inspired by the well-known input–output linearization methodology described above. Since the proposed method in the paper learns LFL block based on input–output data, an LFL block that provides an exact linearization from the newly defined control input \(v\) to the system output \(y\) by means of a feedback control \(u=\gamma \left({\varvec{x}},v\right)\) may not exist. In this sense, the LFL block depicted in Fig. 1 does just define an approximate linearization rather than an exact one. The LFL block used for an approximate linearization is considered in this paper as having the following (discrete time) linear ARMA representation.

$$y^{k} = \sum\nolimits_{n = 1}^{N} {a_{n} y^{k - n} } + \sum\nolimits_{n = 0}^{M} {b_{n} v^{k - n} }$$
(8)

The LFL block of this paper is implemented by a specific algebraic ANN, which has the universal approximation property, namely the feedforward MLP with a single hidden layer shown in Fig. 2. ANN is trained with the training sample set \(\left\{{{\left[{{({\varvec{x}}}^{s})}^{T}{v}^{S}\right]}^{T},u}^{s}\right\}_{s=0}^{S}\). Herein, \({{\varvec{x}}}^{s}\) whose entries are defined in (2) in terms of the plant output is the measured output at different time instants \(k\). The LFL block is identified by training the MLP to learn the above given input–output samples in an offline manner with a batch mode (Levenberg–Marquardt) backpropagation algorithm.

Fig. 2
figure 2

The LFL is designed for the nonlinear plant during learning phase

Full size image

Now, as expressed in SubSect. 2.2, the identification of the augmented plant with an already learned LFL block can be made based on the ARMA model of (8).

2.2 ARMA-based identification of augmented plant

The ARMA model identification of the LFL-based augmented plant is depicted in Fig. 3. The augmented (feedback-linearized) plant identification is formulated as the minimization of the identification error in (9) that is defined by ε-insensitive loss function \({{\ell}}_{1,\varepsilon }\left(\cdot ,\cdot \right)\) given in (10). In contrast to the offline nature of the identification of LFL block, the augmented plant is identified in an online (mini-batch) mode. In this mode, the ARMA parameters of the augmented plant are updated in time in accordance with the minimization of the regularized identification error in (9) for each time interval of \(\left[k,k-K+1\right]\) where \(K\) is the sliding window length.

Fig. 3
figure 3

ARMA plant identification of the augmented plant

Full size image
$$\frac{1}{K}\mathop\sum\nolimits_{s=0}^{K-1}{{\ell}}_{1,\varepsilon }\left(\begin{array}{c}{y}_{a}^{k-s},\sum_{n=1}^{N}{a}_{n}{y}^{k-s-n}\\ +\mathop\sum\nolimits_{n=0}^{M}{b}_{n}{v}^{k-s-n}\end{array}\right)+\lambda {\left\Vert \begin{array}{c}a\\ b\end{array}\right\Vert }_{\begin{array}{c}2\\ \end{array}}^{2}$$
(9)

Herein, ε-insensitive loss function \({{\ell}}_{1,\varepsilon }\left(\cdot ,\cdot \right)\) is a measurement of the distance between the \((k-s)\)th actual output sample \({y}_{a}^{s}\) of the plant and the \((k-s)\)th output sample of the linear ARMA model \({y}^{k-s}={\sum }_{n=1}^{N}{a}_{n}{y}^{k-s-n}+{\sum }_{n=0}^{M}{b}_{n}{v}^{k-s-n}\) of the augmented plant model where \(N {\text\,{and}} M\) standing for the degrees of the ARMA model. As given in [32], the ε-insensitive (absolute value-based) loss function and the regularizing term are defined below.

$$\ell_{1,\varepsilon } \left( {y_{a}^{s} ,y^{s} } \right) = \left\{ {\begin{array}{*{20}c} {\left| {y_{a}^{s} - y^{s} } \right|} & {{\text{if}}} & {\left| {y_{a}^{s} - y^{s} } \right| \ge \varepsilon } \\ 0 & {{\text{if}}} & {\left| {y_{a}^{s} - y^{s} } \right| < \varepsilon } \\ \end{array} } \right.$$
(10)
$${\lambda \left\Vert \begin{array}{c}a\\ b\end{array}\right\Vert }_{2}^{2}=\lambda \left(\mathop\sum\nolimits_{n=1}^{N}{a}_{n}^{2}+\mathop\sum\nolimits_{n=0}^{M}{b}_{n}^{2}\right)$$
(11)

In the above given identification error, ε-insensitiveness is used for providing robustness against noise, disturbances, and small modeling/approximation errors \(\Delta y\mathrm{^{\prime}}{\text{s}}\) to the ARMA model. Herein, the modeling/approximation error \(\Delta y\) is considered as being additive to the output \(y\), which is inaccuracy in the assumption of that the augmented plant model is exactly feedback linearizable by means of the LFL block realized by MLP. The regularization term in (11) is used to provide a smooth augmented plant model by avoiding over-fitting, and so increasing the generalization ability to respond well to the data unseen before [23].

2.3 Learning ARMA controller as a closed-loop system identification

The study presented in this paper considers the system identification problem of the closed-loop system as a controller design which is the only unknown part of the system (Fig. 1). Once the ARMA parameters \(\left\{{\left\{{a}_{n}\right\}}_{n=1}^{N}, {\left\{{b}_{n}\right\}}_{n=1}^{M}\right\}\) of the augmented (linear) plant model are identified, the linear closed-loop system’s ARMA parameters \(\left\{{\left\{{\alpha }_{n}\right\}}_{n=1}^{\widehat{N}}, {\left\{{\beta }_{n}\right\}}_{n=1}^{\widehat{M}}\right\}\) are learned in an online manner, so are the ARMA controller parameters \(\left\{{\left\{{f}_{m}\right\}}_{m=1}^{P}, {\left\{{c}_{m}\right\}}_{m=1}^{R},{\left\{{d}_{m}\right\}}_{m=1}^{Q}\right\}\). The closed-loop system identification error to be minimized by the online (mini-batch mode) learning algorithm is indeed the regularized tracking error given with ε-insensitive loss function \({{\ell}}_{1,\varepsilon }\left(\cdot ,\cdot \right)\) in (12) that is defined for the time interval of \(\left[k,k-L+1\right]\) where \(L\) is sliding window length.

$$\frac{1}{L}\mathop\sum\nolimits_{s=0}^{L-1}{{\ell}}_{1,\varepsilon }\left(\begin{array}{c}{y}_{d}^{k-s},\mathop\sum\nolimits_{n=1}^{\widehat{N}}{\alpha }_{n}{y}^{k-s-n}\\ +\sum_{n=0}^{\widehat{M}}{\beta }_{n}{r}^{k-s-n}\end{array}\right)+\lambda {\left\Vert \begin{array}{c}\alpha \\ \beta \end{array}\right\Vert }_{2}^{2}$$
(12)

Herein, ε-insensitive loss function \({{\ell}}_{1,\varepsilon }\left(\cdot ,\cdot \right)\) is a measure of the distance between the \((k-s)\)th desired output sample, namely the reference, \({y}_{d}^{s}\) of the plant and the \((k-s)\)th actual output sample \({y}^{k-s}={\sum }_{n=0}^{\widehat{N}}{\alpha }_{n}{y}^{k-s-n}+{\sum }_{n=0}^{\widehat{M}}{\beta }_{n}{r}^{k-s-n}\) of the closed-loop system. \(\widehat{N} {\text\,{and}} \;\widehat{M}\) stand for the degrees of the ARMA model. \({\lambda\left \Vert \begin{array}{c}\alpha \\ \beta \end{array}\right\Vert }_{2}^{2}\) is the regularization term. The tracking error in (12) is minimized under the Schur stability constraints \({\alpha }_{0}>\dots >{\alpha }_{2N-1}>{\alpha }_{2N}>0\) to ensure the stability of the closed-loop system [23, 33].

As done in [9], the determination of the ARMA controller parameters \(\left\{{\left\{{f}_{m}\right\}}_{m=1}^{P}, {\left\{{c}_{m}\right\}}_{m=1}^{R},{\left\{{d}_{m}\right\}}_{m=1}^{Q}\right\}\) from already learned ARMA parameters \(\left\{{\left\{{\alpha }_{n}\right\}}_{n=1}^{\widehat{N}}, {\left\{{\beta }_{n}\right\}}_{n=1}^{\widehat{M}}\right\}\) of the closed-loop system and the ARMA parameters \(\left\{{\left\{{a}_{n}\right\}}_{n=1}^{N}, {\left\{{b}_{n}\right\}}_{n=1}^{M}\right\}\) of the augmented (linear) plant model is performed by means of the following straightforward algebraic derivations.

By choosing \({a}_{0}=-1\) without losing the generality, (8) can be written in the implicit form of (13).

$$\sum\nolimits_{n = 0}^{N} {a_{n} y_{a}^{k - n} } + \sum\nolimits_{n = 0}^{M} {b_{n} v^{k - n} } = 0$$
(13)

Assume that the controller (colored as the green block in Fig. 1) admits the following ARMA representation.

$$v^{k} = \sum\nolimits_{m = 1}^{P} {f_{m} v^{k - m} } + \sum\nolimits_{m = 0}^{R} {c_{m} r^{k - m} } + \sum\nolimits_{m = 0}^{Q} {d_{m} y^{k - m} }$$
(14)

Herein, \(v^{k}\) is the output signal of the controller, \(r^{k}\) is the reference signal that is aimed to be tracked by the plant, and \(c_{m} , d_{m} , f_{m}\) denote the controller parameters. With the choice of \(f_{0} = - 1\), then (14) is written in the implicit form of (15).

$$\sum\nolimits_{m = 0}^{P} {f_{m} v^{k - m} } + \sum\nolimits_{m = 0}^{R} {c_{m} r^{k - m} } + \sum\nolimits_{m = 0}^{Q} {d_{m} y^{k - m} } = 0$$
(15)

(16) is obtained by taking the weighted sum of (13) with weights \(f_{m}\).,

$$\mathop \sum \limits_{n = 0}^{P} f_{m} \mathop \sum \nolimits_{n = 0}^{N} a_{n} y_{a}^{k - m - n} + \mathop \sum \nolimits_{n = 0}^{P} f_{m} \mathop \sum \nolimits_{n = 0}^{M} b_{n} v^{k - m - n} = 0$$
(16)

Substitution of the expression for \(v^{k}\) in (14) into (16), (17) is obtained.

$$0 = \sum\nolimits_{n = 0}^{P} {f_{m} } \sum\nolimits_{n = 0}^{N} {a_{n} y_{a}^{k - m - n} } + \sum\nolimits_{n = 0}^{M} {b_{n} } \sum\nolimits_{n = 0}^{M} {b_{n} } \left[ {\sum\nolimits_{m = 0}^{Q} {d_{m} y^{k - m - n} } - \sum\nolimits_{m = 0}^{R} {c_{m} r^{k - m - n} } } \right]$$
(17)

(17) can be simplified by introducing new parameters \(\alpha_{n}\), \(\beta_{n}\) as below.

$$y^{k} = \sum\nolimits_{n = 0}^{{\hat{N}}} {\alpha_{n} y^{k - n} } + \sum\nolimits_{n = 0}^{{\hat{M}}} {\beta_{n} r^{k - n} }$$
(18)

Herein \(\widehat{N}\) =: max \(\left\{P+N, M+Q\right\}\), and \(\widehat{M}=:M+R\) might be chosen for different values of \(P,N,R,M {\text\,{and}} Q\). Without loss of generality, one can assume that \(P=N=R=M= Q\) and \(\widehat{N}=\widehat{M}\). Then, the controller parameters \(\left\{{\left\{{f}_{m}\right\}}_{m=1}^{P}, {\left\{{c}_{m}\right\}}_{m=1}^{R},{\left\{{d}_{m}\right\}}_{m=1}^{Q}\right\}\) can be calculated from the below given Diophantine.

$$\begin{aligned} a_{o} = & 1 + a_{0} f_{0} - b_{0} d_{0} \\ a_{i} = & \sum\nolimits_{j = 0}^{i} {a_{j} f_{i - j} } - \sum\nolimits_{j = 0}^{i} {b_{j} d_{i - j} } \;{\text{for}}\;i \in \left\{ {1,2, \ldots ,N} \right\}\;{\text{for}}\;i \in \left\{ {N + 1, N + 2, \ldots ,2N} \right\} \\ \beta_{i} = & - \sum\nolimits_{j = 0}^{i} {b_{j} c_{i - j} } \;{\text{for}}\;i \in \left\{ {0,1,2, \ldots ,N} \right\} \\ \beta_{i} = & - \sum\nolimits_{j = i - N}^{N} {b_{j} c_{i - j} } \;{\text{for}}\;i \in \left\{ {N + 1, N + 2, \ldots ,2N} \right\} \\ \end{aligned}$$
(19)

3 Simulations and experimental results

The proposed LFL-based stable robust adaptive controller is tested on the ROTPEN model and on a real ROTPEN setup. The performances of LQR, SMC, and the developed controller are compared as the balance controllers in terms of the settling time, overshoot percentage, and mean square error (MSE) of tracking errors. Each balance controller algorithm is used with an energy-based swing-up algorithm. Controller signals in all experiments are saturated \({}_{-}{}^{+}12\) \(V.\) The effect of ε-insensitive loss functions of the proposed controller is investigated for the tracking error minimization under with and without measurement noise and disturbance for ROTPEN.

3.1 Experiment 1: ROTPEN model

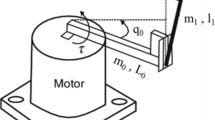
The ROTPEN system is one of the most popular plants used in the field of the nonlinear control. The ROTPEN system model has one input and two outputs. Therefore, the ROTPEN might be represented as a single-input multiple-output (SIMO) system. Hence, the control signal is composed of summing of two controllers used for \(\theta\) and \(\phi\) borrowed from [34]. Either the pendulum angle or the angular position of the arm might be chosen as the output to be controlled. Some parameters of the dynamical system model are shown in a 3D diagram of ROTPEN in Fig. 4. The total force might be written in terms of Newton’s second law for ROTPEN system and dynamical model is given in (20) where \(\theta\) and \(\phi\) stands for the pendulum angle and the rotating arm angle, respectively, \({\tau }_{{\text{output}}}={K}_{t}({V}_{m}-{K}_{m}\dot{\phi })/{R}_{m}\) is used for torque control equation of the dc motor [35]. The ROTPEN system parameters are borrowed from [34] (See Table 1).

$$\begin{aligned} \ddot{\phi }\left( t \right) & = \frac{{rl_{p} M_{p} \cos \left( {\theta \left( t \right)} \right)*\left[ {J_{p} \cos \left( {\theta \left( t \right)} \right)\sin \left( {\theta \left( t \right)} \right)\left( {\dot{\phi }\left( t \right)} \right)^{2} + gl_{p} M_{p} \sin \left( {\theta \left( t \right)} \right)} \right]}}{{J_{p}^{2} \sin^{2} \left( {\theta \left( t \right)} \right) + J_{p} J_{{{\text{eq}}}} - r^{2} l_{p}^{2} Mp^{2} \cos^{2} \left( {\theta \left( t \right)} \right) }} \\ & \quad - \frac{{J_{p} \left[ {rl_{p} M_{p} \sin \left( {\theta \left( t \right)} \right)\left( {\dot{\theta }\left( t \right)} \right)^{2} + 2J_{p} \left( {\dot{\phi }\left( t \right)} \right)\cos \left( {\theta \left( t \right)} \right)\sin \left( {\theta \left( t \right)} \right)\left( {\dot{\theta }\left( t \right)} \right) - \tau_{{{\text{output}}}} } \right]}}{{J_{p}^{2} \sin^{2} \left( {\theta \left( t \right)} \right) + J_{p} J_{{{\text{eq}}}} - r^{2} l_{p}^{2} Mp^{2} \cos^{2} \left( {\theta \left( t \right)} \right) }} \\ \ddot{\theta }\left( t \right) & = \frac{{\left[ {J_{p} \cos \left( {\theta \left( t \right)} \right)\sin \left( {\theta \left( t \right)} \right)\left( {\dot{\phi }\left( t \right)} \right)^{2} + gl_{p} M_{p} \sin \left( {\theta \left( t \right)} \right)} \right]*\left( {J_{p} \sin^{2} \left( {\theta \left( t \right)} \right) + J_{{{\text{eq}}}} } \right)}}{{J_{p}^{2} \sin^{2} \left( {\theta \left( t \right)} \right) + J_{p} J_{{{\text{eq}}}} - r^{2} l_{p}^{2} Mp^{2} \cos^{2} \left( {\theta \left( t \right)} \right) }} \\ & \quad - \frac{{J_{p} \left[ {rl_{p} M_{p} \sin \left( {\theta \left( t \right)} \right)\left( {\dot{\theta }\left( t \right)} \right)^{2} + 2J_{p} \left( {\dot{\phi }\left( t \right)} \right)\cos \left( {\theta \left( t \right)} \right)\sin \left( {\theta \left( t \right)} \right)\left( {\dot{\theta }\left( t \right)} \right) - \tau_{{{\text{output}}}} } \right]}}{{J_{p}^{2} \sin^{2} \left( {\theta \left( t \right)} \right) + J_{p} J_{{{\text{eq}}}} - r^{2} l_{p}^{2} Mp^{2} \cos^{2} \left( {\theta \left( t \right)} \right) }} \\ \end{aligned}$$
(20)
Fig. 4
figure 4

ROTPEN 3-D simplified diagram

Full size image
Table 1 Definitions of ROTPEN plant model parameters and their values
Full size table

By defining \({x}_{1}\left(t\right)=\phi \left(t\right), {x}_{2}\left(t\right)=\dot{\phi }\left(t\right), {x}_{3}\left(t\right)=\theta \left(t\right), {x}_{4}\left(t\right)=\dot{\theta }\left(t\right)\) and then employing forward Euler approach, a discrete time approximation of a state-space form of the differential equation system in (20) can be obtained with \(\Delta T={t}_{k+1}-{t}_{k}\) in the following form

$$\begin{aligned} x_{1}^{k + 1} = & x_{1}^{k} + \Delta T*x_{2}^{k} \\ x_{2}^{k + 1} = & x_{2}^{k} + \Delta T*\left( {\alpha - \beta } \right) \\ x_{3}^{k + 1} = & x_{3}^{k} + \Delta T*x_{4}^{k} \\ x_{4}^{k + 1} = & x_{4}^{k} + \Delta T*\left( {\rho - \sigma } \right) \\ \end{aligned}$$
(21)

Herein \(\alpha ,\beta , \rho , {\text{and}}\; \sigma\) are defined as:

$$\alpha = \frac{{rl_{p} M_{p} \cos \left( {x_{3}^{k} } \right)*\left[ {J_{p} \cos \left( {x_{3}^{k} } \right)\sin \left( {x_{3}^{k} } \right)\left( {x_{2}^{k} } \right)^{2} + gl_{p} M_{p} \sin \left( {x_{3}^{k} } \right)} \right]}}{{J_{p}^{2} \sin^{2} \left( {x_{3}^{k} } \right) + J_{p} J_{eq} - r^{2} l_{p}^{2} Mp^{2} \cos^{2} \left( {x_{3}^{k} } \right) }}$$
$$\beta = \frac{{J_{p} \left[ {rl_{p} M_{p} \sin \left( {x_{3}^{k} } \right)\left( {x_{4}^{k} } \right)^{2} + 2J_{p} \left( {x_{2}^{k} } \right)\cos \left( {x_{3}^{k} } \right) \sin \left( {x_{3}^{k} } \right)\left( {x_{4}^{k} } \right) - \tau_{{{\text{output}}}} } \right]}}{{J_{p}^{2} \sin^{2} \left( {x_{3}^{k} } \right) + J_{p} J_{{{\text{eq}}}} - r^{2} l_{p}^{2} Mp^{2} \cos^{2} \left( {x_{3}^{k} } \right)}}$$
$$\rho = \frac{{\left[ {J_{p} \cos \left( {x_{3}^{k} } \right)\sin \left( {x_{3}^{k} } \right)\left( {x_{2}^{k} } \right)^{2} + gl_{p} M_{p} \sin \left( {x_{3}^{k} } \right)} \right]*\left( {\left( {J_{p} \sin^{2} \left( {x_{3}^{k} } \right)} \right) + J_{{{\text{eq}}}} } \right)}}{{J_{p}^{2} \sin^{2} \left( {x_{3}^{k} } \right) + J_{p} J_{{{\text{eq}}}} - r^{2} l_{p}^{2} Mp^{2} \cos^{2} \left( {x_{3}^{k} } \right) }}$$
$$\sigma = \frac{{rl_{p} M_{p} \cos \left( {x_{3}^{k} } \right) \left[ {rl_{p} M_{p} \sin \left( {x_{3}^{k} } \right)\left( {x_{4}^{k} } \right)^{2} + 2J_{p} \left( {x_{2}^{k} } \right)\cos \left( {x_{3}^{k} } \right)\sin \left( {x_{3}^{k} } \right)\left( {x_{4}^{k} } \right) - \tau_{{{\text{output}}}} } \right]}}{{J_{p}^{2} \sin^{2} (x_{3}^{k} ) + J_{p} J_{{{\text{eq}}}} - r^{2} l_{p}^{2} Mp^{2} \cos^{2} \left( {x_{3}^{k} } \right)}}$$

It should be noted that the obtained discrete-time plant model in (21) is linear in the input variable \({\tau }_{{\text{output}}}\), so it constitutes an affine model with relative degree 1 as a special case of the input–output model in (1) that means that the feedback linearization method presented in (2–8) for discrete-time nonlinear affine systems is applicable to control one of the outputs of the ROTPEN. In the application presented in the paper, the pendulum angle \(({x}_{3}=\theta )\) is chosen as the output to be controlled. For a realistic control, the rotating arm angle \(({x}_{1}=\phi )\), which is the second output of the ROTPEN, is to be controlled simultaneously. As for the balance controller part in Fig. 5, the developed LFL-based stable robust adaptive controller is exerted to control the pendulum angle of the ROTPEN properly. Owing to the reference arm angle assumed as constant, e.g., \({r}_{\phi }^{k}=0\), the SIMO system might be transformed into a SISO system depicted as a cascade control scheme borrowed from [36]. Herein, the rotating arm angle \(\phi\) is controlled by a PD controller. Following the cascade control structure outlined in [36] and referring to Fig. 5, PD controller parameters were calculated using LQR technique [28] as \({K}_{p}=-1\), and \({K}_{d}=-1.2688\) for our case. The PD controller parameters are set to negative values. Thus, the balance control of the rotary inverted pendulum is achieved with the control signal generated by the developed LFL-based stable robust adaptive controller for \({\theta }^{k}\) in Fig. 5 [37]. In light of the cascaded control technique, it would be noted that the control of pendulum angle \(\theta\) is not affected by the speed of the inner loop, because it responds quite faster than the outer loop [38].

Fig. 5
figure 5

LFL-based NARMA controller and ROTPEN block diagram

Full size image

The validity of the above approach of controlling a single output of a SIMO system by considering it as a SISO system for the considered output relies on the following fact. A SIMO system is reduced to a SISO system for the considered output if this output is associated with the slow dynamics of the system such that the fast dynamics are asymptotically stable so tending to the fixed reference points after their relatively short transient periods. For the ROTPEN, this can be seen that when fast dynamics associated with the rotating arm angle \({x}_{1}=\phi (t)\) is settled down, so is its change \({x}_{2}=\dot{\phi }\left(t\right)\), the slow dynamics determined by the last two recursions of (21) in terms of the pendulum angle \({x}_{3}=\theta (t)\) and its change \({x}_{4}=\dot{\theta }\left(t\right)\) becomes to constitute an affine nonlinear SISO system.

In controlling the pendulum angle by the developed data-dependent feedback linearization method, (9) and (12) might be rewritten as (22) and (23), respectively.

$$\frac{1}{K}\mathop\sum\nolimits_{s=0}^{K-1}{{\ell}}_{1,\varepsilon }\left(\begin{array}{c}{\theta }_{a}^{k-s},\sum_{n=1}^{N}{a}_{n}{\theta }^{k-s-n}\\ +\sum_{n=0}^{M}{b}_{n}{v}^{k-s-n}\end{array}\right)+\lambda {\left\Vert \begin{array}{c}a\\ b\end{array}\right\Vert }_{\begin{array}{c}2\\ \end{array}}^{2}$$
(22)
$$\frac{1}{L}\mathop\sum\nolimits_{s=0}^{L-1}{{\ell}}_{1,\varepsilon }\left(\begin{array}{c}{r}_{\theta }^{k-s},\sum_{n=1}^{\widehat{N}}{\alpha }_{n}{\theta }^{k-s-n}\\ +\sum_{n=0}^{\widehat{M}}{\beta }_{n}{{r}_{\theta }}^{k-s-n}\end{array}\right)+\lambda {\left\Vert \begin{array}{c}\alpha \\ \beta \end{array}\right\Vert }_{2}^{2}$$
(23)

An energy-based swing-up algorithm is initially used for the balance control of the pendulum angle \((\theta )\) at the upright position. So, the pendulum angle is kept in a nearly linear range of \(-0.2618\;{\text{rad}}\) and \(0.2618\;{\text{rad}}\). The swing-up algorithm computes total energy of the system to use it as a feedback variable, so the pendulum total energy is driven to the upright position for reaching the linear range. Energy-based swing-up controller algorithm is given as in (24) [35, 39].

$$u_{{{\text{swing}}}} = sat_{\vartheta g} \left[ {\mu \left( {E - E_{d} } \right){\text{sign}}\left( {\dot{\theta }\cos \left( \theta \right)} \right)} \right]$$
(24)

where \({u}_{{\text{swing}}}\) is control signal, \(\mu\) is tunable design parameter, \(E\) is total energy of the system, \({E}_{d}\) is total energy of upright position, and a linear function \(sa{t}_{\vartheta g}\) saturates \({u}_{{\text{swing}}}\) control signal at \({}_{-}{}^{+}\vartheta g\) which \(\vartheta\) is a design parameter and \(g\) is the gravity acceleration for limiting maximum acceleration of pivot. If the initial condition of \(\theta\) is chosen as \(-3.14 \;rad\) and the upright position is chosen as \(0 \;rad\) for \(\theta\), the potential and kinetic energy of the algorithm might be defined as \({E}_{p}={M}_{p}g{l}_{p}(1+{\text{cos}}(\theta ))\) and \({E}_{k}=\frac{1}{2}{J}_{p}{\dot{\theta }}^{2},\) respectively, according to chosen positions, so total energy becomes \(E={E}_{p}+{E}_{k}={M}_{p}g{l}_{p}\left(1+{\text{cos}}\left(\theta \right)\right)+\frac{1}{2}{J}_{p}{\dot{\theta }}^{2}.\) The potential energy is \(0\) when pendulum is at \(-3.14 {\text{rad}}\) and \({E}_{d}=2{M}_{p}g{l}_{p}=0.081 J\) when pendulum is at the upright position. The \(\vartheta\) and \(\mu\) are chosen as \(1\) and \(2.5\), respectively, for the ROTPEN model [28, 39]. The swing-up algorithm is run when out of the linear range while a balance controller algorithm is run in the linear range via switching mechanism. During all experiments, the pendulum angle \(\theta\) is plotted as \({\text{mod}}\left(\theta \left(t\right), 2\pi \right)-\pi\) [28].

After the pendulum has swung up, the proposed adaptive LFL-based NARMA controller takes its place and is applied to control the ROTPEN model as shown in Fig. 5. LFL-based NARMA controller, depicted in Fig. 5, consists of an adaptive ARMA controller and a LFL block as presented in Fig. 1. Here, the LFL block is identified in an offline manner using \(x\left(k\right)\) and \({v}^{k}\) as input and \({u}^{k}\) as output by a suitable MLP-ANN that possesses 2 hidden layers in the “feedforwardnet” structure and each of these layers has 10 neurons as described in Sect. 2.1. This MLP-ANN training has an epoch number of 1000 and 9 s of elapsed time. Besides, for the sliding window mode of the LFL-based NARMA controller, also called online (mini-batch) mode, the identification window of the plant model and the identification window of the control loop are taken as \(K=5\), \(L=30\), respectively, in (22) and (23). These loss functions are minimized so that \(N=M=5\), \(\widehat{N}=\widehat{M}=10\) by using the stochastic gradient descent algorithm borrowed from [40], and the sampling time is set to \(0.001 s\) during the simulation studies. Herein, the learning rate of stochastic gradient descent is 0.01 for minimization processes. As a result of minimization, feedback-linearized plant parameters \(a, b\) and closed-loop system parameters \(\alpha , \beta\) are found, these parameters are evaluated by using (19) in an online manner along the sliding window to calculate the adaptive ARMA controller \({c}_{m}, {d}_{m}\). To test the tracking performance \(\theta\) angle of the proposed controller, \({r}_{\theta }^{k}=0 rad\) is chosen for \(\theta\) and \({r}_{\phi }^{k}=0 rad\). Initial value of \(\theta\) is chosen as − 3.14 rad and initial value of \(\phi\) is chosen as \(0\;{\text{rad}}\).

The results of tracking performance and time evolutions of the developed LFL-based adaptive controller with swing-up algorithm and developed LFL-based adaptive controller signal are depicted for the reference signals in Fig. 6a and b, respectively. As seen from Fig. 6a, the developed controller works well for the balance tracking performance. Time evolutions of the LFL-based linear plant model, the closed-loop, and the controller parameters are illustrated for the constant reference signal as \(0\;rad\) in Fig. 7. The value of regularization term as \(\lambda =0.05\) is found as the most appropriate value out of the set \(\left\{{0, 10}^{-2}, 5\times {10}^{-2},{10}^{-1}\right\}\) for the online mode in order to limit the norm of both plant and controller parameters for better generalization.

Fig. 6
figure 6

a The tracking performance of the developed controller for pendulum angle θ and b developed controller’s control signal

Full size image
Fig. 7
figure 7

a Time evolutions of the plant (\({a}_{n}\),\({b}_{n}\)), b the closed-loop (\({\alpha }_{n}, {\beta }_{n}\)), and c the controller parameters (\({c}_{n},{d}_{n}\))

Full size image

To test the robustness performance of the proposed LFL-based adaptive controller, a white noise that has a 2 \(dB\) “SNR” is applied to the control signal \({v}^{k}\) in (14) and a 40 \(dB\) “SNR” is applied to pendulum angle \(\theta\) via SIMULINK with “awgn” function. The performances of the tracking error for balance control (23) are presented with different ε-insensitiveness values in terms of the MSE results with and without noise given in Table 2 where MSE \(=\frac{1}{S}\sum_{i=1}^{S}{e}^{2}\left(i\right)\) defined in terms of \(S\) number of samples and \(e\left(i\right)\) error signal. The eligible ε-insensitiveness of the tracking error might be used as \(5.1436\times {10}^{-4}\) and \(3.8650\times {10}^{-4}\) in terms of MSE with and without noise, respectively.

Table 2 MSE performance of plant model identification (22) and tracking error (23) with and without noise for different \(\varepsilon-\)insensitiveness
Full size table

To compare the tracking performance of the proposed adaptive controller, LQR controller [28] and coupled SMC [29, 30] are applied to ROTPEN plant model. LQR design is based on the state feedback control signal \(u=-{{\varvec{K}}}_{{\varvec{k}}}{\varvec{x}}\) where \({\varvec{x}}\) is \(N\times 1\) column vector and \({{\varvec{K}}}_{{\varvec{k}}}\) is \(1\times N\) row vector. The goal is to find an optimum \(u\) value that minimizes a quadratic cost function as \(J={\int }_{0}^{\infty }({{\varvec{x}}}^{T}Q{\varvec{x}}+{u}^{T}Ru){\text{d}}t\) where \({\varvec{Q}}\) is chosen as \(\left[\begin{array}{cccc}{Q}_{11}& 0& 0& 0\\ 0& {Q}_{22}& 0& 0\\ 0& 0& {Q}_{33}& 0\\ 0& 0& 0& {Q}_{44}\end{array}\right]\) that should be a positive semi definite matrix and \(R\) is a scalar for \({\varvec{x}}\)= [\(\phi\);\(\theta\);\(\dot{\phi }\);\(\dot{\theta }\)] of the linearized model of ROTPEN from [35]. The simulations are implemented with the parameters given in Table 1 and initial conditions of \({\varvec{x}}=[0; -3.14; 0; 0]. {\varvec{Q}}\) and \(R\) are chosen as \(\left[\begin{array}{cccc}1& 0& 0& 0\\ 0& 1162& 0& 0\\ 0& 0& 0.913& 0\\ 0& 0& 0& 13\end{array}\right]\) and 1, respectively, so that \({{\varvec{K}}}_{{\varvec{k}}}\) is found as \(\left[-1, 57.0528, -1.3636, 6.8465\right]\).

As for the coupled SMC [29, 30], (20) might be written as

$$\begin{gathered} \ddot{\phi }\left( t \right) = f_{\phi } \left( {\phi \left( t \right),\theta \left( t \right),\dot{\phi }\left( t \right),\dot{\theta }\left( t \right)} \right) + g_{\phi } \left( {\phi \left( t \right),\theta \left( t \right)} \right)u \hfill \\ \ddot{\theta }\left( t \right) = f_{\theta } \left( {\phi \left( t \right),\theta \left( t \right),\dot{\phi }\left( t \right),\dot{\theta }\left( t \right)} \right) + g_{\theta } \left( {\phi \left( t \right),\theta \left( t \right)} \right)u \hfill \\ \end{gathered}$$
(25)

and sliding surface \(s\) is chosen as coupled sliding surface as follows

$$s={s}_{\theta }+{\overline{{\lambda }_{u}}s}_{\phi }$$
(26)

where \({s}_{\theta }\) is sliding surface for pendulum angle, \({s}_{\phi }\) is sliding surface for rotary arm angle and state-dependent \(\overline{{\lambda }_{u}}=\lambda {\text{cos}}(\theta (t))\) which has a \({\lambda }_{u}\) constant coupling parameter in the following form

$${s}_{\theta }=\dot{\theta }(t)+{c}_{\theta }\theta (t)$$
(27)
$${s}_{\phi }=\dot{\phi }(t)+{c}_{\phi }\phi (t)$$
(28)

where \({c}_{\theta }\) and \({c}_{\phi }\) are positive coefficients. The control law of the coupled SMC (\({u}_{{\text{smc}}}\)) might be given as follows

$${u}_{{\text{smc}}}=\frac{-\left({f}_{\theta }+{c}_{\theta }\dot{\theta }(t)+\overline{{\lambda }_{u}}\left({f}_{\phi }+{c}_{\phi }\dot{\phi }(t)\right)\right)-k{\text{sign}}\left(s\right)-\dot{\overline{{\lambda }_{u}}}{s}_{\phi }}{{g}_{\theta }+\overline{{\lambda }_{u}}{g}_{\phi }}$$
(29)

where k is a positive design parameter and \(\dot{\overline{{\lambda }_{u}}}\) is time derivative of \(\overline{{\lambda }_{u}}\). \({c}_{\phi }\),\({c}_{\theta }\), \(k\), and \({\lambda }_{u}\) were chosen as 7.5, 1.5, 3, and − 0.35, respectively.

Comparisons of the tracking performances of the developed controller and the other two controllers considered are given in Fig. 8 LFL-based NARMA controller provides good performance in terms of MSE as shown in Table 3. The overshoot percentage of the proposed controller is observed as 0 rad, and it is less than the other controllers’ overshoot percentage values. The settling time of the proposed controller is computed as 2.1 \(s\) according to %2 criterion gives a good response as shown [41] in Table 4. The proposed controller performance might be an acceptable performance during the transient behavior because it avoids the swinging motion visible in the zoomed area in Fig. 8 observed in other controllers.

Fig. 8
figure 8

ROTPEN plant model performance evaluation of controllers

Full size image
Table 3 Comparison of the controller performances in terms of MSE
Full size table
Table 4 Comparison of settling time and overshoot percentage performances of the controllers
Full size table

To compare the performance of the controllers in the presence of measurement noise and disturbance, white noise which has a 2 \({\text{dB}}\) “SNR” is applied to the control signal of LQR, coupled SMC and the developed controllers and a 40 \({\text{dB}}\) “SNR” is applied to pendulum angle \(\theta\) of them via SIMULINK with “awgn” function. The obtained results are given in Table 5 where LFL-based controller provides the minimum MSE value. In addition to the noise and disturbance analysis, ten separate simulations are conducted to evaluate controller performance under parameter uncertainties. In each run, ± 5% uncertainty is randomly added to both pendulum mass \(({M}_{{\text{p}}})\) and length \(({l}_{{\text{p}}})\) of the ROTPEN system, simulating deviations from the nominal model. Table 6 presents the average MSE values across these ten trials. The proposed LFL-based controller with its adaptive manner seems to perform slightly better than the coupled SMC and outperforms LQR since the proposed controller achieves the lowest overall MSE as shown in Table 6. Furthermore, the achievement of performance close to coupled SMC, which is known for its robustness to parameter uncertainties, underscores the significant strength of the proposed method.

Table 5 Comparison of performances of the controllers in the presence of measurement noise and disturbance
Full size table
Table 6 Comparison of performances of the controllers in the presence of parameter uncertainties
Full size table

3.2 Experiment: real ROTPEN Setup

Real ROTPEN setup is an example of a well-known under-actuated mechanical system [34, 42,43,44,45]. Incompletely driven mechanical systems are widely used in the field of robotics, and the main feature of these systems is that they have fewer actuators than degrees of freedom [46]. The inverted pendulum possesses unstable and nonlinear dynamical behaviors inherently. Another important feature that makes the rotary inverted pendulum more interesting is that it forms the basis of many new technologies such as seismometers, humanoid robots, unmanned air vehicles, and rockets. The real ROTPEN setup consists of mechanical design, data acquisition card, and software. The mechanical design of the pendulum is made by SolidWorks software. A direct current motor Maxon DC-max B773D74C44771 is used to rotate the ROTPEN arm horizontally. The pendulum is connected to the pendulum arm by the pivot. Thus, the pendulum will be able to oscillate easily. AVAGO HEDM-5505-j06 two-channel 1024 resolution encoder is located on the shaft. This encoder is used to measure the angle of the pendulum with the horizontal plane and to implement the control system. The end of the L-shaped pendulum arm is mounted on the shaft of the dc motor. Due to the circular rotation of the motor shaft, the pendulum arm can be moved clockwise and counterclockwise. The angle of the arm is calculated with the encoder mounted on the motor. A rotating arm in a horizontal axis and a rotating pendulum which is mounted on arm, in a vertical plane take part in the rotary inverted pendulum [42,43,44]. The final version of the successful ROTPEN setup is given in Fig. 9. For ROTPEN setup, the encoder reading for \(\theta\) angle is set to be the same as the simulation,\(-3.14 {\text{rad}}\) initial condition as updown position and \(0 {\text{rad}}\) as upright position. Theta encoder is set to \(0 {\text{rad}}\) for initial condition. The proposed controller is tested on ROTPEN real plant via real-time desktop interface of SIMULINK environment [47].

Fig. 9
figure 9

ROTPEN real setup and V-DAQ data acquisition card

Full size image

To test the tracking performance of the proposed adaptive controller, it is used together with the swing-up algorithm described in the subSect. 3.1. The feedback-linearized plant model and the closed-loop system model have \(N=M=5\), and \(\widehat{N}=\widehat{M}=10\) degrees, respectively. For the online sliding window mode, the plant model identification window and the closed-loop identification window are taken as \(K=5\), \(L=30\) for (22) and (23), respectively. The loss functions are minimized with the stochastic gradient descent algorithm borrowed from [40], and the sampling time is chosen as 0.001 \(s\). In order to test tracking performance \(\theta {\text{angle}}\) of the proposed controller, \({r}_{\theta }^{k}=0 {\text{rad}}\) is chosen for \(\theta {\text{angle}}\) (pendulum upright position). Herein, the parameters initial values are determined for the online mode after running a batch mode. \(\lambda =0.05\) is found the best as the regularization term out of the set \(\left\{{0;10}^{-2};5\times {10}^{-2};{10}^{-2};{10}^{-1}\right\}\). The results of tracking performance and time evolutions of the developed LFL-based adaptive controller and its signal are depicted for the reference signal in Fig. 10a and b, respectively. Time evolutions of the proposed LFL-based adaptive controller for the considered plant, closed-loop, and the developed controller parameters are depicted in Fig. 11a, b, and c, respectively.

Fig. 10
figure 10

a The tracking performance of the developed controller for pendulum angle θ and b developed controller’s control signal

Full size image
Fig. 11
figure 11

a Time evolutions of the plant (\({a}_{n}\),\({b}_{n}\)), b the closed-loop (\({\alpha }_{n}, {\beta }_{n}\)) and c the controller parameters (\({c}_{n},{d}_{n}\))

Full size image

In order to compare the performance of the LQR, coupled SMC, and the proposed controllers are applied to ROTPEN real plant. The comparison of the performances of the controllers is given in Fig. 12. LFL-based NARMA controller provides lower error than the other controllers according to the MSE error as shown in Table 7. According to Table 8, the overshoot percentage of the proposed controller is observed as − 2.6% which is better than the other controllers. The 5.174 \(s\) settling time of the proposed controller that is found for the proposed controller is better than the other controllers.

Fig. 12
figure 12

ROTPEN real plant performance evaluation of the controllers

Full size image
Table 7 Comparison of the controller performances in terms of MSE
Full size table
Table 8 The evaluations of settling time and overshoot percentage in terms of the controller’s performance
Full size table

4 Conclusions

This paper proposes a novel data-dependent NARMA controller for nonlinear affine systems. The controller parameters are adaptively learned using a sliding window approach. It builds on a previous work for linear systems [23] by extending it to nonlinear affine systems based on the data-dependent implementation of input–output feedback linearization. Firstly, the offline input–output feedback linearization is cascaded to the nonlinear plant to form a linear augmented plant. Subsequently, an online identification process takes place within the sliding window, modeling both the augmented plant, and the overall closed-loop system as linear ARMA models. The controller parameters are determined by considering Schur stability constraints during the closed-loop identification phase, guaranteeing the stability of the entire control system. Furthermore, the ε-insensitive \({{\ell}}_{1,\varepsilon }\left(\cdot ,\cdot \right)\) loss function, employed for minimizing identification and tracking errors in the online learning algorithms, contributes to the NARMA controller's robustness against noise, disturbances, and modeling errors.

The rationale behind the usage of the proposed data- dependent control method based on the artificial neural networks-based approximate feedback linearization lies on the following facts. (1) Not all of the plants have well-defined realistic mathematical models that reflect the effects of all intrinsic nonlinearities, noise, disturbances, and parameter changes. So, there is a need to develop and implement data-dependent control methods that work with measurement data. (2) Usage of learning algorithms provides ways to determine the parameters of the identification model and also the controller model’s parameters in an offline and also online manner. (3) Artificial neural networks with their universal approximation properties provide good candidates with the features such as being realistic, robust, and adaptive both for plant identification and controller models. (4) The performance of the data-dependent nonlinear controller design methods is generally lower than those of the linear ones. So, employing the feedback linearization first and then applying a data-dependent linear controller design method might be a viable approach that is also followed in the presented work.

The proposed NARMA controller is tested on a simulated ROTPEN model and on a real setup for angular pendulum position. Its performance is compared to those of LQR and coupled SMC. The proposed NARMA controller is observed to be superior in comparison with the other two controllers in terms of overshoot percentage and tracking performance in MSE.

The application of the developed NARMA controller is by no means restricted to ROTPEN and has the potential of being used for controlling a large class of SISO nonlinear plants. As future works, the NARMA controller scheme developed for nonlinear SISO plants can be extended into multi–input–multi–output plants which might be non-affine. Developing methods for automatic determination of the sizes of sliding windows in online learning of the parameters of the augmented plant model and controller and investigation of the effects of the sliding window sizes in the tracking performance of the proposed NARMA controller are among possible future research subjects.