Parameters extraction of photovoltaic models using enhanced generalized normal distribution optimization with neighborhood search

Abstract

The photovoltaic system has been widely integrated into electrical power grids to produce clean and sustainable energy sources. Precisely modeling of PV systems is crucial to simulate and asset the performance of such power system. Modeling of PV system is a challenge because the characteristic curve of current and voltage is nonlinear and has unknown parameters due to insufficient data points in manufacture’s data sheet. This work proposes generalized normal distribution optimization based on neighborhood search strategies (NSGNDO) to extract the parameter of single diode model (SDM), double diode model (DDM), and PV module model (PVM). The root means square error (RMSE) is used as a performance indicator. Two commercial PV models like RTC France solar cell and PWP201 are used to validate the ability of NSGNDO to precisely estimated the PV system’s parameters. The results show the superiority of NSGNDO over competitive optimization methods and can reduce the RMSE to 2.05296E-03 for PWP201 and to 9.8248E-04 for RTC France solar cell which prove that NSGNDO can be used as competitor method to identify the parameters of PV solar system. The statistical analysis shows the robustness of NSGNDO through statistical measurements and Wilcoxon rank test.’

1 Introduction

Photovoltaic (PV) systems are widely utilized to produce electric energy from solar energy [1]. As PV systems are exposed to open-air environmental factors such as temperature and global irradiance, which affect the efficiency of solar energy, it is critical to precisely create current–voltage models for managing the systems.

The current–voltage (IV) models primarily use two basic forms namely single diode (SDM) and double diode model (DDM). These models are extensively applied to express the relation between current and voltage. The correct and accurate parameters estimation of these models provide accurate and reliable PV models.

Due to the varying unsteady environment, the process of solar systems and the PV models’ parameters are commonly variable. Accurate estimation of the model parameters is very important. Hence, using efficient methods for this task is required. Consequently, even if the metaheuristic algorithms for the estimation of PV model parameters produced good results, additional studies are required to develop more efficient techniques that can produce better solutions.

An essential phase of improving the efficiency of PV solar cells systems is the optimum design of these systems. Therefore, performing reliable and accurate PV system modeling enhance the system’s working characteristics [2,3,4]. The modeling procedure can be divided into two distinct stages. First, the mathematical modeling is done first; then, extraction of system parameters comes next [5].

Several PV solar cells systems models have nonlinear characteristics. Single diode model (SDM) is the simplest widespread model [6]. Also, the double diode model (DDM) [7] and three-diode model (TDM) are significant ones in the literature [2]. Some other models are less used as the multi-diode model (MDM) [8] and the reverse double diode model (RDDM) [9].

The SDM has smaller number of parameters and provides acceptable accuracy. The DDM model is introduced later; however, it has seven parameters to calculate. The three-diode model has ten parameters and is designed to allow more accurate estimation and PV cell model enhancement that is suitable for production [2].

Even with its complicated design, TDM is regarded as the finest PV solar cell model. Precise PV system representation is a challenging task that relies on mathematical modeling and estimation of PV cell specifications. So when the models are indirectly transcendent, the outcomes are inappropriate, and this debility is hard to fix using traditional standard techniques [10].

Many studies have been recently used in the solar PV systems. The main concern was to find a correctly estimation of the PV system models parameters, i.e., finding the best parameters of the solar cells as well as PV units to develop precise I–V description curve and correctly design the PV system. The PV parameter can be found by three methodologies: (1) analytical [11], (2) numerical [12, 13], and (3) metaheuristic [5]. The first technique use equations that provide mathematical model of the system for fast direct calculation of the PV parameters. It uses the three key points of the I–V curves, i.e., the point of short circuit current, open-circuit voltage, and the maximum power. Analytical approaches are simple and fast, but the accuracy is liable to deterioration if one of the key points is incorrectly specified.

Numerous analytical methods were used, such as the Lambert method-based W- function. It was used for the estimation of PV cells parameters of the SDM and DDM. However, the numerical methods appeared to be more accurate [14, 15]. Various numerical techniques were introduced to find the PV parameter [16, 17]. Mares et al found that numerical method appeared simple and accurate to calculate the parameters of DDM [16].

Numerical methods used nonlinear algorithms, like Newton–Raphson method [18, 19]. Nelder-Mead simplex method [20] and conductivity method (CM) for parameters calculation of the of the PV system [21]. Also, Two-step linear least-squares (TSLLS) have been appeared to be accurate in the estimation of the PV cell parameters [12]. Numerical approaches, requires continuous and differentiable fitness function, hence will face some challenges in parameter extraction of the PV cells. While numerical methods outperform analytical methods in terms of accuracy, the large number of parameters complicates the extraction operation [16, 17, 22].

To overcome the drawbacks and challenges of the first two techniques, metaheuristic methods have been used for optimization of PV parameter estimation. Metaheuristic optimization methods are recognized by their global search and are capable of handling nonlinearity. Furthermore, the gradient computation of the objective function and initializing constraints are not required [23].

Several metaheuristic optimization methods, such as the genetic algorithm, are designated for estimating the parameters of the PV cell [24]. For the genetic algorithm, considerable flaws were found. The computation time and the slow rate of convergence are big concerns.

Particle swarm optimization (PSO) is another metaheuristic method that was used to determine the parameters of solar cells for the SDM and DDM models [25]. Also, simulated annealing (SA) method was used to obtain the parameters of the PV cell’s using the SDM and DDM models [23].

Generalized normal distribution optimization (GNDO), a new metaheuristic method, was used to extract parameters from PV models. The most prominent aspect of GNDO is that it only needs the population size and terminal condition to be defined and does not require any other explicit controlling parameters. The method has a simple structure and uses the traditional generalized normal distribution formula to update the individual’s locations based on population location information. GNDO has been applied for parameter extraction of three photovoltaic models and appeared to outperform the compared algorithms in terms of efficiency and accuracy [26].

A dynamic self-adaptive and mutual comparison teaching learning-based optimization (DMTLBO) outperforms the basic TLBO by improving its teacher and learner stages. In the first stage, two teaching strategies were proposed (differentiated/personalized) according to the learning status. In the second stage, a new strategy was introduced for learning. The learner can communicate and learn with three learners selected randomly. DMTLBO showed better convergence speed and accuracy [27].

Triple-phase teaching learning-based (TPTLBO) adds a third phase (buffer phase) and uses a centroid approach to update the location of middle learners, increasing the exploitation and exploration; learners can select different phases and conduct different methods for learning according to their level of knowledge [28]. Additionally, to improve the search capabilities, a dynamic control parameter takes the role of the rand random parameter. The results reveal that TPTLBO obtains greater performance in terms of accuracy and reliability when tested through the SDM, DDM, and TDM.

Another approach used the Runge Kutta RUN method to estimate the PV parameters. It uses root mean square error (RMSE) by comparing calculated and measured current as the optimization objective function. It significantly outperformed other optimization methods such as the Hunger Games Search (HGS), Chameleon swarm algorithm (CSA), Tunicate swarm algorithm (TSA), Harris Hawk’s Optimization (HHO), Sine–Cosine algorithm (SCA), and gray wolf optimization (GWO). The algorithm was applied on three solar cell models to extract their parameters (single, double and triple diode models) [29].

Gradient-based optimizer (GBO) was used to find the parameters of three common SC models, namely single, double and three-diode models. It efficiently and precisely estimate the parameters of these models [30]. A two flames generation strategy is used to create two different types of target flames for directing the moths flying in an improved moths-flames optimization (IMFO) method. Furthermore, two distinct strategies are used to adjust the moth’s position. This uses probability to select one update strategy for each month at each update, balancing exploitation and exploration. IMFO was used to find the parameters of single, double and PV module models. It indicates better performance compared with other well established methods [31].

The tree growth method (TGA) was used to find the parameters of solar cells and PV modules [32]. The approach performed well for solar cells and typical PV modules when using different diode models, including a SDM, a DDM, and TDM models. The results of TGA technique provide an accurate and efficient estimation of the parameters. Furthermore, the balance between intensification and diversification of the TGA can be achieved by tuning of the algorithm parameters.

The cuckoo search optimization (CSO) and some of its variants were used for estimating parameter of PV cell [33,34,35]. They are used to estimate parameters of (I) photovoltaic (PV) cell: SDM and DDM, and (II) PV module which contains 36 diodes series connected PV cells [35]. Improved cuckoo search optimization (ICSO) and modified cuckoo search optimization (MCSO) techniques were applied to estimate parameters of PV cell models. ICSO applies random walk using adaptive step size coefficient. While MCSO use communication mechanism between top nests. Results show that step size improved the convergence speed of the ICSO algorithm in contrast to CSO algorithm that uses fixed step size. Compared to the CSO and MCSO, ICSO accomplished minimum RMSE, higher accuracy and reliability [35].

An improved queuing search optimization (QSO) algorithm is proposed to overcome the nonlinearity of PV solar cell and to extract optimal parameters’value [36]. The DE algorithm is applied to every obtained solution in order to increase the diversity of the populations. The authors evaluate the algorithm using the manufacturer’s datasheet TFST40 and MCSM. The practical and statistical finding show the reliability and accuracy of the algorithm to find the solution for PVM model.

To identify the unknown parameters in PV model and to solve the nonlinearity behavior, Northern Goshawk optimization algorithm (NGO) was introduced [37]. The algorithm is applied to extract the parameters of triple diode model (TDM) of the PV, module namely Photowatt-PWP201, Kyocers KC200GT and Canadian solar CS65k-280 M. The results reveal that NGO can dramatically reduce the cost functions in terms of RMSE.

The atomic orbital search algorithm (AOS) was introduced to extract the unknown parameters of RTC France solar cell and PVM752 GaAs thin-film cell [38]. The authors present decent basis technique to validate the accuracy of extracting the unknown parameters. The obtained results were compared to RMSE from other methods, and the results show that the AOS can significantly reduce the cost function compared to other methods in the literature.

Table 1 Various method for extracting PV model parameters

According to state-of-the art summarized in Table 1, many metaheuristic techniques have been extensively used to tackle the problem of parameters extraction of PV solar cell. However, there is NO-Free-Lunch which demonstrate that no singular method has the ability to address all optimization problems, based on this fact, one algorithm may have competitive performance on a specific kind of problems, but there is no guarantee to perform well on other problems. Therefore, to tackle the shorting coming of the after mentioned techniques such as premature convergence, poor global search, and complex computation time, this work proposes NSGNDO to overcome the premature convergence of the basic GNDO [26] and to prevent the stuck in local optima.

In addition, the RMSE based on the extracted parameters of PV solar cell has been widely used in the literature for RTC France solar cell and Phowatt-PWP201 PV module. This work employees RMSE as performance and comparison indicator. This performance metric is calculated based on the differences between the measured solar cell output current and the estimated one at different measured voltages (I–V characteristic curve).

The contribution of this work can be summarized as follows

• 1. Local neighborhood search (LNS) strategy to improve the exploitation and convergence rate.

• 2. Global neighborhood search (GNS) strategy to increase the diversity of the population and prevent premature trapped in local minima.

The rest of the paper is organized as follows. Sections 2 and 3 demonstrate the mathematical modeling and formulate the problem, respectively. The standard GNDO is presented in Sect. 4 whereas Sect. 5 presents the proposed NSGNDO. The numerical results and discussion are presented in Sect. 6. Finally, Sect. 7 concludes the paper and presents the future work.

2 Mathematical modeling

Numerous mathematical models have been introduced to demonstrate the characteristics of PV solar cells. The standard models are single diode model (SDM), double diode Model (DDM), and PV model. The most commonly used model is the single diode model because of its simplicity but its accuracy is not high enough. Therefore, the double diode model as well as PV model are proposed to enhance the efficiency of the solar cells. This section shows the problem formulation, presents mathematical modeling of three PV solar cells, and introduces objective function formulation.

2.1 Single diode model

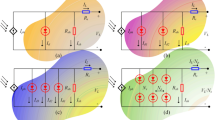
Figure 1a shows the equivalent circuit for SDM. It consists of single diode and an independent current source in parallel. In addition to one series resistance $R_{s}$ and a shunt resistance $R_{\rm sh}$, the output current ($I_{o}$ of the circuit is calculated as follows

Fig. 1

The equivalent circuits of SDM, DDM, and PV models

$$\begin{aligned} I_{o} = I_{\rm ph} - I_{D} - I_{\rm sh} \end{aligned}$$

(1)

Where $I_{\rm ph}$, $I_{D}$, and $I_{\rm sh}$ represent the current of the independent current source, the diode current, and the current of shunt resistance. The diode current $I_{D}$is well defined by Shockley equation as

$$\begin{aligned} I_{D} = I_{\rm sd}\left[exp(\frac{V_{m} + R_{s} I_{m}}{n V_{t}})-1\right] \end{aligned}$$

(2)

Where $I_{\rm sd}$, $V_{m}$, $I_{m}$ are the diode saturation current(A), the measured voltage (V), and the measured current(A), respectively. The diode ideality factor is n, and the thermal voltage is represented by $V_{t}$ and is calculated as

$$\begin{aligned} V_{t} = \frac{K.T}{q} \end{aligned}$$

(3)

Where k represents the Boltzmann constant and equals ($1.3806503 \times 10^{-23}$ J/K), T is the temperature measured in Kelvin, and q is the electron charge (1.60217646 $\times$ $10^{-19}$ C). The shunt resistance current is formulated as

$$\begin{aligned} I_{\rm sh} = \frac{V_{m} + R_{s}.I_{m}}{R_{\rm sh}} \end{aligned}$$

(4)

From Eqs. 1,  2, 3, and  4, the output current of the solar cell can be calculated as

$$\begin{aligned} I_{o} = I_{\rm ph} - I_{\rm sd}\left[exp\left(\frac{V_{m} + R_{s} I_{m}}{n V_{t}}\right)-1\right] - \frac{V_{m} + R_{s}.I_{m}}{R_{\rm sh}} \end{aligned}$$

(5)

In this equation, the unknown five parameters are $X=$($I_{\rm ph}$, $I_{\rm sd}$, $R_{s}$, $R_{\rm sh}$, and n) which have to be optimized.

2.2 Double diode model

DDM is proposed to enhance the solar cell efficiency through considering the influence of leakage current within the depletion region. The equivalent circuit is shown in Fig. 1b. The output current of this circuit $I_{o}$ is calculated by Kirchhoff’s current law as follows

$$\begin{aligned}{} & {} I_{o} = I_{\rm ph} - I_{D1} - I_{D2} - I_{\rm sh} \end{aligned}$$

(6)

$$\begin{aligned}&I_{o} = I_{\rm ph} - I_{\rm sd1}[exp(\frac{V_{m} + R_{s} I_{m}}{n_{1} V_{t}})-1] \\&-\quad I_{\rm sd2}[exp(\frac{V_{m} + R_{s} I_{m}}{n_{2} V_{t}})-1] - \frac{V_{m} + R_{s}.I_{m}}{R_{\rm sh}} \end{aligned}$$

(7)

Where $I_{\rm sd1}$, $I_{\rm sd2}$ are, respectively, the saturation currents (A) of the diode 1 and diode 2. n1 and n2 are denote the ideality of the diode 1 and diode 2, respectively. There are seven unknown parameters within this model and have to be identified $X=$($I_{\rm ph}$, $I_{\rm sd1}$, $I_{\rm sd2}$, $R_{s}$, $R_{\rm sh}$, $n_1$ and $n_2$).

2.3 PV module model

PVM module model is build based on the configuration of SDM. It consists of a number of solar cells arranged in series or/and parallel to increase the efficiency of the energy solar cell. $N_{s}$ describes the number of series cells, and $N_{p}$ presents the number of parallel solar cells. The modeling of the PV solar cell is described in Fig. 1c, and the output current is calculated by the following expression.

$$\begin{aligned}&I_{o} = I_{\rm ph}. N_{p} - I_{\rm sd}.N_{p} [exp(\frac{V_{m} + R_{s} I_{m}.N_{s}/N_{p}}{n V_{t}})-1] \\&\quad -\frac{V_{m} + R_{s}.I_{m}. N_{s}/N_{p}}{R_{\rm sh}. N_{s}/N_{p}} \end{aligned}$$

(8)

$$\begin{aligned}{} & {} V_{t} = \frac{N_{s}. K.T}{q} \end{aligned}$$

(9)

The PVM model has five unknown parameters needed to be optimized similar to SDM which are $X=$($I_{\rm ph}$, $I_{\rm sd}$, $R_{s}$, $R_{\rm sh}$, and n).

3 Problem formulation

The extraction of the unknown parameters of different solar cells models can be regard as optimization problem. In order to measure the accuracy of the extraction process, the objective function should emphasize the differences between the measured current and the current calculated using the estimated parameters.

The different algorithms settings substantially impact the performance of metaheuristic algorithms, and therefore, different performance indicators can be used to evaluate the results from diverse aspects. Literature usually visualizes the accuracy of the extracted parameters against experimental data. Based on the differences between simulation data and experimental data, some general and objective functions are more suitable for evaluation and comparing the algorithms.

The absolute error indicator (AE) is used to represent the difference between the simulated data and the experimental data. The mean absolute error (MAE) emphasizes the situation of the simulated data and the experimental data. The sum squared error (SSE) measures the degree of change in data between the simulated data and the experimental data where the small value of SSE indicates that the simulated data can describe the experimental data with a small error.

The root mean square error (RMSE) describes the degree of dispersion of the simulated data and the experimental data and gives an overall assessment. The Wilcoxon test gives overall assessment from statistical perspectives. In this work, the RMSE is used as the objective function [42] and Wilcoxon test is used to evaluate performance. According to Eqs. 5, 7, and 8, the error function for SDM, DDM, and PV module model can be expressed as follows.

$$\begin{aligned}f_{SD}(V_{m},I_{m},X) &= I_{m} - I_{\rm ph} + I_{\rm sd}[exp(\frac{V_{m} + R_{s} I_{m}}{n V_{t}})-1] \\&\quad +\frac{V_{m} + R_{s}.I_{m}}{R_{\rm sh}} \end{aligned}$$

(10)

$X=$($I_{\rm ph}$, $I_{\rm sd}$, $R_{s}$, $R_{\rm sh}$, and n)

$$\begin{aligned}&f_{DD}(V_{m},I_{m},X) = I_{m} - I_{\rm ph} + I_{\rm sd1}[exp(\frac{V_{m} + R_{s} I_{m}}{n_{1} V_{t}})-1] + \\&I_{\rm sd2}[exp(\frac{V_{m} + R_{s} I_{m}}{n_{2} V_{t}})-1] + \frac{V_{m} + R_{s}.I_{m}}{R_{\rm sh}} \end{aligned}$$

(11)

$X=$($I_{\rm ph}$, $I_{\rm sd1}$, $I_{\rm sd2}$, $R_{s}$, $R_{\rm sh}$, $n_1$ and $n_2$).

$$\begin{aligned}&f_{PV}(V_{m},I_{m},X) = I_{m} - I_{\rm ph}. N_{p} \\&\quad +I_{\rm sd}.N_{p} [exp(\frac{V_{m} + R_{s} I_{m}.N_{s}/N_{p}}{n V_{t}})-1] \\&\quad + \frac{V_{m} + R_{s}.I_{m} . N_{s}/N_{p}}{R_{\rm sh}. N_{s}/N_{p}} \end{aligned}$$

(12)

$X=$($I_{\rm ph}$, $I_{\rm sd}$, $R_{s}$, $R_{\rm sh}$, and n).

In general, the objective function can be regarded as follows

$$\begin{aligned} f_{RMSE}(V_{m},I_{m},X) = \sqrt{\frac{1}{n} \sum _{k=1}^{n} f^{k}_{d}(I^{k}_{m},V^{k}_{m}, X)} \end{aligned}$$

(13)

Where d denotes to single diode model, double diode model, or PV module model, and n is the number of benchmark current.

4 Generalized normal distribution optimization

GNDO is a relatively new optimization algorithm introduced by Zhang et al. in 2020 to extract the unknown parameters of photovoltaic models with high accuracy. The algorithm is inspired by the normal distribution model, and the position of all individuals is considered as random variables obeying normal distribution. Therefore, the search process can be described by multiple normal distributions corresponding to the position of populations. Moreover, GNDO searches the promising solution space through two operators, namely local exploitation, and global exploration.

4.1 Local exploitation

Local exploitation or local search aims to enhance the solution found so far through searching the space around the better solutions where the search space consists of the current positions of all individuals, and the mean positions. Therefore, generalized normal distribution model is built as follows.

$$\begin{aligned} v^{t}_{i} = \mu _{i} + \delta _{i} \times \eta , i=1,2,...,N \end{aligned}$$

(14)

where $v^{t}_{i}$, $\mu _{i}$, $\delta _{i}$ are the new position, generalized mean position, the standard variance of the ith individual at time t, and $\eta$ is penalty factor. Moreover, these parameters care calculated as follows

$$\begin{aligned}{} & {} \mu _{i} = \frac{1}{3}(x^{t}_{i} + x^{t}_{best} + M) \end{aligned}$$

(15)

$$\begin{aligned}{} & {} \delta _{i} = \sqrt{\frac{1}{3}[(x^{t}_{i}-\mu )^2 + (x^{t}_{best}-\mu )^2+(M-\mu )^2]} \end{aligned}$$

(16)

$$\begin{aligned}{} & {} \eta = \left\{ \begin{array}{rcl} \sqrt{-\log (\lambda _{1})} \times cos(2\pi \lambda _{2}) &{} \text{ if } &{} a \le b \\ \sqrt{-\log (\lambda _{1})} \times cos(2\pi \lambda _{2}+\pi ) &{} \text{ otherwise } \end{array}\right. \end{aligned}$$

(17)

$$\begin{aligned}{} & {} M = \frac{\sum _{i=1}^{N}x^{t}_{i}}{N} \end{aligned}$$

(18)

where a, b, $\lambda _{1}$, and $\lambda _{2}$ are random number between 0 and 1. M, $x^{t}_{best}$ are the mean position of the current population and the best current position, respectively, and N is the population size.

4.2 Global exploration

The global exploration searches for new regions to find promising solutions. Three randomly selected individuals are used to update the individual ith position as follows.

$$\begin{aligned} v^{t}_{i} = x^{t}_{i} + \beta \times (|\lambda _{3}| \times v_{1}) + (1-\beta ) \times (|\lambda _{4} \times v_{2}) \end{aligned}$$

(19)

Where $\lambda _{3}$ and $\lambda _{4}$ are two random number between 0 and 1 drawn from normal distribution and the adjustment factor $\beta$ controls the information sharing between local and global operators. Moreover $v_{1}$, and $v_{2}$ can be computed as follows.

$$\begin{aligned}{} & {} v_{1} = \left\{ \begin{array}{rcl} x^{t}_{i}-x^{t}_{p1} &{} \text{ if } &{} f(x^{t}_{i}) < f(x^{t}_{p1}) \\ x^{t}_{p1} - x^{t}_{i} &{} \text{ otherwise } \end{array}\right. \end{aligned}$$

(20)

$$\begin{aligned}{} & {} v_{2} = \left\{ \begin{array}{rcl} x^{t}_{p2}-x^{t}_{p3} &{} \text{ if } &{} f(x^{t}_{p2}) < f(x^{t}_{p3}) \\ x^{t}_{p3} - x^{t}_{p2} &{} \text{ otherwise } \end{array}\right. \end{aligned}$$

(21)

where $x^{t}_{p1}$, $x^{t}_{p2}$, and $x^{t}_{p3}$ are three randomly selected individual from the current population.

Finally, GNDO introduces screening mechanism to keep the better solution in the next generation as follows. Algorithm 1 shows the steps of GNDO.

$$\begin{aligned} x^{t+1}_{i} = \left\{ \begin{array}{rcl} v^{t}_{i}&{} \text{ if } &{} f(v^{t}_{i}) < f(x^{t}_{i}) \\ x^{t}_{i} &{} \text{ otherwise } \end{array}\right. \end{aligned}$$

(22)

Algorithm 1. Standard GNDO

5 Enhanced GNDO with neighborhood search (NSGNDO)

A common drawback of the most stochastic search algorithm is Premature convergence. However, some trapped individuals at local optima can contain the global minimum. Therefore, searching the neighborhood of individuals may find better solutions and lead to find the global solutions. Based on this concept, many neighborhoods search strategies are proposed to enhance both the exploration and exploitation of some natural-inspired algorithms [39,40,41]. Inspired by the work done in [43], NSGNDO is presented with two search strategies namely: local neighborhoods search strategy (LNS) and global neighborhoods search strategy (GNS). The former strategy improves the convergence of the algorithms and makes it converge to near-optimal solutions while the later one makes the algorithm explores more feasible solutions in the search space.

5.1 Local neighborhoods search strategy

LNS improves the exploitation of the algorithm by searching the neighborhood of individuals to accelerate the algorithm’s convergence. Assume that, the individual $x_{i}, i =1,\dots ,N$ where N is the population size and the individuals are organized in a circle topology as shown in Fig 2. After each generation, the neighborhood of individual $x_{i}$ is calculated based on the mean Euclidean distance between $x_{i}$ and every individual in the population as follows

$$\begin{aligned} d_{i} = \frac{\sum _{k=1}^{N} d_{(i,k)}}{N-1} \end{aligned}$$

(23)

Where N is the population size excluding individual $x_{i}$, and the d(i, k) is the Euclidean distance between $x_{i}$ and $x_{j}$. The individual $x_{j}$ is neighbor of $x_{i}$ if the distance d(i, k) is less than $r.d_{i}$ where r is the neighborhood radius and equal to 1. Consequently, the position of individual $x_{i}$ is updated as follows

$$\begin{aligned}{} & {} Lx_{i} = r_{1} x_{i} + r_{2} pbest_{i} + r_{3} v_{1} \end{aligned}$$

(24)

$$\begin{aligned}{} & {} v_{1} = \left\{ \begin{array}{rcl} x_{a}-x_{b} &{} \text{ if } &{} f(x_{a}) < f(x_{b}) \\ x_{b}-x_{a} &{} \text{ otherwise } \end{array}\right. \end{aligned}$$

(25)

Where $pbest_{i}$ is the previous best position of individual $x_{i}$, $x_{a}$ and $x_{b}$ are two randomly selected individuals from the neighborhood of $x_{i}$, $a !=b$, and r1,r2 and r3 are three random numbers generated from uniform distribution, and $r1+r2+r3=1$. Figure 2a demonstrates the local neighborhood search mechanism.

The individual with large step may be easily trapped in local minima. The LNS generates new solution near the current one,which helps the algorithm to find better solution step by step. In general, LNS is helpful when the local minimum is close to the global minimum.

Fig. 2

Neighborhood search strategies

5.2 Global neighborhood search strategy

The GNS is proposed to improve the exploration ability of the standard GNDO by searching new promising region that may contains feasible solutions. The trail position of individual $x_{i}$ is generated as follows

$$\begin{aligned}{} & {} gx_{i} = r_{4} x_{i} + r_{5} gbest_{i} + r_{6} v_{2} \end{aligned}$$

(26)

$$\begin{aligned}{} & {} v_{2} = \left\{ \begin{array}{rcl} x_{c}-x_{d} &{} \text{ if } &{} f(x_{c}) < f(x_{d}) \\ x_{c}-x_{d} &{} \text{ otherwise } \end{array}\right. \end{aligned}$$

(27)

Where $gbest_{i}$ is the global best individual, $x_{c}$ and $x_{d}$ are two randomly selected individuals from the entire population, $c !=d$. The variables r4,r5 and r6 are three random numbers generated from uniform distribution, and $r4+r5+r6=1$. Figure 2b demonstrates the mechanism of global neighborhood search. The GNS prevents the individuals from trapped in local optima and pulls the individuals toward new promising solutions.

Algorithm 2. NSGNDO

5.3 Process of NSGNDO

Algorithm 2 shows the pseudo code for the proposed NSGNDO. Line 1 shows the input to the algorithm where Max_FES denotes the maximum number of function evaluations, N denotes the number of populations, and L and U are the lower and upper limits for each variable. In Line 2, the algorithm randomly initializes the populations. For instance, to estimate a SDM’s parameters, each individual $X_{i}$ can be expressed as $X_{i} =[x_1,x_2,x_3,x_4,x_5,x_6,x_7]$ corresponding to parameters’ values of the SDM which are Iph, $Isd_1$, $Isd_2$, Rs, Rsh, $n_1$, and $n_2$; then, the algorithm randomly initializes the swarm $X_{i}$ according to lower and upper limits based on Table 2. In Line 3, the best individual $X_{best}$, the local best individual $X_{pbest}$ are calculated. From Line 9 to Line 14, the algorithm performs either local search or global search according to Eqs. 14 and 19, respectively. In Line 15, the algorithm performs screening mechanism between $X^{t}_{i}$ and $X^{t+1}_{i}$. From Line 16 to 21, the algorithm performs either local search strategy using Eq. 24 or global search strategy using Eq. 26 according to the value of $p_{n}$. Line 23 selects the best individual using screening mechanism among $X_{i}$, LX, and GX. From Line 23 to 27, the value of FEs, the best individual and the local best individual are updated. In Line 29, the optimal/near-optimal solution is obtained. Figure 3 sum up the whole process of the NSGNDO and highlights the neighborhood local search and neighborhood global search strategies.

Fig. 3

Flow chart of NSGNDO

5.4 The computation complexity of NSGNDO

Computation complexity is one of the most important metrics to measure the running time for any algorithm regardless of the hardware. According to Algorithm 2 and the flowchart shown in Fig. 3, the complexity of NSGNDO consists of the complexity for the basic GNDO plus the complexity of LNS and GNS. The complexity of the GNDO consists of comparing and updating the individuals based on number of function evaluations. There are N individuals position updates and there are N comparisons. Therefore, the total complexity of the basic GNDO is $\mathcal {O}({\rm NDT}_{\max} + {\rm NT}_{\max})$. In the proposed NSGNDO, the calculation for neighborhood is estimated on each iteration from Eq. 23 and mentioned in Line 7 of Algorithm 2. Therefore, the complexity of calculating the neighborhood is ${\rm NT}_{\max}$. Therefore, the total complexity of the proposed NSGNDO is $\mathcal {O}({\rm NDT}_{\max} + 2{\rm NT}_{\max})$

6 Numerical results and discussion

The performance of the proposed NSGNDO has been validated through estimating the parameters of SDM, DDM, and PVM models. The proposed NSGNDO is implemented using MATLAB 2016a software on an Intel Core TM core i7 CPU @ 2.90GHz, 16 GB RAM Laptop.

The simulation results are compared with real time data obtained from [44] and presented in Table 10(see Appendix A). This benchmark is widely used to evaluate different optimization algorithms on estimating the parameters of various solar cells. The experimental data for SDM, and DDM were collected using R.T.C France solar cell with a 57 mm diameter commercial silicon under 1000 W/m$^{2}$ at 33 C$^{\circ }$. For the PVM model, the experimental data were collected for Phowatt-PWP201 that consists of 36 polysilicon cells in series and the data were measured at temperature 45 C$^{\circ }$.

Table 2 The parameters range of the PV models

To have fair comparison between different algorithms, the range of different parameters is shown in Table 2 [45,46,47,48]

The search range for each parameter is given in Table 2 for single diode model, double diode model, and PV module model, respectively. In addition, the performance of the proposed NSGNDO is evaluated against nine sophisticated metaheuristic algorithms including GNDO [26], SSA [49], TLBO [50], NNA [51], MBO [52], GA [53], BSA [54], PSO [55], and CS [56]. For the sake of having fair comparison, the number of function evaluation is set to 35,000, 45,000 and 35,000 for single diode model, double diode model and PV module model. The population size is set to 50 for all algorithms on SDM, DDM, and PV module model, respectively. The control parameters of the compared methods are the same as mentioned in their references. The probability of conducting neighborhood search is set to 0.6 as in [43]. Moreover, each algorithms run independently 30 times on each test benchmark. The best results are indicated by boldface.

6.1 Result analysis for single diode model

Table 3 shows the extracted parameters of SDM model and the corresponding RMSE obtained by different methods. On one hand, both the proposed NGNDO and the standard GNDO are superior to other methods, and they can find the best values of SDM’s parameters that achieve minimum RMSE with value of 9.8602E-04. On the other hand, PSO ranks second with RMSE’s value of 9.8630E-04.

Table 3 The best solution obtained by different algorithms on single diode model

Table 4 Comparing the statistical results obtained by applying different algorithms on single diode

Although NSGNDO and GNDO achieve the same RMSE, NSGNDO can find the best values of the SDM’s parameters with fewer number of function evaluations as indicated by the convergence curve in Fig. 6a. The figure shows that NGNDO has a fast convergence beginning from early iterations compared to GNDO and can obtain the best mean value of RMSE at 10,000 function evaluations. On contrast, the GNDO can reach the best value of RMSE at the 30,000 function evaluations. Furthermore, Fig. 7a shows that NSGNDO has better convergence than other methods for SDM model.

In addition, Table 4 shows the worst, mean, median, best, and Std of RMSE obtained by different methods. The results demonstrate that NSGNDO has a small variation of the results over different function evaluations compared to other methods. In more detail, NSGNDO shows more stability as indicated by the minimum Std with value of 3.098E-17 compared to the basic GNDO which has Std with value of 3.1269E-17.

Furthermore, to have competitive comparison between the simulated results and the experimental data. Figure 4a shows I–V characteristics curve for simulated current and measured current against the measured voltage. The simulated currents are calculated using the values of parameters obtained by applying NSGNDO whereas the measured currents are obtained from [44]. The curve demonstrates that the error between simulated currents and measured current over different voltages are too small. The small value of error gives more inference about the improvement of NSGNDO results because of local and global neighborhood search strategies. Similarly, P-V characteristic curve shown in Fig. 5a demonstrates that the error between the estimated power and the experimental power is very small.

To sum up, the local and global search strategies enable NSGNDO to efficiently search for the promising values of the SDM’s parameters and to identify the optimal values of these parameters. The comparison between the simulated currents, measured current as well as the comparison between simulated power and the measured power give more inference on the improvement of NSGNDO and its search ability to find the best values of the parameters.

Fig. 4

I–V characteristics between the simulated current and measured current obtained by NSGNDO

Fig. 5

Power characteristics between the simulated power and measured power obtained by NSGNDO

Fig. 6

The convergence curves obtained by NSGNDO and GNDO

Fig. 7

The convergence curves obtained by NSGNDO and other methods

6.2 Result analysis for double model

Table 5 shows the values of DDM’s parameters extracted using different methods. The value of RMSE shown in tables indicates the error between the simulated currents that was calculated using values of extracted parameters and the measured current. The results demonstrates that the proposed NSGNDO and the standard GNDO successfully identify the best values of the DDM’s parameters that results in minimum RMSE with value of 9.8248E–04 compared to other methods. The TBLO method comes second with RMSE of 9.8406E–04. Despite NSGNDO and GNDO have similar performance as they achieve the same RMSE NSGNDO converges to the minimum RMSE with fewer number of function evaluations as demonstrated in Fig. 6b. In addition, Fig. 7b demonstrates that NSGNDO can converge to the best solutions with fewer number of iterations compared to other methods.

Although the proposed NSGNDO and GNDO have similar performance as they achieve the same RMSE, but NSGNDO shows high stability over different function evaluations as indicated by Std of value 1.2581E–06 compared to 1.4417E–06 for GNDO as demonstrated in Table 6 In addition, TLBO comes in the third rank with 1.7644E–04 for the Std. To conclude, NSGNDO show high stability over different function evaluations compared to other methods because local and global search strategies help the algorithm to find best parameters’ value in early function evaluations and therefore, RMSE slightly variant over next function evaluations.

Besides NSGNDO has a fast convergence rate, NSGNDO, it also shows high consistence between the simulated currents and the extracted parameters. The I–V characteristics curve in Fig. 4b demonstrates this consistence as the RMSE between the simulated currents and corresponding measured current over different voltage is too small. Furthermore, the P-V characteristics shown in Fig. 5b also confirm this consistence where the calculated power based on simulated currents is too close the experimental power shown in [44].

Table 5 The best solution obtained by different algorithms on double diode model

Table 6 Comparing the statistical results obtained by applying different algorithms on double diode

6.3 Result analysis for PV module model

Table 7 depicts the value of PVM’s parameters corresponding to different methods. The RMSE values are used to measure and compare the performance of each method. The proposed NSGNDO shows a significant improvement in the simulated current estimation as indicated by the minimum RMSE. On one hand, the NSGNDO ranks first and achieve 2.05296E–03 of RMSE compared to 2.42507E-03 for GNDO. On the other hand, PSO ranks third with 2.42508E-03 for RMSE.

In addition, NSGNDO obtains the value of the extracted parameters for PVM with fewer number of function evaluations as demonstrated in Fig. 6c. The figure shows the convergence curves for NSGNDO and GNDO with respect to RMSE. The proposed NSGNDO has fast convergence at the beginning of iteration compared to GNDO. However, both algorithms in some iterations do not have any improvement such as the function evaluations between 60 and 70 that is because the search space becomes so large, and the algorithms need to explore more regions to find the promising solutions. Furthermore, Fig. 7c show that NSGNDO has a better convergence rate compared to other methods. Table 8 shows that stability of NSGNDO over function evaluations starting from early function iteration as indicated by Std value of 1.05495E-17.

The I–V characteristic curve in Fig, 4c demonstrates the consistency between the simulated currents and the measured current against different measured voltage. The small error between the simulated current and measured current infers that although the search space is more complex and so large, the proposed NSGNDO efficiently explores the search space and can find better values of the PVM’s parameters. Furthermore, the P-V characteristics curve shown in Fig. 5c shows that a very small RMSE between the simulated power and the experimental power.

Table 7 The best solution obtained by different algorithms on PV module model

Table 8 Comparing the statistical results obtained by applying different algorithms on PV module model

6.4 Wilcoxon signed-rank test

Table 9 presents the results obtained by Wilcoxon signed-rank test with a significant level $\alpha = 0.05$ to check the null hypothesis that the NSGNDO algorithm do not have significant performance differences compared to other considered algorithms for SDM, DDM, and PVM models.

The results obtained by 30 independent runs are used for this test. The $T^{+}$ represents the sum of ranks for the benchmark in which the NSGNDO algorithm has better performance compared to the corresponding algorithm, whereas $T^{-}$ represents the opposite.

By carefully looking at the results on Table 9, the proposed NSGNDO outperforms the basic GNDO and other methods in all benchmarks. In detail, NSGNDO superior the basic GNDO in 487 out of 500 cases for SDM, 496 out of 500 cases for DDM, and 500 out of 500 cases for PVM models. Furthermore, the p value of 1.19E–70, 1.50E–79, and 1.26E–83 for SDM, DDM, and PVM, respectively, indicates that the superiority of the proposed NSGNDO compared to the standard GNDO is significant.

To sum up, the values of $T^{+}$,$T^{-}$, and p value for SDM, DDM, and PVM demonstrates that the NSGNDO performs better in most cases compared to other methods.

Table 9 The results of Wilcoxon signed-rank test with a significant level $\alpha$=0.05

7 Conclusion

This paper presents an enhanced variant of generalized normal distribution optimization algorithm denoted as NSGNDO to extract the unknown parameters of the photovoltaic models. The NSGNDO algorithm improves the convergence of the basic GNDO and increases the diversity of the population by integrating the neighborhood search strategies within the algorithm. The neighborhood search strategies include LNS for local search, and GNS for global search. The experimental results show consistency of the performance and the stability of NSGNDOcompared to other algorithms in the literature. The NSGNDO is an efficient algorithm and can be applied to solve different optimization problem such as load balancer in fog-computing, disease diagnoses, and image segmentation. Some of the limitations include: the proposed method is not tested on noisy data and is not tested for other PV modules such as polycrystalline STP6-120/36, STP6-40/36, and triple diode model. These limitations will be considered as future work.

Appendix

Table 10 Benchmark data for single, double, and PV module models