1 Introduction

Fault detection and process monitoring have been active areas of the research in the control community over the last several decades [1,2,3]. Due to a large amount of stored data in industrial databases, the data-driven process monitoring approaches have attracted more attention because of their simple design methods and low requirements on the underlying mechanisms [4, 5]. To effectively use the data-driven approaches for process monitoring of large-scale industrial systems with a huge amount of data, it is necessary to perform pre-processing on the collected data to extract information, followed by dimensionality reduction and the selection of the variables that explains a significant part of the observed process variation.

The multivariate statistical process monitoring methods are considered the most popular among data-driven techniques where they directly use the input–output measurements for process monitoring purposes. The basic multivariate statistical process monitoring methods including principal component analysis (PCA) [6, 7], partial least squares (PLS) [8], total projection to latent structures (TPLS) [9], modified partial least squares (MPLS) [10], orthogonal projection to latent structures (O-PLS) [11], modified orthogonal projection to latent structures (MOPLS) [12], expectation-maximization partial robust M-regression (EMPRM) [13], and total principal component regression (TPCR) [14]. All these methods have been successfully applied to many large industrial processes, e.g., chemical plants, water treatment processes, power grids, and cyber-physical systems [15,16,17]. It should be noted that these monitoring methods are efficiently used with linear, single-mode, and time-invariant processes [18].

Today, wind turbine systems have been widely used to convert wind energy into electricity as a renewable energy source [19,20,21]. Some wind turbines can produce power up to 4.8 MW [22]. However, wind turbines can be subjected to several faults whether they are sensor faults, actuator faults, and system faults. For a wind turbine, the sensor faults include pitch position sensor faults, rotor speed sensor faults, and generator speed sensor faults. On the other hand, the actuator faults are due to converter coupling faults and pitch system faults. Furthermore, system faults can be found in the wind turbine drive train. It is worth mentioning that unexpected failures of wind turbine parts are the major cause of increased repair costs [23, 24].

Fault detection and diagnosis in different fields have attracted more attention in the literature. The research papers can be classified according to the used fault detection techniques into statistical techniques [25], machine learning techniques [26], deep learning techniques [27,28,29], vibration analysis techniques [30], and Hybrid techniques [31]. Furthermore, there are two sources of data in these researches that can be either simulated data [32] or SCADA data [33]. Moreover, deep learning methods have been applied in many fields, and among these fields is the field of fault detection and diagnosis. Therefore, its advantages are their ability to improve the accuracy of predictions and decision-making, the ability to learn from unstructured data, such as images, text, and audio, and the ability to automatically learn features from data, eliminating the need for manual feature engineering, but their limitations are their high computational cost and their dependence on the quality and quantity of data used for training.

Recently, data-driven techniques have been applied to a wide range of applications, e.g fault classification [34], signal processing [35], image processing and pattern recognition [36], modeling [37], real-time fatigue life prediction of structures [38], and fuzzy sewage treatment processes [39].

Although significant efforts have been made in the process monitoring of wind turbine systems, to the best knowledge of the authors, there is no systematic comparative studies of data-driven fault detection strategies are available in the literature. Therefore, this is the main motivation behind this study. Due to the nature of this study, the amount of mathematical equations behind the different methodologies have been minimized, as there is a wealth of knowledge in the literature on data-driven methodologies. In addition to that, a detailed description of the benchmark of wind turbines including the models, variables, and faults is presented to be as a reference to other research studies.

The remainder of this study is presented in the following structure. Section 2 gives an overview of the basic data-driven fault detection methods and their variants. Section 3 provides a detailed description of the wind turbine system. The presented fault detection methods are applied to a simulated benchmark of wind turbines, and the comparative results are presented in Sect. 4. Finally, the conclusions are provided in Sect. 5.

2 Overview of data-driven techniques

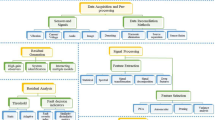
In order to make it easier to compare different data-driven techniques, we categorize them along a standard fault detection and diagnosis (FDD) work-flow for gathering and analyzing measurements from manufacturing process. Additionally, the basic multivariate statistical process monitoring methods including: The principal component analysis (PCA) model is a statistical procedure in which a set of correlated variables is converted into a set of linearly independent variables that are called principal components. Moreover, PCA is regarded as one of the dimensional reduction techniques in which the number of principal components is always lower than the number of original variables. As well known, the fault detection issue in the scope of the statistics is formulated by two hypotheses, the null hypothesis, which represents the fault-free case, and the alternative hypothesis, which represents the faulty-case [40]. Assume that \(J_{\rm index}\) and \(J_{\rm{th,index}}\) are the fault detection index and its corresponding threshold, respectively. Then, the fault detection logic is as follows:

$$\begin{aligned} {\left\{ \begin{array}{ll} J_{\rm index} \le J_{\rm th,index} &{} \text {null hypothesis (fault-free case)},\\ J_{\rm index} >J_{\rm th,index}&{} \text {alternative hypothesis (fault case)}. \end{array}\right. } \end{aligned}$$
(1)

Partial least square (PLS) is a popular input–output technique that is used for modeling, regression, fault detection, and classification purposes. Although the success of the standard PLS model as a monitoring tool for quality-related process problems, it suffers from some problems such as it requires many latent variables that include variations orthogonal to the output Y but are not useful for predicting the output Y [41]. Moreover, residual subspace usually has quite large variations that are not proper to be monitored. [9] proposed the TPLS algorithm to treat the standard PLS model-associated problems. TPLS model works well for characterizing the observed X and is appropriate for monitoring various parts of X. In spite of this, TPLS is not able to totally eliminate impacts. Therefore, as fault amplitude increases, the amount of undesired variability will rise to a point where the post-processing techniques are useless.

MPLS is another variant of PLS in which the orthogonal decomposition on regression variable space is applied to eliminate the useless variations for output prediction. The related computation cost of the modified strategy eliminates the shortcomings of the traditional PLS algorithm and is significantly simpler than that of the standard technique. Orthogonal projection to latent structures (OPLS) has been used to reduce the number of latent variables while maintaining good prediction accuracy. The OPLS approach is a combination between PLS and a pre-processing technique that is used for removing components that orthogonal to the output Y from the input \(X\) [42].

MOPLS methodology is a combination of both OPLS and MPLS algorithms defined in the previous subsections. One of its main advantages is its lower complexity since it reduces the number of latent variables. The EMPRM algorithm has a smaller predicted offset and a more accurate predicted output than the PLS algorithm. The expectation-maximization (EM) phase consists of two steps: the expectation step and the maximization one. In the former, the missing elements are filled with the expected values. In the latter, the expected values are updated using the data in which missing elements are included have been filled in. TPCR model is used to solve the quality-related fault detection issue for linear systems [14]. However, TPCR is inappropriate for automobile applications but is suitable for statistical processes. In the following subsections, the essential mathematical background for the discussed data-driven techniques is presented.

2.1 Principal component analysis

The first step in building a PCA model for the fault detection process is to collect the normal dataset \(X = \left[ x_{1}\,x_{2}\,\ldots \, x_{N} \right] ^{\rm T} \in {\mathfrak {R}}^{{N \times M}}\), with M is the process variables and N is the number of measurements. The second step is to normalize the data matrix X with data mean and variance to ensure that all variables have equal weight and to prevent a set of variables from dominating the fault detection process [43]. The third step is to build the PCA model which can be done by calculating the sample covariance matrix \(S=\frac{1}{N-1} X^{\rm T}X\), and then applying the singular value decomposition (SVD) method to calculate the loading vectors which are considered the new coordinates of the data. Generally, PCA model decomposes the original data measurement space into the principal component subspace (PCS), \({\ S}_{p}\) = \(\text {span}(P)\) and the residual subspace (RS), \({\ S}_{\rm{r}}\) = \(\text {span}({\widetilde{P}})\) [18, 41].

$$\begin{aligned} X = {\widehat{X}}+{\widetilde{X}}= TP^{\rm T} +{\widetilde{T}}{\widetilde{P}} \end{aligned}$$
(2)

where \(T \in {\mathfrak {R}}^{{N \times l}}\) and \({\widetilde{T}} \in {\mathfrak {R}}^{{N \times {M-l}}}\) are the score matrices in the PCS and RS, respectively, and \(l\ll M\) is the number of the principal components that can be determined by using different methods [44]. In general, The PCS contains the data that show the most variation, while the RS typically includes data with little variation, which is primarily noise. For an online sample vector, \(x\in {\mathfrak {R}}^{M}\), the principal and residual components are obtained by projecting \(x\) on both two subspaces, PCS and RS according to the following:

$$\begin{aligned} x={\widehat{x}}+{\widetilde{x}}=PP^{\rm T}x+{\widetilde{P}}{\widetilde{P}}^{\rm T}x=PP^{\rm T}x+\left( I\ - \ PP^{\rm T} \right) x \end{aligned}$$
(3)

where \(I\in {\mathfrak {R}}^{M \times M}\) is an identity matrix. Typically, there are two indices are used to monitor normal the variability in PCS and RS, i.e., Hotelling’s \(T^{2}\) and the squared prediction error SPE. Hotelling’s \({T}^{2}\) captures the variations in the PCS. On the other hand, the \(\text {SPE}\) index measures the variations in RS. Therefore, the two monitoring indices with their thresholds for a given significant level [45, 46] can be calculated as Table 1:

Table 1 PCA monitoring statistics and thresholds
Full size table

2.2 Partial least squares

Generally, the PLS partitions the input space into a principal subspace \(S_{\rm p}\) and a residual subspace \(S_{\rm r}\). Given a measurement data matrix (regression variables) \(X = \left[ x_{1}\,x_{2}\, \ldots \, x_{N} \right] ^{\rm T} \in {\mathfrak {R}}^{\text {NxM}}\) and \(Y = \left[ y_{1}\, y_{2}\,\ldots \, y_{N} \right] ^{\rm T} \in {\mathfrak {R}}^{N \times q}\) consisting of \(N\) samples of \(q\) product quality variables (outputs), the PLS projects both \(X\) and \(Y\) onto a low dimensional subspace defined by a l latent variables. Therefore, both X and Y become:

$$\begin{aligned} X=\text {TP}^{\rm T} + {\widetilde{X}}= \text {XRP}^{\rm T} + {\widetilde{X}} \end{aligned}$$
(4)
$$\begin{aligned} Y=\text {TQ}^{\rm T} + {\widetilde{Y}}=\text {XRQ}^{\rm T} + {\widetilde{Y}} \end{aligned}$$
(5)

where \(T=\left[t_{1}\ldots \ t_{l} \right]\epsilon {\ {\mathfrak {R}}}^{N \times l}\)is the score matrix. \(P\in {\mathfrak {R}}^{M \times l}\) and \(Q\) \(\in \) \({\mathfrak {R}}^{q \times l}\) are the loading vectors of X and Y, respectively. \(P^{\rm T}R= R^{\rm T}P= I_{l}\), \(R\in {\mathfrak {R}}^{M \times l}\). The PLS is implemented using the nonlinear iterative partial least squares algorithm (NIPALS) to calculate P, T, Q, and R matrices [47, 48]. Similarly to the PCA model, there are two indices used for fault detection extracted from PLS model, i.e., Hotelling’s \(T^{2}_{\rm PLS}\) statistic that is used for monitoring the variations in the \(S_{\rm p}\) related to the quality output data Y. On the other side, the residual subspace \(S_{\rm r}\) is monitored by the \(\text {SPE}_{\rm PLS}\) statistic which represents the variations unrelated to Y. Therefore, the two monitoring indices with their thresholds can be calculated as Table 2:

Table 2 PLS monitoring statistics and thresholds
Full size table

2.3 Total projection to latent structures (TPLS)

The main idea of the TPLS model is to decompose the input data space, X, into four parts instead of two parts as in the standard PLS:

$$\begin{aligned} \begin{aligned} X&= T_{y}P_{y}^{\rm T} + T_{\rm o}P_{\rm o}^{\rm T} + T_{\rm{r}}P_{\rm{r}}^{\rm T} + {\widetilde{X}}_{\rm{r}} \\ Y&= {\widehat{Y}}+{\widetilde{Y}}=TQ^{\rm T} + {\widetilde{Y}} \\ \end{aligned} \end{aligned}$$
(6)

where \(T_y\) is a score matrix that is directly correlated with Y in the original T, and \(T_{\rm o}\) is orthogonal to Y in the original T. Furthermore, \(T_{\rm r}\) is the main part in \({\widetilde{X}}\), and \({\widetilde{X}}_{\rm r}= {\widetilde{X}} \left( I - P_{\rm{r}}P_{\rm{r}}^{\rm T} \right) \) is the residual part in \({\widetilde{X}}\) that represents the noise. \(P_{y}\), \(P_{\rm o}\), \(P_{\rm{r}}\) are the loading vectors that span the corresponding subspaces. It is clear that the TPLS model is able to monitor different parts of X. Therefore, there are four monitoring statistics, i.e., \(T_{y}^{2}\), \(T_{\rm{r}}^{2}\), \(T_{\rm o}^{2}\), and \(\text {SPE}_{\rm r}\) with their thresholds that can be calculated according to the following [49] as Table 3:

Table 3 TPLS monitoring statistics and thresholds
Full size table

More details about the TPLS model are given in the research work of [9]. It should be noted that both \(T_{y}^{2}\) and \(\text {SPE}_{\rm r}\) are used to detect the faults related to Y. On the contrary, \(T_{\rm o}\) and \(T_{\rm{r}}\) are used together to detect the faults that are not related to Y. It should be noted that \(\text {SPE}_{\rm r}\) is more sensitive to incipient faults compared with SPE in the standard PLS [9].

2.4 Modified partial least squares (MPLS)

The following desired relation can be calculated:

$$\begin{aligned} Y\ = {\widehat{Y}}\ + {\widetilde{Y}}= \ XM\ + {\widetilde{Y}} \end{aligned}$$
(7)

where M is the matrix of the regression coefficient and contains correlation information between X and Y. Moreover, \({\widehat{Y}}\) and \({\widetilde{Y}}\) are the subspaces that are correlated and uncorrelated with X, respectively. The coefficient matrix, M can be easily calculated as:

$$\begin{aligned} M\ = \left( X^{\rm T}X \right) ^{- 1}X^{\rm T}Y \end{aligned}$$
(8)

By applying the SVD technique, the MPLS model decomposes the original data measurement space into the principal component subspace (PCS), \({\ S}_{p}\) = \(\text {span}(P_{M}\)) and the residual subspace (RS), \({\ S}_{\rm{r}}\) = \(\text {span}({\widetilde{P}}_{M}\)) [50].

$$\begin{aligned} MM^{\rm T} = \begin{bmatrix} {P}_{M} &{} {{\widetilde{P}}_{M}} \\ \end{bmatrix}\begin{bmatrix} \Lambda _{M} &{} 0 \\ 0 &{} 0 \\ \end{bmatrix}\begin{bmatrix} {P}_{M}^{\rm T} \\ {{\widetilde{P}}_{M}^{\rm T}} \\ \end{bmatrix} \end{aligned}$$
(9)

where \({P}_{M}\in {\mathfrak {R}}^{M \times q}\), \({\widetilde{P}}_{M}\) \(\in \) \({\mathfrak {R}}^{M \times (M-q)}\) and \(\Lambda _{M}\in {\mathfrak {R}}^{q \times q}\)

Accordingly, the fault detection process can be achieved using two monitoring statistics, \(T^{2}_{M}\) and \(\text {SPE}_{M}\). It is worth mentioning that \(T^{2}_{M}\) statistic is used for monitoring \({\widehat{X}}\) which enables detecting faults that are related to Y. On the other hand, the \(\text {SPE}_{M}\) statistic is used for monitoring \({\widetilde{X}}\), thus it can detect faults that are unrelated to Y. Therefore, the monitoring statistics, i.e., \(T^{2}_{M}\), \(\text {SPE}_{M}\) with their thresholds can be calculated as Table 4

Table 4 MPLS monitoring statistics and thresholds
Full size table

More details about the MPLS algorithm are given in the research work of [50].

2.5 Orthogonal projection to latent structures (OPLS)

The original measurement data matrix X is converted into a filtered matrix \(X_{\rm opls}\) which in turn is decomposed by the OPLS algorithm into two subspaces \({\widehat{X}}_{\rm opls}\) and \({\widetilde{X}}_{\rm opls}\).

$$\begin{aligned} X_{\rm opls} = {\widehat{X}}_{\rm opls}+{\widetilde{X}}_{\rm opls} \end{aligned}$$
(10)

where \({\widehat{X}}_{\rm opls}\) is highly correlated with Y and \({\widetilde{X}}_{\rm opls}\) is uncorrelated with Y. Similarly, the aforementioned subspaces can be monitored by two indices, i.e., \(T^{2}_{\rm opls}\) and \(\text {SPE}_{\rm opls}\). Therefore, the two monitoring statistics, i.e., \(T^{2}_{\rm opls}\), \(\text {SPE}_{\rm opls}\) with their thresholds can be calculated as Table 5:

Table 5 OPLS monitoring statistics and thresholds
Full size table

2.6 Modified orthogonal projection to latent structures (MOPLS)

In this technique, the process data matrix X is decomposed into orthogonal data, \(X_{\bot }\), and filtered data \({X}_{\rm opls}\). First, the PCA model is used for Monitoring \(X_{\bot }\) that are uncorrelated with the quality variables. This can be done by performing SVD on \((1/N-1)X_{\bot }^{\rm T}X_{\bot }\).

$$\begin{aligned} \left( \frac{1}{N-1}\right) X_{\bot }^{\rm T}X_{\bot } = \begin{bmatrix} \Gamma _{\text {pc}} &{} \Gamma _{\text {res}} \\ \end{bmatrix}\begin{bmatrix} \Lambda _{\rm pc} &{} 0 \\ 0 &{} 0 \\ \end{bmatrix}\begin{bmatrix} \Gamma _{\text {pc}}^{\rm T} \\ \Gamma _{\text {res}}^{\rm T} \\ \end{bmatrix} \end{aligned}$$
(11)

where \(\Gamma _{\text {pc}} \in {\mathfrak {R}}^{\text {Mx}l_{\text {pc}}}\), \(\Gamma _{\text {res}} \in {\mathfrak {R}}^{\text {Mx}{(M - l}_{\text {pc}})}\), \(\Lambda _{\text {pc}}\in {\mathfrak {R}}^{l_{\text {pc}}xl_{\text {pc}}}\), and \(l_{\text {pc}}\) is the number of principal components. For a new data sample \(x \in {\mathfrak {R}}^M\), this subspace can be monitored using two statistics that are \(T_{\bot }^{2}\) and \(\text {SPE}_{\bot }\). Second, the MPLS model is used to monitor \({X}_{\rm opls}\) which in turn decomposed into \({\widehat{X}}_{\rm opls}\) and \({\widetilde{X}}_{\rm opls}\). The monitoring results of \({\widehat{X}}_{\rm opls}\) and \({\widetilde{X}}_{\rm opls}\) reveal quality-related and quality-unrelated faults, respectively. The principal and residual components are obtained by projecting \(x_{\rm opls}\) on both two subspaces, PCS and RS according to the following:

$$\begin{aligned} x_{\rm opls}={\widehat{x}}_{\rm opls}+{\widetilde{x}}_{\rm opls} \end{aligned}$$
(12)

Therefore, there are four monitoring statistics, i.e., \(T_{\bot }^{2}\), \({\ \text {SPE}}_{\bot }\), \(T_{{{\widehat{x}}}_{\text {opls}}}^{2}\), and \(T_{{{\widetilde{x}}}_{\text {opls}}}^{2}\) with their thresholds that can be calculated according to the following [12] as Table 6:

Table 6 MOPLS monitoring statistics and thresholds
Full size table

where \(\theta _{i} = \sum _{j = l_{\rm pc} + 1}^{m}\left( \lambda _{j} \right) ^{2},\ \ i = 1,2,3,\ \ h_{0} = 1 - \frac{2\theta _{1}\theta _{3}}{3{\theta _{2}}^{2}}\). \(\lambda _{j}\) is the diagonal elements of \(\Lambda _{\text {pc}}\). Here, \(t_{{{\widehat{x}}}_{\text {opls}}}\) and \(t_{{{\widetilde{x}}}_{\text {opls}}}\) are considered the score vectors as defined in [12].

2.7 Expectation–maximization partial least squares (EMPRM)

Algebraically, the final regression coefficient vector \(M_{\rm EM}\) is obtained from the last PLS step in the final iteration of EMPRM algorithm that is summarized in [52].

Similarly, by applying the singular value decomposition (SVD) method, the EMPRM model decomposes the original data measurement space X and Y into the principal component subspace (PCS), \({\ S}_{p}\) =  \(\text {span}(P_{\rm EM}\)) and the residual subspace (RS), \({\ S}_{\rm{r}}\) = \(\text {span}({\widetilde{P}}_{\rm EM}\)).

$$\begin{aligned} M_{\rm EM}M_{\rm EM}^{\rm T} = \begin{bmatrix} {P}_{\rm EM} &{} {{\widetilde{P}}_{\rm EM}} \\ \end{bmatrix}\begin{bmatrix} \Lambda _{\rm EM} &{} 0 \\ 0 &{} 0 \\ \end{bmatrix}\begin{bmatrix} {P}_{\rm EM}^{\rm T} \\ {{\widetilde{P}}_{\rm EM}^{\rm T}} \\ \end{bmatrix} \end{aligned}$$
(13)

where \({P}_{\rm EM}\in {\mathfrak {R}}^{M \times q}\), \({\widetilde{P}}_{\rm EM}\) \(\in \) \({\mathfrak {R}}^{M \times (M-q)}\) and \(\Lambda _{\rm EM}\in {\mathfrak {R}}^{q \times q}\)

The fault detection process can be achieved using two monitoring statistics, \(T^{2}_{\rm EM}\) and \(\text {SPE}_{\rm EM}\) for monitoring \({\widehat{X}}\), \({\widetilde{X}}\), respectively. It is worth mentioning that \(T^{2}_{\rm EM}\) statistic which enables detecting faults related to Y. The other statistics \(\text {SPE}_{\rm EM}\) is used for monitoring \({\widetilde{X}}\) that detects unrelated faults to Y. Therefore, the two monitoring statistics with their thresholds can be calculated as Table 7.

Table 7 EMPRM monitoring statistics and thresholds
Full size table

More details about the EMPRM model are given in the research work of [52].

2.8 Total principal component regression (TPCR)

The basic idea of this algorithm is that the original process matrix X is first projected onto the score matrix T by PCA. \(T_{\rm c}\) is a score matrix that is extracted from T by the least squares regression between T and Y. After that, \(X_{\rm c}\) is reconstructed from X by \(T_{\rm c}\) such that \(X_{\rm c}\) is highly correlated with Y, leaving the remaining part \(X_{\rm u}\) is uncorrelated with Y. To build the TPCR model, the PCA is performed on \({\widehat{Y}}\) to get its score matrix \(T_{\rm c}\) and load matrix \(Q_{\rm c}\) such that:

$$\begin{aligned} T_{\rm c} = {\widehat{Y}}Q_{\rm c} = \ TQ^{\rm T}Q_{\rm c} \end{aligned}$$
(14)

where \({\widehat{Y}}\) is the online prediction of Y, \(Q^{\rm T} = \left( T^{\rm T}T \right) ^{- 1}T^{\rm T}Y\), and T is re-projected to \(T_{\rm c}\) by \(Q^{\rm T}Q_{\rm c}\). Next, we reconstruct \(X_{\rm c}\) from \(T_{\rm c}\) by the following steps:

$$\begin{aligned} P_{\rm c}^{\rm T} = \left( T_{\rm c}^{\rm T}T_{\rm c} \right) ^{- 1}T_{\rm c}^{\rm T}{\widehat{X}} \end{aligned}$$
(15)

Thus:

$$\begin{aligned} X_{\rm c} = T_{\rm c}P_{\rm c}^{\rm T} = T_{\rm c}\left( T_{\rm c}^{\rm T}T_{\rm c} \right) ^{- 1}T_{\rm c}^{\rm T}TP^{\rm T} \end{aligned}$$
(16)

And

$$\begin{aligned} X_{\rm u} = X - X_{\rm c} \end{aligned}$$
(17)

By performing PCA on \(X_{\rm u}\), we get its score matrix \(T_{\rm u}\) and load matrix \(P_{\rm u}\) with only the eigenvectors corresponding to zero and extremely small eigenvalues. For each online sample \({\ x}\), the correlated score vector \(t_{\rm c}^{\rm T}\) is calculated as follows:

$$\begin{aligned} t_{\rm c}^{\rm T} = t^{\rm T}Q^{\rm T}Q_{\rm c} = x^{\rm T}PQ^{\rm T}Q_{\rm c} \end{aligned}$$
(18)

Similarly, the score vector of the uncorrelated part is calculated as follows:

$$\begin{aligned} t_{\rm u}^{\rm T} = x_{\rm u}^{\rm T}P_{\rm u} = \left( x^{\rm T} - t_{\rm c}^{\rm T}P_{\rm c}^{\rm T} \right) P_{\rm u} = \left( x^{\rm T} - x^{\rm T}PQ^{\rm T}Q_{\rm c}P_{\rm c}^{\rm T} \right) P_{\rm u} \end{aligned}$$
(19)

Therefore, the two monitoring statistics, i.e., \(T_{\rm c}^{2}\), \(T_{\rm u}^{2}\) of \(X_{\rm c}\) and \(X_{\rm u}\), respectively, with their thresholds can be calculated as Table 8.

Table 8 TPCR monitoring statistics and thresholds
Full size table

To summarize the main components of the fault detection approaches given in this paper, the offline and online phases are described in the following flowchart, see Fig. 1. The main terminologies and abbreviations of the algorithms are summarized in table 15.

Fig. 1
figure 1

Flowchart of the fault detection schemes

Full size image

3 Wind turbine system

It is well known that wind turbines convert the kinetic energy of wind into electrical energy. The main components are the tower, the rotor and hub (including three blades), the nacelle, and the generator as shown in Fig. 2. Wind turbines may generate several GW yearly that are used around the world. Therefore, they have attracted many investments in the field of renewable energy sources. It is worth mentioning that the parts of wind turbines may have malfunctions that should be detected using fault detection schemes. As mentioned in the introduction section, there are two sources of the wind turbine systems data including the SCADA and simulated data. In the paper, we collect the data from a benchmark of a wind turbine system that is popularly used for evaluating the controller and process monitoring schemes [53,54,55]. The wind turbine model consists of a horizontal-axis three-blade turbine with full converter coupling and is connected to the generator via a gearbox, see Fig. 2. The conversion from wind energy to mechanical energy can be controlled using the aerodynamics of the wind turbine. Using the generator coupled to a converter coupling, mechanical energy is converted to electrical energy. The drive train (Gearbox) between the rotor and the generator increases the generator’s speed. Table 9 summarizes the main signals exchanged among the subsystems.

Fig. 2
figure 2

Wind turbine model

Full size image
Table 9 Variables of wind turbine system
Full size table

The wind turbine model consists of different parts, i.e., controller, drive train, generator/converter, wind, blade and pitch subsystems as shown in Fig. 3. The main variables of the wind turbine system are summarized in table 16.

Fig. 3
figure 3

Overview of the benchmark model

Full size image

Moreover, because the wind turbine system is a multi-mode system, the controller has to work in four operating zones, which are determined according to the average wind speed within a certain time window as depicted in Fig. 4 [56]. It is clearly shown from this figure that the turbine is at standstill at Region I and Region II represents the power optimization with partial load. Whenever, Region III and Region IV describe the constant power generation and high wind speed, respectively. In this paper, the wind turbine is assumed to work at Region III which represents the steady-state operation of the wind turbine system. The turbine is controlled at wind speed between 0 and \(v_{rated}\) m/s in order to achieve the optimal power generation. The speed ratio is given by:

$$\begin{aligned} \mu = \frac{\omega _{\rm{r}}\text {.r}}{\upsilon _{\rm{w}}}\ \end{aligned}$$
(20)

where r is the radius of the blades.

Fig. 4
figure 4

Regions of power operation

Full size image

The benchmark model implemented in Simulink is available at the URL address: https://www.mathworks.com/matlabcentral/fileexchange/35130-award-winning-fdi-solution-in-wind-turbines.

The utilization of wind energy for the wind power generation system is a subject of research interest and in the recent years, the focus is on the cost-effective use of wind energy with the aim of providing electricity of high quality and reliability. In the past twenty years, wind turbine sizes have evolved from 20-kW to 5-megawatts, while even more powerful wind turbines are being developed. Therefore, in order to prevent major component failures, fault detection algorithms enable early alarms of mechanical and electrical faults. Side effects on other components can be significantly reduced.

Furthermore, many faults can be detected even when the faulty component is still working. Thus, necessary repairs can be planned in time and do not have to be carried out immediately. Therefore, this is important because wind power generation system is inaccessible because they are located on extremely high towers, typically 20 m or higher [57]. This is also particularly important for wind turbine installations, where adverse weather conditions (storms, high tides, etc.) can prevent repair action for several weeks.

Therefore, maintenance costs and downtime of wind power generation system can be significantly reduced [58]. Therefore, due to the importance of fault detection and diagnosis in wind power generation system (blades, drive train, and generator), this paper is presented to be as a reference to other research studies as shown in Fig. 5 [25, 57]. For illustration, this figure shows the main wind turbine components that are concerned by the above benchmark model.

In summary, the sensors are mainly used for the blade load reduction based on the individual pitch control strategy, especially in offshore wind turbines. The lifetime of the sensors in wind turbine systems is usually not very long. There are several factors that lead to higher failure rates. The strain in the blades can be very high, which affects the gauges themselves and the bonding. Harsh environmental factors such as lightning, salt spray, moisture, corrosion can directly affect the bonding and wiring of the sensors. Maintenance personnel can easily damage the sensors [25].

Fig. 5
figure 5

Wind turbine configuration

Full size image

3.1 Wind model

The combined wind model is [59]:

$$\begin{aligned} \upsilon _{\rm{w}}(t) = \upsilon _{\rm{m}}(t) + \upsilon _{\rm{s}}(t) + \upsilon _{\rm{ws}}(t) + \upsilon _{\rm{ts}}(t) \end{aligned}$$
(21)

where \(\upsilon _{\rm{m}}(t)\) is the mean wind, \(\upsilon _{\rm{s}}\) \((t)\) is the stochastic part, \(\upsilon _{\text {ws}}\) \((t)\) is the wind shear, and \(\upsilon _{\text {ts}}\) \((t)\) is the tower shadow. The wind shear model is:

$$\begin{aligned}{} {} \upsilon _{{\rm ws},i}(t) &= \frac{2\upsilon _{\rm{m}}(t)}{3r^{2}}\left( \frac{r^{3}\sigma }{3H}\Xi + \frac{r^{4}}{4}\sigma \frac{\sigma - 1}{2{\ H}^{2}}\Xi ^{2}\right) \nonumber \\{} & {} \quad+ \frac{2\upsilon _{\rm{m}}(t)}{3r^{2}}\left( \frac{r^{5}}{5}\frac{{(\sigma }^{2} - \sigma )(\sigma - 2)}{6{\ H}^{3}}\Xi ^{3}\right) \end{aligned}$$
(22)

where \(\Xi \ = \cos (\vartheta _{r*}(t)),\ \text {and}\ \vartheta _{r*}\) is the angular position of the three blades, \(\vartheta _{r1}(t)\) =\(\vartheta _{\rm{r}}(t)\), \(\vartheta _{r2}(t)\) =  \(\vartheta _{\rm{r}}(t) + (2/3)\pi \), and \(\vartheta _{r3}\) = \(\vartheta _{\rm{r}}(t)\ + \ (4/3)\pi \). \(\sigma \text { and }H\) are two aerodynamic parameters. Furthermore, the tower shadow model is:

$$\begin{aligned} \upsilon _{{\rm ts},i}(t) = \frac{m{{\overline{\vartheta }}}_{{\rm r},i}(t)}{3r^{2}}(\psi + \upsilon )\ \end{aligned}$$
(23)

where

$$\begin{aligned} \psi= & {}\, 2a^{2}\frac{r^{2} - r_{0}^{2}}{\left( r^{2} + r_{0}^{2} \right) \sin {{({\overline{\vartheta }}}_{{\rm r},i}(t))}^{2} + k^{2})}\ \end{aligned}$$
(24)
$$\begin{aligned} \upsilon= & {}\, 2a^{2}k^{2}\frac{{(r}_{0}^{2} - r^{2})(r_{0}^{2}s\text {in}{{({\overline{\vartheta }}}_{{\rm r},i}(t))}^{2} + k^{2})}{r^{2}\sin {{({\overline{\vartheta }}}_{{\rm r},i}(t))}^{2} + k^{2}}\ \end{aligned}$$
(25)
$$\begin{aligned} m= & {}\, 1 + \frac{\sigma (\sigma - 1){\ r}_{0}^{2}}{8{\ H}^{2}}\ \end{aligned}$$
(26)
$$\begin{aligned} {({\overline{\vartheta }}}_{{\rm r},i}(t)= &\, {} \vartheta _{\rm{r}}(t) + \frac{(i - 1) 2\pi }{3} - \text {floor}\left( \frac{\vartheta _{\rm{r}}(t) + \frac{(i - 1)2\pi }{3}}{2\pi } \right) 2\pi \ \end{aligned}$$
(27)

\(r_{0}\) is the blade hub radius and k is an aerodynamic parameter.

3.2 Blade and pitch model

This model combines the aerodynamic and the pitch models. The aerodynamic subsystem describes the forces that an air flow develops on a wind turbine and transforms the three-dimensional wind field into concentrated forces. As can be seen in the block diagram of Fig. 3, the inputs to this subsystem are the wind speed \(v_{\rm{w}}\), the pitch angle \(\beta \), and the rotation speed of the rotor \(\omega _{\rm r}\). The output of this subsystem is the aerodynamic torque \(\tau _{\rm r}\). The torque equation of this subsystem is [56]:

$$\begin{aligned} \tau _{\rm{r}}(t) = \frac{\rho \pi r^{3}C_{q}(\gamma (t),\beta (t))\upsilon _{\rm{w}}(t)^{2}}{2}\ \end{aligned}$$
(28)

where \(C_{q}(\gamma (t),\beta (t))\) is a map of the torque coefficients that represent a function of the speed ratio with the lead angle and \(\rho \) is the air density. A simple representative is used to model the three blades to obtain their pitch angle value. This assumption suppose that the torque of each blade is one-third of the torque that is given by the three blades. Therefore, the torque equation of this subsystem is:

$$\begin{aligned} \tau _{\rm{r}}(t) = \ \sum _{i = 1}^{3}\frac{\rho \pi r^{3}C_{q}(\gamma (t),\beta _{i}(t))\upsilon _{w,i}(t)^{2}}{6}\ \end{aligned}$$
(29)

where \(\beta _{i}\) is the pitch position.

On the other hand, the pitch subsystem is an actuator that generally rotates all the blades or a part of them. Therefore, the model of the hydraulic pitch system is considered as a closed-loop transfer function between the measured pitch angle (\(\beta _{\rm{m}}\)) and its reference (\(\beta _{\rm{r}}\)). In principle, this subsystem can be modeled by a second-order transfer function [60] as:

$$\begin{aligned} \frac{\beta _{\rm{m}}(s)}{\beta _{\rm{r}}(s)} = \frac{\omega _{n}^{2}}{s^{2} + 2\zeta \omega _{n}s + \omega _{n}^{2}} \end{aligned}$$
(30)

where \(\beta _{\rm{r}}\) is the input to the closed-loop transfer function; \(\beta _{\rm{m}}\) is the output of the transfer function; \(\zeta\)is the damping factor, and \(\omega _{n}\) is the natural frequency.

3.3 Drive train model

A two-mass model of the drive train is used in this benchmark model. The torque from the rotor is transferred to the generator through the drive train. From the low-speed rotor side to the high-speed generator side, the rotational speed is increased using a gearbox. A two-mass drive train model can be represented by:

$$\begin{aligned} J_{\rm{r}}\dot{\omega _{\rm{r}}}(t)= & {} \tau _{\rm{r}}(t) - K_{\text {dt}}\vartheta _{\Delta }(t) - \left( B_{\text {dt}} + B_{\rm{r}} \right) \omega _{\rm{r}}(t) + \frac{B_{\text {dt}}}{N_{\rm{g}}}\omega _{\rm{g}}(t)\ \end{aligned}$$
(31)
$$\begin{aligned} J_{\rm{g}}{\dot{\omega }}_{\rm{g}}(t)= & {} \frac{\eta _{\text {dt}}K_{\text {dt}}}{N_{\rm{g}}}\vartheta _{\Delta }(t) + \frac{\eta _{\text {dt}}B_{\text {dt}}}{N_{\rm{g}}}\omega _{\rm{r}}(t) - \left( \frac{\eta _{\text {dt}}B_{\text {dt}}}{{N_{\rm{g}}}^{2}} + B_{\rm{g}} \right) \omega _{\rm{g}}(t) - \tau _{\rm{g}}(t)\ \end{aligned}$$
(32)
$$\begin{aligned} {\dot{\vartheta }}_{\Delta }(t)= & {} \omega _{\rm{r}}(t) - \frac{1}{N_{\rm{g}}}\omega _{\rm{g}}(t)\ \end{aligned}$$
(33)

where \(J_{\rm{r}} \), \(J_{\rm{g}}\) are the moment of inertia of the low-speed and high-speed shafts, respectively, \({\ K}_{\text {dt}} \) is the torsion stiffness, \(\eta _{\text {dt}}\) is the efficiency, \(B_{\text {dt}}\) is the torsion damping coefficient, \(B_{\rm{r}}\), \(B_{\rm{g}}\) are the viscous friction of the low-speed and high-speed shafts, respectively, \(N_{\rm{g}}\) is the gear ratio, and \(\vartheta _{\Delta }(t)\) is the torsion angle.

3.4 Generator and converter model

The frequency range used in this model is much slower than the electrical system in the wind turbine system. A first-order transfer function can be used to represent the generator and converter dynamics at the wind turbine system level.

$$\begin{aligned} \frac{\tau _{\rm{g}}(s)}{\tau _{g,r}(s)} = \frac{\sigma _{\text {gc}}}{s + \sigma _{\text {gc}}}\ \end{aligned}$$
(34)

where \(\sigma _{\text {gc}}\) is the model parameter of generator and converter.

The generator output power is:

$$\begin{aligned} P_{\rm{g}}(t) = \ \eta _{\rm{g}}\omega _{\rm{g}}(t)\tau _{\rm{g}}(t)\ \end{aligned}$$
(35)

where \(\eta _{\rm{g}}\) is the generator efficiency. Moreover, the controller is implemented in discrete-time form, with a sampling frequency of 100 Hz. The controller changes from mode 1 to mode 2 in the following case:

$$\begin{aligned} P_{\rm{g}}(k)\ \ge P_{\rm{r}}(k)\ \vee \ \omega _{\rm{g}}(k)\ \ge \omega _{\rm{nom}} \end{aligned}$$
(36)

Here, \(\omega _{\rm{nom}}\) is the nominal speed of the generator. The controller changes from mode 2 to mode 1 in the following case:

$$\begin{aligned} \omega _{\rm{g}}(k)\ < \omega _{\rm{nom}} - \ \omega _{\Delta } \end{aligned}$$
(37)

\(\omega _{\Delta }\) is a small offset subtracted from the nominal speed of the generator. At mode 1, the optimal value of \(\gamma \) is represented by \(\gamma _{\text {opt}}\). This optimal value is realized when the pitch reference to zero (\(\beta _{\rm{r}}(k) = \ 0\)), and the reference torque to the converter \(\tau _{g,r}\) is:

$$\begin{aligned} \tau _{g,r}(k)= & {} K_{\text {opt}}\left( \frac{\omega _{\rm{g}}(k)}{N_{\rm{g}}} \right) ^{2}\ \end{aligned}$$
(38)
$$\begin{aligned} K_{\rm{opt}}= & {} \frac{1}{2}\rho *Ar^{3}\frac{C_{\rm{Pmax}}}{\gamma _{\rm{opt}}^{3}} \end{aligned}$$
(39)

A = \(\pi r^{2}\) is the area swept by the wind turbine blades, and \(K_{\rm{opt}}\) is the optimal value of k, \(C_{\rm{Pmax}}\) is the maximum value of the power coefficient. On the other hand, at mode 2, the major control actions are handled by the pitch system using a PI controller trying to keep \(\omega _{\rm{g}}(k)\) at \(\omega _{\text {nom}}\)

$$\begin{aligned} \beta _{\rm{r}}(k) = \beta _{\rm{r}}(k - 1) + K_{\rm{P}}e(k) + (K_{i}T_{\rm{s}} - K_{\rm{P}})e(k - 1) \end{aligned}$$
(40)

\(e(k) = \omega _{\rm{g}}(k) - \omega _{\text{nom}}\), and the controller gains are\(\ K_{\rm{P}} \) and \(K_{i} \). In this case, the converter reference is:

$$\begin{aligned} \tau _{g,r}(k) = \frac{P_{\rm{r}}(k)}{\eta _{\text {gc}}\omega _{\rm{g}}(k)} \end{aligned}$$
(41)

where \(\eta _{\text {gc}} \) is the efficiency of the generator and converter subsystems. Moreover, a stochastic noise component is added to the actual variable value to model each sensor. The parameters used in the benchmark model are listed in Table 10.

Table 10 The benchmark model parameters
Full size table

It is worth mentioning that many fault types are occurring in wind turbine systems including sensor faults, actuator faults, and process faults. This paper is dedicated to studying the efficiency of the presented process monitoring methodologies for sensor faults detection. The sensor faults can be in the pitch position measurements, e.g., \({\beta }_{1,m1\,}{\beta }_{1,m2\,}{\beta }_{2,m1\,}{\beta }_{2,m2\,}{\beta }_{3,m1,} {\beta }_{3,m2}\); in the rotor speed measurements,\({\omega }_{{\rm r},m1}\) and\({\omega }_{{\rm r},m2}\); in the generator speed measurements \({\omega }_{{\rm g},m1}\) and \({\omega }_{{\rm g},m2}\). The details of these faults are listed in Table 11.

Table 11 Sensor faults in the wind turbine system
Full size table

4 Simulation results and discussion

In this simulation study for a wind turbine system, the measurement data are collected from 16 variables at normal operation. The dataset includes \(10^5\) samples, and the fault scenarios are presented at a sample time k = \(5 \times 10^4\) to the end of the simulation. Twenty different fault scenarios are given in Table 11 that occur in the wind turbine system. The rotational speed of the rotor in the drive train is chosen as the quality variable to construct Y matrix (output variable) and the other 15 process variables are chosen as input variables. Furthermore, the different fault scenarios are monitored using the presented data-driven fault detection approaches in this paper and evaluated by using two indices, i.e., fault detection rate (FDR) and false alarm rate (FAR) [9, 43, 61].

$$\begin{aligned} \text {FDR}= & {} \frac{\left. \; \text {No. of samples} \; (J> J_{\text {th}} \right| f \ne 0)}{\text {total samples }(f \ne 0)}\times 100\%\\ \text {FAR}= & {} \frac{\left. \; \text {No. of samples}\; (J > J_{\text {th}} \right| f = 0)}{\text {total samples }(f = 0)}\times 100\%\end{aligned}$$

The number of principal components (PCs) and the number of LVs are selected by using the cumulative percent variance method (CPV) and the cross-validation method, respectively [9, 44, 62]. The design parameters are summarized in Table 12.

Table 12 Design parameters
Full size table

Two fault scenarios are given in details, i.e., F14 and F19. The first fault occurs as a gain factor in the pitch position sensor. Figure 6 shows the fault detection charts of the described monitoring models in this paper. It is clearly shown that the monitoring models achieved FDR with average about \(80\%\). Furthermore, PCA, TPLS recorded the lowest FAR, but the other methods have the highest degree of FAR compared with the PCA and TPLS.

Besides, F19 represents a fixed value in the sensor that measures the generator speed. The fault detection results of the presented methods of this fault are shown in Fig. 7. It is clearly shown that all the tested algorithms showed satisfactory fault detection performance with FDRs of approximately \(99.99\%\) except for PCA algorithm that failed to detect fault successfully as shown in Fig. 7a. As well as, all monitoring methodologies exhibit acceptable FARs.

Fig. 6
figure 6

Process monitoring using different algorithms in case of (F4)

Full size image
Fig. 7
figure 7

Process monitoring using different algorithms in case of (F19)

Full size image

To evaluate the fault detection approaches according to all possible sensor faults, Tables 13 and 14 give the FDRs and FARS. As shown in Table 13, most fault detection methods successfully detected all faults with high FDRs. On the other side, the PCA and TPLS could not detect the faults (F13, F14, F15, F16, F19) and F9, respectively, in which the boldface denotes the lowest FDRs.

Table 13 FDRs \((\%)\) of the wind turbine system
Full size table

It is clearly shown from Table 14 that the FARs of both PCA and TPLS had the lowest FAR rates for all fault scenarios, which means they are the most robust fault detection methods. As well as other algorithms in some fault scenarios have high FARs which are denoted by the boldface.

Table 14 FARs \((\%)\) of the wind turbine system
Full size table

The detectability of the described fault detection approaches in this paper is clearly shown in Fig. 8 that represents the average value of FDR’s of all possible sensor fault cases. The MPLS achieved the highest average FDR comparable to other methodologies. As well as, From the point of view of robustness, Fig. 9 introduces a comparison of the fault detection techniques in terms of FARs. It is well proven that both TPLS and PCA are the most robust fault detection techniques.

In summary, the data-driven methods are tested under the assumption that the wind turbine operates in a steady-state region. Simulation results demonstrate that PLS (Partial Least Squares) and its variants exhibit the highest sensitivity to wind turbine sensor faults. Additionally, most of the fault detection methodologies, including MPLS, EMPRM, MOPLS, TPCR, OPLS, PLS, and TPLS, successfully detected all faults with a high Fault Detection Rate (FDR) with average about 90.57%, 88.55%, 88.52%, 88.12%, 88.09%, 86.55%, and 80.95%, respectively. On the other hand, PCA exhibited the lowest FDR compared to the other methods with average about 68.86%. Additionally, this is because PCA cannot establish the correlation between quality and process variables. However, PCA still outperformed PLS and its variants in terms of robustness to these faults, which directly relates to the False Alarm Rate (FAR), i.e, PCA with average FAR about 1.02% is less than TPCR, MOPLS, PLS, OPLS, EMPRM, and MPLS with average FAR about 14.17%, 14.70%, 17.93%, 19.18%, 19.74%, and 22.96%, respectively, except TPLS has the lowest average FAR of about 0.2%.

Fig. 8
figure 8

Average FDR of the presented algorithms

Full size image
Fig. 9
figure 9

Average FAR of the presented algorithms

Full size image

5 Conclusions

In this paper, we present a comprehensive review and evaluation of the most commonly used multivariate statistical techniques for fault detection, specifically focusing on their application in wind turbines. The primary objective of this study is to conduct a comparative analysis of data-driven fault detection strategies within the context of wind turbine applications. The data-driven methods are tested under the assumption that the wind turbine operates in a steady-state region. Simulation results demonstrate that PLS (Partial Least Squares) and its variants exhibit the highest sensitivity to wind turbine sensor faults. Additionally, most of the fault detection methodologies, including MPLS, EMPRM, MOPLS, TPCR, OPLS, PLS, and TPLS, successfully detected all faults with a high Fault Detection Rate (FDR) averaging around \(90\%\). On the other hand, PCA exhibited the lowest FDR compared to the other methods. However, PCA still outperformed PLS and its variants in terms of robustness to these faults, which directly relates to the False Alarm Rate (FAR). It should be noted that the discussed fault detection methods in this paper are efficient in dealing with single-mode, time-invariant systems. Real wind turbines, however, are multi-mode systems with high nonlinearity. Therefore, future research efforts should focus on the development of process monitoring methods capable of effectively handling these challenges.