1 Introduction

In recent years, convolutional neural networks (CNNs), which represent a very popular class of deep learning techniques, have become pivotal to many computer vision applications. Since the successful design of GPU-based CNNs that exceed human performance [4] and the remarkable victory in 2012 ImageNet image classification challenge [16], this type of deep neural networks has been among the most widespread methods for image classification [14, 28, 30], capable of achieving computation times and error rates described as “superhuman” [13]. CNNs have also proven successful in tasks such as image segmentation [2], object detection [23], predicting the scene depth and surface normals [8] and colorization of grayscale images [37]. As it was projected in the original works on CNNs [17], their application is not limited to analyzing visual imagery, as they can also handle audio [25] and text input [6]. Apart from the popular image processing challenges, CNN-based solutions are working their way into a variety of other practical applications, particularly in the areas of astronomy [7] and medical imaging [33, 9, 31].

Since the introduction of CNNs [17], their key property has been related to the processing of grid-aligned data with the matrix convolution operator. Optionally, the dimension of the resulting maps can be reduced with the maximum-pooling operation. In both of these components, different grid-aligned regions of the input data are processed exactly in the same way. As the design is inspired by the Neocognitron [10], the intermediate layers generate outputs that are based on the local features of the input data. The results of such multilayer local filtering are further summarized by the fully-connected layers that provide the global image classification. Since the crucial part is solely based on the local image features, the CNN as a whole is roughly invariant to the translation of image contents. Apart from the slight impact of the placement of pooling region boundaries in relation to the image features, translated image is expected to yield accordingly translated feature maps, with a similar subset of strongly activated filters. Extensive subsampling used in some of the modern models is known to affect the invariance to small translations [1], but this problem can be significantly reduced with the appropriate anti-aliasing [36].

In this paper, we propose a novel approach to the rotation- and scale-invariant CNN architectures. Our goal is to make the CNN process multiple variants (rotation angles or scaling factors) of data input with similar operations. This approach is intended to imitate the original behavior with respect to image translation, which involves using the same filter at different positions as the convolution operation is performed. The proposed method acts in a similar way, but with multiple angles/scales in addition to the offsets. Additionally, we expect to gain the possibility to recognize multiple local features of presented objects in the same image even in the case when they are subjected to different transformations. As the method does not involve any filter transformations, the learning process remains simple and efficient. The geometric transformations are applied to the intermediate layer outputs. The processing results gained for multiple transformations are summarized by further convolutional layers, which makes the desired invariance fully based on the local image features. This behavior is achieved by utilizing the approximate “reverse geometric transformations”. For increased performance, sequences of geometric transformations are reduced to a single operation and prepared before the data propagation or samples learning—this approach is described as “fast geometric transformations”. The method is verified experimentally and compared to the CNNs without the proposed additions, with various approaches to the manual augmentation of the training set.

2 Related works

For a living observer, objects can usually be recognized not only regardless of their position in the field of view but also regardless of their rotation and size, provided they remain visible and fit in the sight range. It is known that image recognition solutions based on CNNs do not provide invariance to image transformations. Thus, other mechanisms are necessary for handling changes in the rotation [12, 7, 19, 32] or scale of an image [23, 34]. The well-known approach to recognition of multiple rotations or scales is to perform extensive data augmentation [7, 22, 27]. This is equivalent to learning multiple rotations or sizes of the object as if they were independent, and then grouped arbitrarily. Alternatively, the transformation can be applied to the convolutional filters [19, 32], which requires significantly more computations per each processed image, especially in the learning process. Neither of these approaches makes the rotation- or size-invariance in CNNs as efficient and versatile as the translation-invariance.

In this paper, we use data augmentation [27] of the selected data sets both as an alternative and as a supplementary utility for the presented method. The experimental setup that relies exclusively on data augmentation to provide transformation invariance bears a close resemblance to the ones proposed in some of the known works [7, 22]. The comparison with these reference setups is crucial to the experimental verification of the novel models.

There are multiple alternative approaches to the rotation- [12, 7, 19, 32] or scale-invariant CNNs [23, 34]. When only scale is considered, the multi-column approach can be used [34]. However, the processing results computed for different scaling factors are not processed by the further convolutional layers but flattened and concatenated as the fully-connected layer input instead. A very practical yet complex solution is to use the YOLOv3 model [23]. It utilizes the convolutional layers where possible, but does not provide an easy way to extend it for an arbitrary number of scaling factors. CNNs with nothing more but data augmentation can be effectively described as rotation-invariant [7], which is a reasonable decision in the most basic cases. On the other hand, it is possible to use a method designed specifically for a selected data set, as presented in [19], where a remarkably large number of rotations were considered for each processed patch. Notable results were achieved with the rotation of filters [32], but such an approach requires significant adjustments to the CNN learning process. A remarkably different yet successful approach was presented in [19], where the rotation-invariant CNNs were achieved through the specific application of regularization functions. In the present paper, however, both the cost function and the learning method remain similar to the other known CNNs, which guarantees compatibility with any general optimization method such as Adam [15] and adjustments such as Dropout [29].

The approach presented here may be considered as similar to the Siamese Networks [3], which can be based on the Convolutional Neural Networks as well. Both in the presented solutions and in the Siamese Networks, pieces of data that share some properties are processed in the parallel CNN branches. The branches can be experimented with in order to either store independent convolutional filters or share some of the filter matrices. The proposed solution, however, has a remarkably different application. Siamese Networks usually work on the pairs of patches, yielding the binary answer that determines the similarity of inputs in terms of the desired relation. In the proposed solution, however, the inputs of the branches are generated from the same patch, and the network output represents the answer to the image classification task. The knowledge is fully stored in the model, so no reference patch needs to be provided. What is more, the CNNs with geometric transformations embedded into the network architectures operate on images that are different in terms of geometric structure. As a result, the task of summarizing the outputs of the branches is additionally challenging—and the proposed solution is to use “the unification blocks”. For Siamese Networks, the geometric unification of multiple branches for further CNN-like processing would be—depending on the application—either inapplicable or impossible to determine.

3 The novel method

Convolutional neural networks are widely used in the state-of-the-art solutions to many image classification problems, such as ImageNet Large Scale Visual Recognition Challenge [24]. The standard approach guarantees invariance to object translations in all the dimensions where the convolution operator is applied. Since the same filters are used at every position of the image, the positions of activated elements in the feature masks can be translated accordingly. However, as the activation remains present, the patterns can be easily recognized regardless of translation. Recognition of the objects in the image irrespective of their translation is a desired feature of intelligent data processing, as any human observer would achieve that with obvious ease.

The human ability to recognize translated objects extends to the geometric transformations such as rotation and scale. This property, however, is not shared by the convolutional neural networks. If the CNN model is trained with patches that are normalized in terms of rotation and scale, a patch with a rescaled or rotated object—either taken from the training set or previously unknown—will remain unrecognized and possibly randomly misclassified.

In many practical applications, this issue is resolved by training the CNN model with an augmented data set, where both the original and transformed (rotated or scaled) patches are present. Such an approach is, by default, barely different to the one in which multiple independent image classes are arbitrarily joined into one. This task can be performed with a CNN, not unlike training a model that recognizes a greater number of object classes—but the training time, number of required iterations with repeated patches and number of convolutional filters required to achieve the optimal solution are likely to increase. The last aspect directly affects the memory usage and propagation time for a pretrained network as well. Both in the case of large-scale visual recognition and when large numbers of images are processed in batches, the memory usage is an important aspect even in applications with the most modern hardware setups.

3.1 Problem statement

The goal of the presented research is to compare the novel CNN models that are expected to provide the improved invariance to rotation and scale with the standard models that include no such transformations. Both approaches should be tested on networks that have the same number of layers and number of parameters. As we are interested in the comparison of multiple experimental setups, the model should not be overly complex, as then the learning process would take too much time. The simplest popular CNN model is LeNet [17], but it is remarkably outdated considering the capabilities of easily accessible hardware, and it does not provide long enough layer sequences to demonstrate the entirety of our idea. Instead, we use models similar to AlexNet [16]. As this model is designed for the image classification task and features a sequence of five convolutional layers, we can rebuild it for the sake of the proposed method and retrain it for the desired experimental tasks.

The evaluation setup involves the image classification task with augmented test data sets that involve random rotations or scales from selected ranges. The testing is performed on multiple data sets. In principle, the proposed extension to the CNN models may be applied also to tasks other than image classification. The final layers used to generate the neural network output could be replaced in order to solve various image processing problems, which opens up a potential for the further research.

The reference solution is based on the known, AlexNet-based [16] CNN model, both with and without data augmentation applied to the training set. In comparison, the proposed method, which reorganizes the neural network model in a significant way, is tested for both original and augmented training sets.

The proposed approach involves structurally similar neural network models for different data sets. What is more, the neural network model used for AlexNet-based solutions and the novel solutions are kept as similar as possible, which involves the same depth of a network and equal number of adjustable weights. This set of assumptions makes it difficult to make a direct comparison with the related works, but it makes the presented research as clear as possible. The only factor that makes the novel solution different from the reference CNN in the experimental process is related to the additional branches with embedded geometric transformations. Such an experimental setup makes it possible to measure the difference that is made by the proposed method, free from any other differences between the experiments. The proposed fixed conditions are necessary to present the impact of the novel approach objectively.

3.2 Proposed solution

The proposed neural network model is designed to handle rotated and scaled patches without the need to use an excessive number of independent convolutional filters. The innovative solution with geometric transformations embedded in the network architecture offers the possibility to improve on the classification accuracy results achieved by previous CNN models.

In this study, both the existing approach and the proposed solution are analyzed using similar memory restraints and training time. Considering these common constraints, the classification accuracies of the individual setup can be used to measure their effectiveness. These parameters are set in such a way as to achieve the optimal result with the unmodified CNNs. The experiments are intended to verify the hypothesis that the convolutional neural networks with geometric transformations make it possible to perform the classification of rotated or scaled images more accurately.

The proposed solution involves:

  • A neural network based on the existing CNN network models. The crucial adjustable parameters are two-dimensional convolutional layers that consist of multiple matrix convolution filters. The presence of said layers and the gradient-based approach to network learning makes the process similar to that applied in previous CNN models. Thus, it is possible to use the Adam optimizer [15] for supervised learning of the whole network.

  • Neural network models designed specifically for the image classification task. This involves a sequence of fully connected layers used to generate the classifier output.

  • Novel, multi-branch organization of the neural network model, which can be adjusted to a specific range of geometric transformations. This is demonstrated on the selected ranges of rotations and scales, as described in Sect. 3.4.

  • Embedded geometric transformations used for different branches of data processing. Each branch involves fast geometric transformations (Sect. 3.3) in order to address two different tasks. At the beginning of the branch, the input data are transformed in such a way as to enable recognition of objects presented at different angles or scales. Secondly, the branch-specific result is geometrically transformed for further processing, performed on data collected from all the branches. The second operation involves both sequences of geometric transformations and approximate reverse transformations.

The proposed ideas can be implemented as follows. Fast geometric transformations can be used to operate on digital images or convolutional layer outputs. This makes them useful for convolutional neural network models, where additional layers based on the fast geometric transformations can be embedded. The models can be image processing task where CNNs are typically applied. In the present study, the method’s performance is evaluated on the basis of its results in image classification. Such an approach can be applied to all types of image processing tasks that typically employ CNN-based solutions. Here, the performance evaluation is based on the task of image classification.

3.3 Fast geometric transformations

Digital image can be considered as a matrix of elements that belong to the linear space S. The proposed operations require proper approximation of intermediate colors, which can be achieved with color spaces such as linear grayscale, linear RGB, CIEXYZ, CIELAB or hyperspectral data [35]. Let the input image A, be \(n \times m\) matrix over S which is supposed to be transformed into \(p \times q\) output. Any transformation where output pixels are linear combinations of an input pixel can be denoted as such\(f: S^{n \times m} \rightarrow S^{p \times q}\) that:

$$\begin{aligned} f_T(A) = \left( \sum _{t=1}^{n} \sum _{u=1}^{m} T_{rstu} \cdot A_{tu}\right) _{r=1\ldots {}p,\, s=1\ldots {}q}, \end{aligned}$$
(1)

where \(T \in [0; 1]^{p \times q \times n \times m}\).

This formula can be used to modify the color intensity either for the whole image or locally. If the application is limited to geometric transformations only, an additional constraint can be introduced:

$$\begin{aligned} \forall _{r=1\ldots {}p,\, s=1\ldots {}q}~ \sum _{t=1}^{n} \sum _{u=1}^{m} T_{rstu} = 1. \end{aligned}$$
(2)

The weights stored in T operator can be designed in such a way as to implement any pixels permutation, image cutting, translation, scaling, rotation, perspective, polar-logarithmic transformation—and for each of these operations any method of interpolation or anti-aliasing can be applied. The most basic examples are presented in Fig. 1.

Fig. 1
figure 1

Fast geometric transformations used to rotate an example image from SVHN data set [20]. From the left: \(-30^\circ\) rotation, \(-15^\circ\) rotation, original image, \(15^\circ\) rotation and \(30^\circ\) rotation. The precalculated transformations involve filling the image edges based on the nearest pixels, anti-aliasing used for smooth image probing and unsharp filtering that reduces the blur effect caused by said anti-aliasing. All these features are directly described by coefficients of the transformations

Full size image

Precalculating the coefficients in the form of T consumes both time and memory. However, once the T is provided, applying the same geometric transformation to multiple images results in the computational efficiency that is significantly superior to the standard methods of transforming images separately. This approach is crucial in the development of efficient neural network model.

The only disadvantage is potential memory consumption of T dependent on input and output image sizes. This problem can be easily addressed considering that many of the values in T are very close to 0—omitting such values and using associative map for each \(T_{rs}\) with the greatest weights instead yields good approximation that takes much less memory. The weights can be additionally normalized in order to satisfy condition (2). Setting the constant limit for the number of nonzero elements to be stored for each \(T_{rs}\) changes memory complexity from \(O(n \cdot m \cdot p \cdot q)\) to \(O(p \cdot q)\). What is more, for some of the transformations, which include rotation with anti-aliasing and interpolated scaling, the number of nonzero elements is limited by default. In such cases, the approach with associative maps reduces the memory consumption without affecting the precision.

Geometric transformations described by coefficient maps T have some useful properties, which can be listed as follows:

  • Identity is a valid geometric transformation—it is implemented by such T that each \(T_{rsrs}=1\) and all the other elements are 0.

  • A sequence of multiple geometric transformations can be denoted as one transformation with specified T values. The “geometric transformation” operator is associative, not unlike the matrix multiplication.

  • In practical applications, computations with coefficient maps T ca be easily parallelized, which makes them especially efficient when the SIMD-like architecture such as a modern GPU is present.

The structure of geometric transformations is a monoid, but not a group. Consider the “crop” operation that reduces the image by omitting the side pixels. No inverse operator that restores the removed pixels is possible. If any pixel that is absent from probing is restored by interpolation of the surrounding pixels and any linearly-dependent pixels are approximated as similar, we can introduce an approximate inverse operator \(T^{-1}\) for any operator T. This is directly precise for scaling with interpolation and remarkably useful for rotations (as it fills the corners by interpolation).

As a result, any sequence of transformations can be stored as an approximate, associative map-based T for efficient computations, alongside with approximate the inverse operator \(T^{-1}\).

3.4 Embedding geometric transformations into convolutional neural networks

The reference approach to applying additional invariance to the convolutional neural networks—which includes rotation and scale—is data set augmentation. This causes different sections of the network to be activated by different variants (ranges of scaling factor or rotation angle) of the key patterns that are required for object detection. An improved model which would recognize the similarities between rotated or rescaled patches by design can be achieved by making sure that the same filters yield feature mask activations, regardless of the geometric properties of the object in the input image. This problem can be resolved with geometric transformations embedded in the convolutional neural network model.

Fig. 2
figure 2

Diagram of the convolutional neural network with embedded transformations

Full size image

The steps of the data processing performed in the proposed neural network (also presented in Fig. 2), common for the training and test stage, can be described as follows:

Fig. 3
figure 3

“Unified geometric structure” block explanation. The dashed arrows track the geometric effects to be inverted (when going left) or reconstructed (when going right)

Full size image
  1. 1.

    The denoising layer. The initial processing that can denoise the image and partially perform some of the tasks that are common to all the geometric transformations of the object. This step is optional, so for some of the experiments it can be formally replaced with an identity function. However, the initial layers of the convolutional neural networks are known to perform the mentioned task. As a result, practical applications suggest that using one or two convolutional layers for this step simplifies the general computations. This step is described in the diagram as the CNN0 block.

  2. 2.

    Multiple parallel branches. Based on the index at the CNN1\(_i\) block of each branch, the branches visible in the diagram can be considered as “branch a,” “branch b” and “branch c”.

    In all branches (with a possible exception of branch a), an additional geometric transformation is performed by the respective GEOM\(_i\) block. This is implemented as a fast geometric transformation, which is embedded in the convolutional neural network model.

    The transformed feature masks are further processed by the CNN1\(_i\) blocks. The architecture of these blocks is mostly similar (with a possible exception for matrix shape changes performed by the GEOM\(_i\) blocks), and the convolutional filters are shared. In the AlexNet-like experiments [16], each CNN1\(_i\) block represents a sequence of three convolutional layers.

    The final step for each branch is to “unify the geometrical structure”, in order to guarantee that all the branches yield feature maps of the same size and possibly similar visual fields (subsets of associated points) in the input image (UGEOM\(_{i \rightarrow a}\) blocks). This requires a reasonably extensive application of the fast geometric transformations. The function of UGEOM\(_{i \rightarrow a}\) blocks is additionally explained in Fig. 3.

    The outputs of multiple branches with the mentioned properties can be further used as separate channels of the further processing with CNNs (“channels concatenation”).

  3. 3.

    Summarizing convolutional layers. The tuple of matrices collected from multiple branches are processed together by the following convolutional layers. This approach opens up the possibility of merging abstract patterns, such as final objects that are supposed to be detected, from the subpatterns recognized in different rotations or scaled. The invariance is remarkably easy to achieve, as the matrices can be simply summed up. However, depending on the filters used in this step, such a property is not mandatory. Not unlike the summarizing steps that operate on translated patterns in the standard CNNs, this part of processing provides an arbitrary ability to group, merge, subtract or ignore the detected features, depending on the channel considered. The exact behavior depends on the convolutional filters learned in the CNN2 block.

  4. 4.

    The neural network output is based on the feature masks provided by CNN2. In the case of image classification tasks, this can be achieved by fully connected layers, where the last layer should have a number of outputs set to the number of considered classes. When such a numeric vector is computed, the classification result can be obtained by the softmax function.

    The proposed layers have an important advantage: both softmax and fully connected layers can be updated using the gradient methods, with errors and changes calculated with the backpropagation approach. The same applies to the convolutional and pulling layers present in CNN2, CNN1\(_i\) and CNN0 blocks.

    When the existence of inverse geometric transformation is considered, it is possible to process the backpropagation-based errors through the geometric transformations as well—both GEOM\(_i\) and UGEOM\(_{i \rightarrow a}\).

    As a result, all the adjustable parameters of the neural network model back to CNN0 can be updated in a common backpropagation sequence, which makes it remarkably easy to apply the supervised learning with standard gradient descent or Adam optimizer [15].

    This means that all the convolutional filters present in the model are trained with a specific purpose of being useful in the image classification task on a defined data set.

It is worth mentioning that the CNN0, CNN1\(_i\) and CNN2 blocks can be implemented as sequences of multiple convolutional layers and maximum-pooling layers, as it is typical for the convolutional neural network models. The sequence of applied filter groups and pooling sizes should be similar in each of the CNN1\(_i\) block, regardless of the branch considered.

Let us now explain the formal contents of each UGEOM\(_{i \rightarrow a}\) block present in the diagram. In the proposed approach, “branch a” is a reference for all the other branches, as no GEOM\(_a\) block was used in the beginning of the branch, which simplifies the computations. Each UGEOM\(_{i \rightarrow a}\) block reorganizes the structure of CNN1\(_i\) output in order to make it resemble the output of CNN1a. Thus, the hypothetical UGEOM\(_{a \rightarrow a}\) transformation is identity, so it was not included in the diagram. The UGEOM\(_{i \rightarrow a}\) performs an operation equivalent to the following sequence:

  • inverse operation to the “geometric effect” of CNN1\(_i\),

  • approximate inverse of GEOM\(_i\),

  • the “geometric effect” of CNN1a.

The “geometric effect” of a convolutional block (or inverse of such, referred to as “inverted geometric effect”) can be provided for any sequence of convolutional, maximum-pooling and activation layers. The activation functions and same-size convolutions can be considered as identity, as instead of applying any changes to the geometric structure, it detects patterns based on the central index of the filter matrix. Convolutions with either “full” or “true” sizes, when used, can be considered as sides extension or cropping (removal of the side rows and columns). The pooling layers, on the other hand, can be considered as geometrically equivalent to scaling. By this approach, the superposition of CNN1\(_i\) layers can be denoted as equivalent to a single geometric transformation—which is additionally inverted in the first step of UGEOM\(_{i \rightarrow a}\) and used directly in the final step.

Table 1 Python Imaging Library against fast geometric transformations implemented for the purpose of this paper
Full size table
Fig. 4
figure 4

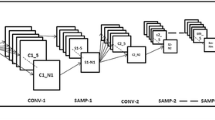
Convolutional neural network used in the reference experiments (without the novel method). The diagram includes convolutional, maximum-pooling, dropout and fully-connected layers. The structure of this model is practically the same as AlexNet [16], the only difference being the naming convention, which is compatible with that used in Fig. 2

Full size image
Fig. 5
figure 5

The novel CNN model. It is similar to the model shown in Fig. 4, but includes GEOM\(_i\), UGEOM\(_{i \rightarrow a}\) as well as the concatenation layers. The groups of convolutional layers inside the dotted rectangles use shared filters

Full size image

As UGEOM\(_{i \rightarrow a}\) performs a sequence of geometric transformations, it can be reduced to a single fast geometric transformation. The coefficients of this transformations are computed once, before the learning process, based strictly on the input size and the model definition. This makes the repeated applications of UGEOM\(_{i \rightarrow a}\) multiple times faster to compute than it would be in the case of a step-by-step application of the definition. The results from Table 1 indicate that fast geometric transformations make the calculations related to the UGEOM\(_{i \rightarrow a}\) layers roughly \(20\times\) faster. However, there is one more crucial advantage of fast geometric transformations that was not covered by the benchmarks—fast transformations are computed on GPU, which makes them readily usable in GPU-based neural network training without the need to transfer data between different computing devices. In terms of the complexity study, it can be summarized that the proposed approach makes each transformation proportional to the number of pixels, with fixed constant. As such, the improvement is purely technical, and we believe that the time measurement from Table 1 is the key illustration of the results.

The complete architectures of the AlexNet-like neural network models without and with the embedded transformations are presented in Figs. 4 and 5, respectively.

The proposed CNN shares the typical properties of AlexNet-like networks with dropout mechanism [29]. As it was explained in the beginning of Sect. 3.4, parts of the model can be considered as “denoising” layers, which directly address the typical kinds of image noise—either related to the image compression or to the white noise component.

4 Evaluation

4.1 Evaluation setup

As the experimental method is the key approach to test the proposed solutions, careful attention was paid to the comparison procedure. In order to evaluate the difference between the proposed models of neural networks as clearly as possible, separate series of experiments were performed for the rotated and rescaled input images.

The experimental setups involved in the presented method apply to the image classification task. Supervised learning of the digital image classifier can be performed with LeNet-like convolutional neural networks, with varying accuracy coefficients reached by the fully trained model. The hyperparemeters of model description, such as the number of layers, number of filters in each layer and the specific optimization method, usually need to be adjusted separately for each data set.

The objective of the experimental evaluation process presented in this paper is to identify the effect of geometric transformations embedded in the model description on the accuracy coefficient. In order to focus on this specific aspect of the neural network model, the roughly optimized model description without embedded geometric transformations is presented for each original data set. Such a basic model is equivalent to the novel network with a single branch, without any blocks parallel to the CNN1a and without any explicit GEOM blocks. This model description can be compared with the practical implementation of the novel approach, where additional branches with linearly independent GEOM blocks are involved.

The difference inducted by the additional branches is tested on the augmented data set, where the additional rotation or scale is applied. Rotations angles and the changes to the magnitude of scale will be selected from the uniform random zero-centered ranges. The typical setup can involve rotations by \(-30^\circ\) to \(30^\circ\) angle or scaling down by the factor from \([50\%, 100\%]\) range. The data set augmentation can apply solely to the test set—to check the automatic aptitude to preserve the correct classifications. More practically, however, the same augmentation method can be applied both to the test set and the training set. Since the data set augmentation is a standard approach to training convolutional neural networks with transformed patches, the basic model description is likely to yield useful results. However, the novel approach is likely to additionally benefit from such a setup, which is expected to result in the best model for the transformed patches.

Each data set and range of geometric transformations is involved in the following setups:

  1. 1.

    Training the reference model (basic CNN) on the original training set.

  2. 2.

    Training the reference model on the augmented training set.

  3. 3.

    Training the novel model (multiple branches with embedded geometric transformations) on the original training set.

  4. 4.

    Training the novel model on the augmented training set.

If the original data set already contains geometric transformations, the points (2.) and (4.) can be considered redundant. Alternatively, if augmented patches were created manually for the purpose of experiment, the models from points (1.) and (3.) can be tested both on the original test set and the augmented test set.

Additional step of the data augmentation can involve transformations different from the rotation/scale, such as adding the white noise. This could prolong the learning process without significant effect on the final accuracy [16], especially when the Dropout mechanism [29] is present in the neural network model.

4.2 Data sets and transformation ranges

In order to confirm the versatility of the presented method, the experimental evaluation is performed on the following data sets:

  • The Street View House Numbers (SVHN) Dataset [20]—over \(600\,000\) digit images extracted from the outside photos; data augmentation is performed manually. The test set without augmentation consists of \(26\,032\) patches.

  • Outex Texture Database [21]—with 68 grayscale textures, 20 patches each. Some geometric transformations are already present in the data set, but the selection of the experimental patches involves additional steps, such as cutting fragments of the original large-surface textures.

  • International Skin Imaging Collaboration: Melanoma Project archive [5]—\(44\,100\) digital images of skin lesions that can be categorized into 7 classes related to the recognized diseases. Classification task on this data set would naturally benefit from the rotation invariance, but data augmentation related to scale needs to be performed manually.

The selected data sets are intended to test the versability of the proposed method with regard to different applications. Fragments of outdoor photography (SVHN), scans of different textures (Outex) and medical imaging (Melanoma Project) are significantly different. The proposed data sets involve both color (SVHN, Melanoma) and grayscale images (Outex). What is more, SVHN is a well known problem for the CNN-based image classification [26, 29], and Outex is widely tested in the case of rotation-invariant image processing solutions [18, 19].

The choice of the data set provides variety to the amounts of noise present in the digital images. The SVHN patches—even if some of them are unsharp or upscaled—are reasonably clean, as they come from the digital camera. Noise is known to be an important concern in the case of the Outex data set, as it was shown in [19]. Amounts of noise that provide a reasonable verification for the presented method are also represented in the Melanoma data set, because of the complex structure of human skin and noise related to the scanning equipment.

In order to address the effect of noise to the method directly, additional experiment was performed for the SVHN data set and rotation invariance (Fig. 8, Table 4).

The most important result to emerge from the classification tasks is the total accuracy achieved on the test set. The accuracy is defined as the ratio of correctly classified test patches to the total number of test patches.

It must be emphasized that the task for each data set is defined as multi-class classification, where all classes are considered equal. This directly reflects the data set properties in the case of SVHN, where recognition of all 10 digits is equally important, and Outex, where all the presented textures are specific materials, with no designated “default background” present in the data set. The same approach is used for Melanoma data set, despite the fact that set of “healthy patients” can be expected to be remarkably the most common in real life. However, considering that multiple diseases are similarly represented in the experiments on ISIC-Melanoma, this remains our key approach. In the usual case, this means that no global precision-and-recall considerations or curve-based analysis can be performed. Precision on each class is directly related to the recall on all the others, and vice versa. In order to review the general shape of the receiver operating characteristic curves describing some of the classifiers, specific consideration of the “malignant neoplasms” class was performed for the ISIC-Melanoma data set—the results are presented in Fig. 9.

Fig. 6
figure 6

Sample rotations of a sample image (based on SVHN [20]) from \(-30^\circ\) to \(30^\circ\). Reference representatives of the three neural network branches are marked with dotted lines

Full size image

The novel CNN models used in the experiments were designed for both rotations and scales. In the case of rotations from \([-30^\circ , 30^\circ ]\) range, the following branches are used:

  • CNN1a: No rotation.

  • CNN1b: \(20^\circ\) rotation clockwise.

  • CNN1c: \(20^\circ\) rotation counterclockwise.

This approach guarantees that each sample from the \([-30^\circ , 30^\circ ]\) is rotated by at most \(10^\circ\) in relation to the basic use of the nearest branch. The selection is illustrated in Fig. 6.

Fig. 7
figure 7

Sample scales of a sample image (based on SVHN [20]) from \(100\%\) to \(50\%\). Reference representatives of the three neural network branches are marked with dotted lines

Full size image

The proposed size transformations involve downscaling only, with \([50\%, 100\%]\) factor range. Equally distributed branches would require using a non-identity transformation for each branch. Instead, the following factors were suggested:

  • CNN1a: No scaling.

  • CNN1b: \(76\%\) scaling (\(\approx 0.5^{0.4}\)).

  • CNN1c: \(57\%\) scaling (\(\approx 0.5^{0.8}\)).

This is an optimal approach with fixed \(100\%\) branch, where each sample has a size factor no lower than \(93\%\) and no greater than \(108\%\) with relation to the closest branch. The selection is illustrated in Fig. 7.

Note that the specific setups of three branches were chosen both for the \([-30^\circ , 30^\circ ]\) angle ranges and \([50\%, 100\%]\) scaling ranges. Different ranges of possible transformations would yield different results and possibly require a different number of processing branches. A fixed setup has been applied to show the effect of using additional branches on the classifier accuracy. The arbitrarily selected ranges are used for all the data sets. The unlimited range of transformations would be especially easy to define in the case of image rotation. However, such a task would be likely to require more than three processing branches.

5 Results

5.1 SVHN data set

The full experimental setup was run on the SVHN [20] data set. AlexNet-like models (Fig. 4) and novel model (Fig. 5) were trained in two experiments each, starting from the randomly initialized parameters obtained with the Xavier method [11]. Due to the parameter sharing explained in Fig. 5, all the models used exactly the same number of adjustable parameters. The number of iterations was fixed for all the experiments in order to provide relevant comparison. The results are displayed in Tables 2 and 3.

Table 2 Classification accuracies achieved for the SVHN experiments with and without rotations used in the data set variants and rotation invariance present in the models
Full size table
Table 3 Classification accuracies achieved for the SVHN experiments with and without scaling used in the data set variants and scale invariance present in the models
Full size table

5.1.1 Manual addition of the noise

Additional question to be researched is related to the possible effect of noise in the input data on the method. The Gaussian noise was added in two phases: as value-based noise with average of 15%, and then as independent RGB-noise of the same magnitude—as it is shown in Fig. 8. The results for the rotation invariance achieved for the additionally noisy data are presented in Table 4. The results are significantly poorer than in the same experiment without noise, which is summarized in Table 2. However, all the conclusions based on the comparisons between achieved values remain valid.

Fig. 8
figure 8

Sample image from the SVHN data set—before and after the manual addition of the noise

Full size image
Table 4 Classification accuracies achieved for the SVHN experiments with and without rotations used in the data set variants and rotation invariance present in the models after the noise was manually added to the original data set, as in Fig. 8
Full size table

5.2 Outex Texture Database

The experiments on Outex Texture Database [21] were used with an additional step of cutting each image into \(3 \times 3\) grid, which resulted in nine times more patches. As a result, each of 68 textures was represented by 180 images. The images were grouped in \(25\%\):\(75\%\) proportions, which yielded \(3\,060\) test samples and \(9\,180\) training samples. The high number of classes (68) and low number of training samples per class (135 without augmentation, 405 in the augmented setups) makes this task especially difficult. The presented accuracies are always related to the top-1 classification matches. The results are displayed in Tables 5 and 6.

Table 5 Classification accuracies achieved for the Outex experiments with and without rotations used in the data set variants and rotation invariance present in the models
Full size table
Table 6 Classification accuracies achieved for the Outex experiments with and without scaling used in the data set variants and scale invariance present in the models
Full size table

5.3 International Skin Imaging Collaboration: Melanoma Project archive

The experiments on International Skin Imaging Collaboration: Melanoma Project archive [5] were conducted in a similar way, with the standard subsets of \(33\,100\) training images and \(11\,000\) test images. The results are displayed in Tables 7 and 8.

Table 7 Classification accuracies achieved for the ISIC-Melanoma experiments with and without rotations used in the data set variants and rotation invariance present in the models
Full size table
Table 8 Classification accuracies achieved for the ISIC-Melanoma experiments with and without scaling used in the data set variants and scale invariance present in the models
Full size table

5.3.1 Receiver operating characteristic curves for the selected class

When the objective of the ISIC-Melanoma data set is considered, one of the seven classes is especially important with regard to the health of the patient—namely, “malignant neoplasms”. Among the data sets considered in this paper, it is the best example to demonstrate the precision and recall of the compared classifiers with regards to one specific class. This comparison was performed in detail for the task with additional rotations, and the result is presented in Fig. 9.

5.4 Summary of the results

In all of the presented experiments (Tables 2, 3, 4, 5, 6, 7, 8), superior accuracy for the tasks involving extended test sets was achieved when data set augmentation and the novel improvements to the model were applied simultaneously. The difference between this setup and the other compared cases was significant.

The novel models without data set augmentation (second row, second column of each table) performed significantly better than the basic CNN models (first rows, second columns) but not nearly as good as the basic CNN with training set augmentation (third row, second column). Such a result suggests that data set augmentation is an important practice and should not be omitted when training the transformation invariant neural network models. However, for both approaches to the training set preparation, using the novel model yielded significant improvements (the most significant difference is presented in Table 6).

The results obtained on the original test set, where all the digits samples were oriented in an approximately similar angle, do not show such dramatic differences. For example, in the most basic version of the SVHN task, the novel model achieved an accuracy level similar to the basic CNN (\(92.6\%\) against \(92.4\%\)). Using data augmentation with the basic CNN resulted in a slightly lower result— \(91.1\%\), which is of no great consequence, but might indicate that the introduction of additional training patches made the problem unnecessarily complex. A greater difference in the global accuracy was noted in the case of novel model with augmented data set. This setup (last row, first column) yielded the best accuracy for the original test set, with a varying margin of difference (see Tables 2 and 7).

The results presented above indicate that the approach involving both the novel model and data augmentation provides significantly smaller differences in accuracy between the original test set and the test set with additional rotations or scales (last row of each table). Therefore, our method demonstrates a substantial improvement in terms of transformation invariance.

6 Conclusions and future work

We have presented a novel approach to the processing of digital images with CNN-like models invariant to the selected geometric transformations. The proposed multi-branch model with embedded fast geometric transformations has been proven to work better in the image classification task in the cases of additional rotations and scales in three different data sets. It has been shown that the novel neural network models improve the classification accuracy, but the best results are achieved when the new models are used in conjunction with data augmentation.

Fig. 9
figure 9

The plots below present the receiver operating characteristic (ROC) curves for the ISIC-Melanoma classifiers with optional rotation invariance, the same as in Table 7. The presented statistics regard the detection of the “malignant neoplasms” class. The x-axis presents the false positive rate (FPR), calculated as the ratio of the false positives of each classifier to all negatives. The y-axis presents the true positive rate (TPR), which is ratio of the true negatives to all negatives. The plotting range covers mostly the values above the \(y=x\) curve, in order to emphasize the differences between classifiers. The default behavior of the multi-class classifier is marked with big \(\mathbf {\times }\) sign for each curve. The other points were generated for FPR and TPR values achieved after scaling neural network output for the “malignant neoplasms” class by factors from \(0.05 \ldots 20.0\) range. The decision of each classifier is always based on the highest class-related output

Full size image

To evaluate the efficiency of the presented method for rotated and rescaled images, both variants have been tested carefully in separate series of experiments. For both transformations, the improvement related to the novel neural network architectures was demonstrated.

The only objective way to test the effect of the proposed method on CNN classification involved a set of common assumptions that were met for all the experiments. Multiple setups were developed using the same technology and designed to consume a similar amount of memory and run at the same computation time. The reference CNN-based models and the novel solutions were similar in terms of neural network depth and number of adjustable parameters. This approach, while yielding meaningful results, required all the computations to be made from scratch, particularly for the comparisons presented.

A number of extensions to the work discussed here present themselves. It has been demonstrated that the method is able to work on diverse image data sets. The current study has only focused on the task of image classification, but the method presented might also be applied to other tasks. Further research is needed to investigate the applicability of multi-branch CNNs with embedded geometric transformations to semantic image segmentation or object detection.

A notable advantage of the method presented is the elastic approach to summarizing the results achieved for different embedded geometric transformations. The parallel branches are unified with special UGEOM transformations to guarantee relatable visual fields among the matrices. In its basic use, the method enables summarizing the subpatterns of different rotations or scales as if they were similar. However, depending on the filter values, it is also possible to achieve more complex results. Instead of “recognizing everything regardless of rotation”, the specific set of filters can limit the further activation to the specific subset of branches, e.g., the range of angles. On the basis of the rotations of the hands of the clock presented in the input image (and possibly shadows—in order to recognize the time of day), the model could be easily trained to recognize a class such as “evening”.

The presented method is capable of making the learning process of the CNN-based classifiers more optimal, as better results were achieved at the same computation time. What is more, the improved classifier yields better results while it utilizes the same amount of memory to store the parameters, which means that the presented solution is more optimal.