Abstract
This study aims to propose a novel model for the determination of depreciation in an environment of uncertainty. In the study, amortization methods were modified through interval type-2 fuzzy, and a new approach was proposed to help investors make decisions in an environment of cash flow uncertainty. We provide options among different depreciation alternatives for the future investment decisions of maritime companies through the revision of the straight-line depreciation method and the double-declining balance depreciation method. The fuzzy depreciation alternatives we suggest in our study are not only suitable for maritime companies, but also companies in different industries.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The concept of depreciation is widely applied to protect working capital. It is related to converting the cost of the asset into expenses to ensure that the fixed asset, which loses its value over time and/or as it wears out due to use, is fully or partially covered. Depreciation is important for enabling self-financing, by ensuring that the depreciation expense is spread out over accounting periods, calculating production costs, and ensuring the actual value of fixed assets (Çankaya and Yilmaz 2014; Engin and Atabay 2018). Depreciation is not only used for fixed asset value, but also cash flow and market value measures of investment performance, such as the internal rate of return and holding period (Bokhari and Geltner 2018). Depreciation also allows the company’s activities to be sustainable. Both cash flow forecasts and the depreciation method used are important for making the right investment decisions in capital-intensive industries. However, managers often make investment decisions in an uncertain environment. One of these uncertainties is often related to the estimated cash flow.
When a tangible asset is purchased, its full cost does not appear in the profit and loss account. If it is considered in terms of accounting, shipping companies would have a huge loss when a ship is purchased. However, the cost of the ship in the company’s balance sheet is registered for each year as a fixed asset, a percentage of its value is charged as a cost in the company’s balance sheet for each year during the accounting period. The cost is called depreciation, although this is not a cash value in accounting, so it is not shown in the cash flow. Furthermore, the profit will be lower than cash flow by this amount. IAS (2021) does not mention exactly how long the economic useful life of a ship is, however, in the market, a merchant ship’s useful life is considered to be about 25–30 years, and some specialized ships have longer useful life spans, though, most commonly, it is taken as 25 years. Therefore, equity investors face a different problem in public shipping companies. If they are a long-term investor, they focus on how much profit can be earned during a period, and so it crucially depends on how much depreciation will be deducted to estimate the profit earned accurately. Therefore, the cost must be deducted from cash flow for each ship wearing out year by year during its useful life. The most common depreciation method used by accountants in the shipping industry is the straight-line depreciation method. However, with this study, it is presented that the double-declining balance depreciation method can be as easily used as an IT2FSs approach as the straight-line depreciation method. In both methods, the ship is written off in defined proportions over its expected life; however, the proportions change depending on the type of depreciation method used. The reason why the company’s trading cash flow cover is so strong that a large proportion of its costs are capital, and a particularly important aspect of cash flow is the method used to pay for the ship. Many shipping companies do not purchase their ships with cash but pay for the vessels using a loan, or leasing agreement, etc. The cash flow profile of the shipping company changes due to the installments and interest of the loan. When cash is tight, purchasing can be deferred, and the ship can be traded on for a few years. When cash is plentiful, more ships can be ordered. This flexibility gives shipping companies financial security (Stopford 2009). Nevertheless, the depreciation calculation method can provide a helpful solution for an investor, for instance, if the double-declining balance depreciation method is considered rather than the straight-line depreciation method, it gives more flexibility in the early years of cash flow in terms of investment. However, applying fuzzy depreciation methods in terms of an investment evaluation perspective can help overcome uncertainty in the high volatility shipping industry. Therefore, IT2FSs can apply as a solution with respect to the uncertainty in future expectations.
Especially due to increasing globalization, firms now operate in a more uncertain environment in which managers need to make important decisions. Decisions are made by managers regarding capital budgeting, capital investment, and the cost of capital, and these affect a firm’s value and plans. One of the important decisions made by managers concerns determining which depreciation method to use. This often depends on accounting standards and is made on practical grounds and affects both the taxable income and shareholder value (Berg et al. 2001). Therefore, determining the depreciation method in an uncertain environment is extremely important because of uncertain in future cash flows.
Accounting principles that firms employ allow them to use different depreciation methods. There are some studies in the literature that examine the choice of method to investigate reducing the present value of tax payments (Jennergren 2018; Kulp and Hartman 2011; Press and Davidson 1964; Wagenhofer 2003). However, there are only a few studies on determining which depreciation method is more appropriate in an environment where future cash flows are uncertain. In this context, some studies which suggest optimal depreciation methods in such conditions are Berg et al. 2001; Berg and Moore 1989. In these studies, the optimal depreciation methods are proposed in different taxation systems. However, the most important problem here is not the preference of different depreciation methods, the important point is the use of the appropriate depreciation method in an uncertain environment.
The various decisions that managers make in uncertain environments are important for firms to survive and gain a competitive advantage. As mentioned, the constant depreciation amount significantly affects firms’ capital investment decisions in times when the amount of future cash flow is uncertain (Jackson 2008; Jackson et al. 2009; Ohrn 2019). Managers often make investment decisions when there is a large imbalance between productivity and capital stock, especially where the investment is irreversible (Samaniego and Sun 2019). On the other hand, using a model in which even the depreciation amount itself is a fuzzy number under different scenarios can help managers make more accurate investment decisions under uncertainty.
The decision-making process in the capital-intensive and highly competitive global maritime industry is crucial because of the inherent uncertainty of the shipping industry. One of the essential difficulties of investments is forecasting cash flows due to the uncertainty of the future. Apart from traditional financial methods that can analyze an investment up to the uncertainty barrier, there are analysis method-based type-1 fuzzy methods, as well as IT2FSs methods. So far, depreciation in the literature has neither been evaluated in terms of investment nor the maritime industry in an interval type-2 fuzzy environment. Conventional depreciation methods and their type-1 fuzzy methods can be insufficient in an environment of uncertainty, such as in future investment evaluation. Fuzzy sets provide wider solution sets than classic methods thanks to their membership functions. Fuzzy sets give wider solution sets than classic methods, though IT2FSs methods give more feasible solutions. The membership functions of type-1 fuzzy sets are in the [0,1] range as a crisp number, and the membership functions of type-1 fuzzy sets are fuzzy numbers. The membership functions of type-1 fuzzy sets are two-dimensional; however, the membership functions of IT2FSs are three-dimensional. Thus, simulating real-life problems with IT2FSs methods obtains more flexibility in the uncertainty of the model by using this third dimension (Zadeh 19651975; Uçal Sari et al. 2013). Accordingly, the membership functions of the proposed model are referred to as ship price and price of scrap metal by using IT2FSs.
There are several studies in the literature claiming that the main reason for choosing the depreciation method is to lower the present value of tax payments (Albonico et al. 2014; Baumol 1971; Berg and Moore 1989; Press and Davidson 1964). However, cash flow is not regular over the years. Even in times of global crisis, such as due to Covid-19, firms may not be able to obtain cash flow to cover depreciation. In an environment of such uncertainty, it is strategically important for management to make the right investment decisions. Unlike previous studies, this study aims to help make more accurate investment decisions by using fuzzy numbers for the amount of future depreciation. More specifically, it proposes a model for evaluating investments not only in times when cash flows are uncertain, but also in times when depreciation is uncertain. As mentioned above, several studies used fuzzy numbers for cash flow (Berg et al. 2001; Berg and Moore 1989; Khalili et al. 2014; Samaniego and Sun 2019) but in these studies, the depreciation amount was fixed or predictable. However, this is unrealistic for periods when cash flow is completely interrupted such as during the Covid-19 pandemic. In this study, we developed a novel model for making investment decisions in times when the depreciation amount is uncertain. In a previous study, depreciating assets were included in the fuzzy system (Khalili et al. 2014), but the IT2FSs approach was not applied in depreciation. As a result, our study varies from others as we integrated the IT2FSs approach into depreciation.
The remaining part of this study is organized as follows: In Sect. 2, we describe studies in the literature. Section 3 provides information about the depreciation method and the theoretical basis of depreciation. In Sect. 4, we explain the methodology of the study and interval type-2 fuzzy sets. The theory development process and the application of the interval type-2 fuzzy straight-line method of depreciation are described in Sects. 5 and 6, respectively. In Sect. 7, we conclude the findings of the study.
2 Literature review
The first studies examining the relationship between depreciation policy and investment date back to the 1960s. Smith (1963), for example, examined the relationship between firms’ investment decisions and depreciation policy, taking into account factors such as the industry in which they operated, the method of depreciation, and tax advantage. Press and Davidson (1964) updated their 1961 article due to legal changes and suggested the “best” method of depreciation under existing laws. In addition to this, several studies have proposed the “best” or optimum method of depreciation (Baumol 1971; Berg et al. 2001; Davidson and Drake 1961; De Waegenaere and Wielhouwer 2002; Stickney 1981; Wakeman 1980).
Companies often operate in an uncertain environment resulting in uncertain cash flows. Several studies associate operating in an uncertain environment with the method of depreciation (Berg et al. 2001; Berg and Moore 1989; Femminis 2008). In an environment of uncertainty, there is a consensus that there is an aggregate economic activity (Samaniego and Sun 2019). Accordingly, it seems that uncertainty significantly affects investment decisions, especially in high-depreciation industries, and it is covered in the literature which focuses on the depreciation method. The negative directional interaction between depreciation and uncertainty provides important evidence for this (Samaniego and Sun 2019).
Capital investment decisions maximize shareholder wealth by increasing the market value of firms, and these decisions are important for securing the long-term survival of firms (Jackson 2008). However, decisions on capital investment are not independent of the depreciation method applied. In this context, there is evidence that there is a significant relationship between the different depreciation methods, the accelerated depreciation method, and the level of capital investments (Jackson et al. 2009). These findings also indicate that the depreciation method is remarkably effective in investment decisions.
Studies have examined various aspects of depreciation. For example, Jackson et al. (2010) examined the relationship between the depreciation method and selling a used capital asset. In the study, decision-makers considered accounting depreciation and historical cost when they sold a used capital asset. Kulp and Hartman (2011) emphasized that the depreciation method was determined by taking into account the present value of expected tax payments, and accelerated methods were preferred. In response to this situation, they developed a model which created conditions in which the straight-line depreciation model could be preferred. Yussof et al. (2014) analyzed the contrast between accounting depression and the tax treatment of capital allowance for Malaysia. According to the result of the study, it was proposed that the government redesigns the capital allowance system. Park (2016) investigated depreciation recovery periods based on the “bonus depreciation” method in the USA. According to the study’s findings, the change in the depreciation method contributed positively to annual investment amounts. Rassenfosse and Jaffe (2018) focused on estimating the depreciation rate with revenues associated with patent applications in Australia. They also analyzed the impact of patent protection on the depreciation rate. The findings showed that the impact of patent protection on the depreciation rate was 2–7%. According to Samaniego and Sun (2019), the number of investments decreases during periods of high uncertainty. This reduction is more evident, especially in industries where capital depreciation is rapid. The findings of their study show that growth is negatively affected by high uncertainty, which also affects depreciation. Ohrn (2019) examined the impact of depreciation policies on the manufacturing sector in the USA. According to the findings of the study, accelerated depreciation policies have an impact on capital investment.
There are various studies in the literature using the type-2 fuzzy method. For instance, the type-2 fuzzy method has been applied in: α-planes optimized in the integration process (Ontiveros-Robles et al. 2021b), implementation of a biogas plant (Karmakar et al. 2021), medical device selection problems (Tolga et al. 2020), medical diagnosis problems (Ontiveros-Robles et al. 2021a; Ontiveros-Robles and Melin 2020), human resource management (Abdullah and Zulkifli 2015), operational performance of some transportation systems (Bakir et al. 2020), a green supplier selection problem (Mousavi et al. 2020), type-2 fuzzy model design (Moreno et al. 2020), occupational safety risk performance in industries (Jana et al. 2019), gravitational search algorithms (Olivas et al. 2019), and another type-2 fuzzy logic application (Mittal et al. 2020).
Several studies in the literature have examined depreciation policy, such as: in advertising (Abdel-Khalik 1975; Falk and Miller 1977; Hirschey and Weygandt 1985; Peles 1971), goodwill amortization period (Hall 1993; Henning and Shaw 2003; Jennings et al. 2001), determinants of goodwill and the effects of goodwill amortization (Ayers et al. 2000; Duvall et al. 1992; Glaum et al. 2015; Huefner and Largay 2004; Vogt et al. 2016), and the valuation of a company and amortization (Gabriel 1937; Lev and Sougiannis 1996). Although such articles examined depreciation in different dimensions, they do not contain information about the optimum method of depreciation for the firm under conditions of uncertainty. With this motivation, the gap in the literature will be filled by the proposed depreciation methods covered in this study.
3 Interval type-2 fuzzy sets
In the section, we describe interval type-2 fuzzy sets briefly. Type-2 fuzzy sets were proposed by Zadeh as an extension of type-1 fuzzy sets having membership grades as type-1 fuzzy sets. A type-2 fuzzy set \(\mathop A\limits^{ \approx }\) in the universe of discourse X can be presented by a type-2 membership function \(\mu_{{\mathop A\limits^{ \approx } }}\), viewed as shown in Eq. (1) (Zadeh 1975; Mendel et al. 2006; Zeng et al. 2007):
where \(J_{x}\) states an interval [0,1]. The type-2 fuzzy set \(\mathop A\limits^{ \approx }\) also can be represented as shown in Eq. (2) (Mendel et al. 2006):
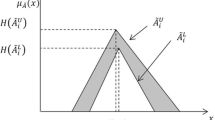
where \(J_{x} \subseteq \left[ {0,1} \right]\) and \(\int {}\) state union over all acceptable x and u. Let \(\mathop A\limits^{ \approx }\) be IT2FSs in the universe of discourse X presented by type-2 membership function \(\mu_{{\mathop A\limits^{ \approx } }}\) If all, \(\mu_{{\mathop A\limits^{ \approx } }} \left( {x,u} \right) = 1\) after \(\mathop A\limits^{ \approx }\) is called an IT2FSs (Zadeh 1975; Buckley 1985). An IT2FSs \(\mathop A\limits^{ \approx }\) can pass for a particular situation of a type-2 fuzzy set, presented as shown in Eq. (3) and in Fig. 1 and Fig. 2 (Mendel et al 2006).
3.1 Triangular interval type-2 fuzzy sets
A triangular IT2FS are defined as \(\mathop {A_{i}}\limits^{ \approx } = \left( {\left( {a_{il}^{U} , \, a_{im}^{U} , \, a_{iu}^{U} ; \, H\left( {\mathop {A_{i}^{U} }\limits^{ \sim } } \right)} \right),\left( {a_{il}^{L} , \, a_{im}^{L} , \, a_{iu}^{L} ; \, H\left( {\mathop {A_{i}^{L} }\limits^{ \sim } } \right)} \right)} \right)\) where \(\mathop {A_{i}^{U} }\limits^{ \sim }\) and \(\mathop {A_{i}^{L} }\limits^{ \sim }\) are type-1 fuzzy sets, \(a_{il}^{U} , \, a_{im}^{U} , \, a_{ir}^{U} ,\)\( \, a_{il}^{L} , \, a_{im}^{L} , \, a_{ir}^{L}\) are the references points of the IT2FSs \(\mathop {A_{i} }\limits^{ \sim } ,\) \(H\left( {\mathop {A_{i}^{U} }\limits^{ \sim } } \right)\) denotes the membership value of the element \(a_{j(j + 1)}^{U}\) in the upper triangular membership function \(\left( {\mathop {A_{i}^{U} }\limits^{ \sim } } \right),\) \(1 \le j \le 2,\) \(H\left( {\mathop {A_{i}^{L} }\limits^{ \sim } } \right)\) denotes the membership value of the element \(a_{j(j + 1)}^{L}\) in the lower triangular membership function \(\left( {\mathop {A_{i}^{L} }\limits^{ \sim } } \right),\)\(1 \le j \le 2,\)\(H\left( {\mathop {A_{i}^{U} }\limits^{ \sim } } \right) \in \left[ {0,1} \right],\)\(H\left( {\mathop {A_{i}^{L} }\limits^{ \sim } } \right) \in \left[ {0,1} \right].\) The membership function of a triangular interval type-2 fuzzy set is given in Fig. 1.
The basic arithmetic operation of interval triangular type-2 fuzzy sets defined \(\mathop {A_{1} }\limits^{ \approx }\) and \(\mathop {A_{2} }\limits^{ \approx }\) are given in Eq. (4–11).
Definition 1:
The addition operation between the two triangular IT2FSs \(\mathop {A_{1} }\limits^{ \approx }\) and \(\mathop {A_{2} }\limits^{ \approx }\) is defined in Eq. (4) as:
Definition 2:
The subtraction operation between two the triangular IT2FSs \(\mathop {A_{1} }\limits^{ \approx }\) and \(\mathop {A_{2} }\limits^{ \approx }\) is defined in Eq. (5) as:
Definition 3:
The multiplication operation between two the triangular IT2FSs \(\mathop {A_{1} }\limits^{ \approx }\) and \(\mathop {A_{2} }\limits^{ \approx }\) is defined in Eq. (6) as:
Definition 4:
The arithmetic operation between the triangular IT2FSs \(\mathop {A_{1} }\limits^{ \approx }\) and a crisp value \(k > 0\) is defined in Eq. (7) and Eq. (8) as:
Definition 5:
The division operation for two the triangular IT2FSs \(\mathop {A_{1} }\limits^{ \approx }\) and \(\mathop {A_{2} }\limits^{ \approx }\) is defined in Eq. (9) as:
Definition 6:
The inverse operation of the triangular IT2FSs \(\mathop {A_{1} }\limits^{ \approx }\) is defined in Eq. (10) as:
Definition 7:
\(n^{th}\) root operation of the triangular IT2FSs \(\mathop {A_{1} }\limits^{ \approx }\) is defined in Eq. (11) as:
3.2 Trapezoidal interval type-2 fuzzy sets
A trapezoidal interval type-2 fuzzy sets are defined as \(\mathop A\limits^{ \approx } = \left( {\left( {a_{i1}^{U} , \, a_{i2}^{U} , \, a_{i3}^{U} , \, a_{i4}^{U} ; \, H_{1} \left( {\mathop {A_{i}^{U} }\limits^{ \sim } } \right), \, H_{2} \left( {\mathop {A_{i}^{U} }\limits^{ \sim } } \right)} \right)} \right.,\)
\(\left. {\left( {a_{i1}^{L} , \, a_{i2}^{L} , \, a_{i3}^{L} , \, a_{i4}^{L} ; \, H_{1} \left( {\mathop {A_{i}^{L} }\limits^{ \sim } } \right), \, H_{2} \left( {\mathop {A_{i}^{L} }\limits^{ \sim } } \right)} \right)} \right)\) where \(\mathop {A_{i}^{U} }\limits^{ \sim }\) and \(\mathop {A_{i}^{L} }\limits^{ \sim }\) are type-1 fuzzy sets, \(a_{i1}^{U} , \, a_{i2}^{U} , \, a_{i3}^{U} ,\)\(a_{i4}^{U} , \, a_{i1}^{L} , \, a_{i2}^{L} , \, a_{i3}^{L} , \, a_{i4}^{L}\) are the references points of the interval trapezoidal type-2 fuzzy sets \(\mathop {A_{i} }\limits^{ \sim } ,\) \(H_{j} \left( {\mathop {A_{i}^{U} }\limits^{ \sim } } \right)\); states the membership estimation of the factor \(a_{j(j + 1)}^{U}\) in the upper trapezoidal membership function \(\left( {\mathop {A_{i}^{U} }\limits^{ \sim } } \right),\)\(1 \le j \le 2,\)\(H_{j} \left( {\mathop {A_{i}^{L} }\limits^{ \sim } } \right)\); also it states the membership estimation of the factor \(a_{j(j + 1)}^{L}\) in the lower trapezoidal membership function \(\left( {\mathop {A_{i}^{L} }\limits^{ \sim } } \right),\)\(1 \le j \le 2,\) \(H_{1} \left( {\mathop {A_{i}^{U} }\limits^{ \sim } } \right) \in \left[ {0,1} \right],\) \(H_{2} \left( {\mathop {A_{i}^{U} }\limits^{ \sim } } \right) \in \left[ {0,1} \right],\) \(H_{1} \left( {\mathop {A_{i}^{L} }\limits^{ \sim } } \right) \in \left[ {0,1} \right],\) \(H_{2} \left( {\mathop {A_{i}^{L} }\limits^{ \sim } } \right) \in \left[ {0,1} \right]\) and \(1 \le j \le n\) (Chen and Lee, 2010). The membership function of a trapezoidal interval type-2 fuzzy set is given in Fig. 2.
The basic arithmetic operation of interval trapezoidal type-2 fuzzy sets defined \(\mathop {A_{1} }\limits^{ \approx }\) and \(\mathop {A_{2} }\limits^{ \approx }\) and are given in Eq. (12–19).
Definition 1:
The addition operation for the two trapezoidal IT2FSs \(\mathop {A_{1} }\limits^{ \approx }\) and \(\mathop {A_{2} }\limits^{ \approx }\) is defined in Eq. (12) as:
Definition 2:
The subtraction operation for two the trapezoidal IT2FSs \(\mathop {A_{1} }\limits^{ \approx }\) and \(\mathop {A_{2} }\limits^{ \approx }\) is defined in Eq. (13) as:
Definition 3:
The multiplication operation for two the trapezoidal IT2FSs \(\mathop {A_{1} }\limits^{ \approx }\) and \(\mathop {A_{2} }\limits^{ \approx }\) is defined in Eq. (14) as:
Definition 4:
The arithmetic operation for the trapezoidal IT2FSs \(\mathop {A_{1} }\limits^{ \approx }\) and a crisp value \(k > 0\) is defined in Eqs. (15) and (16) as:
Definition 5:
The division operation for two the trapezoidal IT2FSs \(\mathop {A_{1} }\limits^{ \approx }\) and \(\mathop {A_{2} }\limits^{ \approx }\) is defined in Eq. (17) as:
Definition 6:
The inverse operation for the trapezoidal IT2FSs \(\mathop {A_{1} }\limits^{ \approx }\) is defined in Eq. (18) as:
Definition 7:
\(n^{th}\) root operation for the trapezoidal IT2FSs \(\mathop {A_{1} }\limits^{ \approx }\) is defined in Eq. (19) as:
3.3 Interval type-2 fuzzy defuzzification
The method of criteria center of area (COA) is considered to defuzzify the lower and upper membership values of IT2FSs into best nonfuzzy performance (BNP) value in the study. The BNP value is worked out in Eqs. (20) and (21) (Bellman and Zadeh 1970; Opricovic and Tzeng 2003; Hsieh et al. 2004). Accordingly, it is calculated by applying arithmetic mean for each defuzzification value of \(\mathop {A_{i}^{U} }\limits^{ \sim }\) and \(\mathop {A_{i}^{L} }\limits^{ \sim }\).
4 Interval type-2 fuzzy depreciation
In this section, straight-line depreciation and double-declining balance (accelerated) methods are described in terms of IT2FSs.
4.1 Classic straight-line depreciation method
The straight-line depreciation method allocates an equal portion of the depreciable value in each period of the asset’s useful life. The assumption of the method is the depreciation is a function of the passage of time rather than the actual productive use of the asset. The depreciation expense for a period is equally calculated by dividing the depreciable cost of the asset by the years of the asset’s useful life. In the method, the depreciable cost is calculated by deducting salvage value from the cost of the asset. Depreciable cost is arrived at by deducting salvage or residual value from the original cost of the asset. So, the value of the asset equals to salvage value when the end of the useful life.
The equation is used for calculating depreciation under the classic straight-line method of depreciation. By modifying Eq. (22) for ship’s deprecation for maritime, the equation is described in Eqs. (22–23):
where D: depreciation ($), C: ship price ($), S: salvage value ($), L: useful life (year)∀ L∉ R and L>0, LDT: light ship displacement, P: price of scrap metal ($)
With respect to the definitions of straight-line depreciation, deprecation (D) means the monetary value of a ship deprecating in maritime industry. Ship price (C) means the monetary value of an asset. Deprecation depends on ship price (C) and salvage value (S) in maritime industry. Also, salvage value (S) depends on light ship displacement (LTD) and price of scrap metal (P). Ship’s useful life (L) is commonly 25 years in maritime industry. Light displacement (LDT) is defined as the weight of the ship excluding cargo, fuel, water, ballast, stores, passengers, crew, but with water in boilers to steaming level. Price of scrap metal (P) means a price of scrap as steel that a ship made from steel which is recyclable.
The interval type-2 fuzzy straight-line depreciation method is defined in Eq. (24). Also, the interval type-2 fuzzy salvage for a ship is defined in Eq. (25).
where \(\mathop D\limits^{{ \simeq }}\): interval type-2 fuzzy depreciation ($), \(\mathop C\limits^{{ \simeq }}\): interval type-2 fuzzy ship price ($), \(\mathop S\limits^{{ \simeq }}\): interval type-2 fuzzy salvage value ($), L: useful life (year)∀ L∉ R and L>0; LDT: light ship displacement, \(\mathop P\limits^{{ \simeq }}\): interval type-2 fuzzy price of scrap metal ($).
4.1.1 Triangular interval type-2 fuzzy straight-line depreciation method
The triangular interval type-2 fuzzy straight-line depreciation method as variable of \(\mathop D\limits^{{ \simeq }}{_{i}}\), \(\mathop C\limits^{{ \simeq }}{_{i}}\), \(\mathop P\limits^{{ \simeq }}{_{i}}\) and \(\mathop S\limits^{{ \simeq }}{_{i}}\) occurred at the time \(i\) as follows and \(\mathop D\limits^{{ \simeq }}{_{i}}\) is defined in Eq. (26):
\(\mathop C\limits^{{ \simeq }}{_{i}}\), \(\mathop P\limits^{{ \simeq }}{_{i}}\) and \(\mathop S\limits^{{ \simeq }}{_{i}}\) are defined for triangular IT2FSs as follows in Eq. (27–29):
4.1.2 Trapezoidal interval type-2 fuzzy straight-line depreciation method
The trapezoidal interval type-2 fuzzy straight-line depreciation method as variable of \(\mathop D\limits^{{ \simeq }}{_{i}}\), \(\mathop C\limits^{{ \simeq }}{_{i}}\), \(\mathop P\limits^{{ \simeq }}{_{i}}\) and \(\mathop S\limits^{{ \simeq }}{_{i}}\) occurred at the time \(i\) as follows and \(\mathop D\limits^{{ \simeq }}{_{i}}\) is defined in Eq. (30):
\(\mathop C\limits^{{ \simeq }}{_{i}}\), \(\mathop P\limits^{{ \simeq }}{_{i}}\) and \(\mathop S\limits^{{ \simeq }}{_{i}}\) are defined for trapezoidal IT2FSs as follows in Eq. (31–33):
4.2 Double-declining balance depreciation method
The method of double-declining balance depreciation is a type of accelerated depreciation doubling the standard depreciation method. It is generally used to depreciate fixed assets more intensely in the early years, allowing the organization to postpone income taxes to the following years. The depreciation factor of the double-declining balance method is the double value of the straight-line expense method. The method of double-declining balance depreciation presents in a larger amount expensed in the earlier years, on the contrary, the later years of an asset’s useful life. So, the value of the asset equals to salvage value when the end of the useful life.
The equation is used for calculating depreciation under the classic double-declining balance depreciation method. By modifying Eq. (34) for ship’s deprecation for maritime, the equation is described in Eqs. (34–36):
where D: depreciation ($), C: ship price ($) (book value at beginning); S: salvage value ($); L: useful life (year)∀ L∉ R and L>0, LDT: light ship displacement, P: price of scrap metal ($), R: double-declining balance depreciation rate.
With respect to the definitions of double-declining balance depreciation, deprecation (D) means the monetary value of a ship deprecating in maritime industry. Ship Price (C) means the monetary value of an asset. Deprecation depends on ship price (C) and salvage value (S) in maritime industry. Also, salvage value (S) depends on light ship displacement (LTD) and price of scrap metal (P). Ship’s useful life (L) is commonly 25 years in maritime industry. Light displacement (LDT) is defined as the weight of the ship excluding cargo, fuel, water, ballast, stores, passengers, crew, but with water in boilers to steaming level. Price of scrap metal (P) means a price of scrap as steel that a ship made from steel which is recyclable.
The interval type-2 fuzzy double-declining balance depreciation method is given in Eq. (37). Also, a double-declining balance depreciation rate is given in Eq. (38), and interval type-2 fuzzy salvage for a ship is given in Eq. (39).
where \(\mathop D\limits^{{ \simeq }}\): interval type-2 fuzzy depreciation ($), \(\mathop C\limits^{{ \simeq }}\): interval type-2 fuzzy ship price ($), \(\mathop S\limits^{{ \simeq }}\): interval type-2 fuzzy salvage value ($), L: useful life (year)∀ L∉ R and L>0, LDT: light ship displacement, \(\mathop P\limits^{{ \simeq }}\): interval type-2 fuzzy price of scrap metal ($), R: double-declining balance depreciation rate
4.2.1 Triangular interval type-2 fuzzy double-declining balance depreciation method
The triangular interval type-2 fuzzy straight-line depreciation method as variable of \(\mathop D\limits^{{ \simeq }}{_{i}}\), \(\mathop C\limits^{{ \simeq }}{_{i}}\), \(\mathop P\limits^{{ \simeq }}{_{i}}\) and \(\mathop S\limits^{{ \simeq }}{_{i}}\) are occurring at the time \(i\) as follows and \(\mathop D\limits^{{ \simeq }}{_{i}}\) is defined in Eq. (40):
\(\mathop C\limits^{{ \simeq }}{_{i}}\), \(\mathop P\limits^{{ \simeq }}{_{i}}\) and \(\mathop S\limits^{{ \simeq }}{_{i}}\) are defined for triangular IT2FSs as follows in Eqs. (41–43).\(\mathop C\limits^{{ \simeq }}{_{i}}\), \(\mathop P\limits^{{ \simeq }}{_{i}}\) and \(\mathop S\limits^{{ \simeq }}{_{i}}\) are defined for triangular IT2FSs as follows in Eqs. (27–29):
4.2.2 Trapezoidal interval type-2 fuzzy double-declining balance depreciation method
The trapezoidal interval type-2 fuzzy straight-line depreciation method as variable of \(\mathop D\limits^{{ \simeq }}{_{i}}\), \(\mathop C\limits^{{ \simeq }}{_{i}}\), \(\mathop P\limits^{{ \simeq }}{_{i}}\) and \(\mathop S\limits^{{ \simeq }}{_{i}}\) are occurring at the time \(i\) as follows and \(\mathop D\limits^{{ \simeq }}{_{i}}\) is defined in Eq. (44):
\(\mathop C\limits^{{ \simeq }}{_{i}}\), \(\mathop P\limits^{{ \simeq }}{_{i}}\) and \(\mathop S\limits^{{ \simeq }}{_{i}}\) are defined for trapezoidal IT2FSs as follows in Eqs. (45–47):
5 Application
The application of straight-line deprecation and double-declining balance depreciation methods are related to a ship in maritime. In application, classic, trapezoidal, and triangular type-2 fuzzy straight-line deprecation and double-declining balance depreciation methods are calculated separately as below. The ship’s characteristics are given in Tables 1 and 2.
5.1 Classic straight-line depreciation method
The classic straight-line depreciation method is calculated from Eq. (22) as follows:
In Tables 2 and 3, the classic straight-line method of depreciation is calculated by breaking down the useful life of the ship.
5.1.1 Triangular interval type-2 fuzzy straight-line depreciation method
The triangular interval type-2 fuzzy straight-line depreciation method is calculated from Eq. (26) as follows:
The triangular interval type-2 fuzzy straight-line depreciation method is defuzzied by calculating from Eq. (21) as follows:
The value of \(D_{11}^{U}\) and value of \(D_{11}^{L}\) are computed by the arithmetic mean and crisp value of \(D\) is computed at the end.
In Table 4, the triangular interval type-2 fuzzy straight-line depreciation is calculated by breaking down for useful life of the ship.
5.1.2 Trapezoidal interval type-2 fuzzy straight-line method depreciation
The trapezoidal interval type-2 fuzzy straight-line depreciation method is calculated from Eq. (27) as follows:
The trapezoidal interval type-2 fuzzy straight-line depreciation method is defuzzied by calculating from Eq. (20) as follows:
The value of \(\mathop {D_{i}^{U} }\limits^{ \sim }\) and value of \(\mathop {D_{i}^{L} }\limits^{ \sim }\) are computed by the arithmetic mean and crisp value of \(D\) is computed at the end.
In Table 5, the trapezoidal interval type-2 fuzzy straight-line depreciation is calculated by breaking down for useful life of the ship.
5.2 Double-declining balance depreciation method
The classic double-declining balance depreciation method was calculated from Eq. (37) as follows:
The double-declining balance depreciation rate is calculated by Eq. (38).
The salvage of the ship is calculated by Eq. (39).
In Tables 2 and 6, the classic double-declining balance depreciation method is calculated by breaking down the useful life of the ship.
5.2.1 Triangular interval type-2 fuzzy double-declining balance depreciation method
The triangular interval type-2 fuzzy double-declining balance depreciation method is calculated from Eq. (26) as follows:
The triangular interval type-2 fuzzy double-declining balance depreciation method is defuzzied by calculating from Eq. (21) as follows:
The value of \(D_{11}^{U}\) and value of \(D_{11}^{L}\) are computed by the arithmetic mean and crisp value of \(D\) is computed at the end.
In Table 7, the triangular interval type-2 fuzzy double-declining balance depreciation method is calculated by breaking down the useful life of the ship.
The triangular interval type-2 fuzzy depreciation of the salvage for the ship is calculated from Eq. (39) as follows. The calculation of the salvage for both methods is the same.
5.2.2 Trapezoidal interval type-2 fuzzy double-declining balance depreciation method
The trapezoidal interval type-2 fuzzy double-declining balance depreciation method is calculated from Eq. (37) as follows:
The trapezoidal interval type-2 fuzzy double-declining balance depreciation method is defuzzied by calculating from Eq. (20) as follows:
The value of \(\mathop {D_{i}^{U} }\limits^{ \sim }\) and value of \(\mathop {D_{i}^{L} }\limits^{ \sim }\) are computed by the arithmetic mean and crisp value of \(D\) is computed at the end.
In Table 8, the double-declining balance depreciation method is calculated by breaking down the useful life of the ship.
The trapezoidal interval type-2 fuzzy of salvage for the ship is calculated from Eq. (39) as follows. The calculation of the salvage is the same for both methods.
Table 2 is related to the ship price, the price of scrap metal, the light ship displacement (LDT), the salvage value off the ship, utilization life of the ship, useful life of the ship, age of the ship, annual depreciation, and annual deprecation defuzzfy. Also, it consists of the values of the classic straight-line depreciation and double-declining balance depreciation methods, the straight-line depreciation and the double-declining balance depreciation methods in triangular interval type-2 fuzzy sets and the straight-line depreciation and the double-declining balance depreciation methods in trapezoidal interval type-2 fuzzy sets.
Table 3 is related to details of breakdown for classic straight-line depreciation method for 25 years. It consists of book value at beginning of the year, depreciation expense, accumulated depreciation, and book value at end of the year. Table 4 is related to details of breakdown for triangular interval type-2 fuzzy for straight-line depreciation method for 25 years. It consists of book value at beginning of the year, depreciation expense, accumulated depreciation, and book value at end of the year. Table 5 is related to details of breakdown for trapezoidal interval type-2 fuzzy for straight-line depreciation method for 25 years. It consists of book value at beginning of the year, depreciation expense, accumulated depreciation, and book value at end of the year. Figure 3 is related to details of the breakdown for the defuzzied straight-line depreciation method.
Table 6 is related to details of breakdown for classic double-declining balance depreciation method for 25 years. It consists of book value at beginning of the year, depreciation expense, accumulated depreciation, and book value at end of the year. Table 7 is related to details of breakdown for triangular interval type-2 fuzzy for double-declining balance depreciation method for 25 years. It consists of details of breakdown for triangular interval type-2 fuzzy for accelerated depreciation method. Table 8 is related to details of breakdown for trapezoidal interval type-2 fuzzy for double-declining balance depreciation method for 25 years. It consists of book value at beginning of the year, depreciation expense, accumulated depreciation, and book value at end of the year. Figure 4 is related to details of breakdown for defuzzied accelerated depreciation method. Because of the characteristic of the double-declining balance depreciation method, the allocation for 24 years.
6 Discussion and conclusion
In this study, we proposed the novel depreciation approach in an environment of uncertainty using the IT2FSs method. There are many studies in the literature related to the IT2FSs method. The IT2FSs method has been applied in the maritime transportation industry (Soner et al. 2017), aircraft selection problems (Kiracı and Akan 2020), sustainable supplier selection (Xu et al. 2019), novel green supplier selection (Liu et al. 2019), and occupational safety risk performance (Jana et al. 2019). However, there have not been any studies where the IT2FSs method has been integrated with any depreciation methods. Recent studies on depreciation in the literature focus on the effect of depreciation on investment (Caballero 2021), depreciation obsolescence of the R&D industry (Chinloy et al. 2020), mortgage depreciation requirements and household indebtedness (Hull 2017), and the depreciation of natural capital (Mardones and del Rio 2019). However, the limited number of studies in which the IT2FSs method was applied to the depreciation method shows that this study is original and will contribute to the literature.
The shipping industry has a naturally uncertain environment as its ecosystem depends on many factors, such as the complication of the shipping investment environment, the volatility of the shipping market, the enormous amount of investment required, and the long payback period. Therefore, to properly carry out ship investment evaluation under uncertain environmental conditions, these factors must be considered by estimating them adequately. However, the uncertainties in shipping affect the evaluation required to make a decision. For instance, the Baltic Dry Index has changed by around 200% since last year (Trading Economics 2021). The dry bulk shipping industry is a highly volatile circular industry and the size and return of investment capital, and freight revenues vary dramatically (Greenwood and Hanson 2015). The demand for service in the shipping industry is volatile and is directed by seaborne trading which, in turn, is connected to the level of global economic activity; nevertheless, there is only a weak correlation between growth in global seaborne trade and global economic growth (Stopford 2009). This is because the trading of bulk commodities, mainly grains, coal, and iron ore, is affected by evolving geographic trade models (the location of commodity users compared to commodity suppliers) and geopolitical events (e.g., the 1967–1975 Suez Canal closure, the 1979 Iranian revolution, the 1990 Gulf War, the 2003 Iraq War, the 2008 economic crisis, and, most recently, the 2019 Covid-19 pandemic). Demand of service in shipping is generally thought to be relatively inelastic because there are few cost-effective alternatives for the international transportation of most bulk goods (Stopford 2009; Greenwood and Hanson 2015). When consideration the shipping industry ecosystem, affects the financial cash flow of the ship directly or indirectly due to the uncertainty it contains.
Merchant ships have a limited lifespan and Stopford (2009) determined the economic life of these ships to be 25 years according to the results of studies. Estimating the future cash flow in ship investment, which requires high capital investment, is very difficult due to the dynamics of the sector. A shipowner as an investor aims to estimate the cash flow values as accurately as possible while making the investment decision. In such environments where uncertainty is high, fuzzy sets provide a wider solution than traditional methods. Therefore, fuzzy sets have been used to provide feasible solutions for evaluating investment decision-making problems that take into consideration the uncertainty of the environment. Furthermore, IT2FSs gives a more specific solution cluster, and decision-makers are not forced to define a single membership function and have greater flexibility to define the membership functions of investment parameters.
Due to the inherent uncertainty of the shipping industry, decision-making processes are more difficult and more crucial than in other industries and decision-makers as investors have always faced the difficulties of uncertainty when making an investment decision. Traditional methods are insufficient for investment evaluation under the uncertainty of the maritime industry (Celik Girgin et al. 2018; Akan and Bayar 2021). Even though there are the investment methods, such as classic, type-1 fuzzy, intuitionistic fuzzy, hesitant fuzzy, and IT2FSs (Ucal Sari and Kahraman 2015), in terms of financial analysis for investment, we have proposed the IT2FSs depreciation methods to literature from the investment perspective. IT2FSs, having three-dimensional membership functions unlike the two-dimensional membership functions of type-1 fuzzy sets, give a more specific solution to decision-makers for making an investment decision evaluation. Thanks to IT2FS having membership functions, all the independent variables of ship price and price of scrap metal for depreciation in terms of ship investment decision-making can be defined as IT2FSs. As a result, the uncertainty of investment in the shipping industry can be managed. Traditional depreciation analysis can be ineffective under such future uncertainty; however, IT2FS methods support decision-makers in making better investment analyses. The results of our study show that the methods give successful results by smoothly computing in an IT2FSs environment.
There are many different depreciation methods in the literature; however, Stopford (2009) mentioned the straight-line depreciation method as one of the most used in calculating depreciation in the shipping industry. In this study, straight-line depreciation and double-declining balance depreciation methods have been proposed in terms of IT2FSs. The proposed IT2FS depreciation and classic depreciation methods were used to calculate a new ship’s depreciation for 25 years. The principal variables for calculating a ship’s depreciation are the ship price, salvage value, and useful life. However, when calculating the depreciation of a ship, the salvage value varies depending on light ship displacement (LDT) and the price of scrap metal. In this study, ship price and salvage value variables were defined as IT2FSs. However, in defining the salvage value, only the price of scrap metal was defined as IT2FSs because a ship’s depreciation calculation, light ship displacement (LTD), and useful life values were fixed and undefined as IT2FSs, as such, these values were defined as determinists.
Uncertainty is related to the future in this study. Therefore, in terms of a ship’s investment evaluation, depreciation will be important in determining the investment strategy of the organization, in its approach to the tax shield, and even in determining the second-hand ship sales strategy. Furthermore, in shipping investment, there are several methods of financing models, such as cash, leasing, KG (Kommanditgesellschaft) system equity, KS (Kommandittselskap) private equity, private equity, public equity, corporate bonds, the ship found, mortgage-backed loans, bank loans, bank financing, unsecured/corporate loans, new building financing, mezzanine, special purpose acquisition companies, high pay-out structures, and master limited partnerships (Stopford 2009; Schinas et al. 2015; Kavussanos and Visvikis 2016). Depreciation must be taken into account when choosing the possible investment model which also depends on the financing model that the organization will choose, the type of ship preferred, and the capacity of the ship. The reason for this is that, in terms of considering the tax shield, an organization that invests using outsourcing may prefer a strategy to show high depreciation, especially in the first years of the investment. Hence, the double-declining balance depreciation method can be preferred. In addition, there may be expectations that arise in subsequent years depending on the cash flow. The organization may prefer the strategy of paying less tax by showing a high-depreciation expense in the first years of the investment. This can protect from possible financial cash flow uncertainty in the first years of the business. When viewed from another aspect, it will be important for public shipping companies, especially those with new investments, to show high profitability. This situation can be evaluated from two aspects: (1) A company that will be newly a public offering may prefer a depreciation model obtaining a higher profitability in the period before it becomes a public offering. Hence, it will highlight the profitability of the company before becoming a public shipping company. (2) The public shipping company may have the choice of strategy to show higher profits in the first years of the new investment. In this case, the value of the company’s stock prices will ensure that the investment is high in the first years. Both situations will change depending on the purpose and strategy of the company. On the other hand, a method of determining the value of a second-hand ship is to determine its second-hand price by deducting the value of a new ship by as much as the depreciation amount for the relevant age of the ship (Beenstock 1985). Along with this relationship, calculating the depreciation value with a more accurate approach, that considers the uncertainties, will help decision-makers. However, there will be differences in depreciation amounts depending on alternative ship types and sizes before the investment because the second-hand price evaluation of the ship type with high-value depreciation will also differ. Depreciation can be a factor in the second-hand values because of the presence of these differences. Therefore, it will also be a criterion when this situation is evaluated by decision-makers.
In all cases, when calculating depreciation, especially in terms of investment along with the natural uncertainties in the shipping industry, the proposed method will increase accuracy when compared to traditional deterministic approaches. This will contribute by allowing decision-makers to make more predictable decisions for the organization because deterministic models are insufficient in the face of uncertainty. For instance, when we look into the future to calculate the scrap value of a ship, one of the best approaches to determine the future value of the depreciation components, which are the Price of Scrap Metal and Value of Assets, will be with fuzzy logic and considering depreciation from an investment perspective is a factor that affects the ship's cash flow.
This study, along with the recommendation of straight-line depreciation and accelerated depreciation methods in IT2FSs methods, will contribute especially to the points where traditional methods are insufficient. Before investment decisions, when determining investment strategies, choosing the depreciation calculation type, and determining the tax strategy, the IT2FSs depreciation methods will provide more accurate input knowledge to the decision-makers.
In this study, interval type-2 triangular and trapezoidal straight-line depreciation and accelerated depreciation methods have been proposed in the literature, and a ship’s depreciation calculations have been carried out and compared to traditional depreciation methods. The results presented demonstrated that IT2FSs can be successfully applied in every aspect. Therefore, with this study, the main contributions to literature are that the IT2FSs depreciation methods have been proposed and applied to a model in the shipping industry with respect to investment evaluation for the first time. In future research, this novel depreciation approach model could be applied to other capital-intensive industries. The other fuzzy set systems integrated into depreciation methods can also be proposed for future studies as they can be applied to any capital-intensive industry. Consequently, a broader perspective can be used to investigate asset investments that require significant capital in uncertain environments.
Data availability
Not applicable.
References
Abdel-Khalik AR (1975) Advertising effectiveness and accounting policy. Account Rev 50(4):657–670
Abdullah L, Zulkifli N (2015) Integration of fuzzy AHP and interval type-2 fuzzy DEMATEL: an application to human resource management. Expert Syst Appl 42(9):4397–4409. https://doi.org/10.1016/j.eswa.2015.01.021
Akan E, Bayar S (2021) An evaluation of ship investment in interval type-2 fuzzy environment. J Oper Res Soc. https://doi.org/10.1080/01605682.2021.1944826
Albonico A, Kalyvitis S, Pappa E (2014) Capital maintenance and depreciation over the business cycle. J Econ Dyn Control 39:273–286. https://doi.org/10.1016/j.jedc.2013.12.008
Ayers BC, Lefanowicz CE, Robinson JR (2000) The effects of goodwill tax deductions on the market for corporate acquisitions. J Am Tax Assoc 22(s-1):34–50. https://doi.org/10.2308/jata.2000.22.s-1.34
Bakir M, Akan Ş, Kiraci K, Karabasevic D, Stanujkic D, Gabrijela P (2020) Multiple-criteria approach of the operational performance evaluation in the airline industry: evidence from the emerging markets. Roman J Econ Forecast XXIII(2):149–172
Baumol WJ (1971) Optimal depreciation policy: pricing the products of durable assets. Bell J Econ Manag Sci 2(2):638–656
Beenstock M (1985) A theory of ship prices. Marit Policy Manag 12(3):215–225
Bellman RE, Zadeh LA (1970) Decision-making in a fuzzy environment. Manage Sci 17(4):141–164
Berg M, Moore G (1989) The choice of depreciation method under uncertainty. Decis Sci 20(4):643–654. https://doi.org/10.1111/j.1540-5915.1989.tb01409.x
Berg M, Waegenaere AD, Wielhouwer JL (2001) Theory and methodology: optimal tax depreciation with uncertain future cash-flows. Eur J Oper Res 132(1):197–209. https://doi.org/10.1016/S0377-2217(00)00132-6
Bokhari S, Geltner D (2018) Characteristics of depreciation in commercial and multifamily property: an investment perspective. Real Estate Econ 46(4):745–782. https://doi.org/10.1111/1540-6229.12156
Buckley JJ (1985) Fuzzy hierarchical analysis. Fuzzy Set Syst 17:233–247
Caballero J (2021) Corporate dollar debt and depreciations: All’s well that ends well? J Bank Finance 130:106185. https://doi.org/10.1016/J.JBANKFIN.2021.106185
Çankaya F, Yilmaz Z (2014) Üretim Miktarına Göre Amortisman Yönteminin Değişken Maliyetler ve Kârlılık Üzerine Etkileri. Bil Derg 8:221–242
Celik Girgin S, Karlis T, Nguyen HO (2018) A critical review of the literature on firm-level theories on ship investment. Int J Financ Stud 6(1):11
Chinloy P, Jiang C, John K (2020) Investment, depreciation and obsolescence of R&D. J Financ Stab 49:100757. https://doi.org/10.1016/J.JFS.2020.100757
Davidson S, Drake DF (1961) Capital budgeting and the “best” tax depreciation method. J Bus 34(4):442–452
de Rassenfosse G, Jaffe AB (2018) Econometric evidence on the depreciation of innovations. Eur Econ Rev 101:625–642. https://doi.org/10.1016/j.euroecorev.2017.11.005
De Waegenaere A, Wielhouwer JL (2002) Optimal tax depreciation lives and charges under regulatory constraints. Or Spectrum 24(2):151–177. https://doi.org/10.1007/s00291-002-0096-0
Duvall, L., Jennings, R., Robinson, J., and Thompson, R. (1992). Can Investors Unravel the Effects of Goodwill Accounting? Accounting Horizons, 6–2.
Trading Economics. (2021). Baltic exchange dry index. https://tradingeconomics.com/commodity/baltic Access: 02 May 2021.
Engin D, Atabay E (2018) Depreciation procedures by accountings systems in turkey and evaluation regarding tax effect. J Account Finance Audit Stud 4(2):67–91
Falk H, Miller JC (1977) Amortization of advertising expenditures. J Account Res 15(1):12–22
Femminis G (2008) Risk-aversion and the investment-uncertainty relationship: the role of capital depreciation. J Econ Behav Organ 65(3–4):585–591. https://doi.org/10.1016/j.jebo.2006.03.003
Gabriel ADP (1937) Valuation and amortization. Account Rev 12(3):209–226
Glaum M, Landsman WR, Wyrwa S (2015) Determinants of goodwill impairment: international evidence. SSRN Electron J. https://doi.org/10.2139/ssrn.2608425
Greenwood R, Hanson SG (2015) Waves in ship prices and investment. Q J Econ 130(1):55–109
Hall SC (1993) Determinants of goodwill amortization period. J Bus Financ Acc 20(4):613–621. https://doi.org/10.1111/j.1468-5957.1993.tb00279.x
Henning SL, Shaw WH (2003) Is the selection of the amortization period for goodwill a strategic choice? Rev Quant Financ Acc 20(4):315–333. https://doi.org/10.1023/A:1024043316292
Hirschey M, Weygandt JJ (1985) Amortization policy for advertising and research and development expenditures. J Account Res 23(1):326–335
Hsieh TY, Lu ST, Tzeng GH (2004) Fuzzy MCDM approach for planning and design tender’s selection in public office buildings. Int J Project Manage 22(7):573–584
Huefner RJ, Largay JA (2004) The effect of the new goodwill accounting rules on financial statements. CPA J 74(10):30–35
Hull I (2017) Amortization requirements and household indebtedness: an application to Swedish-style mortgages. Eur Econ Rev 91:72–88. https://doi.org/10.1016/J.EUROECOREV.2016.09.011
International Accounting Standards (IAS) (2021) IAS 16 — property, plant and equipment. https://www.iasplus.com/en-gb/standards/ias/ias16
Jackson SB (2008) The effect of firms’ depreciation method choice on managers’ capital investment decisions. Account Rev 83(2):351–376. https://doi.org/10.2308/accr.2008.83.2.351
Jackson SB, Liu X, Cecchini M (2009) Economic consequences of firms’ depreciation method choice: evidence from capital investments. J Account Econ 48(1):54–68. https://doi.org/10.1016/j.jacceco.2009.06.001
Jackson SB, Rodgers TC, Tuttle B (2010) The effect of depreciation method choice on asset selling prices. Acc Organ Soc 35(8):757–774. https://doi.org/10.1016/j.aos.2010.09.004
Jana DK, Pramanik S, Sahoo P, Mukherjee A (2019) Interval type-2 fuzzy logic and its application to occupational safety risk performance in industries. Soft Comput 23(2):557–567. https://doi.org/10.1007/S00500-017-2860-8/FIGURES/9
Jennergren LP (2018) A note on the linear and annuity class of depreciation methods. Int J Prod Econ 204(April):123–134. https://doi.org/10.1016/j.ijpe.2018.05.004
Jennings R, LeClere M, Thompson RB (2001) Goodwill amortization and the usefulness of earnings. Financ Anal J 57(5):20–28. https://doi.org/10.2469/faj.v57.n5.2478
Karmakar S, Seikh MR, Castillo O (2021) Type-2 intuitionistic fuzzy matrix games based on a new distance measure: application to biogas-plant implementation problem. Appl Soft Comput 106:107357. https://doi.org/10.1016/j.asoc.2021.107357
Kavussanos MG, Visvikis ID (2016) Shipping markets and their economic drivers. Int Handb Shipp Finance Theory Pract Springer. https://doi.org/10.1057/978-1-137-46546-7_1
Khalili S, Mehrjerdi YZ, Zare HK (2014) Choosing the best method of depreciating assets and after-tax economic analysis under uncertainty using fuzzy approach. Decis Sci Lett 3(4):457–466. https://doi.org/10.5267/j.dsl.2014.8.001
Kiracı K, Akan E (2020) Aircraft selection by applying AHP and TOPSIS in interval type-2 fuzzy sets. J Air Transp Manag 89:101924. https://doi.org/10.1016/J.JAIRTRAMAN.2020.101924
Kulp A, Hartman JC (2011) Optimal tax depreciation with loss carry-forward and backward options. Eur J Oper Res 208(2):161–169. https://doi.org/10.1016/j.ejor.2010.06.040
Lev B, Sougiannis T (1996) The capitalization, amortization, and value-relevance of R&D. J Account Econ 21(1):107–138. https://doi.org/10.1016/0165-4101(95)00410-6
Liu P, Gao H, Ma J (2019) Novel green supplier selection method by combining quality function deployment with partitioned Bonferroni mean operator in interval type-2 fuzzy environment. Inf Sci 490:292–316. https://doi.org/10.1016/J.INS.2019.03.079
Mardones C, del Rio R (2019) Correction of Chilean GDP for natural capital depreciation and environmental degradation caused by copper mining. Resour Policy 60:143–152. https://doi.org/10.1016/J.RESOURPOL.2018.12.010
Mendel JM, John RI, Liu F (2006) Interval type-2 fuzzy logic systems made simple. IEEE Trans Fuzzy Syst 14(6):808–821
Mittal K, Jain A, Vaisla KS, Castillo O, Kacprzyk J (2020) A comprehensive review on type 2 fuzzy logic applications: past, present and future. Eng Appl Artif Intell 95(August):103916. https://doi.org/10.1016/j.engappai.2020.103916
Moreno JE, Sanchez MA, Mendoza O, Rodríguez-Díaz A, Castillo O, Melin P, Castro JR (2020) Design of an interval Type-2 fuzzy model with justifiable uncertainty. Inf Sci 513:206–221. https://doi.org/10.1016/J.INS.2019.10.042
Mousavi SM, Foroozesh N, Zavadskas EK, Antucheviciene J (2020) A new soft computing approach for green supplier selection problem with interval type-2 trapezoidal fuzzy statistical group decision and avoidance of information loss. Soft Comput 24(16):12313–12327. https://doi.org/10.1007/S00500-020-04675-4/TABLES/7
Ohrn E (2019) The effect of tax incentives on U.S. manufacturing: evidence from state accelerated depreciation policies. J Public Econ 180:104084. https://doi.org/10.1016/j.jpubeco.2019.104084
Olivas F, Valdez F, Melin P, Sombra A, Castillo O (2019) Interval type-2 fuzzy logic for dynamic parameter adaptation in a modified gravitational search algorithm. Inf Sci 476:159–175. https://doi.org/10.1016/j.ins.2018.10.025
Ontiveros-Robles E, Melin P (2020) Toward a development of general type-2 fuzzy classifiers applied in diagnosis problems through embedded type-1 fuzzy classifiers. Soft Comput 24(1):83–99. https://doi.org/10.1007/S00500-019-04157-2/TABLES/9
Ontiveros-Robles E, Castillo O, Melin P (2021a) Towards asymmetric uncertainty modeling in designing general type-2 fuzzy classifiers for medical diagnosis. Expert Syst Appl 183:115370. https://doi.org/10.1016/J.ESWA.2021.115370
Ontiveros-Robles E, Melin P, Castillo O (2021b) An efficient high-order α-plane aggregation in general type-2 fuzzy systems using newton-cotes rules. Int J Fuzzy Syst 23(4):1102–1121. https://doi.org/10.1007/S40815-020-01031-4/FIGURES/23
Opricovic S, Tzeng GH (2003) Defuzzification within a fuzzy multicriteria decision model. Int J Uncertain Fuzziness Knowledge-Based Syst 11:635–652
Park J (2016) The impact of depreciation savings on investment: evidence from the corporate alternative minimum tax. J Public Econ 135:87–104. https://doi.org/10.1016/j.jpubeco.2016.02.001
Peles Y (1971) Rates of amortization of advertising expenditures. J Political Econ 79(5):1032–1058
Press C, Davidson S (1964) The " best " tax depreciation method-1964. J Bus 37(3):258–260
Samaniego RM, Sun JY (2019) Uncertainty, depreciation and industry growth. Eur Econ Rev 120:103314. https://doi.org/10.1016/j.euroecorev.2019.103314
Schinas, O., Grau, C., and Johns, M. (2015). HSBA handbook on ship finance. In HSBA Handbook on Ship Finance. https://doi.org/10.1007/978-3-662-43410-9
Smith VL (1963) Tax depreciation policy and investment theory. Int Econ Rev 4(1):80–91
Soner O, Celik E, Akyuz E (2017) Application of AHP and VIKOR methods under interval type 2 fuzzy environment in maritime transportation. Ocean Eng 129:107–116. https://doi.org/10.1016/J.OCEANENG.2016.11.010
Stickney CP (1981) A note on optimal tax depreciation research. Account Rev 56(3):622–625
Stopford M (2009) Maritime economics. Routledge, New York
Tolga AC, Parlak IB, Castillo O (2020) Finite-interval-valued Type-2 Gaussian fuzzy numbers applied to fuzzy TODIM in a healthcare problem. Eng Appl Artif Intell 87:103352. https://doi.org/10.1016/j.engappai.2019.103352
Uçal Sari, I., Öztayşi, B., and Kahraman, C. (2013). Fuzzy analytic hierarchy process using type-2 fuzzy sets: an application to warehouse location selection. In: Doumpos M, rigoroudis E (eds), Multicriteria decision aid and artificial intelligence, pp 285–308. https://doi.org/10.1002/9781118522516.ch12
Ucal Sari I, Kahraman C (2015) Interval type-2 fuzzy capital budgeting. Int J Fuzzy Syst 17(4):635–646. https://doi.org/10.1007/s40815-015-0040-5
Vogt M, Pletsch CS, Morás VR, Klann RC (2016) Determinants of goodwill impairment loss recognition. Revista Contabilidade e Financas 27(72):349–362. https://doi.org/10.1590/1808-057x201602010
Wagenhofer A (2003) Accrual-based compensation, depreciation and investment decisions. Eur Account Rev 12(2):287–309. https://doi.org/10.1080/0963818031000087835
Wakeman LMD (1980) Optimal tax depreciation. J Account Econ 2(3):213–237. https://doi.org/10.1016/0165-4101(80)90003-8
Xu Z, Qin J, Liu J, Martínez L (2019) Sustainable supplier selection based on AHPSort II in interval type-2 fuzzy environment. Inf Sci 483:273–293. https://doi.org/10.1016/J.INS.2019.01.013
Yussof SH, Isa K, Mohdali R (2014) An analysis of the gap between accounting depreciation and tax capital allowance in Malaysia. Procedia Soc Behav Sci 164(August):351–357. https://doi.org/10.1016/j.sbspro.2014.11.087
Zadeh LA (1965) Fuzzy sets. Inf Control 8:338–353
Zadeh LA (1975) The concept of a linguistic variable and its application to approximate reasoning–i. Inf Control 8(3):199–249
Zeng J, Min A, Smith NJ (2007) Application of fuzzy based decision-making methodology to construction project risk assessment. Int J Proj Manage 25:589–600. https://doi.org/10.1016/j.ijproman.2007.02.006
Funding
No funds provided.
Author information
Authors and Affiliations
Contributions
Both authors contributed to introduction, literature, conceptualization, methodology, writing and conclusion.
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Ethical approval
This material is the authors’ own original work, which has not been previously published elsewhere. The paper is not currently being considered for publication elsewhere. The paper reflects the authors’ own research and analysis in a truthful and complete manner.
Informed consent
Not applicable.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Communicated by Hemen Dutta
Rights and permissions
About this article
Cite this article
Akan, E., Kiraci, K. A novel depreciation approach in an uncertain environment: interval type-2 fuzzy sets in the maritime industry. Soft Comput 27, 1941–1969 (2023). https://doi.org/10.1007/s00500-022-06778-6
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00500-022-06778-6