1 Introduction

Over the last century, groundwater systems have faced increasingly severe environmental pressures as a consequence of massive industrial and agricultural development. To release these pressures, collaborative efforts are necessary, involving coordination with authorities and end-users to formulate decisions that prevent the depletion and contamination of aquifers. This poses a challenge that necessitates a comprehensive understanding of the subsurface environment and groundwater systems whose complex spatial distribution can be difficult to characterize (Gómez-Hernández and Wen 1994; Gómez-Hernández et al. 2003). Conventional survey methods, such as water sampling from monitoring wells, may not adequately capture a contaminant plume's structure and spread since they provide little localized information; furthermore, they are invasive, relatively expensive, and time-consuming. As a result, complementary techniques have been developed to overcome these survey-related challenges. Hydrogeophysics has emerged as a powerful, non-invasive and cost-effective tool in the field of contaminant hydrogeology, leveraging geophysical data to gain insights into hydrological processes and the underlying geology that govern the subsurface (Rubin and Hubbard 2005; Vereecken et al. 2006; Hubbard 2011). These methods, such as electrical resistivity tomography (ERT), ground-penetrating radar (GPR), and seismic surveys, enable subsurface imaging and detection of anomalies. Given that polluted groundwater exhibits increased electrical conductivity (Frohlich and Urish 2002; Carpenter et al. 2012), approaches that measure ground electrical conductivity or its reciprocal, electrical resistivity, become particularly interesting when combined with hydrological data. For this reason, ERT is widely used in hydrological studies (e.g., Page 1969; Wilson et al. 2006; Pereira et al. 2023).

Recovering aquifer characteristics and groundwater contaminant information from geophysical data, alongside sparse hydrological data, requires solving a complex geophysical inverse problem. Several deterministic and stochastic methods have been proposed to address these challenges. A comprehensive review of hydrogeology inverse methodologies is available in the works of McLaughlin and Townley (1996), Zimmerman et al. (1998), Carrera et al. (2005), Hendricks Franssen et al. (2009), Zhou et al. (2014) and Gómez-Hernández and Xu (2022). Stochastic inverse methods, such as the geostatistical approach (Kitanidis 1995), offer an effective way of characterizing spatial variability and inferring properties of interest at unsampled locations associated with their uncertainty (Michalak and Kitanidis 2004; El Idrysy and De Smedt 2007; Huysmans and Dassargues 2009; Zhou et al. 2012; Butera et al. 2013; Cupola et al. 2015; Zanini and Woodbury 2016; Visentini et al. 2020). Among the stochastic inversion techniques, the ensemble Kalman filter (Evensen 1994) and the ensemble smoother (Leeuwen and Evensen 1996), have seen a rise in popularity in hydrogeology due to their adaptability and effectiveness (Chen and Zhang 2006; Li et al. 2012, 2019; Crestani et al. 2013, 2015; Xu and Gómez-Hernández 2016, 2018; Chen et al. 2018). In particular, Emerick and Reynolds (2012, 2013) introduced the ensemble smoother with multiple data assimilation (ES-MDA), which involves the iterative assimilation of the same data multiple times, enhancing the applicability and efficacy of the ensemble smoother (Todaro et al. 2019, 2021, 2023; D’Oria et. al, 2022; Xu et al. 2021; Godoy et al. 2022; Chen et al. 2023a, b).

Several works have shown how hydrogeophysics inverse modeling can be used in conjunction with ERT measurements to estimate hydraulic properties such as hydraulic conductivity (Irving et al., 2010; Pollock and Cirpka 2010, 2012), including the use of Kalman-based techniques (Camporese et al. 2011, Crestani et al. 2015; Kang et al. 2019; 2015). However, few studies have focused on utilizing ERT measurements to predict groundwater contamination. Kang et al. (2018) employed the ensemble Kalman filter to simultaneously estimate the distribution of dense non-aqueous phase liquid (DNAPL) saturation and aquifer heterogeneous parameter field using time-lapse ERT data. Tso et al. (2020) employed ES-MDA to detect contaminant leaks utilizing time-lapse ERT measurements. Chen et al. (2023a, b) utilized the ES-MDA to jointly identify contaminant source information and the hydraulic conductivity field by assimilating ERT data in a synthetic heterogeneous aquifer with a time-varying release history. The results underscored the capability of the ES-MDA data assimilation framework to provide a robust inversion of both time-varying release history and hydraulic conductivity estimation.

The aforementioned research findings demonstrated hydrogeophysics' ability to identify pollutant sources and aquifer characteristics. However, one major challenge in inverse modeling is the complexity of the underlying forward models, which are often computationally expensive or analytically unsolvable. Surrogate models present a viable solution to overcome these issues (e.g., Asher et al. 2015; Jamshidi et al. 2020; Secci et al. 2022, 2024). In recent years, neural networks have emerged as a promising tool for replacing full forward models and reducing computational demand. A well-known neural network is the convolutional neural network (CNN) introduced by LeCun et al. (1998). CNNs specialize in processing grid-based data, such as images, exhibiting an inherent capacity to capture and hierarchically represent spatial features in data. For this reason, CNN is a technology widely employed in various fields, including groundwater spatial modeling (e.g., Hong and Liu 2020; Panahi et al. 2020; Lähivaara et al. 2019).

In the literature, only a few studies have explored the potential of coupling CNN with ES-MDA. Tang et al. (2021) combined convolutional post-processing of principal component analysis parameterization and ES-MDA to estimate both a channelized permeability and oil/water rate in petroleum engineering. Zhou et al. (2022) integrated convolutional adversarial autoencoder and ES-MDA to parameterize a non-Gaussian conductivity field and to identify the spatiotemporal extended source of contamination. In this work, the ES-MDA and CNN are coupled to unlock the potential of hydrogeophysics in addressing environmental pollution problems while lowering the computational cost of the inversion procedure. The primary objective is to combine hydrological and ERT data to accurately estimate the spatial distribution of a contaminant within a groundwater system.

The ES-MDA inverse procedure is applied to estimate the plume distribution by employing a well-established geophysical forward model and assimilating both ERT data and sparse concentration values from monitoring points. To enhance efficiency, a CNN is used to replace the part of the forward model that transforms the electrical resistivity of the investigated material into the apparent electrical resistivity that would be deduced from an ERT survey. The proposed methodology is tested by means of a two-dimensional synthetic case study that mimics a tracer test in an unconfined aquifer. Different scenarios are investigated exploring the effect of combining multiple data sources and their abundance.

The structure of this paper is outlined as follows. Section 2 provides a comprehensive overview of the material and methods employed in the proposed inverse approach. Section 3 details the test case set up, the configuration of the CNN end the ES-MDA, as well as the investigated scenarios. Section 4 delves into the presentation and analysis of results. Finally, Sect. 5 presents discussions and conclusions.

2 Material and methods

2.1 Forward model

The forward model has two components. The first is a petrophysical model used to spatially predict the resistivity field associated with a given contaminant plume. The second is a geophysical model utilized to calculate the apparent resistivity (i.e., pseudo-electrical resistivity) that would be observed during an Electrical Resistivity Tomography (ERT) survey associated with a given subsurface electrical resistivity field. In this work, the geophysical model is replaced by a convolutional neural network. The following sections describe the entire forward model in detail.

2.1.1 Petrophysical relationship

Petrophysical models are needed to link geophysical imaging techniques and hydrological models (Vereecken et al. 2006). In this case, the model proposed by Pollock and Cirpka (2012) is used to transform concentration into electrical conductivity (EC) using

$$ {\upsigma }\left( {{\text{t}},{\mathbf{x}}} \right) = {\upsigma }_{0} \left( {\mathbf{x}} \right) + {\upsigma }{\prime} \left( {{\text{t}},{\mathbf{x}}} \right) $$
(1)

where σ(t, x) is the bulk electrical conductivity at specific time t and location x, σ0(x) is the background bulk electrical conductivity (constant through time), and σ’(t, x) is a perturbation resulting from a change in solute concentration c(t, x). σ’(t,x) can be derived from Archie’s law (Archie 1942)

$$ \sigma^{\prime}\left( {{\text{t}},{\mathbf{x}}} \right) = \frac{{\varphi^{{\text{m}}} }}{{\text{a}}}{\text{S}}^{{\text{n}}} \sigma_{{\text{w}}} \;{\text{c}}\left( {{\text{t}},{\mathbf{x}}} \right) $$
(2)

with φ being the porosity, S being the water saturation, σw being the water EC, m and n being two empirical parameters referred to as cementation and saturation exponent, respectively. a is a proportionality constant of the order of 1.

Electrical resistivity (ρ) is the reciprocal of EC

$$\uprho =\frac{1}{\sigma }$$
(3)

2.1.2 Electrical resistivity tomography (ERT): governing equations

A common ERT survey considers four electrodes and consists of injecting electrical current into the ground through two current electrodes (C1 and C2) and measuring the resulting voltage difference at two potential electrodes (P1 and P2). Afterward, the current and voltage measurements are transformed into apparent electrical resistivity, which represents a weighted average resistance of earth materials to electrical current propagation (Loke et al. 2013).

Poisson’s equation can be used to describe the electric potential field generated by a couple of electrodes

$$ - \nabla \cdot {\upsigma }\left( {{\text{x}},{\text{y}},{\text{z}}} \right)\nabla \phi \left( {{\text{x}},{\text{y}},{\text{z}}} \right) = {\text{I}}\left( {{\updelta }\left( {{\text{r}} - {\text{r}}_{ + } } \right) - {\updelta }\left( {{\text{r}} - {\text{r}}_{ - } } \right)} \right) $$
(4)

In which ф represents the potential field; I is the input current; r+ and r– are the locations of the positive and negative electrodes, respectively, and δ(⋅) is the Dirac delta function. Following Pidliskey and Knight (2008), the solution to Eq. 4 yields a vector of electric potential values for each grid location within the considered model. Then, for a given electrode array, the apparent electrical resistivity at a location in the xz plane that is specific to such configuration is computed as

$$ {\uprho }_{{{\text{app}}}} = {\Delta }\hat{\phi } \cdot {\text{K}} $$
(5)

where \(\Delta \widehat{\upphi }\) is the difference of potential recorded between the electrodes P1 and P2, and K is a geometric factor, which is a function of the distance among the four electrodes calculated as follows when the effects of the topography are ignored

$$\text{K}=\frac{2\uppi }{\frac{1}{{\text{d}}_{1}}-\frac{1}{{\text{d}}_{2}}-\frac{1}{{\text{d}}_{3}}+\frac{1}{{\text{d}}_{4}}}$$
(6)

where \({\text{d}}_{1}\) is the distance between the current electrode C1 and the potential electrode P1, \({\text{d}}_{2}\) is the distance between the current electrode C1 and the potential electrode P2, \({\text{d}}_{3}\) is the distance between the current electrode C2 and the potential electrode P1, \({\text{d}}_{4}\) is the distance between the current electrode C2 and the potential electrode P2.

The apparent electrical resistivity values are then visualized in a 2D "pseudo-section" plot, providing a comprehensive view of both horizontal and vertical changes. The horizontal position of each data point corresponds to the midpoint of the electrode set used for measurement, while its vertical position represents a proportionate distance based on electrode separation. For further insight into the specific array configuration, readers are directed to Edwards (1977).

According to Pidliskey and Knight (2008) and assuming no variation along the y-axis (\(\frac{\partial }{\partial \text{y}}\upsigma \left(\text{x},\text{y},\text{z}\right)=0\)), a 2.5D forward ERT model, is used to calculate the apparent electrical resistivity from an electrical resistivity model. The forward geophysical problem is solved using SimPEG (Cockett et al. 2015), an open-source geophysical library.

2.1.3 Surrogate model: convolutional neural network (CNN)

Convolutional Neural Networks (CNNs), first developed by LeCun et al. (1998), represent a class of machine learning models designed for processing and analyzing visual data, making them particularly effective for tasks involving images or spatially structured data. At their core, CNNs leverage convolutional filters: small learnable matrices that slide over the input image, capturing spatial hierarchies and local patterns. This allows CNNs to efficiently recognize complex patterns and spatial relationships within the data. Several review papers have been presented in the last few years, offering comprehensive overviews of the CNN advancements and applications (see e.g., Gu et al. 2018; Khan et al 2020; Alzubaidi et al. 2021). Within the geophysical inversion context, CCNs have been utilized in studies such as Das et al. (2019a, b) and Puzyrev (2019). A CNN comprises an input layer, several hidden layers, and an output layer. The input layer receives the raw input data in the form of images or other grid-like data. Typically, CNN hidden layers consist of convolutional layers, activation functions, pooling layers, and possibly batch normalization. Convolutional layers apply filters to capture local features. The use of activation functions, such as rectified linear units (ReLU), introduces non-linearity to the model, enhancing its ability to capture intricate patterns. Pooling layers with specified pool sizes and strides downsample the spatial dimensions, reducing computational complexity. Batch normalization may be included to normalize the input activations, enhancing training stability. The CNN architecture typically concludes with a fully connected (dense) layer, which takes the features learned by the convolutional layers and combines them to make predictions. Dropout layers can also be included to mitigate overfitting by randomly deactivating a fraction of neurons during training. Ultimately, the output layer produces the final prediction. The training process involves iteratively adjusting the weights of the network using optimization algorithms, such as Adam optimizer (Zhang 2018), to minimize the difference between predicted and target values.

In this study, a CNN is employed to replace the electrical resistivity forward model described in the previous section. The input layer comprises a resistivity map, and the output layer yields apparent resistivity data. The details of the CNN’s architecture employed for this particular application are outlined in the Sect. 3.3.

2.2 ES-MDA inversion approach

The method applied to solve the hydrogeophysical inverse problem is the ensemble smoother with multiple data assimilation (ES-MDA). The ES-MDA is an iterative data assimilation approach that allows the estimation of model parameters using a set of observed measurements and a known relationship between parameters and observations, given by a forward model. A brief description of the method is provided next. For a more detailed description, the reader is referred to Emerick and Reynolds (2013).

The method workflow consists of an initialization phase and an iterative phase; in which each iteration is made up of two steps: a forecast step and an update step. The initialization phase involves the generation of an initial ensemble of parameter realizations  ∈ ℜ Np×Ne, where Np is the number of parameters to be estimated and Ne is the ensemble size, together with an ensemble of observation errors ε ∈ ℜ m×Ne, where m is the number of observations. Moreover, the procedure requires the definition of a priori number of iterations N and a vector of inflation coefficients {αi, i = 1,…,N}. Several schemes can be used to define the set of α, but they must satisfy the condition

$$ \mathop \sum \limits_{{{\text{i}} = 1}}^{{\text{N}}} \frac{1}{{{\upalpha }_{{\text{i}}} }} = 1 $$
(7)

After the initialization step, iterations start. During the forecast step, at each iteration i, for each realization j of the ensemble of parameters Xj, i ∈ ℜ Np, the forward model is run to obtain the model predictions, of which a subset Yj, i ∈ ℜm is extracted coinciding with the same locations and times as the observations  ∈ ℜm

$${\mathbf{Y}}_{\text{j},\text{i}}=\text{g}\left({\mathbf{X}}_{\text{j},\text{i}}\right)$$
(8)

where g (⋅) is an operator that incorporates the forward model as well as a filtering function used to extract the predictions at the m locations where observations have been collected. Next, the ensemble of parameters is updated during the update step according to the equation

$$ {\mathbf{X}}_{{{\text{j}},\;{\text{i}} + 1}} = {\mathbf{X}}_{{{\text{j}},\;{\text{i}}}} + {\mathbf{Q}}_{{{\mathbf{XY}}}}^{{\text{i}}} \left( {{\mathbf{Q}}_{{{\mathbf{YY}}}}^{{\text{i}}} + {\upalpha }_{{\text{i}}} {\mathbf{R}}} \right)^{ - 1} \left( {{\mathbf{D}} + \sqrt {{\upalpha }_{{\text{i}}} } {{\varvec{\upvarepsilon}}}_{{\text{j}}} - {\mathbf{Y}}_{{{\text{j}},\;{\text{i}}}} } \right) $$
(9)

where \({\mathbf{Q}}_{\mathbf{X}\mathbf{Y}}^{\text{i}}\)∈ ℜ Np×m is the cross-covariance matrix between parameters and predictions, \({\mathbf{Q}}_{\mathbf{Y}\mathbf{Y}}^{\text{i}}\) ∈ ℜ m×m is the auto-covariance matrix of predictions and  ∈ ℜ m×m is the auto-covariance matrix of the measurement errors, which are assumed to be uncorrelated. εj ∈ ℜ m is the vector of measurement errors for realization j. \({\mathbf{Q}}_{\mathbf{X}\mathbf{Y}}^{\text{i}}\) and \({\mathbf{Q}}_{\mathbf{Y}\mathbf{Y}}^{\text{i}}\) are computed, from the ensemble of realizations, at each iteration i as

$${\mathbf{Q}}_{\mathbf{X}\mathbf{Y}}^{\text{i}}=\frac{1}{{\text{N}}_{\text{e}}-1}\sum_{\text{j}=1}^{{\text{N}}_{\text{e}}}\left({\mathbf{X}}_{\text{j},\text{i}}-{\overline{\mathbf{X}} }_{i}\right){\left({\mathbf{Y}}_{\text{j},\text{i}}-{\overline{\mathbf{Y}} }_{i}\right)}^{\text{T}}$$
(10)
$${\mathbf{Q}}_{\mathbf{Y}\mathbf{Y}}^{\text{i}}=\frac{1}{{\text{N}}_{\text{e}}-1}\sum_{\text{j}=1}^{{\text{N}}_{\text{e}}}\left({\mathbf{Y}}_{\text{j},\text{i}}-{\overline{\mathbf{Y}} }_{i}\right){\left({\mathbf{Y}}_{\text{j},\text{i}}-{\overline{\mathbf{Y}} }_{i}\right)}^{\text{T}}$$
(11)

where \({\overline{\mathbf{X}} }_{i}\) and \({\overline{\mathbf{Y}} }_{i}\) are the ensemble means, at iteration i, of and , respectively.

The iteration index then advances, and the algorithm returns to the forecast step until the final iteration.

To minimize the number of parameter realizations, since computation time depends on it, covariance and inflation techniques are employed. These methods help prevent issues stemming from small ensemble sizes. The covariance localization involves an element-wise multiplication of the original covariance matrices with selected tapering functions that diminish correlations between points as the distance increases, effectively eliminating spurious long-range spurious correlations beyond a specified threshold. Covariance inflation is additionally taken into account to address issues related to under sampling. At each iteration, it modifies the ensemble of updated parameters by adjusting the ensemble spread, preventing the spread from becoming too narrow with the consequence of collapse and divergence.

The software package genES-MDA developed by Todaro et al. (2022) is used to apply the ES-MDA procedure.

2.3 Coupled hydrogeophysical inverse model

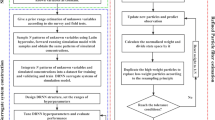
This section summarizes the scheme of the proposed coupled hydrogeophysical inversion, which seeks to estimate the spatial distribution of a tracer plume by integrating available observations (e.g. observed ERT data and concentration values at monitoring points). The methodology comprises several steps detailed below (Fig. 1).

Fig. 1
figure 1

Flowchart of the coupled hydrogeophysical inverse model

Full size image

Step 1. Initialization

The first step involves the generation of the initial parameter realizations. These realizations correspond to different concentration fields, aiming to incorporate available a priori information and adequately represent the specific problem under consideration. The initial concentration maps can be systematically generated through various approaches, ensuring a comprehensive exploration of the subsurface conditions, one can:

  1. (i)

    Assume homogeneity across all parameters. In this scenario, each realization exhibits a distinct constant value drawn from a uniform distribution. This method is straightforward and feasible in situations where no prior information is available.

  2. (ii)

    Run stochastic sequential simulations to generate fields using a semi-variogram model. The semi-variogram can be fitted to existing field data if available, or alternatively, variogram parameters can be selected randomly from a range defined based on prior knowledge. This approach considers the spatial correlations present in the reference dataset, ensuring that the initial ensemble captures the expected patterns of the actual concentration map.

  3. (iii)

    Utilize a numerical transport model to generate diverse realizations by simulating the injection from different locations within the model domain as well as various tracer concentrations, both randomly selected from predefined tailored ranges. This ensures that each realisation considers realistic representation of contaminant distribution in the subsurface.

This step also involves the definition of the number of iterations N, the observation errors, the coefficients αi and the training of the CNN.

Step 2. Forecast: CNN-based forward model.

For each iteration and for every realization, the petrophysical relationship, described in Sect. 2.1.1 is used to transform the concentration maps into electrical resistivity maps. Subsequently, these maps undergo forward modelling with the trained CNN, resulting in apparent electrical resistivity values. A filtering function is employed to extract the subset of prediction data at the observation locations.

Step 3. Update.

At each iteration, the prediction vector is used to update the concentration map following Eqs. 9–11. Upon completing the concentration update, the subsequent iteration starts with the updated ensemble of parameters. Step 2 and Step 3 are repeated until the last iteration.

Step 4. Analysis and interpretation of the results.

The results are analyzed in terms of mean and standard deviation computed from the ensemble, allowing to associate the parameter estimation with their uncertainty.

If a reference solution is available, as is common in synthetic case studies, a thorough comparison is made between the estimated and actual concentration values. The assessment of results employs well-established metrics, specifically, the mean error (ME), the mean absolute error (MAE), the root mean squared error (RMSE) and the determination coefficient (R2) as given by

$$\text{ME}=\frac{1}{{\text{N}}_{\text{p}}}\sum_{\text{k}=1}^{{\text{N}}_{\text{p}}}\left({\widehat{\text{C}}}_{\text{k}}-{\text{C}}_{\text{k}}\right)$$
(12)
$$\text{MAE}=\frac{1}{{\text{N}}_{\text{p}}}\sum_{\text{k}=1}^{{\text{N}}_{\text{p}}}\left|{\widehat{\text{C}}}_{\text{k}}-{\text{C}}_{\text{k}}\right|$$
(13)
$$\text{RMSE}=\sqrt{\frac{1}{{\text{N}}_{\text{p}}}\sum_{\text{k}=1}^{{\text{N}}_{\text{p}}}{\left({\widehat{\text{C}}}_{\text{k}}-{\text{C}}_{\text{k}}\right)}^{2}}$$
(14)
$${\text{R}}^{2}= 1-\frac{{\sum }_{\text{k}=1}^{{\text{N}}_{\text{p}}}{\left({\widehat{\text{C}}}_{\text{k}}-{\text{C}}_{\text{k}}\right)}^{2}}{{\sum }_{\text{i}=1}^{{\text{N}}_{\text{p}}}{\left({\text{C}}_{\text{k}}-\overline{{\text{C} }_{\text{k}}}\right)}^{2}}$$
(15)

where \({\text{N}}_{\text{p}}\) is the number of parameters (in this case is the number of grid nodes), \({\text{C}}_{\text{k}}\) is the actual concentration, \({\widehat{\text{C}}}_{\text{k}}\) is the estimated ensemble-mean concentration and \(\overline{{\text{C} }_{\text{k}}}\) is mean actual concentration.

3 Application

3.1 Set up of the test case

The validity of the proposed methodology is demonstrated by its application to a two-dimensional synthetic model representing the vertical cross section of a heterogeneous unconfined aquifer under fully saturated conditions, where a contaminant plume is present. This model resembles the sandbox developed at the University of Parma’s Hydraulic Laboratory, which has been extensively used in experimental and computational studies (Citarella et al. 2015; Cupola et al. 2015; Chen et al. 2018, 2021; Todaro et al. 2021, 2023; Pereira et al. 2023).

Figure 2 offers a schematic depiction of the synthetic model being discussed. It is discretized into 96 by 1 by 20 cells, each measuring 1 by 10 by 1 cm. The hydraulic conductivity varies in space with three well-defined homogeneous zones differing by two orders of magnitude (Fig. 2 and Table 1), and a uniform porosity equal to 0.37. The boundary conditions are impermeable at the bottom, phreatic surface at the top, and fixed heads at the left and right sides. This setup generates a head loss of 1 cm that induces flow from left to right. The initial condition is zero concentration everywhere. A continuous injection of a conservative non-reactive tracer, with a concentration of 20 mg/L, is introduced into the model from a designated injector point at location (X = 12.5 cm, Z = 10.5 cm). Longitudinal and transverse dispersivity values are assumed to be 0.16 cm and 0.016 cm, respectively. The reference solution is derived from a simulation conducted using MODFLOW (Harbaugh 2005) and MT3DMS (Zheng and Wang 1999) to model the groundwater flow and mass transport process, respectively. Table 1 summarizes the model parameters. The simulation extends for a total duration of 3600 s to achieve a well-developed plume, with the concentration map at the final time step serving as the reference map. The parameters to be estimated correspond to the concentration at each model grid cell (Np = 1920).

Fig. 2
figure 2

Hydraulic conductivity and concentration reference maps. The red grid cells represent the left and right boundary conditions. The cross indicates the injector position

Full size image
Table 1 Flow and transport model parameters
Full size table

The reference electrical resistivity map (Fig. 3) is obtained by applying the petrophysical model described in Sect. 2.1.2. Then, the SimPEG package processes the resulting map to derive the apparent resistivity at 225 locations, representing the observations to be used in the inverse procedure. This estimate is made using Eqs. 4–6 and taking into account a Wenner–Schlumberger acquisition array, which consists of 32 electrodes spaced at 3 cm intervals.

Fig. 3
figure 3

Reference resistivity model and observed pseudo-section. The cross indicates the position of the injector

Full size image

Table 2 summarizes the geophysical and petrophysical parameters used.

Table 2 Geophysical and petrophysical parameters
Full size table

3.2 Investigated scenarios

The idea of the work rises from the necessity to visualize the plume spread into aquifers. One possibility is the interpolation of observed concentrations in the field if they are available. Normally these data are few and spatially sparse. Therefore, the introduction of ERT measurements, which are spatially exhaustive, is considered. In order to assess the capabilities of the proposed approach, five distinct scenarios considering different datasets are developed. Each dataset aimed to emphasize the advantages of employing specific combinations of apparent resistivity measurements (m1) and concentration measurements (m2).

Three monitoring wells are placed along the vertical at x = 23.5, 47.5, and 71.5 cm, each with five equidistant observation points spaced at 3 cm interval, for a total of 15 observation points. In Scenario 1, a limited dataset, comprising only the 15 concentration values, is used to interpolate the concentration map. This map is generated using a kriging-based interpolation method, with the variogram model computed using the 15 concentration observations (m1 = 0, m2 = 15). The intent is to demonstrate how difficult is to obtain a good estimate using a spatially sparse data set. In the other scenarios, parameters are estimated in each cell of the model grid using the ES-MDA hydrogeophysical inversion, with the number of observations varying according to the specific case under examination. In Scenario 2 (m1 = 225, m2 = 0) only ERT data are employed. In Scenario 3 (m1 = 225, m2 = 15) the ERT data are combined with 15 concentration values. In Scenario 4 (m1 = 225, m2 = 9) the ERT data are combined with 9 concentration values. And, in Scenario 5 (m1 = 225, m2 = 3), the ERT data are combined with only 3 concentration values. A summary of the five scenarios is provided in Table 3.

Table 3 Summary of the scenarios. Number of observations used
Full size table

3.3 CNN’s set up

To speed up the execution of the forward model, a CNN is implemented to replace the SimPEG package that converts electrical resistivity into apparent electrical resistivity data (i.e., pseudo- electrical resistivity sections). To train the network, a dataset including 7000 realizations obtained with SimPEG, is considered. This input dataset undergoes preprocessing involving the normalization of input and output data and is then split into training (70%), validation (15%), and test (15%) sets. The CNN architecture is outlined in Table 4. The model is optimized using the Adam optimizer with a learning rate of 0.001, and the mean squared error between predicted and target apparent resistivity values is used as the loss function. The training is performed with a batch size of 18 over 300 epochs. After training, the model is evaluated on the validation set, and predictions are inverse transformed to the original scale. The complete CNN training and validation process tooks approximately 3 h utilizing a computer equipped with Intel i9-10920X CPU 3.5GHz, 32 GB RAM.

Table 4 CNN architecture
Full size table

Figure 4 reports the results of the validation set. It is clear the good agreement between the true and computed apparent resistivities.

Fig. 4
figure 4

CNN Validation, the dashed line is the 1:1 line

Full size image

The computational time of the CNN was compared to that of the 2.5D forward ERT model, showing a substantial reduction for each realization from 2.3 s to approximately 20 ms using the computational infrastructure described above.

Furthermore, to validate the reliability of the presented approach, the inverse problem in Scenario 3 is solved by using both the CNN model and the full forward model (SimPEG), comparing their performance.

3.4 Inverse model set up

For Scenarios 2–5, the ES-MA is performed with six iterations and an ensemble size of 500. In this study, the initial ensemble of parameters is generated following approach ii) described in Sect. 2.3 (Step 1) using the Python package GeostatsPy (Pyrcz et al. 2021), which interfaces the Geostatistical Software Library (GSLIB) with Python. It is employed to generate Gaussian random fields in logarithmic space to prevent negative values, which are subsequently back-transformed into the concentration space. Each realization is based on an anisotropic exponential variogram, with an azimuth for the largest continuity set at 90 degrees. The mean log-concentration is randomly selected from a uniform distribution within the interval [− 2, 2], while the standard deviation is equal to 1.1. The correlation range in the vertical direction is randomly selected from a uniform distribution with ranges [10, 20] (cm), while the anisotropy ratio is sampled within the range [7, 10] (cm).

The observation errors are normally distributed with zero mean and variance equal to 10–4 (Ω m)2 for the apparent electrical resistivity and 0.01 (mg/L)2 for the concentrations. A decreasing α set with values equal to [364.0; 121.3; 40.4; 13.5; 4.5; 1.5] is used. A spatial covariance localization is applied considering a space correlation length of 30 cm. A covariance inflation is applied with a factor equal to 1.01 (refer to Todaro et al., (2023) for a detailed explanation of ES-MDA set up).

4 Results

The comparative analysis of the five scenarios reveals different insights into the efficacy of ES-MDA in estimating the distribution and values of the concentration plume for a given release history. The results are depicted in Fig. 5, where the estimated concentration for Scenarios 2–5 is given by the ensemble mean. Table 5 provides the evaluation metrics, assessed using Eqs. 12–15, alongside the maximum estimated concentration for comparison with the actual value of 20 mg/L. Additionally, it encompasses an assessment of estimate uncertainty as indicated by the standard deviation.

Fig. 5
figure 5

Estimated concentration distribution for the five scenarios. The injector is marked by a cross. Red circles represent the locations of observation wells

Full size image
Table 5 Performance of the proposed approach evaluated for each scenario
Full size table

In the first scenario (Fig. 5a), the concentration map is obtained through kriging interpolation using 15 concentration values; this result provides a baseline for performance evaluation. Moving on to Scenario 2 (Fig. 5b), where ES-MDA is utilized with only apparent resistivity as observations, the results exhibit poorer accuracy in the estimation of the concentration map, compared to the previous one (Fig. 2). While the estimation of the contaminant distribution is satisfactory and the RMSE of 3.69 mg/L is comparable to that of Scenario 1, there is a significant overestimation of the injected concentration, resulting in higher mean error (-0.48 mg/L) and mean absolute error (2.64 mg/L). In particular, the maximum estimated concentration reaches around 32 mg/L, whereas the actual concentration is 20 mg/L. The absence of concentration data highlights the significance of incorporating such information for a more robust estimation. In comparison, the third scenario (Fig. 5c), which combines apparent resistivity data and the 15 concentration values, emerges as the best result in terms of observation estimation and field distribution. When compared to the other scenarios, this integrated approach outperforms the previous ones with a ME = 0.06 mg/L; MAE = 1.56 mg/L; RMSE = 2.74 mg/L; R2 = 0.82, and the best estimate of the maximum concentration of 22 mg/L, which is close to the actual injected. The combination of geophysical data and concentration values improves the model's ability to capture plume distribution. Scenario 4 (Fig. 5d), which is similar to Scenario 3 but considers only 9 concentration observations, reveals a subtle trade-off between data quantity and model accuracy. Although the reduction in concentration data slightly affects accuracy, the overall performance remains good (ME = -0.01 mg/L; MAE = 1.97 mg/L; RMSE = 3.01 mg/L; R2 = 0.79). The limitations of the sparse concentration information become more pronounced in the final scenario (Fig. 5e), where only three concentration data points are used in conjunction with apparent resistivity data. Despite the model's adaptability, the reduced data set compromises the accuracy of the estimated concentration map, as indicated by ME of -0.38 mg/L, MAE of 2.21 mg/L, RMSE of 3.17 mg/L, Max Concentration of 28.62 mg/L, and R2 of 0.76.

Figure 6 shows the scatterplot between true and estimated concentrations at each model grid cell (Np = 1920) for all investigated scenarios. The dispersion data points indicates that there is not a perfect agreement between the estimated and true values. Despite this dispersion, the best linear fit, illustrated by the red line in Fig. 6, indicates that the model's overall predictive ability is good, with slopes ranging from 0.71 (Scenario 4) to 0.80 (Scenario 1). This is also supported by a high R2 value (Table 5). The results of the inversion procedure effectively capture a significant portion of the variation in the true concentration field. However, as highlighted in Fig. 6, the methodology encounters difficulties, particularly in identifying the lower and higher concentration values in some scenarios, pointing out the limits of each application.. The interpolation in Scenario 1 faces a challenge in accurately estimating lower values, while maximum values are quite well represented. Comparing the true contaminant distribution (Fig. 2) and the estimated one (Fig. 5a) it can be noticed that the concentrations in the area upstream of the source location are overestimated, mainly due to the extrapolation by the kriging estimator beyond the position of the available data. In Scenarios 2 to 5 the proposed procedure better estimates the lower values whereas it presents large uncertainty on the maximum concentration (see Fig. 6). In particular, comparing the true concentration map with the estimated one in Scenarios 2–5 (Fig. 5b-e), it is evident that most of the underestimated values are located upstream of the source location. This discrepancy is mainly due to the lack of information in this portion of the field. Moreover, some concentration values are overestimated particularly in Scenario 2, as a result of the assimilation of only apparent resistivity data and the absence of concentration data. Adding concentration information mitigates this issue, as evidenced by the improved estimation of maximum concentration in Scenario 3.

Fig. 6
figure 6

Scatterplot of the estimated vs. observed concentration for all scenarios. The red line is the best linear fit and the black dashed line is the 1:1 line

Full size image

Following a thorough examination of the results and associated metrics, the third scenario, which employs both apparent resistivity data and concentration values, is the best configuration in terms of estimation values and pattern distribution. This comprehensive evaluation emphasizes the importance of integrating different datasets in hydrological studies to achieve a more accurate and reliable estimation of contaminant plume distribution.

Figure 7 represents the agreement between observed values and the corresponding predictions, given by the ensemble mean of the last iteration, for Scenario 2 to Scenario 5. The inclusion of a 45° line serves as a visual benchmark, indicating a perfect fit between the observed and estimated apparent resistivities and concentrations. The proximity of data points to this line signifies the accuracy of the model in reproducing the measured values. The results for Scenario 1 are not explicitly shown as all the points align along the 45° line, since kriging is an exact estimator.

Fig. 7
figure 7

Observed-estimated apparent resisitivity and concentration for scenarios 2–5

Full size image

The uncertainty assessment in the estimation of the concentration map is crucial for a comprehensive understanding of the reliability and robustness of the proposed approach. In this study, the standard deviation serves as a key indicator of the dispersion, or variability, of the estimated concentration maps around their mean (Fig. 8 and Table 5). In Scenario 1, the kriging standard deviation is zero at the observation points and it increases with distance from these points, reaching a maximum of 25.82 mg/L at the borders of the model and the mean of the standard deviation map is 12.51 mg/L. In the remaining scenarios, the standard deviation is computed from the ensemble of the concentration maps. In Scenarios 2 and 5, the standard deviation is high close to the source location where no concentration values are available. Scenario 2 presents a mean value of 2.42 mg/L and a maximum one of 13.62 mg/L. These values are comparable to those in Scenario 5, where the mean and maximum value are 2.10 mg/L and 13.21 mg/L, respectively. Scenario 3 shows the smallest standard deviations with an average value of 1.16 mg/L and a maximum one of 6.18 mg/L. Scenario 4 has a mean (1.43 mg/L) and maximum (6.59 mg/L) values close to those of Scenario 3. The scenario color bar is the same for easy comparison of standard deviation values but is limited to 15 mg/l to optimize the display of Scenarios 3 and 4. In particular, the maximum standard deviation value achieved in Scenario 1 exceeds 25 mg/l, while Scenarios 3 and 4 have values below 7 mg/l. This discrepancy is attributed to Scenario 1 having significantly higher values in the border area, where no concentration information was available.

Fig. 8
figure 8

Standard deviation maps of the estimated concentrations for the five scenarios. The cross denotes the injector. The observation wells are visually depicted by the red circles

Full size image

These results confirm that the combination of ERT and concentration data provides a reliable estimation of the concentration distribution in aquifer. Obviously, the more concentration data there is, the better the result, but even just 3 observations lead to an acceptable result.

4.1 Full forward model (SimPEG) vs CNN

The validity of the proposed inversion approach is further investigated by solving Scenario 3, employing the full forward model instead of the CNN. In Fig. 9a, the estimated plume using the SimPEG forward model is depicted. Figure 9b illustrates the differences in concentration values between the two approaches. Remarkably, differences are negligible except for a small area beneath the source location. The two forward models demonstrate comparable performance in solving the inverse problem across several metrics. Both models showcase RMSE values that are close. The full forward model achieves an RMSE of 2.93 mg/L, while the CNN model slightly outperforms it with an RMSE of 2.75 mg/L, suggesting near-equivalent accuracy in predicting the target variable. Furthermore, the full forward model achieves an R2 of 0.81, closely followed by the CNN model with an R2 of 0.83. Examining the ME and MAE metrics, which gauge the average magnitude of prediction errors, the full forward model exhibits an ME of 0.32 mg/L and an MAE of 1.68 mg/L, while the CNN model showcases an ME of 0.07 mg/L and an MAE of 1.56 mg/L. Delving into the mean and maximum standard deviation, the CNN model marginally outperforms the full model with slightly lower values for both mean standard deviation (1.11 mg/L vs. 1.68 mg/L) and maximum standard deviation (11.39 mg/L vs. 16.41 mg/L). Finally, both models show similar maximum concentration values, with the CNN model slightly higher at 22.35 mg/L compared to 20.37 mg/L for the full forward model. Notably, a significant disparity arises in terms of computational time: the inverse procedure with the SimPEG forward model takes approximately 2 h, whereas the one with CNN completes the task in approximately 5 min ran with a system composed of an Intel i9-10920X 3.5GHz equipped with 32 GB RAM.

Fig. 9
figure 9

a Estimated concentration distribution, Scenario 3—SimPEG forward model. The injector is marked by a cross. Red circles represent the locations of observation wells. b Differences between estimated concentrations (CNN-SimPEG forward model)

Full size image

5 Conclusion

The presented paper investigated the effectiveness of the Ensemble Smoother with Multiple Data Assimilation (ES-MDA) model in addressing the complex challenge of accurately estimate the spatial distribution of a concentration plume. This is achieved through the simultaneous assimilation of observed electrical resistivity tomography (ERT) data and scattered concentration values from monitoring wells. One of the distinguishing features of this approach was the integration of convolutional neural network (CNN) to speed up the forward model.

The study compared five different datasets to evaluate the performance of the proposed approach. These various scenarios enable a thorough examination of the advantages of combining data from multiple sources (Linde and Doetsch 2016), highlighting the effects of different observation datasets on the accuracy of plume distribution assessments. The first scenario used a kriging-based approach to interpolate 15 concentration values, while subsequent scenarios were conducted to evaluate the capability of the proposed inverse hydrogeophysical approach. The second scenario used only apparent resistivity data as observations into the ES-MDA; and the third to fifth scenario combined apparent resistivity data with different subsets of concentration values: 15, 9, and 3, respectively. The third scenario, which combines apparent resistivity with 15 concentration values, emerged as the most promising configuration in terms of accuracy and precision. The least accurate estimates were observed in the case of kriging interpolation (Scenario 1) and ES-MDA utilizing only apparent resistivity data (Scenario 2). A pertinent point to mention, based on the comparison of these results, is the inherent difficulty in relying solely on 15 concentration values derived from a survey for interpolation purposes. This challenge becomes even more pronounced with the use of 9 or 3 values, which are insufficient for constructing the variogram in the case of kriging. These findings suggest that such a limited dataset may not provide sufficient information to capture the spatial variability of subsurface concentration maps accurately, emphasizing the importance of combining multiple data sources.

In addition, the comparison between the full ERT forward model (i.e., SimPEG) and the CNN showcased significant enhancements in computational efficiency using the surrogate model while maintaining robust predictive performance. The overall results demonstrate the efficacy of the proposed inverse methodology in accurately capturing and predicting the plume concentration’s distribution and values, providing a quick tool for supporting optimal strategies for contaminated site remediation.

Considering the factors that influence the accuracy of the results, one must keep in mind the petrophysical relationships that play a key role in determining the reliability of concentration estimates. These models may face some uncertainties that might have an impact on the inversion outcomes (Linde et al. 2017). Furthermore, in this work, simplifications have been made in the geophysical properties of the electrical model that have to be considered in real cases. Another factor that could affect the results is the setup of the CNN. For this reason, future researches will focus on a comprehensive analysis of the influence of CNN parameters and hyperparameters on the inversion procedure. Additionally, upcoming works will explore the potential application of the proposed inverse methodology in laboratory experiments.