1 Introduction

Hydrologic engineering and design are necessarily linked to reliable and robust estimates of extreme rainfall and discharges, to quantitatively assess and manage flood risks. In this context, soon after the development of the index-flood procedure by Dalrymple (1960), statistical estimation of the spatial distribution of extremes, also referred to as regional frequency analysis (see e.g. Hosking and Wallis 1997), has developed to one of the most prominent challenges in statistical hydrology (see e.g. Adamowski 2000; Ahmad et al. 2013; Alila 1999; Benson 1962; Bernardara et al. 2011; Blanchet et al. 2016; Caporali et al. 2008; Carreau et al. 2013; Cong et al. 1993; Cunnane 1988; Deidda et al. 2000; Dinpashoh et al. 2004; Du et al. 2014; Eslamian et al. 2012; Fitzgerald 1989; Gellens 2002; Guttman et al. 1993; Hosking and Wallis 1993, 1997; Madsen et al. 1997a; Malekinezhad et al. 2011; Mascaro 2020; Modarres and Sarhadi 2011; Ngongondo et al. 2011; Perdios and Langousis 2020; Sang and Gelfand 2010; Satyanarayana and Srinivas 2008; Schaefer 1990; Thomas and Benson 1970; Trefry et al. 2005), with particular emphasis on the estimation of hydrologic quantities (i.e. rainfall and discharges) from short recordings, and associated predictions at ungauged locations within a basin; see also the PUB (prediction in ungauged basins) initiative set by the International Association of Hydrological Sciences (IAHS) for the decade 2003–2012 (see https://iahs.info/pub/index.php), aiming at reducing uncertainty in hydrological predictions.

To what concerns extreme rainfall estimation, the intrinsic spatial and temporal variability of rainfall fields induced by the complex interactions of atmospheric processes with topographic features and the land-sea boundary, result in significant parameter estimation uncertainties when fitting extreme type distribution models to maxima series of limited length (see e.g. Coles et al. 2003; Coles and Tawn 1996; Deidda 2010; Emmanouil et al. 2020; Koutsoyiannis 2004b; Langousis et al. 2013, 2016b). Thus, regional frequency analysis approaches based on homogeneous regions (also referred to as regional approaches) became very popular for extreme rainfall estimation at the end of last century (see e.g. the review in Hosking and Wallis 1997), as a means of improving statistical estimation at ungauged locations, including refinements based on the concept of region of influence around each site (Burn 1990; Das 2019).

In brief, regional approaches are based on the assumption that, after proper partitioning of the study area into distinct statistically homogeneous geographical regions, the maxima series at different locations within the same homogeneous region can be described by the same probability distribution when standardized by their mean, or some other index-statistic (e.g. median, 90% -quantile etc.). Under this setting, and at the expense of spatial detail, one can effectively reduce parameter estimation uncertainties induced by short sample lengths, by pooling together the standardized recordings of all stations within a homogeneous region, and fitting a unique distribution model common to all stations (usually referred to as parent distribution) inside each identified region. Selection of homogeneous regions can be conducted through a variety of cluster analysis (CA) techniques, such as hierarchical cluster analysis (HCA), principal component analysis (PCA), factorial analysis (FA), and self-organizing maps (SOM) (see e.g. Baeriswyl and Rebetez 1997; Beaudoin and Rousselle 1982; Comrie and Glenn 1998; Hassan and Ping 2012; Karl et al. 1982; Malekinezhad et al. 2011; Mallants and Feyen 1990; Markonis and Strnad 2020; Modarres and Sarhadi 2011; Munoz-Díaz and Rodrigo 2004; Ngongondo et al. 2011; Pineda-Martínez et al. 2007; Santos et al. 2015; Van Regenmortel 1995), complemented by some type of statistical homogeneity testing; see e.g. Hosking and Wallis (1997) and Sect. 3.3.

While widely used in hydrology due to their computational simplicity and robustness of the obtained estimates, regional approaches are not limitation free. More precisely, independent of the method used to define homogeneous regions, regional approaches result in abrupt shifts of quantile estimates along the boundaries of contiguous regions, due to differences in the regional parameters of the parent distribution (see e.g. Schaefer 1990). Except for the fact that such discontinuities cannot be physically justified, as hydrologic variables, such as precipitation, vary seamlessly in space, the aforementioned issue is of particular importance in engineering applications, as hydrological basins may be consisted by areas belonging to neighboring homogeneous regions, with significantly different distribution parameters. Additional limitations of regional approaches include: (a) the lack of high resolution detail in the spatial variation of rainfall statistics, as the effects of topography and local climatology are smeared out by grouping of stations, (b) the fact that the extent of homogeneous regions, as determined through statistical testing, is necessarily constrained by the length of the available recordings (i.e. when the recordings are short, estimation uncertainties are large enough to shade site-to-site differences of rainfall statistics induced by the topography and local climatology, leading to coarser partitioning of the study area), and (c) the technical limitation that the parent distribution assigned to each homogenous region constitutes an average of different at-site behaviors, leading to quantile overestimation in some parts of the considered region, and underestimation inside the remaining parts.

The aforementioned shortcomings can be remedied, to some extent, by the so-called geostatistical approaches, which allow for a seamless representation of rainfall statistics in space. This is accomplished by fitting a theoretical distribution model to the recordings of each station and, then, spatially interpolating the return levels or distribution parameters over the region of interest. For the latter purpose, different interpolation techniques can be used, such as linear regression based methods (see e.g. Beguería and Vicente-Serrano 2006; Carreau et al. 2013; Van De Vyver 2012), inverse distance weighting schemes (see e.g. Goovaerts 2000), bootstrap techniques (see e.g. Uboldi et al. 2014), spline based regression models (see e.g. Blanchet and Lehning 2010), and kriging (see e.g. Alila 1999; Goovaerts 1999; Libertino et al. 2018; Moral 2010; Prudhomme and Reed 1999). The latter is a geostatistical technique, which was initially proposed by Krige (1951), improved by Matheron (1963) and Mazzetti and Todini (2009), and still remains the most widely used method for spatial interpolation (see e.g. Ceresetti et al. 2012; Das et al. 2020; De Marsily 1986; Furcolo et al. 2016; Mamalakis et al. 2017; Mazzetti and Todini 2009; Panthou et al. 2012; Prudhomme and Reed 1999; Yin et al. 2018).

While promising, estimation of the spatial distribution of rainfall extremes using geostatistical approaches has received limited attention. In this context, the present study aims at assessing the relative performance of regional and hierarchical geostatistical approaches in modeling the general tendencies and spatial variation of the distribution of extreme rainfall. In doing so, two models are progressively developed, a regional and geostatistical one, to describe the spatial variation of extreme rainfall regimes over the island of Sardinia (Italy). The analysis is conducted using annual maxima of daily rainfall from 256 raingauges with at least 30 years of complete recordings, which are fitted using a Generalized Extreme Value (GEV) distribution model. The at-site GEV parameter estimates are spatially interpolated using two versions of kriging: ordinary kriging (OK, the simplest and most widespread version of kriging) and kriging for uncertain data (KUD), which accounts for intrinsic uncertainties of at-site estimates due to measurement errors and/or sampling variability.

The paper is organized as follows. Section 2 presents some necessary information regarding the study area and the available data. In Sect. 3 we summarize background information on extreme value theory, present step-by-step details on the implementation of the regional and geostatistical approaches, and outline the error metrics used to assess the relative performance of the two procedures for extreme rainfall estimation. Section 4 discusses the obtained results, and Sect. 5 summarizes the main findings of the study, and points towards future research directions.

2 Study area and rainfall data

The regional and boundaryless approaches are here implemented using rainfall timeseries recorded in Sardinia (Fig. 1a), the second largest island in Italy with approximate area of 24 000 km2, which is located in the center of the Western Mediterranean sea (see inset in Fig. 1a), between 32° N and 41° N latitude, and between 8° E and 10° E longitude. The topography of Sardinia is rather complex, as illustrated in Fig. 1a. A long mountain range is located in the eastern part of the island, running from North to South, with highest elevation of 1834 m. A secondary and smaller mountain range is located in the southwestern part of the island. Between the two mountain ranges, the Campidano plain is formed.

Fig. 1
figure 1

a Digital Elevation Model of Sardinia (Italy) with an inset illustrating the location of the island in the Mediterranean; black circles indicate the locations of raingauges (total number 229) with more than 50 years of complete daily recordings, while red circles indicate the locations of 27 stations  with 30–50 years of complete data. b Spatial distribution of the mean annual rainfall depth (mm) over the Island. c Spatial distribution of the highest daily rainfall depths in record (mm)

Full size image

The island of Sardinia is characterized by Mediterranean climate, with dry summers and most rainfall occurring during the period from September to May. The central-east and the southwestern coastal zones of the island experience the highest rainfall extremes, due to the interaction of humid air masses from southern Mediterranean with the two main mountain ranges (Chessa et al. 2004), while the local topography, soil structure, land use and intensive coastal urbanization make these areas highly vulnerable to flash floods and landslides.

The available database consists of daily rainfall recordings from 1920 to 2008, collected by Sardinia’s Regional Hydrographic Agencies. During the considered period, more than 400 raingauges evenly distributed over the island have been recording daily precipitation, with some of them experiencing one or more temporal interruptions. For this reason, we conducted a statistical analysis (described in detail in Sect. 4.3) to determine a tradeoff rule between the minimum record length required for including a certain station in a specific phase of the analysis, and the resulting spatial density of the network. As a result, two ensembles of stations were identified. The first one consists of 229 stations with at least 50 years of complete observations (see black circles in Fig. 1), and it was used to estimate distribution parameters controlled by moment orders larger than 1, which are characterized by higher statistical variability. The second ensemble consists of 256 stations (see black and red circles in Fig. 1) with at least 30 years of complete recordings (thus including also all stations pooled in the first ensemble), and it was used to estimate statistical attributes characterized by lower levels of uncertainty; i.e. in our analysis mean rainfall fields.

Figure 1b shows the spatial distribution of the mean annual rainfall depth over the Island, indicating a strong linkage between mean annual rainfall and elevation (compare Fig. 1a to 1b). Mean annual rainfall depths range from about 450 mm per year in low elevation areas, to about 1200 mm in the highest mountain peaks, while the regional mean is approximately 730 mm/yr. A different pattern is depicted in Fig. 1c, which illustrates the spatial distribution of the highest daily rainfall depths recorded. One notices a significant intensification of rainfall extremes at the eastern and southern parts of Sardinia, where cyclonic activity interacts with orographic barriers.

3 Methods

This Section aims at providing essential information regarding the implementation of methods and interpretation of the results presented herein. Hence, for the sake of brevity, we limit discussion solely to methodological and technical aspects used in the present study, whereas for additional details the interested readership is referred to the wide literature on the presented topics. Since the main objective of the study is to propose a geostatistical boundaryless approach and to compare its performance against widely applied regional methods (see e.g. Hosking and Wallis 1997), the common tools for the two approaches are introduced first, namely the selected theoretical distribution model for the purposes of extreme value analysis (Sect. 3.1), and the standardization procedure associated with the index-flood method (Sect. 3.2). Section 3.3 resumes the main principles of regional analysis, and Sect. 3.4 introduces the boundaryless approach based on geostatistical analysis using kriging for uncertain data. Statistical measures and metrics used to evaluate and compare the performances of the two approaches are presented in Sect. 3.5.

3.1 Elements of extreme value theory

The problem of characterizing the probability distribution of hydrological extremes has been addressed in the past using a variety of theoretical probability distribution models. Based on both theory and empirical evidence (see e.g. AghaKouchak and Nasrollahi 2010; Blanchet et al. 2016; Coles 2001; Coles and Dixon 1999; Coles et al. 2003; El Adlouni et al. 2008, 2007; El Adlouni and Ouarda 2010; Engeland et al. 2004; Gubareva and Gartsman 2010; Katz 2013; Katz et al. 2002; Koutsoyiannis 2004a, 2004b; Koutsoyiannis and Langousis 2011; Langousis et al. 2013, 2016b; Lucarini et al. 2016; Mélèse et al. 2018; Onibon et al. 2004; Papalexiou and Koutsoyiannis 2013; Tyralis and Langousis 2019; Veneziano et al. 2009, 2007; Villarini 2012; Villarini et al. 2011, 2012), in the present study we model annual maxima of daily rainfall using the Generalized Extreme Value (GEV) distribution model. In what follows, we recall the essentials of GEV formulation, while referring the interested reader to the wide literature on the topic for a more in-depth discussion (see e.g. Coles 2001; Langousis et al. 2016b; Lucarini et al. 2016). Additional empirical evidence regarding the suitability of the GEV distribution model in describing the statistical attributes of the analyzed dataset are presented in Sect. 4.1, where we discuss some preliminary results of our analysis.

Let Zi be a sequence of independent and identically distributed (iid) random variables, and X: = max(Z1,…,ZM) be the maximum inside a block of length M. For example, if M is the number of observations in one year, as commonly assumed in statistical hydrology, then X corresponds to the annual maximum. If nondegenerate, extreme value theory (see e.g. Coles 2001; Fisher and Tippett 1928; Gnedenko 1943; Jenkinson 1955; Lucarini et al. 2016) determines the specific form of the limiting distribution of X when M tends to infinity; i.e. Gumbel, Fréchet and Weibull distributions. Using the von Mises-Jenkinson parameterization (Jenkinson 1955), the three limiting distributions can be summarized in the following closed form, usually referred to as Generalized Extreme Value (GEV) model:

$${F}_{X}\left(x\right)=\left\{\begin{array}{l}exp\left\{-{\left[1+k\left(\frac{x-\mu }{\sigma }\right)\right]}^{-\frac{1}{k}}\right\} \quad for\;k=0\\ exp\left\{-exp\left[-\left(\frac{x-\mu }{\sigma }\right)\right]\right\} \quad for\;k=0\end{array}\right.$$
(1)

where k ϵ (− ∞, + ∞), σ > 0 and µ ϵ (− ∞, + ∞) are the shape, scale and location parameters of the distribution, respectively.

The specific form of the distribution in Eq. (1) determines the upper tail behavior of random variable X; see e.g. Gumbel (1958), and more recently Coles (2001). For k = 0 the GEV distribution reduces to Gumbel’s (i.e. Extreme Value of type 1, EV1) form with exponential upper tail; for k > 0 (i.e. Frèchet, or EV2 form) the corresponding distribution is lower bounded and exhibits an algebraic upper tail with exponent − 1/k, whereas for k < 0 (i.e. Weibull, or EV3 form) the distribution in Eq. (1) exhibits a finite upper bound.

In the context of extreme daily rainfall characterization, it is worth mentioning the results of Papalexiou and Koutsoyiannis (2013), who analyzed more than 15 000 annual maxima series from different locations worldwide, with lengths varying from 40 to 163 years. The study showed that for very long time series, GEV shape parameter estimates vary in the range between 0 and 0.23 with probability 99%, while the probability of negative shape parameter estimates is well below 1% (i.e. on the order of 0.005). Based on these findings, as well as visual inspection (using Gumbel charts) of the empirical cumulative distribution functions of all analyzed series, we concluded that the few negative shape parameter estimates obtained should be attributed to sampling variability and were set to zero. In this context, please note that from a physical perspective the rainfall process cannot simultaneously exhibit (as implied by negative shape parameter estimates) and not exhibit (as implied by positive shape parameter estimates) an upper bound. Therefore, unless attributed to statistical variability, positive and negative GEV shape parameter values cannot coexist in a region (Emmanouil et al. 2020).

For practical applications, one usually needs to estimate quantiles corresponding to different return levels. This is done by inverting Eq. (1):

$$x\left(F\right)=\left\{\begin{array}{l}\mu -\frac{\sigma }{k}\left[1-{\left(-\mathrm{ln}F\right)}^{-k}\right]\quad for\;k\ne 0\\ \mu -\sigma \mathrm{ln}\left(-\mathrm{ln}F\right) \quad for \; k=0\end{array}\right.$$
(2)

where F denotes the non-exceedance probability. While different definitions of F are possible depending on the problem under consideration (see e.g. Langousis and Kaleris 2014; Langousis et al. 2016a, 2009; Langousis and Veneziano 2007, 2009; Stedinger et al. 1993; Veneziano and Furcolo 2002; Veneziano and Langousis 2005a, 2005b; Willems 2000), for the case of annual maxima, one usually sets F = 1–1/T, where T denotes the return period of the event in years.

3.2 The index-flood method

The index-flood method inherits its name from an application to flood frequency estimation by Dalrymple (1960), but the method has been effectively applied to other hydrological variables, including rainfall; see e.g. Hosking and Wallis (1997) for a general and widely adopted framework for regional frequency analysis, and Fitzgerald (1989), Schaefer (1990), Cong et al. (1993), Guttman et al. (1993) Madsen et al. (1997a), Alila (1999), Deidda et al. (2000), Trefry et al. (2005), Caporali et al. (2008) Satyanarayana and Srinivas (2008), Modarres and Sarhadi (2011), Ngongondo et al. (2011), and Blanchet et al. (2016) for relevant applications to rainfall. In brief, the method is essentially based on the assumption that, after proper at-site standardization, the data originating from different sites belong to the same population, as outlined below.

Let X(i) be a random variable that corresponds to a certain hydrologic quantity at site i = 1, 2, …, N within a homogeneous region. According to the index-flood concept, when properly standardized by a local multiplicative factor m(i), the frequency distribution of the ratio Y: = X(i)/m(i) is assumed to be invariant within the homogeneous region. Since the present study deals with rainfall fields, hereafter the site-specific multiplicative factor m(i) will be referred to as index-rainfall (instead of index-flood; see e.g. Ngongondo et al. (2011)). Hence, under the above assumption, the quantile function x(i)(F) for any specific site i = 1, 2, …, N within a homogeneous region is given by:

$${x}^{\left(i\right)}\left(F\right)={m}^{\left(i\right)} y\left(F\right) \quad i=1,\dots N$$
(3)

where y(F) is a dimensionless quantile function, also referred to as regional growth curve (see e.g. Hosking and Wallis 1997). y(F) is common to all sites inside a homogeneous region, while the multiplicative factor m(i) may vary from site to site, and can be linked to physiographic descriptors, or estimated using interpolation procedures. Although the most popular choice is to use the local mean of the modeled variable X(i) as site-specific factor (i.e. m(i) = E[X(i)]) (see e.g. Cunderlik and Ouarda 2007; Laio et al. 2011; Madsen et al. 1997b; Zaman et al. 2012), occasionally, other statistical measures, such as the median or mode, have also been used (see e.g. Kjeldsen and Jones 2006; Ngongondo et al. 2011). In what follows, we estimate m(i) as the mean value of the annual maxima of daily rainfall, recorded at raingauge i.

By introducing the aforementioned standardization to Eq. (1), the distribution function of the dimensionless random variable Y: = X(i)/m(i) receives the form:

$${F}_{Y}\left(y\right)=\left\{\begin{array}{l}exp\left\{-{\left[1+k\left(\frac{y-{\mu }^{*}}{{\sigma }^{*}}\right)\right]}^{-\frac{1}{k}}\right\} \quad for\; k\ne 0\\ exp\left\{-exp\left[-\left(\frac{y-{\mu }^{*}}{{\sigma }^{*}}\right)\right]\right\} \quad for\; k=0\end{array}\right.$$
(4)

where the shape parameter k, the dimensionless scale parameter σ*: = σ/m, and the dimensionless location parameter µ*: = µ/m remain constant inside each homogeneous region. Again, direct inversion of Eq. (4) results in the dimensionless quantile function of random variable Y:

$$y\left(F\right)=\left\{\begin{array}{l}{\mu }^{*}-\frac{{\sigma }^{*}}{k}\left\{1-{\left(-\mathrm{ln}F\right)}^{-k}\right\} \quad for \; k\ne 0\\ {\mu }^{*}-{\sigma }^{*}\mathrm{ln}\left(-\mathrm{ln}F\right) \quad for \; k=0\end{array}\right.$$
(5)

In addition, since the ratio Y has unit mean value (i.e. mY = E[Y] = E[X(i)/m(i)] = 1), it can be easily proved that the three parameters are linked by the following equation:

$${\mu }^{*}=\left\{\begin{array}{l}1+\frac{{\sigma }^{*}}{k}\left\{1-\Gamma \left(1-k\right)\right\} \quad for\; k\ne 0\\ 1-\gamma {\sigma }^{*} \quad for \; k=0\end{array}\right.$$
(6)

where \(\Gamma (.)\) denotes the gamma function \(\Gamma \left(x\right)= {\int }_{0}^{\infty }{t}^{x-1} {e}^{-t} dt\), and γ = 0.577215665… is the Euler constant. Thus, estimation of k and σ* from the pool of all standardized data in a homogeneous region suffices to fully parameterize Eqs. (4) and (5).

Regarding GEV parameter estimation, common procedures include the method of moments (also referred to as simple moments (SM) or conventional moments), the method of probability-weighted moments (PWM), and maximum likelihood (ML). Here we use the method of L-moments (i.e. a subcase of PWM; see Hosking and Wallis (1997) for a detailed review and relevant formulations), due to its higher robustness against outliers relative to SM (see e.g. Hosking 1992; Sankarasubramanian and Srinivasan 1999; Vogel and Fennessey 1993), and its better performance relative to ML when applied to small samples (see e.g. Bezak et al. 2014; Gubareva and Gartsman 2010; Hosking et al. 1985; Madsen et al. 1997a). Also, similar to simple moments, L-moment ratios can be efficiently used to describe the empirical distribution of samples (see e.g. Deidda and Puliga 2006; Hosking 1990; Hosking and Wallis 1997; Silva Lomba and Fraga Alves 2020; Vogel and Fennessey 1993 among others). In this context, the coefficient of L-variation (L-CV) is defined as:

$$\tau =\frac{{\lambda }_{2}}{{\lambda }_{1}}$$
(7)

where λ1 denotes the mean, and λ2 is the L-moment of order 2. For orders r > 2, the L-moment ratio τr is defined as:

$${\tau }_{r}=\frac{{\lambda }_{r}}{{\lambda }_{2}} \quad r=3, 4,\dots$$
(8)

where λr denotes the L-moment of order r

When interest is in determining the theoretical distribution model that best fits the data, a useful diagnostic is the L-moment ratios diagram proposed by Hosking (1990) (see also Vogel and Fennessey 1993). The latter allows for direct comparison of the empirically estimated L-skewness (τ3 = λ3/λ2) and L-kurtosis (τ4 = λ4/λ2) from the available data, to what is theoretically expected for different distribution models; see also discussion of Fig. 2 in Sect. 4.1.

Fig. 2
figure 2

Theoretical L-moment ratio curves of common distribution models, as compared to the sample L-moment ratios of annual maxima of daily precipitation from the network of 229 stations with more than 50 years of complete recordings (empty circles). The filled large mark corresponds to the regional average of all sample L-moment ratios shown

Full size image

3.3 Regional approach

Any regional approach requires a preliminary identification of homogeneous regions, where the parameters of the distribution function of the dimensionless random variable y (in our case the GEV model in Eq. (4)) can be reasonably assumed constant. Different approaches to group measuring locations of hydrologic quantities into homogeneous regions have been proposed (see Hosking and Wallis 1997 for a review), but no consensus on the best procedure has been still reached, since any approach exhibits advantages and limitations; e.g. regions determined based solely on geographic proximity constraints may not guarantee hydrological or climatological similarity, pure objective criteria based solely on minimization of heterogeneity metrics may lead to fragmented regions, whereas subjective partitioning may be unfeasible in the case of large observational networks. Independent of the grouping criteria used, there is always the necessity for statistical testing to determine whether the standardized series y(i) = x(i)/m(i) at different sites i can be considered to belong to the same population. The spatial coverage of these sites defines the extent of the homogeneous region.

In this study, we have applied a mixture of grouping criteria, trying to take advantage of different techniques. In brief, identification of homogeneous regions was mainly implemented in two steps. The first step relied on purely objective criteria, namely an agglomerative (or “bottom-up”) hierarchical cluster analysis approach based on Ward's method (see e.g. Ahmad et al. 2013; Ercan et al. 2008; Hassan and Ping 2012; Modarres and Sarhadi 2011), coupled with a geographic proximity constraint to avoid excessive fragmentation of regions. Specifically, Ward’s method was used to minimize the total within-group variance of sample L-CV and L-skewness (see e.g. Pearson 1991), starting from clusters containing only one station each, and progressively merging couplets of clusters based on Delaunay's triangulation of the region. More precisely, at each step of the algorithm, we considered as candidates for potential mergers only couplets of previous-step clusters that shared at least one site in the same Delaunay triangle (Tucker et al. 2001). In case needed, a final subjective refinement was applied to the clusters resulting from each step of the algorithm, by exchanging very few sites at cluster boundaries to better reflect orographic features, with particular care not to increase the average error metrics described in Sect. 3.5.

Once the clustering procedure was completed (i.e. all sites were merged into a unique terminal cluster), in the second step of the regionalization procedure, we used a “top–bottom” approach to conclude on the minimum number of homogeneous regions. More in detail, we started by assuming one homogeneous region containing all sites, then two homogeneous regions corresponding to the last two clusters before the final merger, then three clusters etc., to conclude on the partition consisting of the minimum number of clusters where the hypothesis of statistical homogeneity was accepted unanimously at a certain significance level.

To test regional homogeneity within regions, we used the procedure described in Hosking and Wallis (1997). According to this procedure, for each considered region, one first calculates the regional value of L-CV (τ R):

$${\tau }^{R}=\frac{{\sum }_{i=1}^{N}{n}^{\left(i\right)}{\tau }^{\left(i\right)}}{{\sum }_{i=1}^{N}{n}^{\left(i\right)}}$$
(9)

where τ(i) and n(i) denote the sample L-CV and the number of available observations at site i, respectively, and N is the number of sites inside the region. Then, one calculates the dispersion measure V, which corresponds to the weighted standard deviation of L-CV estimates within the region:

$$V={\left[\frac{{\sum }_{i=1}^{N}{n}^{\left(i\right)}{ \left({\tau }^{\left(i\right)}-{\tau }^{R}\right)}^{2}}{{\sum }_{i=1}^{N}{n}^{\left(i\right)}}\right]}^{1/2}$$
(10)

As a final step, one computes the heterogeneity measure:

$$H=\frac{\left(V-{\mu }_{V}\right)}{{\sigma }_{V}}$$
(11)

where µV and σV denote the mean and standard deviation of V, which are usually determined via Monte Carlo simulation, as described below.

To assess statistical homogeneity within a region, Hosking and Wallis (1997) suggest the following three ranges of H values: (i) H < 1 the region is acceptably homogeneous; (ii) 1 ≤ H < 2 the region is possibly heterogeneous; (iii) H ≥ 2 the region can be considered heterogeneous. It is important to note that Hosking and Wallis (1997) suggest the aforementioned ranges as guidelines, rather than acceptance regions for a statistical test. In this (lenient) context, to determine the acceptance region for the null hypothesis of statistical homogeneity at a certain significance level, one can reasonably assume that H follows a standard normal distribution.

For each considered region, the mean µV and standard deviation σV of the dispersion measure V can be obtained using Monte Carlo simulation, as follows. First, a regional probability distribution model (in our case a 4-parameter Kappa distribution (Hosking 1994); see discussion below and Eq. (12)) is fitted to the sample created after pooling together all standardized timeseries y(i) (i = 1, 2,…, N) within the considered region, using the method of L-moments; see e.g. Hosking and Wallis (1997). Then, the fitted regional distribution is used to simulate a large number, in our case Nsim =  10 000, of synthetic timeseries at each location i = 1, 2,…, N, with length equal to that of the corresponding historical series n(i). By construction, and in accordance with the tested null hypothesis of statistical homogeneity, all simulated series originate from a homogeneous random field, free of cross (spatial) and serial (temporal) dependencies. Hence, one can calculate µV and σV in Eq. (11) using the Nsim estimates of the dispersion measure V, obtained by applying Eqs. (9) and (10) to the ensemble of synthetic realizations generated by a 4-parameter Kappa distribution model (Hosking 1994):

$${F}_{Y}\left(y\right)=\left[1-h\left\{1+\frac{k\left(y-\xi \right)}{\alpha }\right\}^{-\frac{1}{k}}\right]^{\frac{1}{h}}$$
(12)

where, ξ and α denote the location and scale parameters of the distribution, respectively, and k and h control the distribution shape (i.e. through skewness and kurtosis).

Selection of a 4-parameter Kappa distribution to model the regional sample for the purposes of Monte Carlo simulation, has been based mainly on the following two reasons (see also Hosking and Wallis 1997): (i) In our analysis, rainfall maxima are modeled using a GEV theoretical distribution with 3 parameters. Hence, to avoid biasing the conducted homogeneity tests through a priori selection of the parent distribution model (i.e. in our case a GEV model), we used a 4-parameter distribution to allow for an additional degree of freedom (a fourth parameter) in describing the shape of the distribution. (ii) The 4-parameter Kappa distribution model is quite flexible in describing a wide range of distribution types used in extreme analysis and beyond, including: the GEV for h = 0, the Generalized Logistic for h = -1, and the Generalized Pareto for h = 1, as sub-cases.

Since the distribution functions of extremes are generally characterized by heavy tails, we decided to complement the homogeneity analysis with two additional dispersion measures (V2 and V3), built using the regional L-skewness (τ3R), and the regional L-kurtosis (τ4R), given by:

$${\tau }_{3}^{R}=\frac{{\sum }_{i=1}^{N}{n}^{\left(i\right)}{\tau }_{3}^{\left(i\right)}}{{\sum }_{i=1}^{N}{n}^{\left(i\right)}}$$
(13)
$${\tau }_{4}^{R}=\frac{{\sum }_{i=1}^{N}{n}^{\left(i\right)}{\tau }_{4}^{\left(i\right)}}{{\sum }_{i=1}^{N}{n}^{\left(i\right)}}$$
(14)

where, similar to Eq. (9), τ3(i), τ4(i) and n(i) denote the sample L-skewness, L-kurtosis and number of available observations at site i, respectively, and N is the number of sites inside the region. Following the same notation as in Hosking and Wallis (1997), we named the additional dispersion measures V2 (i.e. based on L-CV and L-skewness) and V3 (i.e. based on L-skewness and L-kurtosis), and the corresponding heterogeneity measures H2 and H3 (see "Appendix" for details). Similar to heterogeneity measure H, computation of H2 and H3 requires preliminary estimation of the regional mean and variance of V2 and V3 in the tested region, which can be obtained from the generated synthetic realizations.

Once partitioning of the station network into the minimum possible number of homogeneous regions is completed, one pools together the standardized annual rainfall maxima from all stations belonging to each of the identified regions, and fits a unique (for each homogeneous region) GEV model (see Eq. (4)), using the estimated regional L-moments; see Eqs. (9), (13) and (14). The parameters k, σ*, and µ* of the regional distribution are kept constant inside each homogeneous region, while the index-rainfall m varies seamlessly in space, and can be related to physiographic features or estimated through spatial interpolation techniques, as described in the next subsection.

3.4 Boundaryless approach based on geostatistical analysis

As an alternative to the regional approach described in the previous subsection, we propose and test a boundaryless approach based on the hierarchical application of geostatistical interpolation, to obtain seamless estimates of GEV distribution parameters in space.

It is well known that at-site estimates of distribution parameters are affected by uncertainties in statistical estimation, due to the limited length of hydrological timeseries; actually, it is exactly this limitation that motivated the development and application of regional approaches. In this context, we decided to avoid applying ordinary kriging (OK; see e.g. De Marsily 1986; Kitanidis 1997; Matheron 1963), and opt in favor of kriging for uncertain data (KUD); see e.g. De Marsily (1986), Mazzetti and Todini (2009), Furcolo et al. (2016), and Mamalakis et al. (2017). Contrary to OK, which assumes zero estimation variance of statistical quantities at locations where data is available, KUD allows for explicit modeling of intrinsic uncertainties in the data, making the interpolation less sensitive to local sampling effects, while remaining unbiased and minimizing the interpolation error variance. These attributes of KUD make it particularly useful when the data to be interpolated exhibit considerable variability, as it is the case here where we interpolate statistical estimates of distribution parameters, originating from finite samples with different lengths.

A pioneering KUD formulation was first proposed by De Marsily (1986) for homoschedastic fields (i.e. where the error variance is constant), and later extended by Mazzetti and Todini (2009) to apply also to heteroschedastic fields, with variance that varies spatially. According to this last formulation, the KUD estimate of a parameter θ at a certain location is obtained as \(\widehat{\theta }=\sum_{k=1}^{{N}_{s}}{\lambda }_{k}{\theta }_{k}\), where θk is the local parameter estimate at site k, Ns is the number of neighboring sites considered for the interpolation, and λk are weights obtained by solving a system of linear equations similarly to OK. The only difference is that the matrix of coefficients (γ*i,j) and vector of constant terms (γ*i,0) in the KUD system of linear equations are properly modified to account for uncertainties in statistical estimation, receiving the form (see Mazzetti and Todini 2009):

$$\left\{\begin{array}{l}{\gamma }_{i,j}^{*}={\gamma }_{i,j}+\frac{{\sigma }_{i}^{2}+{\sigma }_{j}^{2}}{2} \quad \forall i,j=1, \dots , {N}_{s} \quad and \quad i\ne j \\ {\gamma }_{i,j}^{*}={\gamma }_{i,j}\quad i=j \\ {\gamma }_{i,0}^{*}={\gamma }_{i,0}+\frac{{\sigma }_{i}^{2}}{2} \quad \forall i=1, \dots , {N}_{s}\end{array}\right.$$
(15)

where γi,j is the variogram value between measuring sites i and j, γi,0 is the variogram value between location i and the estimation point, and σi2 denotes the variance of the measuring error at site i.

In the suggested boundaryless approach, KUD is applied to obtain seamless GEV parameter estimates over the study region, following a four-step hierarchical approach:

  1. 1.

    At each measuring location i = 1, 2, …, N, the standardized to mean-1 timeseries of annual rainfall maxima y(i) = x(i)/m(i) are used to fit a GEV model (see Eq. 4), using the method of L-moments.

  2. 2.

    KUD is applied to the GEV shape parameter k estimates from all measuring locations, to obtain a smoothly varying k-field over the study region. The shape parameter estimation variances at the measuring locations (necessary for KUD analysis and interpolation; see Eq. 15 above), are obtained through Monte Carlo simulation. More precisely, at each measuring location, we used the fitted GEV distribution model to simulate 10 000 synthetic series with length equal to that of the corresponding historical series of annual maxima, refitted the GEV model to each of the simulated series, and calculated the variance of the shape parameter estimates.

  3. 3.

    At each site, the interpolated shape parameter value is used to condition estimation of the dimensionless scale parameter σ*. Next, KUD is applied to the newly estimated dimensionless scale parameters σ*, to obtain a smoothly varying σ*-field over the study region. Similar to shape parameter k, the dimensionless scale parameter estimation variance at each measuring location is obtained through Monte Carlo simulation, using the GEV distribution model from step 2 above (i.e. where σ* is estimated conditionally based on the interpolated k value).

  4. 4.

    The interpolated k and σ* fields are used together with Eq. (6), to acquire the dimensionless location parameter µ*-field.

The first step of the suggested approach produces unbiased GEV shape parameter estimates, which are less sensitive to local sampling effects and, also, account for intrinsic uncertainties in the data. The remaining steps reduce propagation of the estimation uncertainty from the shape parameter, which is more sensitive to sampling effects, to the dimensionless scale and location parameters, thus making the interpolation method more robust.

As a final step for the application of both regional and boundaryless approaches, one needs to obtain an interpolated field of the index-rainfall m over the study region, which will be used to multiply the dimensionless quantile function in Eq. (5), or calculate the scale σ and location μ parameters of the GEV distribution at any location inside the study area, from σ* and μ*, respectively. Here we do so by applying KUD analysis to the mean of annual rainfall maxima over the study region.

3.5 Error metrics

The relative effectiveness of the regional and boundaryless approaches in modeling the observed annual rainfall maxima, are evaluated by comparing the empirical and fitted distribution models in each raingauge site in terms of: (i) observed and modeled frequencies over the whole range of historical observations, and (ii) the average error of the estimated quantiles corresponding to the highest values in record. For the sake of brevity, and to facilitate readability, indexing of raingauge sites is omitted in this subsection.

For the first type of comparisons, we selected the Anderson Darling, A2, and the Cramer-von Mises, W2, statistics (see e.g. Ahmad et al. 1988; Anderson and Darling 1952, 1954; Deidda and Puliga 2006, 2009; Laio 2004; Laio et al. 2009; Langousis et al. 2016b; Stephens 1986) to quantify the deviations between the empirical cumulative distribution function (CDF) and the fitted theoretical GEV model FX(x):

$${A}^{2}=-n-\frac{1}{n}\sum_{j=1}^{n}\left(2j-1\right)\left[log\left({F}_{X}\left({x}_{j}\right)\right)+log\left(1-{F}_{X}\left({x}_{n+1-j}\right)\right)\right]$$
(16)
$${W}^{2}=\frac{1}{12n}+\sum_{j=1}^{n}{\left({F}_{X}\left({x}_{j}\right)-\frac{2j-1}{2n}\right)}^{2}$$
(17)

where n denotes the length of the available observations, and xj denotes the j-th ascending order statistic. In Both W2 and A2 the empirical CDF is estimated by applying the Hazen (1914) plotting position formula (see e.g. Barnett 1975, 1976; Harter 1984). W2 assigns equal weights to the whole distribution, while A2 assigns larger weights to observations located at the upper or lower distribution tails.

For the second type of comparisons, we calculated the mean error (ME, see Eq. 18), mean relative error (MEr, see Eq. 19), mean absolute error (MAE, see Eq. 20), and the mean absolute relative error (MAEr, see Eq. 21) in the estimation of the K highest recordings at each station:

$$ME\left(K\right)=\frac{1}{K}\sum_{j=n-K+1}^{n}{{x}^{d}}_{j}-{x}_{j}$$
(18)
$$MEr\left(K\right)=\frac{1}{K}\sum_{j=n-K+1}^{n}\frac{{{ x}^{d}}_{j}-{x}_{j}}{{x}_{j}}$$
(19)
$$MAE\left(K\right)=\frac{1}{K}\sum_{j=n-K+1}^{n}\left|{{x}^{d}}_{j}-{x}_{j}\right|$$
(20)
$$MAEr\left(K\right)=\frac{1}{K}\sum_{j=n-K+1}^{n}\left|\frac{{{ x}^{d}}_{j}-{x}_{j}}{{x}_{j}}\right|$$
(21)

where xdj denotes the theoretical quantile of the j-th ascending order statistic, estimated from Eq. (2) for F = (2j−1)/n according to Hazen (1914) plotting position formula.

The first two metrics (i.e. Eqs. 18 and 19) measure the bias of each approach providing an indication of the locations where the theoretical quantiles from Eq. (2) over- or underestimate the K highest observed maxima, while the third and fourth metrics (i.e. Eqs. 20 and 21) provide an indication of the magnitude of the errors, regardless of their sign. ME and MAE are dimensional, sharing the same units with the analyzed records (i.e. mm), while MEr and MAEr are dimensionless.

All error metrics in Eqs. (18)–(21) were computed for the K = 5 highest annual maxima recorded by each raingauge considered in our analysis, and the performances of the regional and boundaryless approaches were evaluated in terms of the spatial distribution of the considered error metrics, as well as in terms of summary statistics for the overall performances. A leave-one-out cross-validation procedure was also implemented to evaluate performances at ungauged locations, as described in the following Section.

4 Results and discussion

In the following subsections we discuss the main findings and results from the application of the regional and boundaryless approaches described in Sect. 3 to the annual maxima of daily rainfall in the island of Sardinia (Italy). All analyses were conducted using the 229 timeseries with more than 50 years of daily recordings, except for the interpolation of index-rainfall, which was implemented including also shorter series, with at least 30 years of observations (i.e. using the extended network of 256 raingauges; see Sect. 2). Section 4.1 describes the preliminary analysis conducted to conclude on a proper distribution model and parameter estimation method, while Sects. 4.2 and 4.3 focus on the implementation of the regional and boundaryless approaches, respectively. The performances of the two approaches are assessed and compared in Sect. 4.4.

4.1 Local analysis and preliminary investigations

As noted in Sect. 3.1, under proper renormalization and if nondegenerate, the GEV model is the limiting distribution of block maxima when the block size M tends to infinity. In addition, as reviewed in Sect. 3.1, the GEV distribution has been widely applied in statistical hydrology to model annual rainfall maxima. To empirically confirm that the GEV assumption can reasonably describe the analyzed timeseries of annual rainfall, we conducted a preliminary investigation using the diagnostic diagram based on L-moment ratios proposed by Hosking (1990); see discussion in Sect. 3.2.

Figure 2 compares the L-ratio curves (L-skewness, L-kurtosis) for different theoretical distribution models (i.e. GEV, Generalized Logistic, Lognormal, Pearson type III) to the corresponding empirical L-moment ratios. The latter were estimated using the annual maxima series of daily precipitation from the subset of 229 stations with more than 50 years of complete recordings. From visual inspection of Fig. 2, one concludes that the theoretical L-moment ratio curve corresponding to a GEV model is the most representative one in terms of minimum average distance from the empirically estimated (L-skewness, L-kurtosis) combinations. The representativeness of the GEV model is also justified by the fact that the point corresponding to the regional statistics (τR3, τR4) obtained by averaging the at-site L-skewness and L-kurtosis empirical estimates from the 229 stations using Eqs. (13) and (14) (filled large mark in Fig. 2), lies on the GEV theoretical L-moment ratio curve. In addition, Table 1 reports the regional averages of L-moment ratios estimated at the 229 sites, as well as the regional averages of the parameters of the fitted Kappa distribution (see Eq. (12) and Sect. 3.3) to the standardized to mean-1 at-site data, using the PWM method; see Hosking and Wallis (1997). The fact that the regional average of the estimated h parameter of the Kappa distribution is very close to zero, further supports the selection of the GEV distribution as the most representative model for the analyzed annual maxima, as expected by theoretical arguments.

Table 1 Regional values of sample L-moment ratios (\(\tau^{R} ,\tau_{3}^{R} ,\tau_{4}^{R}\)) and Kappa distribution parameter estimates (\(\xi^{R} ,\alpha^{R} ,k^{R} ,h^{R}\)), based on the standardized to mean-1 229 timeseries with more than 50 years of complete recordings; see main text for details
Full size table

Regarding the effectiveness of different methods for GEV parameter estimation, we conducted a preliminary investigation using the methods of Simple Moments (SM), Maximum Likelihood (ML) and Probability Weighted Moments (PWM). Simple moments resulted in significantly biased estimates in cases when the empirical distributions exhibited heavy upper tails and, therefore, were not considered for the remainder of the analysis. With reference to the other two methods, when applied to the standardized to mean-1 timeseries from the 229 sites, our analysis did not reveal any clear competitive advantage of either ML or PWM. In seldom cases where k estimates exhibited small negative values, these were set to zero (see discussion in Sect. 3.1). Figure 3a, b show scatterplots of the ML versus PWM local estimates of k and σ*, respectively. One sees that the two methods produce compatible results, with the corresponding points fluctuating around the 1:1 line. Similarly, good agreement is indicated by the empirical cumulative distribution functions of the estimated k and σ*, when using the ML and PWM methods (see Fig. 3c, d). Based on the aforementioned findings, and the fact that the PWM approach exhibits better performance when dealing with small sample sizes (see Hosking et al. 1985, and Sect. 3.2), we decided to proceed by using the PWM approach for estimation of distribution parameters. In addition, PWM is the parameter estimation method of general choice for regional frequency analysis purposes (see e.g. Hosking and Wallis 1993, 1997) and, therefore, it is used here also when applying the suggested boundaryless approach, to ensure a fair comparison.

Fig. 3
figure 3

Scatterplots (upper panels) and empirical cumulative distribution functions (lower panels) of the GEV distribution parameters k (left column) and σ* (right column) estimated by applying the Maximum Likelihood (ML) and Probability Weighted Moments (PWM) methods to the 229 series of annual maxima with more than 50 years of complete recordings

Full size image

4.2 Results from the regional approach

As discussed in Sect. 3.3, grouping of observational sites in potentially homogeneous regions was conducted by a hierarchical cluster analysis based on Ward's method, in order to minimize the total within-group variance of different combinations of sample L-CV (τ) and L-skewness (τ3) metrics; see discussion below. In order to keep compact sets of stations at each merging step, the condition of territorial continuity was imposed using Delaunay’s triangulation among the raingauge locations, allowing solely aggregation of neighboring stations and/or clusters. In this way, we obtained several cluster configurations by using either the variance of τ as metric, or the weighted average of τ and τ3 variances. In the latter case, to account for the higher statistical variability of τ3 relative to τ estimates, the ratio of the applied weights was set equal to the empirical mean of the ratio of the standard deviations σL-CV and σL-skewness of τ and τ3, respectively (i.e. E[σL-CV /σL-skewness] ≈ 1/3, see below and Fig. 4). The standard deviations of τ and τ3 were obtained by simulating Nsim = 10 000 ensembles of synthetic timeseries at each site i = 1, 2,…, N, with length equal to that of the corresponding historical series n(i), using a Kappa distribution model (see Hosking 1994 and Sect. 3.3) with parameters in Table 1. The empirical probability density function of the obtained ratios is shown in Fig. 4, where one sees that the dispersion around the mean value 1/3 is relatively small. As a matter of fact, we found only minor differences among the outcomes of the cluster analysis based only on τ, or both τ and τ3 metrics (probably due to the high linear correlation, ρ = 0.63, between τ and τ3 estimates) and, subsequently, we made only minor adjustments at the boundaries of homogeneous regions to obtain a common configuration. In doing so, we took into account orographic features and geographical exposure, while minimizing the error metrics described in Sect. 3.5 when using the regional parameters of the GEV distribution in each considered cluster. The resulting adjustments included merging of a cluster facing the eastern coast of Sardinia, with a cluster located at the southwest part of Sardinia with eastward exposition. The merger was initially driven by the fact that both regions are exposed to humid air fluxes induced by Sirocco winds, causing intense precipitation events (sometimes larger than 500 mm in less than 24 h, see also Fig. 1c), but it is also supported by the fact that both regions pool together stations characterized by the highest coefficients of variation and skewness values (Hellies 2016). The reason why the corresponding clusters were not initially merged, is due to the lack of spatial continuity as initially embodied in Delaunay’s triangulation of the station network.

Fig. 4
figure 4

Empirical probability density function of ratio σL-CV/σL-skewness of the standard deviations of τ(σL-CV) and τ3 (σL-skewness), as obtained from 10 000 ensembles of synthetic time series with length equal to that of the corresponding historical ones. The dashed vertical line denotes the ratio 1:3; see main text for details

Full size image

The terminal partitioning of the island of Sardinia into four homogeneous regions is illustrated in Fig. 5a, using different symbols and colors (e.g. the blue diamond symbols indicate region C3, resulting from the merger of the cluster facing the eastern coast of Sardinia, with the cluster at the southwest part of Sardinia with eastward exposition). Table 2 summarizes the statistical characteristics of each homogeneous region, i.e. the regional L-moment ratios τR, τ3R and τ4R; the heterogeneity measures H, H2, and H3 (see Sect. 3.3 and "Appendix"), and the regional value of Kappa distribution parameter h. The latter was found to be very close to zero for all terminal clusters, confirming the suitability of the GEV distribution in modeling the statistical character of annual maxima of daily rainfall in each homogeneous region.

Fig. 5
figure 5

a Final configuration of the 4 contiguous homogeneous regions; b Theoretical L-moment ratio curves of common distribution models, as compared to the sample L-moment ratios of annual maxima of daily precipitation from the network of 229 stations with more than 50 years of complete recordings (colored circles). Colors correspond to different homogeneous regions, as shown in (a). Filled large marks correspond to the regional averages of sample L-moment ratios inside homogeneous areas

Full size image
Table 2 Regional values of sample L-moment ratios (\(\tau^{R} ,\tau_{3}^{R} ,\tau_{4}^{R}\)), heterogeneity measures (H, H2, H3), and Kappa distribution parameter h for each identified  homogeneous region. The IDs of the four terminal clusters (homogeneous regions), the colors used in Fig. 5 to denote station locations, and the number of stations in each terminal cluster are reported in the first and second columns, respectively
Full size table

Figure 5b shows the estimated L-moment ratios τ3 and τ4 for the stations inside each homogeneous region, using the same colors and symbols as in Fig. 5a. In the same L-moment ratios diagram, we used large marks to denote the regional statistics (τR3, τR4) of the terminal clusters (see also Table 2). The latter lie on the theoretical GEV L-moment ratios curve, providing additional confirmation that the GEV distribution can effectively be used to model the statistical character of each homogeneous region, with parameters shown in Table 3.

Table 3 Estimates of GEV distribution parameters (k, σ*, µ*) for the four identified homogeneous regions; see main text for details
Full size table

One sees that region C1 is characterized by the lowest values of shape (k) and dimensionless scale (σ*) regional parameters, probably because it is located far from the coast at the center of the Island (see red circles in Fig. 5), thus being less sensitive to interactions of humid air masses from the sea with orography. On the other hand, region C3 (see blue diamonds in Fig. 5) is characterized by the highest regional values of distribution shape parameters, due to the interaction of cyclonic perturbations with the steep eastward orography gradients, resulting in intense precipitation events.

Application of the regional approach requires parameterization of the GEV model in Eq. (1) using the local scale σ and location µ parameters. These can be obtained by multiplying the σ* and µ* values for each homogeneous region in Table 3, by the index-rainfall m. For this last statistic, we did not find any significant linkage to morphometric properties and, therefore, we decided to interpolate the at-site index-rainfall estimates obtained from the extended sample of 256 timeseries exhibiting more than 30 years of complete recordings, resulting in a seamless index-rainfall field. As discussed in Sect. 3.3, this is a common feature of both regional and boundaryless approaches considered in this study, and it is discussed in the next subsection.

4.3 Results from the boundaryless approach

The proposed boundaryless approach is based on KUD spatial interpolation of the GEV shape and dimensionless scale parameters, and the index-rainfall field, according to the following hierarchical approach (see also Sect. 3.4): (i) First, we focus on the spatial interpolation of the shape parameter k, to obtain a smoothly varying field; (ii) we use the interpolated k estimates from step (i), to condition estimation and proceed with interpolation of the dimensionless scale parameter σ*; (iii) as a final step, we interpolate the index-rainfall m, which characterizes the local scaling factor for both the regional and boundaryless approaches.

To optimize the obtained results in terms of accuracy and robustness, we made some preliminary analyses to select the theoretical variograms that best fits the sample of annual rainfall maxima and, also, determine an optimal setting for our geostatistical analysis (i.e. number of nearest stations to be used for interpolation of distribution parameters, and the lower cut-off threshold regarding the length of the timeseries to be included in the analysis). Preliminary analyses were conducted using both ordinary kriging (OK) and kriging for uncertain data (KUD). Indeed, while OK reproduces the exact values of empirical estimates at the measuring locations, from a theoretical point of view, KUD is expected to perform better when interpolating estimates of distribution parameters, which are affected by sampling variability.

Concerning the choice of the theoretical variogram to be used, after some initial attempts to fit location dependent variograms, we decided to use a unique variogram for the whole study area. The empirical raw variogram was thus built using all possible couples of raingauge stations that exceeded a certain minimum number of observed annual maxima (the tradeoff rule regarding the minimum length of timeseries included in the analysis is discussed below), and then binned together according to 5 km distance intervals (i.e. 0–5 km, 5–10 km, 10–15 km, etc.). The resulting raw variogram was then used to calibrate theoretical stationary and nonstationary candidate variogram models, including the Gaussian, exponential, spherical, hole-effect, power and linear models. The best fit was obtained for the case of the exponential model, which was adopted in our analysis to describe the covariance properties of all statistics used in the boundaryless approach.

Next we investigated the optimal setting for the spatial interpolation of the GEV shape parameter k, dimensionless scale parameter σ*, and index-rainfall m in terms of: (i) number of nearest stations to be considered when building the kriging system of linear equations; (ii) minimum length of the timeseries to be included in the analysis; (iii) estimation method (OK vs KUD), assuming no a priori preference. For each setting, the overall performances were evaluated using a leave-one-out cross-validation procedure, based on the mean absolute error between the at-site empirical estimate and the interpolated one. The latter was obtained by neglecting all applicable information at the considered site, which was instead used as benchmark for error estimation. Figures 6a–c show the mean absolute error resulting from interpolation of the shape k and the dimensionless scale σ* parameters, and the index-rainfall m, respectively, as a function of the number of nearest locations used to build the kriging system of linear equations. Results from the application of OK (KUD) interpolation are noted by empty circles (asterisks), while the effect of the minimum length of the timeseries included in the analyses is indicated by different colors (i.e. the lower the minimum length, the larger the number of stations included in the analysis). An important finding from Fig. 6, is that KUD outperforms OK interpolations for any setting. In addition, a number of 10 nearest stations to be included when building the kriging system of linear equations suffices to minimize the interpolation error of k, σ*, and m. The only difference is that, while for both GEV parameters k and σ* the optimal cut-off threshold regarding the minimum length of timeseries to be included in the analysis is on the order of 50 years, for index-rainfall m the best interpolation performance is attained when including also shorter timeseries, on the order of 30 years.

Fig. 6
figure 6

Mean absolute error of OK (circles) and KUD (stars) estimates of k, σ*, and m as a function of the number of nearest stations used to solve each local kriging system, including only time series with more than Ny = 30, 50, and 70 years of complete recordings (red, black, and blue colors respectively). Results for: a GEV shape parameter k; b GEV dimensionless scale parameter σ*; c index-rainfall m

Full size image

In the light of the aforementioned preliminary analyses, we decided to apply KUD for all relevant parameters (i.e. k, σ* and m) on a regular grid with 1 km spatial resolution, using information from the 10 nearest stations to each grid-point. For interpolation of k and σ* (i.e. where estimation uncertainty is larger) we used information from stations with at least 50 complete years of observations (a total number of 229), while for interpolation of index-rainfall m (characterized by lower sample variability) we applied a lower threshold and used annual maxima series from stations with at least 30 years of complete recordings (a total number of 256); see also Sect. 2.

Despite using KUD interpolation, we observed some noise at sporadic locations of the spatial grid, originating from changes in the coefficients and constant terms of the kriging system of linear equations (i.e. built using information from the 10 nearest stations), as one moves to different locations of the computational grid. To smooth out this local variability, we applied a simple moving average window with dimensions 9 × 9 km. Comparison of the filtered and originally interpolated parameter fields revealed negligible differences at the peaks, with the moving average window allowing for preservation of large scale spatial trends, with the added benefit of continuity in parameter estimates.

The results of the spatial interpolation of the shape parameter k, the dimensionless scale parameter σ*, and the index-rainfall m are shown in Fig. 7. The highest values of parameters k and σ* are located in the eastern and southwestern parts of the Island, which are characterized by intense precipitation events (as already noted in Sect. 2; see also Fig. 1c), while the index-rainfall m exhibits a peak of about 125 mm/d at the eastern part of the Island.

Fig. 7
figure 7

KUD interpolation of GEV parameters k and σ* (using 229 time series with more than 50 years of complete recordings), and index-rainfall m (using 256 time series with more than 30 years of complete recordings)

Full size image

4.4 Comparison between regional and boundaryless approaches

The performances of the regional and boundaryless approaches were evaluated and compared using the error metrics introduced in Sect. 3.5. In this context, Table 4 summarizes the results in terms of average values of error metrics computed at the 229 raingauge locations with at least 50 years of observations, including absolute (relative) errors in estimating the quantiles of the 5 highest observations at each site (i.e. MAE(5) and MAEr(5)), and errors in the whole distribution range (A2 and W2 metrics). The first row in Table 4 reports the errors corresponding to the local fits of the GEV theoretical distribution model, which are reported here as benchmarks, representative of the smallest possible error one may reasonably achieve. Results from the regional and boundaryless approaches are reported in the second and third rows of Table 4, where one sees that the errors of the boundaryless approach are always lower than those of the regional approach, and very close to those of the local fits.

Table 4 Average performance metrics of the local, regional and boundaryless approaches, based on the 229 daily rainfall timeseries with more than 50 years of complete recordings
Full size table

Although results presented in the first rows of Table 4 suggest that the boundaryless approach outperforms the regional one, it must be noted that fair comparison of the tested approaches should refer to ungauged locations. To evaluate the relative performance of the two approaches miming ungauged conditions, we applied a leave-one-out cross-validation (LOOCV) procedure, implementing both the regional and boundaryless approaches N = 229 times to estimate the parent distribution at each raingauge site, using solely information from the remaining N-1 sites with at least 50 years of complete observations. In each iteration, information from the blinded raingauge was only used to evaluate the errors of the estimated parent distribution by applying the same metrics introduced in Sect. 3.5. Specifically, for the regional approach the blinded site was assigned to the same region as the nearest station, and the GEV distribution model in Eq. (4) was consequently parameterized with the corresponding regional estimates. For the boundaryless approach, application of the LOOCV is straightforward since parameterization of Eq. (4) at the location of the blinded raingauge is provided by interpolation of the N-1 parameter estimates at the remaining sites. Finally, for a fair comparison, the local GEV in Eq. (1) was parameterized with the same index-rainfall m for both approaches. A summary of results of the LOOCV procedure is presented in the last two rows of Table 4, which clearly confirms the superiority of the boundaryless approach relative to the regional one at ungauged locations.

More details regarding the outcome of the LOOCV procedure are illustrated in Fig. 8, which shows the spatial distribution of the LOOCV error metric MEr(5) (i.e. the average relative overestimation/underestimation error of the 5 highest recordings at each site) for the regional (left) and boundaryless (right) approaches. The radius of each circle in Fig. 8 is proportional to the error magnitude, while red (blue) color denotes overestimation (underestimation) larger than ± 20%. Evidently, the boundaryless approach performs better than the regional one, with the former resulting in very few stations with relative error larger than ± 20%. This becomes apparent even from visual inspection of Fig. 8a, b, based on the predominance of green color (i.e. relative errors smaller than ± 20%) and the smaller sizes of symbols in Fig. 8b (boundaryless case). To complement the visual comparison between Fig. 8a and 8b, histograms of LOOCV MEr(5), W2 and A2 are presented in Fig. 9a–c, respectively. One sees that, when compared to the regional approach, the boundaryless approach is more robust, characterized by estimation errors that exhibit both lower mean value (i.e. bias) and variance.

Fig. 8
figure 8

Spatial distribution of error metric MEr(5) resulting from the cross-validation procedure of the regional (left) and boundaryless (right) approaches. Symbol sizes are proportional to the absolute value of error metric MEr (5); green color indicates sites  where  error  is lower than +/− 20%, while red and blue colors refer to larger overestimation or underestimation errors, respectively

Full size image
Fig. 9
figure 9

Histograms of error metrics of the regional (blue) and boundaryless (red) approaches: a MEr(5), b W2, c A2

Full size image

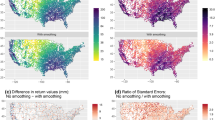
In conclusion, all applied error metrics revealed the superiority of the boundaryless approach relative to the regional one. To make even clearer the advantages of the boundaryless approach in practical applications, Fig. 10 compares the maps of daily rainfall depth (mm) with return period T = 200 yr, obtained using the regional (left panel) and boundaryless (right panel) approaches. As displayed in Fig. 10a, the regional approach results in abrupt discontinuities along the boundaries of homogeneous regions, indicative of rainfall depth shifts that cannot be justified based on physical arguments. Since the location of the boundaries of homogenous regions may vary due to many factors, including the method used for cluster identification, the density and spatial distribution of the network, as well as sampling variability issues and subjective interpretations, it becomes evident that, to what concerns practical applications, any possible assignment of an ungauged site located close to the boundaries to a certain homogeneous region, is subject to large uncertainties. The proposed boundaryless approach overcomes this limitation, as all distribution parameters, and quantiles corresponding to different non-exceedance probability levels, vary seamlessly in space; see Fig. 10b.

Fig. 10
figure 10

Spatial distribution of the quantiles of daily rainfall depth (mm) with return period T = 200 years, as obtained from the regional (left) and boundaryless (right) approaches

Full size image

An additional advantage of the boundaryless approach, is that by avoiding grouping of stations into homogeneous regions, it can more effectively describe the effects of topography and local climatology on the distribution of extreme rainfall, minimizing underestimation/overestimation issues. For example, focusing on the eastern part of Sardinia in Fig. 10a, it becomes apparent that the regional approach introduces some kind of smoothing at the central part of the homogeneous region C3, due to the common regional growth curve; i.e. the spatial variability of the 200 yr rainfall quantiles inside terminal cluster C3 is solely driven by spatial variations of the index-rainfall. This is not the case for the boundaryless approach, where the growth curve varies spatially, allowing for more accurate reproduction of rainfall extremal properties; see Fig. 10b and similarity with Fig. 1c.

5 Summary considerations and conclusions

Assessment and management of flood risks is strictly connected to accurate and robust estimation of extreme rainfall events. Although addressed by many scientists, dating back to the pioneering works on regional frequency analysis (see Introduction), spatial characterization of the frequency of rainfall extremes still exhibits enough room for improvements. Indeed, most studies on the spatial distribution of extreme rainfall limit interest to regional approaches where, except for an at-site dependent index-variable, higher order moments of the parent distribution are considered constant inside wide areas, which are assumed to be homogeneous. Regional frequency analysis based on homogeneous regions became very popular at the end of last century (see e.g. the review in Hosking and Wallis 1997), primarily due to the limited length of available timeseries of observed maxima. Indeed, for short samples, any estimation method of distribution parameters related to higher order moments is affected by significant estimation uncertainties, making site-to-site differences indistinguishable from a statistical point of view, especially inside wide areas exhibiting similar large-scale topographic and climatological characteristics. Under this setting, timeseries corresponding to stations inside homogeneous regions can be properly standardized (e.g. through division by the local mean) to be described by a common distribution model. The parameters of the latter (usually referred to as parent distribution) can be estimated by pooling together all time-series within the identified homogeneous region, significantly reducing the estimation error, in expense of spatial statistical detail.

All aforementioned considerations are certainly true and very appealing if one really deals with ensembles of homogeneous timeseries. However, when processing observations of precipitation, which is the final product of complex interactions of atmospheric processes with orography and the land-sea boundary, the question one should answer is: In such a complex setting, does regional homogeneity really exist? Usually hydrologists answer this question by applying statistical tests, thus a region is considered as homogeneous if the differences among specified parameters, metrics or statistics, derived from different stations belonging to the considered region, are comparable to the magnitude of the estimation error. This also implies that if the analysis is based solely on statistical arguments, one will find that the extent of homogeneous regions depends also on the length of the observation period. Indeed, for short enough timeseries, statistical tests often lead to the acceptance of wide areas as statistically homogeneous regions, because estimation errors will be high enough to hide possible site-to-site differences of the local climatology. Conversely, for long enough timeseries, only when splitting the original region into a number of sub-regions, the null hypothesis of spatial homogeneity will not be rejected. In other words, the longer the timeseries, the larger the number of homogenous regions resulting from statistical tests.

Even ignoring the above reasoning and accepting that any partitioning of the study area into homogenous regions can be revised in the future in the light of additional observations, the regional approach is still subject to serious drawbacks. One is related to abrupt shifts of quantile estimates along the boundaries of contiguous regions, due to differences in the regional parameters of the parent distribution. In most cases, such discontinuities cannot be physically justified, as climatological variables, such as precipitation, vary seamlessly in space. In addition, for practical applications, the presence of such discontinuities is an undesired source of uncertainty and ambiguity; e.g. when one needs to determine the design rainfall for a catchment consisted of sub-catchments belonging to different homogeneous regions.

An additional and, possibly more, critical drawback of the regional approach is that homogeneity tests may fail to detect local rainfall features associated with more intense precipitation events relative to the wider tested region. In such a case, the same coefficient of variation, skewness, etc. will be assigned to any location inside the region and, consequently, rainfall quantiles at some locations can be severely underestimated. This drawback is not surprising, since the final parent distribution in each homogenous region is, to some extent, an average of different at-site behaviors, leading to quantile overestimation in some parts of the considered region, and underestimation inside the remaining parts.

Another important source of uncertainty in the regional approach is related to the selection procedure used to pool together stations in a hypothetically homogeneous region. Indeed, depending on the adopted procedure, stations located at the boundaries of homogeneous regions, will be subject to quantile overestimation/underestimation issues, similar to those discussed above.

We have shown how problems related to application of the regional approach for extreme rainfall estimation can be overcome by implementing a quite simple boundaryless approach based on geostatistical analysis of all distribution parameters, using kriging for uncertain data (KUD). Indeed, the boundaryless approach can better characterize local topographic and climatological features, such as those related to the presence of orographic barriers. For example, as shown in our application, the spatial distribution of quantiles obtained using the boundaryless approach (see Fig. 10b), reliably reproduces the pattern of extreme rainfall events in Sardinia (see Fig. 1c), which are localized due to the interaction of cyclonic activity with the main mountain ranges (see Fig. 1a). Conversely, the quantile estimates obtained using the regional approach at the same locations (Fig. 10a), are smeared out by the assumption of a common growth curve inside the whole homogeneous region (terminal cluster C3).

In addition, we have also shown that the boundaryless approach reproduces in a reliable and seamless fashion the spatial variation of rainfall quantiles (see Fig. 10b), avoiding unrealistic jumps and shifts (Fig. 10a), while minimizing subjective interpretations regarding the boundaries of homogeneous regions. In summary, by applying the boundaryless approach, it is possible to bypass most of the typical drawbacks of the regional approach.

Besides empirical evidence on the superiority and advantages of the boundaryless approach with respect to the regional one, we complemented our analysis by assessing the performances of the two approaches in reproducing the spatial distribution of observed extremes using two classes of error metrics. The first class quantifies the squared differences between the empirical and fitted cumulative distribution functions, whereas the second class quantifies the errors in reproducing the highest observed values in record. The obtained results unanimously confirmed the superiority of the boundaryless approach in assessing the frequency of rainfall extremes at ungauged sites, based on a leave-one-out cross-validation procedure.

It is also worth mentioning that, although many probability distributions have been proposed and applied to describe hydrological extremes, during implementation of the regional and boundaryless approaches, we obtained sufficient evidence regarding the suitability of the Generalized Extreme Value (GEV) distribution for modeling annual maxima of daily rainfall, even under pre-asymptotic conditions (see e.g. Langousis et al. 2013; Veneziano et al. 2009). To account for uncertainties in parameter estimation, in the proposed boundaryless approach interpolations were conducted using kriging for uncertain data (KUD), where at-site error variances of statistical estimates were determined through Monte Carlo simulation. In addition, since parameters controlled by higher order moments are affected by higher estimation errors, the boundaryless approach was implemented in a hierarchical setting: first we interpolated the GEV shape parameter estimates, then we interpolated the GEV scale parameter estimates conditioned on the previously interpolated shape parameters, and lastly the index-rainfall. Finally, to optimize the obtained results in terms of accuracy and robustness, we conducted preliminary analyses to determine the theoretical variogram to be applied, the number of nearest stations to be used when developing the kriging system of linear equations, and the lower cut-off threshold regarding the length of the timeseries to be included in the analysis.

While the superiority of the boundaryless approach relative to the regional one has been quantitatively assessed in a detailed real-world comparison, there is still significant room for improvements, such as the use of locally-dependent anisotropic variogram models to more accurately describe the effects induced by the interaction of humid air masses with orographic barriers, more in-depth assessment of available interpolation schemes, and the statistical linkage among the spatial distributions of daily and smaller duration rainfall estimates. These will form the subjects of future communications.