1 Introduction

Numerical methods for solving differential equations have already been extensively investigated in recent years. The further development of these methods represents an important point to increase their efficiency. Several method can be used for the spatial discretization of the domain. Among them, the finite element method (FEM) is one of the most used one. While FEM is restricted to the usage of regular shaped elements, the recently developed virtual element method (VEM) represents one further step towards a generalization of the finite element method, see [1, 2]. The virtual element method (VEM) allows the usage of meshes with highly irregular shaped elements, including non-convex shapes, as outlined in [2]. The large number of positive properties of VEM increases the variety of possible applications in engineering and science. Recent works on virtual elements have been employed to linear elastic deformations in [2, 3], contact problems in [4, 5], elasto-plastic deformations in [6,7,8], anisotropic materials in [9,10,11], curvilinear virtual elements for 2D solid mechanics applications in [12], hyperelastic materials at finite deformations in [13, 14], crack-propagation for 2D elastic solids at small strains in [15], phase-field modeling of brittle and ductile fracture in [16, 17].

Dynamic behavior has a strong influence on the mechanical behaviour of solids, failure of components and the prediction of their real response. Thus a large amount of work has been devoted to these class of problems, as well from the theoretical side as from the numerical point of view, see e.g. [18,19,20,21,22,23] and [24]. In the range of virtual element methods most of the investigations are related to static problems so far. First investigations in dynamics can be found in [25] who proposed a virtual element method for linear elastodynamics problems. However their formulations are restricted to small strain settings. This has motivated the authors into enlarge the application of VEM from the static to the dynamic case for finite deformations, see [26]. The presented contribution extends now the application of the virtual element method to 3D finite strain dynamic elasto-plastic problems, using a mixed formulation to correctly account for the case of plastic incompressibility.

Typically the construction of a virtual element is divided into a projection step and a stabilization step. Within the projection step, a quantity \(\varphi _h\) is replaced by its projection \(\varphi _\Pi \) onto a polynomial space. Using this projected quantity in the weak formulation or energy functional yields a rank-deficient structure which needs to be stabilized. In the second step, the stabilization term, which is a function of the difference \(\varphi _h - \varphi _\Pi \) between the original variable and the projected quantity needs to be evaluated. Various possibilities exist to evaluate this stabilization term. To this end, Da Veiga et al. [27] proposed a stabilization term, where integrations take place at the element boundaries. Wriggers et al. presented in [14] a novel stabilization technique, based on a triangulated sub-mesh, which uses the same nodes as the original mesh. This formulation however needed an integration within the volume of the virtual element. The stabilization parameters for the latter stabilization were based on an approach first described for finite elements in Nadler and Rubin [28], generalized in Boerner et al. [29] and simplified in Krysl [30] for the stabilization of a reduced order mean-strain hexahedron. The stabilzation method described in [14] is used in this paper as well.

The elasto-plastic dynamic behavior of the solid is modelled on the basis of a numerical integration scheme. Here we utilize the implicit Newmark method as documented in [31, 32]. It has the advantage that mass and tangent stiffness matrix of the virtual element are combined for the solution. Thus a rank deficient mass matrix does not provide any problem once the tangent stiffness matrix is stabilized as described above. Based on this observation it is sufficient to compute the mass matrix only for the consistency part, using the projection \(\ddot{\varphi }_\Pi \), see [1] and [26]. This approach provides some advantage in comparison with [25] who need stabilization of the mass matrix within an explicit time integration scheme.

The structure of the presented work is as follows. In Sect. 2.1 the governing equations for nonlinear dynamic elasto-plasticity are outlined. In addition to the pure displacement formulation, a mixed formulation based on Hu-Washizu functional is introduced. Section 3 summarizes the virtual element method. It includes details on the computation of the element mass-matrix and the algorithmic treatment of finite strain plasticity. To verify the proposed virtual element formulations, a various number of examples are demonstrated and discussed in Sect. 4. Section 5 briefly summarizes the work and gives some concluding remarks.

2 Governing equations for finite strain elasto-plasticity

In this section the kinematical relations and balance laws are described together with the boundary and initial conditions for three-dimensionale solids. Variational forms are provided for the pure displacement and mixed forms as well as constitutive equations for finite plasticity.

2.1 Pure displacement formulation

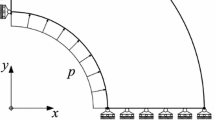
In this section we summarize the finite strain elasto-plastic formulation (see e.g. [6, 7]) and supplement it by the dynamic behavior. For that we first consider an elastic Body \(\Omega \subset {\mathbb {R}}^3\) with boundary \(\Gamma \). This boundary is decomposed into a non-overlapping Dirichlet \(\Gamma _{D}\) and Neumann \(\Gamma _{N}\) boundary, such that \(\Gamma _{D} \cup \Gamma _{N} = \Gamma \), see Fig. 1.

Fig. 1
figure 1

Solid with boundary conditions

Full size image

The position \({{\varvec{x}}}\) of a material point in the current configuration is given by the deformation map

$$\begin{aligned} {{\varvec{x}}} = \varvec{\varphi }({{\varvec{X}}},t) = {{\varvec{X}}} + {{\varvec{u}}}({{\varvec{X}}},t)\,, \end{aligned}$$
(1)

where \({{\varvec{X}}}\) is the position of a material point in the initial configuration and \({{\varvec{u}}}({{\varvec{X}}},t)\) is the displacement and t the time. In the further course of this work we will skip the explicit specification of the dependence of variables on the initial configuration and time thus we will write: \({{\varvec{u}}}={{\varvec{u}}}({{\varvec{X}}},t)\). A key quantity for the description of finite deformations is the deformation gradient \({{\varvec{F}}}\), defined by the Fréchet derivative as

$$\begin{aligned} {{\varvec{F}}} = \text{ Grad }\,\varvec{\varphi } = \nabla _{{{\varvec{X}}}}\, \varvec{\varphi }\,, \end{aligned}$$
(2)

where the gradient is evaluated with respect to the initial configuration \({{\varvec{X}}}\). For elasto-plastic material behavior, the deformation gradient is decomposed into an elastic \({{\varvec{F}}}_e\) and a plastic part \({{\varvec{F}}}_p\) as

$$\begin{aligned} {{\varvec{F}}} = {{\varvec{F}}}_e {{\varvec{F}}}_p\,, \end{aligned}$$
(3)

which is also known as the multiplicative split of the deformation gradient for finite strain plasticity. We further consider the isochoric \(J_2\)-plasticity theory which leads to the fact that the volume change due to plasticity can be neglected

$$\begin{aligned} J_p = \mathrm {det} {{\varvec{F}}}_p =1 \quad \text{ yields } \quad J=J_e J_p=J_e=\mathrm {det} {{\varvec{F}}}_e \,, \end{aligned}$$
(4)

where \(J_e\) and \(J_p\) are the elastic and plastic part of the Jacobian J. Next, the elastic part of the left Cauchy-Green tensor \( {{\varvec{b}}}_e\) is defined as

$$\begin{aligned} {{\varvec{b}}}_e= & {} {J_e}^{2/3} \bar{{{\varvec{b}}}}_e = {{\varvec{F}}}_e {{{\varvec{F}}}_e}^T = {{\varvec{F}}} {{{\varvec{C}}}_p}^{-1} {{\varvec{F}}}^T \quad \text{ with } \nonumber \\ {{\varvec{C}}}_p= & {} {{{\varvec{F}}}_p}^T {{\varvec{F}}}_p \quad \text{ and } \quad \mathrm {det} {{\varvec{b}}}_e={J_e}^2 \,, \end{aligned}$$
(5)

where \(\bar{{{\varvec{b}}}}_e\) is the deviatoric part of the elastic left Cauchy-Green tensor, with \(\mathrm {det} \bar{{{\varvec{b}}}}_e =1\) and \({{\varvec{C}}}_p\) is the plastic part of the right Cauchy-Green tensor.

The solid \(\Omega \) has to satisfy the balance of linear momentum, with the body forces \(\overline{{{\varvec{f}}}}\),

$$\begin{aligned} \text{ Div }\,{{\varvec{P}}} + \overline{{{\varvec{f}}}} = \rho \ddot{{{\varvec{u}}}} \quad \text{ with } \quad {{\varvec{P}}} = {{\varvec{F\,S}}} \; , \end{aligned}$$
(6)

where \({{\varvec{P}}}\), \({{\varvec{S}}}\) are the 1st and 2nd Piola-Kirchhoff stresses, respectively. The right side of the equation (6)\(_1\) is taking the dynamic effects \(\rho \ddot{{{\varvec{u}}}}\) into consideration. The Dirichlet and Neumann boundary conditions are defined by

$$\begin{aligned} {{\varvec{u}}}({{\varvec{X}}},t)&= \bar{{{\varvec{u}}}}({{\varvec{X}}},t) \qquad \text{ on }\ {\Gamma _{D}}\,, \end{aligned}$$
(7)
$$\begin{aligned} {{\varvec{P}}}({{\varvec{X}}},t){{\varvec{N}}}&= \bar{{{\varvec{t}}}}({{\varvec{X}}},t)\qquad \text{ on }\ {\Gamma _{N}}\,, \end{aligned}$$
(8)

here \({{\varvec{N}}}\) is the outward unit normal vector related to the initial configuration, \(\bar{{{\varvec{u}}}}\) represents the prescribed displacement on the Dirichlet boundary \(\Gamma _{D}\), and \(\bar{{{\varvec{t}}}}\) depicts the surface traction at the Neumann boundary \( \Gamma _{N}\), as illustrated in Fig. 1. Furthermore we have the initial conditions at time \(t=0\)

$$\begin{aligned} {{\varvec{u}}}({{\varvec{X}}},0)&= {{\varvec{u}}}_0({{\varvec{X}}}) \qquad \text{ in }\ {\Omega } \end{aligned}$$
(9)
$$\begin{aligned} \dot{{{\varvec{u}}}}({{\varvec{X}}},0)&= \dot{{{\varvec{u}}}}_0({{\varvec{X}}}) \qquad \text{ in }\ {\Omega } \,. \end{aligned}$$
(10)

With the introduction of a strain energy function \(\Psi _e\) for the elastic part of the deformation, the quantities such as the 1st Piola-Kirchhoff stress \({{\varvec{P}}}\) and 2nd Piola-Kirchhoff stress \({{\varvec{S}}}\) can be derived as follows:

$$\begin{aligned} {{\varvec{S}}}=2 \dfrac{\partial {\Psi _e}}{\partial {{{\varvec{C}}}_e}} \quad \text{ and } \quad {{\varvec{P}}}={{\varvec{F}}} {{\varvec{S}}} \end{aligned}$$
(11)

The push forward of the 2nd Piola-Kirchhoff stress to the current configuration yields the Cauchy \(\varvec{\sigma }\) and Kirchhoff stress \(\varvec{\tau }\):

$$\begin{aligned} \varvec{\sigma }=\dfrac{2}{J_e} {{\varvec{F}}}_e \dfrac{\partial {\Psi _e}}{\partial {{{\varvec{C}}}_e}} {{\varvec{F}}}_e^T \quad \text{ and } \quad \varvec{\tau }=J_e \varvec{\sigma } \end{aligned}$$
(12)

A homogeneous compressible isotropic elastic material is considered, here we use the Neo-Hookean strain energy function

$$\begin{aligned} \Psi _e= \frac{\kappa }{4}(J_e^2 -1 - 2\ln {J_e}) + \frac{\mu }{2} (\text{ tr } \,\bar{{{\varvec{b}}}}_e -3) \; , \end{aligned}$$
(13)

in terms of the bulk \(\kappa \) and shear \(\mu \) modulus. The elastic part of the Jacobian \({J_e}\) is computed as

$$\begin{aligned} {J_e} = \sqrt{\det {{\varvec{b}}}_e} \end{aligned}$$
(14)

Next, we use the potential energy function as a starting point for the development of a discretization method for the elastodynamics problem in (6). The static part of the potential is defined for elastic materials as

$$\begin{aligned} U^{stat}({{\varvec{u}}}) = \int \limits _{\Omega } \left[ \Psi _e({{\varvec{u}}}) - \overline{{{\varvec{f}}}}\cdot {{\varvec{u}}}\ \right] \ d\Omega - \int \limits _{\Gamma _N} \bar{{{\varvec{t}}}}\cdot {{\varvec{u}}} \ d\Gamma \, , \end{aligned}$$
(15)

whereas the dynamic part of the potential is the kinetic energy that describes inertial effects takes the form

$$\begin{aligned} {\mathcal {K}}({{\varvec{u}}}) =\frac{1}{2} \int \limits _{\Omega } \rho {\dot{{{\varvec{u}}}}}^2 \ d\Omega \,, \end{aligned}$$
(16)

where \(\rho \) is the density of the solid.

With the above set of equations, the finite strain elasto-dynamic problem is well formulated. Next the model for an elasto-plastic material behavior requires additionally the formulation of a yield function, a hardening law and an evolution equation for the plastic variables. We adopt the following yield function, which follows from the assumption of \(J_2\)-plasticity with nonlinear isotropic hardening,

$$\begin{aligned} \Phi = \sigma _{vM} - \left[ Y_0 + \left( Y_{\infty } - Y_0 \right) \left( 1 - e^{- \delta \alpha } \right) + H \alpha \right] \, , \end{aligned}$$
(17)

with

$$\begin{aligned} \sigma _{vM}= \sqrt{\dfrac{3}{2}} ||{{\varvec{s}}}|| \quad \text{ and } \quad {{\varvec{s}}}=\varvec{\tau }-\dfrac{1}{3} \text{ tr }\, \varvec{\tau }\; {{\varvec{1}}} \, . \end{aligned}$$
(18)

Here, \(\sigma _{vM}\) is the von Mises stress, \(Y_0\) the initial yield limit, \(Y_{\infty }\) the infinite yield stress, \(\delta \) the saturation parameter, H the hardening modulus and \(\alpha \) the hardening variable. The stress \({{\varvec{s}}}\) represents the deviatoric part of the Kichhoff stress. To account for phenomenological hardening/softening response, the equivalent plastic strain \(\alpha \) is defined as a local internal variable. For the formulation of an elasto-plastic problem an equation for the evolution of the plastic variable is needed, which can be written as, see e.g. [33],

$$\begin{aligned} {\mathcal {L}}_v {{\varvec{b}}}_e= & {} -2 {\dot{\gamma }} {{\varvec{n}}} {{\varvec{b}}}_e \quad \quad \text{ with } \quad \quad {{\varvec{n}}}= \dfrac{\partial \Phi }{\partial {{\varvec{s}}}} \quad \quad \text{ and } \nonumber \\ {\dot{\alpha }}= & {} {\dot{\gamma }} \quad \quad \text{ with } \quad \quad {\dot{\alpha }} \ge 0 \, . \end{aligned}$$
(19)

where \({\mathcal {L}}_v {{\varvec{b}}}_e\) denotes the Lie derivative in time of the left Cauchy-Green Tensor, \({\dot{\gamma }} \ge 0\) is the plastic Lagrange multiplier, and \({{\varvec{n}}}\) is the flow direction. For the algorithmic treatment of plasticity, we adopt the Kuhn-Tucker conditions for our model:

$$\begin{aligned} \Phi \le 0 \quad \quad , \quad \quad {\dot{\gamma }} \ge 0 \quad \quad \text{ and } \quad \quad \Phi {\dot{\gamma }} = 0 \, . \end{aligned}$$
(20)

Equation (19) can be written in an equivalent form as, see [33]:

$$\begin{aligned} \dot{{{\varvec{C}}}}_p^{-1} = -2 {\dot{\gamma }} {{\varvec{F}}}^{-1} {{\varvec{n}}} {{\varvec{F}}} {{\varvec{C}}}_p^{-1} \, . \end{aligned}$$
(21)

The evolution equation (21) will be used for the algorithmic treatment of plasticity within the numerical solution algorithm.

2.2 Mixed Hu-Washizu formulation

To obtain a locking free behavior in the framework of \(J_2\)-plasticity, we adopt the Hu-Washizu functional, see [34], for the virtual element formulation. Several mixed formulations were already discussed in the framework of virtual elements in [14] applied to finite strain hyperelastic solids. Here, based on the classical formulations in the context of finite element methods for finite strain plasticity, see [35], the following Hu-Washizu functional will be employed

$$\begin{aligned} U^{stat,HW}({{\varvec{u}}},\Theta ,p)= & {} \int \limits _{\Omega } \left[ \Psi ^{iso}({{\varvec{u}}})+ \Psi ^{p \Theta }({{\varvec{u}}},\Theta ,p) \right. \nonumber \\&\left. + \Psi ^{vol}(\Theta ) - \overline{{{\varvec{f}}}}\cdot {{\varvec{u}}}\ \right] \ d\Omega \nonumber \\&- \int \limits _{\Gamma _N} \bar{{{\varvec{t}}}}\cdot {{\varvec{u}}} \ d\Gamma \, , \end{aligned}$$
(22)

with

$$\begin{aligned} \Psi ^{iso}({{\varvec{u}}})&= \frac{\mu }{2} \, (J_e^{-\frac{2}{3}} \, \text{ tr }\, {{\varvec{b}}}_e -3) \, , \end{aligned}$$
(23)
$$\begin{aligned} \Psi ^{p \Theta }({{\varvec{u}}},\Theta ,p)&= p \, (J_e -\Theta ) \, , \end{aligned}$$
(24)
$$\begin{aligned} \Psi ^{vol}(\Theta )&= \frac{\kappa }{4} \, (\Theta ^2 -1 -2 \, \ln \Theta ) \, . \end{aligned}$$
(25)

In this formulation, the energy is split into an isochoric and volumetric part. In addition to that, a constraint associated with the volumetric deformation is added to the potential. Within this framework, the pressure p and the volume dilatation \(\Theta \) occur as additional independent variables.

3 Formulation of the virtual element method

The virtual element method is using a Galerkin projection, which maps the primary variables to a specific polynomial ansatz space. Unlike the finite element method, the isoparametric mapping for VEM is not simply obtainable. Thus simple polynomial ansatz functions can be given in terms of the coordinates \({{\varvec{X}}}\) in the initial configuration. Since this contributions deals with low order VEM, the virtual element is based on linear functions and therefore contains nodes, which are placed at the element vertices.

3.1 VEM ansatz

In general, for finite strains the deformation map \(\varvec{\varphi }= {{\varvec{X}}} + {{\varvec{u}}}\) has to be discretized (1). But since the coordinates \({{\varvec{X}}}\) in the initial configuration are exactly known, the discretization of the displacement field \({{\varvec{u}}}= u_i\,{{\varvec{E}}}_i\) is sufficient. Here, \({{\varvec{E}}}_i\) are the basis vectors with respect to the initial configuration in the three-dimensional space \(i\in \{1,2,3\}\).

The main concept of the virtual element method is the split of the ansatz space \( {{\varvec{u}}}_h \) into a projected part \({{\varvec{u}}}_{\Pi } \) and a remainder \( {{\varvec{u}}}_h - {{\varvec{u}}}_{\Pi }\) as

$$\begin{aligned} {{\varvec{u}}}_h = {{\varvec{u}}}_{\Pi }+ ( {{\varvec{u}}}_h - {{\varvec{u}}}_{\Pi }) \end{aligned}$$
(26)

For a linear ansatz, the projection \({{\varvec{u}}}_{\,\Pi }\) at element level takes for three-dimensional elements the form

$$\begin{aligned} \mathbf{u} _{\,\Pi } = {\mathbf{H}}\,{\mathbf{a}} \quad \text{ with } \quad {\mathbf{H}}=\begin{bmatrix} {{\varvec{1}}}&{} X {{\varvec{1}}}&{} Y {{\varvec{1}}}&{} Z {{\varvec{1}}}\\ \end{bmatrix} \text {, where }\, {{\varvec{1}}}= \begin{bmatrix} 1 &{} 0 &{} 0 \\ 0 &{} 1 &{} 0 \\ 0 &{} 0 &{} 1 \\ \end{bmatrix} , \end{aligned}$$
(27)

where \({\mathbf{a}}\) represents the twelve unknown virtual parameter \({\mathbf{a}}=\bigcup {\mathbf{a}}_{i\,j}\) which have to be determined. The goal is to express the projection \({{\varvec{u}}}_\Pi \) within a virtual element \(\Omega _v\) in terms of the element degrees of freedom \({\mathbf{u}}_v\):

$$\begin{aligned} \mathbf{u} _{\,\Pi } = {\mathbf{H}}({{\varvec{X}}}) {\mathbf{a}} = {\mathbf{H}}({{\varvec{X}}})\,{\tilde{\varvec{\Pi }}}^\nabla {\mathbf{u}}_v \end{aligned}$$
(28)

where \({\tilde{\varvec{\Pi }}}^\nabla \) is a projection operator that will be computed next.

Fig. 2
figure 2

VEM shape functions for displacements, pressure and dilatation

Full size image

While the VEM ansatz for the displacements is linear, the pressure p and the dilatation \(\Theta \) are considered to be constant over the entire element, see Fig. 2. To determine the virtual parameters, \({{\varvec{u}}}_{\Pi }\) has to fulfil the orthogonality condition (29), see [1]. Thus \(\nabla {{\varvec{u}}}_{\Pi }\) is computed through the Galerkin projection as

$$\begin{aligned} \int _{\Omega _{v}} \nabla {{\varvec{p}}} \cdot (\nabla {{\varvec{u}}}_{\Pi } -\nabla {{\varvec{u}}}_h) \ d\Omega = 0 \, , \end{aligned}$$
(29)

where \({{\varvec{p}}}\) is a polynomial function which has been chosen similarly to the projection \({{\varvec{u}}}_{\,\Pi }\), see (27). Since linear ansatz functions are used, \(\nabla {{\varvec{p}}}\) and \(\nabla {{\varvec{u}}}_{\Pi }\) are constant at element level and can be shifted out of the integral as

$$\begin{aligned} \nabla {{\varvec{u}}}_{\Pi } = \frac{1}{\Omega _v} \int _{\Omega _{v}} \nabla {{\varvec{u}}}_h \ d\Omega \,. \end{aligned}$$
(30)

Applying integration by parts to (30), integral over the element volume can be transformed to an equivalent integral over its boundary, obtaining

$$\begin{aligned} {\nabla {{\varvec{u}}}_{\Pi }}{\mathop {=}\limits ^{\smash {\scriptscriptstyle \mathrm {!}}}}\frac{1}{\Omega _v}\int _{\Gamma _{v}} {{\varvec{u}}}_h \otimes {{\varvec{N}}}\,\ d \Gamma \ , \end{aligned}$$
(31)

Here \({{\varvec{N}}}\) denotes the normal vector on the reference boundary \(\Gamma _e\) of the domain \(\Omega _e\), which belongs to a virtual element e. By employing a low order ansatz, the ansatz space is linear and thus the left hand side of (31) takes the simple form

$$\begin{aligned} {\nabla {{\varvec{u}}}_{\Pi }}= \left[ \begin{matrix} a_{1\,2} &{} a_{1\,3} &{} a_{1\,4} \\ a_{2\,2} &{} a_{2\,3} &{} a_{2\,4} \\ a_{3\,2} &{} a_{3\,3} &{} a_{3\,4}\end{matrix}\right] \,. \end{aligned}$$
(32)

To be able to determine the virtual parameters, (31) needs to be computed on the element boundary. For the 2D case, the right hand side of (31) is evaluated along the straight edges. As the displacements are known at the boundary, which are straight line segments, a linear ansatz for the displacements is used, see [14]. However, in the 3D case, the element boundary consists of polygonal faces. Therefore the evaluation of the integral in (31) is not straight forward, unless an appropriate ansatz is found. For the evaluation, there are many different methods available [3]. One option is to subdivide the element faces into 3 noded triangles, see Fig. 3. The integration is then carried out over the triangles of the polygonal faces by using the standard ansatz function for a linear triangle and Gauss integration, as outlined in [6].:

$$\begin{aligned} {\mathbf{N}}^{{\mathcal {T}}}&= \left( \xi , \eta , 1 - \xi - \eta \right) \end{aligned}$$
(33)
$$\begin{aligned} {{\varvec{u}}}_h^{{\mathcal {T}}}&= {\mathbf{N}}^{{\mathcal {T}}} {\mathbf{u}}_{{\mathcal {T}}}, \qquad {\mathbf{u}}_{{\mathcal {T}}}=\left( {{\varvec{u}}}_I\right) _{\forall I\in {{\mathcal {T}}}} \, . \end{aligned}$$
(34)

Here \({{\varvec{u}}}_h^{{\mathcal {T}}}\) denotes the linear ansatz for the displacements at each triangle of the polygonal faces. \({\mathbf{u}}_{{\mathcal {T}}}\) is a list which contains the three nodal displacement vectors of the triangle \({{\mathcal {T}}}\). \(\xi \) and \(\eta \) are the local reference \(\xi ,\eta \in [0,1]\) coordinates at the triangle level. The local nodes of \({{\mathcal {T}}}\) and the outward normal vector \(\mathbf{N } _i\) are visualized in Fig. 4.

Fig. 3
figure 3

Virtual element faces split into multiple triangles

Full size image

The right hand side of (31) can now be computed. Using (34), the integral in (31) takes the form:

$$\begin{aligned} \frac{1}{\Omega _v}\int \limits _{\Gamma _{v}}{{{\varvec{u}}}_h \otimes {{\varvec{N}}}}\,d{\Gamma }= & {} \frac{1}{\Omega _v} \sum _{k=1}^{n_f}\int \limits _{\Gamma _{k}}{{{\varvec{u}}}_h^{{\mathcal {T}}} \otimes {{\varvec{N}}}_k}\,d {\Gamma } \nonumber \\= & {} \frac{1}{\Omega _v} \sum _{k=1}^{n_f} \sum _{g=1}^{n_g} w_g N_\zeta {{\varvec{u}}}_{h\,g}^{{\mathcal {T}}} \otimes {{\varvec{N}}}_g \end{aligned}$$
(35)

Here \(n_f\) is the number of element faces. For an integration over triangles with linear shape functions (33) one point quadrature with \(n_g=1\) Gauss point and \(w_g = 1/2\) Gauss weight is sufficient. \(N_\zeta \) is the Jacobian of the transformation from the reference to the initial configuration. \(\square _g\) denotes quantities which are evaluated at the Gauss point with the local coordinates \(\xi =1/3\) and \(\eta =1/3\). The normal vector \({{\varvec{N}}}\) and the Jacobian of the isoparametric mapping \(N_\zeta \) are evaluated as follows:

$$\begin{aligned} {{\varvec{X}}}^{{\mathcal {T}}}&= {\mathbf{N}}^{{\mathcal {T}}} \,{\mathbf{X}}_{{\mathcal {T}}} \qquad {\mathbf{X}}_{{\mathcal {T}}}=\left( {{\varvec{X}}}_I\right) _{\forall I\in {{\mathcal {T}}}}, \end{aligned}$$
(36)
$$\begin{aligned} {{\varvec{g}}}_\xi&= \frac{\partial {{\varvec{X}}}^{{\mathcal {T}}}}{\partial \xi },\,\, {{\varvec{g}}}_\eta = \frac{\partial {{\varvec{X}}}^{{\mathcal {T}}}}{\partial \eta },\,\, {{\varvec{g}}}_\zeta = {{\varvec{g}}}_\xi \times {{\varvec{g}}}_\eta \,, \end{aligned}$$
(37)
$$\begin{aligned} N_\zeta&=|{{\varvec{g}}}_\zeta |, \, {{\varvec{N}}}= \frac{{{\varvec{g}}}_\zeta }{N_\zeta }\,. \end{aligned}$$
(38)

All quantities are related to the initial configuration.

Comparing (32) and (35) the unknown virtual parameters \( \left. {\mathbf{a}}=a_{i\,j} \right| _{ i\in (1,\ldots ,3) \wedge j\in (2,\ldots ,4) } \) can be linked to the nodal displacements

$$\begin{aligned} {\mathbf{u}}_v= \left( {{\varvec{u}}}_I\right) _{\forall I\in \lbrace 1,\ldots , n_V\rbrace } = \lbrace {{\varvec{u}}}_1, {{\varvec{u}}}_2, \ldots , {{\varvec{u}}}_{n_V} \rbrace \,, \end{aligned}$$
(39)

since with (34) the nodal degrees of freedom, associated with one surface \({\mathbf{u}}_{{\mathcal {T}}}=\left( {{\varvec{u}}}_I\right) _{\forall I\in {{\mathcal {T}}}}\), are related to the nodal displacements: \({\mathbf{u}}_{{\mathcal {T}}} \in {\mathbf{u}}_v\).

Since only the gradient of the projection \({\nabla {{\varvec{u}}}_{\Pi }}\) is needed to define the strain energy function of the static part, the virtual parameters which are related to the constant parts due not have to be computed in general. However, for the construction of the mass-matrix, the complete ansatz for the projected displacements \({{\varvec{u}}}_{\Pi } \) is necessary which includes the virtual parameters that are related to the constant parts. Thus our formulation has to be supplemented by a further condition to obtain the constants \( \left. {\mathbf{a}}=a_{i\,j} \right| _{ i\in (1,\ldots ,3) \wedge j=1 } \). This condition (see for example [2]) relates the sum of the nodal values of \({{\varvec{u}}}_h\) to the values of the projection \({{\varvec{u}}}_{\Pi } \). This leads for each virtual element \(\Omega _{e}\) to the following condition

$$\begin{aligned} \sum ^{n_{V}}_{I=1} {{\varvec{u}}}_{\Pi } ({{{\varvec{X}}}_I}) = \sum ^{n_{V}}_{I=1}{{\varvec{u}}}_{h}({{{\varvec{X}}}_I}) \,, \end{aligned}$$
(40)

where \(n_V\) is the number of boundary nodes and \({{\varvec{X}}}_I\) are the initial coordinates of the nodal point I. The sum includes all boundary nodes \(n_V\). By substituting (27) in (40) the missing three parameters can expressed in terms of the nodal displacements and the already known virtual parameters \( \left. {\mathbf{a}}=a_{i\,j} \right| _{ i\in (1,\ldots ,3) \wedge j\in (2,\ldots ,4) } \) as:

$$\begin{aligned} {\left( a_{1\,1}, a_{2\,1}, a_{3\,1}\right) } = \frac{1}{n_V} \sum ^{n_{V}}_{I=1} \left( {{\varvec{u}}}_I - {\nabla {{\varvec{u}}}_{\Pi }}\, {{\varvec{X}}}_I \right) \; . \end{aligned}$$
(41)

Finally with equation (35) and (41) the ansatz function \({{\varvec{u}}}_{\Pi } \) of the virtual element is completely defined in terms of the element nodal displacements \({\mathbf{u}}_e\) which can be written with the projector introduced in (28) as

$$\begin{aligned} \mathbf{u} _{\,\Pi } = {\mathbf{H}}({{\varvec{X}}}) \,{\tilde{\varvec{\Pi }}}^\nabla \, {\mathbf{u}}_v\,. \end{aligned}$$
(42)

We note that a matrix formulation of the projector \({\tilde{\varvec{\Pi }}}^\nabla \) can be derived, but it is not necessary since we use the symbolic tool AceGen which does this automatically.

3.2 Construction of the element mass-matrix for VEM

The inertia term in the balance equation (6) leads in a weak sense for a virtual element \(\Omega _v\) to

$$\begin{aligned} \int \limits _{\Omega _v} \rho \ddot{{{\varvec{u}}}}\, \cdot \delta {{\varvec{u}}} \ d\Omega \end{aligned}$$
(43)

where \(\delta {{\varvec{u}}}\) is the test function. Discretization of this term yields a mass-matrix which has to be constructed for the virtual element method. Our starting point is the same split for the accelerations \(\ddot{{{\varvec{u}}}}_h\) as we already used for the displacement in (26):

$$\begin{aligned} \ddot{{{\varvec{u}}}}_h = \ddot{{{\varvec{u}}}}_{\Pi } + (\ddot{{{\varvec{u}}}}_h - \ddot{{{\varvec{u}}}}_{\Pi })\, . \end{aligned}$$
(44)

For a linear ansatz, the projected accelerations \(\ddot{{{\varvec{u}}}}_{\,\Pi }\) at element level take for three-dimensional elements by using (42) the form:

$$\begin{aligned} \ddot{\mathbf{u }}_{\,\Pi } = {\mathbf{H}}({{\varvec{X}}}) \,{\tilde{\varvec{\Pi }}}^\nabla \, \ddot{{\mathbf{u}}}_v \, \end{aligned}$$
(45)

where \({\mathbf{H}}\) is the same ansatz as for the displacements (27) and \(\ddot{{\mathbf{u}}}_e\) are the accelerations of the nodal degrees of freedom.

Fig. 4
figure 4

Virtual element faces split into multiple tetrahedron

Full size image

For the construction of the elastodynamic virtual element, we employ the software tool AceGen, see [36]. It generates code automatically and provides the most efficient element routines when a potential formulation is used. Thus the part of the weak form related to the mass matrix (43) will be expressed by the specific pseudo-potential

$$\begin{aligned} U^{dyn}( \ddot{{{\varvec{u}}}}\,,{{\varvec{u}}}) = \int \limits _{\Omega } \rho \ddot{{{\varvec{u}}}}\, \cdot {{\varvec{u}}} \ d\Omega \, , \end{aligned}$$
(46)

where \(\ddot{{{\varvec{u}}}}\) needs to be hold constant during the first variation to obtain exactly (43).

Inserting both equations (26) and (44) for the displacements and the accelerations in (46) yields for the virtual element \(\Omega _v\)

$$\begin{aligned} U^{dyn}_v( \ddot{{{\varvec{u}}}}\,,{{\varvec{u}}}) = \int \limits _{\Omega _v} \rho \ddot{{{\varvec{u}}}}_\Pi \cdot {{\varvec{u}}}_\Pi \ d\Omega + \int \limits _{\Omega _v} \rho (\ddot{{{\varvec{u}}}}_h - \ddot{{{\varvec{u}}}}_\Pi ) \cdot ({{\varvec{u}}}_h -{{\varvec{u}}}_\Pi ) \ d\Omega \, . \end{aligned}$$
(47)

The coupled terms are zero due to the orthogonality condition, see e.g. [1]. The first term in (47) is the consistency part, whereas the second term is the stabilization part. For the construction of the mass-matrix, it is sufficient to use the consistency term without any stabilization. This is valid, when the problem is not reaction dominated, as stated in [1, 37] and shown in [26].

Using the relationship between the projected values and the unknown values for the displacement (42) and the accelerations (45), the following expression for the consistency part of the pseudo dynamic potential results for one element e

$$\begin{aligned} U^{dyn}_v(\ddot{{{\varvec{u}}}}_\Pi \,, {{\varvec{u}}}_\Pi )= & {} \int \limits _{\Omega _v} \rho \, \ddot{{{\varvec{u}}}}_\Pi \cdot {{\varvec{u}}}_\Pi \ d\Omega \nonumber \\= & {} {\mathbf{u}}_v^T \,\left( {\tilde{\varvec{\Pi }}}^\nabla \right) ^T \left[ \int \limits _{\Omega _v} \rho \, \left[ {\mathbf{H}}({{\varvec{X}}})\right] ^T {\mathbf{H}}({{\varvec{X}}}) \ d\Omega \right] \, {\tilde{\varvec{\Pi }}}^\nabla \, \ddot{{\mathbf{u}}}_v\,. \nonumber \\ \end{aligned}$$
(48)

Note, that the projector \({\tilde{\varvec{\Pi }}}^\nabla \) is constant over the element. Therefore they can be shifted out of the integral. The argument of the integral is a polynomial function up to second order for constant density

$$\begin{aligned}&\left[ {\mathbf{H}}({{\varvec{X}}})\right] ^T {\mathbf{H}}({{\varvec{X}}})= \begin{bmatrix} {{\varvec{1}}}&{} {{\varvec{1}}}X &{} {{\varvec{1}}}Y &{} {{\varvec{1}}}Z \\ {{\varvec{1}}}X &{} {{\varvec{1}}}X^2 &{} {{\varvec{1}}}X Y &{} {{\varvec{1}}}X Z \\ {{\varvec{1}}}Y &{} {{\varvec{1}}}X Y &{} {{\varvec{1}}}Y^2 &{} {{\varvec{1}}}Y Z \\ {{\varvec{1}}}Z &{} {{\varvec{1}}}X Z &{} {{\varvec{1}}}Y Z &{} {{\varvec{1}}}Z^2 \\ \end{bmatrix} , \nonumber \\&\text { where } {{\varvec{1}}}\text { is the Identity } {{\varvec{1}}}= \begin{bmatrix} 1 &{} 0 &{} 0 \\ 0 &{} 1 &{} 0 \\ 0 &{} 0 &{} 1 \\ \end{bmatrix} \end{aligned}$$
(49)

For the evaluation of the integral in (48), several ways can be utilized, see [26]. As in finite element procedures, the mass-matrix for a virtual element \(\Omega _e\) can now be defined

$$\begin{aligned} {\mathbf{M}}_v= \left( {\tilde{\varvec{\Pi }}}^\nabla \right) ^T \left[ \int \limits _{\Omega _v} \rho \, \left[ {\mathbf{H}}({{\varvec{X}}})\right] ^T {\mathbf{H}}({{\varvec{X}}}) \ d\Omega \right] \, {\tilde{\varvec{\Pi }}}^\nabla \,. \end{aligned}$$
(50)

3.3 Construction of the virtual element

As already introduced in Sect. 3.1, the formulation of a virtual element undergoing large deformations is based on a split of the energy into a constant part and an associated stabilization term. Since the nodal degrees of freedom are in each element approximated with one interpolation function per coordinate direction, the consistency part does not lead to a stable formulation. Thus an appropriate stabilization term is required. The idea of stabilizing the formulation is analogous to the stabilization of the classical finite elements with reduced integration, developed by [30]. The starting point for the construction of the virtual element method is the potential function

$$\begin{aligned} U=U^{stat}+U^{dyn} \, . \end{aligned}$$
(51)

The variation of (51) yields exactly the weak form of (6) when considering the nonlinear dependency of the 2nd Piola-Kirchhoff stress \({{\varvec{S}}}\) on the displacement \({{\varvec{u}}}\).

Assembling of all element contributions for the \({n}_v\) virtual elements yields the following expression:

(52)

where \({\mathbf{h}}_v\) denote the plastic history variables at element level.

3.3.1 Consistency part

For the consistency part the projection \({{\varvec{u}}}_\Pi \), introduced in Sect. 3.1, is used and therefore the first part of equation (52) for each element is given by

$$\begin{aligned} U_c\left( {{\varvec{u}}}_{\Pi },{\mathbf{h}}_v \right)= & {} \int \limits _{\Omega _v}{\left[ \Psi ({{\varvec{u}}}_{\Pi },{\mathbf{h}}_v) - \overline{{{\varvec{f}}}} \cdot {{\varvec{u}}}_{\Pi }\right] }{\, d\Omega } \nonumber \\&- \int \limits _{{\Gamma }_v^N}{\bar{{{\varvec{t}}}}\cdot {{\varvec{u}}}_{\Pi }}{\, d\Gamma } + \int \limits _{\Omega _v} \rho \ddot{{{\varvec{u}}}}_\Pi \cdot {{\varvec{u}}}_\Pi \ d\Omega \end{aligned}$$
(53)

The gradient of the projection \({\nabla {{\varvec{u}}}_{\Pi }}\) is constant on the entire domain \(\Omega _e\). Therefore, all kinematic quantities, that steam from \({\nabla {{\varvec{u}}}_{\Pi }}\), such as \({{\varvec{F}}}\), \({{\varvec{b}}}_e\) and \({{\varvec{C}}}_p^{-1}\) are constant as well:

$$\begin{aligned} {{\varvec{F}}}= {{\varvec{1}}}+ {\nabla {{\varvec{u}}}_{\Pi }}\quad \quad \quad \quad {{\varvec{b}}}_e= {{\varvec{F}}} {{\varvec{C}}}_p^{-1} {{\varvec{F}}}^T \ \end{aligned}$$
(54)

Thus the integration of the strain energy function can be simplified as:

$$\begin{aligned} \int \limits _{\Omega _v}{\Psi ({{\varvec{b}}}_e,{\mathbf{h}}_v)}{\, d\Omega } = \Psi ({{\varvec{b}}}_e, {\mathbf{h}}_v) \,\Omega _v \ , \end{aligned}$$
(55)

which is still nonlinear with respect to the unknown nodal degrees of freedom and plastic history variables.

As already mentioned in Sect. 3.2, the third integral in (53) related to the dynamic part can be computed in different ways. In [26] it has been shown, that the evaluation of the third integral in (53) at the centroid \({{\varvec{X}}}_c\) of the virtual element yields sufficient results and needs less computational effort when compared to the other evaluation schemes. Thus the mass-matrix (50) takes the form

$$\begin{aligned} {\mathbf{M}}_v = \rho \, \left( {\tilde{\varvec{\Pi }}}^\nabla \right) ^T \left[ {\mathbf{H}}({{\varvec{X}}}_c)\right] ^T {\mathbf{H}}({{\varvec{X}}}_c) \, {\tilde{\varvec{\Pi }}}^\nabla \Omega _v\,. \end{aligned}$$
(56)

The element residual related to the inertia term is obtained by the first derivative of the dynamic potential \(U^{dyn}= {\mathbf{u}}_v^T {\mathbf{M}}_v \,\ddot{{\mathbf{u}}}_v\), see (48) and (50), holding the acceleration \(\ddot{{\mathbf{u}}}_v\) constant

$$\begin{aligned} {\mathbf{R}}^{dyn}_v = \left. \frac{\partial U^{dyn}({\mathbf{u}}_v)}{\partial {\mathbf{u}}_v} \right| _{\ddot{{\mathbf{u}}}_v = const.}={\mathbf{M}}_v \, \ddot{{\mathbf{u}}}_v \end{aligned}$$
(57)

Before computing the second derivative, the Newmark method, see e.g. [31], is used for the implicit time integration which leads to a approximation of the acceleration \(\ddot{{\mathbf{u}}}_e\) in time within a time increment \(\Delta t = t_{n+1}-t_n\)

$$\begin{aligned} \ddot{{\mathbf{u}}}_v=\dfrac{1}{\zeta \Delta t^2} \left( {\mathbf{u}}_{v,n+1}-{\mathbf{u}}_{v,n}\right) -\dfrac{1}{\zeta \Delta t} \dot{{\mathbf{u}}}_{v,n} -\left( \dfrac{1}{2 \zeta }-1\right) \ddot{{\mathbf{u}}}_{v,n} \end{aligned}$$
(58)

where the Newmark parameters are chosen as \(\zeta =1/4\) and \(\gamma =1/2\).

Thus, the residual for the dynamic part follows as

$$\begin{aligned} {{\varvec{R}}}^{dyn}_v= & {} {\mathbf{M}}_v \, \left[ \dfrac{1}{\zeta \Delta t^2} \left( {\mathbf{u}}_{v,n+1}-{\mathbf{u}}_{v,n}\right) \right. \nonumber \\&\left. -\dfrac{1}{\zeta \Delta t} \dot{{\mathbf{u}}}_{v,n} -\left( \dfrac{1}{2 \zeta }-1\right) \ddot{{\mathbf{u}}}_{v,n} \right] \end{aligned}$$
(59)

The derivative of \({{\varvec{R}}}^{dyn}_v\) with respect to the current displacement \({\mathbf{u}}_{v,n+1}\) leads then to the dynamic part of the tangent for an element \(\Omega _e\)

$$\begin{aligned} \frac{\partial {{\varvec{R}}}^{dyn}_v({\mathbf{u}}_v)}{\partial {\mathbf{u}}_v} = \dfrac{1}{\zeta \Delta t^2} \,{\mathbf{M}}_v \, . \end{aligned}$$
(60)

3.3.2 Algorithmic treatment of finite strain plasticity

The discretized form of (61) follows from [33, 38] and yields together with (20) the local residual:

$$\begin{aligned} {{\varvec{Q}}}_e = {{\varvec{F}}} {{\varvec{C}}}_p^{-1} - \text{ exp }[-2(\alpha -\alpha _n) {{\varvec{n}}}] {{\varvec{F}}} {{\varvec{C}}}_{p,n}^{-1} = 0 \quad \quad \text{ and } \quad \quad \Phi = 0 \, . \end{aligned}$$
(61)

Here, \({{\varvec{C}}}_{p}^{-1}\) and \(\alpha _n\) are the converged history variables from the previous step and therefore given. Equation (61) contains one equation for each of the six unique components of \({{\varvec{C}}}_{p,n}^{-1}\) and one additional equation for the hardening variable \(\alpha \). For \(\Phi < 0\), a pure elastic step follows and therefore the history variables, \({\mathbf{h}}_e\), will remain the same as from the previous time step, i.e. \({{\varvec{C}}}_{p}^{-1}={{\varvec{C}}}_{p,n}^{-1}\) and \(\alpha =\alpha _n\). If \(\Phi > 0\), the set of equations (61) needs to be solved locally at the centroid of the element \(\Omega _v\) which yields to an updated history field array \({{\varvec{h}}}_v=\{ \,{\mathbf{C}}^{\,p-1}\,, \alpha \,\}\).

figure a

The resulting equations, which need to be solved at the centroid of each virtual element \(\Omega _v\), are the residual \({\mathbf{Q}}_v\) in (61) which stem from the plastic routine and the residual \({\mathbf{R}}\) resulting from the first variation of the pseudo-potential (52):

(62)
(63)
Fig. 5
figure 5

Stabilization parameter \(\beta \) as a function of the plastic deformation \(\alpha \)

Full size image
Fig. 6
figure 6

Necking problem

Full size image
Table 1 Material parameters used for the numerical examples
Full size table
Fig. 7
figure 7

Necking problem—force-displacement response for two different meshes

Full size image

The above equations are solved in a nested algorithm, where first (62) needs to be solved locally at the element level in a inner Newton-Raphson loop for a fixed \({\mathbf{u}}_v\) to update the plastic history variables \({\mathbf{h}}_v\) for the current time step \(t=t_{n+1}\). The summary of the finite strain plasticity model, that leads to \({\mathbf{Q}}_v\) is given in Box 1. Thus the local tangent matrix for the inner loop yields:

$$\begin{aligned} {\mathbf{A}}_v = \frac{\partial {\mathbf{Q}}_v ({{\varvec{F}}}, {\mathbf{h}}_v, {\mathbf{h}}_{vn})}{\partial {\mathbf{h}}_v} \, \end{aligned}$$
(64)

Next, the outer Newton-Raphson loop is solved globally by using standard Newton-Rhaphson iteration procedure: \({\mathbf{K}}\Delta {\mathbf{u}} = {\mathbf{R}}\). The residual \({\mathbf{R}}_v^c\) and tangent matrix \({\mathbf{K}}_v\) at each virtual element \(\Omega _v\) (63) are obtained by utilizing AceFEMs automatic differentiation techniques, which will yield to the residual and tangent of the virtual element:

$$\begin{aligned} {\mathbf{R}}^c_v= & {} \left. \frac{\partial U_c( {{\varvec{u}}}_{\Pi },{\mathbf{h}}_v)}{\partial {\mathbf{u}}_v} \right| _{\frac{D{\mathbf{h}}_v}{D{\mathbf{F}}}=0; \, \, \ddot{{\mathbf{u}}}_v=const.}\nonumber \\ {\mathbf{K}}^c_v= & {} \left. \frac{\partial {\mathbf{R}}^c_v ({{\varvec{u}}}_v, {\mathbf{h}}_v, {\mathbf{h}}_{vn})}{\partial {\mathbf{u}}_v} \right| _{\frac{D{\mathbf{h}}_v}{D{\mathbf{F}}}=-{\mathbf{A}}^{-1}_v \frac{\partial {\mathbf{Q}}_v}{\partial {\mathbf{F}}}} \, \end{aligned}$$
(65)

Note that residual \({\mathbf{R}}^c_v\) is obtained by holding history variables \({\mathbf{h}}_v\) constant during differentiation procedure. Additionally, when deriving the tangent \({\mathbf{K}}^c_e\) with respect to the primary variables \({\mathbf{u}}_e\), providing the dependency \(\frac{D{\mathbf{h}}_v}{D{\mathbf{F}}}\) is necessary to ensure a consistent linearization. For further details see [33].

3.3.3 Stabilization part

Using only the consistency term yields a rank deficient stiffness matrix and thus needs to be stabilized. In [14] Wriggers et al. a new positive definite energy \({\hat{U}}\) was introduced, with the help of which the stabilization term is redefined as:

$$\begin{aligned} U_{stab} ({{\varvec{u}}}_h -{{{\varvec{u}}}_{\Pi }},{\mathbf{h}}_v) = {\hat{U}}({{\varvec{u}}}_h,{\mathbf{h}}_v)-{\hat{U}}({{{\varvec{u}}}_{\Pi }},{\mathbf{h}}_v) \end{aligned}$$
(66)

Furthermore, the positive definite energy \({\hat{U}}\) can be defined in terms of a stabilization parameter \(\beta \in [0,1]\) and the \(U_c\):

$$\begin{aligned} {\hat{U}}=\beta \ U_c \end{aligned}$$
(67)

Thus the stabilization term takes the form:

$$\begin{aligned} U_{stab} ({{\varvec{u}}}_h -{{{\varvec{u}}}_{\Pi }},{\mathbf{h}}_v)=\beta U_c({{\varvec{u}}}_h,{\mathbf{h}}_v) - \beta U_c({{{\varvec{u}}}_{\Pi }},{\mathbf{h}}_v) \end{aligned}$$
(68)

Applying equation (68) in equation (52), the final form of the total potential energy function takes the form:

(69)
Fig. 8
figure 8

3D beam—geometry and boundary conditions

Full size image
Fig. 9
figure 9

3D beam—displacement over time response for different element types and mesh discretization in a–c with \(\nu \)=0.3 and d–f with \(\nu \)=0.499999

Full size image
Fig. 10
figure 10

3D beam—error of the maximum displacement over time for different element types and various Poisson’s ratio in (a) to (c)

Full size image

The computation of the first term of equation (69) can be done as explained in Sect. 3.3.1. The second term \(U_c({{\varvec{u}}}_h,{\mathbf{h}}_v)\) needs an approximation. An approach how to compute this part is introduced in [14]. An additional internal Mesh of triangles in 2D and tetrahedrons in 3D is introduced. The approximation of the displacement field is done by standard linear finite element ansatz functions. The nodes of the generated submesh belong to the set of nodes in the virtual element, such that no additional nodes are introduced. The potential \(U_c({\mathbf{u}}_h, {\mathbf{h}}_v)\) can then be calculated on internal/embedded tetrahedron mesh:

$$\begin{aligned} U_c({\mathbf{u}}_h, {\mathbf{h}}_v) = \sum _T^{n_T} \Omega _v^T \Psi ^{stat}_c({{\varvec{u}}}_h^T(\left. {\mathbf{X}}_c\right| _{T}),{\mathbf{h}}_v) \end{aligned}$$
(70)

Based on the triangulated submesh, the displacement gradient is computed as \(\nabla {{\varvec{u}}}_h= \frac{D{{\varvec{u}}}_h^T}{D{{\varvec{X}}}^T}\) by employing standard FEM shape functions \({\mathbf{N}}^T\) (analogous to (34) and (36)) for linear tetrahedron. The stabilization term \(U_c({{{\varvec{u}}}_h},{\mathbf{h}}_v)\) contains both the static \(U_c^{stat}({{{\varvec{u}}}_h},{\mathbf{h}}_v)\) and dynamic part \(U_c^{dyn}({{{\varvec{u}}}_h})\). As the ansatz is linear, the gradient is constant and thus the integral for the static part can be simply evaluated at the centroid \(\left. {\mathbf{X}}_c\right| _{T}\) of each tetrahedron \(n_T\), as sketched in Fig. 4. The plastic history variables need to be computed once \({\mathbf{h}}_e\) and than be used in both parts of the strain energies in (69) and (72). Therefore, the computation of the left Cauchy Green tensor is performed in a approximative way by using the contact plastic strains \({{\varvec{C}}}_{p}^{ -1}({\mathbf{h}}_e)\) from the consistency part. By doing so, this approximation yields in a non-symmetric tangent.

Since \(\beta \in [0,1]\), it can be seen as a ratio parameter. The stabilization parameter \(\beta \) can be chosen freely. For \(\beta =1\) the total energy is computed using only the stabilization part. Thus the tangent results from the internal FEM-submesh with three noded triangles in 2D or four noded tetrahedron in 3D. Using \(\beta =0\) yields in a tangent, which is solely calculated from the projection part. Thus for \(\beta =0\) the computation results in a rank deficient tangent. The choice for the stabilization parameter \(\beta \) for hyperelasticity was analyzed in [6, 7] and it has been shown that the optimal value is in the range \(\beta \in [0.2, 0.6]\). In [6, 7] the stabilization parameter \(\beta \) was chosen as a function of the accumulated plastic strains. Thus, with increasing amount of plastic deformation, the stabilization parameter decreases. For our investigations, we choose the approach from [6, 7].

In both, the pure displacement as well as the Hu-Washizu based element framework, the following equation for \(\beta \) is used.

$$\begin{aligned} \beta = \text {min} \! \! \left[ 0.4,\text {max} \! \! \left[ \frac{\sigma _{VM}}{E \alpha }, \eta \right] \right] \end{aligned}$$
(71)

Here \(\eta =10^{-3}\) denotes the minimum amount of stabilization, see Fig. 5. Without \(\eta \), the stabilization parameter would decrease during the simulation and tend to be zero, which would result in a rank deficient tangent.

Fig. 11
figure 11

Taylor Anvil test—a geometry and boundary value problem, b deformed state (schematic illustration)

Full size image

Due to the combination of both VEM and FEM, the outlined stabilization procedure is called mixed VEM-FEM-Stabilization. The total element residual vector \({\mathbf{R}}_e\) and tangent matrix \({\mathbf{K}}_e\) are obtained as the first and second derivative of the element total energy \(U({{\varvec{u}}}_h,{\mathbf{h}})\) with respect to the global unknowns \({\mathbf{u}}_e\), analogous to (65), keeping the same internal variables and its dependencies as for projected part.

3.3.4 Hu-Washizu VEM

For the Hu-Washizu formulation, the same potential as in (69) is used as well, But it is only necessary to use the mixed formulation only for the consistency part of the virtual element. Thus for the consistency part is exchanged by the Hu-Washizu potential (22). By inserting the projected quantities in to the consistency part, the total energy yields:

(72)

Note that the derivative of (72) needs to be taken with respect to all variables. Looking at (72), it is clear that the Hu-Washizu virtual element is based only on the projection part of the mixed terms. The stabilization is constructed purely on the displacement potential. Test computations have demonstrated that a stabilization of the mixed part is not necessary and additionally such a reduced formulation leads to a more efficient element since the mixed variables need not to be treated within the internal triangular mesh. This leads to an element tangent \({\mathbf{K}}_v\) with the structure

$$\begin{aligned} {\mathbf{K}}_v= \begin{bmatrix} {\mathbf{K}}_{u u} &{} 0 &{}{\mathbf{K}}_{u p}\\ 0 &{}{\mathbf{K}}_{\Theta \Theta } &{}{\mathbf{K}}_{\Theta p}\\ {\mathbf{K}}_{u p}^T&{}{\mathbf{K}}_{\Theta p}^T&{}{\mathbf{0}}\\ \end{bmatrix}. \end{aligned}$$
(73)

Since \(p_\Pi \) and \(\Theta _\Pi \) are constant over the entire virtual element, static condensation can be applied to eliminate these constant variables at element level.

Table 2 Material parameters used for the Taylor Anvil test
Full size table

4 Numerical examples

In this section the performance of the proposed mixed virtual element formulation will be investigated. For comparison purposes results of the standard finite element method (FEM) are also included. The material parameters used in this work are the same for all examples and are provided in Table 1, unless it is otherwise specified.

In this contribution, the following mesh types for first order virtual element discretizations are introduced:

  • VEM H1: A regular shaped 3D virtual element with 8 nodes and linear ansatz. Pure displacement formulation, based on (69).

  • VEM H1JP: A regular shaped 3D virtual element with 8 nodes. This element is using a Hu-Washizu formulation with a linear ansatz for the displacement, constant pressure p and constant dilatation \(\theta \) as additional degrees of freedom, see (72).

  • VEM VO: A 3D voronoi shaped virtual element with arbitrary number of nodes and linear ansatz. Pure displacement formulation, based on (69).

  • VEM VOJP: A 3D voronoi shaped virtual element with arbitrary number of nodes. This element is using a Hu-Washizu formulation with a linear ansatz for the displacement, constant pressure p and constant dilatation \(\theta \) as additional degrees of freedom (72).

For a representative comparison, the following finite element formulations are selected:

  • FEM H1: A regular shaped 3D finite element with 8 nodes and linear ansatz. Pure displacement formulation.

  • FEM H1JP: A regular shaped 3D finite element with 8 nodes. This element is using a Hu-Washizu formulation with a linear ansatz for the displacement, constant pressure p and constant dilatation \(\theta \) as additional degrees of freedom.

  • FEM H2: A regular shaped 3D finite element with 27 nodes and quadratic ansatz. Pure displacement formulation.

The stabilization parameter of the static part \(\beta ^{stat}\) is chosen in all the simulations using (71), unless it is otherwise specified. For the dynamic part the mass-matrix is computed according to (56) without any stabilization.

Fig. 12
figure 12

Taylor Anvil test—deformation state for different elements, showing the accumulated plastic strain

Full size image
Fig. 13
figure 13

Taylor Anvil test—length change over time for different element numbers and formulations

Full size image
Fig. 14
figure 14

Taylor Anvil test—evolution of the mushroom radius \(r_m\) for different element numbers and formulations

Full size image
Table 3 Taylor Anvil test—comparison of different results obtained in the literature
Full size table
Table 4 Taylor Anvil test—comparison of results for different element types
Full size table

4.1 Necking problem

In the first numerical example the proposed element formulations will be tested and compared for the quasi static case. Necking of cylindrical bar due to prescribed displacements along axial direction is considered, see [6]. This example serves to illustrate the robustness of the mixed virtual element method for localization of plastic strains in the necking area.

The geometrical setup and the boundary conditions of the cylindrical bar with diameter \(d = 1\) mm and length \(L = 10\) mm is depicted in Fig. 6. The material parameters can be taken from Table 1.

Figure 7 depicts the load-displacement curves for two different mesh discretization. The prescribed displacement is applied at the center of the cross section. It can be observed that all elements give nearly the same force response until the necking appears. Thereafter at about \({\bar{u}}= 0.7\) mm, the FEM H1 element demonstrates stiffer results compared to all other elements due to an expected locking behaviour. However, the similar, displacement based virtual elements (i.e. VEM H1 and VEM VO) perform way better but still not as good as the reference FEM H2 element with a quadratic ansatz. In this regard, the newly developed mixed VEM formulation produces very good results that compare with the higher order FEM H2 element. The results are even better than the ones using the mixed FEM H1JP element as shown in Fig. 7 for both, coarser and finer meshes.

4.2 3D beam

In the second example a three-dimensional beam is dynamically loaded by a surface load p(t) at the end of the beam, as illustrated in Fig. 8. The load is applied as a half sine function with the time period \(T_0=0.0008\) and an amplitude of 45 N / mm\({}^2\). Thereafter, the force is released and the beam is oscillating around its new position of rest. The time increment is set to \(\Delta t= 1 \mu s\).

The key goal of this test is to demonstrate the performance of the Hu-Washizu formulation for compressible and nearly incompressible material behavior. Different Poisson’s ratios are chosen: \(\nu = \{ 0.3, \, 0.45, \, 0.49, \, 0.499, \, 0.4999, \, 0.49999, \, 0.499999 \} \). The material parameters used in the simulations are listed in Table 1.

Figure 9 shows the time history of the displacement at the tip of the beam. For a compressible material (i.e. \(\nu = 0.3\) outlined in Fig. 9a–c), the bending of the beam converges with increasing nodes number to nearly \(u= 70\) mm, see Fig. 9c).

Nevertheless, the finite and virtual elements, which are based on a pure displacement formulation H1/VO, tend to provide stiffer responses after getting into the plastic regime. Such an observation is in line with the artificial stiffening due to volumetric locking. Since this example is bending dominated bending locking can also appear. By increasing the Poisson’s ratio up to a nearly incompressible material (i.e. \(\nu = 0.499999\) outlined in Fig. 9d–f), a strongly stiffer response is observed for the pure displacement elements in comparison with the stable and robust mixed finite and virtual element formulations. Thus the Hu-Washizu based finite and virtual elements produce a much softer response and hence can handle incompressible material behaviour well.

For a representative comparison between all elements, the relative error of the maximum displacement (related to Fig. 9) is plotted in Fig.10 for different elements and Poisson ratios. Hereby, the error is computed with respect to an overkill solution, that is obtained from the mixed finite element FEM H1JP using 100000 elements. In Fig. 10 a (for \(\nu =0.3\)), the error is remarkably reduced by increasing the number of element for all types. In this regard, the pure displacement elements H1/VO demonstrate a high error in comparison with mixed FEM and VEM formulations in the case of coarse meshes. When increasing the Poisson’s ratio, the error of the pure displacement elements is further increased, reaching its maximum for \(\nu =0.499999\). The mixed finite and virtual elements stay nearly constant and are not effected by any kind of locking phenomena. This illustrates the importance of using a mixed formulation for virtual element, when it comes to elastic and plastic incompressibility.

4.3 Taylor anvil test

The next example presents the Taylor-Anvil problem, which is widely used to test the dynamical behaviour of metals but it is also a validation test for discretization schemes that simulate finite strains elasto-plasticity undergoing dynamic loadings, see [20, 39]. Within this framework, a rod impacts at high velocity a rigid plate. This is modelled by fixing in longitudinal direction one side of the rod and by prescribing an initial velocity to all other parts of the body, as depicted in Fig. 11a.

The material parameters for the simulations are taken from the literature, see [40,41,42,43,44], and summarized in Table 2. Hereby, the saturation parameter is set to zero (\(\delta =0\)), hence the exponential term in (17) disappears and the model is reduced to linear hardening. The initial velocity is set to \(v_0=227\) m/s. The time increment for the dynamic simulation is \(\Delta t=0.01 \mu \text{ s }\). During the impact a plastic front develops and moves upwards leading to a deformed state as shown in Fig. 11 b).

Fig. 15
figure 15

Punch problem—boundary value problem

Full size image

The equivalent plastic strain at the final deformation state for all element formulations is depicted in Fig. 12 and is obtained with 10000 elements. As expected large plastic deformations are observed at the end of the rod, as well documented in the literature [39, 44, 45]. This is due to the influence of the kinetic energy resulting in high stresses at the front of the rod where the essential boundary condition is applied. When a certain energy is dissipated, the stresses are not reaching the yield stress anymore. Therefore some elastic energy is still stored in the upper part of the rod as shown in Fig. 12. From the contour plots, all element yield similar results except the stiffer FEM H1. Figure 13 demonstrates the length change over time for different element formulations and two mesh discretization. All element types show nearly the same displacement curves over time. Locking effects for this impact test occur only for the FEM H1 discretization. For all formulations a small oscillation with low frequency can be observed which is due to the elastic response at the upper part of the rod.

Fig. 16
figure 16

Punch problem—deformation state for different elements, showing the accumulated plastic strain

Full size image
Fig. 17
figure 17

Punch problem. a Time history of maximum displacement at the tip. b Error of the maximum displacement over number of elements. c Maximum displacement over number of elements

Full size image

Figure 14 depicts the development of the mushroom radius at the lower part (\(z=0\)). Good agreement between all element formulations – besides the FEM H1 – is also observed. Again the mixed formulation converges for finite and virtual elements (FEM/VEM H1JP) the best fast and results in the best coarse mesh accuracy, see Fig. 14a.

Next, we illustrate in Table 3 the results obtained by different authors with different methods and compare them with the values from the current work depicted in Table 4. Good agreement is achieved for the proposed mixed virtual element formulation.

4.4 Punch problem

The last test example is concerned with the capability of the proposed mixed VEM formulations to solve dynamic elastic-plastic problems. For this purpose, a punch problem is selected which is subjected to high compression loading. A surface load is applied on one quarter of the block with the geometrical properties \(H=B=L=50\) mm. The boundary and loading conditions can be taken from Fig. 15. For a comprehensive comparison, a convergence study is performed where the number of elements is set to \(N= \{ 64, \, 512, \, 1728, \, 4096, \, 10648, \, 21952, \, 39304 \} \). The load is applied in time as a half-sine function with a time period of \(T_0=0.4\) ms and an amplitude of 2.5 kN/mm\({}^2\). Similar to the previous examples, the force is released after a half sine. The material parameters used for the numerical simulations are same as in the previous examples, see Table 1. The time increment used in this example is \(\Delta t= 1 \mu \)s.

Figure 16 illustrates the accumulated plastic strain \(\alpha \) at the end of the simulation. As expected the pure displacement formulations H1 of FEM and VEM underestimate the large deformation behavior due to locking phenomena, resulting to small maximum values of \(\alpha \), see Fig. 16a, b. For VEM VO with voronoi cells, the locking phenomena is even more significant as depicted in Fig. 16c. This nonphysical behavior is overcome for both, FEM and VEM elements, by the mixed form based on the Hu-Washizu formulation as shown in Fig. 16d–f.

Figure 17a depicts the time history of the displacement at the corner of the block, where the maximum displacement appears. The presented curves are obtained with 40000 elements. It can be seen, that the mixed finite element FEM H1JP leads to the largest deformation followed by the mixed virtual element VEM H1JP. Those elements illustrate a much softer response compared with the pure displacement finite and virtual elements which is related to their locking free behaviour. The same can be seen in Fig. 17b, c, which is showing the maximum displacement at the corner and its relative error for different numbers of elements. The reference solution for the error analyses is computed with the mixed finite element FEM H1JP, using around 100000 elements.

A closer look reveals, that the mixed finite and virtual elements are providing a much softer response, compared to the pure displacement elements. Especially for course mesh, the mixed elements behave softer and thus are not affected by volumetric locking phenomena.

5 Summary and conclusions

A mixed low order virtual element formulation for three-dimensional dynamic elasto-plasticity was developed in this work. The mixed approach is based on a three field Hu-Washizu potential function, which leads to a softer response of the body undergoing large deformations. This yields also for virtual elements a superior caorse grid accuracy in comparision with pure displacement elements. The presented formulation is based on a minimization of a specific pseudo-potential, considering the dynamic behavior of the solid. The treatment of VEM for elasto-plasticity in this contribution is in line with the authors previous works, see [6, 7]. The extension towards dynamic problems was performed using a fast and simple computation of the mass-matrix, see [26].

It has been shown that the mixed formulation for virtual elements, can prevent volumetric locking under elastic and plastic incompressibility conditions, especially for Voronoi shaped virtual elements.