1 Introduction

Computational models for structural analysis are omnipresent in nowadays engineering disciplines. For slender structures, like cars, ships, or airplanes, shell models using the Finite Element Method (FEM) are often used. The geometric design of these structures is typically done using computer-aided design (CAD) software tools, enabling the geometric representation of curves and surfaces using spline techniques. Bridging CAD with FEM by using the geometric constructions of CAD inside FEM, Isogeometric Analysis (IGA) [1] aims to seamlessly integrate these two essential aspects of the design process. In addition, IGA provides a patch-wise globally smooth basis, allowing for higher-order formulations such as rotation-free Kirchhoff–Love (KL) shells [2].

Since the advent of IGA, many contributions have been made to the field of isogeometric shell analysis. For thin shells, the rotation-free isogeometric Kirchhoff–Love shell applying the higher-order continuity of the basis function was developed [2] with extensions for plasticity [3], hyperelasticity [4, 5], peridynamics [6,7,8], composites [9,10,11,12], stiffener embedding [13, 14] and with applications in fluid–structure interaction [15], crash simulations [16], biological tissues [17,18,19] and many more. In addition, investigations on numerical integration to alleviate locking phenomena have been performed [20, 21] using reduced patch-wise integration procedures [22, 23]. For moderately thick shells, the Reissner-Mindlin formulation [24,25,26,27,28,29,30,31,32,33] has been developed, also with extensions for plasticity [33], hyperelasticity [4], peridynamics [34], composites [35,36,37] et cetera. Lastly, the hierarchical shell [38] is a shell concept intelligently modifying the director vector by adding parameters to the formulations to switch between thin, moderately thick, and thick shell formulations. Recent developments for this shell formulation include [39]. Similar to isogeometric shell elements, isogeometric beam elements [40] also benefit from the higher-order continuity of the basis.

Besides the aforementioned shell elements, the isogeometric solid-shell element [41, 42] is based on the work of Sze and co-authors [43], where shear-deformable shell theories are modelled by using a single element in the through-thickness direction. Solid-shell elements in general use the 3D continuum strain measure and 3D constitutive model, which would be particularly useful for the treatment of hyperelastic materials, employing only translational degrees of freedom [44,45,46] and without the need for additional rules to update internal rotations. The model is based on a Total Lagrangian formulation adopting a Green-Lagrange strain measure with a linearization of the strains and a pre-integration along the thickness direction and a modified generalized constitutive matrix. Due to efficiency reasons, in the context of Lagrangian FEMs, solid-shell elements are often based on a linear displacement interpolation that exhibits shear locking as well as trapezoidal and thickness locking. The first two are cured in [43] by utilizing the Assumed Natural Strains method but other approaches are also possible [47]. Thickness locking, typical of solid-like elements, does not vanish with mesh size [47] without changing the constitutive laws as in [43] or enhancing the transversal strain measure.

In the context of IGA shear and membrane locking are cured by properly established patch-wise reduced integration rule which has been extended to large deformation problems in [41]. The concept of patch-wise reduced integration has been also applied in other shell models [21] as well as to avoid overconstraining in patch coupling problems of Kirchhoff–Love shells [20]. Although the solid shell element is almost locking-free, the thickness locking cannot be eliminated by increasing the interpolation order or by mesh refinement, as observed by [42, 47] changing the constitutive laws. In this respect for the classical linear strain–stress relation corresponding to the St. Venant–Kirchhoff-like materials, the pre-integration along the thickness direction and a modified generalized constitutive matrix can effectively be used to eliminate thickness locking [43]. Since the isogeometric solid-shell formulation does not require \(C^1\) continuity across patches—contrary to isogeometric Kirchhoff–Love shells—complex geometries with connections between patches are modelled easily [41]. Moreover, when applying the patch coupling method proposed in [48] in the case of non-matching meshes the penalty energy term is simply quadratic, as it affects displacements only and thus it is particularly beneficial in nonlinear analysis [20]. Additionally, solid-shell models have been successfully applied in Koiter analyses for post-buckling analyses [49,50,51,52], showing notable advantages concerning the reduction of locking phenomena not caused by interpolation [42, 53, 54]. In addition, isogeometric solid-shell models have been widely investigated in [41, 55,56,57,58,59] and have been extended to composites in [60] for which is particularly interesting the case of FGM [61] where the proposed quasi-3D model could be conveniently replaced with this efficient solid-shell model. Further extensions to hyperelasticity, peridynamics, and plasticity have not yet been developed for IGA and require enhancements like those proposed in the present paper.

In general, the performances of the nonlinear numerical models not only depend on the accuracy of the mechanical model but are often affected by the performances of the numerical procedure used for solving the problem. Usually, the performance of displacement-based formulations deteriorates drastically when the slenderness of the structure increases [62]. On the contrary, formulations based on both stress and displacement fields make Newton-based algorithms insensitive to this effect, independently from the FEM formulation. In addition, especially in the context of IGA, the construction of Mixed models is not trivial nor costless. To enhance convergence of non-linear solid-shells [41], Kirchhoff–Love shells [21] and isogeometric beams [40] the so-called Mixed Integration Point (MIP) method, proposed in [54, 63], has been applied. This method relaxes constitutive equations at each integration point such that the stress in every integration point becomes a locally-independent variable during the Newton iterations, speeding up the iterative solution process [21, 64, 65] preserving the accuracy and the discrete operator format of the displacement FEM model. As was found in the previous works on the MIP [20, 21, 54], the formulation enables larger step sizes and results in fewer iterations required to obtain the same accuracy for the equilibrium path-following.

To these authors’ knowledge, no solid-shell-like models for hyperelastic materials have been formulated in the context of IGA yet so, in this work a seven-parameter (7p) model inspired by the hierarchical concept [38, 66] is developed. In particular, a quadratic displacement field along the actual normal direction is introduced so the resulting linear transversal strain component resolves the thickness locking. Similar to the 6p model [41], the proposed 7p model takes benefits from the rotation-free formulation using the full 3D description which simplifies the application of the non-linear constitutive laws. Moreover, the MIP formulation is extended to non-linear elastic materials, accelerating and improving the robustness of the Newton solution process adopted in this work by making its performances independent of the slenderness of the structure and by the magnitude of the constitutive parameters, even near incompressibility. The formulation of a trivial (non-hierarchical) 3D solid-like with quadratic displacement would be possible but at a higher computational cost as it would require nine parameters per control point. In this respect, our model is, evidently, much more efficient. In addition, the proposed model employs a reduced integration rule based on the target space \(\mathcal {S}^p_r\), as in [41], which will be proven to be effective in the hyperelastic 7p model as well. The combination of the enhancement given by the seventh parameter, the extension to constitutive models and the use of MIP and reduced integration makes the proposed model well-performing in the analysis of shells undergoing large deformations and large membrane stretches for which the linear constitutive relations are invalid.

The outline of this paper is as follows. Section 2 provides preliminaries for the solid-shell formulation presented in this work. That is, notations and basics of spline surfaces are presented, as well as generic kinematics for shell elements. In Sect. 3 the solid-shell formulation from [41] is presented, along with the 7p model. Thereafter, Sect. 4 presents the methodology for constitutive modelling of hyperelastic materials for solid shells and Sect. 5 presents a framework for non-linear analysis with hyperelastic 7p solid-shells elements, including the Mixed Integration Point (MIP) method. Section 6 provides relevant benchmark results for the presented solid-shell formulation and Sect. 7 provides the conclusions and future work following from this contribution.

2 Preliminaries

In this section, the kinematic relations for the isogeometric solid shell are presented. Firstly, Sect. 2.1 provides preliminaries from spline surfaces that are used for the isogeometric element formulations. Secondly, Sect. 2.2 presents general shell kinematics, providing strain definitions given deformations provided in curvilinear coordinate systems.

2.1 Preliminaries for spline surfaces

Shell elements are, by definition, related to surface geometries. Given a surface \(\varvec{s}(\varvec{\xi })\) with parametric coordinates \(\varvec{\xi }=(\xi ,\eta )\), the covariant basis vector \(\varvec{a}_i\), \(i\in \{1,2\}\) is defined as:

$$\begin{aligned} \varvec{a}_i = \frac{\partial \varvec{s}}{\partial \varvec{\xi }_i}, \end{aligned}$$
(1)

where \(\varvec{\xi }_i\) denotes the ith parametric coordinate. Furthermore, the contravariant basis of the surface, denoted by \(\varvec{a}^i\) is defined by

$$\begin{aligned} \varvec{a}^i = \{a_{ij}\}^{-1}a_j, \end{aligned}$$
(2)

where Einstein’s summation convention is used and where \(\{a_{ij}\}^{-1}\) denotes the inverse of the metric tensor, which is defined by \(a_{ij}=\varvec{a}_i\cdot \varvec{a}_j\). In computer-aided design, the surface \(\varvec{s}(\varvec{\xi })\) is commonly described by B-splines or related basis functions. Firstly, we consider a B-spline curve \(\varvec{c}(\xi )\) is defined by

$$\begin{aligned} \varvec{u}(\xi )= \sum _{i=1}^{n} N^p_{i}(\xi ) \varvec{P}_i = \varvec{N}(\xi ) \varvec{P}. \end{aligned}$$
(3)

Here \(\varvec{P}_i\), \(i=1\cdots n\) are the control points and \(N^p_{i}(\xi )\) are the set of B-Spline basis functions, which are piecewise polynomial functions of order p. The latter are defined by a set of non-decreasing real numbers \(\Xi =[\xi _1,\xi _2,...,\xi _{n+p+1}]\) known as knot vector. More details on the B-Spline parametrization can be found in [67]. B-spline basis functions are calculated recursively by using the formula

$$\begin{aligned} N^p_{i}(\xi ) =\frac{\xi -\xi _i}{\xi _{i+p}-\xi _i}N_{i}^{p-1}(\xi ) + \frac{\xi _{i+p+1}-\xi }{\xi _{i+p+1}-\xi _{i+1}}N_{i+1}^{p-1}(\xi ),\nonumber \\ \end{aligned}$$
(4)

for \(p\ge 1\), starting from piecewise constant functions (\(p = 0\)) defined as

$$\begin{aligned} N_{i}^0(\xi ) = {\left\{ \begin{array}{ll} 1, &{}\quad \text {if} \,\xi _i \le \xi < \xi _{i+1} \\ 0, &{}\quad \text {otherwise}. \end{array}\right. }. \end{aligned}$$
(5)

B-Spline basis functions have attractive properties: they satisfy the partition of unity that makes them suitable for discretization methods, they have a compact support, and they are non-zero and non-negative within the knot interval \([\xi _i, \xi _{i+p+1}]\). The regularity r between two parametric or physical elements is described by the multiplicity of the associated knot in \(\Xi \). The regularity is given by \(r=p-s\) where p and s are the order used for the basis functions and the multiplicity of the knot \(\xi _i\) respectively.

Since B-splines are piece-wise polynomial functions they are not able to represent circular arcs and conic sections exactly. For this reason, NURBS have been introduced extending the B-spline concept to represent these objects exactly. NURBS are obtained by a projective transformation of B-splines extending Eq. (3) by using as shape functions

$$\begin{aligned} R_{i}^{p}(\xi ) = \frac{N_{i}^{p}(\xi ) w_i}{\sum _{k=1}^{n} N_{k}^{p}(\xi ) w_k}, \end{aligned}$$
(6)

where \(w_i\) are the so-called weights. It is worth noting that all properties of B-Splines are maintained and, in particular, B-Splines are retrieved when all the weights are equal. Similar to the definition of a B-spline surface (see Eq. (3), a surface \(\varvec{s}(\varvec{\xi })\) can be defined by

$$\begin{aligned} \varvec{u}(\xi ,\eta )= & {} \sum _{i=1}^{n} \sum _{j=1}^{m} N_{ij}^{p,q}(\xi ,\eta ) \varvec{P}_{ij} = \varvec{N}(\xi ,\eta ) \varvec{P}, \quad \text {with} \nonumber \\{} & {} \quad {\left\{ \begin{array}{ll} N_{ij}^{p,q}(\xi ,\eta )=\frac{R_i^p(\xi )M_j^q(\eta ) w_{ij}}{\sum _{k,e=1}^{n,m}R_k^p(\xi )M_e^q(\eta ) w_{ke}} &{} \text {NURBS}\\ N_{ij}^{p,q}(\xi ,\eta )=R_i^p(\xi )M_j^q(\eta ) &{} \text {B-splines} \end{array}\right. }, \end{aligned}$$
(7)

where \(\Xi =[\xi _1,\xi _2...\xi _{n+p+1}]\) and \( \mathcal {H} =[\eta _1,\eta _2...\eta _{m+q+1}]\) are two knot vectors, \(R_{i}^p\) and \(M_j^q\) are the one-dimensional B-spline basis functions over these knot vectors, \(\varvec{P}_{ij}\) defines a set of \(n\times m\) control points and \(w_{ij}\) are the corresponding weights. The tensor product of the knot vectors \(\Xi \) and \( \mathcal {H}\) defines a mesh of quadrilateral isogeometric elements.

In this paper we only deal with NURBS with maximum regularity, that is \(r=p-1\). For this reason, in the following sections, the label quadratic is used to denote NURBS with \(p=2\) and \(r=1\), while cubic means \(p=3\) and \(r=2\).

2.2 Shell kinematics

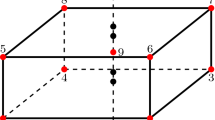
Using a Total Lagrangian formulation, material points in a current (deformed) configuration \(\varvec{x}(\xi , \eta , \zeta )\) are related to the material points in a reference configuration \(\varvec{X}(\xi , \eta , \zeta )\) by a displacement \(\varvec{d}(\xi , \eta , \zeta )\), see Fig. 1

$$\begin{aligned} \varvec{x}(\xi , \eta , \zeta ) = \varvec{X}(\xi , \eta , \zeta ) + \varvec{d}(\xi , \eta , \zeta ). \end{aligned}$$
(8)

Here, \(\varvec{x}\), \(\varvec{X}\) and \(\varvec{d}\) are vectors in a three-dimensional coordinate system, depending on three parametric coordinates.

Fig. 1
figure 1

Undeformed and deformed shell geometry

Full size image

Similar to Eqs. (1) and (2), the covariant basis vectors in the undeformed and deformed configuration can be obtained from the corresponding partial derivatives of the position vectors \(\varvec{X}\) and \(\varvec{x}\) with respect to their parameterizations, respectively

$$\begin{aligned} \varvec{G}_{i} = \varvec{X},_i,\quad \varvec{g}_{i} = \varvec{x},_{i}= \varvec{G}_{i}+ \varvec{d},_i \quad \text{ with } \;i=1,2,3 ,\nonumber \\ \end{aligned}$$
(9)

where \((),_i\) denotes the partial derivative with respect to ith parametric coordinate. The contravariant basis vectors are obtained in a similar way to Eq. (2) but then for three dimensions. The motion of material points from the initial reference configuration to the current configuration is described by the deformation gradient \(\varvec{F}:\,\varvec{x}\rightarrow \varvec{X}\):

$$\begin{aligned} \varvec{F} = \frac{\partial \varvec{x}}{\partial \varvec{X}} = \varvec{g}_i \otimes \varvec{G}^i. \end{aligned}$$
(10)

where the Einstein summation convention is used. Using the deformation gradient in Eq. (10) and the metric tensor coefficients \(g_{ij}\) and \(G_{ij}\), the coefficients of the Green-Lagrange strain tensor \(\varvec{E}=E_{ij}\,\varvec{G}^i \otimes \varvec{G}^j\) can be expressed as

$$\begin{aligned} E_{ij} = \frac{1}{2} \left( \varvec{X},_{i} \cdot \varvec{d},_{j} + \varvec{d},_{i} \cdot \varvec{X},_{j} + \varvec{d},_{i} \cdot \varvec{d},_{j}\right) \quad \text {with}\quad i,j=1, 2, 3\,,\nonumber \\ \end{aligned}$$
(11)

where again \((),_i\) denotes the partial derivative with respect to ith parametric coordinate and \((\cdot )\) is the inner-product between vectors. Note that at this point, we have not made any assumption on the kinematics, thus the form of \(\varvec{X}\) and \(\varvec{d}\).

3 Isogeometric solid-shell model

For different shell models, different assumptions are made to define the position vectors \(\varvec{x}\), \(\varvec{X}\), and \(\varvec{d}\). For example, the Kirchhoff–Love shell model [2] defines the position vector as a surface position plus a contribution in the normal direction. In this section, we first recall the basic kinematics of the standard 6p solid-shell model and then we enhance the kinematics and derive the 7p model, being the main contribution of this paper.

3.1 The 6 parameter (6p) isogeometric solid-shell model

For the solid shell, [41, 43], a linear through-the-thickness interpolation is used to define the position vector is expressed as

$$\begin{aligned} \varvec{X}(\xi ,\eta ,\zeta ) = \varvec{X}_0(\varvec{\xi }) + \zeta \frac{2}{h}\varvec{X}_n(\varvec{\xi }), \end{aligned}$$
(12)

where \(\varvec{\xi }=(\xi ,\eta )\) are the in-plane coordinates, \(\zeta \) is the through-thickness coordinate, h is the shell thickness such that \(\zeta =h/2\) and \(\zeta =-h/2\) identify the top and the bottom surface of the shell respectively. Furthermore, the mid-surface and the normal vector, are respectively defined by

$$\begin{aligned}{} & {} \varvec{X}_0 = \frac{1}{2} \left( \varvec{X}(\xi , \eta , h/2) + \varvec{X}(\xi , \eta , -h/2)\right) ,\nonumber \\{} & {} \quad \varvec{X}_n = \frac{1}{2} \left( \varvec{X}(\xi , \eta , h/2) - \varvec{X}(\xi , \eta , -h/2)\right) . \end{aligned}$$
(13)

Similarly, the displacement field \(\varvec{d}= \varvec{d}_0(\varvec{\xi }) + \zeta \frac{2}{h}\varvec{d}_n(\varvec{\xi }) \) is described as a combination of the displacements

$$\begin{aligned}{} & {} \varvec{d}_0 = \frac{1}{2} \left( \varvec{d}(\xi , \eta , h/2) + \varvec{d}(\xi , \eta , -h/2)\right) ,\nonumber \\{} & {} \quad \varvec{d}_n = \frac{1}{2} \left( \varvec{d}(\xi , \eta , h/2) - \varvec{d}(\xi , \eta , -h/2)\right) . \end{aligned}$$
(14)

Note that in Eq. (14) the symbols \(\varvec{d}(\xi , \eta , \zeta )\) with \(\zeta \in \left[ -h/2,+h/2\right] \) are unknowns of the model. The shell geometry and displacement field are conveniently described, as in other shell models, in terms of the mid-surface and, in this case, a field describing its normal vector. The same convective coordinates \(\varvec{\xi },\zeta \) are used to express the discrete model’s interpolation. Now, using Eqs. (13) and (14), the components of the Green-Lagrange in Eq. (11) strain tensor can be found for the solid-shell.

In the isogeometric concept, \(\varvec{X}\) and \(\varvec{d}\) are defined by splines on an element as follows:

$$\begin{aligned} \varvec{X}(\varvec{\xi },\zeta ) = \varvec{N}_d(\varvec{\xi },\zeta ) \varvec{X}_e, \quad \varvec{d}(\varvec{\xi },\zeta ) = \varvec{N}_d(\varvec{\xi },\zeta ) \varvec{d}_e, \end{aligned}$$
(15)

meaning that \(\varvec{d}_e=(\varvec{d}_{0e}, \varvec{d}_{ne})\) and \(\varvec{X}_e=(\varvec{X}_{0e}, \varvec{X}_{ne})\) are the element control points for, respectively, the geometry and the (unknown) displacements. Furthermore, the matrix \(\varvec{N}_d(\varvec{\xi })\) contains the basis functions with a contribution for the in-plane part \(\varvec{N}(\varvec{\xi })\) and the out-of-plane part \(\zeta \frac{2}{h}\varvec{N}(\varvec{\xi })\):

$$\begin{aligned} \varvec{N}_d(\varvec{\xi },\zeta ) \equiv \begin{bmatrix} \varvec{N}(\varvec{\xi }),\zeta \frac{2}{h}\varvec{N}(\varvec{\xi }). \end{bmatrix} \end{aligned}$$
(16)

.

This model has been proven to be effective also in the context of nonlinear analysis of composite shells too aimed to eliminate thickness locking by means of a modified generalized constitutive matrix [60].

3.1.1 Strain components

Adopting a Voigt notation, the Green-Lagrange covariant strain tensor in Eq. (11) can be written as \(\varvec{E}= [E_{11}, E_{22}, 2E_{12}, E_{33}, 2E_{23}, 2E_{13}]^T\), using Eq. (15) these strains become

$$\begin{aligned} \varvec{E}= \left( \varvec{\mathcal {L}}[\varvec{\xi }] + \frac{1}{2}\varvec{\mathcal {Q}}[\varvec{\xi },\varvec{d}_e]\right) \varvec{d}_e, \end{aligned}$$
(17)

where \(\varvec{\mathcal {L}}[\varvec{\xi }] \equiv \varvec{\mathcal {Q}}[\varvec{\xi }, \varvec{X}_e]\) with

$$\begin{aligned} \varvec{\mathcal {Q}}[\varvec{\xi }, \varvec{d}_e] \equiv \begin{bmatrix} \varvec{d}_e^T \varvec{N}_d,_1^T \varvec{N}_d,_1 \\ \varvec{d}_e^T \varvec{N}_d,_2^T \varvec{N}_d,_2 \\ \varvec{d}_e^T ( \varvec{N}_d,_1^T \varvec{N}_d,_2 + \varvec{N}_d,_2^T \varvec{N}_d,_1)\\ \varvec{d}_e^T \varvec{N}_d,_3^T \varvec{N}_d,_3 \\ \varvec{d}_e^T ( \varvec{N}_d,_3^T \varvec{N}_d,_2 + \varvec{N}_d,_2^T \varvec{N}_d,_3)\\ \varvec{d}_e^T ( \varvec{N}_d,_1^T \varvec{N}_d,_3 + \varvec{N}_d,_3^T \varvec{N}_d,_1)\\ \end{bmatrix}. \end{aligned}$$
(18)

Linearizing the strain tensor from Eq. (17) with respect to \(\zeta \) results in

$$\begin{aligned} \varvec{E}\approx \begin{bmatrix} \varvec{e}(\varvec{\xi }) + \zeta \; \varvec{\chi }(\varvec{\xi })\\ E_{33}(\varvec{\xi }) \\ {\varvec{\gamma }}(\varvec{\xi }) \end{bmatrix}, \end{aligned}$$
(19)

where

$$\begin{aligned}{} & {} \varvec{e}(\xi ,\eta ) \equiv \begin{bmatrix} E_{11}(\xi , \eta , 0)\\ E_{22}(\xi , \eta , 0)\\ 2E_{12}(\xi , \eta , 0) \end{bmatrix},\;\; \varvec{\chi }(\xi ,\eta ) \equiv \begin{bmatrix} E_{11},_{\zeta }(\xi , \eta , 0)\\ E_{22},_{\zeta }(\xi , \eta , 0)\\ 2E_{12},_{\zeta }(\xi , \eta , 0) \end{bmatrix},\nonumber \\{} & {} {\varvec{\gamma }}[\xi ,\eta ] \equiv \begin{bmatrix} 2E_{23}(\xi , \eta , 0)\\ 2E_{13}(\xi , \eta , 0) \end{bmatrix}. \end{aligned}$$
(20)
Fig. 2
figure 2

Seven parameter solid-shell kinematics

Full size image

Using these expressions, the generalized covariant strains at the mid-surface (i.e. \(\zeta =0\)) are found as \(\varvec{\varepsilon }^{6p}(\varvec{\xi }) \equiv \left[ \varvec{e}, E_{33},\varvec{\chi },{\varvec{\gamma }}\right] ^T\). For the sake of notation, the parametric coordinates \(\varvec{\xi }\) are omitted unless needed.

Remark

Curvature thickness locking, as it is already indicated in the name, plays only a role for three-dimensional shell elements with load-induced thickness changes applied to curved structures. For the 6p solid-shell, the through-thickness strain \(E_{33}\) is constant but the in-plane strains have a linear distribution through-thickness. Due to the fact that the constitutive law couples \(E_{33}\) with the in-plane strains, the difference between the constant and linear through-thickness distribution of \(E_{33}\) and the in-plane strains, respectively, causes thickness locking. As surface mesh refinements do not influence the through-thickness precision, thickness locking is not avoided by refining meshes [47].

3.2 The 7 parameter (7p) isogeometric solid-shell model

The previously presented 6p shell model allows for a constant change in thickness direction during the motion. In the context of linear constitutive laws, an effective 6p free from thickness locking is obtained by changing the material law [43]. A decisive advantage of higher-order shell models with at least 7p degrees of freedom per node is the application of complete three-dimensional constitutive laws. Thus, every kinematic variable is linked with its corresponding stress resultant through the material law making curing the curvature thickness locking automatically. In this 7p model, the through-thickness strain is modified by introducing an extra linear through-thickness function, following the approach proposed by [38, 47]. We start by defining the 7th-parameter per node in order to obtain a quadratic transversal displacement in the actual configuration (see Fig. 2 for a schematic overview):

$$\begin{aligned} \varvec{x}^{7p}=\varvec{X}_0+\varvec{d}_0+\zeta \frac{2}{h}(\varvec{X}_n+\varvec{d}_n)+\zeta ^2 w (\varvec{X}_n+\varvec{d}_n). \end{aligned}$$
(21)

Using this definition, the displacement can be written as:

$$\begin{aligned} \varvec{d}^{7p}= \varvec{d}_0 +\zeta \frac{2}{h}\varvec{d}_n + \zeta ^2 w(\varvec{X}_n+\varvec{d}_n). \end{aligned}$$
(22)

Here, we omit the superscript 7p as the 7-parameter model will be the only one considered in the rest of this work. The derivative of the displacements with respect to \(\zeta \) is

$$\begin{aligned} \varvec{d}^{7p}_{,3}= \frac{2}{h}\varvec{d}_n + 2 \zeta w(\varvec{X}_n+\varvec{d}_n). \end{aligned}$$
(23)

Using Eq. (11), the formulation of the transversal linear strain is

$$\begin{aligned} E^{7p}_{33} = \frac{4}{h^2}\varvec{X}_n^T \varvec{d}_n + \frac{2}{h^2}\varvec{d}_n^T \varvec{d}_n +2 \zeta w (\varvec{X}_n +\varvec{d}_n)^T(\varvec{X}_n + \varvec{d}_n). \end{aligned}$$
(24)

Here, the last term of Eq. (23) gives the last contribution of Eq. (24). Moreover, with this hierarchical enhancement of the displacement field, linear terms arise also in the out-of-plane shear strains

$$\begin{aligned} \begin{aligned} 2 E^{7p}_{\alpha 3}&= \varvec{X}_{0,\alpha }^T \varvec{d}_n + \varvec{X}_n^T \varvec{d}_{0,\alpha } +\varvec{d}_n^T\varvec{d}_{0,\alpha }\\&\quad +\varvec{d}_{0,\alpha }^T\varvec{d}_n +\zeta \left( \varvec{X}_{n,\alpha }^T \varvec{d}_n + \varvec{X}_n^T \varvec{d}_{n,\alpha }+\varvec{d}_n^T\varvec{d}_{n,\alpha }+\varvec{d}_{n,\alpha }^T\varvec{d}_n \right. \\&\quad \left. +2 w \left( (\varvec{X}_{0,\alpha }+\varvec{d}_{0,\alpha })^T(\varvec{X}_n+\varvec{d}_n) \right. \right. \\&\quad \left. \left. + (\varvec{X}_n+\varvec{d}_n)^T(\varvec{X}_{0,\alpha }+\varvec{d}_{0,\alpha }) \right) \right) \end{aligned}. \end{aligned}$$
(25)

Then by introducing the interpolation \(w=\varvec{N}_w \varvec{w}\), the term \(\varvec{\mathcal {C}}=2 \zeta w (\varvec{X}_n +\varvec{d}_n)^T(\varvec{X}_n + \varvec{d}_n)\) from Eq. (24) becomes

$$\begin{aligned} \varvec{C}_N=2 \zeta \varvec{N}_w \varvec{w}_e (\varvec{X}_{ne}+\varvec{d}_{ne})^T\varvec{N}^T\varvec{N}(\varvec{X}_{ne}+\varvec{d}_{ne}). \end{aligned}$$
(26)

As a consequence, the first and second variations of this term become

$$\begin{aligned} \begin{aligned} \delta \varvec{\mathcal {C}}&= 2 \zeta \varvec{x}_n^T \varvec{x}_n \delta w + 4\zeta w \varvec{x}_n^T \delta \varvec{d}_n\\ \delta \tilde{\varvec{\mathcal {C}}}&= 4\zeta \delta w \varvec{x}_n^T\dot{\varvec{d}}_n+ 4\zeta \delta \varvec{d}_n^T \varvec{x}_n\dot{w}+4\zeta \delta \varvec{d}_n^T \dot{\varvec{d}}_n w. \end{aligned} \end{aligned}$$
(27)

Evidently, this additional term implies only a small increase in computational costs in terms of element evaluations and storage. To completely describe the computational model the new strain hierarchical term is added to Eq. (19):

$$\begin{aligned} \varvec{E}\approx \begin{bmatrix} \varvec{e}(\varvec{\xi }) + \zeta \; \varvec{\chi }(\varvec{\xi })\\ E_{33}(\varvec{\xi }) +\zeta \bar{E}_{33}(\varvec{\xi })\\ {\varvec{\gamma }}(\varvec{\xi })\\ \end{bmatrix}, \end{aligned}$$
(28)

where \(\bar{E}_{33}=2 w (\varvec{X}_n +\varvec{d}_n)^T(\varvec{X}_n + \varvec{d}_n)\). Finally the generalized covariant strain for the 7p model is \(\varvec{\varepsilon }(\varvec{\xi }) \equiv \left[ \varvec{e},E_{33},\varvec{\chi },{\varvec{\gamma }},\bar{E}_{33}\right] ^T\).

For the problems considered in the present paper, the linear terms in (25) are dropped out. It should be noted that that the linear terms independent from w have been discarded also in previous works [41, 43]. Moreover, it should be stressed that the curvature thickness locking also arises in the linear analysis of curved shells and initially flat shells undergoing large displacements. In Sect. 6.4, a numerical example showing the effectiveness of the proposed cure is given.

3.2.1 Stress conjugate components

Given the 7-parameter kinematic model, the generalized stress components are automatically given by assuring the invariance of the internal work. By collecting the contravariant stress components of the stress tensor \(\varvec{S}=S^{ij}\,\varvec{G}_i\otimes \varvec{G}_j\), in Voight notation being \(\varvec{S}\equiv [S^{11}, S^{22}, S^{12}, S^{33}, S^{23}, S^{13}]^T\), the work conjugate variables with \(\varvec{\varepsilon }\) are obtained by

$$\begin{aligned} \begin{aligned}&\mathcal {W}^{int} = \int _V \varvec{S}^T\varvec{E}dV = \int _\Omega \left( \varvec{\mathcal {N}}^T \varvec{e}+ \varvec{\mathcal {M}}^T \varvec{\chi }\right. \\&\quad \left. + s^{33} E_{33} + \varvec{\mathcal {T}}^T {\varvec{\gamma }}+ \bar{s}^{33} \bar{E}_{33} \right) = \int _\Omega \varvec{\sigma }^T\varvec{\varepsilon }d\Omega , \end{aligned} \end{aligned}$$
(29)

where

$$\begin{aligned} \int _\Omega \left( ... \right) d\Omega = \int _{\xi _i}^{\xi _{i+1}} \int _{\eta _i}^{\eta _{i+1}} \left( ... \right) det(\varvec{J}[\xi , \eta , 0]) d\xi d\eta , \end{aligned}$$
(30)

with \(\varvec{J}\) the Jacobian matrix \(\varvec{J}[\xi , \eta , \zeta ] = [\varvec{G}_1,\; \varvec{G}_2,\; \varvec{G}_3]^T\). The generalized contravariant stresses \(\varvec{\sigma }\equiv \begin{bmatrix} \varvec{\mathcal {N}}, s^{33}, \varvec{\mathcal {M}}, \varvec{\mathcal {T}},\bar{s}^{33} \end{bmatrix}^T\) in Eq. (29) are defined using

$$\begin{aligned} \begin{aligned} \varvec{\mathcal {N}}&\equiv \int _{-h/2}^{h/2} \varvec{\sigma }_{p} d \zeta&\varvec{\mathcal {M}}&\equiv \int _{-h/2}^{h/2} \zeta \varvec{\sigma }_{p} d \zeta \\ s^{33}&\equiv \int _{-h/2}^{h/2} S^{33} d \zeta&\varvec{\mathcal {T}}&\equiv \int _{-h/2}^{h/2} \varvec{\tau }d \zeta \\ \bar{s}^{33}&\equiv \int _{-h/2}^{h/2} \zeta \bar{S}^{33} d \zeta \end{aligned}, \end{aligned}$$
(31)

with

$$\begin{aligned} \varvec{\sigma }_{p} = \begin{bmatrix} S^{11}\\ S^{22}\\ S^{12}\\ \end{bmatrix} \quad \varvec{\tau }= \begin{bmatrix} S^{13}\\ S^{23}\\ \end{bmatrix}. \end{aligned}$$
(32)

Note that in the above, the stress/strain components \(S^{ij}\) and \(E_{ij}\) are written in contravariant/covariant frames and bar \((\bar{\cdot })\) is used for the new 7p model components.

3.3 Variational formulation

The internal work in the solid-shell is given by Eq. (29). Taking the variation of this formulation, we obtain its contribution the virtual work equation, also known as the weak formulation, where

$$\begin{aligned} \begin{aligned} \delta \mathcal {W}^{int}&= \int _\Omega \delta \varvec{\sigma }^T \varvec{\varepsilon }+ \varvec{\sigma }^T \delta \varvec{\varepsilon }d\Omega \end{aligned}. \end{aligned}$$
(33)

Here, \(\delta \varvec{\varepsilon }\) and \(\delta \varvec{\sigma }\) are the variations of the strain and stress tensors, respectively. Following [4], the first variation of the stress and strain fields are linked by

$$\begin{aligned} \delta \varvec{\sigma }= \varvec{D}_\epsilon \delta \varvec{\varepsilon }\end{aligned}$$
(34)

where the subscript \(\epsilon \) means nonlinear dependence on the deformation tensor and where

$$\begin{aligned} \varvec{D}_\epsilon =\begin{bmatrix} \mathcal {\varvec{A}}_0&{} \mathcal {\varvec{D}}_0&{}\mathcal {\varvec{A}}_1&{}\mathcal {\varvec{B}}_0&{} \mathcal {\varvec{D}}_1\\ \mathcal {\varvec{D}}_0&{}\mathcal {R}_0&{}\mathcal {\varvec{D}}_1 &{}\mathcal {\varvec{C}}_0&{}\mathcal {R}_1\\ \mathcal {\varvec{A}}_1^T &{}\mathcal {\varvec{D}}_1^T&{}\mathcal {A}_2&{}\mathcal {\varvec{B}}_1&{} \mathcal {\varvec{D}}_2\\ \mathcal {\varvec{B}}_0^T&{}\mathcal {\varvec{C}}^T_0&{}\mathcal {\varvec{B}}^T_1&{}\mathcal {C}_T&{}\mathcal {\varvec{C}}_1\\ \mathcal {\varvec{D}}_1^T&{}\mathcal {R}_1&{}\mathcal {\varvec{D}}_2^T&{}\mathcal {\varvec{C}}_1^T&{}\mathcal {R}_2 \end{bmatrix}. \end{aligned}$$
(35)

Here, the submatrices are defined by:

$$\begin{aligned} \begin{aligned} \mathcal {A}_{0\alpha \beta }&= \int _{-h/2}^{h/2} \mathbb {C}^{\alpha \beta } dz, \,\,\ \mathcal {A}_{1\alpha \beta } = \int _{-h/2}^{h/2} \mathbb {C}^{\alpha \beta } z dz\,\,\ \mathcal {A}_{2\alpha \beta }\\&= \int _{-h/2}^{h/2} \mathbb {C}^{\alpha \beta } z^2 dz\\ \mathcal {R}_0&= \int _{-h/2}^{h/2} \mathbb {C}^{3333} dz, \,\,\ \mathcal {R}_1 \\&= \int _{-h/2}^{h/2} \mathbb {C}^{3333} z dz, \,\,\ \mathcal {R}_2 = \int _{-h/2}^{h/2} \mathbb {C}^{3333} z^2 dz\\ \mathcal {B}_{0\alpha \beta \gamma }&= \int _{-h/2}^{h/2} \mathbb {C}^{\alpha \beta \gamma 3} dz, \,\,\ \mathcal {B}_{1\alpha \beta \gamma }\\&= \int _{-h/2}^{h/2} \mathbb {C}^{\alpha \beta \gamma 3} z dz \\ \mathcal {C}_{0\gamma }&= \int _{-h/2}^{h/2} \mathbb {C}^{33 \gamma 3} dz, \,\,\ \mathcal {C}_{1\gamma } = \int _{-h/2}^{h/2} \mathbb {C}^{33 \gamma 3} z dz,\\ {}&\,\,\ \mathcal {C}_{T\alpha \beta } = \int _{-h/2}^{h/2} \mathbb {C}^{\alpha 3 \beta 3} z dz \\ \mathcal {D}_{0\alpha \beta }&= \int _{-h/2}^{h/2} \mathbb {C}^{\alpha \beta 33} dz, \,\,\ \mathcal {D}_{1\alpha \beta }\\&= \int _{-h/2}^{h/2} \mathbb {C}^{\alpha \beta 33} z dz, \,\,\ \mathcal {C}_2 = \int _{-h/2}^{h/2} \mathbb {C}^{ij33} z^2 dz \end{aligned} \end{aligned}$$
(36)

Here, the fourth-order tensor \(\mathbb {C}=\mathbb {C}^{ijkl} \varvec{G}_i \otimes \varvec{G}^j\otimes \varvec{G}_k \otimes \varvec{G}^l\) denotes the tangent material tensor. In the following section, the hyperelastic formulations of the stress and tangent material tensors will be provided, given a strain energy density function \(\Psi \).

4 Constitutive modeling

Constitutive models for hyperelastic materials are generally defined by the deformation tensor \(\varvec{C}=\varvec{F}^T\varvec{F}=C_{ij}\,\varvec{G}^i\otimes \varvec{G}^j\)

$$\begin{aligned} S^{ij}_{el}=\frac{\partial \Psi _{el}}{\partial E_{ij}}=2\frac{\partial \Psi _{el}}{\partial C_{ij}}, \end{aligned}$$
(37)

where \(\Psi _{el}(\varvec{C})\) is a proper strain energy function describing an isotropic hyperelastic material. In the following, we present a consistent and general derivation based on the 3D continuum to the solid-shell model. As a consequence, a unified implementation for Kirchhoff–Love [4] and solid-shell is possible by using the same material laws computer library. These implementations are employed to get the results presented in the present paper.

Given the deformation tensor \(\varvec{C}\), the components of the Green-Lagrange strain tensor (11) can be defined as

$$\begin{aligned} E_{ij} = \frac{1}{2}(C_{ij}-G_{ij}). \end{aligned}$$
(38)

Given the coefficients \(E_{ij}\) from Eq. (11), the deformation tensor can be found

$$\begin{aligned} C_{ij} = 2E_{ij}+G_{ij}. \end{aligned}$$
(39)

Such that any assumption in the strain measure leads to a coherent deformation tensor \(\varvec{C}\). Following the variation of the stress tensor from Eq. (34), the tangent material tensor \(\mathbb {C}\) is found as

$$\begin{aligned} \mathbb {C}^{ijkl}=\frac{\partial ^2 \Psi _{el}}{\partial E_{ij}\partial E_{kl}}=4\frac{\partial ^2 \Psi _{el}}{\partial C_{ij}C_{kl}}. \end{aligned}$$
(40)

This representation is particularly convenient in this context of the analysis (IGA) where the model is intrinsically described in terms of curvilinear coordinates. Firstly, from Eq. (28) the strain tensor can be written as a linear function in terms of \(\zeta \):

$$\begin{aligned}{}[E_{ij}]= & {} \begin{bmatrix} \varvec{e}_{1}&{}\varvec{e}_{3}/2&{}{\varvec{\gamma }}_{2}/2\\ \varvec{e}_{3}/2&{}\varvec{e}_{2}&{}{\varvec{\gamma }}_{1}/2\\ {\varvec{\gamma }}_{2}/2&{}{\varvec{\gamma }}_{1}/2&{}E_{33}\\ \end{bmatrix}+ \zeta \begin{bmatrix} \varvec{\chi }_{1}&{}\varvec{\chi }_{3}/2&{}0\\ \varvec{\chi }_{3}/2&{}\varvec{\chi }_{2}&{}0\\ 0&{}0&{}\bar{E}_{33}\\ \end{bmatrix}. \end{aligned}$$
(41)

Similarly, the metric tensor can be written as a linear function in terms of \(\zeta \) too. Recall that,

$$\begin{aligned} \begin{aligned} \varvec{G}_{,\alpha }&=\varvec{X}_{0,\alpha } + \zeta \varvec{X}_{n,\alpha }, \,\,\alpha =1..2\\ \varvec{G}_{,3}&=\varvec{X}_n. \end{aligned} \end{aligned}$$
(42)

Then, the linear expansion of the undeformed metric coefficients can be evaluated as follows

$$\begin{aligned} \begin{aligned} G_{\alpha \beta }&= (\varvec{X}_{0,\alpha }\\&\quad + \zeta \varvec{X}_{n,\alpha })^T(\varvec{X}_{0,\beta } + \zeta \varvec{X}_{n,\beta })\\&=\varvec{X}_{0,\alpha }^T \varvec{X}_{0,\beta } \\&\quad + \zeta \varvec{X}_{0,\alpha }^T \varvec{X}_{n,\beta } + \zeta \varvec{X}_{n,\alpha }^T \varvec{X}_{0,\beta }\\ G_{\alpha 3}&=(\varvec{X}_{0,\alpha } + \zeta \varvec{X}_{n,\alpha })^T \varvec{X}_n\\&=X_{0,\alpha }^T \varvec{X}_n + \zeta \varvec{X}_{n,\alpha }^T \varvec{X}_n\\ G_{33}&=\varvec{X}_n^T \varvec{X}_n \end{aligned}, \end{aligned}$$
(43)

from which it follows that:

$$\begin{aligned}{}[G_{ij}]= & {} \begin{bmatrix} \varvec{X}_{0,1}^T \varvec{X}_{0,1}&{}\varvec{X}_{0,1}^T \varvec{X}_{0,2} &{} \varvec{X}_{0,1}^T \varvec{X}_n\\ \varvec{X}_{0,2}^T \varvec{X}_{0,1}&{}\varvec{X}_{0,2}^T \varvec{X}_{0,2} &{} \varvec{X}_{0,2}^T \varvec{X}_n\\ \varvec{X}_n^T \varvec{X}_{0,1}&{}\varvec{X}_n^T \varvec{X}_{0,2} &{} \varvec{X}_n^T \varvec{X}_n\\ \end{bmatrix}\nonumber \\{} & {} + \zeta \begin{bmatrix} 2\varvec{X}_{0,1}^T \varvec{X}_{n,1} &{}\varvec{X}_{0,1}^T \varvec{X}_{n,2} + \varvec{X}_{n,1}^T \varvec{X}_{0,2}&{} \varvec{X}_{n,1}^T \varvec{X}_n\\ \varvec{X}_{0,2}^T \varvec{X}_{n,1} + \varvec{X}_{n,2}^T \varvec{X}_{0,1}&{}2\varvec{X}_{0,2}^T \varvec{X}_{n,2}&{} \varvec{X}_{n,2}^T \varvec{X}_n\\ \varvec{X}_n^T \varvec{X}_{n,1}&{} \varvec{X}_n^T \varvec{X}_{n,2}&{}0 \end{bmatrix}.\nonumber \\ \end{aligned}$$
(44)

Using Eq. (39), this eventually leads to an expression of the deformation tensor \(\varvec{C}\). In the following, we describe the procedure to obtain the stress and tangent material tensor coefficients, \(S^{ij}\) and \(\mathbb {C}^{ijkl}\), respectively, for compressible materials.

For compressible materials, the stress and material tangent tensors are simply found by evaluating Eqs. (37) and (40) using a strain energy density function of the form

$$\begin{aligned} \Psi (\varvec{C})=\Psi _{iso}(\varvec{C})+\Psi _{\text {vol}}(J), \end{aligned}$$
(45)

with \(\Psi _{iso}\) and \(\Psi _{\text {vol}}\) being the isochoric and volumetric parts of the strain energy density function, respectively [68,69,70].

4.1 Compressible neo-Hookean material

The strain energy density function for the neo-Hookean (nH) material is (see [4])

$$\begin{aligned} \Psi ^{\text {nH}}_{\text {iso}}(\textbf{C}) = \frac{\mu }{2}\left( J^{-\frac{2}{3}}I_1 - 3\right) . \end{aligned}$$
(46)

Then, the derivatives of \(\Psi \) with respect to the components \(C_{ij}\) of the deformation tensor are

$$\begin{aligned} \frac{\partial \Psi ^{\text {nH}}_{\text {iso}}}{\partial C_{ij}}&= \frac{\mu }{2}J^{-\frac{2}{3}} \left( \frac{\partial I_1}{\partial C_{ij}} - \frac{1}{3}\bar{C}^{ij}I_1 \right) \end{aligned}$$
(47)
$$\begin{aligned}&=\frac{\mu }{2}J^{-\frac{2}{3}}\left( G^{ij} - \frac{1}{3}\bar{C}^{ij}I_1 \right) \end{aligned}$$
(48)
$$\begin{aligned} \frac{\partial ^2 \Psi ^{\text {nH}}_{\text {iso}}}{\partial C_{ij}\partial C_{kl}}&=\frac{\mu }{2}J^{-\frac{2}{3}}\left( -\frac{1}{3}\bar{C}^{kl}\left( \frac{\partial I_1}{\partial C_{ij}}- \frac{1}{3}\bar{C}^{ij}I_1 \right) \nonumber \right. \\&\quad \left. -\frac{1}{3}\left( \frac{\partial \bar{C}^{ij}}{\partial C_{kl}}I_1 + \bar{C}^{ij}\frac{\partial I_1}{\partial C_{kl}} \right) \right) \end{aligned}$$
(49)
$$\begin{aligned}&= \frac{1}{9}\frac{\mu }{2}J^{-\frac{2}{3}} \left( I_1 \left( \bar{C}^{ij}\bar{C}^{kl} + \frac{3}{2}\left( \bar{C}^{ik}\bar{C}^{jl} + \bar{C}^{il}\bar{C}^{jk} \right) \right) \nonumber \right. \\&\quad \left. -3\left( G^{ij}\bar{C}^{kl} + \bar{C}^{ij}G^{kl} \right) \right) . \end{aligned}$$
(50)

Here, we used the first invariant \(I_1=\text {tr}(\varvec{C}) = C_{ij}G^{ij}\) with its derivative \(\partial I_1/\partial C_{ij} = G^{ij}\). Furthermore, we recall that \(J=\sqrt{\frac{|g_{ij}|}{|G_{ij}|}}\) with \(g_{ij}={\varvec{g}}_i\cdot {\varvec{g}}_j\, i,j=1,...,3\) the metric tensor of the deformed configuration and \(G_{ij}\) its counterpart in the reference configuration. The notation \(|\cdot |\) denotes the determinant of the coefficient matrices of the metric tensors. The derivative of J is \(\partial J^{k}/\partial C_{ij} = k J^{k}\bar{C}^{ij}/2\) with \(\bar{C}^{ij}\) being the inverse of \(C_{ij}\) as in [4], alternatively computed by \( \bar{C}^{ij}=G^{ik}C_{kl}G^{lj}\), and its derivative is \(\partial \bar{C}^{ij} / \partial C_{kl} = -1/2 (\bar{C}^{ik}\bar{C}^{jl}+\bar{C}^{il}\bar{C}^{jk})\).

4.2 Compressible Mooney–Rivlin material

The strain energy density function is

$$\begin{aligned} \Psi ^{\text {MR}}_{\text {iso}}(\textbf{C}) = \frac{c_1}{2}\left( J^{-\frac{2}{3}}I_1 - 3\right) + \frac{c_2}{2}\left( J^{-\frac{4}{3}}I_2 - 3\right) . \end{aligned}$$
(51)

Then, the derivatives of \(\Psi \) with respect to the components \(C^{ij}\) of the deformation tensor are

$$\begin{aligned} \frac{\partial \Psi ^{\text {MR}}_{\text {iso}}}{\partial C_{ij}}&= \frac{c_1}{2}J^{-\frac{2}{3}} \left( \frac{\partial I_1}{\partial C_{ij}} - \frac{1}{3}\bar{C}^{ij}I_1 \right) \nonumber \\&\quad + \frac{c_2}{2}J^{-\frac{4}{3}}\left( \frac{\partial I_2}{\partial C_{ij}} -\frac{2}{3}\bar{C}^{ij}I_2 \right) \end{aligned}$$
(52)
$$\begin{aligned}&=\frac{c_1}{2}J^{-\frac{2}{3}}\left( G^{ij} - \frac{1}{3}\bar{C}^{ij}I_1 \right) \nonumber \\&\quad +\frac{c_2}{2} J^{-\frac{4}{3}}\left( \frac{\partial I_2}{\partial C_{ij}}-\frac{2}{3} I_2 \varvec{a}r{C}^{ij}\right) \end{aligned}$$
(53)
$$\begin{aligned} \frac{\partial ^2 \Psi ^{\text {MR}}_{\text {iso}}}{\partial C_{ij}\partial C_{kl}}&= \frac{c_1}{2}J^{-\frac{2}{3}}\left( -\frac{1}{3}\bar{C}^{kl}\left( \frac{\partial I_1}{\partial C_{ij}} - \frac{1}{3}\bar{C}^{ij}I_1 \right) \nonumber \right. \\&\left. \quad -\frac{1}{3}\left( \frac{\partial \bar{C}^{ij}}{\partial C_{kl}}I_1 + \bar{C}^{ij}\frac{\partial I_1}{\partial C_{kl}} \right) \right) \end{aligned}$$
(54)
$$\begin{aligned}&\quad + \frac{c_2}{2}J^{-\frac{4}{3}}\left( -\frac{2}{3}\bar{C}^{kl} \left( \frac{\partial I_2}{\partial C_{ij}} - \frac{2}{3}\bar{C}^{ij}I_2 \right) \right. \nonumber \\ {}&\left. \quad + \frac{\partial ^2 I_2}{\partial C_{ij} \partial C_{kl}} - \frac{2}{3}\left( \frac{\partial I_2}{\partial C_{kl}}\bar{C}^{ij}+ \frac{\partial \bar{C}^{ij}}{\partial C_{kl}} \right) \right) \end{aligned}$$
(55)
$$\begin{aligned}&= \frac{1}{9}\frac{c_1}{2}J^{-\frac{2}{3}} \left( I_1 \left( \bar{C}^{ij}\bar{C}^{kl} + \frac{3}{2}\left( \bar{C}^{ik}\bar{C}^{jl} + \bar{C}^{il}\bar{C}^{jk} \right) \right) \right. \nonumber \\ {}&\left. -3\left( G^{ij}\bar{C}^{kl} + \bar{C}^{ij}G^{kl} \right) \right) \end{aligned}$$
(56)
$$\begin{aligned}&+\frac{1}{9}\frac{c_2}{2} J^{-\frac{4}{3}}\left( 4 I_2 \bar{C}^{ij}\bar{C}^{kl}+3I_2\bar{C}^{ik}\bar{C}^{jl}+3I_2\bar{C}^{il}\bar{C}^{jk}\nonumber \right. \\&\left. -6\frac{\partial I_2}{\partial C_{ij}}\bar{C}^{kl}-6\frac{\partial I_2}{\partial C_{kl}}\bar{C}^{ij}+9\frac{\partial ^2 I_2}{\partial C_{ij}C_{kl}} \right) , \end{aligned}$$
(57)

where the second invariant is \(I_2=1/2 (\text {tr}(\varvec{C})^2 - \text {tr}(\varvec{C}^2))\) and its derivatives are \(\partial I_2/\partial C_{ij} = I_1 G^{ij}-C_{ij}\) [71] and \(\partial ^2 I_2/ \partial C_{ij}\partial C_{kl} = 1/2(G^{ik}G^{jl}+G^{il}G^{jl}-2\,G^{ij}G^{kl})\).

4.2.1 Volumetric strain energy density

For the volumetric strain energy density, \(\Psi _{\text {vol}}\) we use [70]

$$\begin{aligned} \Psi _{\text {vol}} = K \beta ^{-2} \left( \beta \log {J} + J^{-\beta } - 1 \right) , \end{aligned}$$
(58)

with \(K=2\mu (1 + \nu )/(3 - 6\nu )\), such that

$$\begin{aligned} \frac{\partial \Psi _{\text {vol}}}{\partial C_{ij}}&= \frac{1}{2}K \beta ^{-1} \left( 1 - J^{-\beta } \right) \bar{C}^{ij}\end{aligned}$$
(59)
$$\begin{aligned} \frac{\partial ^2 \Psi _{\text {vol}}}{\partial C_{ij}\partial C_{kl}}&= \frac{1}{2}K \beta ^{-1} \left( \frac{1}{2}\beta J^{-\beta }\bar{C}^{ij}\bar{C}^{kl} + \left( 1-J^{-\beta }\right) \frac{\partial \bar{C}^{ij}}{\partial C_{kl}}\right) , \end{aligned}$$
(60)

such that for \(\beta =-2\), a common value, we get

$$\begin{aligned} \Psi _{\text {vol}}&= \frac{1}{4}K \left( -2\log {J} + J^{2} - 1 \right) \end{aligned}$$
(61)
$$\begin{aligned} \frac{\partial \Psi _{\text {vol}}}{\partial C_{ij}}&= \frac{1}{4}K \left( 1 - J^{2} \right) \bar{C}^{ij}\end{aligned}$$
(62)
$$\begin{aligned} \frac{\partial ^2 \Psi _{\text {vol}}}{\partial C_{ij}\partial C_{kl}}&= \frac{1}{4}K \left( J^{2}\bar{C}^{ij}\bar{C}^{kl} + \left( J^{2}-1\right) \frac{\partial \bar{C}^{ij}}{\partial C_{kl}}\right) . \end{aligned}$$
(63)
Fig. 3
figure 3

Flowchart of the nonlinear solver employed. Parameters \(\beta _0, \lambda _{max}\) are set at the beginning of the analysis depending on the test, and \(\beta \), eventually, could be updated within the analysis

Full size image

5 Nonlinear analysis framework

In this section, we provide the non-linear analysis framework for the solid-shell element in large strains, starting from the internal virtual work equation and its variation in Eqs. (29) and (33). For more details, we refer to [41, 63].

The variational formulation of the problem is obtained from the equilibrium of internal and external virtual work,

$$\begin{aligned} \delta \mathcal {W}(u, \delta u)=\delta \mathcal {W}^{int}-\delta W^{ext}=0, \end{aligned}$$
(64)

where \(\delta \mathcal {W}\) is the total virtual work in the system, \(\delta \mathcal {W}^{int}\) is the internal virtual work given by Eq. (33) and \(\delta \mathcal {W}^{ext}\) is defined by

$$\begin{aligned} \delta \mathcal {W}^{ext} = \lambda \int _\Omega f\, \delta u \end{aligned}$$
(65)

here, \(\lambda \) is a magnification factor and f is a load acting on the structure. Using Eq. (64), the interpolation assumed it gives

$$\begin{aligned} \varvec{r}(\varvec{d},\,\lambda )\equiv \varvec{s}(\varvec{d})-\lambda \,{\varvec{f}}= \textbf{0}, \quad \text {with} \quad \left\{ \begin{aligned}&\varvec{s}^T\delta \varvec{d}\equiv \delta \mathcal {W}^{int}\\&{\varvec{f}}^T\delta \varvec{d}\equiv \delta \mathcal {W}^{ext}\\ \end{aligned} \right. \end{aligned}$$
(66)

Here, \({\varvec{r}}:\mathbb {R}^{N+1}\rightarrow \mathbb {R}^N\) is the discrete residual vector, is the internal force vector, and \({\varvec{f}}\) the reference load vector. Note that Eq. (66) represents a system of N equations with \(N+1\) unknowns, represented by the displacements \(\varvec{d}\) and the load multiplier \(\lambda \) on so-called equilibrium paths. To trace such paths, Arc-length methods can be employed, with the most commonly known as the Riks and Crisfield methods [72, 73], starting from a known initial configuration \(\varvec{d}^0\) corresponding to \(\lambda = 0\). Arc-length methods typically solve a Newton iteration on each step to find a solution interval represented by \(\Delta \varvec{d}\) and \(\Delta \lambda \), requiring the tangential stiffness matrix which is obtained from linearizing Eq. (66).

Given Eq. (33), variations of the strain and stress tensors \(\varvec{\varepsilon }\) and \(\varvec{\sigma }\), respectively \(\delta \varvec{\varepsilon }\) and \(\delta \varvec{\sigma }\) are required. The first variation of the strain in matrix form is given, using Eqs. (17) and (18) and the first of Eq. (27) by the following:

$$\begin{aligned} \delta \varvec{\varepsilon }= \varvec{B}(\varvec{d}_e) \delta \varvec{d}_e, \end{aligned}$$
(67)

such that the elemental contribution to the internal force vector is obtained by introducing the interpolations in (64)

$$\begin{aligned} \begin{aligned} \delta \mathcal {W}_e^{int}[u] = \int _{\Omega _e}\left( \delta \varvec{\varepsilon }^T \varvec{\sigma }_{el}\right) d\Omega _e = \delta \varvec{d}_e^T \varvec{s}_e[\varvec{d}_e]. \end{aligned} \end{aligned}$$
(68)
Fig. 4
figure 4

Tensile test. Geometry

Full size image
Fig. 5
figure 5

Results for the uniaxial tension test. The tests are performed for different values of Poisson’s ratio \(\nu \). The markers denote the results of the Kirchhoff–Love (KL) shell formulation and the lines denote the results of the solid-shell (SS) formulation

Full size image
Table 1 Tensile test
Full size table

Following [41], the second variation of the strain tensor is given by

$$\begin{aligned} \delta \tilde{\varvec{\varepsilon }} = \varvec{Q}(\varvec{d}_e, \tilde{\varvec{d}}_e) \delta \varvec{d}_e = \varvec{Q}(\varvec{d}_e, \delta \varvec{d}_e) \tilde{\varvec{d}}_e, \end{aligned}$$
(69)

where Eq. (18) and the second of Eq. (27) should be introduced and where its k-th component can be evaluated, introducing the symmetric matrix \(\varvec{\Psi }_k(\varvec{d}_e)\), as

$$\begin{aligned} \delta \tilde{\varepsilon }_k = \tilde{\varvec{d}}_e^T \varvec{\Psi }_k(\varvec{d}_e) \delta \varvec{d}_e, \end{aligned}$$
(70)

where \(\delta \varvec{d}\) and \(\tilde{\varvec{d}}\) are the discrete vectors corresponding to generic variations \(\delta u\) and \(\tilde{u}\) of the configuration field u. From Eq. (33), it can be seen that the term \(\varvec{\sigma }^T \delta \tilde{\varvec{\varepsilon }}\) needs to be evaluated. Hence, from (37)

$$\begin{aligned} \varvec{\sigma }(\varvec{d}_e)= \varvec{\sigma }_{el}= & {} \int _{-\frac{h}{2}}^{\frac{h}{2}}[S_{el}^{11}, S_{el}^{22}, S_{el}^{12}, S_{el}^{33}, z S_{el}^{11}, z S_{el}^{22}, z S_{el}^{12},\nonumber \\ {}{} & {} S_{el}^{13}, S_{el}^{13}, z S_{el}^{33}]^T dz, \end{aligned}$$
(71)

it follows that

$$\begin{aligned} \varvec{\sigma }_{el}^T \delta \tilde{\varvec{\varepsilon }} \equiv \sum _k \sigma _{kel} \delta \tilde{\varepsilon }_k = \tilde{\varvec{d}}_e^T \varvec{\mathcal {G}}(\varvec{d}_e,\varvec{\sigma }_{el}) \delta \varvec{d}_e, \end{aligned}$$
(72)

with

$$\begin{aligned} \varvec{\mathcal {G}}(\varvec{d}_e, \varvec{\sigma }_{el}) = \sum _k \sigma _{elk} \varvec{\Psi }_k(\varvec{d}_e). \end{aligned}$$
(73)

Using Eqs. (34) and (33), the linearization of (68) can be written as

$$\begin{aligned} \int _{\Omega _e}\left( \delta \varvec{\varepsilon }^T \varvec{D}_\epsilon \tilde{\varvec{\varepsilon }} + \delta \tilde{\varvec{\varepsilon }}^T \varvec{\sigma }_{el} \right) d\Omega _e = \delta \varvec{d}_e^T \varvec{K}_e(\varvec{d}_e) \tilde{\varvec{d}}_e, \end{aligned}$$
(74)

Finally, by introducing Eqs. (67) and (72) the tangent stiffness matrix calculated as

$$\begin{aligned} \varvec{K}_e(\varvec{d}_e) \equiv \int _{\Omega _e}\left( \varvec{B}(\varvec{d}_e)^T \varvec{D}_\epsilon \varvec{B}(\varvec{d}_e) + \varvec{\mathcal {G}}(\varvec{d}_e, \varvec{\sigma }_{el}) \right) d\Omega _e. \end{aligned}$$
(75)

The discrete operators involved in the evaluation of the internal force vector and stiffness matrix are defined by means of the strain variations. To avoid locking, the patch-wise reduced integrations proposed in [21] are used to evaluate the integrals in Eqs. (68) and (75).

Fig. 6
figure 6

Initial geometry of the inflation of a balloon benchmark. The geometry is one-eighth part of a sphere with radius \(R=10\) and this part is modelled with \(4\times 4\) cubic elements

Full size image
Fig. 7
figure 7

Results for the inflated balloon benchmark

Full size image

5.1 The iterative scheme with mixed integration points

In [21] it was found that the patch-wise reduced integration rule provides an accurate and efficient discrete approximation. Besides from obtaining the discrete operators, efficiency can also be gained from a reduction in the number of iterations performed in the non-linear solution procedures. From [54, 62], it is known that Newton procedures generally converge slowly for slender elastic structures under large displacements when a purely displacement-based formulation is used, referred to as locking of the Newton method by [41] since the method’s performance decreases with increasing slenderness. As discussed in this work, this iterative behavior is caused by the stresses when obtained by constitutive laws \(\varvec{\sigma }_g(\varvec{d}_e)\) in the tangent stiffness matrix \(\varvec{K}_e(\varvec{\sigma }_g(\varvec{d}_e),\varvec{d}_e)\) which are constrained to satisfy (introducing an overconstraint) the constitutive equations at each iteration loop.

A remedy to solve the problem of poor convergence of Newton’s method for slender structures is called the Mixed Integration Point method and was proposed in [63] and extended and tested in [21, 41, 74, 75]. The idea behind the MIP is to relax the constitutive equations at the level of each iteration point during iterations. In the case of hyperelastic materials, the formulation is not evident as in the case of linear materials. For a formal derivation and a deep discussion in this context, a recent paper [76] can be referred to for details. In particular, the stresses at each integration point \(\varvec{\sigma }_g\) are introduced as independent variables to relax the constitutive e relations as in the standard MIP format, which however can be condensed out at the element level without any additional cost.

Fig. 8
figure 8

Different deformations of the inflated balloon, for \(\lambda =510.221\), \(\lambda =29233.871\) and \(\lambda =41537.189\)

Full size image
Fig. 9
figure 9

Geometry of the cantilever square plate. The plate is clamped on the bottom-left side and free on the other sides. A line-load in out-of-plane direction is added on the top-right side. The plate is modelled using \(3\times 3\) cubic elements

Full size image
Fig. 10
figure 10

Load–displacement curve for the cantilever plate with the load factor \(\lambda \) on the vertical axis and the vertical displacement of the mid-point of the loaded edge \(w_A\) on the horizontal axis

Full size image

The stresses in the MIP are an extrapolation of the previous equilibrium points, like displacements, and are updated during the iterations with the following correction term [76]

$$\begin{aligned} \dot{\varvec{\sigma }}_g=\varvec{D}_g \varvec{B}^j_g \dot{\varvec{d}}_e + \varvec{\sigma }_{elg}-\varvec{\sigma }_g \end{aligned}$$
(76)

which results from equating the internal force contribution with the displacement formulation, as is the philosophy of the MIP and then assuring the same accuracy and matrix sparsity.

To simplify the implementation to the reader a flowchart is depicted in Fig. 3.

It can be observed that the FEM framework for nonlinear analysis with MIP is closely related to the classical displacement-based procedures.

6 Results

This section presents several numerical tests using different compressible and nearly-incompressible materials. All benchmark problems are compared and validated against the compressible Kirchhoff–Love (KL) shell model from [4]. Firstly the present formulation is evaluated on the uniaxial tensile test and the inflation of a balloon. These tests serve the purpose of checking with originally analytical solutions with respect to the evaluation of the stretches and thickness changes by the comparison with the KL model of [4]. Thereafter, a benchmark of the bending of a plate is used to validate the present model for bending-dominated against thickness locking. The last test, which represents the pinching of a cylinder, shows the difference with respect to the KL shell model due to the presence of out-of-plane shear and transverse normal stresses. In all comparisons, the Kirchhoff–Love shell is integrated with a \(S^{3}_0\) [21] reduced integration rule, while for the present model the \(S^{4}_1\) reduced integration is employed [41].

Fig. 11
figure 11

Cantilever plate. Deformed shapes of the cantilever plate for the a solid-shell model and b the KL model

Full size image
Fig. 12
figure 12

Cantilever plate. Contravariant stress components S\(^{11}\) (left) and covariant strains \(E_{33} + \zeta \bar{E}_{33}\) (right) for the inward case at \(\lambda \) = 0.667

Full size image

6.1 Uniaxial tensile test

As a first example Fig. 4, we simulate a simple uniaxial tensile test, the reference solution is compared in [4] with the analytical one so that the comparison between the KL shell model and the present one is meaningful. The unit square membrane of thickness \(h=0.01\) is subjected to uniaxial unit tensile loading and different constitutive models are employed. Are considered simply supported boundary conditions in transversal direction while in plane is simply restrained the rigid body motion. The domain is modelled using a single cubic solid-shell element with the neo-Hookean (nH, Eq. (46)) model having material parameter \(\mu \) = 1.5 10\(^6\). In all cases given different values for the Poisson ratios \(\nu = \{0.45, 0.49, 0.499\}\) are considered. The actual thickness \(h^*\) can be evaluated using the formula \(h^*=\lambda _{33}h\).

In Fig. 5, the results are provided for different values of the Poisson ratios, in particular, are shown the thickness change factors \(\lambda _{33}\) against the load amplifier \(\lambda \) and, as usual, the load–displacement (\(u_A-\lambda \)) curves.

Fig. 13
figure 13

The initial geometry of the cylinder for the pinched cylinder benchmark. The cylinder has radius \(R=9\), length \(L=30\), and a line-load \(q=\pm 2\) is applied on the top and the bottom of the cylinder. The sign of the line-load is changed to create inward or outward displacements. The geometry is modelled by a quarter, as indicated, with symmetry conditions on both sides and with 8 elements in the radial direction and 16 in the longitudinal direction

Full size image
Fig. 14
figure 14

Load–displacement curves for the pinched cylinder for both the inward and outward loading case. The vertical axis represents the load magnitude \(\lambda \) and the horizontal axis represents the vertical deflection of the mid-point of the top boundary of the domain, \(w_A\)

Full size image

As can be seen from these results, a perfect agreement with the Kirchhoff–Love shell model can be observed for all values. In particular, the cumulative iteration numbers of the present model and the Kirchhoff–Love shell model are presented in table 1 for different values of the Poisson ratios. As seen in this table, the number of iterations is not influenced by the material’s compressibility, as well as for the Kirchhoff–Love shell. The small deviations in iteration numbers are due to the variability of the step size of the arch-length method here implemented.

6.2 Inflation of a balloon

In this benchmark problem, the inflation of a balloon is modelled. The geometry of the balloon is simplified by a sphere with initial radius \(R=10\) of which 1/8th section is modelled using 4x4 cubic elements, as highlighted in Fig. 6. The balloon is subjected to an internal unit pressure acting in the normal direction. Since the balloon is represented by a perfect sphere, this benchmark represents a bi-axial membrane stress state, of which an analytical solution is given in [70] and has been already compared with the KL model in [4] making the comparison with this model meaningful. For this test, we consider a nearly incompressible neo-Hookean material as well as a nearly incompressible Mooney–Rivlin material. The near incompressibility is applied as in the previous case by choosing \(K=K(\nu )\) and \(\nu =0.499659\). As material property we choose \(\mu =4.225\cdot 10^5\), \(c_1 = 0.4375\mu \), and \(c_2 = 0.0625\mu \), (thus \(c_1/c_1\) =7) as reported in [4].

The load–displacement and pressure-membrane stretch curves are provided in Fig. 7 for the present solid-shell model and the KL shell model as proposed in [4]. As can be seen from these results, the proposed solid-shell model performs well in comparison with the results obtained with the KL shell model. Finally, Fig. 8 shows the one-eighth analyzed portion deformed shape for different load levels for the case of nearly-incompressible Neo-Hookean material.

6.3 Cantilever plate

To assess the proposed model in a bending-dominated benchmark, a cantilever plate subjected to a uniformly distributed load at the free end is studied, see Fig. 9. The plate has unit-thickness as proposed by [77] and material parameter \(\mu =2\) for compressible neo-Hookean (nH) material with \(\nu =0.49\) for the solid-shell model and an incompressible nH model for the KL shell model. In [43], the plate is modelled using 4 quadratic \(C^0\) elements in the longitudinal direction whereas in the present benchmark we use 3x3 and 4x4 cubic elements for the solid-shell model and 24x24 cubic elements for the KL shell model as very fine reference mesh. The solution obtained by employing the 6p model is included for comparison. This model, as can be seen from Fig. 10, does not provide accurate results. It is worth noting that, in contrast to classical locking effects, the severe thickness locking observed is unsolvable by mesh refinement [47].

Figures 10 and 11 show the load–displacement curves of the cantilever plate. As can be seen in these figures, there is a good correspondence between the KL shell model and the solid-shell model for a nearly compressible model. Only a small deviation in the tail of the curve is observed in the case of the mesh 3x3, because of the coarse mesh for the solid-shell model and a perfect match with the 6x6 one. This is as expected because, for both models, thickness locking has been correctly resolved.

Fig. 15
figure 15

Deformed geometry of the pinched cylinder subject to an inward load

Full size image
Fig. 16
figure 16

Deformed geometry of the pinched cylinder subject to an outward load

Full size image

The smoothness of the stress and strain fields in Fig. 12 demonstrates that locking is resolved accurately. In fact, the locking effects are usually shown by stress field oscillations [78].

Fig. 17
figure 17

Pinching of a cylinder. Contravariant stress components S\(^{11}\) (left) and covariant strains \(E_{33} + \zeta \bar{E}_{33}\) (right) for the inward case at \(\lambda \) = 0.667

Full size image

6.4 Pinching of a cylinder

The last benchmark of this work involves the pinching of a cylinder. This bending-dominated problem was proposed by [79] and also modelled in [4]. The cylinder has radius \(R=9\), length \(L=30\), and thickness \(t=0.2\) and is modelled using a fully symmetric model (i.e. 1/4th of the cylinder) with line-loads on the top and bottom as shown in Fig. 13, to simplify reproducibility of the results. The geometry is represented by \(8\times 16\) cubic elements in respectively radial and longitudinal directions. We analyze the load case of both inward and outward-directed loads, and we use a compressible neo-Hookean material is used, defined by the following strain energy function:

$$\begin{aligned}{} & {} \Psi _{el} =\frac{\mu }{2}(tr(\varvec{C}) - 3) - \mu \ln (\sqrt{\text {det}(\varvec{C})})+\frac{\Lambda }{4}(\text {det}(\varvec{C})\nonumber \\ {}{} & {} -1-2\ln (\sqrt{\text {det}(\varvec{C})})) \end{aligned}$$
(77)

with \(\mu \) = 60 and \(\Lambda \) = 240 as the Lamé constants.

In Fig. 14, the load–displacement diagrams of the pinched cylinder are presented, with the inward-facing loads on the left and the outward-facing loads on the right. The results are again compared to a Kirchhoff–Love shell formulation derived from [4]. Furthermore, Figs. 15 and 16 show the deformed shapes of the pinched cylinder with inward and outward-facing loads, respectively. In these plots, only the computed part of the cylinder is plotted with contour plots. From the results of the pinched cylinder in comparison with the KL shell model, we can see that the models compare very well.

Also for this benchmark, see Fig. 17 the stress and strain fields are smooth. This demonstrates the adequate efficiency of the proposed model in removing the thickness locking.

To show the difference in the behavior of the solid-shell model and the KL shell model, the pinched cylinder benchmark is slightly modified. The geometry is kept the same, but in addition to the previous symmetric boundary conditions, the points B and \(B'\) in Fig. 13 are fixed. The results of this test, for inward load case only, are given in Fig. 18 in terms of load–displacement curves. The deformed geometries are given in Fig. 19, evidently showing a different solution as in Fig. 15 without the added fixed points. Given the results from Fig. 18, it can be seen that the differences in the load–displacement curves of the solid-shell and KL shell models are more evident. Indeed, fixing the additional points of the cylinder reveals the differences between the two models with respect to capturing shear deformation effects and transverse normal stresses, which are captured more accurately in the proposed 7p solid-shell model.

Fig. 18
figure 18

Load–displacement curve of the pinched cylinder subject to an inward load, with points B and \(B'\) (see Fig. 13) constrained. The vertical axis represents the load magnitude \(\lambda \) and the horizontal axis represents the vertical deflection of the mid-point of the top boundary of the domain, \(w_A\)

Full size image
Fig. 19
figure 19

Deformed geometry of the pinched cylinder subject to an inward load, with points B and \(B'\) (see Fig. 13) constrained

Full size image

7 Conclusions

The present paper presents an effective hierarchic seven-parameter solid-shell model for hyperelastic materials under large strains. This hierarchic extension adds an extra parameter for the transversal displacement field on each control point which eliminates the thickness locking observed in the six-parameter model. The model presented in this paper benefits, also, from the reduced integration rule which has never been experimented with in this context as well as the Mixed Integration Point strategy, which has been extended for fully non-linear constitutive laws. Via numerous benchmark examples, the model has been examined against an existing hyperelastic Kirchhoff–Love shell formulation. From these benchmark examples, it can be concluded that the present model works as expected for compressible and nearly incompressible materials. Furthermore, in the last benchmark of the pinching of a cylinder, we compared the present model against the Kirchhoff–Love shell model, providing slightly different results since the present model takes shear deformations into account. In the derivations of the presented formulations, linear shear components have been neglected for the purpose of a simplified model which only involves the linear normal strain enhancement. As an extension, future work includes the application of shells with thickness variability for challenging applications.