Embedding physical knowledge in deep neural networks for predicting the phonon dispersion curves of cellular metamaterials

Abstract

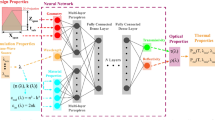
Phononic metamaterials have the capability to manipulate the propagation of mechanical waves. The traditional finite element (FE) analysis-based methods for predicting phonon dispersion curves are computationally expensive for structure optimization that may require thousands of design evaluations, especially when applied to high-resolution metamaterial models with a large number of elements. To address this issue, this paper presents two physics-embedded deep convolutional neural networks to predict the phonon dispersion curves of 2D metamaterials: (1) a transfer learning-based convolutional neural network (TLCNN) and (2) a physics-guided convolutional neural network (PGCNN). The physics knowledge is embedded into the two proposed models by modifying the loss function of the convolutional neural network (CNN). A comparative study among CNN, TLCNN and PGCNN is conducted to understand the relative merits. The effectiveness of the physics-embedded methods is evaluated by comparing the predicted normalized eigenfrequencies with those obtained by direct numerical simulations (DNS) using FE simulation. Furthermore, a comparison of the computational costs, which include computing time and memory usage, is presented among DNS, CNN, TLCNN and PGCNN. It is demonstrated that the proposed TLCNN and PGCNN have the potential to improve prediction accuracy with a limited amount of input data. However, the computational costs of the “offline” model training are still significant. Among the three methods, PGCNN shows the best prediction accuracies on both the training and test sets.

Appendix

1.1 Hyperparameters related to the structure of three models

See Table 3.

Table 3 The dimensionality of each layer in the proposed models

1.2 Training result of the structure-elasticity model (the source model of the TL model)

Figure 7 shows the accuracy of the structure-elasticity model (source model). The predicted elastic stiffness constants against the ground truth values obtained by FE simulation are plotted. The ${R}^{2}$ values are shown in Table 4. The structure-elastic stiffness constants model shows satisfactory prediction accuracies.

Fig. 7

Predicted elastic stiffness constants ${C}_{11}$, ${C}_{22}$, ${C}_{12}$, ${C}_{44}$ versus the ground truth values

Table 4 R squared value of the predictions of the elastic stiffness constants ${C}_{11}$, ${C}_{22}$, ${C}_{12}$, ${C}_{44}$

1.3 Convergence study for choosing $\boldsymbol{\alpha }$

A convergence study is conducted to determine the $\alpha$ value in the loss function of PGCNN. We test a series of $\alpha$ values with the same training and test sets. We compare the performances of these models by the metrics discussed in Sect. 4.3. Figure 8 shows the performances of PGCNN with different $\alpha$ values. We observe the highest accuracy occurring when $\alpha =10$. Therefore, we choose 10 as the value of $\alpha$ in Eq. 19.

Fig. 8

Convergence study to determine the value of $\alpha$

1.4 Convergence test on the choice of the characteristic length ${\varvec{l}}$

When using reduced-order metamaterial unit sample, Eq. 18 does not hold and will be replaced by:

$$sum\left\{abs\left[\left(\overline{{\varvec{K}} }-{\left(\frac{2\pi Cf}{l}\right)}^{2}\overline{{\varvec{M}} }\right){\varvec{v}}\right]\right\}=\epsilon $$

(22)

where $\epsilon$ represents the residual error of using reduced-order metamaterial unit sample, $l$ represents the characteristic length, which is defined as the side length of the metamaterial unit in pixel. When using the 250 $\times$ 250 pixels metamaterial unit samples for the calculation of $\overline{{\varvec{K}} }$, $\overline{{\varvec{M}} }$ and ${\varvec{v}}$, $\epsilon$ should be equal to 0. A convergence test is conducted for choosing the characteristic length $l$ which balances the computational cost and the induced residual error. We randomly select 50 metamaterial unit samples from the dataset and calculate their corresponding $\overline{{\varvec{K}} }$, $\overline{{\varvec{M}} }$ and ${\varvec{v}}$ matrices with different characteristic length $l$. The averaged residual error $\epsilon$ of 50 samples are calculated and the averaged memory usage for the storage of $\overline{{\varvec{K}} }$, $\overline{{\varvec{M}} }$ and ${\varvec{v}}$ are recorded as well. As shown in Figure 9, with the characteristic length $l$ increases, the memory usage for storing the physics-related matrices increases. The curve of residual error converges at $l=20$. To balance the memory usage and the accuracy, we choose $l=20$ as the characteristic length of the reduced-order metamaterial unit samples.

Fig. 9

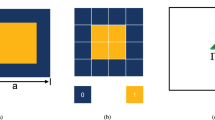
a Convergence test on characteristic length $l$ of the reduced-order calculation of $\overline{{\varvec{K}} }$, $\overline{{\varvec{M}} }$ and ${\varvec{v}}$. The curve of residual error shows that the residual error converges at $l=20$. The curve of averaged storage memory usage increases with characteristic length $l$ increases. b One representative structure and its corresponding morphology under different characteristic length $l$

1.5 A zoom-in view of the predicted and ground truth phonon dispersion curves

The phonon dispersion curves of one representative structure are separated into three parts by different frequency regions: low frequency region, medium frequency region and high frequency region, as shown in Fig. 10.

Fig. 10

A detailed phonon dispersion curves of the predicted structure

1.6 Comparison among multiple purely data-driven CNN models

See Table 5.

Table 5 Comparison of the CNN used in this work and other popular CNN models: the accuracies of predicting the normalized frequencies under different normalized wave vectors