Proper generalized decomposition solutions for composite laminates parametrized with fibre orientations

Abstract

Composite materials are gaining popularity as an alternative to classical materials in many different applications. Moreover, their design is even more flexible due to the potential of additive manufacturing. Thus, one can produce a tailored composite laminate with the optimal values of some design parameters providing the desired mechanical performance. In this context, having a parametric numerical model for the mechanical response of the composite laminate is essential to compute the optimal parameters. In the present paper, the design parameters under consideration are the angles describing the orientation of the reinforcement fibers in different layers or patches of the composite laminates. We obtain a generalized solution using Proper Generalized Decomposition (PGD) which is adopted to provide solutions with explicit parametric dependence. The Tsai-Wu failure criterion is used to estimate first ply failure. In this context, Tsai-Wu criterion is used as the objective function for the optimization of the fibre orientations in the laminate. The PGD solution provides also sensitivities for a gradient-based optimization algorithm. The potentiality and efficiency of the presented approach is demonstrated through some numerical tests.

1 Introduction

The progress of additive manufacturing allows producing tailored composite laminates, for instance with different fiber orientations in each layer or patch. Thus, the designer of the laminate has the freedom of selecting a number of parameters, e.g., angles describing the fiber orientation in each zone. In order to properly determine the optimal choice for these parameters, there is a need for modeling the mechanical behavior of a given composite laminate for any possible value of the parameters. To achieve such model, the selected parameters are considered as independent variables (extra-coordinates or extra-dimension) in the problem formulation resulting in a multidimensional problem. Generally, solving a mechanical model using mesh based techniques in 3D is computationally expensive and at some point it could become infeasible when the problem is multidimensional. In spite of the existence of very well established theories that simplify the analysis of 3D composite laminate bodies through 2D or even into 1D structural theories, a 3D analysis is often compulsory to capture all the physics through the thickness and around the boundaries [1]. Furthermore, if the problem under consideration is an application requiring multiple queries such as optimization, inverse problems, or uncertainty quantification, the direct problem is solved numerous times increasing drastically the computational burden.

In the present work, the design parameters under consideration are the angles describing the orientation of the reinforcement fibers in different layers or patches of the composite laminates. Classical engineering approaches to the optimization of fibre orientations in composite laminates have been addressed in many different studies. The approaches could be divided into six main parts: buckling load maximization (eg. [2, 3]), vibrational characteristics enhancement (eg. [4, 5]), weight minimization (eg. [6, 7]), strength and stiffness maximization (eg. [8, 9]), deflection minimization (eg. [10]), and stress minimization (eg. [11, 12]).

The approach adopted in the current study is the maximization of the strength of the composite structure. Early work by Pedersen has been dedicated to solve the optimization problem of the orientation of orthotropic material analytically using a strain based objective function [13]. Pedersen continued his work and devised a FEM and optimization procedure to solve the aforementioned problem and also to solve the thickness-orientation optimization problem [14, 15]. Recent work by Huang et al. on the optimization of fibre orientation, using a load bearing approach, used the Tsai-Wu criterion as the objective function [16]. It was followed by the work of Groenwold and Haftka on the optimization of different failure criteria [8]. The work by Bruynmeel consisted in optimizing the fibre orientation using strength based criteria, such as Tsai-Hill and Tsai-Wu, showing that a direct parameterization of the problem in the design variables is favorable over the parameterization using lamination parameters where the space is not completely known [17]. Bruynmeel extended his work and argued that the optimization of the fibres in a non-homogeneous domain is very sensitive to the initial guess of gradient based methods and that one could end up with a local solution. Bruynmeel also reported that the more the number of design variables increases the more the optimization problem becomes expensive, especially if the optimization method employed is a non-deterministic method to obtain global solutions [18].

In the current study, we aim to investigate the effect of the fibre configuration on the Tsai-Wu failure index that is presented as the objective function of the optimization problem. Note that here we are not predicting final failure of the laminates, which would require a progressive damage model, but rather first ply failure. While the Tsai-Wu criterion is not the most accurate failure criterion available (invariant-based failure criteria are more accurate, especially for the fiber-kinking failure mode), it’s mathematical representation makes it suitable to be used in combination with the Proper Generalized Decomposition technique. Accordingly, an optimization technique should be applied to efficiently find the best fibre orientation in the laminate. The fibre orientation in a laminate is one of many design parameters affecting the structural performance. For example, the variation of the stacking sequence, material density and layer thickness has a direct effect on the mechanical performance of composite laminates. For this reason, it is of paramount importance to consider their optimization either individually or simultaneously [19] to achieve better designs.

In terms of optimization techniques, recent work done by Hwang et al. addressing the optimization of fibre orientation in each layer using the Genetic Algorithm (GA) and it was reported that the optimization algorithm behaves well in such problems [5]. It was shown by Li et al. in a recent research that a hybrid optimization method consisting in the genetic algorithm and the particle swarm optimization efficiently finds the optimal solution [20]. Another recent work combining topology optimization with fibre orientation optimization by minimizing the compliance. They use gradient-based method which leads to local solutions. Moreover, solving the system and the computation of the sensitivities every iteration could lead to a computationally expensive problem depending on the size of the system and the number of design variables [21]. A recent study by Diniz et al. focuses on the design optimization using the Tsai-Wu failure criterion as the objective function coupled with Artificial Neural Networks (ANN) [22]. The work done by Shen et al. is competitive and it shows the optimization of fibre orientation using the compliance as the objective function. However, it is reported that the solution is easily affected by the initial guess since the work employs a gradient-based method to obtain the optimal fibre orientation. They overcome this issue by providing the gradient-based method with the principle directions as initial guess. Moreover, in each iteration they solve the complete system, which could become computationally challenging if the system is large [23]. There is a vast literature on methodologies and different approaches for the optimization of the design of composite laminates; and for deeper insight the reader is referred to the review paper by Nikbakt et al. [24] and the references therein.

The present paper focuses on composite laminates and it aims to ultimately find the best fibre orientations to minimize the Tsai-Wu failure index. These aims naturally lead us to an optimization problem that has to be solved a large number of times, corresponding to different choices of the design parameters. Thus, the computational complexity of this procedure blows up with the number of design parameters, resulting in the so-called curse of the dimensionality [25]. The use of a Model Order Reduction (MOR) technique is advocated to alleviate the mentioned computational burden. Particularly, the Proper Generalized Decomposition (PGD) method is selected as a MOR technique because it provides a solution with explicit dependence on the parameters of the problem.

The layout of the present paper is as follows. Section 2 presents the problem statement of the full 3D linear elasticity problem, showing the parametric dependence, and a brief introduction to the failure criterion used along with the optimization problem to be solved. Section 3 introduces the encapsulated PGD concept and shows how the problem in hand is adapted to it. Section 4 shows some numerical examples to demonstrate the potentiality of the methodology and finally in Sect. 5 we address some concluding remarks.

2 Problem statement

2.1 Equilibrium equations and constitutive law

Given a 3D domain , the linear elasticity problem consists in finding the displacement ${\varvec{u}}$ satisfying,

$$\begin{aligned} {\left\{ \begin{array}{ll} {\varvec{\nabla }}^{\textsf {T}}_S{\varvec{\sigma }}+{\varvec{b}}={\varvec{0}} &{} \text {in } \varOmega \\ {\varvec{u}}={\varvec{u}}_D &{} \text {on } \varGamma _D\\ {\varvec{n}}^\textsf {T}{\varvec{\sigma }}={\varvec{t}}_N &{} \text {on } \varGamma _N \end{array}\right. } \end{aligned}$$

(1)

with ${\varvec{\sigma }}={\mathcal {C}}{\varvec{\varepsilon }}$ and ${\varvec{\varepsilon }}={\varvec{\nabla }}_S{\varvec{u}}$,

where ${\varvec{\nabla }}_S$ is a $6 \times 3$ symmetric gradient matrix operator (see for example [26]), ${\varvec{\sigma }}$ is the stress field, ${\varvec{b}}$ is the body forces vector; ${\varvec{u}}_D$ is the displacement field prescribed on the Dirichlet boundary, ${\varvec{t}}_N$ is the prescribed the traction applied on the Neumann boundary, ${\varvec{n}}$ is the $6\times 3$ matrix representation of the normal (in analogy with the ${\varvec{\nabla }}_S$ operator); ${\mathcal {C}}$ is the elasticity tensor, and ${\varvec{\varepsilon }}$ is the strain field. The stresses and strains are expressed in the engineering Voigt’s notation; and therefore the elasticity tensor is expressed as a $6 \times 6$ matrix. For orthotropic materials the constitutive relation reads

$$\begin{aligned} \begin{bmatrix} \sigma _{xx} \\ \sigma _{yy}\\ \sigma _{zz}\\ \tau _{yz}\\ \tau _{xz}\\ \tau _{xy} \end{bmatrix} = \begin{bmatrix} {\mathcal {C}}_{11} &{} {\mathcal {C}}_{12} &{} {\mathcal {C}}_{13} &{} 0 &{} 0 &{} 0\\ &{} {\mathcal {C}}_{22} &{} {\mathcal {C}}_{23} &{} 0 &{} 0 &{} 0\\ &{} &{} {\mathcal {C}}_{33} &{} 0 &{} 0 &{} 0\\ &{} \text {Sym.} &{} &{} {\mathcal {C}}_{44} &{} 0 &{} 0\\ &{} &{} &{} &{} {\mathcal {C}}_{55} &{} 0\\ &{} &{} &{} &{} &{} {\mathcal {C}}_{66} \end{bmatrix} \begin{bmatrix} \epsilon _{xx} \\ \epsilon _{yy}\\ \epsilon _{zz}\\ \gamma _{yz}\\ \gamma _{xz}\\ \gamma _{xy} \end{bmatrix} \end{aligned}$$

(2)

The weak form of the elastic problem (1) reads, find ${\varvec{u}} \in U$ such that,

$$\begin{aligned} \begin{aligned}&\int _{\varOmega }({\varvec{\nabla }}_S{\varvec{w}})^\textsf {T}{\varvec{{\mathcal {C}}\nabla }}_{S}{\varvec{u}}\;d\varOmega \\&\quad =\int _{\varGamma _N}{\varvec{w}}^\textsf {T}{\varvec{t}}_N\;d\varGamma +\int _{\varOmega }{\varvec{w}}^\textsf {T}{\varvec{b}}\;d\varOmega \qquad \forall {\varvec{w}}\; \in U_o \end{aligned} \end{aligned}$$

(3)

where the spaces are defined as $U=\{{\varvec{u}}|{\varvec{u}} \in \big (H_1(\varOmega )\big )^3,\;{\varvec{u}}={\varvec{u}}_D \quad \textsf {on}\;\varGamma _D \}$ and $U_0=\{{\varvec{w}}|{\varvec{w}} \in \big (H_1(\varOmega )\big )^3,\;{\varvec{w}}=0 \quad \textsf {on}\;\varGamma _D \}$. The discrete approximation ${\varvec{u}}_h$ to ${\varvec{u}}$ is associated with a tessellation of $\varOmega$ in elements $\varOmega ^e$, $e=1,\dots ,\texttt {n}_{\texttt {el}}$. The number of degrees of freedom within each element is denoted by $\texttt {n}_{\texttt {edof}}$. For any point ${\varvec{x}}$ in element $\varOmega ^e$, the restriction of ${\varvec{u}}_h$ to the e-th element reads

$$\begin{aligned} {\varvec{u}}^e_h({\varvec{x}})={\varvec{N}}^e ({\varvec{x}}){\varvec{d}}^e \end{aligned}$$

(4)

where ${\varvec{N}}^e({\varvec{x}})$ is a $3\times \texttt {n}_{\texttt {edof}}$ element shape function matrix, and ${\varvec{d}}^e$ is a $\texttt {n}_{\texttt {edof}}\times 1$ vector of element nodal displacements.

Following the derivations in [26], the corresponding element stiffness matrix ${\varvec{K}}^e$ and force vector ${\varvec{f}}^e$ read,

$$\begin{aligned} {\varvec{K}}^e= & {} \int _{\varOmega ^e}{\varvec{B}}^{e\textsf {T}} {\varvec{{\mathcal {C}}}} {\varvec{B}}^e\;d\varOmega \end{aligned}$$

(5)

$$\begin{aligned} {\varvec{f}}^e= & {} \int _{\varOmega ^e}{\varvec{N}}^{e\textsf {T}} {\varvec{b}}\;d\varOmega + \int _{\varGamma _N \bigcap {\bar{\varOmega }}^e}{\varvec{N}}^{e\textsf {T}} {\varvec{t}}\;d\varGamma \end{aligned}$$

(6)

where ${\varvec{B}}^e$ is the strain-displacement matrix containing the symmetric gradient of the shape functions.

The global number of degrees of freedom is denoted by $\texttt {n}_{\texttt {d}}$. The global stiffness matrix ${\varvec{K}}$ is obtained assembling the element matrices ${\varvec{K}}^e$, $e=1,\dots ,\texttt {n}_{\texttt {el}}$. Here, the assembly operator is represented by $\texttt {n}_{\texttt {edof}}\times \texttt {n}_{\texttt {d}}$ Boolean matrices ${\varvec{L}}^e$, containing only ones and zeros, such that they restrict a global vector into a local one defined within each element; for example ${\varvec{d}}^e={\varvec{L}}^e {\varvec{d}}$ for the global and local nodal displacement vectors. The force vectors are treated similarly and, therefore, the global system of equations reads

$$\begin{aligned} {\varvec{K}} {\varvec{d}} = {\varvec{f}} \end{aligned}$$

(7)

where

$$\begin{aligned} {\varvec{K}}:=\sum _{e=1}^{\texttt {n}_{\texttt {el}}}{\varvec{L}}^{e \textsf {T}} {\varvec{K}}^e {\varvec{L}}^e \text { and } {\varvec{f}}:= \sum _{e=1}^{\texttt {n}_{\texttt {el}}}{\varvec{L}}^{e \textsf {T}} {\varvec{f}}^e \end{aligned}$$

(8)

2.2 Parameterization of the problem

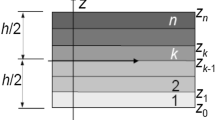
It is assumed in the following that fibres always lie in planes parallel to the $1-2$ plane in a $\{O,1,2,3\}$ material coordinate system (see Fig.  1), where direction 1 is always the fibres’ longitudinal direction. The existence of the fibres is modelled using a transversely isotropic material assumption. The reference coordinate system (or global axes) is denoted by $\{O,x,y,z\}$ and axis z coincides with axis 3, consequently, plane $\{O,x,y\}$ coincides with plane $\{O,1,2\}$, as shown in Fig.  1.

Fig. 1

Global coordinate system $\{O,x,y,z\}$ and material coordinate system $\{O,1,2,3\}$

The angle $\theta$ is the orientation of the family of fibres belonging to the material coordinate system with respect to the global coordinate system. Note that, the domain could be divided into many subdomains (layers or patches), hence, $\theta$ could take a specific value for each specific subdomain with respect to the global coordinate system.

The elasticity tensor ${\varvec{{\mathcal {C}}}}$ in (??) when expressed in the material axes $\{O,1,2,3\}$ in terms of the Young’s moduli, shear moduli, and Poisson’s ratios, is denoted as ${\varvec{{\mathcal {C}}}}_0$. Since our problem is defined with respect to the global axes $\{O,x,y,z\}$ and we aim at having different fiber orientations in different parts of the domain, ${\varvec{{\mathcal {C}}}}_0$ has to be also expressed in the global reference. Thus, the question is how to represent ${\varvec{{\mathcal {C}}}}(\theta )$ as a function of ${\varvec{{\mathcal {C}}}}_0$ and $\theta$.

The transformation of ${\varvec{{\mathcal {C}}}}_0$ to ${\varvec{{\mathcal {C}}}}(\theta )$ is a result of the transformation of stresses and strains from material to global axes. These transformations are well established in the literature [27, 28] and make use of a transformation matrix ${\varvec{T}}(\theta )$. The matrix ${\varvec{T}}$ is applied to stresses and strains as follows

$$\begin{aligned} \begin{aligned} {\varvec{\sigma }}_{123}&= {\varvec{T}}(\theta ){\varvec{\sigma }}_{xyz}\\ {\varvec{\varepsilon }}_{123}&= {\varvec{T}}^{-\textsf {T}}(\theta ){\varvec{\varepsilon }}_{xyz} \end{aligned} \end{aligned}$$

(9)

where the subscript “123" refers to the material axes and “xyz" refers to the global axes. Given that $\textit{c}:= \cos (\theta )$ and $\textit{s}:= \sin (\theta )$, we could then define the matrix ${\varvec{T}}$ as

$$\begin{aligned} {\varvec{T}}(\theta )= \begin{bmatrix} \textit{c}^2 &{} \textit{s}^2 &{} 0 &{} 0 &{} 0 &{} 2\textit{c}{} \textit{s}\\ \textit{s}^2 &{} \textit{c}^2 &{} 0 &{} 0 &{} 0 &{} -2\textit{c}{} \textit{s}\\ 0 &{} 0 &{} 1 &{} 0 &{} 0 &{} 0\\ 0 &{} 0 &{} 0 &{} \textit{c}&{} -\textit{s} &{} 0\\ 0 &{} 0 &{} 0 &{} \textit{s}&{} \textit{c} &{} 0\\ -\textit{c}{} \textit{s} &{} \textit{c}{} \textit{s} &{} 0 &{} 0 &{} 0 &{} \textit{c}^2-\textit{s}^2 \end{bmatrix} \end{aligned}$$

(10)

The inverse transpose of ${\varvec{T}}(\theta )$ is explicitly given by the following expression

$$\begin{aligned} {\varvec{T}}^{-\textsf {T}}(\theta )= \begin{bmatrix} \textit{c}^2 &{} \textit{s}^2 &{} 0 &{} 0 &{} 0 &{} \textit{c}{} \textit{s}\\ \textit{s}^2 &{} \textit{c}^2 &{} 0 &{} 0 &{} 0 &{} -\textit{c}{} \textit{s}\\ 0 &{} 0 &{} 1 &{} 0 &{} 0 &{} 0\\ 0 &{} 0 &{} 0 &{} \textit{c}&{} \textit{s} &{} 0\\ 0 &{} 0 &{} 0 &{} -\textit{s}&{} \textit{c} &{} 0\\ -2\textit{c}{} \textit{s} &{} 2\textit{c}{} \textit{s} &{} 0 &{} 0 &{} 0 &{} \textit{c}^2-\textit{s}^2 \end{bmatrix} \end{aligned}$$

(11)

Given the following relation,

$$\begin{aligned} \begin{aligned} {\varvec{\sigma }}_{123}=&{\varvec{{\mathcal {C}}}}_0{\varvec{\varepsilon }}_{123}\\ \end{aligned} \end{aligned}$$

(12)

The elasticity tensor ${\varvec{{\mathcal {C}}}}(\theta )$ could be derived by substituting the stress and strain tensors in (12) by the ones in (9) which results in the following,

$$\begin{aligned} \begin{aligned} {\varvec{T}}(\theta ){\varvec{\sigma }}_{xyz}=&{\varvec{{\mathcal {C}}}}_0{\varvec{T}}^{-\textsf {T}}(\theta ){\varvec{\varepsilon }}_{xyz}\\ \end{aligned} \end{aligned}$$

(13)

Multiplying both sides by ${\varvec{T}}^{-1}(\theta )$ yields,

$$\begin{aligned} \begin{aligned} {\varvec{\sigma }}_{xyz}=&{\varvec{T}}^{-1}(\theta ){\varvec{{\mathcal {C}}}}_0{\varvec{T}}^{-\textsf {T}}(\theta ){\varvec{\varepsilon }}_{xyz}\\ \end{aligned} \end{aligned}$$

(14)

Thus, the relation between the elasticity tensor in the global axes and in the one in the material axes reads,

$$\begin{aligned} {\varvec{{\mathcal {C}}}}(\theta )={\varvec{T}}^{-1}(\theta ) {\varvec{{\mathcal {C}}}}_0{\varvec{T}}^{-\textsf {T}}(\theta ) \end{aligned}$$

(15)

In the remainder of the paper, we divide the domain into several different subdomains (layers or patches) and, as parameters to be optimized, we assume the fibre orientation angle in each single subdomain (layer or patch). Thus, the number of layers (or patches) $\texttt {n}_{\texttt {p}}$ is the number of parameters characterizing the domain denoted by $\theta _i$, such that $i=1,\dots ,\texttt {n}_{\texttt {p}}$. Each parameter $\theta _i$ ranges in a real interval and describes the fiber orientation in a subdomain $\varOmega _i \subset \varOmega$ (note that the notation for the finite elements is $\varOmega ^e$, $e=1,\dots ,\texttt {n}_{\texttt {el}}$, and typically many elements $\varOmega ^e$ are inside a subdomain $\varOmega _i$).

The $\texttt {n}_{\texttt {p}}$ parameters are gathered in the vector ${\varvec{\theta }}=[\theta _1,\theta _2,...,\theta _{\texttt {n}_{\texttt {p}}}]^\textsf {T}$. Note that ${\varvec{\theta }}$ ranges in the multidimensional parametric domain .

Recalling (5), for every element e such that $\varOmega ^e \subset \varOmega _i$, the element stiffness matrix reads

$$\begin{aligned} {\varvec{K}}^e(\theta _i) = \int _{\varOmega ^e} {\varvec{{B}^{e\textsf {T}}}}{\varvec{{\mathcal {C}}}}(\theta _i){\varvec{B}}^e d\varOmega \end{aligned}$$

(16)

The parametric linear system of equations is derived using the parametric expression of the element stiffness matrix (16) in the assembly described in (8) resulting in

$$\begin{aligned} {\varvec{K}}({\varvec{\theta }}){\varvec{d}}({\varvec{\theta }})={\varvec{f}} \end{aligned}$$

(17)

It is worth noting that in this particular problem statement the force term ${\varvec{f}}$ does not depend on the parameters.

2.3 Failure criterion and optimization

The design analysis of a composite laminate is performed by comparing the stresses due to the applied loads with an allowable strength of the material [28, 29]. To achieve this comparison, many failure criteria were proposed for different types of materials. For example, the classical Von Mises stress invariant is very popular for isotropic materials, such as steel and aluminium alloys. Anisotropic materials require more sophisticated criteria, such as the maximum stress and strain criteria, the Tsai-Hill criterion, and the Tsai-Wu criterion, see [27,28,29,30] and references therein for a deeper discussion on the comparison of the different approaches. The Tsai-Wu criterion accounts for all the interactions between different stress states, in particular tensile and compressive states, and it has been proven to fit the experimental data best. Consequently, in the following, the Tsai-Wu criterion is chosen as the objective function for our optimization problem with the goal of finding the best fibre orientation in the laminate.

2.3.1 Tsai-Wu criterion

In our context, the Tsai-Wu criterion is intended to be a descriptive tool for us to have a general notion of the load-bearing capacity of structures for design purposes. The criterion has been widely applied as an optimization objective function for different applications [8, 16, 31,32,33,34,35]. The failure criterion was first proposed by Tsai and Wu [36] and it is based on the scalar failure index ${\mathcal {I}}_{\texttt {f}}$ defined as function of the stress ${\varvec{\sigma }}$ as follows:

$$\begin{aligned} {\mathcal {I}}_{\texttt {f}}\big ({\varvec{\sigma }} \big )= {\varvec{\sigma }}^\textsf {T}{\varvec{ {\mathcal {F}} \sigma }} + {\varvec{\sigma }}^\textsf {T}{\varvec{F}} \end{aligned}$$

(18)

In particular, the criterion states that the material at point ${\varvec{x}}$ is not at failure if and only if ${\mathcal {I}}_{\texttt {f}}({\varvec{\sigma }}) \le 1$. The dependency of the failure index on the position ${\varvec{x}}$ is through the stress state ${\varvec{\sigma }}({\varvec{x}})$. The strength tensors ${\varvec{{\mathcal {F}}}}$ and ${\varvec{F}}$ are fourth and second order tensors respectively (expressed as a matrix and a vector, when using the engineering Voigt’s notation). In the case of transversal isotropy, the forms of ${\varvec{{\mathcal {F}}}}$ and ${\varvec{F}}$ with respect to the material axes, denoted by ${\varvec{{\mathcal {F}}}}_0$ and ${\varvec{F}}_0$, are

$$\begin{aligned} {\varvec{{\mathcal {F}}}}_0= & {} \begin{bmatrix} F_{11} &{} F_{12} &{} F_{12} &{} 0 &{} 0 &{} 0\\ &{} F_{22} &{} F_{23} &{} 0 &{} 0 &{} 0\\ &{} &{} F_{22} &{} 0 &{} 0 &{} 0\\ &{} \text {Sym.} &{} &{} 2(F_{22}-F_{23}) &{} 0 &{} 0\\ &{} &{} &{} &{} \dfrac{1}{\tau _{\texttt {y}}^2} &{} 0\\ &{} &{} &{} &{} &{} \dfrac{1}{\tau _{\texttt {y}}^2} \end{bmatrix} \end{aligned}$$

(19)

$$\begin{aligned} {\varvec{F}}_0= & {} \begin{bmatrix} F_{1} \\ F_{2}\\ F_{2}\\ 0\\ 0\\ 0 \end{bmatrix} \end{aligned}$$

(20)

Remark 1

Tensors ${\varvec{{\mathcal {F}}}}_0$ and ${\varvec{F}}_0$ are material characteristics that have to be determined in the laboratory. This is achieved by applying uni-axial and bi-axial stresses in tension and compression and measuring the failure strengths [36]. In particular

$$\begin{aligned} F_{11}= & {} \frac{1}{\sigma _{\texttt {y}}^{Lt}\sigma _{\texttt {y}}^{Lc}}, \quad F_1=\frac{1}{\sigma _{\texttt {y}}^{Lt}}-\frac{1}{\sigma _{\texttt {y}}^{Lc}} \end{aligned}$$

(21)

$$\begin{aligned} F_{22}= & {} \frac{1}{\sigma _{\texttt {y}}^{Tt}\sigma _{\texttt {y}}^{Tc}}, \quad F_2=\frac{1}{\sigma _{\texttt {y}}^{Tt}}-\frac{1}{\sigma _{\texttt {y}}^{Tc}} \end{aligned}$$

(22)

$$\begin{aligned} F_{12}= & {} -\frac{1}{2}\sqrt{F_{11}F_{22}}, \quad F_{23} = -\frac{1}{2}\sqrt{F_{22}F_{33}} \end{aligned}$$

(23)

where, $\sigma _{\texttt {y}}^{Lt}$, $\sigma _{\texttt {y}}^{Lc}$, $\sigma _{\texttt {y}}^{Tt}$, $\sigma _{\texttt {y}}^{Tc}$ and $\tau _{\texttt {y}}$ are the longitudinal tensile, longitudinal compressive, transverse tensile, transverse compressive and shear yielding strength of the material respectively, and the subscript “y" stands for yield state of the strength.

The criterion in (18) is non-homogeneous, meaning that it has a quadratic term and a linear term, where the latter takes into account the internal stresses that differentiate between tensile and compressive stress states [36]. It was demonstrated in [8] that sometimes the Tsai-Wu criterion is load dependent. This means that for applied loads under a certain threshold the criterion in (18) is dominated by the linear term, and thus, leading to inaccurate counter-intuitive optimization results. To alleviate this problem, the failure criterion may be alternatively expressed in terms of a scalar load multiplier $\lambda$. The load multiplier (or safety factor) $\lambda$ produces a stress state $\overline{{\varvec{\sigma }}}=\lambda {\varvec{\sigma }}$, such that, the applied stress scales by a factor $\lambda$ to match the yielding state of the material at the onset of failure (see [8] for details). Consequently, the goal now is to find the best fibre orientation that maximizes the safety factor $\lambda$, and therefore, design the laminate based on the maximum load capacity of the structure just before failure. Thus, the corresponding failure index reads

$$\begin{aligned} {\mathcal {I}}_{\texttt {f}}\big (\overline{{\varvec{\sigma }}}\big )={\mathcal {I}}_{\texttt {f}}\big (\lambda {\varvec{\sigma }}\big ) = \lambda ^2 {\varvec{\sigma }}^\textsf {T}{\varvec{{\mathcal {F}}}} {\varvec{\sigma }} + \lambda {\varvec{\sigma }}^\textsf {T}{\varvec{F}} \end{aligned}$$

(24)

At each point ${\varvec{x}}$, the critical value of $\lambda$ corresponds to the onset of failure ${\mathcal {I}}_{\texttt {f}}\big (\overline{{\varvec{\sigma }}}\big )=1$. This results in a polynomial equation of the second degree for $\lambda$ where its explicit solution is available. Assuming that ${\varvec{{\mathcal {F}}}}$ is symmetric positive definite, ${\varvec{\sigma }}^\textsf {T}{\varvec{{\mathcal {F}}}} {\varvec{\sigma }} \ge 0$, there is a unique positive root of the equation ${\mathcal {I}}_{\texttt {f}}\big (\overline{{\varvec{\sigma }}}\big )=1$. The smallest positive root is the safety factor, denoted by $\lambda _s$ and reads

$$\begin{aligned} \lambda _s = \frac{1}{2 {\varvec{\sigma }}^\textsf {T}{\varvec{{\mathcal {F}}}} {\varvec{\sigma }}} \left( \sqrt{({\varvec{\sigma }}^\textsf {T}{\varvec{F}})^2 + 4 \, {\varvec{\sigma }}^\textsf {T}{\varvec{{\mathcal {F}}}} {\varvec{\sigma }}} - {\varvec{\sigma }}^\textsf {T}{\varvec{F}} \right) \end{aligned}$$

(25)

Note that the safety factor depends on the choice of the parameters ${\varvec{\theta }}$ and the point ${\varvec{x}}$ where the stress is evaluated; and thus the notation $\lambda _s({\varvec{x}},{\varvec{\theta }})$ is adopted in the following. To emphasize the dependence of the failure criterion in (18) on the fibre orientation (our parameters), we explicitly express the strength tensors in (19) and (20) with respect to the global axes. Thus, in an arbitrary point ${\varvec{x}}\in \varOmega _i$ where the fiber orientation angle is $\theta _i$, or in any element $\varOmega ^e\subset \varOmega _i$, the expressions of ${\varvec{{\mathcal {F}}}}$ and ${\varvec{F}}$ with respect to the global axes are obtained using the transformation matrices introduced in (10) and (11), namely

$$\begin{aligned} \begin{aligned} {\varvec{{\mathcal {F}}}}(\theta _i)&= {\varvec{T}}^{\textsf {T}}(\theta _i) {\varvec{{\mathcal {F}}}}_0{\varvec{T}}(\theta _i)\\ {\varvec{F}}(\theta _i)&={\varvec{T}}^{\textsf {T}}(\theta _i) {\varvec{F}}_0 \end{aligned} \end{aligned}$$

(26)

It is worth noting that the dependence of ${\mathcal {I}}_{\texttt {f}}({\varvec{\sigma }})$ on ${\varvec{\theta }}$ does not only come from ${\varvec{\sigma }}({\varvec{x}},{\varvec{\theta }})$ but also from ${\varvec{{\mathcal {F}}}}(\theta _i)$ and ${\varvec{F}}(\theta _i)$ where they depend only on the local $\theta _i$ because they are material properties. Marking explicitly the parametric dependence, for ${\varvec{x}}\in \varOmega _i$, Eq. (18) is rewritten as

$$\begin{aligned} \begin{aligned}&{\mathcal {I}}_{\texttt {f}}\big ({\varvec{\sigma }}({\varvec{x}},{\varvec{\theta }})\big )\\&\quad ={\varvec{\sigma }}({\varvec{x}},{\varvec{\theta }})^\textsf {T}{\varvec{{\mathcal {F}}}}(\theta _i) {\varvec{\sigma }}({\varvec{x}},{\varvec{\theta }}) + {\varvec{\sigma }}({\varvec{x}},{\varvec{\theta }})^\textsf {T}{\varvec{F}}(\theta _i) . \end{aligned} \end{aligned}$$

(27)

2.3.2 Optimization problem

Following [8], two alternative optimization problems are considered to find the optimal values of the parameters ${\varvec{\theta }}$. The first choice is to find ${\varvec{\theta }}$ that minimizes the maximum value of ${\mathcal {I}}_{\texttt {f}}\big ({\varvec{\sigma }}({\varvec{x,\theta }})\big )$ evaluated at all points ${\varvec{x}}$ in $\varOmega$. Thus, the optimization problem reads

$$\begin{aligned} {\varvec{\theta }}_{\texttt {f}}^{\texttt {Opt}} = \textsf {arg}\,\underset{{\varvec{\theta }}}{\text {min}} \;\; \underset{{\varvec{x}}}{\text {max}} \; {\mathcal {I}}_{\texttt {f}}\big ({\varvec{\sigma }}({\varvec{x,\theta }})\big ) \end{aligned}$$

(28)

where superscript “Opt" is used to indicate the optimal choice and subscript “f" is a label to indicate that the objective function is based on the failure index.

Alternatively, the second choice is to find ${\varvec{\theta }}$ that maximizes the minimum value of $\lambda _s({\varvec{x}},{\varvec{\theta }})$ evaluated at all points ${\varvec{x}}$ in $\varOmega$. The corresponding optimal choice (labeled by subscript “s" for safety) is

$$\begin{aligned} {\varvec{\theta }}_\texttt {s}^\texttt {Opt} = \textsf {arg}\,\underset{{\varvec{\theta }}}{\text {max}} \;\; \underset{{\varvec{x}}}{\text {min}} \; \lambda _s({\varvec{x}},{\varvec{\theta }}) \end{aligned}$$

(29)

These objective functions as defined in the parametric space ${\varvec{I}}_{{\varvec{\theta }}}$ are not necessarily smooth or regular, and they are not expected to have nice convexity properties. Thus, the optimization algorithm has to be carefully selected to avoid stalling at local extrema which often happens to gradient-based methods if the initial guess is not accurate enough. On the other hand, having an accurate solution is also desirable and is achieved by using global methods (such as the Genetic Algorithm), however, they are often exhibiting a slow convergence rate. Thus, a smart combination of different methodologies is probably the best strategy.

3 Proper generalized decomposition

This section briefly describes the Proper Generalized Decomposition (PGD) as a tool to obtain a parametric solution of the problem described in Sect. 2 that depends explicitly on the fibre orientation. This explicit parametric solution allows expressing in a compact form the solutions corresponding to all possible values of parameters ${\varvec{\theta }}$. In a nutshell, the main concepts behind the PGD approach are summarized in three steps as follows [25, 37]:

• First, the parameters are taken as extra coordinates, stating the problem in a multidimensional framework; this means finding an approximation to ${\varvec{d}}({\varvec{\theta }})$ in solution of (17). Consequently, the multidimensional character of the problem drastically increases its computational complexity.

  Standard discretization techniques have severe computational difficulties dealing with the number of degrees of freedom produced by the discretization of the multidimensional domain (the number of degrees of freedom is the product of the number of degrees of freedom in each parametric dimension). This happens even for a small number of parameters (1 or 2).

• Second, in order to reduce the computational complexity, the solution is sought in a separable format. This means that the solution is written as a sum of products of sectional functions each depending only on one of the parameters; each term is referred to as a rank-one term. Thus, the actual number of degrees of freedom reduces to the sum of the number of degrees of freedom in each parametric dimension, multiplied by the number of terms. Although, the number of terms is usually small and it does not grow exponentially with the number of dimensions.

• Third, the algorithm to solve this problem is based on a greedy strategy (computing one rank-one term at a time) and an alternating directions methods to solve the nonlinear rank-one problems.

The PGD-solution is typically computed in an offline phase that may take important computational resources. The interesting aspect of the PGD is that once the explicit parametric solution is available, exploring the parametric space (e.g. for an optimization problem) is a simple postprocess, which is extremely fast, and it can be conducted online in real time. In the following we show the encapsulated concept, presented in [38, 39], where a set of algebraic tools operate with multidimensional tensors in a separable format. Subsequently, we present the process of separation of input for the encapsulated PGD and, finally, we introduce the post-process steps to compute the failure index and the optimization problem.

3.1 Encapsulated PGD

The PGD approach is presented here following the encapsulated concept presented in [38, 39], where it provides tools that directly produce the generalized solution for the high-dimensional tensor data. The encapsulated PGD concept allows to define PGD objects, which are quantities defined in a multidimensional setting representing multiparametric functions, and it provides a toolbox¹ of algebraic routines to directly operate with these objects. Thus, the general methodology permits the performance of non-trivial operations (e.g. solving linear systems of equations, compression, etc...) for multidimensional tensors, see [39]. For example, the input parametric matrix ${\varvec{K}}({\varvec{\theta }})$ in (17) has to be provided in (or approximated by) a separated form, that is

$$\begin{aligned} {\varvec{K}}({\varvec{\theta }})\approx {\varvec{K}}^\texttt {sep}({\varvec{\theta }})= \sum _{k=1}^{\texttt {n}_{\texttt {k}}}{\varvec{K}}^k\prod _{j=1}^{\texttt {n}_{\texttt {p}}}\varphi _j^k(\theta _j) \end{aligned}$$

(30)

where superscript “sep" indicates that the quantity (in this case the matrix) is stored in a separated form. For each term $k=1,\dots ,\texttt {n}_{\texttt {k}}$, matrices ${\varvec{K}}^k$ and functions $\varphi _j^k$, for $j=1,\dots ,\texttt {n}_{\texttt {p}}$ are the spatial and the parametric modes, respectively, describing the parametric dependence of the global stiffness matrix using an affine decomposition with $\texttt {n}_{\texttt {k}}$ terms.

One of the routines in the toolbox is the linear solver, having as input ${\varvec{K}}^\texttt {sep}({\varvec{\theta }})$ and ${\varvec{f}}$ (possibly ${\varvec{f}}^\texttt {sep}({\varvec{\theta }})$) and yielding as output a separable approximation to the unknown vector of generalized displacements ${\varvec{d}}({\varvec{\theta }})$, namely

$$\begin{aligned} \begin{aligned} {\varvec{d}}({\varvec{\theta }})&\approx {\varvec{d}}_\texttt {PGD}^n({\varvec{\theta }})=\sum _{m=1}^{n}\beta ^m {\varvec{d}}^m\prod _{j=1}^{\texttt {n}_{\texttt {p}}}G_j^m(\theta _j)\\&= {\varvec{d}}_\texttt {PGD}^{n-1}({\varvec{\theta }})+\beta ^n{\varvec{d}}^n G_1^n(\theta _1)G_2^n(\theta _2)...G_{\texttt {n}_{\texttt {p}}}^n(\theta _{\texttt {n}_{\texttt {p}}}) \end{aligned} \end{aligned}$$

(31)

where, ${\varvec{d}}_\texttt {PGD}^n$ is a separated approximation with n terms; ${\varvec{d}}^m$ is the spatial mode, and $G_j^m$ are the parametric modes where $m=1,\dots ,n$ and $j=1,\dots ,\texttt {n}_{\texttt {p}}$. Modes ${\varvec{d}}^m$ and $G_j^m$ are normalized and $\beta ^m$ collects the amplitude of each term. Amplitude $\beta ^m$ accounts for the importance of term m and is also used to decide when to stop the greedy algorithm (one stops computing new terms once $\beta ^m$ is small enough, with respect to $\beta ^1$). Despite this stopping criterion is only strictly valid for elliptic problems [40], it is used in practice for any equation with good results.

Often, the PGD solution has redundant information as orthogonality between successive terms is not enforced; whereas it is enforced, for instance, in the Singular Value Decomposition (SVD can be seen as a particular case of PGD). The PGD compression is a methodology that post-processes any PGD object, aiming to alleviate the excess of PGD terms associated with this redundancy (reduce a too large value of n in (31)). It consists in least-squares approximation following the same PGD philosophy, see [38, 41, 42]. In a nutshell, for any solution provided by the PGD solver like ${\varvec{d}}^n_\texttt {PGD}$ (as solution of (31)) the goal is to find a PGD-type approximation ${\varvec{d}}^{\texttt {n}_{\texttt {c}}}_{\texttt {com}}$ such that the following discrepancy is minimized

$$\begin{aligned} \begin{aligned}&\Vert {\varvec{d}}^{\texttt {n}_{\texttt {c}}}_{\texttt {com}}-{\varvec{d}}^n_\texttt {PGD}\Vert _{L^2(I_{\varvec{\theta }})}\\&\quad =\int _{I_1}\dots \int _{I_{\texttt {n}_{\texttt {p}}}} ({\varvec{d}}^{\texttt {n}_{\texttt {c}}}_{\texttt {com}}-{\varvec{d}}^n_\texttt {PGD})^2\;d\theta _{\texttt {n}_{\texttt {p}}}\dots d\theta _1 . \end{aligned} \end{aligned}$$

(32)

Note that the number of terms, $\texttt {n}_{\texttt {c}}$, in the compressed solution ${\varvec{d}}^{\texttt {n}_{\texttt {c}}}_{\texttt {com}}$ is expected to be significantly lower than the original one ($\texttt {n}_{\texttt {c}}\ll n$).

3.2 Separated input for encapsulated PGD

As indicated above, the input of the encapsulated PGD routines is made of separated PGD objects, as the stiffness matrix described in (30). In the present case, the parametric dependence of the input matrix ${\varvec{K}}({\varvec{\theta }})$ on the parameters $\theta _i$, $i=1,\dots ,\texttt {n}_{\texttt {p}}$ arises from the parametric dependence of the elasticity tensor ${\varvec{\mathcal {C(\theta )}}}$; which depends on the value of the fiber orientation at the material point where it is evaluated. A separated representation of ${\varvec{\mathcal {C(\theta )}}}$ is required in order to build up a separated representation of matrix ${\varvec{K}}({\varvec{\theta }})$ as in (30).

Recalling Sect. 2.2, it is assumed that the subdomains $\varOmega _i$, $i=1,\dots ,\texttt {n}_{\texttt {p}}$, where the angle of the fiber orientation is $\theta _i$, do cover the whole domain $\varOmega$; that is ${\bar{\varOmega }}=\bigcup \limits _{i=1}^{\texttt {n}_{\texttt {p}}} {\bar{\varOmega }}_{i}$. Thus, the elasticity tensor depends at each point ${\varvec{x}}\in \varOmega _i$ on the parameter $\theta _i$, and it is expressed in a separable format as

$$\begin{aligned} {\varvec{{\mathcal {C}}}}(\theta _i) = \sum _{\ell =1}^{\texttt {n}_{\texttt {t}}}{\varvec{{\mathcal {C}}}}^\ell \prod ^{\texttt {n}_{\texttt {p}}}_{j=1}\phi _j^{\ell ,i}(\theta _j) \end{aligned}$$

(33)

where the fact that ${\varvec{{\mathcal {C}}}}(\theta _i)$ depends only on $\theta _i$ results in the condition $\phi _j^{\ell ,i}(\theta _j) \equiv 1$ for $j \ne i$, see Appendix A for details.

Moreover, any point ${\varvec{x}}$ belonging to some element $\varOmega ^e \subset \varOmega _i$, such that the element index, e, $e=1,\dots ,\texttt {n}_{\texttt {el}}$, is in relation with subdomain index i.

This formal convention identifying element e with material subdomain i allows replacing (33) in the expression for ${\varvec{K}}^e(\theta _i)$ provided by (16), and this results in

$$\begin{aligned} {\varvec{K}}^e(\theta _i) =\sum _{\ell =1}^{\texttt {n}_{\texttt {t}}}\Big [ \int _{\varOmega _e}{\varvec{B}}^{e\textsf {T}}{\varvec{{\mathcal {C}}}}^\ell {\varvec{B}}^e d\varOmega \Big ] \prod ^{\texttt {n}_{\texttt {p}}}_{j=1}\phi _j^{\ell ,i}(\theta _j) \end{aligned}$$

(34)

Then, assembling the local matrices as indicated in (4), one gets

$$\begin{aligned} \begin{aligned}&{\varvec{K}}(\theta _1,\theta _2,...,\theta _{\texttt {n}_{\texttt {p}}})\\&\quad = \sum ^{\texttt {n}_{\texttt {el}}}_{e=1} {\varvec{L}}^{e\textsf {T}}{\varvec{K}}^e(\theta _i) {\varvec{L}}^e\\&\quad =\sum ^{\texttt {n}_{\texttt {el}}}_{e=1} \sum _{\ell =1}^{\texttt {n}_{\texttt {t}}}\Big [\int _{\varOmega _e}{\varvec{L}}^{e\textsf {T}}{\varvec{B}}^{e\textsf {T}}{\varvec{{\mathcal {C}}}}^\ell {\varvec{B}}^e{\varvec{L}}^{e}\;d\varOmega \Big ] \prod ^{\texttt {n}_{\texttt {p}}}_{j=1}\phi _j^{\ell ,i}(\theta _j) \end{aligned} \end{aligned}$$

(35)

which provides a separable expression for ${\varvec{K}}({\varvec{\theta }})$ that is used as input for the encapsulated PGD routines. In particular, the linear solver for algebraic equations provides as output ${\varvec{d}}^n_\texttt {PGD}({\varvec{\theta }})$.

3.3 Post-process and sensitivities

Once the parametric solution ${\varvec{d}}^n_\texttt {PGD}({\varvec{\theta }})$ is obtained in the form of a generalized solution (31), it has to be used to compute the parametric expressions of the failure index ${\mathcal {I}}_{\texttt {f}}$, see (18), and the safety factor, $\lambda _s$, see (25). In order to solve the optimization problems (28) and (29) with gradient-based methods, the sensitivities (gradients and Hessian matrices with respect to the parameters) need to be computed.

In a first step, the strain tensor has to be computed as a postprocess of the parametric displacements ${\varvec{d}}^n_\texttt {PGD}({\varvec{\theta }})$. In practice, the strain field is computed in a set of $\texttt {n}_{\texttt {g}}$ points in domain $\varOmega$, typically the integration points of the finite element mesh which are indexed with $g=1,\dots ,\texttt {n}_{\texttt {g}}$. At each of these points, the strain tensor is a vector of 6 components (using Voigt’s notation), which is a linear function of the displacement field. Thus, globally the strain field is described by a $6 \times \texttt {n}_{\texttt {g}}$ matrix depending on the parameters, ${\varvec{\varepsilon }}({\varvec{\theta }})$. Each column of this matrix is a $6 \times 1$ vector denoted ${\varvec{\varepsilon }}_g({\varvec{\theta }})$ and represents the strain tensor at point g.

Assuming that point g is in element $\varOmega ^e$, the strain at point g is a linear output of the overall displacements ${\varvec{d}}$, namely

$$\begin{aligned} {\varvec{\varepsilon }}_g = {\varvec{B}}^e_g {\varvec{L}}^e {\varvec{d}} \end{aligned}$$

where ${\varvec{B}}^e_g$ is matrix ${\varvec{B}}^e$ (same as in Eq. (5)) evaluated at point g and ${\varvec{L}}^e$ is the Boolean operator localizing global displacements to element d.o.f. Consequently, using the parametric expression of the displacements in (31) results in the following expression for the parametric strains at point g:

$$\begin{aligned} {\varvec{\varepsilon }}_g({\varvec{\theta }}) = \sum _{m=1}^{n}\beta ^m{\varvec{\varepsilon }}^m_g\prod _{j=1}^{\texttt {n}_{\texttt {p}}}G_j^m(\theta _j) \end{aligned}$$

(36)

where ${\varvec{\varepsilon }}^m_g={\varvec{B}}^e_g {\varvec{L}}^e {\varvec{d}}^m$.

The format of the strain field ${\varvec{\varepsilon }}({\varvec{\theta }})$, that is a $6\times \texttt {n}_{\texttt {g}}$ matrix, with columns ${\varvec{\varepsilon }}_g({\varvec{\theta }})$ representing strains at point g, is replicated to describe the stresses. Thus, stresses are stored in a $6\times \texttt {n}_{\texttt {g}}$, ${\varvec{\sigma }}({\varvec{\theta }})$, such that each column of this matrix is a $6 \times 1$ vector ${\varvec{\sigma }}_g({\varvec{\theta }})$ representing the stress tensor at point g.

The relation between strains and stresses at point g is given by the corresponding elasticity tensor ${\varvec{{\mathcal {C}}}}$. Thus, the stresses at point g, ${\varvec{\sigma }}_g({\varvec{\theta }})= {\varvec{{\mathcal {C}}}}(\theta _i) {\varvec{\varepsilon }}_g({\varvec{\theta }})$ become, using (33) and (36),

$$\begin{aligned} {\varvec{\sigma }}_g({\varvec{\theta }})=\sum _{m=1}^{n}\sum _{\ell =1}^{\texttt {n}_{\texttt {t}}} \beta ^m {\varvec{{\mathcal {C}}}}^\ell {\varvec{\varepsilon }}^m_g \prod _{j=1}^{\texttt {n}_{\texttt {p}}}\phi _j^{\ell ,i}(\theta _j) G_j^m(\theta _j) \end{aligned}$$

(37)

where it is worth noting that, similarly as in the previous equations, index i is associated with index g, in the sense that it is assumed that point g is in subdomain $\varOmega _i$. Sorting the terms with a single index $q=1,\dots ,n \cdot \texttt {n}_{\texttt {t}}$ instead of the two indices m and $\ell$, (37) is rewritten as

$$\begin{aligned} {\varvec{\sigma }}_g({\varvec{\theta }})=\sum _{q=1}^{n \cdot \texttt {n}_{\texttt {t}}}{\bar{\beta }}^q{\varvec{\sigma }}^q_g\prod _{j=1}^{\texttt {n}_{\texttt {p}}}Q_j^q(\theta _j) \end{aligned}$$

(38)

where it is assumed that there is an explicit association between a pair $(m,\ell )$ and index q (for instance $q=m+(\ell -1)\cdot n$); ${\varvec{\sigma }}^q_g$ is equal to ${\varvec{{\mathcal {C}}}}^\ell {\varvec{\varepsilon }}^m_g$ divided by its norm, $Q_j^q(\theta _j)$ is the product $\phi _j^{\ell ,i}(\theta _j) G_j^m(\theta _j)$ also normalized; and ${\bar{\beta }}^q$ collects the product of $\beta ^m$ and the normalization factors.

In the remainder, a similar strategy is employed to compute the parametric dependence of ${\mathcal {I}}_{\texttt {f}}\big ({\varvec{\sigma }}_g({\varvec{\theta }})\big )$, see (18) in Sect. 2.3.1. A parametric separated expression of the transformation matrix ${\varvec{T}}(\theta _i)$ is needed as a first step to compute the parametric expression for the strength tensor and vector, ${\varvec{{\mathcal {F}}}}$ and ${\varvec{F}}$, see (26), namely

$$\begin{aligned} {\varvec{T}}(\theta _i)=\sum _{r=1}^{\texttt {n}_{\texttt {r}}}{\varvec{T}}^r \prod ^{\texttt {n}_{\texttt {p}}}_{j=1}Z_j^{r,i}(\theta _j) \end{aligned}$$

(39)

where $\texttt {n}_{\texttt {r}}$ is the number of terms required to express the transformation matrix in a separated fashion, and similar to the definition of $\phi ^{\ell ,i}_j$ in (33), $Z_j^{r,i}(\theta _j)\equiv 1$ for $i\ne j$. The explicit expressions of all the terms are given in Appendix A. Using (39) in (26), results in

$$\begin{aligned} {\varvec{{\mathcal {F}}}}(\theta _i) = \sum _{s=1}^{\texttt {n}_{\texttt {r}}}\sum _{r=1}^{\texttt {n}_{\texttt {r}}}({\varvec{T}}^r{}^\textsf {T}{\varvec{{\mathcal {F}}}}_0{\varvec{T}}^s) \prod ^{\texttt {n}_{\texttt {p}}}_{j=1}Z_j^{r,i}(\theta _j)Z_j^{s,i}(\theta _j) \end{aligned}$$

(40)

Analogously as with ${\varvec{\sigma }}_g$, (40) is rewritten using a single index notation (index pair (r, s) is mapped into a single index p, $p=1,\dots ,\texttt {n}_{\texttt {r}}^2$), that is

$$\begin{aligned} {\varvec{{\mathcal {F}}}}(\theta _i) =\sum _{p=1}^{\texttt {n}_{\texttt {r}}^2}{\bar{\alpha }}^p{\varvec{{\mathcal {F}}}}^p\prod ^{\texttt {n}_{\texttt {p}}}_{j=1} P_j^{p,i}(\theta _j) \end{aligned}$$

(41)

The same is carried out for ${\varvec{F}}$ and results in

$$\begin{aligned} {\varvec{F}}(\theta _i) = {\varvec{T}}^\textsf {T}(\theta _i){\varvec{F}}_0 =\sum _{r=1}^{\texttt {n}_{\texttt {r}}}{\tilde{\alpha }}^r({\varvec{T}}^r{}^\textsf {T}{\varvec{F}}_0)\prod ^{\texttt {n}_{\texttt {p}}}_{j=1}Z_j^{r,i}(\theta _j) \end{aligned}$$

(42)

The failure index given in (18) is divided in two terms, one linear and one quadratic, namely

$$\begin{aligned} \begin{aligned} {\mathcal {I}}_{\texttt {L}}\big ({\varvec{\sigma }}_g({\varvec{\theta }})\big ) =&{\varvec{\sigma }}_g^\textsf {T}{\varvec{F}}(\theta _i)\\ {\mathcal {I}}_{\texttt {Q}}\big ({\varvec{\sigma }}_g({\varvec{\theta }})\big ) =&{\varvec{\sigma }}_g^\textsf {T}{\varvec{{\mathcal {F}}}}(\theta _i){\varvec{\sigma }}_g \end{aligned} \end{aligned}$$

(43)

The expression for ${\varvec{\sigma }}_g$ and ${\varvec{{\mathcal {F}}}}$ in (38) and (41) are used in (43) to obtain the following expression for ${\mathcal {I}}_{\texttt {Q}}$

$$\begin{aligned} \begin{aligned} {\mathcal {I}}_{\texttt {Q}}\big ({\varvec{\sigma }}_g({\varvec{\theta }})\big ) =&\sum _{p=1}^{\texttt {n}_{\texttt {r}}^2}\sum _{w=1}^{n \cdot \texttt {n}_{\texttt {t}}}\sum _{q=1}^{n \cdot \texttt {n}_{\texttt {t}}} {\bar{\alpha }}^p{\bar{\beta }}^w{\bar{\beta }}^q ({\varvec{\sigma }}_g^{q \,\textsf {T}}{\varvec{{\mathcal {F}}}}^p{\varvec{\sigma }}_g^w)\\&\cdots \prod _{j=1}^{\texttt {n}_{\texttt {p}}}P_j^{p,i}(\theta _j)Q_j^{w,i}(\theta _j)Q_j^{q,i}(\theta _j) \end{aligned} \end{aligned}$$

(44)

Again, transforming the three indices (p, w, q) into one index b, $b=1,\dots ,\texttt {n}_{\texttt {r}}^2 n^2 \texttt {n}_{\texttt {t}}^2$, the following expression is obtained

$$\begin{aligned} {\mathcal {I}}_{\texttt {Q}}\big ({\varvec{\sigma }}_g({\varvec{\theta }})\big ) = \sum _{b=1}^{ \texttt {n}_{\texttt {r}}^2 n^2 \texttt {n}_{\texttt {t}}^2}{\tilde{\gamma }}^b \tilde{A}_g^b \prod _{j=1}^{\texttt {n}_{\texttt {p}}}\tilde{H}_j^{b,i}(\theta _j) \end{aligned}$$

(45)

where $\tilde{A}_g^b$ and $\tilde{H}_j^{b,i}(\theta _j)$ are the normalized versions of ${\varvec{\sigma }}_g^{q \,\textsf {T}}{\varvec{{\mathcal {F}}}}^p{\varvec{\sigma }}_g^w$ and $P_j^{p,i}(\theta _j)Q_j^{w,i}(\theta _j)Q_j^{q,i}(\theta _j)$ respectively, and ${\tilde{\gamma }}^b$ collects the amplitude ${\bar{\alpha }}^p{\bar{\beta }}^w{\bar{\beta }}^q$ and all the normalization factors.

Analogously, for the linear part of the failure index, ${\mathcal {I}}_{\texttt {L}}$, we have

$$\begin{aligned} \begin{aligned}&{\mathcal {I}}_{\texttt {L}}\big ({\varvec{\sigma }}_g({\varvec{\theta }})\big ) \\&\quad =\sum _{q=1}^{n \cdot \texttt {n}_{\texttt {t}}}\sum _{r=1}^{\texttt {n}_{\texttt {r}}} {\bar{\beta }}^q {\tilde{\alpha }}^r ({\varvec{\sigma }}_g^q{}^\textsf {T}{\varvec{F}}^{r}) \prod _{j=1}^{\texttt {n}_{\texttt {p}}}Q_j^{q,i}(\theta _j) Z_j^{r,i}(\theta _j) \end{aligned} \end{aligned}$$

(46)

that in a single index format (associating (q, r) to v, $v=1,\ldots ,n\cdot \texttt {n}_{\texttt {t}}\cdot \texttt {n}_{\texttt {r}}$) results in

$$\begin{aligned} {\mathcal {I}}_{\texttt {L}}\big ({\varvec{\sigma }}_g({\varvec{\theta }})\big ) = \sum _{v=1}^{n\cdot \texttt {n}_{\texttt {t}}\cdot \texttt {n}_{\texttt {r}}} {\hat{\gamma }}^v {\hat{A}}^v_g \prod _{j=1}^{\texttt {n}_{\texttt {p}}}{\hat{H}}_j^{v,i}(\theta _j) \end{aligned}$$

(47)

where we define $\texttt {n}_{\texttt {L}}:=\texttt {n}_{\texttt {r}}\cdot n \cdot \texttt {n}_{\texttt {t}}$ to ease the notation. The expression for the failure index ${\mathcal {I}}_{\texttt {f}}$ is readily recovered by summing up (45) and (47), that is

$$\begin{aligned} \begin{aligned} {\mathcal {I}}_{\texttt {f}}\big ({\varvec{\sigma }}_g({\varvec{\theta }})\big )&= {\mathcal {I}}_{\texttt {Q}}\big ({\varvec{\sigma }}_g({\varvec{\theta }})\big ) + {\mathcal {I}}_{\texttt {L}}\big ({\varvec{\sigma }}_g({\varvec{\theta }})\big )\\&= \sum _{f=1}^{\texttt {n}_{\texttt {Q}}+\texttt {n}_{\texttt {L}}} \gamma ^f A^f_g \prod _{j=1}^{\texttt {n}_{\texttt {p}}}H_j^{f,i}(\theta _j) \end{aligned} \end{aligned}$$

(48)

where the quantities $\gamma ^f$, $A^f_g$ and $H_j^{f,i}(\theta _j)$ are equal to the ones in (45) or (47) depending on the index f,

$$\begin{aligned} \gamma ^f,\,A^f_g,\,H^f_g = {\left\{ \begin{array}{ll} {\tilde{\gamma }}^f,\tilde{A}^f_g,\tilde{H}^f_g &{} \text {if} f\le \texttt {n}_{\texttt {Q}}\\ {\hat{\gamma }}^{f-\texttt {n}_{\texttt {Q}}},{\hat{A}}^{f-\texttt {n}_{\texttt {Q}}}_g,{\hat{H}}^{f-\texttt {n}_{\texttt {Q}}}_g &{} \text {if } f>\texttt {n}_{\texttt {Q}}\end{array}\right. } \end{aligned}$$

and, for the sake of shortening the writing, the number of PGD terms needed to express ${\mathcal {I}}_{\texttt {Q}}$ is introduced as $\texttt {n}_{\texttt {Q}}:=\texttt {n}_{\texttt {r}}^2 n^2 \texttt {n}_{\texttt {t}}^2$.

Once ${\mathcal {I}}_{\texttt {f}}\big ({\varvec{\sigma }}_g({\varvec{\theta }})\big )$ is obtained in the form of (48), the multiple queries required to solve the optimization problem defined in (28) (or in (29)) may be performed very fast, as a simple post-processing.

Moreover, an additional advantage of the PGD solutions is that it is possible computing the derivatives of the explicit parametric dependence of the objective function provided by (48). That is, the sensitivities needed in the implementation of the gradient-based optimization methods.

At any sampling point g, the gradient of the failure index is denoted as $\nabla _\theta {\mathcal {I}}_{\texttt {f}}({\varvec{\theta }})$ and contains all partial derivatives of ${\mathcal {I}}_{\texttt {f}}$ with respect to $\theta _k$, for $k=1,\dots ,\texttt {n}_{\texttt {p}}$. Using the expression (48), these derivatives read

$$\begin{aligned} \frac{\partial {\mathcal {I}}_{\texttt {f}}({\varvec{\theta }})}{\partial \theta _k}= & {} \sum _{f=1}^{\texttt {n}_{\texttt {Q}}+\texttt {n}_{\texttt {L}}}\gamma ^f A^f_g \left[ \frac{d H_k^{f,i}}{d \theta _k}(\theta _k)\right] \prod _{j \ne k}^{\texttt {n}_{\texttt {p}}} H_j^{f,i}(\theta _j) \end{aligned}$$

(49)

$$\begin{aligned} \frac{\partial ^2 {\mathcal {I}}_{\texttt {f}}({\varvec{\theta }})}{\partial \theta _k \partial \theta _{\tilde{k}}}= & {} \sum _{f=1}^{\texttt {n}_{\texttt {Q}}+\texttt {n}_{\texttt {L}}} \gamma ^f A^f_g \left[ \frac{d H_k^{f,i}}{d \theta _k}(\theta _k) \, \frac{d H_{\tilde{k}}^{f,i}}{d \theta _{\tilde{k}}}(\theta _{\tilde{k}})\right] \nonumber \\&\cdots \prod _{j \ne k , {\tilde{k}}}^{\texttt {n}_{\texttt {p}}} H_j^{f,i}(\theta _j) \end{aligned}$$

(50)

$$\begin{aligned} \frac{\partial ^2 {\mathcal {I}}_{\texttt {f}}({\varvec{\theta }})}{{\partial \theta _k}^2}= & {} \sum _{f=1}^{\texttt {n}_{\texttt {Q}}+\texttt {n}_{\texttt {L}}} \gamma ^f A^f_g \left[ \frac{d^2 H_k^{f,i}}{{d \theta _k}^2}(\theta _k) \right] \prod _{j \ne k}^{\texttt {n}_{\texttt {p}}} H_j^{f,i}(\theta _j) \end{aligned}$$

(51)

Moreover, for the strategies requiring the Hessian matrix, all its components consist in second order derivatives, which are readily computed in a similar fashion.

The derivatives of the parametric modes $H_k^{f,i}$ in Eq. (49) are performed numerically. Typically, the modes are stored in terms of vectors of nodal variables, following the Finite Elements philosophy. Thus, assuming that the nodal values of function $H_k^{f,i}(\theta _k)$ are collected in vector ${\varvec{h}}$, the question is how to compute the derivatives. In other words, assuming that $\dfrac{d H_k^{f,i}}{d \theta _k}$ is stored in the same fashion in the vector of nodal values ${\varvec{g}}$, how to compute ${\varvec{g}}$ from ${\varvec{h}}$? Note that the parametric range for $\theta _k$, $I_k$, is typically 1D (a subset of ) and therefore explicit numerical differentiation node-wise is straightforward. A more consistent approach is based on the least-squares projection on the initial discrete functional space of the sectional approximation. Recall that the adjective sectional is used in this context to refer to operations in a single parametric dimension. In summary, the derivation of the function described by ${\varvec{h}}$ consists in computing ${\varvec{g}}$ such that

$$\begin{aligned} {\varvec{M}} {\varvec{g}} = {\varvec{D}}{\varvec{h}} \end{aligned}$$

(52)

where ${\varvec{M}}$ is the sectional mass matrix and ${\varvec{D}}$ is the sectional gradient matrix. Both ${\varvec{M}}$ and ${\varvec{D}}$ are very simple matrices (in the usual case of being $I_k$ a 1D sectional domain discretized with linear finite elements, they are tridiagonal matrices). In a more general case, they result of assembling element matrices having the form

$$\begin{aligned} \begin{aligned} {\varvec{M}}^{e}=\int _{I_k}{\varvec{\tilde{N}}}^{e \,\textsf {T}} {\varvec{\tilde{N}}}^e\;d\theta \\ {\varvec{D}}^{e}=\int _{I_k} {\varvec{\tilde{N}}}^e\frac{d{\varvec{\tilde{N}}}^e}{d\theta }\;d\theta \end{aligned} \end{aligned}$$

where ${\varvec{\tilde{N}}}^e$ is the vector of element shape functions in each element discretizing $I_k$, that is the parametric counterpart of the shape functions introduced in Eq. (4) for the space approximation.

The sensitivities provided by Eqs. (49) and (51) are extremely useful for gradient-based methods. However, the optimization problem defined in (28) is in general non-convex and therefore gradient-based methods are extremely sensitive to initial guesses, and the iterative procedure is often non-convergent. In order to carry out a first global inspection of the parametric domain providing a proper initial guess, it is interesting to consider some evolutionary strategies as Genetic Algorithms (GA), or Simulated Annealing (SA). In a second phase, and starting from a fair initial guess, a gradient-based algorithm is a robust complementary approach converging fast to an accurate solution. This combination of algorithms is very efficient as the evolutionary (genetic) algorithm is used to identify the region were the optimum lies and then the gradient-based one is intended to gain accuracy.

4 Numerical examples

Two examples are presented next to show the capabilities of the techniques described in previous sections. Both are based on composite laminates parameterized with the orientation of the fibers in different subdomains. The first example (Sect. 4.1) has only two parameters and therefore it is affordable to compute its parametric solution using Finite Elements (FE) for each point in the parametric space. Whereas the evaluation of the PGD solution is extremely fast, the FE solution requires a full solve for each parametric value. This first example is used to quantify the accuracy of PGD with respect to FE.

The second example (Sect. 4.2) involves a problem with 4 parameters. While PGD provides a solution in $\sim 6$ hours, the cost of computing FE at every parametric point would be approximately $\sim 10^6$ hours and thus becomes impractical.

4.1 Plate under tensile load

This example considers a two-layered composite parameterized by the fibre orientation at each layer. The domain corresponds to a square plate subjected to a tensile load as shown in Fig. 2. Parameters are independent and therefore the material properties at each layer has the form (15) and the final separated expression of the operator is that in (33).

Fig. 2

Plate under tensile load of 45$^{\circ }$

Parameters $\theta _1$ and $\theta _2$ determine the fibre orientation of layers 1 and 2 respectively as shown in Fig. 2. The parameters take values in the range $\theta _1 \in I_1 = \left[ -90^{\circ },90^{\circ }\right]$ and $\theta _2 \in I_2 = \left[ -90^{\circ },90^{\circ }\right]$.

This particular parameterization is symmetric in the sense that the first and second parameters can be interchanged without modifying the solution, as shown in Figs. 3c and 3d. This allow to validate the solution and, also to keep a similar parameterization in the two examples; PGD requires coupling the dimensions when the parametric domain is not a cartesian product of the individual parameters domains.

The discretization of space involves 800 hexahedral Serendipity elements (4725 nodes) and discretization of both parameters is done with a uniform $1^{\circ }$ spaced grid (181 points). Note that, despite the parametric space is two dimensional, because of the separated structure of the problem, each parameter dimension is discretized independently as one dimensional grid.

The mechanical properties of the materials are relative to carbon fibre reinforced ABS [43] and are reported in Appendix B. The plate is under a $45^{\circ }$ tensile load with respect to the x-axis.

Results of the PGD parametric solution show an excellent agreement with those obtained by Finite Elements (FE) having a global error around 0.1% with 87 modes in the PGD solution (shown by the blue curve in Fig. 3a). The comparison is done by measuring the norm of the difference between the PGD and FE solutions, $\varDelta {\varvec{d}}={\varvec{d}}_\texttt {PGD}-{\varvec{d}}_\texttt {FE}$, integrated in space and parameters as,

$$\begin{aligned} \begin{aligned} e =\frac{\sum \limits _{\text {S}_i}\sum \limits _{\text {S}_j}\varDelta {\varvec{d}}^\textsf {T}(\theta _i,\theta _j){\varvec{M}}\varDelta {\varvec{d}}(\theta _i,\theta _j)}{\sum \limits _{\text {S}_i}\sum \limits _{\text {S}_j}{\varvec{d}}_\texttt {FE}^\textsf {T}(\theta _i,\theta _j){\varvec{M}}{\varvec{d}}_\texttt {FE}(\theta _i,\theta _j)}, \end{aligned} \end{aligned}$$

(53)

where the ${\varvec{M}}$ matrix is a mass matrix for the space dimension. Note that the error is estimated based on subsets of the parametric grids, $\text {S}_i \in I_1$ and $\text {S}_j \in I_2$. This is done to reduce the number of FE problems that is required to solve. Here we use subsets $\text {S}_i$ and $\text {S}_j$ with one value every $3^{\circ }$ and therefore the solutions are compared at $60\times 60=3600$ parametric points.

In Fig. 3a, the convergence curve of the displacements (blue curve) reaches a plateau after $\sim 30$ modes and the error does not decrease when adding new modes. This minimum error is usually controlled by the tolerances imposed in the PGD algorithm (enrichment tolerance = $10^{-4}$). Stricter tolerances produce a plateau at smaller error values. Moreover, we show in Fig. 3a the evolution of both the maximum error and the error at the optimal solution of the goal function with the number of modes. We could deduce that the more we increase the number of modes, the more we get a smaller error.

Fig. 3

Plate under tensile load at 45$^{\circ }$: The labeled points correspond to the optimal values of the two objective functions

The amplitude of the terms in the PGD solution is shown in Fig. 3b. There we can see how the importance of the terms is reduced. Note that, the convergence curve Fig. 3a reaches stagnation after 30 modes, while the amplitude curve Fig. 3b continues decreasing, therefore, implying that the amplitude cannot be used as a direct estimator of the error. The curve shown in Fig. 3b has undergone a post-process usually called PGD-compression [39]. This is a standard procedure that projects the solution into the same space using an $L^2$ projection to remove redundant modes. The compression is done once the PGD solution process has finished.

Panels (c) and (d) of Fig. 3 show maps of the maximum failure criterion (to be minimized) and the minimum safety factor (to be maximized) in the structure introduced in Sect. 2.3.1. Once the PGD solution has been obtained it is extremely fast to evaluate it for any value of the parameters and, therefore, one can evaluate the criterion (or the safety factor) at every parameter value of a fine grid and produce those plots easily. The optimization in this simple case can be done by direct observation of the maps, where local and global minimum/maximum are readily identified. In this simple case, the critical point is located at the fibre orientations $(\theta _1,\theta _2)=(45^{\circ },45^{\circ })$ as expected. The failure indices based on the PGD solution can be easily used in combination with an optimization procedure, such as the Genetic Algorithm or a gradient based method, to obtain the critical point automatically.

Note that the computing time to obtain the PGD solution is $\sim 2.5$ hours and the map is generated in seconds. If one aims at producing the same maps based on a FE solution, this would require $181\times 181=32761$ FE solves, that would take $\sim 6.5$ days using the same computer power as in the PGD case.

It is also worth noting that if the accuracy used to obtain the PGD solution is relaxed, the accuracy of the inverse solver is deteriorated. This is interesting as it shows that the location of the minimum of the function to be minimized is affected by the accuracy of the surrogate.

4.2 Plate with circular hole under tensile load

The second example of the current section involves four parameters. The parameters in this case correspond to patches in the material. The discretization of the four-dimensional parametric space becomes impractically expensive if standard techniques are applied, because the number of points increases exponentially with the number of dimensions. The separable character of the PGD solution, on the other hand, makes this problem tractable as every dimension is discretized independently.

This example involves a plate with a circular hole in the middle subjected to tensile load oriented parallel to the x-axis as shown in Fig.  4. Using the symmetry of the problem we solve only for half of the domain. This symmetry condition brings the implicit assumption that the part not modeled depends on the same four parameters with an angle with opposite sign. This parameterization is reasonable when the traction applied is parallel to the symmetry axis.

The plate is divided into four subdomains, each one with its independent fibre orientation determined by the corresponding parameter $\theta _i \in I_i$ with $i=1,\ldots , 4$. The range of all parameters $\theta _i$, is $I_i = \left[ -90^{\circ },90^{\circ }\right]$, for $i=1,\ldots ,4$. The material properties are the same as in the previous example in Sect. 4.1. Space discretization has 390 hexahedral Serendipity elements and the discretization of each parametric dimension is the same as in the previous example, that is, $I_i$ is represented using a uniform grid of $1^{\circ }$ spacing (181 points). Note that the discretization of the coupled four-dimensional parametric space would require $181^4 > 10^9$ points, whereas the separated representation requires $181\times 4$. The parametric part of the solution is stored in $181\times 4 \times m$ points, being m the number of terms used in the solution (170 terms for this example).

Fig. 4

Symmetric half of a square plate with a circular hole

Fig. 5

Amplitudes and convergence curves of plate with hole

The parametric PGD solution has been computed with the same tolerances as in the previous example and, after compression, the solution has 170 modes. Amplitudes of the modes are shown in Fig. 5a. In this case integrating the error in the parametric domain is too expensive as the number of FE solves is enormous. As a reference, in Fig. 5b we provide a convergence curve of the error in space for one given point in the parametric space, ${\varvec{\theta }}^\texttt {Opt}$, that happens to be the optimal solution found as described next. In this four-dimensional case it is not possible to find the critical point of the objective functions by inspection, and thus some optimization algorithm must be employed. As we have seen in the previous example, the objective functions defined by the failure criterion are not convex and local minima/maxima are present. Therefore we obtain the critical point in two steps, first we use the Genetic Algorithm to perform a global minimization/maximization without large accuracy. Second, we use a gradient method to reach the minimum/maximum starting from the solution of the first step. Both optimization methods where implemented using general built-in Matlab functions (ga and fmincon). The optimal fibre orientations are shown in Fig. 6 and presented in Table 1.

Fig. 6

Optimal fibre orientations on the deformed domain obtained by a global maximization of the safety factor ($\lambda _s$) using first a Genetic Algorithm and then a gradient based method starting from the first solution

The output angles of the optimization in Table 1 for the Genetic Algorithm are integer numbers because the population of the input are integers as well.

Table 1 Optimized angles for square plate with circular hole

The number of evaluations of the objective function is approximately 10,000 out of a total around $1\times 10^9$ possible evaluations. Using this result as the initial guess for the gradient method, we obtain a very robust and precise solution in an efficient way. Once the parametric function is computed by PGD, its evaluation for any parametric point is extremely fast and, therefore, the feasible number of evaluations of the objective function is very large.

The optimization problem is naturally evaluating the forward problem numerous times. The great advantage of PGD is that, through the generalized solution, the whole parametric space is available and browsing it for any value of the set of parameters is very fast. Generally speaking, mesh based techniques are more accurate than PGD, however very expensive in a multi-query application, like optimization, especially when the number parameters is large. It is worth recalling that the computational complexity scales linearly with the increase of the number of parameters in PGD whereas it varies exponentially when using standard mesh based techniques such as FE. Fig. 7 shows the CPU time needed for the PGD and standard FE to explore the whole parametric space; and for standard FE to explore a reduced parametric space ($30\%$ of the full parametric space). We could deduce from the trend of the graph that the PGD is by far computationally cheaper than standard FE when considering a number of parameters more than two.

Fig. 7

CPU time evolution of PGD vs standard FEM

5 Conclusions

We presented a method based on the Proper Generalized Decomposition that efficiently obtains solutions for the deformation of composite laminates parameterized with fibre orientations. This is relevant for the mechanical optimization of 3D printed components. The proposed methodology is able to handle cases where the application of standard discretization techniques would be impractical due to its computational burden. The optimality of the structure is determined here using the Tsai-Wu criterion that acts as a general indicator for the load-carrying capacity of the structure. In practice, the objective function of the optimization problem is non-convex, and therefore, a global optimization is costly and many evaluations of the objective functions are required. The extremely fast evaluation of the parametrized solution once it has been obtained by PGD, makes this optimization possible and fast.

Appendices

Appendix A: separation terms of the elasticity tensor and the transformation matrix

The separation of ${\varvec{{\mathcal {C}}}}$ results in the following summation for a given $\theta _i \subset \varOmega _i$

$$\begin{aligned} {\varvec{{\mathcal {C}}}}(\theta _i)=\sum _{\ell =1}^{9}{\varvec{{\mathcal {C}}}}^\ell \prod ^{\texttt {n}_{\texttt {p}}}_{j=1}\phi _j^{\ell ,i}(\theta _j) \end{aligned}$$

with $\phi _j^{\ell ,i}(\theta _j) \equiv 1$ for $j \ne i$.

The separation process of ${\varvec{{\mathcal {C}}}}$ to obtain the spatial terms and the parametric terms apart was carried out by hand with the aid of the symbolic tool of Matlab^®. The separation process yielded 9 unique terms and they are as follows,

$$\begin{aligned} {\varvec{{\mathcal {C}}}}^1= & {} \begin{bmatrix} a_{11} &{} a_{12} &{} 0 &{} 0 &{} 0 &{} 0\\ &{} a_{22} &{} 0 &{} 0 &{} 0 &{} 0\\ &{} &{} 0 &{} 0 &{} 0 &{} 0\\ &{} \text {Sym.} &{} &{} 0 &{} 0 &{} 0\\ &{} &{} &{} &{} 0 &{} 0\\ &{} &{} &{} &{} &{} a_{66} \end{bmatrix} \; \phi _i^{1,i}(\theta _i) = \cos ^4(\theta _i)\\ {\varvec{{\mathcal {C}}}}^2= & {} \begin{bmatrix} b_{11} &{} b_{12} &{} 0 &{} 0 &{} 0 &{} 0\\ &{} b_{22} &{} 0 &{} 0 &{} 0 &{} 0\\ &{} &{} 0 &{} 0 &{} 0 &{} 0\\ &{} \text {Sym.} &{} &{} 0 &{} 0 &{} 0\\ &{} &{} &{} &{} 0 &{} 0\\ &{} &{} &{} &{} &{} b_{66} \end{bmatrix} \; \phi _i^{2,i}(\theta _i) = \sin ^4(\theta _i) \\ {\varvec{{\mathcal {C}}}}^3= & {} \begin{bmatrix} d_{11} &{} d_{12} &{} 0 &{} 0 &{} 0 &{} 0\\ &{} d_{22} &{} 0 &{} 0 &{} 0 &{} 0\\ &{} &{} 0 &{} 0 &{} 0 &{} 0\\ &{} \text {Sym.} &{} &{} 0 &{} 0 &{} 0\\ &{} &{} &{} &{} 0 &{} 0\\ &{} &{} &{} &{} &{} d_{66} \end{bmatrix} \; \phi _i^{3,i}(\theta _i) = \cos ^2(\theta _i)\sin ^2(\theta _i) \\ {\varvec{{\mathcal {C}}}}^4= & {} \begin{bmatrix} 0 &{} 0 &{} e_{13} &{} 0 &{} 0 &{} 0\\ &{} 0 &{} e_{23} &{} 0 &{} 0 &{} 0\\ &{} &{} 0 &{} 0 &{} 0 &{} 0\\ &{} \text {Sym.} &{} &{} e_{44} &{} 0 &{} 0\\ &{} &{} &{} &{} e_{55} &{} 0\\ &{} &{} &{} &{} &{} 0 \end{bmatrix} \; \phi _i^{4,i} = \cos ^2(\theta _i) \\ {\varvec{{\mathcal {C}}}}^5= & {} \begin{bmatrix} 0 &{} 0 &{} g_{13} &{} 0 &{} 0 &{} 0\\ &{} 0 &{} g_{23} &{} 0 &{} 0 &{} 0\\ &{} &{} 0 &{} 0 &{} 0 &{} 0\\ &{} \text {Sym.} &{} &{} g_{44} &{} 0 &{} 0\\ &{} &{} &{} &{} g_{55} &{} 0\\ &{} &{} &{} &{} &{} 0 \end{bmatrix} \; \phi _i^{5,i}(\theta _i) = \sin ^2(\theta _i) \\ {\varvec{{\mathcal {C}}}}^6= & {} \begin{bmatrix} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} h_{16}\\ &{} 0 &{} 0 &{} 0 &{} 0 &{} h_{26}\\ &{} &{} 0 &{} 0 &{} 0 &{} 0\\ &{} \text {Sym.} &{} &{} 0 &{} 0 &{} 0\\ &{} &{} &{} &{} 0 &{} 0\\ &{} &{} &{} &{} &{} 0 \end{bmatrix} \; \phi _i^{6,i}(\theta _i) = \cos ^3(\theta _i)\sin (\theta _i) \\ \end{aligned}$$

$$\begin{aligned} {\varvec{{\mathcal {C}}}}^7= & {} \begin{bmatrix} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} k_{16}\\ &{} 0 &{} 0 &{} 0 &{} 0 &{} k_{26}\\ &{} &{} 0 &{} 0 &{} 0 &{} 0\\ &{} \text {Sym.} &{} &{} 0 &{} 0 &{} 0\\ &{} &{} &{} &{} 0 &{} 0\\ &{} &{} &{} &{} &{} 0 \end{bmatrix} \; \phi _i^{7,i}(\theta _i) = \cos (\theta _i)\sin ^3(\theta _i) \\ {\varvec{{\mathcal {C}}}}^8= & {} \begin{bmatrix} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0\\ &{} 0 &{} 0 &{} 0 &{} 0 &{} 0\\ &{} &{} 0 &{} 0 &{} 0 &{} l_{36}\\ &{} \text {Sym.} &{} &{} 0 &{} l_{45} &{} 0\\ &{} &{} &{} &{} 0 &{} 0\\ &{} &{} &{} &{} &{} 0 \end{bmatrix} \; \phi _i^{8,i}(\theta _i) = \cos (\theta _i)\sin (\theta _i) \\ {\varvec{{\mathcal {C}}}}^9= & {} \begin{bmatrix} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0\\ &{} 0 &{} 0 &{} 0 &{} 0 &{} 0\\ &{} &{} q_{33} &{} 0 &{} 0 &{} 0\\ &{} \text {Sym.} &{} &{} 0 &{} 0 &{} 0\\ &{} &{} &{} &{} 0 &{} 0\\ &{} &{} &{} &{} &{} 0 \end{bmatrix} \;\; \phi _i^{9,i}(\theta _i) = 1 \end{aligned}$$

Note that the components a, b, d, e, g, h, k, l, q are function of the material characteristics, i.e. Young’s moduli, shear moduli, and Poisson’s ratios, for transversely isotropic material (Table 2).

Similarly, the separation of the transformation matrix ${\varvec{T}}$ results in the following summation for a given $\theta _i \subset \varOmega _i$

$$\begin{aligned} {\varvec{T}}(\theta _i)=\sum _{r=1}^{7}{\varvec{T}}^r\prod ^{\texttt {n}_{\texttt {p}}}_{j=1}Z_j^{r,i}(\theta _j) \end{aligned}$$

Table 2 Carbon fibre reinforced ABS material characteristics

taking $Z_j^{r,i}(\theta _j)\equiv 1$ for $j\ne i$. This separation process outputs 7 unique terms that are as follows,

$$\begin{aligned} {\varvec{T}}^1= & {} \begin{bmatrix} 1 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0\\ &{} 1 &{} 0 &{} 0 &{} 0 &{} 0\\ &{} &{} 0 &{} 0 &{} 0 &{} 0\\ &{} \text {Sym.} &{} &{} 0 &{} 0 &{} 0\\ &{} &{} &{} &{} 0 &{} 0\\ &{} &{} &{} &{} &{} 0 \end{bmatrix} \; Z_i^{1,i}(\theta _i) = \cos ^2(\theta _i) \\ {\varvec{T}}^2= & {} \begin{bmatrix} 0 &{} 1 &{} 0 &{} 0 &{} 0 &{} 0\\ &{} 0 &{} 0 &{} 0 &{} 0 &{} 0\\ &{} &{} 0 &{} 0 &{} 0 &{} 0\\ &{} \text {Sym.} &{} &{} 0 &{} 0 &{} 0\\ &{} &{} &{} &{} 0 &{} 0\\ &{} &{} &{} &{} &{} 0 \end{bmatrix} \; Z_i^{2,i}(\theta _i) = \sin ^2(\theta _i)\\ {\varvec{T}}^3= & {} \begin{bmatrix} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0\\ &{} 0 &{} 0 &{} 0 &{} 0 &{} 0\\ &{} &{} 1 &{} 0 &{} 0 &{} 0\\ &{} \text {Sym.} &{} &{} 1 &{} 0 &{} 0\\ &{} &{} &{} &{} 0 &{} 0\\ &{} &{} &{} &{} &{} 0 \end{bmatrix} \; Z_i^{3,i}(\theta _i) = \cos (\theta _i)\\ {\varvec{T}}^4= & {} \begin{bmatrix} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0\\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0\\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0\\ 0 &{} 0 &{} 0 &{} 0 &{} -1 &{} 0\\ 0 &{} 0 &{} 0 &{} 1 &{} 0 &{} 0\\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \end{bmatrix} \;\; Z_i^{4,i}(\theta _i) = \sin (\theta _i)\\ {\varvec{T}}^5= & {} \begin{bmatrix} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 2\\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} -2\\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0\\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0\\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0\\ -1 &{} 1 &{} 0 &{} 0 &{} 0 &{} 0 \end{bmatrix} \; Z_i^{5,i}(\theta _i) = \cos (\theta _i)\sin (\theta _i)\\ {\varvec{T}}^6= & {} \begin{bmatrix} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0\\ &{} 0 &{} 0 &{} 0 &{} 0 &{} 0\\ &{} &{} 0 &{} 0 &{} 0 &{} 0\\ &{} \text {Sym.} &{} &{} 0 &{} 0 &{} 0\\ &{} &{} &{} &{} 0 &{} 0\\ &{} &{} &{} &{} &{} 1 \end{bmatrix} \; Z_i^{6,i}(\theta _i) = \cos ^2(\theta _i)-\sin ^2(\theta _i)\\ {\varvec{T}}^7= & {} \begin{bmatrix} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0\\ &{} 0 &{} 0 &{} 0 &{} 0 &{} 0\\ &{} &{} 1 &{} 0 &{} 0 &{} 0\\ &{} \text {Sym.} &{} &{} 0 &{} 0 &{} 0\\ &{} &{} &{} &{} 0 &{} 0\\ &{} &{} &{} &{} &{} 0 \end{bmatrix} \; Z_i^{7,i}(\theta _i) = 1 \end{aligned}$$

Appendix B: elasticity tensor characteristic values

The elasticity tensor is described by characteristic values of the material such as Young’s modulii, Poison’s ratios, and shear modulii. The elasticity tensor has the following format for orthotropic materials,

$$\begin{aligned} {\mathcal {C}}_0= \begin{bmatrix} \dfrac{1-\nu _{23}\nu _{32}}{E_{2}E_{3}\varDelta } &{} \dfrac{\nu _{21}-\nu _{23}\nu _{31}}{E_{2}E_{3}\varDelta } &{} \dfrac{\nu _{31}-\nu _{21}\nu _{32}}{E_{2}E_{3}\varDelta } &{} 0 &{} 0 &{} 0\\ &{} \dfrac{1-\nu _{13}\nu _{31}}{E_{1}E_{3}\varDelta } &{} \dfrac{\nu _{32}-\nu _{12}\nu _{31}}{E_{1}E_{3}\varDelta } &{} 0 &{} 0 &{} 0\\ &{} &{} \dfrac{1-\nu _{12}\nu _{21}}{E_{1}E_{2}\varDelta } &{} 0 &{} 0 &{} 0\\ &{} \text {Sym.} &{} &{} G_{23} &{} 0 &{} 0\\ &{} &{} &{} &{} G_{13} &{} 0\\ &{} &{} &{} &{} &{} G_{12} \end{bmatrix} \end{aligned}$$

where,

$$\begin{aligned} \varDelta = \frac{1-\nu _{12}\nu _{21}-\nu _{23}\nu _{32}-\nu _{13}\nu _{31}-2\nu _{21}\nu _{32}\nu _{31}}{E_{1}E_{2}E_{3}} \end{aligned}$$

Note that, for transversely isotropic material with plane 2-3 as the plane of isotropy, the following relations hold

$$\begin{aligned} \begin{aligned} E_2&= E_3, \quad \nu _{12}=\nu _{13}, \quad \nu _{32}=\nu _{23}, \quad \nu _{21}=\frac{E_2}{E_1}\nu _{12}\\ \nu _{31}&=\nu _{21}, \quad G_{12}=G_{13}, \quad \text {and} \quad G_{23}=\frac{E_{2}}{2(1+\nu _{23})} \end{aligned} \end{aligned}$$

In this work, we used a material close to carbon fibre ABS material in our simulations, and the characteristics have the following values: