Abstract
In this paper, mixed formulations are presented in the framework of isogeometric Reissner–Mindlin plates and shells with the aim of alleviating membrane and shear locking. The formulations are based on the Hellinger-Reissner functional and use the stress resultants as additional unknowns, which have to be interpolated in appropriate approximation spaces. The additional unknowns can be eliminated by static condensation. In the framework of isogeometric analysis static condensation is performed globally on the patch level, which leads to a high computational cost. Thus, two additional local approaches to the existing continuous method are presented, an approach with discontinuous stress resultant fields at the element boundaries and a reconstructed approach which is blending the local control variables by using weights in order to compute the global ones. Both approaches allow for a static condensation on the element level instead of the patch level. Various numerical examples are investigated in order to verify the accuracy and effectiveness of the different approaches and a comparison to existing elements that include mechanisms against locking is carried out.
Similar content being viewed by others
1 Introduction
Isogeometric Analysis (IGA) was introduced by Hughes et al. [1] with the aim of unifying the design and analysis process. This is achieved by using for both the same higher order basis functions that are common in CAD tools, such as Non-Uniform Rational B-splines (NURBS). Since then, isogeometric analysis has been successfully implemented in structural mechanics and many other fields, e.g. in fluid mechanics [2], contact mechanics [3] and fracture mechanics [4].
Especially in the context of shell structures, isogeometric analysis offers many advantages. The higher continuity of splines over the patch is essential for the correct computation of the shell’s curvature and the surface’s normal. Furthermore, free form structures can now be computed with a significantly lower computational cost. Thus, in the past years a lot of effort was put in integrating isogeometric analysis into the existing shell formulations. The first step was done with the Kirchhoff-Love shells, see [5,6,7,8] and later with the Reissner–Mindlin shells in [9,10,11,12,13] and the solid-shells in [14,15,16].
Even though splines are very advantageous due to their higher order and continuity, they suffer from the same locking effects as Lagrange shape functions, see [17]. Locking leads to an artificial stiffening of the system, an underestimation of the deformation and oscillations in the stress resultants. Various methods have been proposed in order to eliminate these undesirable effects in the framework of isogeometric analysis. The easiest one is to use higher order shape functions, however, this approach does not eliminate locking completely and at the same time increases the computational cost, see [10, 17, 18]. An attempt to overcome locking effects on the theoretical level by using hierarchic formulations was made in the framework of Reissner–Mindlin and 3D shells in [19,20,21,22]. Even though these formulations were able to avoid transverse shear and curvature thickness locking ab initio, additional methods had to be implemented for the elimination of membrane locking. In [23, 24] the classical Timoshenko beam problem was reformulated to a single differential equation with only one primal variable in order to avoid shear locking by construction. A mixed displacement method that avoids the geometrical locking effects ab initio was presented in Bieber et al. [25].
In addition to these formulations, methods that have been valuable in the classical finite element analysis for the elimination of locking effects have been extended to isogeometric analysis, like the Assumed Natural Strain (ANS) method in [26, 27], the Discrete Shear Gap (DSG) approach in [17, 20] and the Enhanced Assumed Strain (EAS) method [28]. Non-uniform integration techniques were implemented for isogeometric Reissner–Mindlin shells in [12, 29] in order to overcome locking and increase the efficiency of the formulations. However, the latter method fails for general non-uniform knot vectors and is thus not relevant for industrial applications. Reduced integrated fields were applied for a solid-shell in [30] in combination with a moving least square approach to project them back onto the fully integrated space. The use of adjusted approximation spaces for the displacements and the rotations in Reissner–Mindlin plates and shells was able to eliminate transverse shear locking, see [31, 32].
The \({\bar{B}}\) method, one of the most popular methods for the finite element analysis, was introduced for isogeometric analysis in Elguedj et al. [33] along with an \({\bar{F}}\) projection in order to alleviate locking in nearly incompressible linear and nonlinear elasticity and plasticity problems. Later, it was extended to straight and curved Timoshenko beams in Bouclier et al. [34] and in Greco et al. [35] to plane curved Kirchhoff rods. A first attempt to apply the \({\bar{B}}\) method to isogeometric 2D solid shells was made in Bouclier et al. [18]. As it was often stated in these works, the \({\bar{B}}\) method within the framework of isogeometric analysis leads to a linear system where a matrix defined on the patch level has to be inverted and the resulting stiffness matrix is fully populated, which increases the computational cost. This led to the introduction of local \({\bar{B}}\) formulations, where the \({\bar{B}}\)-projection is applied locally and the global variables are obtained from the local ones using reconstruction algorithms. Such a local \({\bar{B}}\) formulation was first introduced in Bouclier et al. [15] for a NURBS-based solid-shell. A local \({\bar{B}}\) formulation based on the Bézier projection proposed by Thomas et al. [36] was presented in Miao et al. [37] to alleviate transverse shear locking in Timoshenko beams and volumetric locking in nearly incompressible elastic solids. In addition, Miao et al. presented a non-symmetric Bézier \({\bar{B}}\) projection, where the variation of the assumed variables is discretized with the dual basis functions. This way, the assumed variables are directly condensed out without the need of an inversion and lead to a sparse stiffness matrix with a slightly higher bandwidth. This method was later applied to geometrically nonlinear Reissner–Mindlin shells in Zou et al. [38]. A much simpler reconstruction algorithm which is also based on the work of Thomas et al. [36] can be found in Greco et al. [35, 39] for plane curved Kirchhoff rods and Kirchhoff-Love shells. There the local variables are directly interpolated with local B-spline functions without a Bézier projection and transformation to the Bernstein basis. Local \({\bar{B}}\) formulations where the locking strains or stresses are projected onto interpolation spaces with the lowest possible order for each element leading to different projection spaces for the inner, corner and boundary elements are presented in Hu et al. [40, 41]. Antolin et al. [42, 43] used discontinuous polynomial spaces for the projection of the strains.
Mixed formulations, which are equivalent to the \({\bar{B}}\) formulations for linear cases as stated in [15, 44], were implemented in the context of isogeometric analysis for a solid-shell in order to eliminate membrane, shear and thickness locking in linear [15] and geometrically nonlinear cases [45]. Echter et al. [20] and Rafetseder et al. [46] used a mixed formulation to overcome membrane locking in hierarchic shells and Kirchhoff-Love shells, respectively. Mixed variational formulations for nearly incompressible solids were implemented in [47, 48]. However, as it is for the \({\bar{B}}\) method, mixed methods involve static condensation on the patch level due to the high continuity of the shape functions in isogeometric analysis. This includes the inversion of a matrix on the patch level and leads to a fully populated stiffness matrix. In order to overcome these issues and reduce the computational cost, in this work, two approaches are presented based on the two-field Hellinger-Reissner variational principle which perform static condensation on the element level. In the first one, the stress fields are defined discontinuously (\(C^{-1}\)) across the element boundaries. The resulting stiffness matrix is sparse and has the same bandwidth as the standard displacement-based shell which additionally reduces the computational cost. The second approach is based on the reconstruction algorithm used by Greco et al. [35, 39] in the framework of a \({\bar{B}}\) method. Here, it is reformulated for the mixed method with the stress resultants as additional unknowns and is extended to the case of Reissner–Mindlin plates and shells where membrane and transverse shear locking occur. The resulting stiffness matrix has a slightly higher bandwidth than the standard displacement-based formulations. Both methods can be applied for any polynomial degree. They are compared to the mixed formulation where static condensation is performed on the patch level.
The paper is organized as follows. In Sect. 2, the Reissner–Mindlin shell formulation from [11, 32] is briefly summarized. In Sect. 3, the isogeometric mixed formulation based on the Hellinger-Reissner variational principle is presented for alleviating membrane and shear locking. The two methods for performing static condensation on the element level are presented, and the existing approach, where static condensation is performed on the patch level is recalled. In Sect. 4, the performance of the different approaches is compared on the basis of various numerical examples. Finally, in Sect. 5, conclusions are drawn and an outlook for future research is presented.
2 Reissner–Mindlin shell formulation
2.1 Kinematics and basis systems
The shell formulation presented in this section is based on the Reissner–Mindlin shell theory and can be found in [11, 32]. It is derived from continuum mechanics and the shell structure is defined with respect to its mid-surface. In order to describe the thickness direction, the so-called director vector, see Fig. 1, is used. The director vector of the reference configuration \({\varvec{D}}\) coincides with the normal vector of the shell’s surface, whereas the director vector of the current configuration is defined by a difference vector formulation
since only linear problems are considered. The difference vector reads
and depends on the rotational parameter \(\varvec{\omega }\) of the shell’s mid-surface and the reference director vector \({\varvec{D}}\). Only small rotations are considered and the inextensibility condition in thickness direction is fulfilled in the sense of \(|{\varvec{d}}|\simeq |{\varvec{D}}|=1\).
Using the director vector, the reference position vector of an arbitrary point on the shell is given as
where \(i=1,2,3\), \(\xi ^a\) with \(\alpha =1,2\) are the two in-plane coordinates of the convected curvilinear coordinate system of the mid-surface, \(-\frac{t}{2}\le \xi ^3\le \frac{t}{2}\) is the thickness coordinate and \({\varvec{X}}(\xi ^\alpha )\) is the position vector of the mid-surface in the reference configuration. In the same manner, the displacement vector \(\varvec{{\tilde{u}}}\) of an arbitrary point on the shell is defined as
where \({\varvec{u}}(\xi ^\alpha )\) is the displacement vector of the mid-surface. The current position vector \({\varvec{x}}(\xi ^\alpha )\) and the displacement vector \({\varvec{u}}(\xi ^\alpha )\) are linked to each other in the following way
The covariant basis vectors \({\varvec{G}}_i\) of the shell are defined with respect to \(\xi ^i\) as follows
while the contravariant basis vectors \({\varvec{G}}^j\) form their dual basis system with \({\varvec{G}}_i\cdot {\varvec{G}}^j=\delta _i^j\) and \(\delta _i^j\) the Kronecker delta symbol. However, an orthonormal basis system is needed for the constitutive relation, thus, a local basis system \({\varvec{A}}_i\) is introduced, see Fig. 1. It is defined with respect to the local Cartesian coordinate system \(\theta ^i\) and is computed as close as possible to the convected basis system using the lamina coordinate system, see [11]. In this sense, the displacement and position vectors in Eqs. (3)–(4) are now defined with respect to the new coordinate system \(\theta ^i\).
The definition of the Jacobian matrix \({\varvec{J}}\) is necessary for the computation of the derivatives with respect to the local Cartesian coordinate system as well as for the transformation of the stress resultant components in Sec. 3. Its entries \(J_{\alpha \beta }\) are defined as
Since only smooth surfaces are considered, the unknown deformation is summed up in the following deformation vector
where \(u_i\) are the displacements and \(\beta _{\alpha }\) the rotations. In the case of surfaces with kinks the third rotation \(\beta _3\) should be considered additionally.
2.2 Strains and stresses
The strains and stresses are expressed with respect to the local Cartesian basis system \({\varvec{A}}_i\) and its dual basis system \({\varvec{A}}^i={\varvec{A}}_i\). Since only linear problems are considered the linearized Green-Lagrange strain tensor is used and the strain tensor with respect to \({\varvec{A}}^i\) is defined as
The components \(E_{ij}\) are split into the in-plane and transverse shear strains as follows
\(E_{33}\) is zero due to the inextensibility constraint. In Eq. (10) \(\varepsilon _{\alpha \beta }\) denote the membrane strains
and \(\kappa _{\alpha \beta }\) the curvatures
The second-order curvatures, which are denoted as
are neglected here because only thin shells are considered and their contribution to the strain energy tends to zero. The shear strains \(\gamma _{\alpha }\) in Eq. (11) are given as
The different strain components are assembled in Voigt notation in the strain vector
The corresponding stress resultant vector in Voigt notation includes the membrane forces \(n^{\alpha \beta }\), the bending moments \(m^{\alpha \beta }\) and the shear forces \(q^{\alpha }\)
Since a linear elastic material is considered, the relation between the stress resultants and the strains is defined as \(\varvec{\sigma }=\bar{{\varvec{D}}}\cdot \varvec{\varepsilon }\), where \(\bar{{\varvec{D}}}\) is the constitutive matrix, see [12].
3 Isogeometric displacement-stress mixed method for alleviating membrane and shear locking
3.1 Hellinger-Reissner variational formulation
In contrast to classical displacement-based formulations, mixed formulations include as additional unknowns the stresses or strains (Hellinger–Reissner) or both the stresses and the strains (Hu–Washizu). The approximation spaces for these additional unknowns must be chosen accordingly, with the aim of alleviating locking effects. In this work, the Hellinger–Reissner functional is used within the framework of an isogeometric Reissner–Mindlin shell formulation, in order to alleviate membrane and shear locking.
The mixed formulation based on the Hellinger-Reissner principle from [49] and [50] reads
with \(\bar{{\varvec{p}}}_0\) the surface loads, \(\bar{{\varvec{t}}}_0\) the boundary tractions and \({\varvec{v}} = \left[ \begin{array}{c}{\varvec{u}}\\ \varvec{\beta } \end{array}\right] =\left[ \begin{array}{ccccc}u_1,&u_2,&u_3,&\beta _1,&\beta _2\end{array}\right] ^T\) the deformation vector. The strains \(\varvec{\varepsilon }\) and their variations \(\delta \varvec{\varepsilon }\) are functions of the unknown displacements and rotations \({\varvec{v}}\) and their variations \(\delta {\varvec{v}}\), respectively. The formulation results from the principle of minimum complementary energy when employing Lagrangian multipliers in order to additionally include the equilibrium and traction boundary conditions in the expression. The Hellinger-Reissner functional leads to a saddle point type problem, thus, the existence of a unique solution and the stability of the system are only guaranteed when fulfilling additional conditions, see [51]. In particular, the Babuška-Brezzi condition (inf-sup condition), see [52] and [53], which ensures the stability of the system should be verified. Here, the condition was not examined, however, since the results obtained in the numerical examples in Sect. 4 were accurate and robust it is assumed that the condition is fulfilled. Nevertheless, in order to ensure the stability of the proposed mixed formulations in general, a mathematical verification of the condition should be carried out in future work. The corresponding variational formulation for a classical displacement-based approach of an isogeometric Reissner–Mindlin shell formulation can be found in [32].
The stress resultant components that are considered as additional unknowns and interpolated with adjusted approximation spaces are those that correspond to the occurring locking effect. In other words, for shear locking the unknown stress resultants include \(\varvec{\sigma }=\left[ q^1, q^2\right] \), for membrane locking \(\varvec{\sigma }=\left[ n^{11}, n^{22}, n^{12}\right] \) and in the case where both locking effects occur, e.g. in shells, the unknowns include \(\varvec{\sigma }=\left[ n^{11}, n^{22}, n^{12}, q^1, q^2\right] \).
In the following, the formulation is presented for the case that shear and membrane locking occur. However, in the numerical examples of Sect. 4 all three versions have been implemented and used for the corresponding examples. The equations are then adjusted. Furthermore, in the case of shells, the bending parts could be also considered as additional unknowns. Here, this does not lead to a significant improvement of the results and increases the computational cost considerably. Thus, only the membrane and shear terms are considered. However, in cases where the membrane and bending terms are coupled the consideration of the bending terms as additional unknowns is mandatory, see [51]. They are then interpolated in the same manner as the membrane terms.
The Hellinger-Reissner variational formulation from Eq. (18) is now modified for the case where membrane and shear locking is expected
Here, \(\varvec{\varepsilon }_{\varepsilon \gamma }^T=\left[ \varepsilon _{11},\varepsilon _{22},2\varepsilon _{12},\gamma _{1},\gamma _{2}\right] \) are the corresponding strains to \(\varvec{\sigma }\) and \(\varvec{\kappa }^T=\left[ \kappa _{11},\kappa _{22},2\kappa _{12}\right] \) the curvatures. The strains \(\varvec{\varepsilon }_{\varepsilon \gamma }\), \(\varvec{\kappa }\) and their variations \(\delta \varvec{\varepsilon }_{\varepsilon \gamma }\), \(\delta \varvec{\kappa }\) are functions of the unknown displacements and rotations \({\varvec{v}}\) and their variations \(\delta {\varvec{v}}\), respectively. The isotropic linear elastic material tensor is also split into the part that corresponds to the membrane and transverse shear strains
and the part that corresponds to the curvatures
where E is Young’s modulus, \(\nu \) is Poisson’s ratio, t is the shell’s thickness and \(\kappa _s=\frac{5}{6}\) is the shear correction factor.
In the framework of isogeometric analysis, the appropriate shape functions for the stress resultant fields are, in the relevant direction, one order lower than the ones used for the interpolation of the deformation, see Table 1. There also exists the possibility to reduce the polynomial degree in both directions by one, see [15, 43]. However, this version is not considered here. The resulting approximation spaces for the different stress resultant components for a polynomial degree of \(p = 3\) and \(q = 2\) is depicted in Fig. 2. It should be noted that all approximation spaces have the same number of elements and the same number of Gauss points as the deformation mesh. However, the number of control points and their location is different for each approximation space.
Here, NURBS shape functions are used for the approximation of the deformation and the stress resultants, see [54, 55]. The shape functions for the stress resultant components \(\varvec{\sigma }=\left[ n^{11}, n^{22}, n^{12}, q^1, q^2\right] \) are summed up in the following way

where the color indicates the corresponding approximation space from Fig. 2 and p, q are the polynomial degrees of the deformations in the first and second direction.  ,
,  and
and  include the shape function’s values at all control points
include the shape function’s values at all control points  ,
,  and
and  . This way, the stress resultants \(\varvec{\sigma }\) are defined with respect to the covariant basis \({\varvec{G}}_{\alpha }\). However, they need to be defined with respect to the local Cartesian basis \({\varvec{A}}_{\beta }\), thus, the transformation matrix \({\varvec{T}}_{\sigma }\) is introduced
. This way, the stress resultants \(\varvec{\sigma }\) are defined with respect to the covariant basis \({\varvec{G}}_{\alpha }\). However, they need to be defined with respect to the local Cartesian basis \({\varvec{A}}_{\beta }\), thus, the transformation matrix \({\varvec{T}}_{\sigma }\) is introduced
where the entries of the Jacobian matrix \(J_{\alpha \beta }\) are evaluated at the integration points and are defined in Eq. (7). The new resulting shape functions for the stress resultants read \(\hat{{\varvec{N}}}_{\sigma }={\varvec{T}}_{\sigma }\,{\varvec{N}}_{\sigma }\). Finally, the interpolations of \({\varvec{v}}\) and \(\varvec{\sigma }\) are given in matrix notation as follows
where \(\hat{{\varvec{v}}}\) includes the 5 nodal degrees of freedom of all the control points in the deformation mesh and \(\hat{\varvec{\sigma }}\) includes the stress resultant components of all the control points in the different stress resultant meshes.
Isogeometric analysis uses the same shape functions for the design and analysis which leads to an exact representation of the geometry. Thus, the interpolated values of \({\varvec{X}}\) and \({\varvec{D}}\) are not approximations but exact values and are denoted without \((...)^h\). In order to interpolate the difference vector \({\varvec{b}}^h\), the interpolation of the rotational parameter \(\varvec{\omega }^h\) from Eq. (2) has to be calculated first. It depends on the nodal transformation matrix \({\varvec{T}}_{3I}=\left[ \begin{array}{c c} {\varvec{A}}_{1I}&{\varvec{A}}_{2I} \end{array}\right] \), which includes the nodal Cartesian system \({\varvec{A}}_{\alpha I}\) at the \(I-th\) control point. These nodal values \({\varvec{A}}_{\alpha I}\) are calculated using a method proposed by Dornisch et al. [11]. There, the nodal Cartesian basis systems are defined in a way that their interpolated values at any point of the surface coincide as well as possible with the basis system defined by the geometry. In this sense, the resulting interpolated rotational parameter reads
where nen is the number of shape functions that are non zero for a given element.
The strain-deformation matrices \({\varvec{B}}^{\varepsilon \gamma }\) and \({\varvec{B}}^{\kappa }\) provide a relation between the strains and the nodal deformation
Eqs. (26,27) are given in matrix notation and \({\varvec{B}}^{\varepsilon \gamma }\), \({\varvec{B}}^{\kappa } \) include the values for all the control points \(I=1,n_{cp}\) of the deformation mesh

Inserting the interpolated values from Eqs. (23-24) and Eqs. (26-27) in Eq. (19) leads to the discrete weak form of the Hellinger-Reissner variational formulation
The linear system of equations that results from Eq. (30) and has to be solved is given as follows
with the different stiffness parts defined as
and the force vector defined as
Applying static condensation on the patch level, a new mixed stiffness matrix \({\varvec{K}}_{Mixed}\) can be defined
that has the same dimension as the stiffness matrix from the classical displacement-based formulation. This way, the unknowns to be calculated are again only the deformations. In the following three different approaches to perform the static condensation are presented.
3.2 Continuous approach
In the first approach, the approximation spaces for the stress resultant components \(\hat{\varvec{\sigma }}\) are chosen to be one level of continuity lower than the approximation space of the deformation. In other words, the continuity of the deformation across an interior element boundary is \(C^{p-1}\), while for the stress resultant components the continuity can take the value \(C^{p-2}\) depending on the direction. The high continuity of the NURBS shape functions, which is one of the advantages for using isogeometric analysis, is now an obstacle when doing the static condensation in Eq. (31). In the standard \(C^0\) continuous finite element method, static condensation can be done on the element level since the stress resultant components are discontinuous across the element boundaries. However, in isogeometric analysis, due to the higher continuity, static condensation has to be performed on the patch level. Thus, the stiffness matrix components in Eqs. (32-35) are going to have the following dimension
-
\({\varvec{K}}_{vv}\) has the dimension \((ncp_v\cdot ndf)\times (ncp_v\cdot ndf)\), where \(ncp_v\) is the total number of control points from the displacement/rotation mesh and \(ndf=5\) are the degrees of freedom per control point.
-
\({\varvec{K}}_{v\sigma }\) and \({\varvec{K}}_{\sigma v}^T\) have the dimension \((ncp_v\cdot ndf)\times (ncp_s)\), where here \(ncp_s\) includes the total number of control points \(ncp_{11}\), \(ncp_{22}\), \(ncp_{12}\) from the stress resultant component meshes. Depending on the locking phenomena to be alleviated, \(ncp_s\) can take different values, as can be seen in Table 2.
-
\({\varvec{K}}_{\sigma \sigma }\) has the dimension \(ncp_s\times ncp_s\).
This way, also the stress resultant components \(\hat{\varvec{\sigma }}\) are defined on the patch level
where
with \({\varvec{n}}^{11}=\left[ \begin{array}{c}n^{11}_1,...,n^{11}_{ncp_{11}} \end{array}\right] \), \({\varvec{n}}^{22}=\left[ \begin{array}{c}n^{22}_1,...,n^{22}_{ncp_{22}} \end{array}\right] \), \({\varvec{n}}^{12}=\left[ \begin{array}{c}n^{12}_1,...,n^{12}_{ncp_{12}} \end{array}\right] \), \({\varvec{q}}^{1}=\left[ \begin{array}{c}q^{1}_1,...,q^{1}_{ncp_{11}} \end{array}\right] \) and \({\varvec{q}}^{2}=\left[ \begin{array}{c}q^{2}_1,...,q^{2}_{ncp_{22}} \end{array}\right] \). The inversion of \({\varvec{K}}_{\sigma \sigma }\) on the patch level requires a significantly higher computational time since the size of the matrix increases very quickly, see Table 2. Furthermore, the resulting stiffness matrix \({\varvec{K}}_{Mixed}\) is not a banded matrix anymore but a full one, which additionally increases the computational cost, see Sect. 3.5.
Since here only linear problems are considered, the continuous mixed formulation is equivalent to the global \({\bar{B}}\) formulation firstly presented in [33] and later used in [15] in the framework of an isogeometric NURBS-based solid-shell with the aim of alleviating membrane, shear and thickness locking. It was later extended to the case of large rotations and large displacements in [45]. Another continuous mixed formulation can be found in the work of Echter et al. [20], where it was applied to a hierarchic family of shells and in the work of Rafetseder et al. [46], where it was implemented to an isogeometric Kirchhoff-Love shell. In both approaches, the aim was to alleviate membrane locking.
Advantages: The results are in general more accurate than for the following two approaches as it will be seen in Sect. 4.
Disadvantages: Higher computational cost since \({\varvec{K}}_{\sigma \sigma }\) is inverted on the patch level and the resulting stiffness matrix is full.
3.3 Discontinuous approach
In the discontinuous approach, the shape functions for the stress resultant components are again chosen with one order lower in the relevant direction than the shape functions for the deformations. However, this time, in order to enable static condensation on the element level, the continuity between internal element boundaries is reduced so that the elements are discontinuous again. This is achieved by repeating the internal entries of the knot vector until a continuity of \(C^{-1}\) is reached. A discontinuous stress resultant field for the component \(n^{11}\) and \(q^1\) is depicted in Fig. 3 in comparison to the corresponding continuous deformation field.
Eqs. (32-35) are now defined on the element level, thus, the integrals are computed within the element limits, i.e. \(\int _{\varOmega _e}d\varOmega _e\). The stiffness matrix components have the following dimension
-
\({\varvec{K}}_{vv}\) has the dimension \((nen_v\cdot ndf)\times (nen_v\cdot ndf)\), where \(nen_v=(p+1)\cdot (q+1)\) is the number of nonzero shape functions for an element in the deformation mesh.
-
\({\varvec{K}}_{v\sigma }\) and \({\varvec{K}}_{\sigma v}^T\) have the dimension \((nen_v\cdot ndf)\times (ncp_s)\), where \(ncp_s\) includes the number of nonzero shape functions \(nen_{11}=p\cdot (q+1)\), \(nen_{22}=(p+1)\cdot q\), \(nen_{12}=p\cdot q\) for an element in the stress resultant component meshes. Again, \(ncp_s\) varies based on the locking phenomena that have to be alleviated, see Table 2.
-
\({\varvec{K}}_{\sigma \sigma }\) has the dimension \(ncp_s\times ncp_s\).
The stress resultant components \(\hat{\varvec{\sigma }}^e\) are now defined on the element level
where \(e=1, numel\) and
with \({\varvec{n}}^{11}=\left[ \begin{array}{c}n^{11}_1,...,n^{11}_{nen_{11}} \end{array}\right] \), \({\varvec{n}}^{22}=\left[ \begin{array}{c}n^{22}_1,...,n^{22}_{nen_{22}} \end{array}\right] \), \({\varvec{n}}^{12}=\left[ \begin{array}{c}n^{12}_1,...,n^{12}_{nen_{12}} \end{array}\right] \), \({\varvec{q}}^{1}=\left[ \begin{array}{c}q^{1}_1,...,q^{1}_{nen_{11}} \end{array}\right] \) and \({\varvec{q}}^{2}=\left[ \begin{array}{c}q^{2}_1,...,q^{2}_{nen_{22}} \end{array}\right] \). The inversion of \({\varvec{K}}_{\sigma \sigma }^e\) is now computationally much cheaper than for the continuous approach and the resulting stiffness matrix \({\varvec{K}}_{Mixed}\) has the same bandwidth of \(2\cdot p+1\) as the displacement-based formulation, which additionally reduces the computational cost, see Sect. 3.5. However, due to the discontinuity of the stress resultant fields, locking is not completely eliminated, as will be shown in Sect. 4.
In the framework of the \({\bar{B}}\) method, a discontinuous approach was presented in [35] for plane curved Kirchhoff rods in order to alleviate membrane locking. However, there, the assumed strain field is not directly implemented discontinuously from the beginning. The strains are computed on the element level using a local \(L^2\)-projection or a collocation method where only the control variables which have an influence on the given element are considered. Across the element boundaries the continuity of the shape functions for the assumed strains are still one continuity lower than the ones for the displacements. This way the formulation becomes quasi discontinuous. Discontinuous local basis functions as the ones presented here were used in [26] in the context of an Assumed Natural Strain method for solid shell NURBS-based elements and in [43] again for isogeometric solid shells. Furthermore, Antolin et al. [42] chose for the projection space of the volumetric strain piecewise discontinuous polynomials, however, they were built on a coarser mesh than the displacements.
Advantages: Static condensation can be performed on the element level. The resulting stiffness matrix is banded and has the same bandwidth as the displacement-based formulation. Thus, the computational cost is low.
Disadvantages: The discontinuity of the stress resultants seems to reduce the accuracy of the results. Larger input file due to the additional control points.
3.4 Reconstructed approach
In order to achieve a low computational cost as in the discontinuous approach while maintaining a high accuracy as in the continuous approach, a reconstruction algorithm is implemented. Reconstruction algorithms have been introduced mainly in the framework of the \({\bar{B}}\) method when using local approaches. One of these algorithms is presented in the work of Greco et al. [39] for a B-spline based isogeometric Kirchhoff-Love shell with the aim of alleviating membrane locking. There, the assumed membrane strains are first defined with a local \(L^2\) - projection and later reconstructed by blending the local control variables using weights in order to get the global ones. Even though this method is based on the algorithm proposed by Thomas et al. [36] it is much simpler and easier to implement. In Thomas’ method, first, Bézier extraction is applied to project the spline basis functions onto the Bernstein basis of each element. In a next step, the Bézier local control points are converted to spline control points using an element reconstruction operator and then weighted in order to compute the global spline control values. On the other hand, Greco et al. directly interpolates the local variables with local B-spline functions and later blends them using the same weights proposed by Thomas.
The Bézier projection algorithm from Thomas was also implemented in the framework of the \({\bar{B}}\) method in order to alleviate transverse shear locking in Timoshenko beams and volumetric locking in nearly incompressible solids in Miao et al. [37]. There, a non-symmetric Bézier \({\bar{B}}\)-projection method was additionally proposed where the variation of the assumed variables is discretized with the dual basis that correspond to the spline basis functions. This way, the assumed variables are condensed out using the orthogonality property of the Bézier dual bases and an inversion of a matrix is not necessary anymore. This method was extended to a geometrically nonlinear isogeometric Reissner–Mindlin shell element to alleviate shear and membrane locking in the work of Zou et al. [38]. Another reconstruction algorithm that could be compared to the one proposed in this work is the local \({\bar{B}}\) formulation presented in the work of Bouclier et al. [15] for a NURBS-based solid-shell to alleviate membrane, shear and thickness locking. A local least squares method is applied to each element and afterwards the resulting local variables are smoothed over the global structure using the average of the shared local degrees of freedom, as it is proposed in the work of Mitchell et al. and Govindjee et al. [56, 57]. However, the weights proposed by Thomas are more exact compared to the ones proposed by Govindjee and lead to more accurate results as stated in [36]. Here, the procedure presented by Greco et al. [39] is adopted to the mixed formulation with stress resultants as additional unknowns and is then extended to the case of the Reissner–Mindlin shell.
As in the continuous approach, the stress resultant fields are in the relevant direction one order and one level of continuity lower than the deformation field. However, static condensation is still performed on the element level, as in the discontinuous approach. Thus, the stress resultant components \(\hat{\varvec{\sigma }}^e\) are defined for each element as
where \(e=1, numel\) and
with \({\varvec{n}}^{11}=\left[ \begin{array}{c} n^{11}_1,...,n^{11}_{nen_{11}} \end{array}\right] \), \({\varvec{n}}^{22}=\left[ \begin{array}{c} n^{22}_1,...,n^{22}_{nen_{22}} \end{array}\right] \), \({\varvec{n}}^{12}=\left[ \begin{array}{c} n^{12}_1,...,n^{12}_{nen_{12}} \end{array}\right] \), \({\varvec{q}}^{1}=\left[ \begin{array}{c} q^{1}_1,...,q^{1}_{nen_{11}} \end{array}\right] \) and \({\varvec{q}}^{2}=\left[ \begin{array}{c} q^{2}_1,...,q^{2}_{nen_{22}} \end{array}\right] \).
In order to reconstruct again a continuous stress resultant field on the patch level, the local stress resultant control variables are blended with a weighted average as follows
where \(D_I\) includes the elements where the I-th NURBS shape function is not zero. The weights \(w_{I,e}^{\alpha \beta }\) are specified according to the work of Thomas et al. [36] as the volume included by the graph of the I-th shape function defined on the element e divided by the volume included by the graph of the I-th shape function defined on the whole patch:
where \({\hat{\varOmega }}\) is the parametric domain of the patch while \({\hat{\varOmega }}^e\) is the parametric domain of the element e.
Control points of the stress resultant component \(q^1\) with polynomial degrees \(p=1\), \(q=2\) and \(2\times 2\) elements and their weights \(w^{11}\) for each element according to Thomas et al. [36]. The reconstruction of \(q^1\) for the \(5^{th}\) control point is demonstrated
In comparison, the weights proposed in the local least squares method of Mitchell et al. [56] and Govindjee et al. [57] are defined as the average of the shared local degrees of freedom
where \(n^{11}_I\), \(n^{22}_I\), \(n^{12}_I\) are the number of elements in the support of the I-th shape function.
Control points of the stress resultant component \(q^1\) with polynomial degrees \(p=1\), \(q=2\) and \(2\times 2\) elements and their weights \(w^{11}\) for each element according to Mitchell et al. [56] and Govindjee et al. [57]. The reconstruction of \(q^1\) for the \(5^{th}\) control point is demonstrated
The reconstructed stress resultant components \(\hat{\varvec{\sigma }}^{rec}\), which include again the control variables of the whole patch are used for the definition of \({\varvec{K}}_{Mixed}\) in Eq. (37). An example for the reconstruction algorithm is given for a plate in Fig. 4. There the control points of the stress resultant component \(q^1\) with polynomial degrees \(p=1\), \(q=2\) and \(2\times 2\) elements are depicted with their weights \(w^{11}\) for each element. The reconstruction of \(q^1\) for the \(5^{th}\) control point is demonstrated. The same example is in addition illustrated in Fig. 5 for the case that the weights of Mitchell et al. [56] and Govindjee et al. [57] are used, see Eq. (49).
The dimension of the stiffness matrix components in Eqs. (32–35) are now partly defined as in the continuous method and partly as in the discontinuous method. \({\varvec{K}}_{\sigma \sigma }\) and \({\varvec{K}}_{\sigma v}\) are defined as in the discontinuous method on the element level. Thus, the computational cost for the inversion of \({\varvec{K}}_{\sigma \sigma }\) is low. On the other hand \({\varvec{K}}_{v\sigma }\) is defined as in the continuous method on the patch level. This way, the resulting stiffness matrix \({\varvec{K}}_{Mixed}\) is not symmetric anymore. However, \({\varvec{K}}_{Mixed}\) is again a banded matrix with a bandwidth slightly higher than in the discontinuous case, which additionally reduces the computational time, see Sect. 3.5. The exact value of the bandwidth is \(6\cdot p-3\) as stated in [15].
Advantages: Accuracy almost as good as for the continuous approach, see Sect. 4. The inversion of \({\varvec{K}}_{\sigma \sigma }\) is done on the element level which reduces the computational cost. The resulting stiffness matrix is banded which reduces the computational cost compared to the continuous method.
Disadvantages: The weights for the reconstruction algorithm have to be defined beforehand and stored. The resulting stiffness matrix is not symmetric anymore. Loss of physical meaning since Betti-Maxwell’s theorem is not valid anymore.
3.5 Computational time
In the previous sections, while describing the advantages and disadvantages of the different approaches to the static condensation, the computational time was often mentioned as an argument. In this section the computational cost is discussed in more detail. In particular, the computational time for the inversion of the \({\varvec{K}}_{\sigma \sigma }\) matrix, the computation of \({\varvec{K}}_{Mixed}\) and the solution of the equations is going to be the main focus since they can increase rapidly depending on the approach that is used.
The computational complexity for the inversion of an \(n\times n\) matrix, based on the Gauss-Jordan elimination algorithm is \(O(n^3)\). There also exist other algorithms which are slightly better concerning the computational time, for instance the Strassen algorithm (\(O(n^{2.807})\)) or the Coppersmith-Winograd algorithm (\(O(n^{2.376})\)), see [58]. In the framework of this comparison, only algorithms for the direct inversion of a matrix are considered. Preconditioned iterative solvers or multigrid solvers are not taken into account, since their application to shell problems is often problematic and not straightforward, see e.g. [59] and [60]. Here, the Gauss-Jordan elimination algorithm is used for the inversion. The dimension of \({\varvec{K}}_{\sigma \sigma }\) is \(ncp_s\times ncp_s\), where \(ncp_s\) was defined for the continuous and the discontinuous method as well as for different locking effects in Table 2. It can be seen that for the continuous approach where \(ncp_s\) depends on the number of control points from the different stress resultant meshes, the dimension of \({\varvec{K}}_{\sigma \sigma }\) and thus the computational time increases rapidly when increasing the number of elements. On the other hand, for the discontinuous and the reconstructed approach, where static condensation is performed on the element level, the dimension of the \({\varvec{K}}_{\sigma \sigma }\) matrix is constant for a fixed polynomial degree, regardless of the number of elements. Thus, in this case the total cost for the inversion increases linearly with an increasing number of elements numel (if \(t_1\) the computational time for the inversion of \({\varvec{K}}_{\sigma \sigma }\) for one element, the total time for the inversions is \(numel\cdot t_1\)).
The computation of the new mixed stiffness matrix \({\varvec{K}}_{Mixed}\) in Eq. (37) requires the matrix multiplication of \({\varvec{K}}_{\sigma \sigma }^{-1}\), \({\varvec{K}}_{\sigma v}\) and \({\varvec{K}}_{v \sigma }\). The computational complexity for the multiplication of two \((n\times m)\) and \((m\times k)\) matrices is, when using the simplest algorithm, O(nmk). Thus, if the matrices are defined on the patch level as in the continuous approach, the computational cost for computing \({\varvec{K}}_{Mixed}\) is a lot higher than for the discontinuous approach where they are defined on the element level. The reconstructed approach, as defined in Sect. 3.4, is going to be in between the continuous and the discontinuous approach since \({\varvec{K}}_{\sigma \sigma }^{-1}\) and \({\varvec{K}}_{\sigma v}\) are defined on the element level whereas \({\varvec{K}}_{v \sigma }\) is defined on the patch level.
The resulting stiffness matrices for the continuous, discontinuous and reconstructed approach have the same dimension, however, in the first case the stiffness matrix is full, while in the last two cases the stiffness matrix is banded, see Sect. 4.4. This has an influence on the computational time for the solution of the equations. In particular, fast solvers like the pardiso solver, where only the non zero entries of the matrix are stored and used and which are running parallel can not be applied when the matrix is full. This additionally increases the total computational time for the continuous approach.
Regarding the question which of these operations is going to dominate the total computational time and which computational complexity should be expected for each method, the following has been observed:
-
Mixed Continuous method: The operations that dominate in the mixed continuous method are the inversion of \({\varvec{K}}_{\sigma \sigma }\) and the computation of \({\varvec{K}}_{v\sigma }({\varvec{K}}_{\sigma \sigma })^{-1}{\varvec{K}}_{\sigma v}\) on the patch level. The expected computational complexity is going to be a combination of the computational complexities of these operations, i.e. \(O(ncp_s^3)+O((ncp_v\cdot ndf)\cdot ncp_s^2)+O((ncp_v\cdot ndf)^2\cdot ncp_s)\) with \(ncp_s\) as defined in Table 2 for the continuous method. The values \(ncp_s\) and \(ncp_v\) depend on the polynomial degrees p, q and the number of elements per direction \(nel_x\), \(nel_y\), i.e. the total number of elements \(numel=nel_x\cdot nel_y\). In the case where the polynomial degrees are fixed and the number of elements is increased, the computational complexity can be rewritten depending on numel as \(O(numel^3)\). This cubic increase of the computational time when the number of elements is increased is going to be demonstrated in Sect. 4.4 for the case of a pinched cylinder. In Table 3 the computational complexity is defined additionally for the case that the number of elements and the polynomial degree q are constant while the polynomial degree p is changing.
-
Mixed Discontinuous method: The operations that dominate the total time are the inversion of \({\varvec{K}}_{\sigma \sigma }^e\) and the computation of \({\varvec{K}}_{v\sigma }^e({\varvec{K}}_{\sigma \sigma }^e)^{-1}{\varvec{K}}_{\sigma v}^e\) on the element level. Since these operations are carried out for each element, the computational complexity is going to be a combination of \(numel\cdot O(ncp_s^3)+numel\cdot O((nen_v\cdot ndf)\cdot (ncp_s)^2)+numel\cdot O((nen_v\cdot ndf)^2\cdot ncp_s)\), with \(ncp_s\) as defined in Table 2 for the discontinuous method. This time \(ncp_s\) as well as \(nen_v\) only depend on the polynomial degrees p, q. In the case where the polynomial degrees are fixed and the number of elements is increased, the computational complexity is going to be O(numel). This linear increase in computational time when increasing the number of elements is going to be observed in Sect. 4.4 for the case of a pinched cylinder. The computational complexity for the case where the polynomial degree q and the number of elements numel is fixed and only p is changing is given in Table 3.
-
Mixed Reconstructed method: Since in the mixed reconstructed method the inversion of \({\varvec{K}}_{\sigma \sigma }^e\) and the matrix multiplication \(({\varvec{K}}_{\sigma \sigma }^e)^{-1}{\varvec{K}}_{\sigma v}^e\) are carried out on the element level, the computational time which is going to dominate is from the matrix multiplication on the patch level in order to compute \({\varvec{K}}_{Mixed}\). The computational complexity for this is \(O((ncp_v\cdot ndf)^2\cdot ncp_s)\), where \(ncp_s\) is defined as for the continuous method in Table 2. Thus, \(ncp_s\) and \(ncp_v\) depend on the polynomial degrees p, q and the number of elements numel. In the case where the polynomial degrees are fixed and the number of elements is increased, the computational complexity can be rewritten depending on numel as \(O(numel^3)\). This is also shown in Sect. 4.4 for the case of a pinched cylinder. In Table 3 the complexity is additionally defined for the case that numel and q are constant and p is changing.
It is important to notice that the computational complexity only describes how the computational time is going to grow as the input grows. The actual value of the computational time for each method depends on the example. A case study is given in Sect. 4.4 for the pinched cylinder. Furthermore, the computational cost should always be considered in relation to the accuracy of a method as shown in Sect. 4.4.
4 Numerical examples
In this section, the presented mixed formulation with its different ways of performing the static condensation is tested and compared to other existing models. The elements and their corresponding abbreviations which are going to be used in the examples are summarized in the following
-
\(\omega \)-shell. The isogeometric 5-parameter Reissner–Mindlin shell formulation proposed by Dornisch et al. [11]. It does not include any measures against locking.
-
Mixed Conti. Mixed continuous formulation presented in Sect. 3.2.
-
Mixed Discont. Mixed Discontinuous formulation presented in Sect. 3.3.
-
Mixed Recon. Mixed reconstructed formulation as presented in Sect. 3.4.
-
AAS shell. The isogeometric Reissner–Mindlin shell formulation with adjusted approximation spaces for the displacements and the rotations proposed in [32]. The polynomial degrees \(p_u\), \(q_u\) correspond to the displacements \(u_i\) while the rotations \(\beta _{\alpha }\) are interpolated with one order lower polynomials in the relevant direction.
-
Pian/Sumihara. 4 node plane stress element based on the work of Pian and Sumihara, see [61], which uses a mixed formulation.
4.1 Cook’s membrane
In the first example, Cook’s membrane [62] is examined, which has been widely used as a benchmark example to evaluate, among other things, the sensitivity of an element to geometric distortions. It was also investigated in the original work of Pian et al. [61]. Cook’s membrane consists of a tapered panel which is clamped at one edge and subjected to a uniformly distributed shear load on the opposite edge, see Fig. 6. The material parameters are given as follows: \(E=1\), \(\nu =0.33333\), \(t=1\). The total load on the right side has the value \(F=1\). Here, the plane stress version of Cook’s membrane is considered.
The deflection of the panel is examined at two different points, the middle point A of the right edge and the lower point B of the right edge as shown in Fig. 6. As a reference solution, the result of Pian/Sumihara’s element is considered with a refinement of \(200\times 200\) elements and has a value of \(u_{2,ref}^A=23.9659\), \(u_{2,ref}^B=23.2162\), respectively. The total number of equations neq for the solution includes the total number of degrees of freedom related to displacements and rotations. It is the same for the mixed formulations, since the additional degrees of freedom related to the stress resultants are condensed out. As expected, a significant improvement is observed when using the Pian/Sumihara compared to the \(\omega \)-shell with \(p=q=1\), see Figs. 7 and 8. For \(p=q=2\) the \(\omega \)-shell has better results than the Pian/Sumihara element, which uses linear basis functions. However, both formulations are surpassed by the mixed formulations presented in this work. Namely, Mixed Discont with \(p=q=2\) is already slightly better than the \(\omega \)-shell in both points A and B. Even more accurate are Mixed Conti and Mixed Recon with \(p=q=2\). Kinks that occur in their error distributions in Figs. 7 and 8, arise because the deflection first converges from above, then crosses the reference solution to converge again from below. Overall, the mixed formulations, especially Mixed Conti and Mixed Recon, lead to very satisfying results.
4.2 Clamped plate with point load
In this example a rectangular plate is considered which is clamped at all edges and subjected to a point load at the center. The material parameters are given as: \(E=1\cdot 10^4\), \(\nu =0.3\). The plate has a length of \(L=100\) and a thickness of \(t=0.1\) and the point load at the center of the plate has a value of \(F=16.367\cdot 10^{-3}\), see Fig. 9. Due to symmetry only one quarter of the plate is modeled. Here, shear locking is expected and the aim is to validate the ability of the presented mixed formulations to alleviate this effect in comparison to another proven approach, the AAS shell, which includes adjusted approximation spaces for the interpolation of the displacements and the rotations, see [32]. For this purpose, first, the error of the center deflection is evaluated for the polynomial degrees \(p=q=2\) and \(p=q=3\). The analytical solution is set, according to the Kirchhoff-Love theory, to \(u_{3,ref}=1\), see [63]. All figures have been plotted in double logarithmic scale.
In the case of \(p=q=2\) transverse shear locking is very profound. This is visible in Fig. 10, where the \(\omega \)-shell is underestimating the deflection, leading to a high error especially for a low number of elements. The AAS shell on the other hand is much more accurate and has a constant convergence rate which indicates that it is locking free. Regarding the mixed methods, Mixed Discont is showing a slight locking behavior for a low number of elements, which is quickly overcome when increasing the elements. However, its performance is still significantly better than the \(\omega \)-shell’s. The best results are obtained with Mixed Conti and Mixed Recon, which both have a constant convergence rate. Another interesting point is that the three mixed approaches have the same starting point, since the formulations are identical for a single-element mesh.
In the second case, where the polynomial degree is increased to \(p=q=3\), a slightly different behavior can be observed, see Fig. 11. The \(\omega \)-shell does not exhibit locking as profound as in the first case since the increase of the polynomial degree is a way to reduce locking, see Sect. 1. Mixed Discont, which was significantly better than the \(\omega \)-shell for \(p=q=2\) is now only slightly improving the results. The AAS shell is again able to overcome locking as well as Mixed Conti and Mixed Recon. The latter two methods exhibit again the best behavior and their results lie very close together.
In conclusion, even though for a low polynomial degree Mixed Discont delivers good results, for higher polynomial degrees it seems that the discontinuity of the stress resultant fields hinders the complete elimination of locking. Another interesting observation that can be made is that the convergence rate of the AAS shell is lower than for all the other methods. This is due to the fact that while the polynomial degrees \(p_u\), \(q_u\) of the displacements are the same as for the other methods, the rotations \(\beta _1\), \(\beta _2\) are interpolated, in the relevant direction, with one polynomial degree less. This slows down the convergence of the method compared to the others.
As it was outlined in the work of Oesterle et al. [22], locking does not only distort the results of the displacements but also the stresses. Its effect is even more severe and visible for the stresses since oscillations occur with high amplitudes. This phenomenon is now examined for the different element types. In Figs. 12(a–e) the shear force \(q^1\) is presented for the different methods with \(p=q=2\) and \(10 \times 10\) elements. In Fig. 12(a) it can be seen that for the \(\omega \)-shell the shear force \(q^1\) exhibits a strong oscillating behavior due to locking. The amplitudes of the oscillations have even higher values than the shear force at the center of the plate where the point load is applied. On the other hand, the AAS shell in Fig. 12(b) successfully eliminates these oscillations. Regarding the mixed methods, Mixed Discont reduces the amplitudes of the oscillations, which are now more concentrated around the center of the plate, see Fig. 12(c). This makes sense since Mixed Discont was not able to completely eliminate transverse shear locking for the center deflection, see Fig. 10. Mixed Conti and Mixed Recon which led to the best results when considering the center deflection, eliminate almost all oscillations as seen in Figs. 12(d) and (e). However, compared to the AAS shell there are still some minor oscillations visible across the midlines.
4.3 Cylindrical shell strip
In this example a cylindrical shell strip that is clamped at one edge and subjected to a constant line load \({\hat{q}}\) at the other is investigated, see Fig. 13. The material parameters are \(E=1000\) and \(\nu =0\). The shell strip has a radius of \(R=10\) and a width of \(b=1\). The radial displacement \(u_{1P}\) is computed for different slenderness values R/t. Here, both membrane and transverse shear locking are expected. These locking effects depend strongly on the slenderness of the shell, i.e. they are more pronounced the thinner the structure is. Thus, locking is going to be more pronounced for higher slenderness values. A reference solution based on Bernoulli beam theory yields \(u_{ref}=0.9451\). The applied line load \({\hat{q}}=0.1\) is scaled with \(t^3\) in order to receive the same reference solution independent of the slenderness. The geometry is refined with 10 elements in circumferential direction and 1 element in axial direction.
In Fig. 14 the results are computed for the different element types. As can be seen, the \(\omega \)-shell, which first matches the reference solution for a slenderness of \(R/t=10\), quickly exhibits locking behavior, which is worsen the thinner the shell gets. To be more specific, for the case of \(p=q=2\) the radial displacement is strongly underestimated and reaches almost the value 0 for a slenderness of \(R/t=10000\). An improvement is visible when using the higher polynomial degree \(p=3\), however, locking is still present and visible for an increasing slenderness. On the other hand, Mixed Discont with \(p=q=2\) significantly improves the results compared to the \(\omega \)-shell, though locking is not completely eliminated, as can be seen for a higher slenderness. When using a higher polynomial degree \(p=3\) Mixed Discont shows a slight improvement in the results which is more visible for the highest slenderness, however, it does not reach such significant differences to the \(\omega \)-shell as for \(p=2\). Hence, as it was also observed for the previous example where only shear locking occurred, Mixed Discont should be preferred when using lower polynomial degrees. The higher the polynomial degree the smaller the improvement of the solution compared to the \(\omega \)-shell. The AAS shell, which includes a mechanism to eliminate shear locking but has nothing against membrane locking is also illustrated for a polynomial degree \(p_u=3\), \(q_u=2\) for the displacements. As can be seen, for low and medium slenderness values its behavior is very similar to the one of the \(\omega \)-shell and Mixed Discont. However, for the highest slenderness the displacement is strongly underestimated since membrane locking is more profound. Mixed Conti and Mixed Recon successfully eliminate transverse shear and membrane locking and lead to the correct displacement regardless of the slenderness.
4.4 Pinched Cylinder
This example is part of the shell obstacle course of Belytschko et al. [64] and is a good test to validate the performance of an element in the case of inextensional bending modes and complex membrane states. This numerical benchmark consists of a cylinder with a radius of \(R=300\), a length of \(L=600\) and a thickness \(t=3\). The material parameters are given as \(E=3\cdot 10^6\), \(\nu =0.3\). The cylinder has at both ends a rigid diaphragm and is subjected to a point load \(F=1\) in radial direction. Due to symmetry only one eighth of the geometry is used, see Fig. 15. The reference solution \(u_{ref} = -1.82889 \cdot 10^{-5}\) is obtained by a computation with \(100\times 100\) elements of polynomial order \(p=q=4\).
As in the previous example, membrane and shear locking are expected. This example is used to show again the ability of the proposed methods to alleviate these locking effects and in addition to take a closer look on the computational cost of each method. In Fig. 16 the error of the deflection under the point load is shown for a varying number of equations neq in double logarithmic scale. As expected, the \(\omega \)-shell strongly underestimates the deflection, especially for the lower polynomial degree \(p=q=2\). Again, the solution can be improved to a certain extent when increasing the polynomial degree to \(p=3\), \(q=2\). Mixed Discont, on the other hand, significantly improves the results compared to the \(\omega \)-shell. Even for the polynomial degree \(p=3\), \(q=2\) the improvement is clearly visible and much greater than, e.g. in the case of the clamped plate, since here, in addition to the transverse shear locking, membrane locking is alleviated. Mixed Conti and Mixed Recon lead to the best results and lie very close together. Here, in addition to the mixed continuous method with static condensation, the case of the mixed continuous method is depicted when no static condensation is performed and the full system of equations is solved with the stress resultants as additional unknowns. In this case the total number of equations is \(neq_{tot}=neq+2\cdot ncp_{11}+2\cdot ncp_{22}+ncp_{12}\), where \(ncp_{11}\) is the number of control points of the stress resultant components \(n^{11}\) and \(q^1\), \(ncp_{22}\) the number of control points of \(n^{22}\) and \(q^2\) and \(ncp_{12}\) is the number of control points of \(n^{12}\). The curve is shifted to the right and is in between Mixed Recon and Mixed Discont.
A comparison of the mixed methods proposed in this work with other existing methods against locking is depicted in Fig. 17. The chosen methods are the Non-uniform integration technique from Dornisch et al. [12], the local \({\bar{B}}\) method presented in Bouclier et al. [15] and the ANS method from Caseiro et al. [26]. The focus lies on the deformation under the point load when considering an increasing number of control points per edge. As can be seen in Fig. 17, Mixed Discont lies very close to the Non-uniform integration method from Dornisch et al. [12], which uses a carefully chosen set of integration points in order to reduce locking. Both methods have a better convergence behavior than the ANS method from Caseiro et al. [26]. More accurate results are achieved by the local \({\bar{B}}\) method from Bouclier et al. [15], which uses a local least-squares method for each element and afterwards applies the weights proposed by Mitchell et al. [56] and Govindjee et al. [57] in order to reconstruct the global variables from the local ones. However, this method is not accurate enough for a very low number of control points per edge. The best results are achieved by Mixed Conti and Mixed Recon. However, it should be mentioned here that the methods from Dornisch et al., Bouclier et al. and Caseiro et al. use in both directions quadratic basis functions. On the other hand, the mixed methods proposed here use quadratic basis functions in the axial direction whereas in circumferential direction cubic basis functions are applied. For these methods the control points per edge in Fig. 17 are the ones from the edge with cubic basis functions.
Regarding the computational cost of Mixed Conti, Mixed Discont and Mixed Recon, a comparison is made in Figs. 18 and 19 for \(p=3\), \(q=2\). The computational time which is considered here includes a) the time for inversion of \({\varvec{K}}_{\sigma \sigma }\) b) the time for the computation of \({\varvec{K}}_{Mixed}\) c) the time for triangular decomposition d) the time for the solution of the equations. Time is defined in CPU seconds on one core of an Intel®\(\text {Core}^{\text {TM}}\) i7-3520M CPU (\(\text {Core}^{\text {TM}}\)i7 \(\text {vPro}^{\text {TM}}\)).
In Fig. 18, first, a comparison of the total computational time over the number of equations neq is made between Mixed Conti and Mixed Recon. It can be seen that Mixed Conti has a rapid, almost cubic increase of the computational time when neq increases. This is in line with the observations made in Sect. 3.5. There it was mentioned that a cubic computational complexity should be expected in the case where the polynomial degrees are fixed and the number of elements is increased. Here it is also observed, as expected, that the resulting stiffness matrix is full, see Fig. 21.
On the other hand, the computational time for Mixed Recon increases much slower than for Mixed Conti. The reason for this is again explained in Sect. 3.5 with reference to the reduced matrix dimension of \({\varvec{K}}_{\sigma \sigma }\) and \({\varvec{K}}_{\sigma v}\). Furthermore, the resulting stiffness matrix is banded, as it is shown in Fig. 22, which additionally reduces the overall computational time. The best time, however, is obtained with Mixed Discont, see Fig. 19. There, an almost linear increase of the computational time over neq is depicted. This is due to the performance of the static condensation and the definition of \({\varvec{K}}_{Mixed}\) on the element level, which leads to a constant dimension of \({\varvec{K}}_{\sigma \sigma }\), \({\varvec{K}}_{\sigma v}\) and \({\varvec{K}}_{v \sigma }\) regardless of the number of elements, see Sect. 3.5. In addition, the resulting stiffness matrix is banded and has the same bandwidth as the standard displacement-based method (\(\omega \)-shell), see Fig. 20.
Considering now Fig. 16 and Figs. 18, 19 at the same time, it can be seen that in order to achieve a desired accuracy as fast as possible, it is often better to use Mixed Recon than Mixed Conti, especially for a higher neq. On the other hand, if a very large neq is considered it is even advisable to use Mixed Discont, since it is going to reduce the computational time significantly.
Here, the time depicted in Figs. 18, 19 should provide an idea on the increase of the computational time for the three different approaches. Of course, depending on how efficient the code is programmed and on the system that is used, the values for the time can slightly vary. However, the relation between the three different approaches should stay the same.
4.5 Partly clamped hyperbolic paraboloid
In the last example, the partly clamped hyperbolic paraboloid which was introduced in [65] and further investigated e.g. in [66], is considered. The geometry of the hyperbolic paraboloid is given as \(Z = X^2-Y^2\) with \((X,Y) \in [(-L/2, L/2)]^2\). The edge \(X = -L/2\) is clamped and the structure is subjected to its self-weight, see Fig. 23. Due to symmetry only one half of the shell is considered with respective symmetry boundary conditions along \(Y = 0\). The thickness of the shell is \(t=0.0001\) and the length is set to \(L = 1\). The material parameters are \(E = 2\cdot 10^{11}\), \(\nu = 0.3\) and \(\rho = 8000\). The thinnest version of this shell is chosen since it is expected that locking is going to be more severe for this case.
The aim of this example is to evaluate the two superior mixed methods, i.e. Mixed Conti and Mixed Recon, for the case of a double curved surface. In Fig. 24 the error of the vertical displacement at point P (\(X = 0.5\), \(Y = 0\), \(Z = 0.25\)) is depicted in relation to the number of equations. The plot is given in double logarithmic scale. As a reference solution, the vertical displacement obtained at point P using a \(100\times 50\) mesh of \(\omega \)-shell elements with \(p = q = 6\) is used (\(u_{3,ref}=-5.3049\cdot 10^{-1}\)). As it can be seen, the \(\omega \)-shell with polynomial degrees \(p=q=2\) and \(p=q=3\) strongly underestimates the displacement, especially for a low number of elements, due to membrane and shear locking. The AAS shell, which alleviates transverse shear locking, only improves the results for a higher number of elements since for a low number membrane locking is still profound. On the other hand, Mixed Conti and Mixed Recon strongly improve the results for a low and moderate number of elements, which indicates that both membrane and shear locking have been alleviated. However, the convergence rate of the mixed methods is lower than for the other formulations, creating a point of intersection from where the other methods lead to better results. In addition, for a high number of elements the error curves of the mixed methods seem to flatten. The reason for this is that the matrix \({\varvec{K}}_{\sigma \sigma }\), which has to be inverted, is, in this example, ill-conditioned. This has an influence on the results especially for a high number of elements. This behavior is not observed e.g. for the mixed and the local \({\bar{B}}\) method presented in [15] for a solid-shell, where thicker versions of this example were examined and a better convergence behavior was observed. The choice of a thicker shell does not improve the results. A combination of Mixed Conti or Mixed Recon for membrane locking and AAS for transverse shear locking could at least reduce this problematic and should be examined in future work.
5 Conclusion
In this work, a displacement-stress mixed method is presented in the framework of an isogeometric Reissner–Mindlin shell formulation in order to alleviate membrane and shear locking. The method was derived using the Hellinger-Reissner functional and by choosing appropriate approximation spaces for the different stress resultant components. One main issue which was discussed here, is the performance of the static condensation. Three different approaches were presented, a continuous approach which performs static condensation on the patch level, a discontinuous approach which performs static condensation on the element level and a reconstructed approach which tries to combine the advantages of the previous two approaches and uses weights for the local control variables in order to get blended global ones. The advantages and disadvantages for using each approach were outlined.
Several numerical examples were investigated in order to test the accuracy and efficiency of the different approaches. They range from a simple panel subjected to an in-plane loading to a plate and shell examples. Depending on the example, different stress resultant components were considered as additional unknowns for the mixed formulation. A comparison to existing elements with mechanisms against locking was additionally carried out. It was shown that the mixed discontinuous approach, while leading to good results for low polynomial degrees, does not improve the results as much for higher polynomial degrees. It seems that the discontinuity of the stress resultant fields hinders the alleviation of locking in those cases. On the other hand, the mixed continuous and the mixed reconstructed approaches surpassed in terms of accuracy every other formulation that was examined here. However, considering the computational effort for the continuous approach which leads to a full stiffness matrix and is computed on the patch level, the use of the reconstructed approach which leads to a banded stiffness matrix and is computed partly on the element level should be considered.
An extension of the proposed mixed formulation to nonlinear problems with large deformations is going to be the focus of future work.
References
Hughes TJR, Cottrell JA, Bazilevs Y (2005) Isogeometric analysis: CAD, finite elements, NURBS, exact geometry and mesh refinement. Comput Methods Appl Mech Eng 194:4135–4195
Gomez H, Hughes TJR, Nogueira X, Calo VM (2010) Isogeometric analysis of the isothermal Navier–Stokes–Korteweg equations. Comput Methods Appl Mech Eng 199:1828–1840
Temizer İ, Wriggers P, Hughes TJR (2011) Contact treatment in isogeometric analysis with NURBS. Comput Methods Appl Mech Eng 200:1100–1112
Kikis G, Ambati M, De Lorenzis L, Klinkel S (2021) Phase-field model of brittle fracture in Reissner–Mindlin plates and shells. Comput Methods Appl Mech Eng 373:113490
Kiendl J, Bletzinger K-U, Linhard J, Wüchner R (2009) Isogeometric shell analysis with Kirchhoff–Love elements. Comput Methods Appl Mech Eng 198:3902–3914
Benson DJ, Bazilevs Y, Hsu M-C, Hughes TJR (2011) A large deformation, rotation-free, isogeometric shell. Comput Methods Appl Mech Eng 200:1367–1378
Nguyen-Thanh N, Kiendl J, Nguyen-Xuan H, Wüchner R, Bletzinger K-U, Bazilevs Y, Rabczuk T (2011) Rotation free isogeometric thin shell analysis using PHT-splines. Comput Methods Appl Mech Eng 200:3410–3424
Duong TX, Roohbakhshan F, Sauer RA (2017) A new rotation-free isogeometric thin shell formulation and a corresponding continuity constraint for patch boundaries. Comput Methods Appl Mech Eng 316:43–83
Uhm T-K, Youn S-K (2009) T-spline finite element method for the analysis of shell structures. Int J Numer Methods Eng 80:507–536
Benson DJ, Bazilevs Y, Hsu M-C, Hughes TJR (2010) Isogeometric shell analysis: the Reissner–Mindlin shell. Comput Methods Appl Mech Eng 199:276–289
Dornisch W, Klinkel S, Simeon B (2013) Isogeometric Reissner–Mindlin shell analysis with exactly calculated director vectors. Comput Methods Appl Mech Eng 253:491–504
Dornisch W, Müller R, Klinkel S (2016) An efficient and robust rotational formulation for isogeometric Reissner–Mindlin shell elements. Comput Methods Appl Mech Eng 303:1–34
Kiendl J, Marino E, De Lorenzis L (2017) Isogeometric collocation for the Reissner–Mindlin shell problem. Comput Methods Appl Mech Eng 325:645–665
Hosseini S, Remmers JJC, Verhoosel CV, de Borst R (2013) An isogeometric solid-like shell element for nonlinear analysis. Int J Numer Methods Eng 95:238–256
Bouclier R, Elguedj T, Combescure A (2013) Efficient isogeometric NURBS-based solid-shell elements: Mixed formulation and \({\bar{B}}\)-method. Comput Methods Appl Mech Eng 267:86–110
Hosseini S, Remmers JJC, Verhoosel CV, de Borst R (2014) An isogeometric continuum shell element for non-linear analysis. Comput Methods Appl Mech Eng 271:1–22
Echter R, Bischoff M (2010) Numerical efficiency, locking and unlocking of NURBS finite elements. Comput Methods Appl Mech Eng 199:374–382
Bouclier R, Elguedj T, Combescure A (2013) On the development of NURBS-based isogeometric solid shell elements: 2D problems and preliminary extension to 3D. Comput Mech 52:1085–1112
Long Q, Bornemann PB, Cirak F (2012) Shear-flexible subdivision shells. Int J Numer Methods Eng 90:1549–1577
Echter R, Oesterle B, Bischoff M (2013) A hierarchic family of isogeometric shell finite elements. Comput Methods Appl Mech Eng 254:170–180
Beirão Da Veiga L, Hughes TJR, Kiendl J, Lovadina C, Niiranen J, Reali A, Speleers H (2015) A locking-free model for Reissner-Mindlin plates: analysis and isogeometric implementation via NURBS and triangular NURPS. Math Models Methods Appl Sci 25:1519–1551
Oesterle B, Ramm E, Bischoff M (2016) A shear deformable, rotation-free isogeometric shell formulation. Comput Methods Appl Mech Eng 307:235–255
Kiendl J, Auricchio F, Hughes TJR, Reali A (2015) Single-variable formulations and isogeometric discretizations for shear deformable beams. Comput Methods Appl Mech Eng 284:988–1004
Kiendl J, Auricchio F, Reali A (2018) A displacement-free formulation for the Timoshenko beam problem and a corresponding isogeometric collocation approach. Meccanica 53:1403–1413
Bieber S, Oesterle B, Ramm E, Bischoff M (2018) A variational method to avoid locking-independent of the discretization scheme. Int J Numer Methods Eng 114:801–827
Caseiro JF, Valente RAF, Reali A, Kiendl J, Auricchio F, Alves de Sousa RJ (2014) On the Assumed Natural Strain method to alleviate locking in solid-shell NURBS-based finite elements. Comput Mech 53:1341–1353
Caseiro JF, Valente RAF, Reali A, Kiendl J, Auricchio F, Alves de Sousa RJ (2015) Assumed Natural Strain NURBS-based solid-shell element for the analysis of large deformation elasto-plastic thin-shell structures. Comput Methods Appl Mech Eng 284:861–880
Cardoso RPR, Cesar de Sa JMA (2012) The enhanced assumed strain method for the isogeometric analysis of nearly incompressible deformation of solids. Int J Numer Methods Eng 92:56–78
Adam C, Bouabdallah S, Zarroug M, Maitournam H (2015) Improved numerical integration for locking treatment in isogeometric structural elements. Part II: Plates and shells. Comput Methods Appl Mech Eng 284:106–137
Cardoso RPR, Cesar de Sa JMA (2014) Blending moving least squares techniques with NURBS basis functions for nonlinear isogeometric analysis. Comput Mech 53:1327–1340
Beirão Da Veiga L, Buffa A, Lovadina C, Martinelli M, Sangalli G (2012) An isogeometric method for the Reissner–Mindlin plate bending problem. Comput Methods Appl Mech Eng 209–212:45–53
Kikis G, Dornisch W, Klinkel S (2019) Adjusted approximation spaces for the treatment of transverse shear locking in isogeometric Reissner–Mindlin shell analysis. Comput Methods Appl Mech Eng 354:850–870
Elguedj T, Bazilevs Y, Calo VM, Hughes TJR (2008) \({\bar{B}}\) and \({\bar{F}}\) projection methods for nearly incompressible linear and non-linear elasticity and plasticity using higher-order NURBS elements. Comput Methods Appl Mech Eng 197:2732–2762
Bouclier R, Elguedj T, Combescure A (2012) Locking free isogeometric formulations of curved thick beams. Comput Methods Appl Mech Eng 245–246:144–162
Greco L, Cuomo M, Contrafatto L, Gazzo S (2017) An efficient blended mixed B-spline formulation for removing membrane locking in plane curved Kirchhoff rods. Comput Methods Appl Mech Eng 324:476–511
Thomas DC, Scott MA, Evans JA, Tew K, Evans EJ (2015) Bézier projection: A unified approach for local projection and quadrature-free refinement and coarsening of NURBS and T-splines with particular application to isogeometric design and analysis. Comput Methods Appl Mech Eng 284:55–105
Miao D, Borden MJ, Scott MA, Thomas DC (2018) Bézier \({\bar{B}}\) projection. Comput Methods Appl Mech Eng 335:273–297
Zou Z, Scott MA, Miao D, Bischoff M, Oesterle B, Dornisch W (2020) An isogeometric Reissner-Mindlin shell element based on Bézier dual basis functions: Overcoming locking and improved coarse mesh accuracy. Comput Methods Appl Mech Eng 370:113283
Greco L, Cuomo M, Contrafatto L (2018) A reconstructed local \({\bar{B}}\) formulation for isogeometric Kirchhoff-Love shells. Comput Methods Appl Mech Eng 332:462–487
Hu P, Hu Q, Xia Y (2016) Order reduction method for locking free isogeometric analysis of Timoshenko beams. Comput Methods Appl Mech Eng 308:1–22
Hu Q, Xia Y, Natarajan S, Zilian A, Hu P, Bordas SPA (2020) Isogeometric analysis of thin Reissner–Mindlin shells: locking phenomena and B-bar method. Comput Mech 65:1323–1341
Antolin P, Bressan A, Buffa A, Sangalli G (2017) An isogeometric method for linear nearly-incompressible elasticity with local stress projection. Comput Methods Appl Mech Eng 316:694–719
Antolin P, Kiendl J, Pingaro M, Reali A (2020) A simple and effective method based on strain projections to alleviate locking in isogeometric solid shells. Comput Mech 65:1621–1631
Simo JC, Hughes TJR (1986) On the Variational Foundations of Assumed Strain Methods. J Appl Mech 53:51–54
Bouclier R, Elguedj T, Combescure A (2015) An isogeometric locking-free NURBS-based solid-shell element for geometrically nonlinear analysis. Int J Numer Methods Eng 101:774–808
Rafetseder K, Zulehner W (2019) A new mixed approach to Kirchhoff-Love shells. Comput Methods Appl Mech Eng 346:440–455
Taylor RL (2011) Isogeometric analysis of nearly incompressible solids. Int J Numer Methods Eng 87:273–288
Fahrendorf F, Morganti S, Reali A, Hughes TJR, De Lorenzis L (2020) Mixed stress-displacement isogeometric collocation for nearly incompressible elasticity and elastoplasticity. Comput Methods Appl Mech Eng 369:113112
Hellinger E (1914) Die allgemeinen Ansätze der Mechanik der Kontinua, Enzyklopädie der Mathematischen Wissenschaften, 601–694. Teubner, Leipzig
Reissner E (1950) On a variational theorem in elasticity. J Math Phys 29:90–95
Andelfinger U (1991) Untersuchungen zur Zuverlässigkeit hybrid-gemischter Finiter Elemente für Flächentragwerke (Ph.D. thesis), Institute for Structural Mechanics - University of Stuttgart
Babuška I, Aziz A (1972) Survey lectures on the mathematical foundations of the finite element method, The mathematical foundations of the finite element method with applications to partial differential equations, 3–363. Academic Press, New York
Brezzi F (1974) On the existence, uniqueness and approximation of saddle-point problems arising from Lagrangian multipliers. RAIRO Analyse Numérique 8:129–151
Piegl L, Tiller W (1997) The NURBS Book, second ed., In: Monographs in Visual Communications, Springer, Berlin
Cottrell JA, Hughes TJR, Bazilevs Y (2009) Isogeometric analysis: toward integration of CAD and FEA. Wiley, Chichester
Mitchell TJ, Govindjee S, Taylor RL (2011) A method for enforcement of Dirichlet boundary conditions in isogeometric analysis. In: D. Mueller-Hoeppe, S. Loehnert, S. Reese (Eds.), Recent Developments and Innovative Applications in Comput. Mech., 283–293. Springer-Verlag, Berlin
Govindjee S, Strain J, Mitchell TJ, Taylor RL (2012) Convergence of an efficient local least squares fitting method for bases with compact support. Comput Methods Appl Mech Eng 213–216:84–92
Petković MD, Stanimirović PS (2009) Generalized matrix inversion is not harder than matrix multiplication. J Comput Appl Math 230:270–282
Gee M, Ramm E, Wall WA (2005) Parallel multilevel solution of nonlinear shell structures. Comput Methods Appl Mech Eng 194:2513–2533
Saint-Georges P, Warzee G, Notay Y, Beauwens R (1999) Problem-dependent preconditioners for iterative solvers in FE elastostatics. Comput Struct 73:33–43
Pian THH, Sumihara K (1984) Rational approach for assumed stress finite elements. Int J Numer Methods Eng 20:1685–1695
Cook RD (1974) Improved two-dimensional finite element. J Struct Div ASCE 100:1851–1863
Timoshenko S (1940) Theory of Plates and Shells. In: Engineering Societies monograph, McGraw-Hill Book Company, New York
Belytschko T, Stolarski H, Liu WK, Carpenter N, Ong JS-J (1985) Stress projection for membrane and shear locking in shell finite elements. Comput Methods Appl Mech Eng 51:221–258
Chapelle D, Bathe K-J (1998) Fundamental considerations for the finite element analysis of shell structures. Comput Struct 66:19–36
Bathe K-J, Iosilevich A, Chapelle D (2000) An evaluation of the MITC shell elements. Comput Struct 75:1–30
Acknowledgements
The financial support of the DFG (German Research Foundation) under Grant No. KL1345/7-1 is gratefully acknowledged by the first author.
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Kikis, G., Klinkel, S. Two-field formulations for isogeometric Reissner–Mindlin plates and shells with global and local condensation. Comput Mech 69, 1–21 (2022). https://doi.org/10.1007/s00466-021-02080-8
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00466-021-02080-8


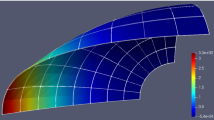

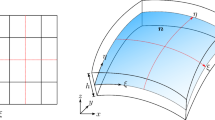


 ) and the stress resultant components
) and the stress resultant components  ),
),  ) and
) and  )
)




















