Mixed peridynamic formulations for compressible and incompressible finite deformations

Abstract

The large flexibility of meshfree solution schemes makes them attractive for many kinds of engineering applications, like Additive Manufacturing or cutting processes. While numerous meshfree methods were developed over the years, the accuracy and robustness are still challenging and critical issues. Stabilization techniques of various kinds are typically used to overcome these problems, but often require the tuning of unphysical parameters. The Peridynamic Petrov–Galerkin method is a generalization of the peridynamic theory of correspondence materials and offers a stable and robust alternative. In this work, the stabilization free approach is extended to three dimensional problems of finite elasticity. Locking-free mixed formulations for nearly incompressible and incompressible materials are developed and investigated in convergence studies. In general, an efficient implicit quasi-static framework based on Automatic Differentiation is presented. The numerical examples highlight the convergence properties and robustness of the proposed formulations.

1 Introduction

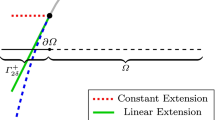
In last decades many different methods for the approximate solution of partial differential equations were developed and applied to various engineering problems. The Finite Element Method (FEM) is well accepted for the solution of a wide range of problems in industry. However, for complex evolving domains it is advantageous to have a more flexible discretization scheme. For instance in the fast growing field of Additive Manufacturing like Selective Laser Melting, the production process is accompanied by evolving surfaces, large deformations and phase changes. A promising discretization approach consists in meshfree methods which include the Smoothed Particle Hydrodynamics (SPH) introduced by Lucy [24] and Gingold and Monaghan [13], the Reproducing Kernel Particle Method (Liu et al. [23]), the Element Free Galerkin method (Belytschko et al. [2]) and the more recent non-ordinary state-based peridynamic correspondence approach (see Silling et al. [31]) where each of them has their specific advantages and drawbacks. Peridynamics is a non-local field theory based on integro-differential equations which is idealized and widely used to model discontinuities as occurring in fracture simulations (see e.g. Silling [28] and Silling [29]) and in recent years the area of applications rapidly increased. For a review on Peridynamics the reader is referred to Javili et al. [17].

Besides the advantage of flexibility in discretization, the efficiency and accuracy of the meshbased FEM is hard to achieve. Some reasons are consistency, stability and the imposition of boundary conditions which are challenging aspects in the scope of meshfree methods. Rank deficiency which result in spurious zero or low energy modes is often addressed by corrections to gain stability (see e.g. the works of Littlewood [22], Breitenfeld et al. [5], Silling [30], Weißenfels and Wriggers [35]). However, unphysical parameters have to be determined that can be case sensitive and reduce the accuracy of the solution.

In the context of the peridynamic correspondence model, approaches were developed to overcome the rank deficiency without the use of such corrections in the last years. Tupek and Radovitzky [33] proposed an extended correspondence formulation based on Seth-Hill strains. A higher order approximation using modified weight functions has been developed in Yaghoobi and Chorzepa [38]. Chowdhury et al. [11] adressed the low-energy modes by means of separation of the so-called family which is the neighborhood of a particle (see Fig. 1) into subdivisions. The use of bond-level and bond-associated deformation gradients is studied in Breitzman and Dayal [6], Chen [9], Gu et al. [14], Madenci et al. [27] and Chen and Spencer [10]. A stress-point method to overcome the rank deficiency was presented in Luo and Sundararaghavan [25]. Hillman et al. [15] unified the peridynamic deformation gradient with the implicit gradient approximation, studied the convergence of the differential operations and proposed a reproducing kernel peridynamic method.

In a further approach the Peridynamic Petrov–Galerkin (PPG) method was introduced, see Bode et al. [4]. It is based on the principle of virtual displacements applied to the peridynamic momentum equation and depicts good accuracy and suffers no oscillations when applied within large deformations. In case of linear ansatz functions it reduces to the commonly used correspondence formulation of Peridynamics. Hence it is applicable to any local material models. In addition, the Petrov–Galerkin formulation enables to a certain extent knowledge transfer from the well established FEM.

In this paper the PPG method is extended to three dimensions and more efficient interpolating Moving Least Square shape functions are utilized. Furthermore, the regime of incompressible material behavior is investigated. Like in the FEM, pure displacement-based peridynamic approaches exhibit locking phenomenas as e.g. a stiffer response or divergence. Mixed displacement-pressure formulations are known to overcome these problems and possess good convergence rates (see Simo et al. [32]). Therefore, mixed PPG formulations for weakly compressible and incompressible material behavior are presented and the convergence and robustness is compared to Finite Elements. The resulting formulations can be viewed as a non-ordinary state-based correspondence model incorporating local constraint equations by means of Lagrange multipliers. The structure of the paper is as follows. The governing equations for nonlinear elasticity are presented in Sect. 2. Section 3 presents the PPG discretization and formulates the mixed formulations based on Automatic Differentiation (AD). Numerical convergence studies for compressible and incompressible benchmark test as well as a numerical inf-sup test are considered in Sect. 4. The paper closes with concluding remarks in Sect. 5.

2 Governing equations for finite elasticity

The peridynamic correspondence theory is based on the nonlocal peridynamic momentum equation. However, it can be applied to constitutive models from the local theory. Therefore, the local kinematic description of the continuum can be used (see e.g. Wriggers [36] and Holzapfel [16]). For an elastic body $\Omega$ the current position of a material point $\mathbf {x}$ is given by

$$\begin{aligned} \mathbf {x} = \mathbf {X} + \mathbf {u} \end{aligned}$$

(1)

with the initial position $\mathbf {X}$ and the displacement $\mathbf {u}$. The deformation gradient is defined as

$$\begin{aligned} \mathbf {F} = \frac{\partial \mathbf {x}}{\partial \mathbf {X}} = {\text {Grad}}\,\mathbf {x} \ \ \ \ \ \text {with}\ \ \ \ \ J = {\text {det}}\,\mathbf {F}\, \end{aligned}$$

(2)

where the Jacobian J describes the volumetric part. We also define the right Cauchy-Green tensor $\mathbf {C}$ by

$$\begin{aligned} \mathbf {C} = {\mathbf {F}}^T \cdot {\mathbf {F}} \end{aligned}$$

(3)

and its isochoric part as

$$\begin{aligned} \mathbf {C}^{iso} = J^{-\frac{2}{3}} \mathbf {C}. \end{aligned}$$

(4)

The body $\Omega$ is subject to the momentum equation at each particle $\mathbf {X}$. It states in the non-local peridynamic form

$$\begin{aligned} \int _{H} \left( \mathbf {t} - \mathbf {t}' \right) \ d H + \rho _{0} \overline{\mathbf {b}} = \mathbf {0} \end{aligned}$$

(5)

as an integral over momentum transfers with neighboring material points. Herein, $\mathbf {t}$ and $\mathbf {t}'$ are called the pairwise force densities. While $\mathbf {t}$ stands for the force acting on $\mathbf {X}$ exerted by a neighboring material point $\mathbf {X}'$ inside the family H (see Fig. 1), the pairwise part $\mathbf {t}'$ arises from the collective deformation of family $H'$ of $\mathbf {X}'$ and is considered by means of Newton’s third law. $\rho _{0}\overline{\mathbf {b}}$ is a body force acting on $\mathbf {X}$. The local counterpart is defined with respect to the initial configuration as

$$\begin{aligned} {\text {Div}}\,\mathbf {P} + \rho _{0} \overline{\mathbf {b}} = \mathbf {0} \end{aligned}$$

(6)

with the first Piola–Kirchhoff stress tensor $\mathbf {P}$. A correspondence formulation $\mathbf {t} = \mathbf {t} \left( \mathbf {P}\right)$ links the first Piola–Kirchhoff stress with a state of pairwise force densities in the discretized form (see for instance Silling et al. [31], Madenci and Oterkus [26] and Bode et al. [4]). By applying the principle of virtual displacements on equations (5) and (6) the peridynamic virtual strain energy yields

$$\begin{aligned} \int _{H} \left( \mathbf {t} - \mathbf {t}' \right) \ d H \cdot \delta \mathbf {u} + \rho _{0} \overline{\mathbf {b}}\cdot \delta \mathbf {u} = 0 \end{aligned}$$

(7)

and the local counterpart excluding surface forces

$$\begin{aligned} -\mathbf {P}:\delta \mathbf {F} + \rho _{0} \overline{\mathbf {b}}\cdot \delta \mathbf {u} = 0. \end{aligned}$$

(8)

Using the correspondence formulation, the constitutive laws can be based on the local theory for elastic finite deformations. In case of incompressible material behavior the Neo-Hookean strain energy function

$$\begin{aligned} \Psi ^{i} = \frac{\mu }{2}\left( {\text {tr}}\left( \mathbf {C}^{iso}\right) -3\right) \end{aligned}$$

(9)

is used and in case of compressible material behavior extended to

$$\begin{aligned} \Psi = \frac{\mu }{2}\left( {\text {tr}}\left( \mathbf {C}^{iso}\right) -3\right) + \frac{K}{4} \left( J-1-2\ln {J}\right) . \end{aligned}$$

(10)

The bulk modulus K and the shear modulus $\mu$ can be calculated from the Young’s modulus E and the Poisson’s ratio $\nu$ or lame constants $\lambda$ and $\mu$. The derivation of the strain energy function with respect to the deformation gradient yields the first Piola–Kirchhoff stress

$$\begin{aligned} \mathbf {P} = \frac{\partial \Psi }{\partial \mathbf {F}}. \end{aligned}$$

(11)

3 Formulation of the peridynamic Petrov–Galerkin method

The PPG method is based on a subdivision of the body $\Omega$ into a finite number of discrete particles. Considering collocation, these particles serve both as material points and nodes (see Fig. 1). The connectivity between particles is established by so-called families which define the surrounding neighborhood of each particle. A particle k interacts only with the neighbors inside its family $H^{k}$. The local linear momentum preservation is ensured if these interactions are always pairwise, i.e. each particle j inside family $H^{k}$ has to have particle k in its own family $H^{j}$. Such a pairwisity is usually fulfilled by having spherical families with a radius of the so-called horizon $\delta$ which is constant inside body $\Omega$. However, the PPG method is not restrictive to spherical family shapes. In this work, for irregular particle distributions the families are made up of the nearest $N=20$ particles (for three dimensions). To ensure pairwisity, all pairwise particles which are not already inside a family are added afterwards. In case of uniform particle patterns, a horizon $\delta$ of 1.51 times the particle spacing is used.

Fig. 1

The connectivity between particles with their representative volume V is established by the family H and the bonds $\Delta \mathbf {X}$. Internal forces acting on a particle are considered in terms of the pairwise force densities $\mathbf {t}$

The non-local kinematics of a family $H^{k}$ consists of the bonds $\Delta \mathbf {X}^{kj} = \mathbf {X}^{j} - \mathbf {X}^{k}$, i.e. the distance vector from particle k to its neighbor j. Analogously, the deformed bonds $\Delta \mathbf {x}^{kj}=\mathbf {x}^{j}-\mathbf {x}^{k}$ and the displacement differences $\Delta \mathbf {u}^{kj} = \mathbf {u}^{j}-\mathbf {u}^{k} = \Delta \mathbf {x}^{kj} - \Delta \mathbf {X}^{kj}$ are defined. For enforcing local constitutive laws, the non-local kinematics have to be transformed to a local defined measure like the deformation gradient $\mathbf {F}$. This transformation is performed by the following approximations for the actual and virtual deformation gradient:

$$\begin{aligned} \mathbf {F}^{kj}= & {} \mathbf {1} + \sum _{i=0}^{N^k} \mathbf {u}^{i} \otimes \frac{\partial N_{u}^{kji}}{\partial \mathbf {X}} \ \ \ \ \ \text {and}\ \nonumber \\ \ \ \ \ \delta \mathbf {F}^{k}= & {} \sum _{j=0}^{N^k} \Delta \delta \mathbf {u}^{kj} \otimes \frac{\partial N_{\delta u}^{kkj}}{\partial \mathbf {X}} \end{aligned}$$

(12)

where $F^{kj}$ stands for the deformation gradient at the position of particle j with respect to family $H^{k}$. As the virtual deformation gradient is evaluated only at the master particle k a single superscript is used. The i-th ansatz function of family $H^{k}$ at the position of particle j is written as $N^{kji}$, where the subscript u and $\delta u$ stand for the trial and test shape function, respectively. With this ansatz, the aforementioned correspondence formulation can be derived. It relates the first Piola–Kirchhoff stress tensor $\mathbf {P}^{kj}$ from a local material model to the non-local pairwise force densities $\mathbf {t}^{kj}$. This relation is based on the equivalence of the virtual work of Eq. (7) and (8) and states

$$\begin{aligned} \mathbf {t}^{kj} = -\frac{1}{V^{k}} \mathbf {P}^{kj} \cdot \frac{\partial N_{\delta u}^{jjk}}{\partial \mathbf {X}}. \end{aligned}$$

(13)

Inserting the pairwise force density relation into the peridynamic momentum equation and integrating over the particle volume $V^{k}$ yields the discretized form in the PPG method at particle level

$$\begin{aligned} \sum _{j=0}^{N^{k}} \left( V^{j} \mathbf {P}^{kj}\cdot \frac{\partial N_{\delta u}^{jjk}}{\partial \mathbf {X}} - V^{k} \mathbf {P}^{jk}\cdot \frac{\partial N_{\delta u}^{kkj}}{\partial \mathbf {X}} \right) = \rho _{0}^{k} \overline{\mathbf {b}}^{k} V^{k}. \end{aligned}$$

(14)

3.1 PPG shape functions

The choice of shape functions for test and trial functions is a crucial point in the PPG method. It can decide over rank deficiency, stability, the accurate imposition of Dirichlet and Neumann boundaries and the convergence rate. In Bode et al. [4] it was shown that in case of a linear Weight Least Square (WLS) functions, the PPG method reduces to the non-ordinary state based peridynamic method for correspondence materials.

The key features for convergence to an accurate solution consists of consistency, i.e. the property to exactly reproduce a polynomial space (see Krongauz and Belytschko [20] and Belytschko et al. [3]). Further necessary requirements on discretization schemes consist in the absence of rank deficiency and an exact imposition of boundary conditions. While at least linear consistency is fulfilled by most meshfree shape functions, the second and third aspects are more challenging for meshfree methods. Rank deficiency and the resulting low-energy modes are oftentimes addressed by stabilization techniques which usually include a tuning parameter and lead to an artificial stiffness. In general the PPG method does not need a stabilization, provided that the trial function ansatz is not linear which would lead to a constant deformation gradient inside a family. This is the case for many shape functions as e.g. second order WLS functions, Moving Least Square (MLS) functions, Local Maximum Entropy (LME) approximants (see Arroyo and Ortiz [1]).

Regarding the exact imposition of boundary conditions, one has to differentiate between Dirichlet and Neumann boundaries. The latter one can be imposed accurately by fulfilling the integration constraint (see Bode et al. [4] and Weißenfels [34]). The peridynamic form states

$$\begin{aligned} \sum _{j=0}^{N^k} V^k \frac{\partial N^{kkj}_{\delta u} }{\partial \mathbf {X}} - V^j \frac{\partial N^{jjk}_{\delta u} }{\partial \mathbf {X}} = \mathbf {N}^k A^k = \left\{ \begin{array}{ll} \mathbf {0} &{}\text {on}\ \Omega \\ A^k \mathbf {N}^k &{}\text {on}\ \partial \Omega \end{array} \right. \,,\nonumber \\ \end{aligned}$$

(15)

where $A^k$ is the surface of particle k. This value is only non zero, if the particle is located at the surface of the body $\Omega$. The vector $\mathbf {N}^{k}$ is the corresponding unit normal vector at the boundary node. Dirichlet boundaries can be imposed accurately by using the Kronecker-$\delta$ property of the test functions (see also Bode et al. [4]). In the following, an interpolating MLS approach based on differences is proposed.

WLS and MLS are fitting techniques for arbitrary point clouds (see Lancaster and Salkauskas [21]). Within these techniques, a field is approximated by a linear combination of shape functions, like for instance monomials. The coefficients are determined in such a way that the squared error at the data points is minimized. In case of WLS the errors are weighted statically and in case of MLS dependent on the evaluation point. For the evaluation at particle j inside family $H^{k}$ this is performed via the minimization of the functional

$$\begin{aligned} E^{kj} := \sum _{i=0}^{N^k} \omega ^{ji} \left( \epsilon ^{ki}\right) ^2 V^i \end{aligned}$$

(16)

where the approximation errors $\epsilon ^{ki} = \Delta {\hat{u}}^{k}\left( \Delta \mathbf {X}^{kj}\right) - \Delta u^{ki}$, volume weights $V^{i}$ and distance weights $\omega ^{ji}$ were introduced. As in the PPG method shape functions are only used to approximate derivatives, the fitting can be done with respect to differences which leads to an enforcement of the interpolation at the reference particle. In a MLS sense, this perspective $\mathbf {X}^{j}$ can move with the according weights $\omega ^{ji}$ which results in the ansatz monomials of first order

$$\begin{aligned} \mathbf {p}^{ji} = \left[ \Delta X^{ji}, \Delta Y^{ji}, \Delta Z^{ji}\right] ^{T}. \end{aligned}$$

(17)

The distance weights $\omega ^{ji}$ regulate the influence of the neighboring particles. A localized fitting can be introduced by a weighting function that decreases with increasing distance. The weights can be set to

$$\begin{aligned} \omega ^{ji}_{p} = \left\{ \begin{array}{ll} \frac{1}{\left( \Delta \mathbf {X}^{ji} \cdot \Delta \mathbf {X}^{ji}\right) ^{p}} &{} \forall \ i \ne j \\ 0 &{}\forall \ i = j \\ \end{array} \right. \end{aligned}$$

(18)

with $p=2$, or in case of regular meshes even more localized with $p=5$. From Eq. (16), applied to the displacement difference field in family $H^{k}$, follows the approximation

$$\begin{aligned}&\Delta \mathbf {u}^{kj} = \sum _{i=0}^{N^k} \left[ \omega ^{ji} \mathbf {p}^{ji} \cdot {\mathbf {M}^{kj}}^{-1} \cdot \mathbf {p}^{jj} V^i \right] \Delta \mathbf {u}^{ki}\nonumber \\&\quad = \sum _{i=0}^{N^k} N^{kji} \Delta \mathbf {u}^{ki} \end{aligned}$$

(19)

where $N^{kji}$ is the i-th ansatz function of family $H^{k}$ evaluated at particle j. The mass matrix, which is also called shape tensor in Peridynamics or correction matrix in SPH, ensures consistency up to the order of completeness of the ansatz monomials. It depends on the position inside the family and is given by

$$\begin{aligned} {\mathbf {M}}^{kj} = \sum _{i=0}^{N^k} \omega ^{ji}\ \mathbf {p}^{ji} \otimes \mathbf {p}^{ji} V^i. \end{aligned}$$

(20)

Utilizing zeroth order consistency, to the gradient of the displacement difference approximation (19) yields the standard approach for the displacement gradient with respect to the reference configuration

$$\begin{aligned} {\text {Grad}}^{kj} \mathbf {u} = \sum _{i=0}^{N^{k}} \Delta \mathbf {u}^{ki} \otimes \frac{\partial N^{kji}}{\partial \mathbf {X}} = \sum _{i=0}^{N^k} \mathbf {u}^{i} \otimes \frac{\partial N^{kji}}{\partial \mathbf {X}}. \end{aligned}$$

(21)

The gradient of the shape functions $\frac{\partial N^{kji}}{\partial \mathbf {X}}$ at data points follows from (19) and the application of the zeroth order consistency condition

$$\begin{aligned} \frac{\partial N^{kji}}{\partial \mathbf {X}} = \left\{ \begin{array}{ll} \omega ^{ji} V^i \mathbf {p}^{ji} \cdot {\mathbf {M}^{kj}}^{-1} \cdot \frac{\partial \mathbf {p}^{jj}}{\partial \mathbf {X}} &{} \forall \ i \ne j \\ - \sum _{l=0, l\ne j}^{N^k} \frac{\partial N^{kjl}}{\partial \mathbf {X}} &{}\forall \ i = j \\ \end{array} \right. . \end{aligned}$$

(22)

3.2 Mixed PPG formulations

By integrating the peridynamic virtual strain energy (7) over the body $\Omega$, a general weak form can be formulated:

$$\begin{aligned} \delta U = \int _{\Omega } \left[ \int _{H} \left( \mathbf {t} - \mathbf {t}' \right) \ d H - \rho _{0}\overline{\mathbf {b}}\right] \cdot \delta \mathbf {u} \ d\Omega . \end{aligned}$$

(23)

With this an implicit quasi-static framework can be derived from the discretized form by separating the body $\Omega$ into a set of $n^{p}$ particles with the corresponding volume of $V^{k}$. Then, the approximate weak form yields

(24)

The discretized virtual strain energy $\delta W^{k}$ is based on the concept of pairwisity exploiting the correspondence formulation of Eq. (13)

$$\begin{aligned} \delta W^{k}= & {} \sum _{j=1}^{N^{k}} V^{j} \left( \mathbf {t}^{kj} - \mathbf {t}^{jk}\right) \cdot \delta \mathbf {u}^{k} = - \sum _{j=1}^{N^{k}} V^{j} \mathbf {t}^{kj} \cdot \Delta \delta \mathbf {u}^{kj} \nonumber \\= & {} \sum _{j=1}^{N^{k}} V^{j} \left( \frac{1}{V^{k}} \mathbf {P}^{kj} \cdot \frac{\partial N^{jjk}_{\delta \mathbf {u}}}{\partial \mathbf {X}} \right) \cdot \Delta \delta \mathbf {u}^{kj}. \end{aligned}$$

(25)

Utilizing the extended strain energy function (10) yields a displacement based PPG formulation. In case of using MLS trial and test functions of first order, this formulation will be termed “PPG Unl”, since the approach for the actual displacements $\mathbf {u}$ is nonlinear (nl).

Next, a mixed displacement-pressure-dilation formulation motivated by the Q1P0/H1P0 finite elements (see Simo et al. [32]) is presented. It is based on an additive split of the strain energy into an isochoric and volumetric part which leads to an additive split of the pairwise force densities

$$\begin{aligned} \mathbf {t}^{kj} = \mathbf {t}^{kj}_{iso} + \mathbf {t}^{kj}_{vol}. \end{aligned}$$

(26)

The isochoric part is handled analogously to the pure displacement based formulation using the isochoric Neo-Hookean strain energy function of Eq. (9). The volumetric part is now derived from the Hu-Washizu potential

$$\begin{aligned} U_{h\ vol} = \int _{\Omega } \left[ p \left( J - \Theta \right) + \frac{K}{2} \left( \Theta - 1\right) ^{2}\right] \ d\Omega . \end{aligned}$$

(27)

By applying particle discretization the discrete form states

(28)

where the pressure $p^{k}$ and the dilation $\Theta ^{k}$ are independent variables of particle k. The resulting formulation will further be denoted as “PPG UnlP0”. In case of incompressible material behavior, i.e. $\nu = 0.5$, the dilation $\Theta ^{k} =1$ which yields the “PPG IUnlP0” formulation. Both formulations satisfy the conservation of linear momentum as the volumetric residual results in pairwise force densities $\mathbf {t}^{kj}_{vol}$. A proof is provided in “Appendix A”, which also shows the additive split of the pairwise force densities into

$$\begin{aligned}&\mathbf {t}^{kj}_{iso} = -\frac{1}{V^{k}} \mathbf {P}^{kj}_{iso} \cdot \frac{\partial N_{\delta u}^{jjk}}{\partial \mathbf {X}} \ \ \ \ \ \text {and}\nonumber \\&\mathbf {t}^{kj}_{vol} = - \frac{1}{V^{k}} \mathbf {P}_{vol}^{j} \cdot \frac{\partial N^{jjk}}{\partial \mathbf {X}}. \end{aligned}$$

(29)

Table 1 summarizes the presented formulations and abbreviations.

Table 1 Overview of abbreviations and involved equations of the presented PPG formulations

3.3 Residual and tangent

The weak form (24) is minimized by means of the Newton-Raphson method. Therefore, the global residual vector and the tangent matrix can be either computed numerically (see e.g. Brothers et al. [7]) or by a consistent linearization (see Bode et al. [4]). In this work, the residual and tangent matrix are assembled family-wise where the linearization is performed with the symbolic Automatic Differentiation (AD) tool AceGen, see Korelc and Wriggers [19]. Hence, for the PPG Unl formulation the residual and tangent matrix follows

$$\begin{aligned} \mathbf {R}^{H^{k}}=\frac{\partial \delta U_{h}^{k}}{\partial \delta \mathbf {u}^{H^{k}}}\ \ \ \ \ \text {and}\ \ \ \ \ \mathbf {K}^{H^{k}}=\frac{\partial \mathbf {R}^{H^{k}}}{\partial \mathbf {u}^{H^{k}}}. \end{aligned}$$

(30)

Note, that the first derivation of the weak form leads back to the residual of Eq. (14). In addition to the family-wise residual and stiffness matrix (30), the part due to volumetric forces for the mixed PPG UnlP0 and PPG IUnlP0 formulations can again be derived with AD to

$$\begin{aligned} \mathbf {R}_{vol}^{H^{k}}= & {} \frac{\partial U_{h\ vol}^{k}}{\partial \mathbf {p}^{k}}\ \ \ \ \ \text {and}\ \ \ \ \ \mathbf {K}_{vol}^{H^{k}}=\frac{\partial \mathbf {R}_{vol}^{H^{k}}}{\partial \mathbf {p}^{k}}\ \ \ \ \ \text {with}\ \ \ \ \ \nonumber \\ \mathbf {p}^{k}= & {} \left[ {\mathbf {u}^{H^{k}}}^{T},p^{k},\Theta ^{k} \right] ^{T} . \end{aligned}$$

(31)

Therefore, the family-wise stiffness matrix for the PPG UnlP0 and PPG IUnlP0 approach yields

$$\begin{aligned} \mathbf {K}^{H^{k}}_{PPG\ UnlP0}= & {} \left( \begin{array}{ccc} \mathbf {K}_{uu} &{} \mathbf {K}_{up} &{} \mathbf {0} \\ \mathbf {K}_{pu} &{} 0 &{} K_{p \Theta } \\ \mathbf {0} &{} K_{\Theta p} &{} K_{\Theta \Theta } \end{array} \right) \ \ \ \ \ \text {and}\ \ \ \ \nonumber \\ \mathbf {K}^{H^{k}}_{PPG\ IUnlP0}= & {} \left( \begin{array}{cc} \mathbf {K}_{uu} &{} \mathbf {K}_{up} \\ \mathbf {K}_{pu} &{} 0 \\ \end{array} \right) . \end{aligned}$$

(32)

In the first case on the left of Eq. (32), the pressure and the dilation can be eliminated at family-level by means of static condensation which leads to a higher efficiency and a better conditioning.

4 Numerical examples

In this section, the new formulations are tested by means of several examples. First, the locking behavior is investigated. Second, the convergence is compared to FEM solutions for regular and irregular particle distributions. Third, the robustness is demonstrated in a torsion test and finally, a numerical inf-sup test is performed.

4.1 Punch problem

The first example investigates a punch into a block of solid material as shown in Fig. 2 (cf. Wriggers [37]). The block has the dimensions $0.1\,m\times 0.1\,m\times 0.05\,m$ and a Young’s modulus of $E = 4.8293\,\frac{N}{m^{2}}$. The locking behavior is investigated for four different Poisson’s ratios of $\nu = \left\{ 0.4,\, 0.499,\, 0.49999,\, 0.5 \right\}$. A load of $q=9\,\frac{N}{m^{2}}$ is applied in negative z-direction on an additional layer of particles (red). These particles are fixed in x- and y-directions (see also Fig. 2). At the bottom an additional layer of wall particles (purple) is used to model a wall where the z-direction is fixed. Free moving particles are colored green. When applying the load, the block undergoes large deformations. In Fig. 2 the final configuration as well as a cross section is depicted for the PPG IUnlP0 formulation with a discretization of 24948 particles. The displacement in z-direction is colored, see legend in Fig. 2d.

Fig. 2

On the left: Geometry and boundary conditions of the punch problem. Dirichlet boundary conditions are prescribed for purple particles and external forces are applied to the red particles. On the right: Exemplary deformed configuration and cross section for $N = 9$ for the PPG IUnlP0 formulation. The vertical displacement in meter is colored

The convergence of the nodal displacement in z-direction in the middle of the block at the upper surface is analyzed. Figure 3 depicts the convergence behavior for the different formulations using MLS1 with $\omega _5$ as both test and trial functions, see Table 1. The displacement based PPG Unl formulation is only pictured for a Poisson’s ratio of $\nu = 0.4$ as it fails to converge or does almost not deform due to locking in the incompressible regime. However, the PPG UnlP0 formulation as well as the incompressible PPG IUnlP0 formulation are free of locking and converge at about the same rate as those of FEM H1P0.

Fig. 3

Convergence study: The minimal vertical displacement is plotted over the number of nodes. Different approaches of the PPG method are compared to the mixed H1P0 Finite Element for various Poisson’s ratios

4.2 Cook’s membrane problem

The second example is Cook’s membrane problem. As depicted in Fig. 4, a tapered cantilever beam is clamped on the left (fixed purple particles) and loaded at the right (red particles) in a single step with a load of $q=4\,\frac{N}{m^{2}}$ in positive z-direction. The block is modeled as a Neo-Hookean solid with the Lame constants $\mu =40\,\frac{N}{m^{2}}$ and $\lambda = 100\,\frac{N}{m^{2}}$. The final configuration in case of the PPG UnlP0 formulation with a regular discretization using 95, 904 particles is shown in Fig. 4 where the displacement in z-direction is colored.

Fig. 4

On the left: Geometry and boundary conditions of the three dimensional Cook’s membrane problem consisting of free moving (green), fixed (purple) and force applied (red) particles. On the right: Vertical displacement field on the deformed body in case of a regular discretization into $72\times 72\times 18$ free moving particles. (Color figure online)

Fig. 5

Deformed configuration of the Cook’s membrane for the finest irregular and regular discretization using $n_{p}$ particles. The contours of the von Mises stress in Newton per square meter are depicted by the particle colors

In a convergence study the PPG UnlP0 formulation compares regular meshes, using $\omega _{2}$ and $\omega _{5}$ distance weights, with an irregular particle distribution (PPG UnlP0-d) using the $\omega _{2}$ weight function. The finest irregular and regular particle distribution are depicted in Fig. 5 showing the von Mises stress in the final configuration. The stresses are highly concentrated at the weak singularity at the upper left edge and exhibit a smooth transition over the whole beam.

Figure 6 shows the displacement of the right upper front edge over the number of nodes. The convergence rate of the PPG formulations is comparable to the H1P0 Finite Element while it converges from the opposite side. In case of strongly localized $\omega _{5}$ distance the converged displacement matches the one of FEM, for more smoothing $\omega _{2}$ weights a slight discrepance is observed.

Fig. 6

Convergence study: The vertical displacement at the upper right front edge of Cook’s membrane is plotted over the number of nodes. Different discretizations and weight functions in the PPG method are compared to the mixed H1P0 Finite Elements

4.3 Torsion problem

The third example demonstrates the robustness of the mixed PPG UnlP0 in a torsion test given in Kadapa et al. [18]. The beam of dimensions $0.001\,m\times 0.001\,m\times 0.005\,m$ is clamped at the top and bottom and rotated at the top end (see Fig. 7). As material parameters a bulk modulus of $K = 5\cdot 10^{8}\,\frac{N}{m^{2}}$ and a shear modulus of $\mu = 1.61148\cdot 10^{8}\,\frac{N}{m^{2}}$ are used. In Fig. 7 the von Mises stress is depicted for a rotation angle of 360 degrees both for the PPG UnlP0 and FEM H1P0 solutions. The stress distribution looks very similar and has a minimum in the center and maximal values in the middle of each side.

Fig. 7

On the left: Geometry of the torsion problem where particles underlying displacement boundary conditions are colored purple and free moving particles green. On the right: Exemplary configuration for a twisting angle of 360 degrees with the mixed PPG UnlP0 and FEM H1P0 formulations. The von Mises stress in Newton per square meter is colored

Via adaptive load stepping, the twisting angle is increased until the convergence fails for a further increment of at least one degree. The total angle as well as the maximal angle that can be applied in a single load step are shown in Table 2 for a discretization into $16\times 16 \times 5 \cdot 16$ particles and elements, respectively. Both measures show the superiority of the mixed formulations over the pure displacement based approaches. While the FEM H1 and PPG Unl formulations need small load steps which soon fall below one degree, the FEM H1P0 and especially the PPG UnlP0 approaches can deal with very large load steps. The peridynamic approach is even more robust and effective for large deformations compared to standard finite element methods.

4.4 Numerical inf-sup test

In mixed FE methods, the inf-sup or Ladyzhenskaya-Babuška-Brezzi condition ensures together with the ellipticity condition the existence, uniqueness and stability of the regarding discretization. For nearly incompressible material behavior in linear elasticity, the inf-sup condition (see Fortin and Brezzi [12]) states

$$\begin{aligned} \inf _{p_{h}\in P_{h}} \sup _{\mathbf {u}_{h}\in U_{h}} \frac{\int _{\Omega } p_{h} {\text {Div}}\,\mathbf {u}_{h} \ d\Omega }{\left| \left| p_{h}\right| \right| _{L^{2}}\ \left| \left| \mathbf {u}_{h}\right| \right| _{H^{1}}} \ge \beta > 0\,, \end{aligned}$$

(33)

where $P_{h}$ and $U_{h}$ are finite dimensional spaces of trial pressure and displacement fields, respectively. Due to the complexity of meshless shape functions, an analytical proof whether the condition is satisfied is difficult to state. However, Chapelle and Bathe [8] proposed a numerical test which can give a prediction for the satisfaction. Therefore, a bloc of material with the applied essential boundaries as shown in Fig. 9a is discretized by a series of regular and distorted particle distributions consisting of $N \times N$ particles or elements with $N= \left\{ 2,4,8,16,32 \right\}$ (see Fig. 9b, c).

Table 2 Robustness study: failure angle and maximal converging angle in a single load step in degrees for displacement based and mixed PPG and FE approaches

The limit $\beta$ of the inf-sup condition of Eq. (33) can be determined from the following generalized eigenvalue problem:

$$\begin{aligned} \mathbf {T}_{h} \cdot \mathbf {U}_{h} = \lambda \mathbf {S}_{h} \cdot \mathbf {U}_{h}\,, \end{aligned}$$

(34)

where $\mathbf {U}_{h}$ is the global vector of nodal displacements. The matrix $\mathbf {S}_{h}$ results from the $H^{1}$ norm of the discrete displacement field

$$\begin{aligned} \left| \left| \mathbf {u}_{h}\right| \right| _{H^{1}}^{2} = \mathbf {U}_{h} \cdot \mathbf {S}_{h} \cdot \mathbf {U}_{h} \end{aligned}$$

(35)

and $\mathbf {T}_{h}$ corresponds to the discrete pressure projection

$$\begin{aligned} \left| \left| p_{h}\right| \right| _{L^{2}}^{2} = \mathbf {U}_{h} \cdot \mathbf {T}_{h} \cdot \mathbf {U}_{h}. \end{aligned}$$

(36)

Fig. 8

Inf-sup values of the model problem of Fig. 9, where the logarithm of the inf-sup value is plotted over the logarithm of the inverse of the number of particles in each dimension for regular and distorted (-d) particle and node distributions, respectively. While the Q1P0 element exhibits an inf-sup value converging towards zero, the inf-sup value of the PPG UnlP0 formulation is bounded from below by a non-zero value

Fig. 9

On the left: Model problem for numerical inf-sup test. On the right: exemplary discretizations for regular and irregular particle distributions. The Dirichlet boundary conditions are applied by and additional layer of wall particles. The displacements of blue colored particles are fixed horizontally and the purple particle is fixed in both horizontal and vertical direction

Considering the range of small strains and using static condensation, it states

(37)

The inf-sup value of a particular resolution computes to the smallest non-zero eigenvalue of the generalized eigenvalue problem defined in Eq. (34):

$$\begin{aligned} {\tilde{\beta }} = \sqrt{\lambda _{k}}. \end{aligned}$$

(38)

where $k-1$ is the number of zero-eigenvalues. The number of spurious pressure modes can be determined from

$$\begin{aligned} k_{pm} = k-\left( n_{u} -n_{p} +1 \right) \end{aligned}$$

(39)

with the number of global displacement and pressure degrees of freedom $n_{u}$ and $n_{p}$. Figure 8 depicts the inf-sup values of the model problem of Fig. 9. Whereas the Q1P0 element violates the inf-sup condition, the UnlP0 formulation passes the numerical inf-sup test as the inf-sup value is bounded from below and $k_{pm}=0$ for both uniform and irregular particle distributions. In case of the distorted particle distribution, the same neighborhood as in the according regular distribution is choosen. The satisfaction of the numerical inf-sup test is in agreement with the presented examples where no locking phenomenas in the range of nearly incompressible material behavior were observed.

5 Summary

In this work, the novel Peridynamic Petrov–Galerkin method is extended to three dimensional problems and a special kind of interpolating Moving Least Square approximation of derivatives based on differences is proposed. The locking behavior of a pure displacement based formulation is investigated and by transferring knowledge from the Finite Element technology mixed displacement-dilation-pressure formulations are developed. An implicit quasi-static framework based on efficient Automatic Differentiation is presented. The numerical examples show that the proposed approach achieves good performance concerning robustness and convergence while maintaining the advantages of meshfree particle methods.

Proof of momentum preservation

The preservation of linear momentum is ensured by the concept of pairwise forces. As the isochoric part of the strain energy is handled in the standard pure displacement based way, the momentum preservation is automatically fulfilled and it remains to show that the volumetric part of the residual can also be written in terms of pairwise force densities. Thus, starting from the local volumetric potential

$$\begin{aligned} U^{k}_{vol} = V^{k} \left[ p^{k} \left( J^{k} - \Theta ^{k}\right) + \frac{K}{2} \left( \Theta ^{k} - 1\right) ^{2}\right] \,, \end{aligned}$$

(40)

the residual contribution to particle j can be computed as the derivative with respect to the particles displacement

$$\begin{aligned} \frac{\partial U^{k}_{vol}}{\partial \mathbf {u}^{j}} = V^{k} p^{k} \frac{\partial J^{k}}{\partial \mathbf {F}^{k}}:\frac{\partial \mathbf {F}^{k}}{\partial \mathbf {u}^{j}} \end{aligned}$$

(41)

where the chain rule is used. Inserting the deformation gradient approach (12) and switching to index notation yields

$$\begin{aligned} \frac{\partial U^{k}_{vol}}{\partial u^{j}_{a}} = V^{k} p^{k} J^{k} {F^{k}_{bc}}^{-T} \sum _{i=0}^{N^{k}} \frac{\partial u^{i}_{b}}{\partial u^{j}_{a}} \frac{\partial N^{kki}}{\partial X_{c}}. \end{aligned}$$

(42)

The resulting pull-back of the volumetric Cauchy-stress can be exchanged by the first Piola–Kirchhoff stress tensor.

$$\begin{aligned} \frac{\partial U^{k}_{vol}}{\partial \mathbf {u}^{j}} = V^{k} p^{k} J^{k} {\mathbf {F}^{k}}^{-T} \cdot \frac{\partial N^{kkj}}{\partial \mathbf {X}} = V^{k} \mathbf {P}^{k}_{vol} \cdot \frac{\partial N^{kkj}}{\partial \mathbf {X}} \end{aligned}$$

(43)

Analogous to the contribution to the nodal residual of particle j, the corresponding contribution to particle k follows

$$\begin{aligned} \frac{\partial U^{k}_{vol}}{\partial \mathbf {u}^{k}} = V^{k} \mathbf {P}^{k}_{vol} \cdot \frac{\partial N^{kkk}}{\partial \mathbf {X}} = - \sum _{j=1}^{N^{k}} V^{k} \mathbf {P}^{k}_{vol} \cdot \frac{\partial N^{kkj}}{\partial \mathbf {X}} \end{aligned}$$

(44)

where the zeroth order consistency conditions is utilized. The internal force acting on particle k can now be assembled from the potentials of its neighboring particles and rearranged to

$$\begin{aligned} \mathbf {R}^{k}_{vol}= & {} \sum _{j=1}^{N^{k}} V^{j} \mathbf {P}^{j}_{vol} \cdot \frac{\partial N^{jjk}}{\partial \mathbf {X}} - V^{k} \mathbf {P}^{k}_{vol} \cdot \frac{\partial N^{kkj}}{\partial \mathbf {X}} \nonumber \\= & {} - V^{k} \sum _{j=1}^{N^{k}} \left[ \mathbf {t}^{kj}_{vol} - \mathbf {t}^{jk}_{vol} \right] V^{j} \end{aligned}$$

(45)

where the volumetric pairwise force density states

$$\begin{aligned} \mathbf {t}^{kj}_{vol} = - \frac{1}{V^{k}} \mathbf {P}_{vol}^{j} \cdot \frac{\partial N^{jjk}}{\partial \mathbf {X}}. \end{aligned}$$

(46)

As the inner forces acting on a particle can be expressed with pairwise force densities, the linear momentum preservation holds if pairwisity is fulfilled.