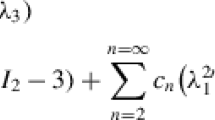1 Introduction

In the Finite Element Method (FEM), a constitutive model is defined to describe the response for each component. The isothermal, quasi-static and rate-independent behaviour of rubber, and materials of a similar phenomenological description, is described by a hyperelastic constitutive model. When more complex behaviour is considered (viscoelasticity, plasticity or damage), the hyperelastic response may represent the equilibrium elastic behaviour [29, 40].

Hyperelastic constitutive models typically define a Helmholtz free energy function, dependent only on the state of strain. Hence, they are often referred to as strain energy (density) functions. These may be categorised as either micro-mechanical or phenomenological [15, 30, 42], depending on whether or not their parameters are physically defined. Otherwise, they may be categorised by their strain measure [21]. Hyperelastic constitutive models defined in terms of principal stretches are of particular interest, as this class of model has been shown to capably predict the elastic response of rubber [10, 18, 23, 25, 33, 35, 46]. However, a definitive numerical implementation with explicit validation is not known from literature.

The implementation of a constitutive model within an implicit FEM requires the definition of a stress tensor and its consistent tangent moduli, in a form that is dependent on the solver. The consistent tangent moduli for hyperelastic constitutive models are defined by an elasticity tensor and any additional terms required for objectivity [14]. For isotropic hyperelasticity in principal stretches, various forms of the elasticity tensor are known from literature. This ambiguity is due to the nature of the principal stretches. The squared principal stretches and associated principal directions are found from the Cauchy-Green deformation tensors, where they are equivalent to eigenvalues and eigenvectors respectively. The original derivation [3, 4, 34] of the elasticity tensor relies on the explicit calculation of these eigenvalues and eigenvectors. However, the seminal implementation in the FEM developed by Simo and Taylor [41] avoided explicit calculation of the eigenvectors, due to the required computational effort, and developed alternative elasticity tensors. Though Simo [39] later stated that explicit calculation of eigenvectors by a Jacobi method should be preferred. This is due to the known numerical instabilities of the alternative elasticity tensors and eigenvector replacements [12, 16, 39]. Despite this, direct methods based on Simo and Taylor [41] have found continued use [5, 7, 8, 16, 18, 23, 26, 36].

In this paper an efficient implementation of isotropic hyperelasticity in principal stretches is proposed and validated. Fortran programs are created to investigate the numerical implementation in reference and current configurations. The commercial FEM software Abaqus is used to further investigate the numerical implementation. Abaqus enables the implementation of user defined constitutive models through UMAT subroutines, written in Fortran 77 standard. The stress and elasticity tensors are derived by explicit calculation of the principal stretches and associated principal directions. These are computed using an efficient Jacobi method algorithm from Kopp [22] (provided open-source). The stress and elasticity tensors are first derived in the reference configuration in terms of the material 2nd Piola-Kirchhoff stress tensor and associated elasticity tensor. These tensors are transformed into the current configuration in terms of the spatial Kirchhoff stress and the elasticity tensor is defined in terms of the Oldroyd rate of the Kirchhoff stress. Transformations to the Cauchy stress and the Jaumann rate of the Cauchy stress are defined, as these are the stress and elasticity tensors required by Abaqus. It is assumed throughout that the constitutive model is defined by an isochoric-volumetric split [9]. The developed expressions are therefore given in terms of isochoric principal stretches and the volumetric contributions are defined for completeness.

The developed numerical implementation has some novel features: the stress and elasticity coefficients are efficiently implemented, symmetric dyadic products of the principal directions are utilised, and the numerical instabilities associated with equal and similar principal stretches are resolved by derived approximations with L’Hôpital’s rule. The implementation is validated by evaluating the stress and elasticity tensors for constitutive models typically described in terms of Cauchy-Green invariants. By expressing these constitutive models in terms of principal invariants, the presented implementation can be compared to the well-established implementation of Cauchy-Green invariants, which are not subject to numerical instabilities for deformations with equal and similar principal stretches. This form of validation is not otherwise known from literature.

2 Isotropic hyperelasticity in principal stretches

In this section, the stress and elasticity tensors for isotropic hyperelasticity in principal stretches are defined. The complete derivations are omitted but referenced throughout. The material tensors are defined with respect to the reference configuration, then transformed to their spatial equivalent form in the current configuration by a push-forward operation. Some additional aspects of the developed numerical implementation are also detailed, including the treatment of numerically similar and equal eigenvalues. Firstly, the kinematics of hyperelasticity are defined.

2.1 Kinematical description of hyperelasticity

In three-dimensional real coordinate space \({\mathbb {R}}^3\), a reference configuration \({\varvec{\Omega }}_0\) and a current configuration \(\varvec{\Omega }\) are defined for a body of interest. A material point \(\mathbf X \), in the reference configuration \(\mathbf X {\in }\varvec{{{\Omega }}_0}\), is mapped to its current position \(\mathbf x \), in the current configuration \(\mathbf x {\in }{\Omega }\), by \(\varvec{\upchi }\), where \(\varvec{\upchi }\ {:}{{\Omega }}_0\rightarrow \, {\mathbb {R}}^3\) and therefore \(\mathbf x = \varvec{\upchi }\left( \mathbf X \right) \). The motion \(\varvec{\upchi }\) describes the both the deformation and the rigid body motions (translation and rotation). To remove translation, the two-point deformation gradient tensor, defined by \(\mathbf F = {\partial \varvec{\upchi }}/{\partial \mathbf X }\) is used. The volume ratio \(J = {V}/{V_0}\) is calculated by its determinant \(J = \mathrm{det}\left( \mathbf F \right) \).

The polar decomposition of the deformation gradient splits \(\mathbf F \) into pure stretch and pure rotation tensors by \(\mathbf F = \mathbf RU \) and \(\mathbf F = \mathbf vR \). Here, \(\mathbf U \) and \(\mathbf v \) are the symmetric positive definite right and left stretch tensors, respectively. Tensor \(\mathbf R \) defines the rigid body rotation and is a proper orthogonal tensor, which implies the relations \(\mathbf{R }^{\mathrm{T}}{} \mathbf R = \mathbf R \mathbf{R }^{\mathrm{T}} = \mathbf 1 \), where \(\varvec{1}\) is the 2nd-order identity tensor and the superscript indicates the transpose of a tensor. With these relations, two further symmetric pure stretch tensors in the material and spatial descriptions may be respectively defined in terms of \(\mathbf F \) as

$$\begin{aligned} \displaystyle&\mathbf C =\mathbf{F }^\mathrm{T}{} \mathbf F =\left( \mathbf UR ^\mathrm{T} \right) \left( \mathbf RU \right) =\mathbf{U }^{{2}}, \end{aligned}$$
(1)
$$\begin{aligned}&\mathbf b =\mathbf F \mathbf{F }^\mathrm{T}=\left( \mathbf vR \right) \left( \mathbf R ^\mathrm{T}{} \mathbf v \right) =\mathbf{v }^{{2}}. \end{aligned}$$
(2)

These are the right and left Cauchy-Green deformation tensors respectively. Due to their symmetry, the spectral decomposition may be used to represent these tensors in terms of real eigenvalues \({{\lambda }_a}^2\) and sets of mutually orthogonal eigenvectors \(\mathbf{N }_{a}\) and \(\mathbf{n }_{a}\)

$$\begin{aligned}&\mathbf C =\sum ^3_{a=1}{{{\lambda }_a}^2\left( \mathbf{N }_{a} {\otimes }\mathbf{N }_{a}\right) },&\end{aligned}$$
(3)
$$\begin{aligned}&\mathbf b =\sum ^{{3}}_{a{=1}}{{{\lambda }_a}^{{2}} \left( \mathbf{n }_{a}{\otimes }\mathbf{n }_{a}\right) }. \end{aligned}$$
(4)

The eigenvalues of both Cauchy-Green deformation tensors \({{\lambda }_a}^2\) are the squared principal stretches. The eigenvectors \(\mathbf{N }_{{a}}\) and \(\mathbf{n }_{{a}}\) are the principal directions. They are related by \(\mathbf{n }_{a} = \mathbf R \mathbf{N }_{a}\) and of unit length \(\left| \mathbf{N }_{a}\right| = \left| \mathbf{n }_{a}\right| = 1\), which is equivalent to the identity

$$\begin{aligned} {{\mathbf{N}}_{a}} \cdot {{\mathbf{N}}_{a}} = 1;a = 1,2,3 \end{aligned}$$
(5)

In the proposed implementation, these eigenvalues and eigenvectors are computed explicitly using an iterative Jacobi method. The algorithm for the Jacobi method was provided as open-source code from Kopp [22]. This algorithm was developed for the explicit purpose of computing the real eigenvalues and eigenvectors of symmetric 3\(\times \)3 matrices, and is therefore suited to this application.

Although the deformation gradient is generally not symmetric, it may also be described by the real eigenvalues and orthogonal eigenvectors by the following

$$\begin{aligned} \mathbf F =\mathbf RU =\sum ^3_{a=1}{{\lambda }_a\left( \mathbf R \mathbf{N }_{a}\otimes \mathbf{N }_{a}\right) }=\sum ^3_{a=1}{{\lambda }_a\left( \mathbf{n }_{a}\otimes \mathbf{N }_{a}\right) } \end{aligned}$$
(6)

This expression is used in the push-forward operations of the material stress and elasticity tensors along with (5).

2.2 Definition of stress tensors

Hyperelasticity assumes the existence of a Helmholtz free-energy function \(\psi \) that is a function of the mechanical strain only. The material stress and elasticity tensors are derived with respect to the derivatives of this strain energy function [4, 14, 41]. Due to rubber’s near incompressibility, the strain energy function is additively decomposed into the isochoric and volumetric contributions \(W\left( {\overline{\lambda }}_1,{\overline{\lambda }}_2,{\overline{\lambda }}_3\right) \) and \(U\left( J\right) \), as proposed by Flory [9]. The total strain energy is therefore defined as the sum

$$\begin{aligned} \psi =W\left( {\overline{\lambda }}_1,{\overline{\lambda }}_2, {\overline{\lambda }}_3\right) +U\left( J\right) \end{aligned}$$
(7)

Here, the isochoric contribution to the energy is computed using isochoric principal stretches defined as

$$\begin{aligned} {\overline{\lambda } _a} = {J^{ - \frac{1}{3}}}{\lambda _a} \end{aligned}$$
(8)

Material stress tensor In the reference configuration, the 2nd Piola-Kirchhoff stress tensor \(\mathbf S \) defines the material stress. For a hyperelastic constitutive model this is calculated as the derivative of the energy \(\psi \) with respect to the right Cauchy-Green deformation tensor \(\mathbf C \)

$$\begin{aligned} \mathbf S =2\frac{\partial \psi }{\partial \mathbf C } \end{aligned}$$
(9)

The stress tensor is also additively decomposed into isochoric and volumetric components \(\mathbf{S }_{iso}\) and \(\mathbf{S }_{vol}\) and given by

$$\begin{aligned} \mathbf S =\mathbf{S }_{iso}+ \mathbf{S }_{vol}=2\frac{\partial W\left( {\overline{\lambda }}_1,{\overline{\lambda }}_2,{\overline{\lambda }}_3\right) }{\partial \mathbf C }+2\frac{\partial U\left( J\right) }{\partial \mathbf C } \end{aligned}$$
(10)

These components are both calculated using well-known identities and the chain rule, see Simo and Taylor [41] and the references therein for a complete derivation. This results in the following expression for the isochoric stress tensor

$$\begin{aligned} {{\mathbf{S}}_{iso}} = 2\sum \limits _{a,b = 1}^3 {\frac{{\partial W}}{{\partial {{\bar{\lambda } }_a}}}} \frac{{\partial {{\bar{\lambda } }_a}}}{{\partial {\lambda _b}}}\frac{{\partial {\lambda _b}}}{{\partial {\mathbf{C}}}} = \sum \limits _{a = 1}^3 {{\beta _a}} {\lambda _a}^{ - 2}{{\mathbf{N}}_{{a}}} \otimes {{\mathbf{N}}_{a}} \end{aligned}$$
(11)

In this expression the principal directions \(\mathbf{N }_{a}\) and squared principal stretches \({{\lambda }_a}^2\) are found from the right Cauchy-Green deformation tensor \(\mathbf C \) defined in (3), using the iterative Jacobi algorithm from Kopp [22]. The stress coefficients \({\beta }_a\) are defined as

$$\begin{aligned} {\beta }_a={\overline{\lambda }}_a\frac{\partial W}{\partial {\overline{\lambda }}_a}-\frac{1}{3}\sum ^3_{b=1}{{\overline{\lambda }}_b\frac{\partial W}{\partial {\overline{\lambda }}_b}} \end{aligned}$$
(12)

The volumetric stress tensor is given as

$$\begin{aligned} {{\mathbf{S}}_{{vol}}} = 2\frac{{\partial U}}{{\partial J}}\frac{{\partial J}}{{\partial {\mathbf{C}}}} = J\frac{{\partial U}}{{\partial J}}{{\mathbf{C}}^{ - 1}} \end{aligned}$$
(13)

Spatial stress tensors The spatial stress tensor is first defined in terms of the Kirchhoff stress, \(\varvec{\tau }\). This stress tensor is related to the 2nd Piola-Kirchhoff stress tensor by

$$\begin{aligned} \varvec{\uptau }=\mathbf FS \mathbf{F }^{\mathrm{T}} \end{aligned}$$
(14)

The volumetric Kirchhoff stress tensor is found using this relationship alone to give

$$\begin{aligned} {\varvec{\uptau }}_{vol}=J\frac{\partial U}{\partial J}\varvec{1}&\end{aligned}$$
(15)

For the isochoric Kirchhoff stress tensor, the identities (5) and (6) are used in (11) to give

$$\begin{aligned} {{{\uptau }}_{{iso}}} = \sum \limits _{a = 1}^3 {{\beta _a}\left( {{{\mathbf{n}}_{{a}}} \otimes {{\mathbf{n}}_{{a}}}} \right) }&\end{aligned}$$
(16)

The stress coefficients \({\beta }_a\) are as previously defined. The principal directions \(\mathbf{n }_{a}\) and the squared principal stretches \({{\lambda }_a}^2\) for the current metric are found from the left Cauchy-Green deformation tensor \(\mathbf b \), defined in (4), using the Jacobi method [22].

The spatial Cauchy stress tensor \(\varvec{\upsigma }\) is required for implementation into Abaqus. By summation of the isochoric and volumetric Kirchhoff stress tensors (15) and (16), the Cauchy stress tensor is calculated from the total Kirchhoff stress tensor as follows

$$\begin{aligned} {\varvec{\upsigma }} = {J^{ - 1}}{\varvec{\uptau }} \end{aligned}$$
(17)

2.3 Definition of elasticity tensors

Unlike the stress tensors, the elasticity tensor appears in various forms in the literature. This is due to differences in the calculation of the principal directions. Here, the elasticity tensor is defined explicitly in terms of the principal directions, which are calculated from the relevant Cauchy-Green tensor by the Jacobi algorithm. In other definitions of the elasticity tensor with explicit calculation of the principal directions [3, 4, 14], the derivation is based on the use of the rate form of the material stress and deformation tensors, \(\dot{\mathbf{S }}\) and \(\dot{\mathbf{C }}\) respectively. These quantities are connected to the material elasticity tensor \(\mathbb {C}\) by

$$\begin{aligned} \dot{\mathbf{S }}=\mathbb {C}:\dot{\mathbf{C }}/2 \end{aligned}$$
(18)

However, due to the rate-independence of hyperelasticity and the objective nature of the material elasticity tensor, this may be defined equivalently by differentiation of the 2nd Piola-Kirchhoff stress tensor with respect to the right Cauchy-Green deformation tensor.

$$\begin{aligned} {\mathbb {C}=2\frac{\partial \mathbf S }{\partial \mathbf C }} \end{aligned}$$
(19)

The spatial elasticity tensors are obtained using a push-forward operation and the inclusion of additional terms for objectivity.

Material Elasticity Tensor The material elasticity tensor is defined using the additive split of isochoric and volumetric contributions as

$$\begin{aligned} \mathbb {C}={\mathbb {C}}_{iso} {+}{\mathbb {C}}_{vol} \end{aligned}$$
(20)

For the isochoric component, the isochoric 2nd Piola-Kirchhoff stress, defined in (11), is differentiated with respect to the right Cauchy-Green tensor. Using the chain rule, this may be defined by the following three terms

$$\begin{aligned} {\mathbb {C}}_{iso}&= 2\frac{{\partial {{\mathbf{S}}_{{{iso}}}}}}{{\partial {\mathbf{C}}}} = 2\left( {\sum \limits _{a = 1}^3 {\frac{{\partial {\beta _a}}}{{\partial {\mathbf{C}}}}} {\lambda _a}^{ - 2}\left( {{{\mathbf{N}}_{{a}}} \otimes {{\mathbf{N}}_{{a}}}} \right) } \right) \nonumber \\&\quad + \, 2\left( {\sum \limits _{a = 1}^3 {{\beta _a}} \frac{{\partial {\lambda _a}^{ - 2}}}{{\partial {\mathbf{C}}}}\left( {{{\mathbf{N}}_{{a}}} \otimes {{\mathbf{N}}_{{a}}}} \right) } \right) \nonumber \\&\quad + \, 2\left( {\sum \limits _{a = 1}^3 {{\beta _a}} {\lambda _a}^{ - 2}\frac{\partial }{{\partial {\mathbf{C}}}}\left( {{{\mathbf{N}}_{{a}}} \otimes {{\mathbf{N}}_{{a}}}} \right) } \right) \end{aligned}$$
(21)

The first and second terms are derived with reference to Simo and Taylor [41]. The third term appears in the explicit derivations where the rate form (18) is used [3, 14, 34] and may be derived using linear perturbation theory Kato [20]. This results in the following isochoric elasticity tensor

$$\begin{aligned} {\mathbb {C}}_{iso}&= \sum \limits _{a,b = 1}^3 \left( {{\gamma _{ab}}\lambda _a^{ - 2}\lambda _b^{ - 2} {-} 2{\delta _{ab}}{\beta _a}\lambda _a^{ - 4}} \right) \nonumber \\&\qquad \left( {{{\mathbf{N}}_{{a}}} \otimes {{\mathbf{N}}_{{a}}} \otimes {{\mathbf{N}}_{{b}}} \otimes {{\mathbf{N}}_{{b}}}} \right) \nonumber \\&\quad +\,\sum \limits _{a,b = 1{;} a \ne b}^3 \frac{{{\beta _b}\lambda _b^{ - 2} {-} {\beta _a}\lambda _a^{ - 2}}}{{\lambda _b^2 {-} \lambda _a^2}}\nonumber \\&\qquad \left[ {\left( {{{\mathbf{N}}_{{a}}} \otimes {{\mathbf{N}}_{{b}}}} \right) \otimes \left( {{{\mathbf{N}}_{{a}}} \otimes {{\mathbf{N}}_{{b}}} + {{\mathbf{N}}_{{b}}} \otimes {{\mathbf{N}}_{{a}}}} \right) } \right] \end{aligned}$$
(22)

With the isochoric elasticity coefficients \({\gamma }_{ab}\) defined as

$$\begin{aligned} \begin{aligned} {\gamma _{ab}} =&\left[ {{{\overline{\lambda } }_b}\left( {{{\overline{\lambda } }_a}\frac{{\partial W}}{{\partial {{\overline{\lambda } }_a}}}} \right) \frac{{\partial W}}{{\partial {{\overline{\lambda } }_b}}}} \right] + \frac{1}{9}\sum \limits _{c,d = 1}^3 {\left[ {{{\overline{\lambda } }_d}\left( {{{\overline{\lambda } }_c}\frac{{\partial W}}{{\partial {{\overline{\lambda } }_c}}}} \right) \frac{{\partial W}}{{\partial {{\overline{\lambda } }_d}}}} \right] } \\&\quad - \frac{1}{3}\sum \limits _{c = 1}^3 {\left[ {{{\overline{\lambda } }_c}\left( {{{\overline{\lambda } }_a}\frac{{\partial W}}{{\partial {{\overline{\lambda } }_a}}}} \right) \frac{{\partial W}}{{\partial {{\overline{\lambda } }_c}}} + {{\overline{\lambda } }_b}\left( {{{\overline{\lambda } }_c}\frac{{\partial W}}{{\partial {{\overline{\lambda } }_c}}}} \right) \frac{{\partial W}}{{\partial {{\overline{\lambda } }_b}}}} \right] } \end{aligned} \end{aligned}$$
(23)

In (22) when the squared principal stretches are equal, the second term will result in a numerical divide by zero error. In general, a numerical treatment such as eigenvalue perturbation [26] may be used. However, for the explicitly defined elasticity tensor, an analytical solution is obtained by applying L’Hôpital’s rule [14, 34]. As the squared principal stretches tend towards one another, this rule enables the second term in (22) to be approximated by

$$\begin{aligned} {\mathop {\mathrm {lim}}_{{\lambda }_a\rightarrow {\lambda }_b} \frac{{\beta }_b{{\lambda }_b}^{-2}-{\beta }_a{{\lambda }_a}^{-2}}{{{\lambda }_b}^2-{{\lambda }_a}^2}\ }=\frac{\partial \left( {\beta }_b{{\lambda }_b}^{-2}\right) }{\partial {{\lambda }_b}^2}-\frac{\partial \left( {\beta }_a{{\lambda }_a}^{-2}\right) }{\partial {{\lambda }_b}^2}&\end{aligned}$$
(24)

This equation is further developed to be approximated in terms of the stress and elasticity coefficients as follows

$$\begin{aligned} {\mathop {\mathrm {lim}}_{\lambda _a\rightarrow {\lambda }_b} \frac{{\beta }_b{{\lambda }_b}^{-2}-{\beta }_a{{\lambda }_a}^{-2}}{{{\lambda }_b}^2-{{\lambda }_a}^2}\ }&= {{\lambda }_b}^{-4}\left( \frac{1}{2}{\gamma }_{bb}-{\beta }_b\right) \nonumber \\&\quad -\,\frac{1}{2}{{\lambda }_a}^{-2}{{\lambda }_b}^{-2}{\gamma }_{ab} \end{aligned}$$
(25)

The numerical implementation of this requires consideration of a means of detecting the numerical similarity of the squared principal stretches with an associated numerical tolerance. This is discussed further in Sect. 2.4.

The volumetric elasticity tensor is also defined in terms of a chain rule. The volumetric 2nd-Piola-Kirchhoff stress, defined in (13), is differentiated with respect to the right Cauchy-Green tensor. This is given as

$$\begin{aligned} {\mathbb {C}}_{vol} = 2\frac{{\partial {{\mathbf{S}}_{{{vol}}}}}}{{\partial {\mathbf{C}}}} = 4\left[ {\frac{{\partial U}}{{\partial J}}\left( {\frac{{\partial ^2 J}}{{\partial {\mathbf{C}}\partial {\mathbf{C}}}}} \right) + \frac{{{\partial ^2}U}}{{\partial {J^2}}}\left( {\frac{{\partial J}}{{\partial {\mathbf{C}}}} \otimes \frac{{\partial J}}{{\partial {\mathbf{C}}}}} \right) } \right]&\end{aligned}$$
(26)

Using various identities, see Holzapfel [14] for full derivation, this leads to the expression

$$\begin{aligned} {\mathbb {C}}_{{vol}}&= J\left( {\frac{{\partial U}}{{\partial J}}{\mathrm{+ }}\frac{{{\partial ^2}U}}{{\partial {J^2}}}J} \right) \left( {{{\mathbf{C}}^{{\mathrm{- 1}}}} \otimes {{\mathbf{C}}^{{\mathrm{- 1}}}}} \right) \nonumber \\&\quad - 2\frac{{\partial U}}{{\partial J}}J\left( {{{\mathbf{C}}^{{\mathrm{- 1}}}} \odot {{\mathbf{C}}^{{\mathrm{- 1}}}}} \right)&\end{aligned}$$
(27)

The symmetric 4th-order dyadic product is applied, which is defined in index notation for two arbitrary 2nd-order tensors \(\mathbf A \) and \(\mathbf B \) as

$$\begin{aligned} {\left( {{\mathbf{A}} \odot {\mathbf{B}}} \right) _{ijkl}}{\mathrm{= }}\frac{{\mathrm{1}}}{{\mathrm{2}}}\left( {{A_{ik}}{B_{jl}}{\mathrm{+ }}{A_{il}}{B_{jk}}} \right) \end{aligned}$$
(28)

Spatial elasticity tensors The spatial elasticity tensor may be defined in various forms due to differences in the stress and strain tensors and the choice of objective rate. The spatial elasticity tensor is first defined in terms of the Oldroyd rate of the Kirchhoff stress, \(\mathrm {c}\). This is connected to the material elasticity tensor, in index notation, by

$$\begin{aligned} {\mathrm {c}}_{ijkl}=F_{iI}F_{jJ}F_{kK}F_{lL}{\mathbb {C}}_{IJKL} \end{aligned}$$
(29)

Using (29), the volumetric component of the spatial elasticity tensor \({\mathrm {c}}_{\varvec{vol}}\) is defined as

$$\begin{aligned} {{\mathrm{c}}_{{{vol}}}} = J\left( {\frac{{\partial U}}{{\partial J}}{\mathrm{+ }}\frac{{{\partial ^2}U}}{{\partial {J^2}}}J} \right) \left( {{\mathbf{1}} \otimes {\mathbf{1}}} \right) {\mathrm{- 2}}\frac{{\partial U}}{{\partial J}}J\left( {{\mathbf{1}} \odot {\mathbf{1}}} \right)&\end{aligned}$$
(30)

The isochoric elasticity tensor \({\mathrm {c}}_{iso}\) is derived using (29) and the identities (5) and (6) to give

$$\begin{aligned} \displaystyle {{\mathrm{c}}_{{{iso}}}} =&\sum \limits _{a,b = 1}^3 {\left( {{\gamma _{ab}} {-} 2{\delta _{ab}}{\beta _a}} \right) \left( {{{\mathbf{n}}_{{a}}} \otimes {{\mathbf{n}}_{{a}}} \otimes {{\mathbf{n}}_{{b}}} \otimes {{\mathbf{n}}_{{b}}}} \right) } \nonumber \\&+ \sum \limits _{a,b = 1 {;} a \ne b}^3 \frac{{{\beta _b}\lambda _a^{ 2} {-} {\beta _a}\lambda _b^{ 2}}}{{\lambda _b^2 {-} \lambda _a^2}}\nonumber \\&\qquad \left[ {\left( {{{\mathbf{n}}_{{a}}} \otimes {{\mathbf{n}}_{{ b}}}} \right) \otimes \left( {{{\mathbf{n}}_{{a}}} \otimes {{\mathbf{n}}_{{b}}} + {{\mathbf{n}}_{{b}}} \otimes {{\mathbf{n}}_{{a}}}} \right) } \right] \end{aligned}$$
(31)

The elasticity coefficients \({\gamma }_{ab}\) are defined in (23). This elasticity tensor is also subject to divide by zero errors if two or more principal stretches are equal. L’Hôpital’s rule may be applied, which is obtained by push-forward of the expression used for the reference configuration (25) as

$$\begin{aligned} \mathop {{\mathrm{lim}}}\limits _{{\lambda _a} \rightarrow {\lambda _b}} \frac{{{\beta _b}{\lambda _a}^2 - {\beta _a}{\lambda _b}^2}}{{{\lambda _b}^2 - {\lambda _a}^2}}\; = {\lambda _a}^2{\lambda _b}^{ - 2}\left( {\frac{1}{2}{\gamma _{bb}} - {\beta _b}} \right) - \frac{1}{2}{\gamma _{ab}}&\end{aligned}$$
(32)

The implementation of this approximation also requires consideration of detecting numerical similarity with definition of a numerical tolerance, discussed in Sect. 2.4.

In Abaqus, the spatial elasticity tensor is defined in terms of the Jaumann rate of the Cauchy stress, denoted here as \({\mathrm {c}}^{\varvec{J}}\). To obtain this spatial elasticity tensor, the complete spatial elasticity tensor \(\mathrm {c}\), defined as the sum of (30) and (31), is transformed by

$$\begin{aligned} {{\mathrm{c}}^{{J}}} = {J^{ - 1}}\left( {{{\mathrm{c}}_{{{iso}}}} + {{\mathrm{c}}_{{{vol}}}}} \right) + \left( {{\varvec{\upsigma }} \odot {\varvec{1}}} \right) + \left( {{\varvec{1}} \odot {\varvec{\upsigma }}} \right) \end{aligned}$$
(33)

2.4 Aspects of numerical implementation

With the stress and elasticity tensors defined in reference and current configurations, these terms may be implemented in numerical methods. Some additional considerations are now discussed regarding particular aspects of the developed numerical implementation for any hyperelastic constitutive model defined in terms of principal stretches. The first consideration is the simplified implementation of the isochoric stress and elasticity coefficients \({\beta }_a\) and \({\gamma }_{ab}\). The next is the use of symmetric dyadic products of the principal directions, which enables Voigt notation and reduces the computational effort. The final consideration is the required algorithm for detection of numerical similarity in the squared principal stretches and employment of the L’Hôpital’s rule approximations to avoid numerical instability. These features can be understood in more depth by examining the developed programs and subroutines available in the referenced dataset [6].

Implementation of isochoric stress and elasticity coefficients In the proposed implementation, the required user input is minimised. In other implementations [18, 23, 41], the stress coefficients \({\beta }_a\) are required. Here it is noted from (12) that the use of a generic expression for \(\frac{\partial W}{\partial {\overline{\lambda }}_a}\) may be defined by considering a specified principal stretch e.g. \(\frac{\partial W}{\partial {\overline{\lambda }}_1}\). As, due to isotropy, this derivative is symbolically equivalent to \(\frac{\partial W}{\partial {\overline{\lambda }}_2}\) and \(\frac{\partial W}{\partial {\overline{\lambda }}_3}\), a general expression is therefore defined to compute all three derivatives. The stress coefficients \({\beta }_a\) are then computed using these derivatives, as defined in (12).

Similarly, in other implementations the elasticity coefficients \({\gamma }_{ab}\) are defined in full. It is observed here that in the definition of \({\gamma }_{ab}\) in (23), the derivatives expand to the same form

$$\begin{aligned} {\bar{\lambda } _b}\left( {{{\bar{\lambda } }_a}\frac{{\partial W}}{{\partial {{\bar{\lambda } }_a}}}} \right) \frac{\partial }{{\partial {{\bar{\lambda } }_b}}} = \left( {\frac{{{\partial ^2}W}}{{\partial {{\bar{\lambda } }_a}\partial {{\bar{\lambda } }_b}}}{{\bar{\lambda } }_a}{{\bar{\lambda } }_b} + \frac{{\partial W}}{{\partial {{\bar{\lambda } }_a}}}{\delta _{ab}}{{\bar{\lambda } }_b}} \right)&\end{aligned}$$
(34)

Only the second derivatives of the isochoric energy function \(\frac{{\partial }^2W}{\partial {\overline{\lambda }}_a\partial {\overline{\lambda }}_b}\) require definition, which may be defined for the two possibilities: \(a = b\) and \(a{\ne } b\). As in the definition of the stress coefficients, the derivatives may be obtained by considering specific principal stretches (e.g. \(\frac{{\partial }^2W}{\partial {\overline{\lambda }}_1\partial {\overline{\lambda }}_1}\) and \(\frac{{\partial }^2W}{\partial {\overline{\lambda }}_1\partial {\overline{\lambda }}_2}\)) before generalising. The elasticity coefficients are therefore implemented using the expanded expression

$$\begin{aligned} {\gamma _{ab}} \, =&\, \left( {\frac{{{\partial ^2}W}}{{\partial {{\bar{\lambda } }_a}\partial {{\bar{\lambda } }_b}}}{{\bar{\lambda } }_a}{{\bar{\lambda } }_b} + \frac{{\partial W}}{{\partial {{\bar{\lambda } }_a}}}{\delta _{ab}}{{\bar{\lambda } }_b}} \right) \nonumber \\&+ \, \frac{1}{9}\sum \limits _{c,d = 1}^3 {\left( {\frac{{{\partial ^2}W}}{{\partial {{\bar{\lambda } }_c}\partial {{\bar{\lambda } }_d}}}{{\bar{\lambda } }_c}{{\bar{\lambda } }_d} + \frac{{\partial W}}{{\partial {{\bar{\lambda } }_c}}}{\delta _{cd}}{{\bar{\lambda } }_d}} \right) } \nonumber \\&- \, \frac{1}{3}\sum \limits _{c = 1}^3 {\left( {\frac{{{\partial ^2}W}}{{\partial {{\bar{\lambda } }_a}\partial {{\bar{\lambda } }_c}}}{{\bar{\lambda } }_a}{{\bar{\lambda } }_c} + \frac{{\partial W}}{{\partial {{\bar{\lambda } }_c}}}{\delta _{ac}}{{\bar{\lambda } }_c}} \right) } \nonumber \\&- \, \frac{1}{3}\sum \limits _{c = 1}^3 {\left( {\frac{{{\partial ^2}W}}{{\partial {{\bar{\lambda } }_b}\partial {{\bar{\lambda } }_c}}}{{\bar{\lambda } }_b}{{\bar{\lambda } }_c} + \frac{{\partial W}}{{\partial {{\bar{\lambda } }_b}}}{\delta _{bc}}{{\bar{\lambda } }_c}} \right) } \end{aligned}$$
(35)

Using the aforementioned simplifications, an incompressible hyperelastic constitutive response defined in principal stretches may be modelled. The user is required to define the isochoric derivatives of the strain energy density function \(\frac{\partial W}{\partial {\overline{\lambda }}_1}\), \(\frac{{\partial }^2W}{\partial {\overline{\lambda }}_1\partial {\overline{\lambda }}_1}\) and \(\frac{{\partial }^2W}{\partial {\overline{\lambda }}_1\partial {\overline{\lambda }}_2}\) in general form. To include compressive behaviour, the derivatives \(\frac{\partial U}{\partial J}\) and \(\frac{{\partial }^2U}{\partial J^2}\) require user input.

Symmetric dyadic products of principal directions For all variations of the elasticity tensors defined in this paper, the stress and deformation tensors used in their derivation are symmetric. For computational efficiency, symmetric 2nd-order tensors may be defined using Voigt notation. This notation allows 2nd-order tensors to be represented by six component matrices, and hence 4th-order tensors are defined by six by six matrices. In the presented numerical implementation, the convention used by Abaqus is followed where the integers 1 to 6 represent the 1,1; 2,2; 3,3; 1,2; 1,3; and 2,3 components, respectively.

The stress tensors are defined in terms of the stress coefficients and the dyadic products of the relevant principal directions, \(\mathbf{n }_{a}\otimes \mathbf{n }_{a}\) or \(\mathbf{N }_{a}\otimes \mathbf{N }_{a}\). These dyadic products are inherently symmetric since they are constructed from the same vectors, as \(\mathbf a \otimes \mathbf b = {\left( \mathbf a \otimes \mathbf b \right) }^{\mathrm{T}}\) if \(\mathbf a = \mathbf b \). These can therefore be represented in Voigt notation. However, the definition of the elasticity tensors, (22) and (31), contains several non-symmetric 2nd-order tensors, for example, in (22), \(\mathbf{N }_{{a}}\otimes \mathbf{N }_{{b}}\) where \({a}{\ne } {b}\) and by the nature of eigenvectors \(\mathbf{N }_{{a}}{\ne }\mathbf{N }_{{b}}\) for \({a}{\ne } {b}\). In this form, these cannot be represented in Voigt notation and nor can their 4th-order dyadic products, e.g. \(\mathbf{N }_{{a}}\otimes \mathbf{N }_{{b}}\otimes \mathbf{N }_{{a}}\otimes \mathbf{N }_{{b}}\). A modification is therefore required.

It is known that all elasticity tensors defined previously contain both minor symmetries, such that \({\mathrm {c}}_{ijkl}={\mathrm {c}}_{jikl}={\mathrm {c}}_{ijlk}\), due to the symmetric definitions of the stress and deformation tensors. Furthermore, due to isotropy, the elasticity tensor also contains major symmetry such that \({\mathrm {c}}_{ijkl}={\mathrm {c}}_{klij}\). Therefore, using the concept that any tensor may be decomposed into a symmetric tensor and a skew symmetric tensor [14], the sum of the components of the isochoric elasticity tensors, (22) and (31), must result in the cancellation of all skew symmetric parts. This permits the use of only the symmetric parts of the dyadic products. The symmetric part of a 2nd-order tensor \(\mathbf A \) is found as the halved sum of itself and its transpose

$$\begin{aligned} \mathrm{sym}\left( {\mathbf{A}} \right) = \frac{1}{2}\left[ {{\mathbf{A}} + {{\mathbf{A}}^{\mathrm{T}}}} \right]&\end{aligned}$$
(36)

Applying this to the dyadic product of the principal directions gives

$$\begin{aligned} \mathrm{sym}\left( {{{\mathbf{N}}_{{a}}} \otimes {{\mathbf{N}}_{{b}}}} \right) =\,&\mathrm{sym}\left( {{{\mathbf{N}}_{{b}}} \otimes {{\mathbf{N}}_{{a}}}} \right) \nonumber \\ = \,&\frac{1}{2}\left[ {\left( {{{\mathbf{N}}_{{a}}} \otimes {{\mathbf{N}}_{{b}}}} \right) + \left( {{{\mathbf{N}}_{{b}}} \otimes {{\mathbf{N}}_{{a}}}} \right) } \right] \end{aligned}$$
(37)

This observation allows for the symmetric dyadic products of the principal directions to be represented as tensors in Voigt notation. Also, only three of these 2nd tensors require calculation, opposed to six. Furthermore, in the calculation of the 4th-order elasticity tensor, (22) or (31), there are only three unique 4th-order dyadic products of the principal directions, opposed to twelve otherwise. This equivalence is shown for the indices 1 & 2 as follows

$$\begin{aligned}&\mathrm{sym}\left( {{{\mathbf{N}}_{\mathrm{1}}} \otimes {{\mathbf{N}}_{\mathrm{2}}}} \right) \otimes \mathrm{sym}\left( {{{\mathbf{N}}_{\mathrm{1}}} \otimes {{\mathbf{N}}_{\mathrm{2}}}} \right) \nonumber \\&\quad = \, \mathrm{sym}\left( {{{\mathbf{N}}_{\mathrm{1}}} \otimes {{\mathbf{N}}_{\mathrm{2}}}} \right) \otimes \mathrm{sym}\left( {{{\mathbf{N}}_{\mathrm{2}}} \otimes {{\mathbf{N}}_{\mathrm{1}}}} \right) \nonumber \\&\quad = \, \mathrm{sym}\left( {{{\mathbf{N}}_{\mathrm{2}}} \otimes {{\mathbf{N}}_{\mathrm{1}}}} \right) \otimes \mathrm{sym}\left( {{{\mathbf{N}}_{\mathrm{2}}} \otimes {{\mathbf{N}}_{\mathrm{1}}}} \right) \nonumber \\&\quad = \, \mathrm{sym}\left( {{{\mathbf{N}}_{\mathrm{2}}} \otimes {{\mathbf{N}}_{\mathrm{1}}}} \right) \otimes \mathrm{sym}\left( {{{\mathbf{N}}_{\mathrm{1}}} \otimes {{\mathbf{N}}_{\mathrm{2}}}} \right) \end{aligned}$$
(38)

The same can be shown for the other two unique pairs of indices 1 & 3 and 2 & 3. The symmetries used here simplify the implementation significantly by permitting the use of Voigt notation throughout. This approach has not previously been used in literature.

Equal and similar principal stretches When two or three of the squared principal stretches (eigenvalues of the Cauchy-Green deformation tensors) are equal, the elasticity tensors result in a divide by zero error. In a numerical method, the finite floating-point precision limit of the computation means that the solution also encounters numerical inaccuracy when the eigenvalues are numerically similar. With equal eigenvalues, the application of L’Hôpital’s rule provides an exact alternative solution, though numerically similar eigenvalues require additional consideration. It is therefore necessary to find an approximate numerical tolerance at which the use of L’Hôpital’s rule gives an approximation more accurate than the original function. There is also a requirement for an algorithm to compare the similarity of the eigenvalues.

The proposed algorithm is based on an eigenvalue perturbation algorithm by Miehe [26]. Eigenvalue perturbation is an alternative means of avoiding divide by zero errors, but is less accurate and stable [13] than the method used here. The proposed algorithm uses a similar method for the detection of equal and similar eigenvalues, but employs approximations by L’Hôpital’s rule if the absolute difference between eigenvalues is less than the defined tolerance value. It also includes additional checks for three equal or similar eigenvalues, as it is possible numerically that \(\left( \left| {\lambda }_1-{\lambda }_2\right| \right) \le tol\) and \(\left( \left| {\lambda }_1-{\lambda }_3\right| \right) \le tol\) are true but \(\left( \left| {\lambda }_2-{\lambda }_3\right| \right) \le tol\) is false, repeated for all combinations. The proposed algorithm is defined in Table 1 for the spatial elasticity tensor, where tol is the magnitude of the numerical tolerance.

Table 1 Proposed algorithm for robust computation of the spatial elasticity tensor
Full size table

An equivalent algorithm is used in the numerical implementation of the isochoric material elasticity tensor defined in (22). Both can be found in the dataset [6]. The algorithm prevents divide by zero errors provided that a suitable tolerance value is selected. Optimisation of the tolerance value is investigated in Sect. 3.3.

3 Numerical validation

The implementation of hyperelasticity in principal stretches defined in Sect. 2 is investigated and validated. Throughout these investigations hyperelastic constitutive models defined in terms of the first and second isochoric Cauchy-Green invariants are used, for which the isochoric-volumetric implementation is well-established [19, 24, 27]. The stress and elasticity tensors for these are defined in “Appendix A”. Any constitutive model defined in terms of these isochoric strain invariants may also be defined, and therefore implemented, by isochoric principal stretches using the following identities

$$\begin{aligned} \displaystyle&{\overline{I}}_{1}={\mathrm {tr} \overline{\mathbf{C }}} ={\mathrm {tr} \overline{\mathbf{b }}\ }={{\overline{\lambda }}_1}^2 +{{\overline{\lambda }}_2}^2+{{\overline{\lambda }}_3}^2 \end{aligned}$$
(39)
$$\begin{aligned}&{\bar{I}_{\mathrm{2}}} = \frac{1}{2}\;\left[ {{{\left( {{\mathrm{tr}}\overline{\mathbf{C}} \;} \right) }^2} - {\mathrm{tr}}\left( {{{\overline{\mathbf{C}} }^{{2}}}} \right) \;} \right] = {\bar{\lambda } _1}^{ - 2} + {\bar{\lambda } _2}^{ - 2} + {\bar{\lambda } _3}^{ - 2} \end{aligned}$$
(40)
$$\begin{aligned}&{\overline{I}}_{3}={\mathrm {det} \overline{\mathbf{C }}\ }={{\overline{\lambda }}_1}^2{{\overline{\lambda }}_2}^2{{\overline{\lambda }}_3}^2=1 \end{aligned}$$
(41)

A comparison can therefore be made between the implementations, which is otherwise unknown from literature, despite its usefulness; the invariant implementation is unambiguous and is not subjected to numerical difficulties for deformations with equal or similar principal stretches. The invariant implementation therefore provides a stable and accurate solution from which the principal stretch implementation is validated. Additionally they are used to optimise the numerical tolerance of L’Hôpital’s rule.

This numerical investigation is divided into three studies, all of which use Fortran programs. These programs allow computation of the stress and elasticity tensors for a user defined deformation gradient with a chosen constitutive model and definition of its parameters and derivatives. The error is then computed by using an equivalent Cauchy-Green invariant implementation. The proposed implementation is first validated for unique eigenvalues, then compared for two and three equal eigenvalues. The tolerance value is then optimised using similar eigenvalues. The validated and optimised implementation is then used to create UMAT user subroutines to investigate performance in the FEM using Abaqus in Sect. 4.

The Fortran programs and UMAT user subroutines used in these investigations, as well as templates for a generic implementation of isochoric-volumetric constitutive models, are provided in the dataset [6]. Both Cauchy-Green invariant and principal stretch variations are included.

3.1 Unique eigenvalues

The validity is assessed in the reference configuration, the current configuration defined in terms of the Oldroyd rate of the Kirchhoff stress and in terms of the Jaumann rate of the Cauchy stress. To compute the error for the stress tensors calculated in terms of principal stretches, the relative error of each of the 6 components in Voigt notation is calculated by comparison to the invariant implementation. The sum of the error \(E_{\mathbf{S}}\) of these components is then computed using

$$\begin{aligned} {E_{\mathbf{S}}}{\mathrm{= }}{\left[ {\sum \limits _{I{{= 1}}}^{\mathrm{6}} {{{\left( {{{\mathrm{S}}^{\bar{\lambda } }}_I{{- }}{{\mathrm{S}}^{{{\bar{I}}_{12}}}}_I} \right) }^{\mathrm{2}}}} } \right] ^{\frac{{\mathrm{1}}}{{\mathrm{2}}}}} / {\left[ {\sum \limits _{I{\mathrm{= 1}}}^{\mathrm{6}} {{{\left( {{{\mathrm{S}}^{{{\bar{I}}_{12}}}}_I} \right) }^{\mathrm{2}}}} } \right] ^{\frac{{\mathrm{1}}}{{\mathrm{2}}}}} \end{aligned}$$
(42)

Here the components in Voigt notation are denoted by I to represent the indices 1 to 6, as defined previously. The 2nd Piola-Kirchhoff stress tensors \({\varvec{\mathrm {S}}}^{\overline{\varvec{\lambda }}}\) and \({\varvec{\mathrm {S}}}^{{\overline{\varvec{I}}}_{\varvec{12}}}\) represent the components computed in terms of principal stretches and Cauchy-Green invariants respectively. The same method is applied for calculating the error of the spatial Kirchhoff and Cauchy stress tensors, \(E_{\varvec{\uptau }}\) and \(E_{\varvec{\upsigma }}\) respectively.

To validate the elasticity tensors, the relative error computation is modified to account for all 36 components of the material elasticity tensor \(\mathbb {C}\) in Voigt notation as

$$\begin{aligned} E_{\mathbb {C}}={\left[ {\sum \limits _{I,J{\mathrm{= 1}}}^{\mathrm{6}} {{{\left( {{\mathbb {C}^{\bar{\lambda } }}_{IJ}{\mathrm{- }}{\mathbb {C}^{{{\bar{I}}_{12}}}}_{IJ}} \right) }^{\mathrm{2}}}} } \right] ^{\frac{{\mathrm{1}}}{{\mathrm{2}}}}}/{\left[ {\sum \limits _{I,J{\mathrm{= 1}}}^{\mathrm{6}} {{{\left( {{\mathbb {C}^{{{\bar{I}}_{12}}}}_{IJ}} \right) }^{\mathrm{2}}}} } \right] ^{\frac{{\mathrm{1}}}{{\mathrm{2}}}}}&\end{aligned}$$
(43)

The notations are defined analogously to the stress tensor. The error is also calculated equivalently for the spatial Oldroyd rate and Jaumann rate tensors, \(E_{\mathrm {c}}\) and \(E_{{\mathrm {c}}^{\varvec{J}}}\) respectively.

To validate the developed expressions and their numerical implementation, as defined in Section 2, the stress and elasticity tensors are computed for two deformation gradients. The first deformation gradient \(\mathbf{F }_{{1}}\) represents an isochoric shear deformation and the second \(\mathbf{F }_{{2}}\) is a shear deformation with dilation. These are defined as follows

$$\begin{aligned} {{\mathbf{F}}_{{{1}}}} = \begin{bmatrix} 3&1&0 \\ 1&1&0 \\ 0&0&0.5 \end{bmatrix} ; \qquad {{\mathbf{F}}_{{{2}}}} = \begin{bmatrix} 1.1&0.2&0.2 \\ 0&0.9535&0.2 \\ 0&0&0.9535 \end{bmatrix} \end{aligned}$$
(44)

To ensure the validity of the use of symmetric dyadic products for the eigenvectors, the deformation gradients are rotated. The method for rotation is equivalent to that of Tanaka et al. [43, 44]. The rotated deformation gradient \(\mathbf{F }_{\text {R}{1}}\) is computed by

$$\begin{aligned} {\mathbf{F }_{{\text {R}1}}} = \mathbf{Q}{{\mathbf{F}}_{{1}}}&\end{aligned}$$
(45)

The rotation tensor \(\varvec{\mathrm {Q}}\) is a product of three rotation matrices

$$\begin{aligned} {{\mathbf{Q}}}= & {} \begin{bmatrix} \cos \frac{\pi }{4}&-{\sin \frac{\pi }{4}}&0 \\ \sin \frac{\pi }{4}&\cos \frac{\pi }{4}&0 \\ 0&0&1 \end{bmatrix} \begin{bmatrix} \cos \frac{\pi }{3}&0&\sin \frac{\pi }{3} \\ 0&1&0 \\ {- \sin \frac{\pi }{3}}&0&\cos \frac{\pi }{3} \\ \end{bmatrix}\nonumber \\&\cdot \begin{bmatrix} 1&0&0 \\ 0&\cos \frac{\pi }{6}&{- \sin \frac{\pi }{6}} \\ 0&\sin \frac{\pi }{6}&\cos \frac{\pi }{6} \\ \end{bmatrix} \end{aligned}$$
(46)

The chosen constitutive model for this comparison is the neo-Hookean model [37]. This is conventionally represented in terms of the first isochoric Cauchy-Green invariant as

$$\begin{aligned} {W_{nH}} = {C_{\mathrm{1}}}\left( {{{\bar{I}}_{\mathrm{1}}}{\mathrm{- 3}}} \right) \end{aligned}$$
(47)

However, it may also be expressed in terms of the isochoric principal stretches using (39). As the volumetric components are consistent for both implementations, which are mutually defined in terms of the volume ratio J, they are omitted from the comparisons.

The sum of the relative error of the stress tensor is shown in Table 2. Given that these were calculated using double precision, their accuracy is close to the finite precision limit \(\sim {10}^{-16}\). These low errors are due to rounding. The stress tensors can therefore be said to be consistent and accurate for the principal stretch implementation. There is also no notable difference between the accuracy for isochoric and dilational deformations. As the stress tensors are generally well-agreed upon, this result is as anticipated.

Table 2 Error of stress tensors: material (2nd Piola-Kirchhoff), spatial (Kirchhoff), and spatial (Cauchy)
Full size table

The validation of the elasticity tensor and its numerical implementation is of particular interest, as some aspects are novel and have not previously been validated. The error of the elasticity tensors for both deformation gradients and all configurations are given in Table 3. The error is of similar scale to the finite precision limit for both isochoric and dilational deformations. This suggests that the developed elasticity tensors and their numerical implementation is consistent with the invariant implementation for deformations with unique eigenvalues.

Table 3 Error of elasticity tensors: material, spatial (Oldroyd), and spatial (Jaumann)
Full size table

3.2 Equal eigenvalues

With equal squared principal stretches, the algorithm of Table 1 is required to avoid undefined divide by zero errors for all variations of the elasticity tensors. As the eigenvectors are identical, any tolerance value N is acceptable for which \(1+N>1\) is true. The computation of the stress tensor is not affected by equal or similar eigenvalues and is therefore not considered henceforth. The eigenvalue and eigenvector computation would be a cause of concern in these scenarios. However, the Jacobi method algorithm is known to be stable and accurate [22].

The accuracy of the elasticity tensor is investigated by a similar method to Sect. 3.1. Here, the Mooney-Rivlin [31] model is used, which is defined in terms of the isochoric Cauchy-Green invariants as

$$\begin{aligned} {W_{MR}} = {C_{\mathrm{1}}}\left( {{{\bar{I}}_{\mathrm{1}}}{\mathrm{- 3}}} \right) + {C_{\mathrm{2}}}\left( {{{\bar{I}}_2}{\mathrm{- 3}}} \right) \end{aligned}$$
(48)

The Mooney-Rivlin constitutive model may also be expressed in terms of isochoric principal stretches through identities (39) and (40). The rotation of the deformation gradient defined in (45) is used and isochoric and dilational deformations are considered for both two and three equal eigenvalues. The pre-rotation deformation gradients for two equal eigenvalues are the isochoric and dilational uniaxial tension deformations, \(\mathbf{F }_{\mathrm {3}}\) and \(\mathbf{F }_{{\mathrm {4}}}\), defined by

$$\begin{aligned} {\mathbf{F }_{{{3}}}} = \begin{bmatrix} 0.25&0&0 \\ 0&2&0 \\ 0&0&2 \end{bmatrix} ; \qquad {\mathbf{F }_{{{4}}}} = \begin{bmatrix} 4&0&0 \\ 0&0.45&0 \\ 0&0&0.45 \end{bmatrix} \end{aligned}$$
(49)

For three equal eigenvalues, the pre-rotation deformation gradients \(\mathbf{F }_{{\mathrm {5}}}\) and \(\mathbf{F }_{{\mathrm {6}}}\) correspond to an undeformed configuration and a hydrostatic compression, respectively defined as

$$\begin{aligned} {{\mathbf{F}}_{{{5}}}} = \begin{bmatrix} 1&0&0 \\ 0&1&0 \\ 0&0&1 \end{bmatrix} ; \qquad {{\mathbf{F}}_{{{6}}}} = \begin{bmatrix} 0.5&0&0 \\ 0&0.5&0 \\ 0&0&0.5 \end{bmatrix} \end{aligned}$$
(50)

For two and three equal principal stretches, the summed errors for each variation of the elasticity tensors are given in Tables 4 and 5 respectively. It is shown that the error throughout is of a similar order to the finite precision limit. The accuracy is of a similar order for isochoric and dilational deformations in the case of two and three equal eigenvalues. The derived approximations by L’Hôpital’s rule and their numerical implementation is therefore assumed to be valid and accurate for the cases of equal eigenvalues.

Table 4 Error of elasticity tensors with two equal eigenvalues
Full size table
Table 5 Error of elasticity tensors with three equal eigenvalues
Full size table
Fig. 1
figure 1

Relative error of the proposed implementation in principal stretches to the Cauchy-Green invariant implementation for perturbed uniaxial deformations with varying \(\lambda \)

Full size image

3.3 Eigenvalue similarity tolerance

Finding an appropriate tolerance value for numerically similar eigenvalues is required to complete the proposed implementation of hyperelasticity in principal stretches. The cases of two and three similar eigenvalues are investigated in each configuration. To achieve numerically similar eigenvalues, a perturbation is applied to the deformation gradients. For two similar eigenvalues, a uniaxial tension deformation gradient is used with a perturbation of the two non-zero, equal components prior to rotation. For three similar eigenvalues, the perturbation is applied to two of the non-zero components of the undeformed deformation gradient prior to its rotation. These may be defined respectively by \(\mathbf{F }_{{\mathrm {7}}}\), with the absolute perturbation magnitude \(\varepsilon \), for \(\uplambda =2\) and \({\uplambda }\mathrm { = 1}\) in the equation

$$\begin{aligned} {{\mathbf{F}}_{{{7}}}} = \begin{bmatrix} \lambda&0&0 \\ 0&{\frac{1}{{\sqrt{{\lambda }} }} + \varepsilon }&0 \\ 0&0&{\frac{1}{{\sqrt{{\lambda }} }} - \varepsilon } \end{bmatrix} \end{aligned}$$
(51)

The perturbation magnitude \(\varepsilon \) is decreased exponentially from \({10}^{-2}\) to \({10}^{-16}\) using only integer powers, as perturbations lower than \({10}^{-16}\) result in \(1+\varepsilon \ngtr 1\) for double precision. The elasticity tensors are calculated with and without L’Hôpital’s rule for increasingly similar eigenvalues and compared to the stable solution obtained from a Cauchy-Green invariant implementation. For this investigation, the Gent model [11] is used, defined by

$$\begin{aligned} W_G = -\frac{1}{2}\mu J_m{\mathrm {ln} \left( 1-\frac{\left( {\overline{I}}_{1}-3\right) }{J_m}\right) \ }&\end{aligned}$$
(52)

For two and three similar eigenvalues, it is found that as the perturbation magnitude tends towards zero, for all configurations, without L’Hôpital’s rule the error increases and with L’Hôpital’s rule the error decreases. Both are shown for the spatial (Jaumann-Cauchy) elasticity tensor in Fig. 1a, b. The optimal tolerance magnitude is therefore that which employs L’Hôpital’s rule at the point where these lines intersect. It is seen from Fig. 1 that the intercept of the lines for these deformation gradients occurs around \(\varepsilon = {10}^{-6}\). This is then checked further for what are considered to be the approximate limits of physical deformations, with \(\uplambda =10\) and \(\uplambda =0.05\). As shown in Fig. 1c, d, the magnitude of the intercept does not diverge significantly from the intercept of \(\varepsilon = {10}^{-6}\).

The algorithm presented in Table 1 is designed such that the tolerance value corresponds to the perturbation magnitude. The optimal tolerance magnitude is therefore approximated as \({10}^{-6}\), the results for which are also plotted in Fig. 1. For the four deformation gradients, assumed to be the limits of physical deformations, and for all configurations, the elasticity tensor is computed accurately, with a maximum error of less than \({10}^{-10}\).

4 Finite Element Method investigation

The proposed implementation has been validated in the previous section in that it is numerically accurate and stable and remains so for deformations with equal and similar eigenvalues. Two Finite Element benchmark simulations are performed to allow for further validation and an assessment of computational efficiency. The simulated Finite Element models represent an inhomogeneous tensile test and a combined tension-torsion test. Abaqus/Standard with UMAT user subroutines is used for this investigation. As in the previous studies, the comparisons are made by the use of implementations of hyperelasticity in terms of both principal stretches and the Cauchy-Green invariants. Additionally, an implementation based on that of Simo and Taylor [41] is included in the comparison. The implementation directly computes eigenvalue bases and uses eigenvalue perturbation from Miehe [26] to avoid numerical instabilities.

Fig. 2
figure 2

Inhomogeneous tension test von Mises stress Finite Element solutions: a undeformed mesh 3, b built-in model c developed principal stretch implementation

Full size image

To assess the computational efficiency of the various implementations, their relative solve times are compared to a built-in constitutive model. This also provides further validation of the numerical accuracy. The hyperelastic constitutive model used throughout these investigations is a cubic function of the first isochoric invariant, often referred to as the Yeoh model [48], given by

$$\begin{aligned} W_Y = C_{1}\left( {\overline{I}}_{1}-3\right) +C_{2}{\left( {\overline{I}}_1-3\right) }^2+C_3{\left( {\overline{I}}_1-3\right) }^3 \end{aligned}$$
(53)

The three model parameters are defined for a fit to Treloar’s experimental data [45] of an unfilled natural rubber as \(C_{1} = 0.214\)MPa, \(C_{2} = -1.617\times {10}^{-2}\)MPa and \(C_{3} = 1.204\times {10}^{-3}\)MPa.

4.1 Inhomogeneous tension test

The first benchmark simulation is a 3D inhomogeneous tension test of a rubber specimen. The cuboidal specimen has a 1 mm by 1 mm cross-section and is 1.5 mm long. One of the 1 mm by 1 mm faces of the specimen is fully fixed and a displacement load of 1 mm is applied to the opposing face in the longitudinal direction in a minimum of 10 increments using automatic incrementation. The body is meshed by hybrid, higher-order tetrahedral elements (C3D10H) to further ensure that the principal directions are computed appropriately. The model is solved for five levels of mesh refinement, giving additional insight into any differences in computational effort. Incompressibility is assumed such that only the isochoric constitutive model requires consideration.

In the incremental solution of the inhomogeneous tensile test, the built-in model, the presented implementation and the Cauchy-Green invariant implementation achieve convergence in the specified minimum of 10 increments for all levels of mesh refinement, with the same number of total iterations. However, the Simo and Taylor [41] implementation achieves convergence in 10 increments for only the simplest mesh, where it requires additional iterations the solution of the first increment. For an increasingly refined mesh, the Simo and Taylor [41] implementation requires additional increments due to the numerical instability in the early increments of the solution. The difference between the implementations is present only in their elasticity tensors, however, and so the converged simulation results are identical for all tested outputs at each level of mesh refinement across the four implementations.

The von Mises stress results are shown for the third mesh with 5617 elements in Fig. 2 for solved models using the built-in model and the proposed implementation. For this mesh, the maximum residual forces during convergence have a maximum difference of \(\Delta F\le {10}^{-7}\ N\) between the presented implementation’s model and the built-in model. There are therefore no observable differences between the solved models for all increments.

The computational effort of the implementations are compared by their solve times relative to that of the built-in model. The results for the five levels of mesh refinement are shown in Fig. 3. In this figure, the Cauchy-Green invariant implementation is labelled as “Invariants”, the presented implementation is labelled as “Lambda” and the Simo and Taylor [41] implementation is labelled “S&T”. Throughout, the built-in model is found to be the most computationally efficient, shown by all relative solve times being greater than one. Following this the invariant implementation requires the least computational effort, which is to be expected since it does not require the computation of the eigenvalues and eigenvectors. The most significant result is that the presented implementation has a significantly lower computation time than the implementation based on that of Simo and Taylor [41]. The presented implementation also does not require significant additional computational effort when compared with the invariant implementation, which decreases with increasing mesh refinement.

Fig. 3
figure 3

Solve times of the three user subroutine implementations relative to a built-in model for increasing mesh density of an inhomogeneous tension test

Full size image
Fig. 4
figure 4

Combined tension-torsion test maximum principal stress Finite Element solutions: a undeformed mesh 3, b built-in model c developed principal stretch implementation

Full size image

4.2 Combined tension-torsion test

The second Finite Element benchmark model is of a combined tension-torsion test using a specimen geometry defined within Miehe and Göktepe [28]. A coupling is used on the top face of the specimen with reference to the centre node. In a minimum of 10 increments using automatic incrementation, the reference node is displaced 10mm in the y-direction and rotated \(90^\circ \) around the y axis, the top face is otherwise fixed from expanding or contracting. The bottom face of the specimen is fully fixed. The specimen is meshed by hybrid, first-order hexahedral elements (C3D8H) and is assumed to be incompressible. As with the previous model, five levels of mesh refinement are used.

Fig. 5
figure 5

Solve times of the three user subroutine implementations relative to a built-in model for increasing mesh density of a combined tension-torsion test

Full size image

The combined tension torsion-test reveals similar findings to the previous simulated model. The minimum number of increments are required for the built-in model, the Cauchy-Green invariant implementation and the presented implementation for all levels of mesh refinement, each with the same number of total iterations. The implementation of Simo and Taylor [41] requires additional increments for all meshes and a higher number of total iterations. As in the previous example, the physical results are seemingly identical in the converged solutions. The maximum principal stress results are shown for the third mesh with 5376 elements in Fig. 4, showing seemingly identical results for the built-in and the proposed implementation models.

The computational effort is compared using solve times relative to the built-in model. The results are shown for the five levels of mesh refinement in Fig. 5 with the same labelling as before. It is confirmed that increasing mesh density leads to a smaller difference in solve times for all implementations. However, the developed implementation remains significantly more computationally efficient compared with that based on Simo and Taylor [41] due to its more stable form requiring fewer total increments and iterations. It does have a higher computation time compared with the Cauchy-Green invariant implementation and the latter implementation should be preferred for a constitutive model that is expressible in terms of the Cauchy-Green invariants.

4.3 Discussion

The numerical validation and Finite Element Method investigation results show that the developed implementation is accurate and of satisfactory computational efficiency. Although it is noted that the proposed implementation is not optimised for computational efficiency. The priority of the developed programs and user subroutines is the ease of user implementation. If all implementations were optimised for computational efficiency then the results may differ.

In the case of equal and similar eigenvalues, it is shown that the approximated terms using L’Hôpital’s rule are accurate and valid. It is apparent that in the case of similar eigenvalues that the algorithm and tolerance value could be optimised and improved. However, this would result in imperceptible changes to the accuracy of the Finite Element result and is not considered to be necessary. The developed algorithm and the approximate tolerance of \({10}^{-6}\) is found to produce converging solutions with a maximum error in the order of \({10}^{-11}\).

The spatial elasticity tensor is given in two forms convenient to the derivation. However, it also exists in several other forms due to the requirement of fulfilling objectivity, which is not inherent as in the reference configuration [38]. The developed spatial elasticity tensors are both known to be objective. However, a possible concern is that they may not satisfy work-conjugacy [1, 2, 17, 32, 47] due to a missing volumetric term in both of the objective rates of the elasticity tensors used in this implementation. The error is therefore insignificant for near and full incompressibility. If the compressive behaviour is not negligible, the modification outlined in Bažant et al. [2] should be applied.

5 Conclusions

A Finite Element implementation of hyperelasticity in principal stretches has been proposed. The implementation involves simple user input while attaining numerical robustness and accuracy. The user input is unchanged in the definition of constitutive models in the reference and current configurations. The user is required only to define the derivatives of the isochoric and volumetric strain energy functions with respect to the isochoric principal stretches and the volume ratio. The isochoric principal stretches and associated principal directions are computed explicitly using an iterative Jacobi method. Explicit computation requires additional computational effort, compared with a direct method, but is shown to require less total computational effort due to its improved numerical stability and accuracy. Compared with a built-in model and a Cauchy-Green invariant implementation, the computational effort is satisfactory, which is in part due to the novel use of symmetric dyadic products of the principal directions. These enable Voigt notation to be used throughout, reducing the overall number of computations.

The proposed implementation was validated by numerical investigations of hyperelastic constitutive models that are typically defined in terms of the Cauchy-Green invariants. Evaluations were made between the proposed implementation and a conventional Cauchy-Green invariant implementation. The evaluations show that the proposed implementation is accurate, stable and of similar computational effort. These evaluations were also beneficent in developing and validating the proposed algorithm for applying approximations derived from L’Hôpital’s rule when principal stretches are numerically equal or similar, as to avoid numerical instability and divide by zero errors. The FEM implementation in Abaqus, through use of a UMAT subroutine, shows that the method produces the desired numerical results, with acceptable solve times. This demonstrates that the proposed implementation is suitable for implementing isotropic hyperelastic constitutive models in terms of principal stretches for the FEM.