On the Contractibility of Random Vietoris–Rips Complexes

Abstract

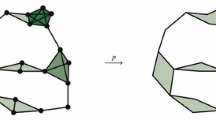
We show that the Vietoris–Rips complex ${\mathcal R}(n,r)$ built over n points sampled at random from a uniformly positive probability measure on a convex body $K\subseteq \mathbb R^d$ is a.a.s. contractible when $r\ge c({\ln n}/{n})^{1/d}$ for a certain constant that depends on K and the probability measure used. This answers a question of Kahle (Discrete Comput. Geom. 45(3), 553–573 (2011)). We also extend the proof to show that if K is a compact, smooth d-manifold with boundary—but not necessarily convex—then ${\mathcal R}(n,r)$ is a.a.s. homotopy equivalent to K when $c_1(\ln n/{n})^{1/d} \le r\le c_2$ for constants $c_1=c_1(K)$, $c_2=c_2(K)$. Our proofs expose a connection with the game of cops and robbers.