Abstract
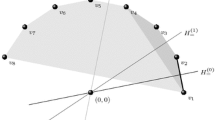
A somewhat fundamental sequence of antiprisms is defined, the d-th antiprism having dimension d, each being a base of the next. The f-vectors of these polytopes are determined. In particular, it is shown that the number of faces of the d-th antiprism is the number of partitions of \(2^{d+1}\) into powers of 2. In order to better understand the structure of the face lattices of these polytopes and their interrelationship, it is convenient also to introduce a countably infinite lattice, the elements of which correspond to the partitions of powers of 2 into powers of 2. This lattice has the property that it is isomorphic to its lattice of intervals, and it is the smallest such lattice.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
Andreev, E.M.: On convex polyhedra in Lobačevskiĭ spaces. Math. Sb. (N.S.) 81(123), 445–478 (1970)
Andrews, G.E., Lawrence, J.: Binary partitions and binary partition polytopes. Aequationes Math. 91(5), 859–869 (2017)
Below, A.: Complexity of Triangulations. PhD thesis, ETH Zürich (2002)
Broadie, M.N.: A theorem about antiprisms. Linear Algebra Appl. 66, 99–111 (1985)
Dobbins, M.G.: Antiprismless, or: Reducing combinatorial equivalence to projective equivalence in realizability problems for polytopes. Discrete Comput. Geom. 57(4), 966–984 (2017)
Etherington, I.M.H.: On non-associative combinations. Proc. R. Soc. Edinb. 59, 153–162 (1939)
Fukuda, K., Weibel, C.: On \(f\)-vectors of Minkowski additions of convex polytopes. Discrete Comput. Geom. 37(4), 503–516 (2007)
Grünbaum, B.: Convex Polytopes. Pure and Applied Mathematics, vol. 16. Interscience, New York (1967)
Koebe, P.: Kontaktprobleme der konformen Abbildung. Ber. Math. Phys. Kl. Sächs Akad. Wiss. Leip. 88, 141–164 (1935)
Lawrence, J.: Parity representations of posets (submitted)
Lindström, B.: Problem P73. Aequationes Math. 6, 113 (1971)
Minc, H.: A problem in partitions: enumeration of elements of a given degree in the free commutative entropic cyclic groupoid. Proc. Edinb. Math. Soc. (2) 11, 223–224 (1958/1959)
Minc, H.: The free commutative entropic logarithmetic. Proc. R. Soc. Edinb. Sect. A 65, 177–192 (1959)
Schramm, O.: How to cage an egg. Invent. Math. 107(3), 543–560 (1992)
Schulte, E.: Analogues of Steinitz’s theorem about noninscribable polyhedra. In: Böröczky, K., Fejes Tóth, G. (eds.) Intuitive Geometry. Colloquia Mathematica Societatis János Bolyai, vol. 48, pp. 503–516. North-Holland, Amsterdam (1987)
Sloane, N.J.A.: The on-line encyclopedia of integer sequences. http://oeis.org
Stanton, D., White, D.: Constructive Combinatorics. Undergraduate Texts in Mathematics. Springer, New York (1986)
Thurston, W.P.: The Geometry and Topology of Three-Manifolds. Lecture Notes. Princeton University, Princeton (1977/1978)
Thurston, W.P.: The geometry and topology of three-manifolds. http://www.msri.org/publications/books/gt3m
Ziegler, G.M.: Lectures on Polytopes. Graduate Texts in Mathematics, vol. 152. Springer, New York (1994)
Ziegler, G.M.: Convex Polytopes: Extremal Constructions and \(f\)-Vector Shapes. Geometric Combinatorics. IAS/Park City Mathematics Series, vol. 13, pp. 617–691. American Mathematical Society, Providence (2007)
Acknowledgements
The paper benefited from comments of Elie Alhajjar, George Andrews, Michael Dobbins, and an unknown referee.
Author information
Authors and Affiliations
Corresponding author
Additional information
Editor in Charge: János Pach
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Lawrence, J. Dual-Antiprisms and Partitions of Powers of 2 into Powers of 2. Discrete Comput Geom 61, 465–478 (2019). https://doi.org/10.1007/s00454-019-00070-5
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00454-019-00070-5