Skip to main content
SpringerLink
Log in

Universality for critical KCM: infinite number of stable directions

  • Published:
Probability Theory and Related Fields Aims and scope Submit manuscript

Abstract

Kinetically constrained models (KCM) are reversible interacting particle systems on \({{\mathbb {Z}}} ^d\) with continuous-time constrained Glauber dynamics. They are a natural non-monotone stochastic version of the family of cellular automata with random initial state known as \({{\mathscr {U}}}\)-bootstrap percolation. KCM have an interest in their own right, owing to their use for modelling the liquid-glass transition in condensed matter physics. In two dimensions there are three classes of models with qualitatively different scaling of the infection time of the origin as the density of infected sites vanishes. Here we study in full generality the class termed ‘critical’. Together with the companion paper by Hartarsky et al. (Universality for critical KCM: finite number of stable directions. arXiv e-prints arXiv:1910.06782, 2019) we establish the universality classes of critical KCM and determine within each class the critical exponent of the infection time as well as of the spectral gap. In this work we prove that for critical models with an infinite number of stable directions this exponent is twice the one of their bootstrap percolation counterpart. This is due to the occurrence of ‘energy barriers’, which determine the dominant behaviour for these KCM but which do not matter for the monotone bootstrap dynamics. Our result confirms the conjecture of Martinelli et al. (Commun Math Phys 369(2):761–809. https://doi.org/10.1007/s00220-018-3280-z, 2019), who proved a matching upper bound.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6

Similar content being viewed by others

Notes

  1. For the lower bound of \(T_{\mathrm {rel}}\) one does not need to use the boostrap percolation results, as \(T_{\mathrm {rel}}\geqslant q^{-\min _{U\in {{\mathscr {U}}}}|U|}/|{{\mathscr {U}}}|\) by plugging the test function \({\mathbb {1}} _{\{\omega _0=0\}}\) in Definition 2.5.

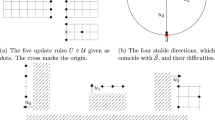
  2. Note that, since the Duarte update rules contain only the North, South and West neighbours of the origin, the constraint at a site x does not depend on the sites with abscissa larger than the abscissa of x.

  3. Actually these references focus on the study of \(T_{\mathrm {rel}}\). A matching upper bound for \({{\mathbb {E}}} (\tau _0)\) follows from (10). The lower bound for \({{\mathbb {E}}} (\tau _0)\) follows easily from the lower bound for \({{\mathbb {P}}} (\tau _0>t)\) with \(t=\exp {(\log (q)^2/2\log 2)}\) obtained in the proof of Theorem 5.1 of [11].

  4. The conjecture involuntarily asks for a positive power of \(\log q\), which we do not expect to be systematically present (see Conjecture 7.1).

  5. For the 3-rule model alluded to in Sect. 3 stable sets consist precisely of Young diagrams and the directions \({{\mathscr {S}}}\) provided by Lemma 4.1 can be arbitrarily close to the four axis directions, yielding Young diagrams.

  6. Associativity was referred to as commutativity by previous authors [8].

References

  1. Aizenman, M., Lebowitz, J.L.: Metastability effects in bootstrap percolation. J. Phys. A 21(19), 3801–3813 (1988). http://stacks.iop.org/0305-4470/21/3801

  2. Aldous, D., Diaconis, P.: The asymmetric one-dimensional constrained Ising model: rigorous results. J. Stat. Phys. 107(5–6), 945–975 (2002). https://doi.org/10.1023/A:1015170205728

    Article  MathSciNet  MATH  Google Scholar 

  3. Bakry, D.: Functional inequalities for Markov semigroups. In: Probability measures on groups: recent directions and trends, pp. 91–147. Tata Inst. Fund. Res., Mumbai (2006)

  4. Balister, P., Bollobás, B., Przykucki, M., Smith, P.: Subcritical \({\cal{U}}\)-bootstrap percolation models have non-trivial phase transitions. Trans. Amer. Math. Soc. 368(10), 7385–7411 (2016). https://doi.org/10.1090/tran/6586

    Article  MathSciNet  MATH  Google Scholar 

  5. Berthier, L., Biroli, G.: Theoretical perspective on the glass transition and amorphous materials. Rev. Mod. Phys. 83, 587–645 (2011). https://doi.org/10.1103/RevModPhys.83.587

    Article  Google Scholar 

  6. Bollobás, B., Duminil-Copin, H., Morris, R., Smith, P.: The sharp threshold for the Duarte model. Ann. Probab. 45(6B), 4222–4272 (2017). https://doi.org/10.1214/16-AOP1163

    Article  MathSciNet  MATH  Google Scholar 

  7. Bollobás, B., Duminil-Copin, H., Morris, R., Smith, P.: Universality of two-dimensional critical cellular automata. Proc. Lond. Math. Soc. (to appear)

  8. Bollobás, B., Smith, P., Uzzell, A.: Monotone cellular automata in a random environment. Combin. Probab. Comput. 24(4), 687–722 (2015). https://doi.org/10.1017/S0963548315000012

    Article  MathSciNet  MATH  Google Scholar 

  9. Cancrini, N., Martinelli, F., Roberto, C., Toninelli, C.: Kinetically constrained spin models. Probab. Theory Related Fields 140(3–4), 459–504 (2008). https://doi.org/10.1007/s00440-007-0072-3

    Article  MathSciNet  MATH  Google Scholar 

  10. Cancrini, N., Martinelli, F., Roberto, C., Toninelli, C.: Facilitated spin models: recent and new results. In: Methods of contemporary mathematical statistical physics, Lecture Notes in Math., vol. 1970, pp. 307–340. Springer, Berlin (2009)

  11. Cancrini, N., Martinelli, F., Schonmann, R., Toninelli, C.: Facilitated oriented spin models: some non equilibrium results. J. Stat. Phys. 138(6), 1109–1123 (2010). https://doi.org/10.1007/s10955-010-9923-x

    Article  MathSciNet  MATH  Google Scholar 

  12. Chleboun, P., Faggionato, A., Martinelli, F.: Time scale separation and dynamic heterogeneity in the low temperature East model. Commun. Math. Phys. 328(3), 955–993 (2014). https://doi.org/10.1007/s00220-014-1985-1

    Article  MathSciNet  MATH  Google Scholar 

  13. Chleboun, P., Faggionato, A., Martinelli, F.: Relaxation to equilibrium of generalized East processes on \({\mathbb{Z}}^d\): renormalization group analysis and energy-entropy competition. Ann. Probab. 44(3), 1817–1863 (2016). https://doi.org/10.1214/15-AOP1011

    Article  MathSciNet  MATH  Google Scholar 

  14. Chung, F., Diaconis, P., Graham, R.: Combinatorics for the East model. Adv. Appl. Math. 27(1), 192–206 (2001). https://doi.org/10.1006/aama.2001.0728

    Article  MathSciNet  MATH  Google Scholar 

  15. Faggionato, A., Martinelli, F., Roberto, C., Toninelli, C.: The East model: recent results and new progresses. Markov Process. Related Fields 19(3), 407–452 (2013)

    MathSciNet  MATH  Google Scholar 

  16. Fredrickson, G.H., Andersen, H.C.: Kinetic Ising model of the glass transition. Phys. Rev. Lett. 53, 1244–1247 (1984). https://doi.org/10.1103/PhysRevLett.53.1244

    Article  Google Scholar 

  17. Garrahan, P., Sollich, P., Toninelli, C.: Kinetically constrained models. In: Berthier, L., Biroli, G., Bouchaud, J.P., Cipelletti, L., van Saarloos, W. (eds.) Dynamical heterogeneities in Glasses, colloids and granular media and jamming transitions, International series of monographs on physics 150, pp. 341–369. Oxford University Press (2011). https://hal.archives-ouvertes.fr/hal-00563884

  18. Harris, T.E.: A lower bound for the critical probability in a certain percolation process. Proc. Camb. Philos. Soc. 56, 13–20 (1960)

    Article  MathSciNet  Google Scholar 

  19. Hartarsky, I.: \({\cal{U}}\)-bootstrap percolation: critical probability, exponential decay and applications. arXiv e-prints arXiv:1806.11405 (2018)

  20. Hartarsky, I., Martinelli, F., Toninelli, C.: Universality for critical KCM: finite number of stable directions. arXiv e-prints arXiv:1910.06782 (2019)

  21. Hartarsky, I., Mezei, T.: Complexity of 2D bootstrap percolation difficulty: Algorithm and NP-hardness. arXiv e-prints arXiv:1809.01525 (2018)

  22. Holroyd, A.E.: Sharp metastability threshold for two-dimensional bootstrap percolation. Probab. Theory Related Fields 125(2), 195–224 (2003). https://doi.org/10.1007/s00440-002-0239-x

    Article  MathSciNet  MATH  Google Scholar 

  23. Jäckle, J., Eisinger, S.: A hierarchically constrained kinetic Ising model. Z. Phys. B Con. Mat. 84(1), 115–124 (1991). https://doi.org/10.1007/BF01453764

    Article  MATH  Google Scholar 

  24. Liggett, T.M.: Interacting particle systems. Classics in Mathematics. Springer-Verlag, Berlin (2005). https://doi.org/10.1007/b138374. Reprint of the 1985 original

  25. Marêché, L., Martinelli, F., Toninelli, C.: Exact asymptotics for Duarte and supercritical rooted kinetically constrained models. Ann. Probab. (to appear)

  26. Martinelli, F., Morris, R., Toninelli, C.: Universality results for kinetically constrained spin models in two dimensions. Commun. Math. Phys. 369(2), 761–809 (2019). https://doi.org/10.1007/s00220-018-3280-z

    Article  MathSciNet  MATH  Google Scholar 

  27. Martinelli, F., Toninelli, C.: Towards a universality picture for the relaxation to equilibrium of kinetically constrained models. Ann. Probab. 47(1), 324–361 (2019). https://doi.org/10.1214/18-AOP1262

    Article  MathSciNet  MATH  Google Scholar 

  28. Morris, R.: Bootstrap percolation, and other automata. Eur. J. Combin. 66, 250–263 (2017). https://doi.org/10.1016/j.ejc.2017.06.024

    Article  MathSciNet  MATH  Google Scholar 

  29. Morris, R.: Monotone cellular automata. In: Surveys in combinatorics 2017, London Math. Soc. Lecture Note Ser., vol. 440, pp. 312–371. Cambridge Univ. Press, Cambridge (2017)

  30. Mountford, T.S.: Critical length for semi-oriented bootstrap percolation. Stoch. Process. Appl. 56(2), 185–205 (1995). https://doi.org/10.1016/0304-4149(94)00061-W

    Article  MathSciNet  MATH  Google Scholar 

  31. Ritort, F., Sollich, P.: Glassy dynamics of kinetically constrained models. Adv. Phys. 52(4), 219–342 (2003). https://doi.org/10.1080/0001873031000093582

    Article  Google Scholar 

  32. Sollich, P., Evans, M.R.: Glassy time-scale divergence and anomalous coarsening in a kinetically constrained spin chain. Phys. Rev. Lett. 83, 3238–3241 (1999). https://doi.org/10.1103/PhysRevLett.83.3238

    Article  Google Scholar 

Download references

Acknowledgements

We wish to thank Fabio Martinelli for numerous and enlightening discussions and the Departement of Mathematics and Physics of University Roma Tre for its kind hospitality.

Author information

Authors and Affiliations

  1. DMA UMR 8553, École Normale Supérieure, PSL University, CNRS, 45 rue d’Ulm, 75005, Paris, France

    Ivailo Hartarsky

  2. CEREMADE UMR 7534, Université Paris-Dauphine, PSL University, CNRS, Place du Maréchal de Lattre de Tassigny, 75775, Paris Cedex 16, France

    Ivailo Hartarsky & Cristina Toninelli

  3. LPSM UMR 8001, Université Paris Diderot, Sorbonne Paris Cité, CNRS, 75013, Paris, France

    Laure Marêché

Authors
  1. Ivailo Hartarsky
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Laure Marêché
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Cristina Toninelli
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Ivailo Hartarsky.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

This work was supported by European Research Council Starting Grant 680275 MALIG and by Agence Nationale de la Recherche-15-CE40-0020-01.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Hartarsky, I., Marêché, L. & Toninelli, C. Universality for critical KCM: infinite number of stable directions. Probab. Theory Relat. Fields 178, 289–326 (2020). https://doi.org/10.1007/s00440-020-00976-9

Download citation

  • Received:

  • Revised:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00440-020-00976-9

Keywords

Mathematics Subject Classification

Search

Navigation