Abstract
We introduce and study the inhomogeneous exponential jump model—an integrable stochastic interacting particle system on the continuous half line evolving in continuous time. An important feature of the system is the presence of arbitrary spatial inhomogeneity on the half line which does not break the integrability. We completely characterize the macroscopic limit shape and asymptotic fluctuations of the height function (= integrated current) in the model. In particular, we explain how the presence of inhomogeneity may lead to macroscopic phase transitions in the limit shape such as shocks or traffic jams. Away from these singularities the asymptotic fluctuations of the height function around its macroscopic limit shape are governed by the GUE Tracy–Widom distribution. A surprising result is that while the limit shape is discontinuous at a traffic jam caused by a macroscopic slowdown in the inhomogeneity, fluctuations on both sides of such a traffic jam still have the GUE Tracy–Widom distribution (but with different non-universal normalizations). The integrability of the model comes from the fact that it is a degeneration of the inhomogeneous stochastic higher spin six vertex models studied earlier in Borodin and Petrov (Higher spin six vertex model and symmetric rational functions, doi:10.1007/s00029-016-0301-7, arXiv:1601.05770 [math.PR], 2016). Our results on fluctuations are obtained via an asymptotic analysis of Fredholm determinantal formulas arising from contour integral expressions for the q-moments in the stochastic higher spin six vertex model. We also discuss “product-form” translation invariant stationary distributions of the exponential jump model which lead to an alternative hydrodynamic-type heuristic derivation of the macroscopic limit shape.












Similar content being viewed by others
Notes
But not always: a notable open problem is to find an integrable structure in ASEP (a two-sided generalization of TASEP) with particle-dependent jump rates.
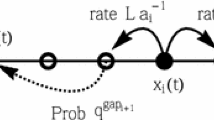
Here and below we say that a certain event has rate \(\mu >0\) if it repeats after independent random time intervals which have exponential distribution with rate \(\mu \) (and mean \(\mu ^{-1}\)). That is, \(\mathbb {P}(\hbox {time between occurrences}>\Delta t) =e^{-\mu \Delta t}\). These independent exponentially distributed random times are also assumed independent from the rest of the system.
By stationary we mean distributions which do not change under the corresponding stochastic evolution, and translation invariance means invariance under spatial translations of \(\mathbb {R}\).
Though for \(\alpha =\upomega ^\circ _{\tau ,x}\) this roadblock changes the fluctuation distribution at \(x=\sigma \) from the GUE Tracy–Widom to a BBP one.
Throughout the paper we use the q-Pochhammer symbol notation \((z;q)_{m}=\prod _{i=0}^{m-1}(1-zq^{i})\), \(m\in \mathbb {Z}_{\ge 0}\). Since \(0<q<1\) it makes sense for \(m=+\,\infty \), too.
Here and below \(B,B_1,B_2,\ldots \) and \(c,c',c'',c_1,c_2,\ldots \) are positive constants which may depend on q, the parameters of the models, or the data in the formulation of the statements (such as the angle \(\varphi \), etc.).
The change of variables in a neighborhood of \(\upomega ^\circ _{\tau ,x}\) introduces a scaling factor \({\uplambda }^{-\frac{2}{3}}(d^{\mathrm {TW}}_{\tau ,x})^{-2}\) coming from dz in the kernel itself and from the integrals over \(w,w'\), cf. (2.12). This scaling of the kernel is reflected in the notation \(\sqrt{dw\,dw'}\) which we will also use below in similar situations.
The assumption that there are no roadblocks makes sense because we expect that \(\mathbf {X}^{\mathbb {R}}\) should describe local behavior under the inhomogeneous exponential jump model from Sect. 2.1, and roadblocks cannot accumulate locally.
References
Aggarwal, A.: Current fluctuations of the stationary ASEP and six-vertex model (2016). arXiv:1608.04726 [math.PR]
Aggarwal, A., Borodin, A.: Phase transitions in the ASEP and Stochastic six-vertex model (2016). arXiv:1607.08684 [math.PR]
Andjel, E.: Invariant measures for the zero range process. Ann. Probab. 10(3), 525–547 (1982)
Andjel, E., Kipnis, C.: Derivation of the hydrodynamical equation for the zerorange interaction process. Ann. Probab. 12(2), 325–334 (1984)
Baik, J.: Painlevé formulas of the limiting distributions for nonnull complex sample covariance matrices. Duke Math J. 133(2), 205–235 (2006). arXiv:math/0504606 [math.PR]
Baik, J., Ben Arous, G., Péchée, S.: Phase transition of the largest eigenvalue for nonnull complex sample covariance matrices. Ann. Probab. 33(5), 1643–1697 (2005). arXiv:math/0403022 [math.PR]
Barraquand, G.: A phase transition for q-TASEP with a few slower particles. Stoch. Process. Appl. 125(7), 2674–2699 (2015). arXiv:1404.7409 [math.PR]
Barraquand, G., Corwin, I.: The \(q\)-Hahn asymmetric exclusion process. Ann. Appl. Probab. 26(4), 2304–2356 (2016). arXiv:1501.03445 [math.PR]
Basu, R., Sidoravicius, V., Sly, A.: Last passage percolation with a defect line and the solution of the slow bond problem (2014). arXiv:1408.3464 [math.PR]
Baxter, R.: Exactly Solved Models in Statistical Mechanics. Courier Dover Publications, Mineola (2007)
Bengrine, M., Benyoussef, A., Ez-Zahraouy, H., Krug, J., Loulidi, M., Mhirech, F.: A simulation study of an asymmetric exclusion model with disorder. MJ Condens. Matter 2(1), 117–126 (1999)
Blank, M.: Exclusion-type spatially heterogeneous processes in continua. In: Jour. Stat. Mech. 2011.06 (2011). arXiv:1105.4232 [math.DS], P06016
Blank, M.: Discrete time TASEP in heterogeneous continuum. Markov Process. Relat. Fields 18(3), 531–552 (2012)
Bornemann, F.: On the numerical evaluation of Fredholm determinants. Math. Comp. 79(270), 871–915 (2010). arXiv:0804.2543 [math.NA]
Borodin, A.: Stochastic higher spin six vertex model and Madconald measures (2016). arXiv:1608.01553 [math-ph]
Borodin, A.: On a family of symmetric rational functions. Adv. Math. 306, 973–1018 (2017). arXiv:1410.0976 [math.CO]
Borodin, A., Bufetov, A., Wheeler, M.: Between the stochastic six vertex model and Hall-Littlewood processes (2016). arXiv:1611.09486 [math.PR]
Borodin, A., Corwin, I.: Macdonald processes. Prob. Theory Relat. Fields 158, 225–400 (2014). arXiv:1111.4408 [math.PR]
Borodin, A., Corwin, I., Ferrari, P.: Free energy fluctuations for directed polymers in random media in \(1 + 1\) dimension. Commun. Pure Appl. Math. 67(7), 1129–1214 (2014). arXiv:1204.1024 [math.PR]
Borodin, A., Corwin, I., Gorin, V.: Stochastic six-vertex model. Duke J. Math. 165(3), 563–624 (2016). arXiv:1407.6729 [math.PR]
Borodin, A., Corwin, I., Petrov, L., Sasamoto, T.: Spectral theory for the q-Boson particle system. Compos. Math. 151(1), 1–67 (2015). arXiv:1308.3475 [mathph]
Borodin, A., Ferrari, P.: Anisotropic growth of random surfaces in 2+1 dimensions. Commun. Math. Phys. 325, 603–684 (2014). arXiv:0804.3035 [math-ph]
Borodin, A., Ferrari, P., Sasamoto, T.: Two speed TASEP. J. Stat. Phys. 137(5), 936–977 (2009). arXiv:0904.4655 [math-ph]
Borodin, A., Petrov, L.: Higher spin six vertex model and symmetric rational functions (2016). doi:10.1007/s00029-016-0301-7, arXiv:1601.05770 [math.PR]. (To appear in Selecta Mathematica, New Series)
Borodin, A., Petrov, L.: Lectures on integrable probability: stochastic vertex models and symmetric functions (2016). arXiv:1605.01349 [math.PR]
Corwin, I.: The Kardar–Parisi–Zhang equation and universality class. In: Random Matrices Theory Appl., vol 1 (2012). arXiv:1106.1596 [math.PR]
Corwin, I., Petrov, L.: Stochastic higher spin vertex models on the line. Commun. Math. Phys. 343(2), 651–700 (2016). arXiv:1502.07374 [math.PR]
Costin, O., Lebowitz, J., Speer, E., Troiani, A.: The blockage problem. Bull. Inst. Math. Acad. Sin. (New Series) 8(1), 47–72 (2013). arXiv:1207.6555 [math-ph]
Dong, J., Zia, R., Schmittmann, B.: Understanding the edge effect in TASEP with mean-field theoretic approaches. J. Phys. A 42(1), 015002 (2008). arXiv:0809.1974 [cond-mat.stat-mech]
Duits, M.: The Gaussian free field in an interlacing particle system with two jump rates. Commun. Pure Appl. Math. 66(4), 600–643 (2013). arXiv:1105.4656 [math-ph]
Ferrari, P., Spohn, H.: Random growth models. In: Akemann, G., Baik, J., Di Francesco, P. (eds.) Oxford Handbook of Random Matrix Theory. Oxford University Press (2011). arXiv:1003.0881 [math.PR]
Ferrari, P., Veto, B.: Tracy–Widom asymptotics for q-TASEP. Ann. Inst. H. Poincaré, Probabilités et Statistiques 51(4), 1465–1485 (2015). arXiv:1310.2515 [math.PR]
Gasper, G., Rahman, M.: Basic Hypergeometric Series. Cambridge University Press, Cambridge (2004)
Georgiou, N., Kumar, R., Seppäläinen, T.: TASEP with discontinuous jump rates. ALEA Lat. Am. J. Probab. Math. Stat. 7, 293–318 (2010). arXiv:1003.3218 [math.PR]
Ghosal, P.: Hall-Littlewood-PushTASEP and its KPZ limit (2017). arXiv:1701.07308 [math.PR]
Gwa, L.-H., Spohn, H.: Six-vertex model, roughened surfaces, and an asymmetric spin Hamiltonian. Phys. Rev. Lett. 68(6), 725–728 (1992)
Helbing, D.: Traffic and related self-driven many-particle systems. Rev. Mod. Phys. 73(4), 1067–1141 (2001). arXiv:cond-mat/0012229 [cond-mat.stat-mech]
Johansson, K.: Shape fluctuations and random matrices. Commun. Math. Phys. 209(2), 437–476 (2000). arXiv:math/9903134 [math.CO]
Knizel, A., Petrov, L.: In preparation (2017)
Krug, J.: Phase separation in disordered exclusion models. Braz. J. Phys. 30(1), 97–104 (2000). arXiv:cond-mat/9912411 [cond-mat.stat-mech]
Krug, J., Ferrari, P.A.: Phase transitions in driven diffusive systems with random rates. J. Phys. A Math. Gen. 29(18), L465 (1996)
Kulish, P., Reshetikhin, N., Sklyanin, E.: Yang–Baxter equation and representation theory: I. Lett. Math. Phys. 5(5), 393–403 (1981)
Landim, C.: Hydrodynamical limit for space inhomogeneous one-dimensional totally asymmetric zero-range processes. Ann. Probab. 24(2), 599–638 (1996)
Liggett, T.: An infinite particle system with zero range interactions. Ann. Probab. 1(2), 240–253 (1973)
Liggett, T.: Interacting Particle Systems. Springer, Berlin (2005)
MacDonald, C., Gibbs, J., Pipkin, A.: Kinetics of biopolymerization on nucleic acid templates. Biopolymers 6(1), 1–25 (1968)
Mangazeev, V.: On the Yang–Baxter equation for the six-vertex model. Nucl. Phys. B 882, 70–96 (2014). arXiv:1401.6494 [math-ph]
Matetski, K., Quastel, J., Remenik, D.: The KPZ fixed point (2017). arXiv:1701.00018 [math.PR]
Okounkov, A.: Infinite wedge and random partitions. Sel. Math. New Ser. 7(1), 57–81 (2001). arXiv:math/9907127 [math.RT]
Okounkov, A., Reshetikhin, N.: Correlation function of Schur process with application to local geometry of a random 3-dimensional Young diagram. J. Am. Math. Soc. 16(3), 581–603 (2003). arXiv:math/0107056 [math.CO]
Orr, D., Petrov, L.: Stochastic higher spin six vertex model and \(q\)-TASEPs (2016). arXiv:1610.10080 [math.PR]
Quastel, J., Spohn, H.: The one-dimensional KPZ equation and its universality class. J. Stat. Phys. 160(4), 965–984 (2015). arXiv:1503.06185 [math-ph]
Rezakhanlou, F.: Hydrodynamic limit for attractive particle systems on \(\mathbb{Z}^{d}\). Commun. Math. Phys. 140(3), 417–448 (1991)
Seppäläinen, T.: Existence of hydrodynamics for the totally asymmetric simple Kexclusion process. Ann. Probab. 27(1), 361–415 (1999)
Seppäläinen, T.: Hydrodynamic profiles for the totally asymmetric exclusion process with a slow bond. J. Stat. Phys. 102(1–2), 69–96 (2001). arXiv:math/0003049 [math.PR]
Spitzer, F.: Interaction of Markov processes. Adv. Math. 5(2), 246–290 (1970)
Spohn, H.: Large Scale Dynamics of Interacting Particles. Springer, Berlin (1991)
Tracy, C., Widom, H.: Level-spacing distributions and the Airy kernel. In: Comm. Math. Phys. 159.1, pp. 151–174 (1994). arXiv:hep-th/9211141, issn: 0010-3616
Tracy, C., Widom, H.: Asymptotics in ASEP with step initial condition. Commun. Math. Phys. 290, 129–154 (2009). arXiv:0807.1713 [math.PR]
Tracy, C., Widom, H.: On ASEP with step Bernoulli initial condition. J. Stat. Phys. 137, 825–838 (2009). arXiv:0907.5192 [math.PR]
Veto, B.: Tracy–Widom limit of q-Hahn TASEP. Electronic Journal of Probability 20(102), 22 (2015). arXiv:1407.2787 [math.PR]
Acknowledgements
The authors are grateful to discussions with Guillaume Barraquand, Ivan Corwin, Michael Blank, Tomohiro Sasamoto, Herbert Spohn, Kazumasa Takeuchi, and Jon Warren. The research was carried out in part during the authors’ participation in the Kavli Institute for Theoretical Physics program “New approaches to non-equilibrium and random systems: KPZ integrability, universality, applications and experiments”, and consequently was partially supported by the National Science Foundation PHY11-25915. A. B. is supported by the National Science Foundation grant DMS-1607901 and by Fellowships of the Radcliffe Institute for Advanced Study and the Simons Foundation.
Author information
Authors and Affiliations
Corresponding author
Appendices
Appendix A: q-polygamma functions
Here we list a number of formulas related to the q-gamma and q-polygamma functions which are used throughout the paper. The q-gamma function is defined by (we always assume \(q\in (0,1)\))
We have \(\lim _{q\nearrow 1}\Gamma _q(z)=\Gamma (z)\). The log-derivative of \(\Gamma _q(z)\) (the q-digamma function) is denoted by
It is straightforward that
which is a meromorphic function in z having poles when \(q^{z+k}=1\) (and the series converges for any z except these poles thanks to the factors \(q^k\)).
The following formula is an alternative series representation for derivatives of \(\psi _q(z)\) (the so-called q-polygamma functions):
e.g., see [8, Lemma 2.1] for the computation. In contrast with (A.1), this series converges only when \(|q^{z}|<1\), i.e., when \(\mathop {\mathrm {Re}}z>0\).
It is convenient to replace \(q^{z}\) by w, and define for any \(n\ge 0\):
We thus have
The latter formula gives an analytic continuation of the series (A.3) to a meromorphic function of \(w\in \mathbb {C}\) having poles of order \(n+1\) at \(w=q^{-k}\), \(k\in \mathbb {Z}_{\ge 0}\).
Several useful properties of the functions \(\phi _n\) are summarized below:
Proposition A.1
We have
The functions \(\phi _{0}(w)\) and \(\phi _{1}(w)\) are negative for negative real w, and \(\phi _{1}(w)\) and \(\phi _{3}(w)\) are positive for positive real \(w\notin q^{\mathbb {Z}_{\le 0}}\), while \(\phi _{2}(w)\) is positive for \(w\in (0,1)\). Moreover, \(\phi _{n}(0)=0\) for all n.
Proof
The claim about the derivatives is straightforward from either (A.3) or (A.4). To check the signs of the \(\phi _n\)’s, let us use the series (A.1) and its derivatives to get formulas for \(\phi _n(w)\) valid for all w. We have
This immediately implies all the remaining claims. \(\square \)
Appendix B: Translation invariant stationary distributions
1.1 B.1 Preliminaries
Here we perform computations related to translation invariant stationary distributions of homogeneous versions of our particle systems on the whole (discrete or continuous) line. Classification of translation invariant stationary distributions for rather general zero range processes (in the sense of [56]) on \(\mathbb {Z}\) is well-known, e.g., see [3]. In particular, under mild conditions on the process every translation invariant stationary distribution is a mixture of product measures. Here by a product measure we mean assigning random independent identically distributed numbers of particles at each location in \(\mathbb {Z}\) (such a random configuration is clearly translation invariant).
While neither the half-continuous stochastic higher spin six vertex model nor the exponential jump model are zero range, the existence (for suitable initial configurations) of these processes on \(\mathbb {Z}\) and \(\mathbb {R}\), respectively, can be established similarly to [3, 44]. The main observation is that our process on \(\mathbb {Z}\) (denote it by \(\mathbf {X}_{\mathrm {hc}}^{\mathbb {Z}}(t)\)) is “slower” than the zero range process (with the geometric jumping distribution) obtained by dropping the interaction of the flying particles with the sitting ones. In the case of the continuous space, our process (denote it by \(\mathbf {X}^{\mathbb {R}}(t)\)) is “slower” than simply the process of independent particles each of which jumps to the right by an exponentially distributed random distance after exponentially distributed time intervals. Therefore, to show the existence of both \(\mathbf {X}_{\mathrm {hc}}^{\mathbb {Z}}\) and \(\mathbf {X}^{\mathbb {R}}\) one can essentially repeat the estimates of [44] or [3] (with suitable modifications in the case of the continuous space). This also implies that product measures on \(\mathbb {Z}\) or their analogues on \(\mathbb {R}\), marked Poisson processes (see Definition B.2 below), can serve as (random) initial configurations for \(\mathbf {X}_{\mathrm {hc}}^{\mathbb {Z}}\) and \(\mathbf {X}^{\mathbb {R}}\), respectively, provided that the random number of points at a single location has, say, two finite first moments.
Here we do not attempt to classify all translation invariant stationary distributions of \(\mathbf {X}_{\mathrm {hc}}^{\mathbb {Z}}\) and \(\mathbf {X}^{\mathbb {R}}\), but instead show that certain specific product measures or marked Poisson processes are indeed stationary under our systems. We also obtain formulas for particle density and particle current (sometimes also called particle flux) for these measures which (in the case of \(\mathbf {X}^{\mathbb {R}}\)) are employed in the heuristic derivation of the macroscopic limit shape for the height function in Sect. 2.2 ( based on the assumption that these measures describe local behavior of the inhomogeneous exponential jump model).
1.2 B.2 Stationary distributions for half-continuous vertex model
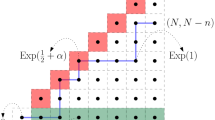
Let \(\mathbf {X}_{\mathrm {hc}}^{\mathbb {Z}}(t)\) be the homogeneous version of the half-continuous stochastic higher spin six vertex model (described in Sect. 3.3) which is well-defined on a suitable subset of \(\mathrm {Conf}_{\bullet }^{\sim }(\mathbb {Z})\), the space of possibly countably infinite particle configurations in \(\mathbb {Z}\) with multiple (but finitely many) particles per location allowed. This process depends on parameters \(\upxi _i\equiv \upxi >0\) and \(\mathsf {s}_i\equiv \mathsf {s}\in (-1,0)\).
For any \(c\ge 0\), let \({\varvec{\upvarphi }}^{\mathrm {hc}}_{c,\mathsf {s}^2}\) be the probability distribution on \(\left\{ 0,1,2,\ldots \right\} \) defined as
The fact that these quantities sum to one follows from the q-binomial theorem [33, (1.3.2)]. When \(\mathsf {s}=0\), \({\varvec{\upvarphi }}^{\mathrm {hc}}_{c,\mathsf {s}^2}\) turns into the distribution \((c;q)_{\infty }c^j/(q;q)_j\) which is often called the q-geometric distribution. The latter in turn becomes the usual geometric distribution \((1-c)c^j\) when \(q=0\).
Let \({\mathfrak {m}}^{\mathrm {hc}}_{c,\mathsf {s}^2}=({\varvec{\upvarphi }}^{\mathrm {hc}}_{c,\mathsf {s}^2})^{\otimes \mathbb {Z}}\) be the product probability measure on \(\left\{ 0,1,2,\ldots \right\} ^{\mathbb {Z}}\) corresponding to the number of particles at each location distributed as \({\varvec{\upvarphi }}^{\mathrm {hc}}_{c,\mathsf {s}^2}\), all of them being independent.
Proposition B.1
For any \(c\ge 0\), the measure \({\mathfrak {m}}^{\mathrm {hc}}_{c,\mathsf {s}^2}\) on \(\mathrm {Conf}_{\bullet }^{\sim }(\mathbb {Z})\) is stationary under the process \(\mathbf {X}_{\mathrm {hc}}^{\mathbb {Z}}(t)\) with the matching parameter \(\mathsf {s}\) and arbitrary \(\upxi \).
Proof
It suffices to consider the evolution of the distribution of the number of particles at a given location in \(\mathbb {Z}\). If there are \(k\ge 0\) particles at this location, then one particle leaves it at rate
Let us compute \({\mathrm {Rate}}(k\rightarrow k+1)\). Let \(Y^{\mathrm {hc}},Y_1^{\mathrm {hc}},Y_2^{\mathrm {hc}},\ldots \) be independent random variables distributed as \({\varvec{\upvarphi }}^{\mathrm {hc}}_{c,\mathsf {s}^2}\). The rate at which a particle joins a stack of k particles has the following form:

One readily sees that
and thus the sum in (B.2) simplifies to
The desired stationarity now follows from the identity which can be readily verified:
( if \(k=0\), then by agreement \( {\mathrm {Rate}}(0\rightarrow -1) = {\mathrm {Rate}}(-1\rightarrow 0) = 0 \)). \(\square \)
Let us now compute the particle density \({\rho }^{\mathrm {hc}}(c)\) and the particle current \({\jmath }^{\mathrm {hc}}(c)\) associated with the product measure \({\mathfrak {m}}^{\mathrm {hc}}_{c,\mathsf {s}^2}\) (a similar computation appears in [61]). The particle current is the average number of particles jumping over any given location per unit time. This quantity is given by the sum in the right-hand side of (B.2) without the last factor \((1-\mathsf {s}^2q^k)\), and hence
The particle density is the average number of particles per location, it is equal to
where in the last equality we used (A.6). We will not further pursue formulas for the discrete model, and instead in the next two subsections turn to the exponential jump model as it is the main object of the present paper.
1.3 B.3 Stationary distributions for the exponential jump model
The homogeneous exponential jump model \(\mathbf {X}^{\mathbb {R}}(t)\) on the whole line depends on parameters \({\varvec{\upxi }}(x)\equiv {\varvec{\upxi }}>0\) and \({\uplambda }>0\), and we assume that there are no roadblocks.Footnote 8 We will use the following analogue of product measures on the continuous line:
Definition B.2
A marked Poisson process with marks following a probability distribution \({\varvec{\upvarphi }}\) on \(\mathbb {Z}_{\ge 1}\) is a probability measure on \(\mathrm {Conf}_{\bullet }^{\sim }(\mathbb {R})\) (i.e., a random particle configuration in \(\mathbb {R}\)) obtained as follows. Take a (homogeneous) Poisson process on \(\mathbb {R}\) with some rate \(\mu >0\), and at each point of this Poisson process put a random number of particles according to the distribution \({\varvec{\upvarphi }}\) on \(\mathbb {Z}_{\ge 1}\), independently for each point of the Poisson process.
As explained in Sect. 3.4, the exponential jump model arises from the half-continuous vertex model as \(\mathsf {s}^2=e^{- {\uplambda }\varepsilon }\rightarrow 1\), \(-\upxi \mathsf {s}={\varvec{\upxi }}\) is fixed, and the discrete space is rescaled by \(\varepsilon \) to become continuous. In this limit regime the distribution \({\varvec{\upvarphi }}^{\mathrm {hc}}_{c,\mathsf {s}^2}\) (B.1) behaves as follows:
and for any \(j\ge 1\) we have
In other words, the product measure \({\mathfrak {m}}^{\mathrm {hc}}_{c,\mathsf {s}^2}\) from “Appendix B.2” turns into a marked Poisson process with rate \({\uplambda }\phi _0(c)\) and marking distribution
Denote this marked Poisson process by \(\mathfrak {m}_{c,{\uplambda }}\).
Proposition B.3
For any \(c\ge 0\) the measure \(\mathfrak {m}_{c,{\uplambda }}\) on \(\mathrm {Conf}_{\bullet }^{\sim }(\mathbb {R})\) is stationary under the process \(\mathbf {X}^{\mathbb {R}}(t)\) with the matching parameter \({\uplambda }\) and arbitrary parameter \({\varvec{\upxi }}\).
Proof
The proof is a continuous space modification of the one of Proposition B.1. However, as the continuous space computations are somewhat more involved, let us give some details. Fix \(x\in \mathbb {R}\), and consider the evolution of the distribution of the number of particles in \((x,x+dx)\). First, if there are \(k\ge 1\) particles there, then the rate at which one particle leaves is
Let \(Y,Y_1,Y_2,\ldots \) be independent random variables distributed as \({\varvec{\upvarphi }}_{c}\), and also let \(x>p_1>p_2>\ldots \) be all points of the Poisson process of rate \({\uplambda }\phi _0(c)\) to the left of our x. We have, similarly to (B.2):

The last factor \(1-q^k e^{- {\uplambda }dx}\) serves two cases: for \(k=0\), the probability that the flying particle stops in \((x,x+dx)\) is \({\uplambda }dx+O(dx^2)\) (which is small), while for \(k\ge 1\) it is \(1-q^k+O(dx)\). We have
where in the last equality we used (A.6). Next, observe that \(x-p_i\) is a sum of i independent exponential random variables with parameter \({\uplambda }\phi _0(c)\) (denote one such variable by \(Y'\) ), and so
Thus, (B.4) turns into
The desired stationarity follows from the identities
which are readily verified. \(\square \)
Let us now write down the particle density \(\rho (c)\) and the particle current j(c) under the measure \(\mathfrak {m}_{c,{\uplambda }}\). We have
where we employed (A.5). The particle current is given by the sum in the right-hand side of (B.4) without the last factor \(1-q^k e^{- {\uplambda }dx}\), and so is equal to
From Proposition A.1 it readily follows that \(\phi _1:[0,1]\rightarrow [0,+\infty ]\) is one to one and increasing. Let \(\phi _1^{-1}\) denote the inverse. From (B.5) and (B.6) we see that the dependence of the current on the density is
1.4 B.4 Verification of the macroscopic limit shape
Recall the inhomogeneous exponential jump model on \(\mathbb {R}_{>0}\) defined in Sect. 2.1 depending on the speed function \({\varvec{\upxi }}(x)\) and the jump distance parameter \({\uplambda }>0\). Let us assume that there are no roadblocks, and, moreover, that \({\varvec{\upxi }}(x)\) is continuous at \(x=0\). Let us take a slightly more general model in which \({\uplambda }\) also depends on the location \(x\in \mathbb {R}_{>0}\) as \(\tilde{\uplambda }(x)L\), where L is a large parameter and \(\tilde{\uplambda }(x)\) is a positive continuous function bounded away from zero and infinity. We also rescale the continuous time as \(t=\tau L\).
Assume that in the limit as \(L\rightarrow +\infty \) there is a limiting density of particles \(\rho (\tau ,x)\in [0,+\infty ]\). Moreover, assume that locally at each \(x\in \mathbb {R}_{>0}\) where \(\rho (\tau ,x)< +\infty \) the behavior of the particle system is described by the translation invariant stationary distribution \(\mathfrak {m}_{c,\tilde{\uplambda }(x)}\) defined in “Appendix B.3”. Under these assumptions and using (B.7), one naturally expects (following the hydrodynamic treatment of driven interacting particle systems in, e.g., [4, 34, 43, 53] ) that the limiting density satisfies the following partial differential equation:
with the initial condition \(\rho (0,x)=0\) (\(x>0\)) and the boundary condition \(\rho (\tau ,0)=+\infty \) (\(\tau \ge 0\)).
Remark B.4
The case \(\tilde{\uplambda }(x)\equiv 1\) considered in the main part of the paper does not restrict the generality. Indeed, let \(\Lambda (x):=\int _0^x {\uplambda }(u)du\). This is a strictly increasing function, and let \(\Lambda ^{-1}\) denote its inverse. If \(\rho (\tau ,x)\) satisfies (B.8) then a straightforward computation shows that
satisfies the same Eq. (B.8) in the variables \((\tau ,y)\), with \(\tilde{\uplambda }\) replaced by 1, and with the modified speed function \(\check{\varvec{\upxi }}(y):={\varvec{\upxi }}(\Lambda ^{-1}(y))\).
By virtue of Remark B.4, we assume that \(\tilde{\uplambda }(x)\equiv 1\), and consider the following equation for the density:
with initial condition \(\rho (0,x)=0\) (\(x>0\)) and boundary condition \(\rho (\tau ,0)=+\infty \) (\(\tau \ge 0\)).
Let us verify that the limiting density coming from the asymptotic analysis of the Fredholm determinant in Sect. 4 satisfies (B.9). Recall that in the absence of roadblocks the macroscopic limit shape \(\mathscr {H}(\tau ,x)\) for the height function is given as follows. First, let \(x_e=x_e(\tau )\ge 0\) be the edge point, i.e., the unique solution to \(\tau =\int _{0}^{x_e}\frac{dy}{(1-q){\varvec{\upxi }}(y)}\). Let also \(w=\upomega ^{\circ }_{\tau ,x}\) for \(0<x<x_e\) be the root of \(\tau w=\int _0^x\phi _2\bigl (w/{\varvec{\upxi }}(y)\bigr )dy\) on the segment \(\bigl (0,\mathop {\mathrm {ess\,inf}}_{y\in [0,x)}{\varvec{\upxi }}(y)\bigr )\) (by Proposition 2.5 this root exists and is unique). The limit shape is
Proposition B.5
The density defined as \(\rho (\tau ,x):=-\frac{\partial }{\partial x}\mathscr {H}(\tau ,x)\) satisfies equation (B.9) (whenever all derivatives involved make sense).
Proof
Assume that \(0<x<x_e(\tau )\), otherwise the density is zero and thus trivially satisfies the equation. Differentiating \(\mathscr {H}(\tau ,x)\) in \(\tau \) and x and using Proposition A.1 together with the definition of \(\upomega ^{\circ }_{\tau ,x}\), we obtain
Therefore, we can write
or, inverting \(\phi _1\):
Differentiating the last equality in x we arrive at Eq. (B.9) for \(\rho (\tau ,x)\). \(\square \)