1 Introduction

In numerous engineering exercises, various forms of disks are used for different purposes. Metal cutting disks, disk brakes, rotating motion transferring disks, or related applications can be given as examples. The number of studies in the literature about disks is quite large due to this wide range of applications. Although these components have been thoroughly studied, there are still some missing points in the scientific literature. This paper is planned to fill in some of these points. Prior to revealing the technical details of this work, it is convenient to refer to what has been researched heretofore.

Firstly, it is pertinent to briefly touch on the studies earlier than 1990s that have been written. The stress distribution of orthotropic rotating constant thickness disks has been analytically modeled by Genta and Gola [1]. For rotating circular and elliptical disk geometries of orthotropic material, closed form solutions are available [2, 3]. In another early study [4], stress distributions have been presented for rotating orthotropic disk with and without a circular hole at the center. In the article of Misra and Achari [5], exact solutions have been carried out for thermal stress analysis of orthotopic circular disk subjected to rotating heat source, in which infinite series and stress function approaches have been utilized. In another thermal stress analysis [6], orthotropic cylinders have been examined under plane temperature distribution.

It is appropriate to refer to more recent studies following the early ones. In this context, Lubarda [7] has put forward a general analytical solution for the elastic response of curvilinearly orthotropic pressurized annular disks, cylinders, and spheres, where both plane strain and plane stress assumptions have been applied. Likewise, Zenkour [8] has investigated rotating orthotropic cylinders having variable thickness profiles and constant solid cores. The stresses and displacements have been examined for five different cases in which various core and material (isotropic and orthotropic) combinations have been considered. In the article of Abd-Alla et al. [9], a long cylinder made of orthotropic material has been considered. The constant thickness cylinder has been subjected to various boundary and loading conditions, which are solid cylinder, cylinder on a rigid shaft, and cylinder with a central hole. Exact solutions of rotating strain hardening orthotropic cylinders have been exhibited by Leu and Hsu [10]. Therein, Voce hardening law and Hill’s yield criterion have been used. Additionally, exact solutions have been validated with Abaqus, and matching results have been achieved. In the paper of Nie et al. [11], material tailoring is discussed to acquire desired stress and displacement field of rotating orthotopic fiber reinforced disk of variable thickness geometry. As known, rotating disks may become unstable at some angular velocities. In the study of Tutuncu [12], influence of anisotropy on the instability of polar orthotopic rotating disks has been addressed. In a similar manner, Tutuncu and Ozturk [13] have analyzed stress redistributions and instabilities of orthotopic cylinders. In the last two mentioned articles, it has been seen that when the classical solutions have been considered, second-order nonhomogeneous differential equations need to be solved. On the other hand, when instabilities have been taken into account, these differential equations have been replaced with Bessel differential equations. Apart from instabilities, singularities may take place in the examinations of disks and shells due to mathematical modeling and various material parameters. In the research of Jain et al. [14], the aim is to investigate singularities of rotating orthotropic disks and solids where Young’s modulus in tangential direction (\({E}_{\theta }\)) is smaller than the one in the radial direction (\({E}_{\rm{r}}\)). According to the authors statements when \({E}_{\theta }\ge {E}_{\rm{r}}\) no singularity has been observed. Similarly, Alexandrova et al. [15] have focused on the singularities of rotating constant thickness orthotropic disk under temperature gradient.

Another related topic is the thermomechanical analysis of orthotopic disks and cylinders. Recently, Sharifi [16] has modeled the rotating orthotopic disk under thermal shock via Lord-Shulman theory of thermoelasticity. El-Naggar et al. [17] have examined the thermal stresses of rotating orthotropic cylinders by combining analytical expressions with finite difference approach. The problem of multilayered orthotropic cylindrical geometry subjected to dynamic thermal loading has been investigated analytically by Abd-Alla et al. [18]. Wherein, thermoelastic stress and displacement have been observed at different time frames. Ding et al. [19] have carried out solutions for the orthotropic and isotropic cylindrical shells subjected to dynamic thermoelastic loads under plane strain assumption. Rotating orthotropic cylinders under magneto-thermoelastic loads has been studied by Abd-Alla and Mahmoud [20]. In the article, the authors have conducted semi-analytical methods. Besides the mentioned mechanical and thermal loads on orthotopic disks and cylinders, from a broader frame, there are some studies that cover the vibration and stability of these orthotopic geometries [21,22,23,24]. In addition to orthotropy, some investigations [25,26,27,28] have considered rotating functionally graded polar orthotopic disks.

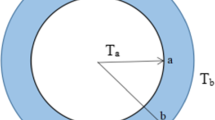
It has been seen from the mentioned articles that most studies generally pay attention to the elastic stresses not the stresses at the onset of plastic yield or elastic–plastic stresses. Additionally, disks with constant thickness geometry have mostly been considered for the orthotropic disks. In this study, elastic stresses at the onset of plastic yield are investigated comprehensively with the variable thickness consideration. Two different analytical solutions and finite element method (FEM) approaches are performed. The considered geometry is portrayed in Fig. 1, and the geometric function (\(\mathcalligra{h}(r)\)) is given below

$$\mathcalligra{h}(r)={\mathcalligra{h}}_{{r}_{\rm{o}}}{\left[\frac{r}{{r}_{\rm{o}}}\right]}^{\mathcalligra{g}},$$
(1)

in which \({\mathcalligra{h}}_{{r}_{\rm{o}}}\) is the thickness of the disk at the outer radius \({r}_{\rm{o}}\) and \({r}_{\rm{i}}\) is the inner radius, \(\mathcalligra{g}\) is the parameter of geometry. Depending on the value of \(\mathcalligra{g}\), the disk takes convex (\(\mathcalligra{g}<0\)), annular (\(\mathcalligra{g}=0\)), and concave (\(\mathcalligra{g}>0\)) forms. This function is a common model that can be seen in other related research papers as well [26, 29,30,31] and is called power-law function in the literature. The solution procedure (analytical, semi-analytical, or fully numerical) varies depending on the geometric function and material property variations.

Fig. 1
figure 1

Illustration of the orthotropic disk geometry

Full size image

Following the introduction, this paper continues as follows: in the next section, governing relations are given, and two different solution methods are presented. In Sect. 3, numerical results are exhibited utilizing analytical solutions. In Sect. 4, analytical and FEM approaches are compared. In the last Sect. 5, obtained results are summarized.

2 Governing relations

The disk component is thin enough to apply plane stress conditions, which indicates that the stress in the axial direction is negligible, \({\sigma }_{z}=0\). Additionally, it is considered that the applied mechanical load, angular rotation, causes small deformations on the disk geometry. Due to the circular geometry of the component, cylindrical polar coordinate system (\(r,\theta ,z\)) has been used for designating relations. Accordingly, the geometric relations between strain and displacement can be expressed as

$${\epsilon}_{\rm{r}}=\frac{{\text{d}}\mathcalligra{u}}{{\text{d}}r}, {\epsilon}_{\theta }=\frac{\mathcalligra{u}}{r}.$$
(2)

wherein, \(\mathcalligra{u}=\mathcalligra{u}(r)\) is the displacement in radial direction, \(d\) is the differential operator, \({\epsilon}_{\rm{r}}={\epsilon}_{\rm{r}}(r)\) and \({\epsilon}_{\theta }={\epsilon}_{\theta }(r)\) are the strains in radial (\(r\)) and tangential (\(\theta\)) directions respectively. Followingly, strain–stress relation via utilizing generalized Hooke’s law is expressed

$${\epsilon}_{\rm{r}}=\frac{{\text{d}}\mathcalligra{u}}{{\text{d}}r}=\frac{1}{{E}_{\rm{r}}}{\sigma}_{\rm{r}}-\frac{{v}_{\theta r}}{{E}_{\theta }}{\sigma}_{\theta },$$
(3)
$${\epsilon}_{\theta }=\frac{\mathcalligra{u}}{r}=-\frac{{v}_{r\theta }}{{E}_{\rm{r}}}{\sigma}_{\rm{r}}+\frac{1}{{E}_{\theta }}{\sigma}_{\theta }.$$
(4)

In the above two equations, \({\sigma}_{\rm{r}}={\sigma}_{\rm{r}}(r)\) and \({\sigma}_{\theta }={\sigma}_{\theta }(r)\) are the stresses in radial and tangential directions. \({E}_{\rm{r}}\), \({E}_{\theta }\), \({v}_{r\theta }\), and \({v}_{\theta r}\) are the mechanical properties of the orthotropic disk, which are changing with the direction of the material. Herein, \(E\) and \(v\) denote Young’s modulus and Poisson’s ratio. Additionally, subscripts of these mechanical properties correspond to the related directions. By rearranging strain–stress relations, associated stress–strain relations are found, which are

$${\sigma}_{\rm{r}}=\frac{{E}_{\rm{r}}}{1-{v}_{r\theta }{v}_{\theta r}}{\epsilon}_{\rm{r}}+\frac{{{E}_{\rm{r}}v}_{\theta r}}{1-{v}_{r\theta }{v}_{\theta r}}{\epsilon}_{\theta },$$
(5)
$${\sigma}_{\theta }=\frac{{E}_{\theta }{v}_{r\theta }}{1-{v}_{r\theta }{v}_{\theta r}}{\epsilon}_{\rm{r}}+\frac{{E}_{\theta }}{1-{v}_{r\theta }{v}_{\theta r}}{\epsilon}_{\theta }.$$
(6)

The introduced Poisson’s ratios have connecting relations, in other words Poisson’s ratios are not independent of each other. Due to the Maxwell relations, see reference [32], the following expression can be written

$$\frac{{v}_{\theta r}}{{E}_{\theta }}=\frac{{v}_{r\theta }}{{E}_{\rm{r}}} \to \frac{{E}_{\theta }}{{E}_{\rm{r}}}=\frac{{v}_{\theta r}}{{v}_{r\theta }}={\mathbb{O}},$$
(7)

in which \({\mathbb{O}}\) is the orthotrophy index. In the case of \({\mathbb{O}}>1\), the material is stiffer in the tangential direction. Similarly, \({\mathbb{O}}<1\) case indicates radial stiffness in the material. Additionally, orthotropy index cannot be equal to zero or smaller than zero. While the material is obeying Hooke’s law within the elastic limits, all the load applied to the solid body is stored as strain energy. Due to the positive definiteness of this energy, Young’s moduli are positive, and Poisson’s ratios are constrained by

$$0<{v}_{r\theta }{v}_{\theta r}<1.$$
(8)

Owing to Eqs. (7) and (8), properties should fulfill [7, 27],

$$\left|{v}_{\theta r}\right|<\sqrt{\frac{{E}_{\theta }}{{E}_{\rm{r}}}}=\sqrt{\mathbb{O}}, \left|{v}_{r\theta }\right|<\sqrt{\frac{{E}_{\rm{r}}}{{E}_{\theta }}}=\sqrt{\frac{1}{\mathbb{O}}}.$$
(9)

From Eq. (7), properties can be connected as

$${E}_{\theta }={\mathbb{O}}{E}_{\rm{r}}, {v}_{\theta r}={\mathbb{O}}{v}_{r\theta }.$$
(10)

Substituting the above two expressions into the strain–stress relations yields to

$${\epsilon}_{\rm{r}}=\frac{1}{{E}_{\rm{r}}}{[\sigma}_{\rm{r}}-{v}_{r\theta }{\sigma}_{\theta }],$$
(11)
$${\epsilon}_{\theta }=\frac{1}{{E}_{\rm{r}}}[\frac{1}{\mathbb{O}}{\sigma}_{\theta }-{v}_{r\theta }{\sigma}_{\rm{r}}].$$
(12)

Utilizing the newly introduced strain–stress relations, stress–strain relations become

$${\sigma}_{\rm{r}}=\frac{{E}_{\rm{r}}}{1-{\mathbb{O}}{{v}_{r\theta }}^{2}}{\epsilon}_{\rm{r}}+\frac{{\mathbb{O}}{E}_{\rm{r}}{v}_{r\theta }}{1-{\mathbb{O}}{{v}_{r\theta }}^{2}}{\epsilon}_{\theta },$$
(13)
$${\sigma}_{\theta }=\frac{{\mathbb{O}}{E}_{\rm{r}}{v}_{r\theta }}{1-{\mathbb{O}}{{v}_{r\theta }}^{2}}{\epsilon}_{\rm{r}}+\frac{{\mathbb{O}}{E}_{\rm{r}}}{1-{\mathbb{O}}{{v}_{r\theta }}^{2}}{\epsilon}_{\theta }.$$
(14)

Subsequent to defining elastic relations, in order to obtain a convenient solution, equilibrium equation and compatibility condition should be satisfied with the applied boundary conditions. Let’s begin by introducing the equilibrium equation in radial direction

$$\frac{{\text{d}}}{{\text{d}}r}\left[\mathcalligra{h}\left(r\right)r{\sigma}_{\rm{r}}\left(r\right)\right]-\mathcalligra{h}\left(r\right){\sigma}_{\theta }\left(r\right)=-\mathcalligra{h}\left(r\right)\varphi {\omega }^{2}{r}^{2},$$
(15)

where \(\varphi\) is the density of the disk material and \(\omega\) is the angular rotation. The compatibility condition is

$$\frac{{\text{d}}}{{\text{d}}r}[r{\epsilon}_{\theta }]-{\epsilon}_{\rm{r}}=0.$$
(16)

As given in Fig. 1, the disk is rigidly fixed on a rotating inclusion and the outer radius is in traction free conditions. Under these circumstances, boundaries take the following forms

$$\mathcalligra{u}\left({r}_{\rm{i}}\right)=0, {\sigma}_{\rm{r}}\left({r}_{\rm{o}}\right)=0.$$
(17)

After presenting the essential governing relations, we can now get into the analytical solutions. In order to acquire the stress and displacement functions, two different analytical solutions are introduced. Each of them is given in detail below.

2.1 Solution Method 1 (SM1)

In this method, the solution is initiated by introducing a stress function, \(\psi =\psi (r)\), which is of the form

$$\psi =\mathcalligra{h}\left(r\right)r{\sigma}_{\rm{r}}\left(r\right).$$
(18)

This function or a similar form of the function can be seen in some related articles as well, see [14, 27, 29, 31]. By using this identity with Eq. (15), directional stresses can be presented as

$${\sigma}_{\rm{r}}=\frac{\psi }{r\mathcalligra{h}}, {\sigma}_{\theta }=\frac{1}{\mathcalligra{h}}\frac{{\text{d}}\psi }{{\text{d}}r}+\varphi {\omega }^{2}{r}^{2}.$$
(19)

Let’s insert the above radial and tangential stress terms into Eqs. (11) and (12), which results in

$${\epsilon}_{\rm{r}}=\frac{1}{{E}_{\rm{r}}}[\frac{\psi }{r\mathcalligra{h}}-{v}_{r\theta }\frac{1}{\mathcalligra{h}}\frac{{\text{d}}\psi }{{\text{d}}r}-{v}_{r\theta }\varphi {\omega }^{2}{r}^{2}],$$
(20)
$${\epsilon}_{\theta }=\frac{1}{{E}_{\rm{r}}}\left[\frac{1}{\mathbb{O}}\frac{1}{\mathcalligra{h}}\frac{{\text{d}}\psi }{{\text{d}}r}+\frac{1}{\mathbb{O}}\varphi {\omega }^{2}{r}^{2}-{v}_{r\theta }\frac{\psi }{r\mathcalligra{h}}\right].$$
(21)

Substituting the above radial and tangential strain terms into Eq. (16) with Eq. (1) renders to the below differential equation

$${r}^{2}\frac{{d}^{2}\psi }{d{r}^{2}}+{\mathcal{A}}_{1}r\frac{{\text{d}}\psi }{{\text{d}}r}+{\mathcal{A}}_{2}\psi ={\mathcal{A}}_{3}{r}^{\mathcalligra{g}+3},$$
(22)

Here, \({\mathcal{A}}_{j}\) terms are the real constants of the differential equation. These terms are

$${\mathcal{A}}_{1}=1-\mathcalligra{g},$$
$${\mathcal{A}}_{2}={\mathbb{O}}[\mathcalligra{g}{v}_{r\theta }-1],$$
$${\mathcal{A}}_{3}=-\frac{\varphi {\omega }^{2}{\mathcalligra{h}}_{{r}_{\rm{o}}}}{{{r}_{\rm{o}}}^{\mathcalligra{g}}}[3+{\mathbb{O}}{v}_{r\theta }].$$
(23)

Solution of Eq. (22) provides the stress function

$$\psi ={\mathcal{C}}_{1}{r}^{{\mathcal{A}}_{4}}+{\mathcal{C}}_{2}{r}^{{\mathcal{A}}_{5}}+{\mathcal{A}}_{6}{r}^{\mathcalligra{g}+3}.$$
(24)

\({\mathcal{C}}_{1}\) and \({\mathcal{C}}_{2}\) are the integration constants and new \({\mathcal{A}}_{j}\) terms are

$${\mathcal{A}}_{4}=\frac{1}{2}\left\{1-{\mathcal{A}}_{1}-\sqrt{{[{\mathcal{A}}_{1}-1]}^{2}-4{\mathcal{A}}_{2}}\right\},$$
$${\mathcal{A}}_{5}=\frac{1}{2}\left\{1-{\mathcal{A}}_{1}+\sqrt{{[{\mathcal{A}}_{1}-1]}^{2}-4{\mathcal{A}}_{2}}\right\},$$
$${\mathcal{A}}_{6}=\frac{{\mathcal{A}}_{3}}{{\mathcalligra{g}}^{2}+\mathcalligra{g}\left[5+{\mathcal{A}}_{1}\right]+6+3{\mathcal{A}}_{1}+{\mathcal{A}}_{2}}.$$
(25)

Combining Eqs. (1), (19), and (24), stress in radial and tangential directions become

$${\sigma}_{\rm{r}}={\mathcal{C}}_{1}\frac{{{r}_{\rm{o}}}^{\mathcalligra{g}}}{{\mathcalligra{h}}_{{r}_{\rm{o}}}}{r}^{{\mathcal{A}}_{4}+\mathcalligra{g}-1}+{\mathcal{C}}_{2}\frac{{{r}_{\rm{o}}}^{\mathcalligra{g}}}{{\mathcalligra{h}}_{{r}_{\rm{o}}}}{r}^{{\mathcal{A}}_{5}+\mathcalligra{g}-1}+\frac{{{{\mathcal{A}}_{6}r}_{\rm{o}}}^{\mathcalligra{g}}}{{\mathcalligra{h}}_{{r}_{\rm{o}}}}{r}^{2},$$
(26)
$${\sigma}_{\theta }={\mathcal{C}}_{1}\frac{{\mathcal{A}}_{4}{{r}_{\rm{o}}}^{\mathcalligra{g}}}{{\mathcalligra{h}}_{{r}_{\rm{o}}}}{r}^{{\mathcal{A}}_{4}+\mathcalligra{g}-1}+{\mathcal{C}}_{2}\frac{{\mathcal{A}}_{5}{{r}_{\rm{o}}}^{\mathcalligra{g}}}{{\mathcalligra{h}}_{{r}_{\rm{o}}}}{r}^{{\mathcal{A}}_{5}+\mathcalligra{g}-1}+\frac{{\mathcal{A}}_{6}{{r}_{\rm{o}}}^{\mathcalligra{g}}\left[3+\mathcalligra{g}\right]+{\mathcalligra{h}}_{{r}_{\rm{o}}}\varphi {\omega }^{2}}{{\mathcalligra{h}}_{{r}_{\rm{o}}}}{r}^{2}.$$
(27)

Substituting the above two stresses into Eq. (12) and multiplying by \(r\), see Eq. (1), radial displacement turns out to be

$$\mathcalligra{u}={\mathcal{C}}_{1}\frac{{{r}_{\rm{o}}}^{\mathcalligra{g}}[{\mathcal{A}}_{4}-{\mathbb{O}}{v}_{r\theta }]}{{\mathcalligra{h}}_{{r}_{\rm{o}}}{E}_{\rm{r}}{\mathbb{O}}}{r}^{{\mathcal{A}}_{4}-\mathcalligra{g}}+{\mathcal{C}}_{2}\frac{{{r}_{\rm{o}}}^{\mathcalligra{g}}[{\mathcal{A}}_{5}-{\mathbb{O}}{v}_{r\theta }]}{{\mathcalligra{h}}_{{r}_{\rm{o}}}{E}_{\rm{r}}{\mathbb{O}}}{r}^{{\mathcal{A}}_{5}-\mathcalligra{g}}+\frac{{\mathcal{A}}_{6}{{r}_{\rm{o}}}^{\mathcalligra{g}}\left[3+\mathcalligra{g}-{\mathbb{O}}{v}_{r\theta }\right]+{\mathcalligra{h}}_{{r}_{\rm{o}}}\varphi {\omega }^{2}}{{\mathcalligra{h}}_{{r}_{\rm{o}}}{E}_{\rm{r}}{\mathbb{O}}}{r}^{3}.$$
(28)

Applying boundary conditions in Eq. (17) to Eqs. (26) and (28), the integration constants are found

$${\mathcal{C}}_{1}=\frac{{{r}_{\rm{i}}}^{3+\mathcalligra{g}}{{r}_{\rm{o}}}^{{\mathcal{A}}_{5}}[{\mathcal{A}}_{6}{{r}_{\rm{o}}}^{\mathcalligra{g}}\left(3+\mathcalligra{g}-{\mathbb{O}}{v}_{r\theta }\right)+{\mathcalligra{h}}_{{r}_{\rm{o}}}\varphi {\omega }^{2}]-{{r}_{\rm{i}}}^{{\mathcal{A}}_{5}}{{r}_{\rm{o}}}^{3+2\mathcalligra{g}}{\mathcal{A}}_{6}\left[{\mathcal{A}}_{5}-{\mathbb{O}}{v}_{r\theta }\right]}{{{r}_{\rm{i}}}^{{\mathcal{A}}_{5}}{{r}_{\rm{o}}}^{{\mathcal{A}}_{4}+\mathcalligra{g}}\left[{\mathcal{A}}_{5}-{\mathbb{O}}{v}_{r\theta }\right]+{{r}_{\rm{i}}}^{{\mathcal{A}}_{4}}{{r}_{\rm{o}}}^{{\mathcal{A}}_{5}+\mathcalligra{g}}[{\mathbb{O}}{v}_{r\theta }-{\mathcal{A}}_{4}]},$$
$${\mathcal{C}}_{2}=\frac{{{r}_{\rm{i}}}^{{\mathcal{A}}_{4}}{{r}_{\rm{o}}}^{3+2\mathcalligra{g}}{\mathcal{A}}_{6}\left[{\mathcal{A}}_{4}-{\mathbb{O}}{v}_{r\theta }\right]-{{r}_{\rm{i}}}^{3+\mathcalligra{g}}{{r}_{\rm{o}}}^{{\mathcal{A}}_{4}}[{\mathcal{A}}_{6}{{r}_{\rm{o}}}^{\mathcalligra{g}}\left(3+\mathcalligra{g}-{\mathbb{O}}{v}_{r\theta }\right)+{\mathcalligra{h}}_{{r}_{\rm{o}}}\varphi {\omega }^{2}]}{{{r}_{\rm{i}}}^{{\mathcal{A}}_{5}}{{r}_{\rm{o}}}^{{\mathcal{A}}_{4}+\mathcalligra{g}}\left[{\mathcal{A}}_{5}-{\mathbb{O}}{v}_{r\theta }\right]+{{r}_{\rm{i}}}^{{\mathcal{A}}_{4}}{{r}_{\rm{o}}}^{{\mathcal{A}}_{5}+\mathcalligra{g}}[{\mathbb{O}}{v}_{r\theta }-{\mathcal{A}}_{4}]}.$$
(29)

As can be seen, the analytical solution has been derived by integrating stress function into the problem.

2.2 Solution Method 2 (SM2)

Another analytical approach is presented in this subsection. Let’s first insert radial and tangential strains in Eq. (2) to Eqs. (13) and (14) then we acquire stress-displacement relations

$${\sigma}_{\rm{r}}=\frac{{E}_{\rm{r}}}{1-{\mathbb{O}}{{v}_{r\theta }}^{2}}\frac{{\text{d}}\mathcalligra{u}}{{\text{d}}r}+\frac{{\mathbb{O}}{E}_{\rm{r}}{v}_{r\theta }}{1-{\mathbb{O}}{{v}_{r\theta }}^{2}}\frac{\mathcalligra{u}}{r},$$
(30)
$${\sigma}_{\theta }=\frac{{\mathbb{O}}{E}_{\rm{r}}{v}_{r\theta }}{1-{\mathbb{O}}{{v}_{r\theta }}^{2}}\frac{{\text{d}}\mathcalligra{u}}{{\text{d}}r}+\frac{{\mathbb{O}}{E}_{\rm{r}}}{1-{\mathbb{O}}{{v}_{r\theta }}^{2}}\frac{\mathcalligra{u}}{r}.$$
(31)

Applying Eqs. (1), (30), and (31) to the equilibrium equation in (15), one acquires

$${r}^{2}\frac{{d}^{2}\mathcalligra{u}}{d{r}^{2}}+{\mathcal{B}}_{1}r\frac{{\text{d}}\mathcalligra{u}}{{\text{d}}r}+{\mathcal{B}}_{2}\mathcalligra{u}={\mathcal{B}}_{3}{r}^{3}.$$
(32)

As in the above SM1 approach, some abbreviations are used as well. In order to avoid any misunderstanding issue, instead of \({\mathcal{A}}_{j}\), \({\mathcal{B}}_{j}\) denotation is employed. Here,

$${\mathcal{B}}_{1}=1+\mathcalligra{g},$$
$${\mathcal{B}}_{2}={\mathbb{O}}[\mathcalligra{g}{v}_{r\theta }-1],$$
$${\mathcal{B}}_{3}=\frac{\varphi {\omega }^{2}}{{E}_{\rm{r}}}[{\mathbb{O}}{{v}_{r\theta }}^{2}-1].$$
(33)

Solution of Eq. (32) is of the form

$$\mathcalligra{u}={\mathcal{K}}_{1}{r}^{{\mathcal{B}}_{4}}+{\mathcal{K}}_{2}{r}^{{\mathcal{B}}_{5}}+{\mathcal{B}}_{6}{r}^{3}.$$
(34)

Above function is the general solution of the radial displacement. Terms \({\mathcal{K}}_{1}\) and \({\mathcal{K}}_{2}\) are the integration constants and \({\mathcal{B}}_{4}\), \({\mathcal{B}}_{5}\) and \({\mathcal{B}}_{6}\) are

$${\mathcal{B}}_{4}=\frac{1}{2}\left\{1-{\mathcal{B}}_{1}-\sqrt{{[{\mathcal{B}}_{1}-1]}^{2}-4{\mathcal{B}}_{2}}\right\},$$
$${\mathcal{B}}_{5}=\frac{1}{2}\left\{1-{\mathcal{B}}_{1}+\sqrt{{[{\mathcal{B}}_{1}-1]}^{2}-4{\mathcal{B}}_{2}}\right\},$$
$${\mathcal{B}}_{6}=\frac{{\mathcal{B}}_{3}}{6+3{\mathcal{B}}_{1}+{\mathcal{B}}_{2}}.$$
(35)

Making use of Eq. (2) with Eq. (34), strains turn out to be

$${\epsilon}_{\rm{r}}=\frac{{\text{d}}\mathcalligra{u}}{{\text{d}}r}={\mathcal{K}}_{1}{\mathcal{B}}_{4}{r}^{{\mathcal{B}}_{4}-1}+{\mathcal{K}}_{2}{\mathcal{B}}_{5}{r}^{{\mathcal{B}}_{5}-1}+{3\mathcal{B}}_{6}{r}^{2},$$
(36)
$${\epsilon}_{\theta }=\frac{\mathcalligra{u}}{r}={\mathcal{K}}_{1}{r}^{{\mathcal{B}}_{4}-1}+{\mathcal{K}}_{2}{r}^{{\mathcal{B}}_{5}-1}+{\mathcal{B}}_{6}{r}^{2}.$$
(37)

Inserting the above strains into Eqs. (13) and (14), stresses become

$${\sigma}_{\rm{r}}={\mathcal{K}}_{1}\frac{{E}_{\rm{r}}[{\mathcal{B}}_{4}+{\mathbb{O}}{v}_{r\theta }]}{1-{\mathbb{O}}{{v}_{r\theta }}^{2}}{r}^{{\mathcal{B}}_{4}-1}+{\mathcal{K}}_{2}\frac{{E}_{\rm{r}}[{\mathcal{B}}_{5}+{\mathbb{O}}{v}_{r\theta }]}{1-{\mathbb{O}}{{v}_{r\theta }}^{2}}{r}^{{\mathcal{B}}_{5}-1}+\frac{{\mathcal{B}}_{6}{E}_{\rm{r}}[3+{\mathbb{O}}{v}_{r\theta }]}{1-{\mathbb{O}}{{v}_{r\theta }}^{2}}{r}^{2},$$
(38)
$${\sigma}_{\theta }={\mathcal{K}}_{1}\frac{{E}_{\rm{r}}{\mathbb{O}}[{\mathcal{B}}_{4}{v}_{r\theta }+1]}{1-{\mathbb{O}}{{v}_{r\theta }}^{2}}{r}^{{\mathcal{B}}_{4}-1}+{\mathcal{K}}_{2}\frac{{E}_{\rm{r}}{\mathbb{O}}[{\mathcal{B}}_{5}{v}_{r\theta }+1]}{1-{\mathbb{O}}{{v}_{r\theta }}^{2}}{r}^{{\mathcal{B}}_{5}-1}+\frac{{\mathcal{B}}_{6}{E}_{\rm{r}}{\mathbb{O}}[3{v}_{r\theta }+1]}{1-{\mathbb{O}}{{v}_{r\theta }}^{2}}{r}^{2}.$$
(39)

Using boundary conditions in Eq. (17) with Eqs. (34) and (38), \({\mathcal{K}}_{1}\) and \({\mathcal{K}}_{2}\) render as

$${\mathcal{K}}_{1}=-\frac{{r}_{\rm{i}}^{{\mathcal{B}}_{5}}{r}_{\rm{o}}^{3}{\mathcal{B}}_{6}\left[3+{\mathbb{O}}{v}_{r\theta }\right]-{r}_{\rm{i}}^{3}{r}_{\rm{o}}^{{\mathcal{B}}_{5}}{\mathcal{B}}_{6}[{\mathcal{B}}_{5}+{\mathbb{O}}{v}_{r\theta }]}{{r}_{\rm{i}}^{{\mathcal{B}}_{5}}{r}_{\rm{o}}^{{\mathcal{B}}_{4}}\left[{\mathcal{B}}_{4}+{\mathbb{O}}{v}_{r\theta }\right]-{r}_{\rm{i}}^{{\mathcal{B}}_{4}}{r}_{\rm{o}}^{{\mathcal{B}}_{5}}[{\mathcal{B}}_{5}+{\mathbb{O}}{v}_{r\theta }]},$$
$${\mathcal{K}}_{2}=\frac{{r}_{\rm{i}}^{{\mathcal{B}}_{4}}{r}_{\rm{o}}^{3}{\mathcal{B}}_{6}\left[3+{\mathbb{O}}{v}_{r\theta }\right]-{r}_{\rm{i}}^{3}{r}_{\rm{o}}^{{\mathcal{B}}_{4}}{\mathcal{B}}_{6}[{\mathcal{B}}_{4}+{\mathbb{O}}{v}_{r\theta }]}{{r}_{\rm{i}}^{{\mathcal{B}}_{5}}{r}_{\rm{o}}^{{\mathcal{B}}_{4}}\left[{\mathcal{B}}_{4}+{\mathbb{O}}{v}_{r\theta }\right]-{r}_{\rm{i}}^{{\mathcal{B}}_{4}}{r}_{\rm{o}}^{{\mathcal{B}}_{5}}[{\mathcal{B}}_{5}+{\mathbb{O}}{v}_{r\theta }]}.$$
(40)

2.3 Orthotropic yield criterion

After two different analytical solutions have been revealed, the elastic limits of the component are obtained utilizing one of these solutions. In order to estimate these limits, Hill’s yield criterion is considered. The criterion, \({\sigma }_{\mathcal{H}}={\sigma }_{\mathcal{H}}(r)\), is

$${\sigma }_{\mathcal{H}}={\mathbb{G}}{\left({\sigma}_{\rm{r}}\right)}^{2}+{\mathbb{F}}{\left({\sigma}_{\theta }\right)}^{2}+{\mathbb{H}}{\left({\sigma}_{\rm{r}}-{\sigma}_{\theta }\right)}^{2}={\left({\sigma }_{\mathcal{Y}}\right)}^{2}.$$
(41)

\({\mathbb{G}}\), \({\mathbb{F}}\), and \({\mathbb{H}}\) are the dimensionless parameters of the criterion, and \({\sigma }_{\mathcal{Y}}\) is the equibiaxial tensile yield strength of the material. The parameters should obey

$${\mathbb{G}}+{\mathbb{F}}=1, {\mathbb{G}}*{\mathbb{F}}+{\mathbb{H}}>0.$$
(42)

The first constituent of the above equation stands for consistency, and the second is necessary for an elliptical yield locus, for details see [33, 34]. When \({\sigma }_{\mathcal{H}}={\left({\sigma }_{\mathcal{Y}}\right)}^{2}\) takes places, the rotating component reaches to its elastic limit. The angular velocity magnitude that satisfies \({\sigma }_{\mathcal{H}}={\left({\sigma }_{\mathcal{Y}}\right)}^{2}\) condition is the limit velocity.

3 Numerical evaluations

In this section, numerical examples are generated to understand the behavior of various parameters on the disk. Throughout the examples including Figs. 2, 3, 4, 5, 7 and Table 1, normalized forms are used which are

Table 1 Comparison of normalized stress and displacement fields obtained by SM1 and SM2 in which \(\mathcalligra{g}={\mathbb{O}}={\mathbb{H}}={\mathbb{G}}=0.50\)
Full size table
$$\overline{{\sigma }_{\mathcal{H}}}=\frac{{\sigma }_{\mathcal{H}}}{{\left({\sigma }_{\mathcal{Y}}\right)}^{2}}, \overline{{\sigma }_{\rm{r}}}=\frac{{\sigma}_{\rm{r}}}{{\sigma }_{\mathcal{Y}}}, \overline{{\sigma }_{\theta }}=\frac{{\sigma}_{\theta }}{{\sigma }_{\mathcal{Y}}}, \overline{\mathcalligra{u}}=\frac{\mathcalligra{u}{E}_{\rm{r}}}{{r}_{\rm{o}}{\sigma }_{\mathcal{Y}}}, \overline{r }=\frac{r}{{r}_{\rm{o}}}, \overline{\Omega }=\sqrt{\frac{\varphi }{{\sigma }_{\mathcal{Y}}}{(\omega {r}_{\rm{o}})}^{2}}.$$
(43)

In these expressions, the first four terms are the stresses and radial displacement, \(\overline{r }\) and \(\overline{\Omega }\) are the non-dimensional disk radius and angular velocity. For the disk, geometric and material parameters are taken as \({r}_{\rm{i}}=50\) mm, \({r}_{\rm{o}}=100\) mm, \({v}_{r\theta }=0.25\), \(\varphi =2000\) kg/m3 \({E}_{\rm{r}}=35*{10}^{9}\) Pa, \({\sigma }_{\mathcal{Y}}=300*{10}^{6}\) Pa. These parameters are fixed throughout the samples. Other parameters, \(\mathcalligra{g}, {\mathbb{O}},{\mathbb{H}}\), and \({\mathbb{G}}\), are altered one by one to analyze their effect individually. Prior to detailing the numerical evaluations, firstly, let’s compare the results obtained from SM1 and SM2 to validate the accuracy of the proposed methods. For this purpose, an example is expressed in Table 1 where \(\mathcalligra{g}= {\mathbb{O}}={\mathbb{H}}={\mathbb{G}}=0.50.\) Under these conditions, limit angular velocity is calculated as \(\overline{\Omega }=1.2975\) for both SM1 and SM2. It is observed from the tabulated results that both stress and displacement fields are in nearly perfect agreement. Only difference occurs at the inner radius of the displacement and outer radius of the radial stress. These small changes most possibly have occurred due to number rounding or digit cutting differences.

In addition to SM1 and SM2 approaches, the results have been compared with another study, see [35]. In the reference, orthotropic rotating discs subjected to radial thermal loads with free-free boundary conditions have been investigated. In order to apply these boundaries, instead of Eq. (17), \({\sigma}_{\rm{r}}\left({r}_{\rm{i}}\right)=0\) and \({\sigma}_{\rm{r}}\left({r}_{\rm{o}}\right)=0\) conditions have been utilized. The disk in the reference has a constant thickness. Hence, the geometric parameter has been taken as \(\mathcalligra{g}=0.00\). Additionally, instead of finding the limit angular velocity, it has been assigned as constant, \(\omega =94.25\) rad/s. Geometric and material properties have been considered as \({r}_{\rm{i}}=40\) mm, \({r}_{\rm{o}}=100\) mm, \({v}_{\theta r}=0.15\), \(\varphi =2030\) kg/m3 \({E}_{\rm{r}}=21.80*{10}^{9}\) Pa and \({E}_{\theta }=26.95*{10}^{9}\) Pa. The results can be compared once the conditions and values mentioned above are applied to this examination. At the inner radius of the disk, the radial stress, tangential stress, and radial displacement from both examinations are given in Table 2. Wherein, instead of normalization, dimensions have been utilized to be compatible with the reference. As can be seen from the tabulated results, the obtained difference is less than one percent. Consequently, high accuracy has been acquired.

Table 2 Comparison of radial stress, tangential stress, and radial displacement at \(r={r}_{\rm{i}}\)
Full size table

After the above verification procedures, we may begin the analysis. In the first example, disk profile is taken into account. Influence of the profile on the stresses and radial displacement at the onset of plastic yield is examined. Depending on geometric parameter \(\mathcalligra{g}\), Fig. 2 is plotted. Therein, other parameters are set as \({\mathbb{O}}={\mathbb{H}}={\mathbb{G}}=0.50.\) The reason of setting other parameters to the same number is for simplicity. Yet, it is appropriate to mention what setting these parameters to \(0.50\) means. \({\mathbb{O}}= 0.50\) implies that the disk is less stiff in tangential direction, see Eq. (10). \({\mathbb{H}}\) and \({\mathbb{G}}\) are the parameters belonging to the yield criterion in Eq. (41). These two parameters should satisfy conditions in Eq. (42). Using \({\mathbb{G}}=0.50\) and the first constituent of Eq. (42), \({\mathbb{F}}\) becomes \(0.50\) as well. From the second constituent of the same equation, we have \({\mathbb{G}}*{\mathbb{F}}+{\mathbb{H}}>0\). The mathematical case \({\mathbb{F}}={\mathbb{H}}={\mathbb{G}}=0.50\) satisfies the inequality. Under these conditions, Fig. 2 and its constituents are observed by manipulating parameter \(\mathcalligra{g}\). According to the first constituent 2a, the disk reaches its limit at the contacting inner radius with the inclusion. In Eq. (43), it is stated that \(\overline{{\sigma }_{\mathcal{H}}}={\sigma }_{\mathcal{H}}/{\left({\sigma }_{\mathcal{Y}}\right)}^{2}\). If the yield criterion in Eq. (41) and the mentioned normalized quantity are observed together, it is apparent that when \(\overline{{\sigma }_{\mathcal{H}}}=1\) happens, yield commences. The figure is plotted for five different \(\mathcalligra{g}\) values, and the corresponding normalized angular velocities are given at the figure constituent. For instance, when \({\mathbb{O}}={\mathbb{H}}={\mathbb{G}}=0.50\) and \(\mathcalligra{g}=-0.50\), the calculated angular velocity is \(\overline{\Omega }=1.60894\). The corresponding angular velocities, which are calculated with Eq. (41), can be tracked for other assigned values as well. According to the obtained velocity values, one may express that negative \(\mathcalligra{g}\) values cause higher \(\overline{\Omega }\) acquisition. Therefrom, it can be interpreted that convex geometry is more favorable if the disk is designed for high velocities. In other words, tapering the geometry along the outer radius may result in higher yielding possibilities. In the second constituent 2(b), corresponding radial stresses are given. As expected, the component is radially stress-free at the outer radius in harmony with the implemented boundary condition. However, the interesting part is that the disk reaches higher values than its yield limits at the inner radius (@ \(\overline{r }=\overline{{r }_{\rm{i}}}\), \(\overline{{\sigma }_{\rm{r}}}>1\)). This phenomenon can be explained by digging deeper into the yield criterion. Essentially, a yield criterion is the combination of stresses. When these combinations reach a certain limit, which is the yield limit of the material, we state that the component has arrived at its elastic limit. Depending on the material characteristics, further load may cause linear hardening, nonlinear hardening, or sudden rapture. These stress combinations are highly influenced by the yield criteria parameters \({\mathbb{F}},{\mathbb{H}}\) and \({\mathbb{G}}\) which are going to be discussed in the following examples. Depending on these parameters, shape of the yield locus alters and consequently stress combinations get affected. This interpretation is valid from a mathematical perspective. Another explanation is a physical possibility. The disk holds the rigid inclusion tightly around the inner diameter of the disk; thus, stress concentrations occur along the inner perimeter. In the third constituent 2(c), tangential stresses are shown. This stress is rather smaller than the radial ones in terms of magnitudes. Also, their distributions are considerably different than the radial ones. In fact, this magnitude comparison reveals the similarity between the distribution of the yield stress and the radial stress. It is previously mentioned that the yield stress is the combination of stresses, and the radial stress’ magnitude is considerably higher than the tangential one. In the case of these combinations, the distribution profile of the yield stress is, of course, going to be similar to the radial one. In the fourth constituent 2(d), radial displacement is illustrated. Due to rigid fixation around the inclusion the displacement around the inner diameter is zero, also, see the first boundary condition in Eq. (17). It is apparent from the figure that displacement gets to its maximum at or around the outer diameter. When parameter \(\mathcalligra{g}\) is smaller, the displacement tends to increase. From a physical point of view, this occurrence is expected. When the value of \(\mathcalligra{g}\) is negative, it means that the component is tapered along the radius. In other words, the thickness of the disk reduces. For positive values of \(\mathcalligra{g}\), the disk thickens along radius. Therefore, the tapering profile formed in thickness causes an increase in displacement toward the outer edge of the disk rotating at high speed. What is seen in the figure contains compatibility with this interpretation.

Fig. 2
figure 2

Effect of disk geometry parameter on the normalized a yield function, b radial stress, c tangential stress, and d radial displacement where \({\mathbb{O}}={\mathbb{H}}={\mathbb{G}}=0.50\)

Full size image

After the geometric discussions about the disk profile, material effects on the stress fields, particularly the effect of orthotropy is handled. As in the previous example, parameters are set to the same number, \(\mathcalligra{g}={\mathbb{H}}={\mathbb{G}}=0.50\) and orthotropy parameter \({\mathbb{O}}\) is altered. Parameter \(\mathcalligra{g}=0.50\) prescribes that the disk is concave and as mentioned earlier \({\mathbb{H}}\), \({\mathbb{G}}\) and \({\mathbb{F}}\) are in an acceptable numerical range. After these arrangements, parameter \({\mathbb{O}}\) is examined. Since \({\mathbb{O}}\) must be greater than zero, firstly, it is set to a relatively small number 0.01 then it is observed up to 1. In Fig. 3a, yield function distributions are given at the elastic limits. The calculated limiting angular velocity values are presented in the figure constituent as well. Accordingly, yielding begins at \(\overline{r }=\overline{{r }_{\rm{i}}}\) for the illustrated cases. The radial stress variations are given in Fig. 3b. Therefrom, it is noticed that increment in parameter \({\mathbb{O}}\) also rises the stresses in this direction. Additionally, higher than yield limit stress happening at the inner diameter is seen as well. From a physical perspective, this incident can be described as the orthotropy increment in the tangential direction increasing the radial limit stresses in the disk. When \({\mathbb{O}}=1\), disk becomes isotropic, Young’s moduli and Poisson’s ratios turn out to be \({E}_{\theta }={E}_{\rm{r}}=E, {v}_{\theta r}={v}_{r\theta }=v.\) Followingly, tangential stresses are given in Fig. 3c. It is seen from the plotting that higher orthotropy values notably rises the stress in tangential direction. While the magnitude of tangential stress at the inner and outer radius are close to each other, at an arbitrary radial location stress magnitude gets to its apex value. Lastly, radial displacement is shown in Fig. 3d. Wherein, it is observed that considerably small alterations occur by changing parameter \({\mathbb{O}}.\)

Fig. 3
figure 3

Effect of orthotropy parameter on the normalized a yield function, b radial stress, c tangential stress, and d radial displacement where \(\mathcalligra{g}={\mathbb{H}}={\mathbb{G}}=0.50\)

Full size image

In the next step, yield criterion parameters are focused on. For this purpose, we may begin by examining parameter \({\mathbb{H}}\), while other parameters are kept constant as \(\mathcalligra{g}={\mathbb{O}}={\mathbb{G}}=0.50\). Parameter \({\mathbb{H}}\) is changed in between zero to one with 0.25 increments. As in the former examples, yield function distributions are presented in Fig. 4a. Calculated limit angular velocity values are available in this figure as well. Accordingly, when \({\mathbb{H}}=0\) the disk reaches its highest \(\overline{\Omega }.\) In order to apprehend this occurrence, one should consider the criterion in Eq. (41). Mathematically, \({\mathbb{H}}=0\) implies that the term in front of \({\mathbb{H}}\) which is \({\left({\sigma}_{\rm{r}}-{\sigma}_{\theta }\right)}^{2}\) vanishes. Therefore, the magnitude that comes from \({\left({\sigma}_{\rm{r}}-{\sigma}_{\theta }\right)}^{2}\) is eliminated. Apparently, calculated \(\overline{\Omega }\) value from this elimination increases the magnitude of \(\overline{\Omega }\). As the assigned value to \({\mathbb{H}}\) increases velocity tends to decrease. In the subsequent constituent Fig. 4b, radial stresses are demonstrated. According to the constituent, it is obvious that parameter \({\mathbb{H}}\) prominently effects the magnitude of the estimated limit radial stresses. Especially, when \({\mathbb{H}}=0\), radial stress goes up to 40 percent greater than the yield limit. From a mathematical perspective, this is possible. However, from a physical perspective, it is not likely. This much difference may cause plasticization in radial direction. If we take a look at other distribution such as \({\mathbb{H}}=0.75\) or \({\mathbb{H}}=1\), it is seen that radial stress at the inner diameter is less than the yield limit. These cases are much likely to happen. \({\mathbb{H}}=0.50\) case is also acceptable but \({\mathbb{H}}=0.00\) and \({\mathbb{H}}=0.25\) cases are mathematically possible but physically exaggerated incidents. Next, tangential stresses are shown in Fig. 4c. Thereat, it is observed that increment in \({\mathbb{H}}\) value reduces the limit stress approximations in tangential direction. In the last figure part, Fig. 4d, radial displacements are shown. As in the stress distributions, for the displacements, we observe reduced displacement distributions with greater \({\mathbb{H}}\) values. Overall, it is apparent that \({\mathbb{H}}\) is a prominent parameter that influences both stresses and displacements.

Fig. 4
figure 4

Effect of yield criterion parameter \({\mathbb{H}}\) on the normalized a yield function, b radial stress, c tangential stress, and d radial displacement where \(\mathcalligra{g}={\mathbb{O}}={\mathbb{G}}=0.50\)

Full size image

In the subsequent step, another yield parameter, \({\mathbb{G}}\), is going to be discussed. Within the scope of this discussion, other parameters are fixed to the same numerical value, \(\mathcalligra{g}={\mathbb{O}}={\mathbb{H}}=0.50\). Before detailing effects of parameter \({\mathbb{G}}\), it should be clarified that manipulating \({\mathbb{G}}\) means indirectly altering parameter \({\mathbb{F}}\) since \({\mathbb{G}}+{\mathbb{F}}=1\) from Eq. (42). Due to \({\mathbb{F}}=1-{\mathbb{G}}\), when a number is assigned to \({\mathbb{G}}\) we automatically obtain a value for \({\mathbb{F}}\). So, in this part of the research, we not only examine parameter \({\mathbb{G}}\) but also parameter \({\mathbb{F}}\). In Fig. 5a, normalized yield function is depicted. As in the above case, for values between zero and one, five different values have been set to parameter \({\mathbb{G}}\). According to the figure, yielding initiates at the inner diameter and when the value of \({\mathbb{G}}\) is smaller or \({\mathbb{F}}\) greater, disk yields at higher value of \(\overline{\Omega }\). Since there is no restriction at the outer diameter of the disk, combination of stresses reduces along the radius. In the ensuing plot, Fig. 5b, radial stresses are demonstrated. When \({\mathbb{G}}\) is zero or close to zero, radial stress exceeds the yield limit considerably. This is once again mathematically possible, yet unlikely to occur. Value of \({\mathbb{G}}\) around 0.50 to 1.00 is much more possible. In the case of \({\mathbb{G}}=0\), the term \({\left({\sigma}_{\rm{r}}\right)}^{2}\) in Eq. (41) vanishes. Similarly, when \({\mathbb{G}}=1,\) \({\left({\sigma}_{\theta }\right)}^{2}\) disappears. Having these two extreme cases may cause imbalances and yield to unsatisfactory interpretations. Next, tangential stresses are displayed in Fig. 5c. One observes from the figure that the stresses at the onset of plastic yield in this direction are prone to reduction with incrementing parameter \({\mathbb{G}}\). This comment is valid for the radial displacements as well, see Fig. 5d.

Fig. 5
figure 5

Effect of yield criterion parameter \({\mathbb{G}}\) on the normalized a yield function, b radial stress, c tangential stress, and d radial displacement where \(\mathcalligra{g}={\mathbb{O}}={\mathbb{H}}=0.50\)

Full size image

4 Finite element method-based analysis

Up to this point, analytical methods have been utilized to understand the behavior of the stress fields of the rotating disk. Here, using Autodesk Inventor Nastran 2024, FEM-based solution of the disk is examined. Followingly, analytical and FEM solutions have been compared. In the samples, annular disk geometry is taken into account, in other words \(\mathcalligra{g}=0.00\). The orthotropy parameter is assigned as \({\mathbb{O}}=0.285.\) In the program, in order to track the yield envelope, von Mises stress is available. If the parameters of Eq. (41) are set as \({\mathbb{G}}={\mathbb{H}}={\mathbb{F}}=0.50\) then the criterion is converted to von Mises (\({\sigma }_{\mathcalligra{v}{\mathcal{M}}}\)) in principal directions, which is

$${\sigma }_{\mathcalligra{v}{\mathcal{M}}}=\sqrt{{\left({\sigma}_{\rm{r}}\right)}^{2}+{\left({\sigma}_{\theta }\right)}^{2}-{\sigma}_{\rm{r}}{\sigma}_{\theta }}={\sigma }_{\mathcal{Y}}.$$
(44)

The criterion in normalized form can be expressed as \(\overline{{\sigma }_{\mathcalligra{v}{\mathcal{M}}}}={\sigma }_{\mathcalligra{v}{\mathcal{M}}}/{\sigma }_{\mathcal{Y}}\). In the FEM analysis, other parameters remain the same, which are \({r}_{\rm{i}}=50\) mm, \({r}_{\rm{o}}=100\) mm, \({v}_{r\theta }=0.25\), \(\varphi =2000\) kg/m3 \({E}_{\rm{r}}=35*{10}^{9}\) Pa, \({\sigma }_{\mathcal{Y}}=300*{10}^{6}\) Pa. Following these arrangements, the obtained results are presented in Fig. 6’s constituents. At the first constituent (a) instead of Hill’s criterion von Misses is given. In part (b), (c) and (d) corresponding radial stress, tangential stress and displacement are exhibited. On the left side of these figure parts, numerical color label chart is shown. By using the stress linearization tool of the commercial program, from one selected node to another along the radius of the disk, the stress distributions in radial, tangential, and axial directions can be tracked. It should be noted that since the disk is considerably thin compared to radial distance, the stress in the axial direction is zero; in other words, plane stress conditions are valid. In the program, the stress linearization tool is unfortunately not available for displacements yet. Thus, in order to track the displacements, the data points in radial and tangential directions which are gathered by stress linearization are combined with the analytical relations to obtain the displacement. As can be seen from Fig. 6 and its associative parts, the stress and displacements are not presented in normalized form. However, normalized distributions are utilized to this point. The data points obtained from the program are converted to normalized form to be in harmony. Followingly, analytical and FEM results are compared in Fig. 7. Overall, both analytical and FEM results are confirming each other with an acceptable difference. The differences have mostly occurred somewhere arbitrary along the radius. At the inner and outer diameters analytical and FEM results are matching. In order to achieve close results, considerably fine meshing is applied to the disk. As mesh geometry parabolic mesh elements are applied. In the computational procedure, 1,877,643 nodes and 1,394,680 elements have been utilized. The computational procedure took around 8 min. However, this time is only around 30 s in Mathematica 8 with an efficiently written mathematical code. It is obvious that for a simple axisymmetric geometry where the analytical solution is available, analytical solution is much preferable. Additionally, in some cases, assigning material parameters to the software is not a simple task since they generally require a considerable number of parameters to do calculations. On the other hand, when the analytical solution is not present or difficult to attain, clearly, FEM analysis is a more suitable option.

Fig. 6
figure 6

Stress and displacement fields of the orthotropic annular disk a von Mises stress, b radial stress, c tangential stress, and d radial displacement where \({\mathbb{G}}={\mathbb{H}}={\mathbb{F}}=0.50\)

Full size image
Fig. 7
figure 7

Comparison of the normalized stress and displacement fields of the orthotropic annular disk a von Mises stress, b radial stress, c tangential stress, and d radial displacement where \({\mathbb{G}}={\mathbb{H}}={\mathbb{F}}=0.50\)

Full size image

5 Results and discussion

In this study, stress analysis of variable thickness disk of orthotropic material is examined via both analytical and FEM approaches. Various parameters have been taken into account and effect of each parameter is investigated. In the parametric investigation, while manipulating one parameter other parameters have been fixed. So that, each parameter’s influence can be comprehended separately. Consequently, achieved results are summarized below:

  1. (I)

    Geometric parameter \(\mathcalligra{g}\) is an important constant that effects both stresses and displacements. For the considered disk geometry function, having negative values of \(\mathcalligra{g}\) is preferable. Negative \(\mathcalligra{g}\) values cause decreasing thickness or in other words tapered geometry on the disk. When this geometry is employed, the limit angular velocity rises.

  2. (II)

    Orthotropy parameter \({\mathbb{O}}\) is the material parameter that influences mostly stresses, particularly the ones in tangential direction. When the orthotropy parameter is increased the disk yields at higher angular velocities. Another way to describe this occurrence is tangentially dominant orthotropy results in higher velocity values.

  3. (III)

    Parameters \({\mathbb{H}}\) and \({\mathbb{G}}\) are substantial parameters of the yield criterion. Interestingly, for some values of \({\mathbb{H}}\) and \({\mathbb{G}}\), radial stress may go considerably higher than the effective yield stress at the inner diameter of the disk at the limit velocities. A little higher radial stress magnitude than the yield limit at the inner diameter may occur; however, considerable differences are not much likely in a realistic sense. These cases are rather mathematical possibilities.

  4. (IV)

    In the numerical examples, both analytical and FEM approaches have been compared. In both approaches, good agreement with some differences has been reached. Nevertheless, when the analytical solution is available, it is much preferred over FEM in terms of computation time and accuracy.