Skip to main content

Advertisement

SpringerLink
Log in

Modal analysis of a rotating twisted and tapered Rayleigh beam

  • Original
  • Published:
Archive of Applied Mechanics Aims and scope Submit manuscript

Abstract

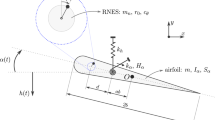
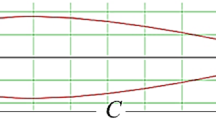
Free vibration analysis of a twisted, double-tapered blade mounted on a rotating disk undergoing overall motion is presented here. The Lagrangian approach is adapted to study the modal characteristics of the blade modeled as a rotating Rayleigh beam. The expressions for the kinetic energy and potential energy of the cantilever blade are derived using hybrid deformation variables. The continuous deformation variables in these equations are discretized using a series of basis functions that satisfy all boundary conditions of the cantilever beam. The equations governing the coupled stretch–bending–torsion motion of the rotating blade are derived using Lagrange’s approach. The equations are then transformed into a non-dimensional form which are then solved for the eigenvalue problem for the modal characteristics of the blade. The results of the present model are verified with the results available in the literature. The variation of the natural frequencies with the rotating speed, taper ratio and pre-twist angle is presented. The tuned angular speed of the blade at which the angular frequency matches with any of the natural frequency of the blade resulting in the resonance is investigated. The Campbell diagram is plotted for the specific problem to identify the resonance where the natural frequency matches with the harmonics of the rotating speed.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16
Fig. 17
Fig. 18
Fig. 19
Fig. 20
Fig. 21
Fig. 22
Fig. 23
Fig. 24
Fig. 25

Similar content being viewed by others

References

  1. Carnegie, W., Thomas, J.: The effects of shear deformation and rotary inertia on the lateral frequencies of cantilever beams in bending. J. Eng. Ind. 94(1), 267–278 (1972)

    Article  Google Scholar 

  2. Yardimoglu, B., Inman, D.: Coupled bending-bending-torsion vibration of a pre-twisted beam with aerofoil cross-section by the finite element method. Shock Vib. 10(4), 223–230 (2003)

    Article  Google Scholar 

  3. Chung, J., Yoo, H.: Dynamic analysis of a rotating cantilever beam by using the finite element method. J. Sound Vib. 249(1), 147–164 (2002)

    Article  Google Scholar 

  4. Fan, J., Zhang, D., Shen, H.: Dynamic modeling and simulation of a rotating flexible hub-beam based on different discretization methods of deformation fields. Arch. Appl. Mech. 90(2), 291–304 (2020)

    Article  Google Scholar 

  5. Huo, Y., Wang, Z.: Dynamic analysis of a rotating double-tapered cantilever timoshenko beam. Arch. Appl. Mech. 86(6), 1147–1161 (2016)

    Article  MATH  Google Scholar 

  6. Rao, J., Carnegie, W.: Solution of the equations of motion of coupled-bending bending torsion vibrations of turbine blades by the method of Ritz-Galerkin. Int. J. Mech. Sci. 12(10), 875–882 (1970)

    Article  MATH  Google Scholar 

  7. Subrahmanyam, K., Kulkarni, S., Rao, J.: Coupled bending-torsion vibrations of rotating blades of asymmetric aerofoil cross section with allowance for shear deflection and rotary inertia by use of the Reissner method. J. Sound Vib. 75(1), 17–36 (1981)

    Article  MATH  Google Scholar 

  8. Zhu, T.: The vibrations of pre-twisted rotating timoshenko beams by the Rayleigh-Ritz method. Comput. Mech. 47(4), 395–408 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  9. Rao, J.: Coupled bending torsion vibrations of cantilever beams. J. Aeronaut. Soc. India 24(1), 265–275 (1972)

    Google Scholar 

  10. Hodges, D., Rutkowski, M.: Free-vibration analysis of rotating beams by a variable-order finite-element method. AIAA J. 19(11), 1459–1466 (1981)

    Article  MATH  Google Scholar 

  11. Seo, S., Yoo, H.: Dynamic analysis of flexible beams undergoing overall motion employing linear strain measures. AIAA J. 40(2), 319–326 (2002)

    Article  Google Scholar 

  12. Sharf, I.: Geometric stiffening in multibody dynamics formulations. J. Guid. Control Dyn. 18(4), 882–890 (1995)

    Article  MathSciNet  MATH  Google Scholar 

  13. Kim, H., Chung, J.: Nonlinear modeling for dynamic analysis of a rotating cantilever beam. Nonlinear Dyn. 86(3), 1981–2002 (2016)

    Article  Google Scholar 

  14. Zhao, G., Wu, Z.: Coupling vibration analysis of rotating three-dimensional cantilever beam. Comput. Struct. 179, 64–74 (2017)

    Article  Google Scholar 

  15. Thomas, O., Sénéchal, A., Deü, J.-F.: Hardening/softening behavior and reduced order modeling of nonlinear vibrations of rotating cantilever beams. Nonlinear Dyn. 86(2), 1293–1318 (2016)

    Article  Google Scholar 

  16. Kane, T., Ryan, R., Banerjee, A.: Dynamics of a cantilever beam attached to a moving base. J. Guid. Control Dyn. 10(2), 139–151 (1987)

    Article  Google Scholar 

  17. Yoo, H., Ryan, R., Scott, R.: Dynamics of flexible beams undergoing overall motions. J. Sound Vib. 181(2), 261–278 (1995)

    Article  MATH  Google Scholar 

  18. Yoo, H., Shin, S.: Vibration analysis of rotating cantilever beams. J. Sound Vib. 212(5), 807–828 (1998)

    Article  Google Scholar 

  19. Yoo, H., Park, J., Park, J.: Vibration analysis of rotating pre-twisted blades. Comput Struct. 79(19), 1811–1819 (2001)

    Article  Google Scholar 

  20. Yoo, H., Lee, S., Shin, S.: Flapwise bending vibration analysis of rotating multi-layered composite beams. J. Sound Vib. 286(4–5), 745–761 (2005)

    Article  MATH  Google Scholar 

  21. Zhu, T.: Free flapewise vibration analysis of rotating double-tapered Timoshenko beams. Arch. Appl. Mech. 82(4), 479–494 (2012)

    Article  MATH  Google Scholar 

  22. Liu, J., Hong, J.: Dynamic modeling and modal truncation approach for a high-speed rotating elastic beam. Arch. Appl. Mech. 72(8), 554–563 (2002)

    Article  MATH  Google Scholar 

  23. Huang, C., Lin, W., Hsiao, K.: Free vibration analysis of rotating euler beams at high angular velocity. Comput. Struct. 88(17–18), 991–1001 (2010)

    Article  Google Scholar 

  24. Invernizzi, D., Dozio, L.: A fully consistent linearized model for vibration analysis of rotating beams in the framework of geometrically exact theory. J. Sound Vib. 370, 351–371 (2016)

    Article  Google Scholar 

  25. Oh, Y., Yoo, H.: Vibration analysis of a rotating pre-twisted blade considering the coupling effects of stretching, bending, and torsion. J. Sound Vib. 431, 20–39 (2018)

    Article  Google Scholar 

  26. Özdemir, Ö., Kaya, M.: Flapwise bending vibration analysis of a rotating double-tapered Timoshenko beam. Arch. Appl. Mech. 78(5), 379–392 (2008)

    Article  MATH  Google Scholar 

  27. Dawson, B., Carnegie, W.: Modal curves of pre-twisted beams of rectangular cross-section. J. Mech. Eng. Sci. 11(1), 1–13 (1969)

    Article  Google Scholar 

  28. Gupta, R., Rao, S.: Finite element eigenvalue analysis of tapered and twisted Timoshenko beams. J. Sound Vib. 56(2), 187–200 (1978)

    Article  MATH  Google Scholar 

  29. Young, T.: Dynamic resppnse of a pretwisted, tapered beam with non-constant rotating speed. J. Sound Vib. 150(3), 435–446 (1991)

    Article  Google Scholar 

  30. Downs, B.: Transverse vibrations of cantilever beams having unequal breadth and depth tapers. J. Appl. Mech. 44(4), 737–742 (1977)

    Article  Google Scholar 

  31. Subrahmanyam, K., Rao, J.: Coupled bending-bending vibrations of pretwisted tapered cantilever beams treated by the Reissner method. J. Sound Vib. 82(4), 577–592 (1982)

    Article  Google Scholar 

  32. Lee, S., Kuo, Y.: Bending vibrations of a rotating non-uniform beam with an elastically restrained root. J. Sound Vib. 154(3), 441–451 (1992)

    Article  MATH  Google Scholar 

  33. Özdemir, Ö., Kaya, M.: Flapwise bending vibration analysis of double tapered rotating Euler-Bernoulli beam by using the differential transform method. Meccanica 41(6), 661–670 (2006)

    Article  MATH  Google Scholar 

  34. Özdemir, Ö., Kaya, M.: Flapwise bending vibration analysis of a rotating tapered cantilever Euler-Bernoulli beam by differential transform method. J. Sound Vib. 289(1–2), 413–420 (2006)

    Article  MATH  Google Scholar 

  35. Ramezani, A., Alasty, A., Akbari, J.: Effects of rotary inertia and shear deformation on nonlinear vibration of micro/nano-beam resonators. 128, 611–615 (2006)

  36. Tian, J., Su, J., Zhou, K., Hua, H.: A modified variational method for nonlinear vibration analysis of rotating beams including coriolis effects. J. Sound Vib. 426, 258–277 (2018)

    Article  Google Scholar 

  37. Banerjee, J.: Development of an exact dynamic stiffness matrix for free vibration analysis of a twisted timoshenko beam. J.Sound Vib. 270(1–2), 379–401 (2004)

    Article  MATH  Google Scholar 

  38. Stoykov, S., Ribeiro, P.: Nonlinear forced vibrations and static deformations of 3d beams with rectangular cross section: the influence of warping, shear deformation and longitudinal displacements. Int. J. Mech. Sci. 52(11), 1505–1521 (2010)

    Article  Google Scholar 

  39. Boresi, A., Schmidt, R., Sidebottom, O.: Advanced Mechanics of Materials. Wiley, New York (1985)

    MATH  Google Scholar 

  40. Hodges, Dewey H, Pierce, G Alvin: Introduction to structural dynamics and aeroelasticity, vol. 15. Cambridge university press, Cambridge (2011)

    Book  Google Scholar 

  41. Ozgumus, O., Kaya, M.: Vibration analysis of a rotating tapered timoshenko beam using dtm. Meccanica 45(1), 33–42 (2010)

    Article  MATH  Google Scholar 

  42. Ozgumus, O., Kaya, M.: Flapwise bending vibration analysis of a rotating double-tapered timoshenko beam. Arch. Appl. Mech. 78(5), 379–392 (2008)

    Article  MATH  Google Scholar 

  43. Hodges, D., Pierce, G.: Introduction to structural dynamics and aeroelasticity, vol. 15. Cambridge university press, Cambridge (2011)

    Book  Google Scholar 

  44. Kim, H., Yoo, H., Chung, J.: Dynamic model for free vibration and response analysis of rotating beams. J. Sound Vib. 332(22), 5917–5928 (2013)

    Article  Google Scholar 

  45. Lacarbonara, W., Arvin, H., Bakhtiari-Nejad, F.: A geometrically exact approach to the overall dynamics of elastic rotating blades part 1: linear modal properties. Nonlinear Dyn. 70(1), 659–675 (2012)

    Article  MathSciNet  Google Scholar 

  46. Wang, G., Wereley, N.: Free vibration analysis of rotating blades with uniform tapers. AIAA J. 42(12), 2429–2437 (2004)

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Defence Institute of Advanced Technology, Pune, 411025, India

    Lokanna Hoskoti & Ajay Misra

  2. Indian Institute of Technology, Hyderabad, 502285, India

    Mahesh M. Sucheendran

Authors
  1. Lokanna Hoskoti
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Ajay Misra
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Mahesh M. Sucheendran
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Lokanna Hoskoti.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Supplementary Information

Below is the link to the electronic supplementary material.

Supplementary material 1 (rar 10785 KB)

Appendices

A coefficient matrices of Eq. 15

$$\begin{aligned}&\text {Mass matrices} \nonumber \\&\quad M^{11}_{ij} = \int _0^L \rho A \psi _{1i}\psi _{1j} dx, \nonumber \\&\quad M^{22}_{ij} = \int _0^L \rho A \psi _{2i}\psi _{2j} dx + \int _0^L \rho I_3 \psi '_{2i}\psi '_{2j} dx, \nonumber \\&\quad M^{23}_{ij} = \int _0^L \rho I_{23} \psi '_{2i}\psi '_{3j} dx, \nonumber \\&\quad M^{32}_{ij} =\int _0^L \rho I_{23} \psi '_{3i}\psi '_{2j} dx, \nonumber \\&\quad M^{33}_{ij} = \int _0^L \rho A \psi _{2i}\psi _{2j} dx+ \int _0^L \rho I_2 \psi '_{3i}\psi '_{3j} dx, \nonumber \\&\quad M^{44}_{ij} =\int _0^L \rho J \psi _{4i}\psi _{4j} dx, \nonumber \\&\text {Gyroscopic matrices} \nonumber \\&\quad G^{12}_{ij} = 2\varOmega \int _0^L \rho A \psi _{1i}\psi _{2j} dx, \nonumber \\&\quad G^{21}_{ij} = 2\varOmega \int _0^L \rho A \psi _{2i}\psi _{1j} dx, \nonumber \\&\quad G^{24}_{ij} = 2\varOmega \int _0^L \rho I_{23} \psi '_{2i}\psi _{4j} dx, \nonumber \\&\quad G^{34}_{ij} = 2\varOmega \int _0^L \rho I_{2} \psi '_{3i}\psi _{4j} dx, \nonumber \\&\quad G^{42}_{ij} = 2\varOmega \int _0^L \rho I_{23} \psi _{4i}\psi '_{2j} dx, \nonumber \\&\quad G^{43}_{ij} = 2\varOmega \int _0^L \rho I_{2} \psi _{4i}\psi '_{3j} dx, \nonumber \\&\text {Stiffness matrices} \nonumber \\&\quad K^{11}_{ij} = \int _0^L EA \psi '_{1i}\psi '_{1j} dx - \varOmega ^2\int _0^L \rho A \psi _{1i}\psi _{1j} dx \nonumber \\&\quad K^{22}_{ij} = \varOmega ^2\int _0^L \rho A \Big [r(L-x) + \frac{1}{2}(L^2-x^2)\Big ] \psi '_{2i}\psi '_{2j} dx \nonumber \\&\qquad \qquad - \varOmega ^2\int _0^L \rho A \psi _{2i}\psi _{2j} dx + \varOmega ^2\int _0^L \rho I_3 \psi '_{2i}\psi '_{2j} dx \nonumber \\&\qquad \qquad + \int _0^L EI_3 \psi _{2i}''\psi _{2j}'' dx, \nonumber \\&\quad K^{23}_{ij} = \int _0^L EI_{23} \psi _{2i}''\psi _{3j}'' dx-\varOmega ^2\int _0^L \rho I_{23} \psi '_{2i}\psi '_{3j} dx \nonumber \\&\quad K^{33}_{ij} = \varOmega ^2\int _0^L \rho A \Big [r(L-x) + \frac{1}{2}(L^2-x^2)\Big ] \psi '_{3i}\psi '_{3j} dx \nonumber \\&\qquad \qquad - \varOmega ^2\int _0^L \rho I_2 \psi '_{3i}\psi '_{3j} dx + \int _0^L EI_2 \psi _{3i}''\psi _{3j}'' dx, \nonumber \\&\quad K^{32}_{ij} = \int _0^L EI_{23} \psi _{3i}''\psi _{2j}'' dx-\varOmega ^2\int _0^L \rho I_{23} \psi '_{3i}\psi '_{2j} dx \nonumber \\&\quad K^{44}_{ij} = \varOmega ^2\int _0^L \rho A \Big [r(L-x) + \frac{1}{2}(L^2-x^2)\Big ] \psi '_{4i}\psi '_{4j} dx \nonumber \\&\qquad \qquad -\varOmega ^2\int _0^L \rho I_2 \psi _{4i}\psi _{4j} dx + \int _0^L GK \psi '_{4i}\psi '_{4j} dx. \end{aligned}$$
(31)

B coefficient matrices of Eq. 22

$$\begin{aligned} \begin{aligned}&\text {Mass matrices} \\&\quad {\bar{M}}^{11}_{ij} = \int _0^1 {\bar{A}} {\bar{\psi }}_{1i}{\bar{\psi }}_{1j} d{\bar{x}}, \\&\quad {\bar{M}}^{22}_{ij} = \int _0^1 {\bar{A}} {\bar{\psi }}_{2i}{\bar{\psi }}_{2j} d{\bar{x}} + \beta ^2 \int _0^1 {\bar{I}}_3 {\bar{\psi }}'_{2i}{\bar{\psi }}'_{2j} d{\bar{x}},\\&\quad {\bar{M}}^{23}_{ij} = \beta ^2\int _0^1 {\bar{I}}_{23} {\bar{\psi }}'_{2i}{\bar{\psi }}'_{3j} d{\bar{x}},\\&\quad {\bar{M}}^{32}_{ij} = \beta ^2\int _0^1 {\bar{I}}_{23} {\bar{\psi }}'_{3i}{\bar{\psi }}'_{2j} d{\bar{x}},\\&\quad {\bar{M}}^{33}_{ij} = \int _0^1 {\bar{A}} {\bar{\psi }}_{2i}{\bar{\psi }}_{2j} d{\bar{x}}+ \beta ^2\int _0^1 {\bar{I}}_2 {\bar{\psi }}'_{3i}{\bar{\psi }}'_{3j} d{\bar{x}},\\&\quad {\bar{M}}^{44}_{ij} = \int _0^1 {\bar{\psi }}_{4i}{\bar{\psi }}_{4j} d{\bar{x}},\\&\text {Gyroscopic matrices} \\&\quad {\bar{G}}^{12}_{ij} = 2\gamma \int _0^1 {\bar{A}} {\bar{\psi }}_{1i}{\bar{\psi }}_{2j} d{\bar{x}},\\&\quad {\bar{G}}^{21}_{ij} = 2\gamma \int _0^1 {\bar{A}} {\bar{\psi }}_{2i}{\bar{\psi }}_{1j} d{\bar{x}},\\&\quad {\bar{G}}^{24}_{ij} = 2\gamma \beta ^2 \int _0^1 {\bar{I}}_{23} {\bar{\psi }}'_{2i}{\bar{\psi }}_{4j} d{\bar{x}},\\&\quad {\bar{G}}^{34}_{ij} = 2\gamma \beta ^2 \int _0^1 {\bar{I}}_{2} {\bar{\psi }}'_{3i}{\bar{\psi }}_{4j} d{\bar{x}},\\&\quad {\bar{G}}^{42}_{ij} = 2\gamma \beta ^2 \int _0^1 {\bar{J}}_{23} {\bar{\psi }}_{4i}{\bar{\psi }}'_{2j} d{\bar{x}},\\&\quad {\bar{G}}^{43}_{ij} = 2\gamma \beta ^2 \int _0^1 {\bar{J}}_{2} {\bar{\psi }}_{4i}{\bar{\psi }}'_{3j} d{\bar{x}},\\\\&\text {Stiffness matrices} \\&\quad {\bar{K}}^{11}_{ij} = \beta ^{-2}\int _0^1 {\bar{\psi }}'_{1i}{\bar{\psi }}'_{1j} d{\bar{x}} - \gamma ^2\int _0^1 {\bar{A}} {\bar{\psi }}_{1i}{\bar{\psi }}_{1j} d{\bar{x}}\\&\quad {\bar{K}}^{22}_{ij} = \gamma ^2\int _0^1 {\bar{A}} F {\bar{\psi }}'_{2i}{\bar{\psi }}'_{2j} d{\bar{x}} - \gamma ^2\int _0^1 {\bar{A}} {\bar{\psi }}_{2i}{\bar{\psi }}_{2j} d{\bar{x}} \\&\qquad \qquad -\beta ^2\gamma ^2\int _0^1 {\bar{I}}_3 {\bar{\psi }}'_{2i}{\bar{\psi }}'_{2j} d{\bar{x}} + \int _0^1 {\bar{I}}_3 {\bar{\psi }}_{2i}''{\bar{\psi }}_{2j}'' d{\bar{x}}, \\&\quad {\bar{K}}^{23}_{ij} = \int _0^1 {\bar{I}}_{23} {\bar{\psi }}_{2i}''{\bar{\psi }}_{3j}'' d{\bar{x}}- \beta ^2 \gamma ^2\int _0^1 {\bar{I}}_{23} {\bar{\psi }}'_{2i}{\bar{\psi }}'_{3j} d{\bar{x}}, \\&\quad {\bar{K}}^{32}_{ij} = \int _0^1 {\bar{I}}_{23} {\bar{\psi }}_{3i}''{\bar{\psi }}_{2j}'' d{\bar{x}}- \beta ^2 \gamma ^2\int _0^1 {\bar{I}}_{23} {\bar{\psi }}'_{3i}{\bar{\psi }}'_{2j} d{\bar{x}}\\&\quad {\bar{K}}^{33}_{ij} = \gamma ^2\int _0^1 {\bar{A}} F {\bar{\psi }}'_{3i}{\bar{\psi }}'_{3j} d{\bar{x}} - \beta ^2\gamma ^2\int _0^1 {\bar{I}}_2 {\bar{\psi }}'_{3i}{\bar{\psi }}'_{3j} d{\bar{x}} \\&\qquad \qquad + \int _0^1 {\bar{I}}_2 {\bar{\psi }}_{3i}''{\bar{\psi }}_{3j}'' d{\bar{x}}, \\&\quad {\bar{K}}^{44}_{ij} = \gamma ^2\int _0^1 {\bar{A}} F {\bar{\psi }}'_{4i}{\bar{\psi }}'_{4j} d{\bar{x}} - \gamma ^2\int _0^1 {\bar{J}}_2 {\bar{\psi }}_{4i}{\bar{\psi }}_{4j} d{\bar{x}} \\&\qquad \qquad + \eta \beta ^{-2} \int _0^1 \bar{J_3}{\bar{\psi }}'_{4i}{\bar{\psi }}'_{4j} d{\bar{x}} \end{aligned} \end{aligned}$$
(32)

where

$$\begin{aligned} \begin{aligned} \beta&=\frac{I_{30}}{A_0L^2}, \eta = \frac{GK_t}{EI_{30}}, {\bar{A}} = (1-c_b{\bar{x}})(1-c_h{\bar{x}})\\ F&= \Big [\delta (1-{\bar{x}}) + \frac{1}{2}(1-{\bar{x}}^2)\Big ] \\ {\bar{I}}_2&= \frac{1}{2}\big (1-c_b{\bar{x}}\big )\big (1-c_h{\bar{x}}\big ) \Big [\kappa \big (1-c_h{\bar{x}}\big )^{2} + \big (1-c_b{\bar{x}}\big )^{2} \Big ]\\&\qquad \quad +\frac{1}{2}\big (1-c_b{\bar{x}}\big )\big (1-c_h{\bar{x}}\big ) \Big [\kappa \big (1-c_h{\bar{x}}\big )^{2} - \big (1-c_b{\bar{x}}\big )^{2} \Big ]\cos (2\theta _t {\bar{x}}), \\ {\bar{I}}_3&= \frac{1}{2}\big (1-c_b{\bar{x}}\big )\big (1-c_h{\bar{x}}\big ) \Big [\kappa \big (1-c_h{\bar{x}}\big )^{2} + \big (1-c_b{\bar{x}}\big )^{2} \Big ]\\&\quad \qquad -\frac{1}{2}\big (1-c_b{\bar{x}}\big )\big (1-c_h{\bar{x}}\big ) \Big [\kappa \big (1-c_h{\bar{x}}\big )^{2} - \big (1-c_b{\bar{x}}\big )^{2} \Big ]\cos (2\theta _t {\bar{x}}), \\ {\bar{I}}_{23}&= \frac{1}{2}\big (1-c_b{\bar{x}}\big )\big (1-c_h{\bar{x}}\big ) \Big [\kappa \big (1-c_h{\bar{x}}\big )^{2} - \big (1-c_b{\bar{x}}\big )^{2} \Big ]\sin (2\theta _t {\bar{x}}) \\ {\bar{J}}_{23}&= {\bar{I}}_{23}/ \big (1-c_b{\bar{x}}\big )\big (1-c_h{\bar{x}}\big ) \Big [\kappa \big (1-c_h{\bar{x}}\big )^{2} + \big (1-c_b{\bar{x}}\big )^{2} \Big ] \\ {\bar{J}}_{2}&= {\bar{I}}_2/ \big (1-c_b{\bar{x}}\big )\big (1-c_h{\bar{x}}\big ) \Big [\kappa \big (1-c_h{\bar{x}}\big )^{2} + \big (1-c_b{\bar{x}}\big )^{2} \Big ] \\ {\bar{J}}_{3}&= {\bar{I}}_3/ \big (1-c_b{\bar{x}}\big )\big (1-c_h{\bar{x}}\big ) \Big [\kappa \big (1-c_h{\bar{x}}\big )^{2} + \big (1-c_b{\bar{x}}\big )^{2} \Big ]. \end{aligned} \end{aligned}$$
(33)

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Hoskoti, L., Misra, A. & Sucheendran, M.M. Modal analysis of a rotating twisted and tapered Rayleigh beam. Arch Appl Mech 91, 2535–2567 (2021). https://doi.org/10.1007/s00419-021-01902-8

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00419-021-01902-8

Keywords

Search

Navigation