Nonlocal and surface effects on nonlinear vibration response of a graded Timoshenko nanobeam

Abstract

The free and forced vibration of a graded geometrically nonlinear Timoshenko nanobeam supported by on a nonlinear foundation is considered in this paper. The main contribution of this study is to propose a new formulation for the dynamic response of this beam by combining nonlocal and surface elasticity in addition to employing the physical neutral axis method which eliminates the quadratic nonlinearity from the equation of motion. Using the principle of virtual work, a fourth-order nonlinear partial differential equation is formulated and Galerkin technique is employed to yield a fourth-order ordinary differential equation with cubic nonlinearity in the temporal domain. The method of multiple scales is employed to obtain the analytical expression of the nonlinear frequency of the beam and its frequency response curve from a primary resonance analysis. To assess the accuracy of this analytical solution, it is compared with a numerical solution obtained using the differential quadrature method. The obtained analytical results are successfully validated for particular cases of the considered problem with results published by other authors. The effects of surface elasticity, nonlocality, the physical neutral axis, the beam aspect ratio, the power-law index and the elastic foundation coefficients on the free and forced vibration response of the graded Timoshenko nanobeam are thoroughly investigated for different types of boundary conditions .

1 Introduction

Miniature beams have been used in many electromechanical systems such as biosensors, ultra-thin films, micro-switches, micro-actuators, nanowires, micro-electromechanical systems (MEMS) and nanoelectromechanical system (NEMS) as the primary structural elements [1,2,3,4]. It is well known that a classical continuum model does not have the capability to handle length scale effects. As a result, many models have been proposed during the last few decades that incorporated the size-dependency effects, namely nonlocal theory [5,6,7], modified coupled stress theory [8, 9], strain gradient theory [10, 11] or a combination of these theories such as the nonlocal strain gradient theory [12].

Functionally graded material (FGM) is a kind of composite material in which the volume fraction of the constituent materials changes from one surface to the other. Thus, FGM provides a smooth transition change in properties in a specified direction that leads to less stress concentration and consequently to fracture [13]. FGMs have been used in several engineering applications such as marine risers [14], biomedical applications [15], energy applications [16] and aerospace applications [17], and a detailed review can be found in [18]. In addition, FGMs have been recently employed in several micro/nanoapplications [19,20,21,22].

Using Eringen’s nonlocal model, several investigators have focused on the linear dynamic response of functionally graded (FG) nanobeams. Eltaher et al. [23] performed a free vibration analysis of a nonlocal nanobeam using the finite element method (FEM). Navier’s method was used by Uymaz [24] to investigate the dynamic response of a FG Euler–Bernoulli nanobeam. The same method was employed by Rahmani and Pedram [25] to examine the vibration behavior of a Timoshenko graded beam. A free vibration study was conducted by Nejad and Hadi [26] on a nanobeam graded in two directions in which they employed the generalized differential quadrature method (GDQM) to solve the equations of motion. Yao et al. [27] investigated the free vibration and wave propagation of an axially moving functionally graded Timoshenko microbeam. Generally, the nonlocal model induces a softening type of behavior; however, Li et al. [28] demonstrated that a cantilever Euler–Bernoulli beam can exhibit either a softening or a hardening type of behavior depending on the applied loading. Recently, Arefi et al. [29] conducted a free vibration analysis of graded polymer composite curved nanobeams reinforced with graphene nanoplatelets to predict their dynamic characteristics. Very recently, Luo et al. [30] conducted transverse vibration of an axisymmetric graded circular nanoplate with radial uniform loads. Esen et al. [31] investigated the vibrational characteristics of functionally graded (FG) cracked microbeam rested on elastic foundation and subjected to thermal and magnetic fields. On the other hand, the literature is abundant with studies using the strain gradient theory such as, for instance, the works among others of Arefi and Zenkour who performed dynamic and bending analyses for the sandwiched microbeams [32,33,34] and FG Timoshenko’s sandwiched microbeams [35]. There are also several published papers which used the modified couple stress theory in studying the dynamic behavior of Timoshenko beams such as the recent work of Abdelrahman et al. [36] who investigated the dynamic behavior of perforated Timoshenko microbeams in a thermal environment and that of Abo-bakr et al. [37] who studied the static and dynamic behavior of axially graded microbeams with nonuniform cross section. The recent literature witnessed additional papers related to the nonlocal strain gradient theory. For instance, Daikh et al. [38] studied the static stability, free vibration and bending response of multilayer functionally graded carbon nanotubes reinforced using composite nanoplates.

Many authors studied the nonlinear dynamic response of graded nanobeams by considering the von Kármán geometric nonlinearity. He’s variational method was employed by Simsek [39] to predict the nonlinear vibration response of a Euler–Bernoulli graded nanobeam. A similar method was used by Niknam and Aghdam [40] to determine the nonlinear response of a free vibration and buckling load of a Euler–Bernoulli graded beam supported by nonlinear elastic springs. Using the method of multiple scales (MMS), the nonlinear nonlocal free vibration response of a Euler–Bernoulli FG nanobeam was investigated by Nazemnezhad and Hosseini-Hashemi [41]. MMS was also used by El-Borgi et al. [42] who examined the nonlinear nonlocal free and forced vibration of a Euler–Bernoulli FG nanobeam supported by elastic foundation effects. A similar problem was solved by Trabelssi et al. [43, 44] by employing both the locally adaptive differential quadrature method (LaDQM) and the regular differential quadrature method (DQM). These studies were extended by the same main authors to investigate the free and forced vibration response of a Timoshenko graded beam based on the weak quadrature element method [45].

In the last few years, several authors have been investigating the incorporation of surface effects on the behavior of nanostructures. These effects can become quite important due to abrupt changes in the surface area-to-volume ratio at the nanoscale dimensions. Overall, it was observed that the surface elasticity properties can influence the properties of the size-dependent materials at nanoscale [46,47,48,49,50]. The nonlinear response of the nonlinear free vibration of FG nanobeams while considering only surface effects was studied by [51]. The nonlinear vibration frequencies of a Timoshenko nanobeam were investigated by [52, 53] in which the combined effects of nonlocal parameter, surface elasticity and residual surface stress were taken into account. The nonlinear vibration response of graded nanobeams was examined by Hosseini-Hashemi et al. [54] by emphasizing on the coupling between nonlocal and surface effects. In the above literature, it was assumed that the geometrical neutral axis coincides with the physical neutral axis for the undeformed plane of the beam. However, this assumption is valid only for uniform material properties along a given direction of a beam. This assumption was shown to result in an error up to 10$\%$ in the natural frequencies of a FG beam [55]. Recently, few researchers have recently adopted in their models the physical neutral axis in FG beams instead of using the geometrical central axis [55,56,57,58,59,60,61]. Lately, Arefi et al. [62, 63] employed the concept of the physical neutral axis to study, respectively, the static behavior of graded piezoelectric plates and the vibration response of graded piezoelectric face-sheets. More recently, Shen et al. [64] investigated the vibration and stability response of graded nanoplates by considering physical neutral plane. The use of such technique can eliminate stretching–bending coupling effect due to nonuniform material distribution along the given direction in the beam.

From the above review and to the best of the authors’ knowledge, it can be summarized that very few researchers have investigated the nonlinear free and forced vibration response of FG Timoshenko nanobeams by considering both nonlocal and surface effects [48] or surface effects only [49, 51]. However, combining the aforementioned effects along with the physical neutral axis location for predicting the nonlinear dynamic behavior of FG beams has not been investigated thus far for deep beams. It was, however, investigated by the authors [65] for slender Euler–Bernoulli beams where shear effects were neglected. The effect of the neutral axis is expected to be more pronounced for a deep beam especially when shear effects are considered. For low aspect ratio, the effect of the neutral axis may cause further deviation from the standard model. To bridge these gaps, this study aims to introduce the physical neutral axis concept while considering both surface elasticity and nonlocality to study the nonlinear dynamic response of a deep Timoshenko beam by employing the method of multiple scales (MMS). Such a solution is based on the linear classical modeshape Galerkin technique. A DQM-based numerical solution proposed by Trabelssi et al. [44] is employed based on the actual nonclassical modeshape for the purpose of assessing the accuracy of the MMS solution. Therefore, the novelty of this study can be summarized as follows: (a) propose a new formulation for the dynamic response of a geometrically nonlinear TBT beam with a nonlinear foundation combining nonlocal and surface elasticity in addition to physical neutral axis, (b) develop an MMS-based analytical solution for the current problem and validate it using DQM, (c) explore low aspect ratios of the beam while remaining within the assumptions of the TBT beam theory, (d) study the effect of surface stress on the neutral axis position, (e) conduct a thorough and detailed parametric study covering all the nondimensional parameters governing the physics of the investigated problem. The proposed formulation can be potentially applied to several applications such as MEMS and NEMS devices [66] in addition to carbon nanotubes (CNTs) such as sensors, actuators, electromagnetics, electroacoustic and hydrogen storage [67] as well as protein microtubules surrounded by an elastic matrix [68].

This paper is structured as follows. Sects. 2 and 3 provide, respectively, the derivation of the motion equations for both the classical and the nonlocal Timoshenko beam theory by considering surface elasticity and the physical neutral axis location. Section 4 summarizes the solution formulation of vibration response of the nanobeam using MMS. Section 5 outlines the DQM formulation used to assess the accuracy of the MMS solution. In Sect. 6, the obtained analytical results are validated with published data for specific cases of the considered problem and then a detailed parametric study is presented to examine the effect of the various parameters on the free and forced vibration nonlinear response of the nanobeam. Finally, a summary of this investigation and main conclusions is provided in Sect. 7.

2 Classical Timoshenko beam with surface effects

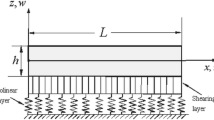
A graded nanobeam is considered in this study whose length, width and height are denoted L, b and h, respectively. The nanobeam is resting on a nonlinear elastic foundation as shown in Fig. 1. The considered boundary condition is either simply supported (S-S) or clamped–clamped (C-C). Due to the characteristics of the graded material, the beam’s mid-plane does not match with the neutral axis of the beam, and hence, two separate frames of reference need to be considered in this study:

• ($x_{m}$,$y_{m}$,$z_{m}$) is a reference coordinate system with the axis $x_{m}$ running through the geometrical mid-plane axis of the beam and $y_m$ and $z_m$ are two axes of symmetry defining the cross-sectional area of the beam, as depicted in Fig. 1.

• (x,y,z) is a secondary reference coordinate system with the axis $x=x_m$ running through the neutral axis of the beam and $y=y_m$ and $z=z_m-h_0$ are two axes of symmetry as shown in Fig. 1. Here, $h_0$ is the distance separating the neutral axis to the mid-plane of the nanobeam.

Fig. 1

Schematic of simply supported FG beam on nonlinear elastic foundation

For a Timoshenko beam with varying mechanical properties varying along z, it is assumed that the elastic and shear moduli, E and G, the surface elastic modulus $E^{s}$ and the density $\rho$ follow a power-law function as given below

$$\begin{aligned} E(z_m)&=(E_{U}-E_{L})\left( \frac{z_m}{h}+\frac{1}{2}\right) ^{n}+E_{L} \quad G(z_m)= \frac{E(z_m)}{2(1+\nu )} \end{aligned}$$

(1a)

$$\begin{aligned} E^{s}(z_m)&=(E_{U}^{s}-E_{L}^{s})\left( \frac{z_m}{h}+\frac{1}{2}\right) ^{n}+E_{L}^{s} \quad \rho (z_m)=(\rho _{U}-\rho _{L})\left( \frac{z_m}{h}+\frac{1}{2}\right) ^{n}+\rho _{L} \end{aligned}$$

(1b)

where L and U denote, respectively, the lower and upper layers of the nanobeam. $\nu$ is the Poisson’s coefficient assumed to be a constant [69]. The parameter n denotes the material gradation index.

According to the Timoshenko beam theory (TBT), the displacement field can be expressed as follows:

$$\begin{aligned} \mathbf{u(x,t)}=\left[ u(x,t)+z\phi (x,t)\right] \hat{\mathbf{e}}_{x}+w(x,t)\hat{\mathbf{e}}_{z} \end{aligned}$$

(2)

where u and w are, respectively, the displacements along x and z coordinates, $\phi$ is the shear angle, and $\hat{\mathbf{e}}_{x}$ and $\hat{\mathbf{e}}_{z}$ are, respectively, unit vectors along the x- and z-axes. Here, t designates the time variable. Within the assumptions of the small deformation and displacement theory, the strain tensor can be expressed as follows:

$$\begin{aligned} \mathbf{E}\approx \varvec{\varepsilon }=\left( \varepsilon _{xx}\right) \hat{\mathbf{e}}_{x}\hat{\mathbf{e}}_{x}+\left( \gamma _{xz}\right) \hat{\mathbf{e}}_{x}\hat{\mathbf{e}}_{z} \end{aligned}$$

(3)

where

$$\begin{aligned} \varepsilon _{xx}=\varepsilon _{xx}^{(0)} + z \varepsilon _{xx}^{(1)}, \varepsilon _{xx}^{(0)}=\frac{\partial u}{\partial x}+\frac{1}{2}\left( \frac{\partial w}{\partial x}\right) ^{2},\varepsilon _{xx}^{(1)}=\frac{\partial \phi }{\partial x},\gamma _{xz}=\phi +\frac{\partial w}{\partial x} \end{aligned}$$

(4)

In a Hookean solid, the stress–strain law for a Timoshenko beam can be written as

$$\begin{aligned} \sigma _{{ xx}}&=E\left( z\right) \varepsilon _{xx}\nonumber \\ \sigma _{{ xz}}&=G\left( z\right) K_s\gamma _{xz} \end{aligned}$$

(5)

where $K_s$ is the shear correction factor with a value of 5/6 for a rectangular section. The beam surface elasticity along the longitudinal direction is represented by [48]

$$\begin{aligned} \sigma ^{s}= E^{s}\left( z\right) \varepsilon _{xx} \end{aligned}$$

(6)

It is worth emphasizing that the beam is assumed to be geometrically nonlinear (i.e., with van Karman strain nonlinearity appearing in Eq. (4)) but with a linear stress–strain behavior (i.e., Eq. (5)) and a nonlinear foundation.

Applying the principle of virtual work for the Timoshenko beam and integrating its expression by parts and separating the different components of the displacement field yield the following equations of motion:

$$\begin{aligned} \frac{\partial M_{xx}^{(0)}}{\partial x}&=m_{0}\frac{\partial ^{2}u}{\partial t^{2}} \end{aligned}$$

(7a)

$$\begin{aligned} \frac{\partial M_{xz}^{(0)}}{\partial x}+\frac{\partial }{\partial x}\left[ M_{xx}^{(0)}\frac{\partial w}{\partial x}\right] +f_{z}&=m_{0}\frac{\partial ^{2}w}{\partial t^{2}}+c\frac{\partial w}{\partial t} \end{aligned}$$

(7b)

$$\begin{aligned} \frac{\partial M_{xx}^{(1)}}{\partial x}-M_{xz}^{(0)}&=m_{2}\frac{\partial ^{2}\phi }{\partial t^{2}} \end{aligned}$$

(7c)

where $M_{xx}^{(0)}$, $M_{xx}^{(1)}$ and $M_{xz}^{(0)}$ are stress resultants and $m_{0}$ and $m_{2}$ are mass inertia which can be expressed as

$$\begin{aligned} M_{xx}^{(i)}&=\int _{A}(z)^{i}\sigma _{xx}dA+\oint \limits _{\Gamma }(z)^{i}\sigma ^{s}ds,(i=0,1),M_{xz}^{(0)}=\int _{A}\sigma _{xz}dA \end{aligned}$$

(8a)

$$\begin{aligned} m_{0}&=\int _{A}\rho \,dA=\rho \,A,\quad m_{2}=\int _{A}\rho z^{2}\,dA \end{aligned}$$

(8b)

in which $A=bh$ denotes the area of the beam’s cross section. By employing the expressions from (2) to (6), the resultants of the stress components can be formulated as a function of the displacements

$$\begin{aligned} M_{xx}^{(0)}&={\tilde{A}}\left[ \frac{\partial u}{\partial x}+\frac{1}{2}\left( \frac{\partial w}{\partial x}\right) ^{2}\right] +{\tilde{B}}\left( \frac{\partial \phi }{\partial x}\right) \end{aligned}$$

(9a)

$$\begin{aligned} M_{xx}^{(1)}&={\tilde{B}}\left[ \frac{\partial u}{\partial x}+\frac{1}{2}\left( \frac{\partial w}{\partial x}\right) ^{2}\right] +{\tilde{D}}\left( \frac{\partial \phi }{\partial x}\right) \end{aligned}$$

(9b)

$$\begin{aligned} M_{xz}^{(0)}&= {\tilde{G}}\left( \phi +\frac{\partial w}{\partial x}\right) \end{aligned}$$

(9c)

where

$$\begin{aligned} {\tilde{A}}&=\int _{A}E(z)\,dA+\oint \limits _{\Gamma }E^{s}(z)ds,\ \ {\tilde{B}}=\int _{A}E(z)z\,dA+\oint \limits _{\Gamma }E^{s}(z)zds,\ \nonumber \\ {\tilde{D}}&=\int _{A}E(z)z^{2}\,dA+\oint \limits _{\Gamma }E^{s}(z)z^{2}ds,\ {\tilde{G}}=\int _{A}G(z)K_s\,dA \end{aligned}$$

(10)

The neutral axis location is derived by setting that the total axial force is equal to zero along the longitudinal axis. Therefore, Eq. (9a) can be rewritten as

$$\begin{aligned} M_{xx}^{(0)} ={\tilde{A}}\left[ \frac{\partial u}{\partial x}+\frac{1}{2}\left( \frac{\partial w}{\partial x}\right) ^{2}\right] +{\tilde{B}}\left( \frac{\partial \phi }{\partial x}\right) =0 \end{aligned}$$

(11)

To determine the neutral axis location, the axial displacement is ignored and higher-order terms are neglected (i.e., first term of the above equation is neglected). Thus, Eq. (11) can be reduced to a closed-form expression for the position of the neutral axis

$$\begin{aligned}&h_{0}= -\frac{h \left[ \left( b \left( n^2+3 n+2\right) +2 h n\right) \left( E^s_L-E^s_U\right) +b h n (E_L-E_U)\right] }{2 (n+2) \left( b n E^s_L+b E^s_L+b n E^s_U+b E^s_U+2 h n E^s_L+2 h E^s_U+b h n E_L+b h E_U\right) } \end{aligned}$$

(12)

Details about the calculation of $h_0$ can be found in Appendix A, and the expressions of ${\tilde{A}}$, ${\tilde{D}}$ and ${\tilde{G}}$ appearing in (10) are written in a simpler form in Appendix B.

To combine the motion equations (8a) and (8b), a relation between the axial and transverse displacements is developed using the von Kármán nonlinearity. Based on a method proposed by [70], the displacement along the axial direction u is eliminated from the motion equations resulting in a constant von Kármán nonlinear term. To this end, the following assumptions are made in the study: (1) The inertia term ($m\ddot{u}$) is very small and can be ignored; (2) the beam is supported at $x=0$ and $x=L$, and hence, the displacements along the longitudinal direction at the boundaries are zero, i.e., $u(0,t)=0 \text{ and } u(L,t)=0$. The first assumption along with (8a) results in $M_{xx}^{(0)}$ being a constant. In light of that, the following equations of motion can be obtained after further mathematical manipulations:

$$\begin{aligned} {\tilde{G}}\left( \phi '+w''\right) +{\tilde{A}}c_{1}w''+f_{z}= & {} m_{0}\ddot{w}+c{\dot{w}} \end{aligned}$$

(13a)

$$\begin{aligned} {\tilde{D}}\phi ''-{\tilde{G}}\left( \phi +w'\right)= & {} m_{2}\ddot{\phi } \end{aligned}$$

(13b)

Here, dot ($^{.}$) represents differentiation with respect to t and prime ($'$) denotes differentiation with respect to x. Details of this simplification are provided in Appendix C. The force $f_{z}$ in Eq. (13a) comprises both the applied force and the elastic foundation reaction force, and its expression can be written as [71]

$$\begin{aligned} f_{z}=-k_{L}w-k_{NL}w^{3}+k_{s}w''+F\cos (\theta t) \end{aligned}$$

(14)

where $k_{L}$, $k_{NL}$ and $k_{s}$ represent, respectively, the linear, nonlinear and shear coefficients of the elastic foundation and F is the magnitude of the harmonic force.

Finally, the following normalization is adopted:

$$\begin{aligned} {\hat{x}}=\frac{x}{L},\quad {\hat{t}}=\frac{t}{\tau },\quad {\hat{w}}=\frac{w}{r}\quad {\hat{\phi }}=\frac{L}{r}\phi \end{aligned}$$

(15)

where r=$\sqrt{\frac{I}{A}}$ is the radius of gyration of the cross section and $I=\frac{bh^{3}}{12}$ is the second moment of inertia. The equation of motion in dimensionless form in terms of the nondimensional parameters is given by

$$\begin{aligned} \frac{1}{s^{2}}\left( {\hat{\phi }}'+{\hat{w}}''\right) -{\hat{k}}_{L}{\hat{w}}-{\hat{k}}_{NL}{\hat{w}}^{3}+{\hat{k}}_{s}{\hat{w}}''+{\hat{F}}\cos ({\hat{\theta }}{\hat{t}})+ {\hat{w}}''\int _{0}^{1}\left[ \kappa _{0}\left( {\hat{w}}'\right) ^{2}\right] d{\hat{x}}= & {} \ddot{{\hat{w}}}+{\hat{c}}\dot{{\hat{w}}} \end{aligned}$$

(16a)

$$\begin{aligned} {\hat{\phi }}''-\frac{1}{s^{2}}\left( {\hat{\phi }}+{\hat{w}}'\right)= & {} {\hat{\alpha }}\ddot{{\hat{\phi }}} \end{aligned}$$

(16b)

where

$$\begin{aligned}&{\hat{\alpha }}=\frac{m_{2}}{m_{0}L^{2}};\ \ \tau =L^{2}\sqrt{\frac{m_{0}}{{\tilde{D}}}};\ \ {\hat{c}}=\frac{c\tau }{m_{0}};\ \ {\hat{k}}_{s}=\frac{k_{s}\tau ^{2}}{m_{0}L^{2}};\ \ {\hat{k}}_{L}=\frac{k_{L}\tau ^{2}}{m_{0}}; \nonumber \\&{\hat{k}}_{NL}=\frac{k_{NL}r^{2}\tau ^{2}}{m_{0}};\ \ {\hat{F}}=\frac{F\tau ^{2}}{m_{0}r};\ \ {\hat{\theta }}=\theta \tau ;\ s^{2}=\frac{{\tilde{D}}}{L^{2}{\tilde{G}}};\ \ \kappa _{0}={\tilde{A}}\frac{r^{2}\tau ^{2}}{2m_{0}L^{4}} \end{aligned}$$

(17)

3 Nonlocal Timoshenko beam theory with surface effects

Eringen [5, 6] introduced the nonlocal theory which states that the stress $\varvec{\sigma }$ at a given point x in an elastic domain is not only a function of the local strain at that point $\varvec{\varepsilon }$ but is a function of the strains at all points in the domain. Based on this theory, the nonlocal stress can be expressed as follows:

$$\begin{aligned} \bar{\varvec{\sigma }}=\int _{\Omega }K(\vert \mathbf{x}'-\mathbf{x}\vert ,\tau )\,\varvec{\sigma }(\mathbf{x}')\,d\mathbf{x}' \end{aligned}$$

(18)

where $\varvec{\sigma }(\mathbf{x}')$ is the local stress at point $\mathbf{x}'$ and $K(\vert \mathbf{x}'-\mathbf{x}\vert ,\tau )$ is the nonlocal modulus, $\vert \mathbf{x}'-\mathbf{x}\vert$ denotes the distance between x and x’, and $\tau$ is a material constant. Eringen [6] also introduced an equivalent form of the differential model which can be written as

$$\begin{aligned} \bigl (1-\mu _{0}^{2}\nabla ^{2}\bigr )\bar{\varvec{\sigma }}=\mathbf{C}:{\varvec{\varepsilon }},\quad \mu _{0}=\tau ^{2}\ell ^{2}=e_{0}^{2}a^{2} \end{aligned}$$

(19)

where $e_{0}$ is a material constant, a is an internal characteristic length, $\ell$ is an external characteristic length and $\mu _0$ is the nonlocal parameter, and $\nabla ^{2}$ is the Laplacian operator. In addition, for a beam-type structure, it is reasonable to assume that the size-dependent effect is dominant along the axial direction. Thus, Eq. (19) can be simplified to the following:

$$\begin{aligned} {\bar{\sigma }}_{xx}-\mu _{0}\frac{d^{2}{\bar{\sigma }}_{xx}}{\partial x^{2}}=&E(z)\varepsilon _{xx} \end{aligned}$$

(20a)

$$\begin{aligned} {\bar{\sigma }}_{xz}-\mu _{0}\frac{d^{2}{\bar{\sigma }}_{xz}}{\partial x^{2}}=&G(z)\gamma _{xz}^{(0)} \end{aligned}$$

(20b)

where the operator $\nabla ^{2}$ is substituted with $\partial ^{2}/\partial x^{2}$ and ${\tilde{A}}$, ${\tilde{D}}$ and ${\tilde{G}}$ are given by (B.1) and the expressions of ${\tilde{A}}$ and ${\tilde{D}}$ incorporate surface effects. Integration of the above relations over the section of the beam yields the nonlocal stress resultants as a function of the strain components which can be written as

$$\begin{aligned} {{\bar{M}}}^{(0)}_{xx}&=\mu _0 {\partial ^2 {{\bar{M}}}^{(0)}_{xx}\over \partial x^2}+ {{\tilde{A}}}\, {\varepsilon }^{(0)}_{xx} \end{aligned}$$

(21a)

$$\begin{aligned} {{\bar{M}}}^{(1)}_{xx}&=\mu _0 {\partial ^2 {{\bar{M}}}^{(1)}_{xx}\over \partial x^2} + {{\tilde{D}}}\, {\varepsilon }^{(1)}_{xx} \end{aligned}$$

(21b)

$$\begin{aligned} {{\bar{M}}}^{(0)}_{xz}&=\mu _0 {\partial ^2 {{\bar{M}}}^{(0)}_{xz}\over \partial x^2} + {{\tilde{G}}}\gamma _{xz}^{(0)} \end{aligned}$$

(21c)

Substituting (2) and (4) into the above equations yields the nonlocal stress resultants as a function of displacements

$$\begin{aligned} {{\bar{M}}}^{(0)}_{xx}&=\mu _0 {\partial ^2 {{\bar{M}}}^{(0)}_{xx}\over \partial x^2}+ {\tilde{A}}\left[ \frac{\partial u}{\partial x}+\frac{1}{2}\left( \frac{\partial w}{\partial x}\right) ^{2}\right] \end{aligned}$$

(22a)

$$\begin{aligned} {{\bar{M}}}^{(1)}_{xx}&=\mu _0 {\partial ^2 {{\bar{M}}}^{(1)}_{xx}\over \partial x^2} + {\tilde{D}} \frac{\partial \phi }{\partial x} \end{aligned}$$

(22b)

$$\begin{aligned} {{\bar{M}}}^{(0)}_{xz}&=\mu _0 {\partial ^2 {{\bar{M}}}^{(0)}_{xz}\over \partial x^2} +{\tilde{G}} \left( \phi +\frac{\partial w}{\partial x}\right) \end{aligned}$$

(22c)

By employing the principle of virtual displacement, the following nonlocal equations of motion are obtained [44]:

$$\begin{aligned} \frac{\partial \bar{M}_{xx}^{(0)}}{\partial x}&=m_{0}\frac{\partial ^{2}u}{\partial t^{2}} \end{aligned}$$

(23a)

$$\begin{aligned} \frac{\partial \bar{M}_{xz}^{(0)}}{\partial x}+\frac{\partial }{\partial x}\left[ \bar{M}_{xx}^{(0)}\frac{\partial w}{\partial x}\right] +f_{z}&=m_{0}\frac{\partial ^{2}w}{\partial t^{2}}+c\frac{\partial w}{\partial t} \end{aligned}$$

(23b)

$$\begin{aligned} \frac{\partial M_{xx}^{(1)}}{\partial x}-M_{xz}^{(0)}&=m_{2}\frac{\partial ^{2}\phi }{\partial t^{2}} \end{aligned}$$

(23c)

Taking the derivative of the above equations with respect to x and substituting the expressions of $\frac{\partial ^{2}{\bar{M}}_{xx}^{(0)}}{\partial x^{2}}$, $\frac{\partial ^{2}{\bar{M}}_{xx}^{(1)}}{\partial x^{2}}$ and $\frac{\partial ^{2}{\bar{M}}_{xz}^{(0)}}{\partial x^{2}}$ into (22a), (22b) and (22c) give

$$\begin{aligned} \bar{M}_{xx}^{(0)}=&\, {\tilde{A}}\,\left[ \frac{\partial u}{\partial x}+\frac{1}{2}\left( \frac{\partial w}{\partial x}\right) ^{2}\right] +\mu _{0}\left( m_{0}\frac{\partial ^{3}u}{\partial x\partial t^{2}}\right) \end{aligned}$$

(24a)

$$\begin{aligned} \bar{M}_{xx}^{(1)}=&\,{\tilde{D}}\,\frac{\partial \phi }{\partial x} +\mu _{0}\left( m_{2}\frac{\partial ^{3}\phi }{\partial x\partial t^{2}}+m_{0}\frac{\partial ^{2}w}{\partial t^{2}}+c\frac{\partial w}{\partial t}-\frac{\partial }{\partial x}\left[ \bar{M}_{xx}^{(0)}\frac{\partial w}{\partial x}\right] -f_{z}\right) \end{aligned}$$

(24b)

$$\begin{aligned} \bar{M}_{xz}^{(0)}=&\,{\tilde{G}}\,\left( \phi +\frac{\partial w}{\partial x}\right) +\mu _{0}\left( m_{0}\frac{\partial ^{3}w}{\partial x\partial t^{2}}+c\frac{\partial ^{2}w}{\partial x\partial t}-\frac{\partial ^{2}}{\partial x^{2}}\left[ \bar{M}_{xx}^{(0)}\frac{\partial w}{\partial x}\right] -\frac{\partial f_{z}}{\partial x}\right) \end{aligned}$$

(24c)

The assumptions listed in Sect. 2 are used to remove the axial displacement u from (24a) and yield the stress resultants as a function of the vertical deflection w and the shear angle $\phi$. The above equations reduce to the following:

$$\begin{aligned} \bar{M}_{xx}^{(0)} =&\,{\tilde{A}}\,c_{1}(t) \end{aligned}$$

(25a)

$$\begin{aligned} \bar{M}_{xx}^{(1)} =&\,{\tilde{D}}\,\frac{\partial \phi }{\partial x} +\mu _{0}\left( m_{2}\frac{\partial ^{3}\phi }{\partial x\partial t^{2}}+m_{0}\frac{\partial ^{2}w}{\partial t^{2}}+c\frac{\partial w}{\partial t}-{\tilde{A}}c_{1}\frac{\partial ^{2}w}{\partial x^{2}}-f_{z}\right) \end{aligned}$$

(25b)

$$\begin{aligned} \bar{M}_{xz}^{(0)}=&\, {\tilde{G}}\,\left( \phi +\frac{\partial w}{\partial x}\right) +\mu _{0}\left( m_{0}\frac{\partial ^{3}w}{\partial x\partial t^{2}}+c\frac{\partial ^{2}w}{\partial x\partial t}-{\tilde{A}}c_{1}\frac{\partial ^{3}w}{\partial x^{3}}-\frac{\partial f_{z}}{\partial x}\right) \end{aligned}$$

(25c)

where the expression of $c_{1}(t)$ is provided in (C.3). Substituting the above equations into (23b) and (23c) yields the nonlocal equations of motion of the nanobeam

$$\begin{aligned} {\tilde{G}}\left( \phi '+w''\right) +{\tilde{A}}c_{1}(t)\left( w''-\mu _{0}w''''\right) +\left( f_{z}-\mu _{0}f_{z}''\right)&=m_{0}\left( \ddot{w}-\mu _{0}\ddot{w}''\right) +c\left( {\dot{w}}-\mu _{0}{\dot{w}}''\right) \end{aligned}$$

(26a)

$$\begin{aligned} {\tilde{D}}\phi ''-{\tilde{G}}\left( \phi +w'\right)&=m_{2}\left( \ddot{\phi }-\mu _{0}\ddot{\phi }''\right) \end{aligned}$$

(26b)

The dimensionless parameters introduced in equation (15) are substituted in the above equations to yield the following nondimensional equations of motion:

$$\begin{aligned} \frac{1}{s^{2}}\left( {\hat{\phi }}'+{\hat{w}}''\right) +\left( {\hat{f}}_{z}-{\hat{\mu }}_{0}{\hat{f}}_{z}''\right) +\left( {\hat{w}}''-{\hat{\mu }}_{0}w''''\right) \int _{0}^{1}\left[ \kappa _{0}\left( {\hat{w}}''\right) ^{2}\right] d{\hat{x}}&=\left( \ddot{{\hat{w}}}-{\hat{\mu }}_{0}\ddot{{\hat{w}}}''\right) +{\hat{c}}\left( \dot{{\hat{w}}}-{\hat{\mu }}_{0}\dot{{\hat{w}}}''\right) \end{aligned}$$

(27a)

$$\begin{aligned} {\hat{\phi }}''-\frac{1}{s^{2}}\left( {\hat{\phi }}+{\hat{w}}'\right)&={\hat{\alpha }}\left( \ddot{{\hat{\phi }}}-{\hat{\mu }}_{0}\ddot{{\hat{\phi }}}''\right) \end{aligned}$$

(27b)

where ${\hat{f}}_{z}={\hat{k}}_{L}{\hat{w}}+{\hat{k}}_{NL}{\hat{w}}^{3}-{\hat{k}}_{s}w''+{{\hat{F}}}\cos ({\hat{\theta }}{\hat{t}})$ and ${\hat{\mu }}_{0}=\frac{\mu _{0}}{L^{2}}$ is the dimensionless nonlocal parameter and the remaining quantities have been defined in (17). When ${\hat{\mu }}_{0}=0$, then the nonlocal equations of motion of the nanobeam reduce to the equations of motion given by (16).

4 Analytical solution using MMS

4.1 Galerkin discretization

It is possible to combine the above equations of motion system into a single partial differential equation in terms of only ${\hat{w}}$. To this end, the expression of ${\hat{\phi }}'$ is extracted from (27a) and then injected into the ${\hat{x}}$ derivative of Eq. (27b). The resulting equation can be written as

$$\begin{aligned}&{\ddot{W}}_{L}^{*}-m{\ddot{W}}_{L}^{''}+{\hat{c}}{\dot{W}}_{L}^{*}+{\hat{w}}^{''''}-\left( f\kappa +{\hat{k}}_{s}\right) W_{L}^{*''}+{\hat{k}}_{L}W_{L}^{*}+{\hat{k}}_{NL}W_{NL}^{*}\nonumber \\&\qquad -2ms^{2}\dot{f\kappa }\left( {\dot{W}}_{L}^{''}-{\hat{\mu }}_{0}{\dot{W}}_{L}''''\right) -ms^{2}\ddot{f\kappa }\left( W_{L}^{''}-{\hat{\mu }}_{0}W_{L}''''\right) \nonumber \\&\quad =\left[ F_{L}\left( 1-ms^{2}{\hat{\omega }}^{2}\right) -s^{2}F_{L}^{''}\left( 1-m{\hat{\omega }}^{2}{\hat{\mu }}_{0}\right) \right] \cos ({\hat{\theta }}{\hat{t}}) \end{aligned}$$

(28)

where

$$\begin{aligned} f'&=\frac{\partial }{\partial {\hat{x}}}f({\hat{x}},{\hat{t}})\quad {\dot{f}}=\frac{\partial }{\partial \tau }f({\hat{x}},{\hat{t}})\quad \forall f({\hat{x}},{\hat{t}})\\ f\kappa&\equiv f\kappa ({\hat{t}})=\int _{0}^{1}\kappa _{0}{\hat{w}}''^{2}d{\hat{x}}\\ W_{L}&={\hat{w}}-{\hat{\mu }}_{0}{\hat{w}}^{''}\\ W_{NL}&={\hat{w}}^{3}-3{\hat{\mu }}_{0}\left( {\hat{w}}^{''}{\hat{w}}{}^{2}+2{\hat{w}}^{'}{}^{2}{\hat{w}}\right) \\ W_{L}^{*}&=W_{L}-s^{2}W_{L}^{''}+ms^{2}\left( {\ddot{W}}_{L}-{\hat{\mu }}_{0}{\ddot{W}}_{L}^{''}\right) \\ W_{NL}^{*}&=W_{NL}-s^{2}W_{NL}^{''}+ms^{2}\left( {\ddot{W}}_{NL}-{\hat{\mu }}_{0}{\ddot{W}}_{NL}^{''}\right) \\ F_{L}&={\hat{F}}-{\hat{\mu }}_{0}{\hat{F}}^{''} \end{aligned}$$

By employing Galerkin technique, the transverse displacement is assumed to be written as ${\hat{w}}({\hat{x}},{\hat{t}})=\psi ({\hat{x}})q({\hat{t}})$ and the resulting equation (28) can be transformed into an ordinary differential equation with time being the independent variable. The term $\psi ({\hat{x}})$ is expressed as a classical linear beam modeshape. Table 1 lists these linear modeshapes corresponding to the either simply supported (S-S) or clamped–clamped (C-C). The aforementioned assumption is substituted into (28), and the resulting equation is integrated over the beam domain

Table 1 Linear classical modeshape functions of a uniform beam for different boundary conditions

$$\begin{aligned}&\frac{d^{4}q}{d{\hat{t}}^{4}}+\mu _{1}\frac{d^{3}q}{d{\hat{t}}^{3}}+\beta _{1}\frac{d^{2}q}{d{\hat{t}}^{2}}+\mu _{2}\frac{dq}{d{\hat{t}}}+\beta _{2}q+\beta _{3}q^{3}+\beta _{4}\frac{d^{2}q}{d{\hat{t}}^{2}}q^{2}+\beta _{5}\left( \frac{dq}{d{\hat{t}}}\right) ^{2}q=\left( \mu _{3}+\mu _{4}{\hat{\omega }}^{2}\right) \bar{F}_{1}\cos ({\hat{\theta }}{\hat{t}}) \end{aligned}$$

(29)

where the coefficients $\beta _{i}\ (i=1,5)$ and $\mu _{i}\ (i=1,4)$ are defined in Appendix D and $\mu _{1}$ and $\mu _{2}$ contain the damping coefficient ${\hat{c}}$. In the above equation, $\bar{F}_{1} = \frac{{\hat{F}}}{\psi _{F}({\hat{x}})}$ is the amplitude of ${\hat{F}}({{\hat{x}}})$, and $\psi _{F}({\hat{x}})$ is a function used to describe the applied force distribution along the x-axis. However, in general, this distribution is set as $\psi _{F}({\hat{x}})=1$.

4.2 Free vibration solution

To study the free vibration response of the nanobeam, the damping term and the external force are removed from (29). Adding the initial conditions gives

$$\begin{aligned}&\frac{d^{4}q}{d{\hat{t}}^{4}}+\beta _{1}\frac{d^{2}q}{d{\hat{t}}^{2}}+\beta _{2}q+\beta _{3}q^{3}+\beta _{4}\frac{d^{2}q}{d{\hat{t}}^{2}}q^{2}+\beta _{5}\left( \frac{dq}{d{\hat{t}}}\right) ^{2}q=0 \end{aligned}$$

(30a)

$$\begin{aligned}&q(0)=A,\ \ {\dot{q}}(0)=0,\ \ \ddot{q}(0)=0,\ \ \dddot{q}(0)=0 \end{aligned}$$

(30b)

where A represents the amplitude of vibration. An approximate analytical solution for equation (30a) is achieved using the method of multiple scales [70]. The solution is obtained through an expansion of both the time variable ${{\hat{t}}}$ and the dependent variable $q({\hat{t}})$. This expansion requires that the system response is expressed as a function of several independent variables called time scales. The solution is expressed in terms of this expansion as follows:

$$\begin{aligned} q({\hat{t}})=\varepsilon q_{0}(T_{0},T_{1},T_{2})+\varepsilon ^{2}q_{1}(T_{0},T_{1},T_{2})+\varepsilon ^{3}q_{2}(T_{0},T_{1},T_{2})+.... \end{aligned}$$

(31)

where $\varepsilon$ is a small scaling term. The fast time scale $T_{0}={\hat{t}}$ is defined as the time scale of the primary oscillation, and the slow time scales $T_{n}=\varepsilon ^{n}{\hat{t}},n\ge 1$, are the times used to account for amplitude and phase modulation. Substituting (31) into (30a) and then gathering the powers of $\varepsilon$ result in a system of three differential equations

$$\begin{aligned} \varepsilon ^{1}:\ \ \ D_{0}^{4}q_{0}+\beta _{1}D_{0}^{2}q_{0}+\beta _{2}q_{0}=&0 \end{aligned}$$

(32a)

$$\begin{aligned} \varepsilon ^{2}:\ \ \ D_{0}^{4}q_{1}+\beta _{1}D_{0}^{2}q_{1}+\beta _{2}q_{1}=&-4D_{1}D_{0}^{3}q_{0}-2\beta _{1}D_{0}D_{1}q_{0} \end{aligned}$$

(32b)

$$\begin{aligned} \varepsilon ^{3}:\ \ \ D_{0}^{4}q_{2}+\beta _{1}D_{0}^{2}q_{2}+\beta _{2}q_{2}=&-\left( 4D_{2}D_{0}^{3}+6D_{1}^{2}D_{0}^{2}\right) q_{0}-\beta _{1}\left( D_{1}^{2}+2D_{2}D_{0}\right) q_{0}\nonumber \\&-\beta _{4}\zeta _{0}^{2}D_{0}^{2}q_{0}-4D_{1}D_{0}^{3}q_{1}-2\beta _{1}D_{1}D_{0}q_{1}\nonumber \\&-\beta _{3}q_{0}^{3}-\beta _{5}\left( D_{0}q_{0}\right) ^{2}q_{0} \end{aligned}$$

(32c)

where $D_{i}$ $(i=0,1,2)$ indicates a differentiation with respect to time and the subscript i denotes the scale of time. The solution of Eq. (32a) may be written as

$$\begin{aligned} q_{0}(T_{0},T_{1},T_{2})=A_{1}(T_{1},T_{2})\mathrm {e}^{i\omega _{1}T_{0}}+A_{2}(T_{1},T_{2})\mathrm {e}^{i\omega _{2}T_{0}}+cc \end{aligned}$$

(33)

where cc designates the complex conjugate of the first two terms and $\omega _{1}$ and $\omega _{2}$ are linear frequencies which are given by

$$\begin{aligned} \omega _{1}^{2}&=\frac{\beta _{1}}{2}-\sqrt{\frac{\beta _{1}^{2}}{4}-\beta _{2}} \end{aligned}$$

(34a)

$$\begin{aligned} \omega _{2}^{2}&=\frac{\beta _{1}}{2}+\sqrt{\frac{\beta _{1}^{2}}{4}-\beta _{2}} \end{aligned}$$

(34b)

Substituting the solution given by (33) into (32b) and then setting the secular terms $\left( \mathrm {e}^{i\omega _{1}T_{0}},\mathrm {e}^{i\omega _{2}T_{0}}\right)$ to zero lead to the following conditions:

$$\begin{aligned} D_{1}A_{1}(T_{1},T_{2})=0,\,\,\,\,D_{1}A_{2}(T_{1},T_{2})=0 \end{aligned}$$

(35)

which simplify to

$$\begin{aligned} A_{1}\left( T_{1},T_{2}\right) =A_{1}(T_{2}),\,\,\,\,A_{2}\left( T_{1},T_{2}\right) =A_{2}(T_{2}) \end{aligned}$$

(36)

Substituting (35) into (32b) gives $q_{1}(T_{0},T_{1},T_{2})=0$. Then, substituting the solutions of (32a) and (32b) and applying the above conditions given by (35) into the differential equation (32c) then dropping the secular terms $\left( \mathrm {e}^{i\omega _{1}T_{0}},\mathrm {e}^{i\omega _{2}T_{0}}\right)$, the following equations are obtained:

$$\begin{aligned}&2i\omega _{1}\left( 2\omega _{1}^{2}-\beta _{1}\right) D_{2}A_{1}+3\left( \beta _{4}\omega _{1}^{2}-\beta _{3}-\frac{1}{3}\beta _{5}\omega _{1}^{2}\right) A_{1}^{2}\bar{A}_{1} \nonumber \\&\quad +2\left[ \beta _{4}\left( \omega _{1}^{2}+2\omega _{2}^{2}\right) -3\beta _{3}-\beta _{5}\omega _{2}^{2}\right] A_{1}A_{2}\bar{A}_{2}=0 \end{aligned}$$

(37a)

$$\begin{aligned}&2i\omega _{2}\left( 2\omega _{2}^{2}-\beta _{1}\right) D_{2}A_{2}+3\left( \beta _{4}\omega _{2}^{2}-\beta _{3}-\frac{1}{3}\beta _{5}\omega _{2}^{2}\right) A_{2}^{2}\bar{A}_{2}\nonumber \\&\quad +2\left[ \beta _{4}\left( \omega _{2}^{2}+2\omega _{1}^{2}\right) -3\beta _{3}-\beta _{5}\omega _{1}^{2}\right] A_{1}\bar{A}_{1}A_{2}=0 \end{aligned}$$

(37b)

Here, $A_{1}$ and $A_{2}$ are given in polar forms as

$$\begin{aligned} A_{1}\left( T_{2}\right) =\frac{1}{2}a_{1}\left( T_{2}\right) \mathrm {e}^{i\theta _{1}\left( T_{2}\right) },\,\,\,A_{2}\left( T_{2}\right) =\frac{1}{2}a_{2}\left( T_{2}\right) \mathrm {e}^{i\theta _{2}\left( T_{2}\right) } \end{aligned}$$

(38)

where $a_{j}$ and $\theta _{j}$ $(j=1,2)$ are reals. Substituting $A_{1}$ and $A_{2}$ into (37a) and (37b) and then separating into real and imaginary parts, it can be concluded that $a_{1}$ and $a_{2}$ are constants and $\theta _{1}$ and $\theta _{2}$ are given by

$$\begin{aligned} \theta _{1}\left( T_{2}\right) =\delta _{1}T_{2}+\theta _{10},\,\,\,\,\theta _{2}\left( T_{2}\right) =\delta _{2}T_{2}+\theta _{20} \end{aligned}$$

(39)

In the above equations, $\theta _{10}$ and $\theta _{20}$ are constants and $\delta _{1}$ and $\delta _{2}$ are given by

$$\begin{aligned} \delta _{1}&=\frac{1}{8}\frac{\left( 3\beta _{4}\omega _{1}^{2}-\beta _{5}\omega _{1}^{2}-3\beta _{3}\right) a_{1}^{2}+2\left[ \beta _{4}\left( \omega _{1}^{2}+2\omega _{2}^{2}\right) -\beta _{5}\omega _{2}^{2}-3\beta _{3}\right] a_{2}^{2}}{\omega _{1}(2\omega _{1}^{2}-\beta _{1})} \end{aligned}$$

(40a)

$$\begin{aligned} \delta _{2}&=\frac{1}{8}\frac{2\left[ \beta _{4}\left( \omega _{2}^{2}+2\omega _{1}^{2}\right) -\beta _{5}\omega _{1}^{2}-3\beta _{3}\right] a_{1}^{2}+\left( 3\beta _{4}\omega _{2}^{2}-\beta _{5}\omega _{2}^{2}-3\beta _{3}\right) a_{2}^{2}}{\omega _{2}(2\omega _{2}^{2}-\beta _{1})} \end{aligned}$$

(40b)

Substituting (39) into (38) yields the following expressions of $A_{1}$ and $A_{2}$:

$$\begin{aligned} A_{1}=\frac{1}{2}a_{1}\mathrm {e}^{\left( i\varepsilon ^{2}\delta _{1}{\hat{t}}+i\theta _{10}\right) },\,\,\,A_{2}=\frac{1}{2}a_{2}\mathrm {e}^{\left( i\varepsilon ^{2}\delta _{2}{\hat{t}}+i\theta _{20}\right) } \end{aligned}$$

(41)

Here, $T_{2}=\varepsilon ^{2}{\hat{t}}$. Substituting $A_{1}$ and $A_{2}$ into (33), the overall solution given by Eq. (31) becomes

$$\begin{aligned} q\left( {\hat{t}}\right) =\varepsilon \left( a_{1}\cos (\Omega _{1}{\hat{t}}+\theta _{10})+a_{2}\cos (\Omega _{2}{\hat{t}}+\theta _{20})\right) +O(\varepsilon ^{3}) \end{aligned}$$

(42)

where the nonlinear frequencies $\Omega _{j}$ $(j=1,2)$ are given by

$$\begin{aligned} \Omega _{j}=\omega _{j}+\varepsilon ^{2}\delta _{j} \end{aligned}$$

(43)

To obtain the unknown constants $a_{1},a_{2},\theta _{10}$ and $\theta _{20}$, solving Eq. (42) by applying the initial conditions provided in (30b) and gathering like powers of $\varepsilon$

$$\begin{aligned} \varepsilon \left( a_{1}\cos \left( \theta _{1}\right) +a_{2}\cos \left( \theta _{2}\right) \right) +O(\varepsilon ^{3})&=A \end{aligned}$$

(44a)

$$\begin{aligned} \varepsilon \left( a_{1}\omega _{1}\sin \left( \theta _{1}\right) +a_{2}\omega _{2}\sin \left( \theta _{2}\right) \right) +O(\varepsilon ^{3})&=0 \end{aligned}$$

(44b)

$$\begin{aligned} \varepsilon \left( a_{1}\omega _{1}^{2}\cos \left( \theta _{1}\right) +a_{2}\omega _{2}^{2}\cos \left( \theta _{2}\right) \right) +O(\varepsilon ^{3})&=0 \end{aligned}$$

(44c)

$$\begin{aligned} \varepsilon \left( a_{1}\omega _{1}^{3}\sin \left( \theta _{1}\right) +a_{2}\omega _{2}^{3}\sin \left( \theta _{2}\right) \right) +O(\varepsilon ^{3})&=0 \end{aligned}$$

(44d)

The solution of the above system of equations can be written as

$$\begin{aligned} a_{1}=\frac{\omega _{2}^{2}A}{\varepsilon \left( \omega _{2}^{2}-\omega _{1}^{2}\right) },\,\,\,\,a_{2}=\frac{\omega _{1}^{2}A}{\varepsilon \left( \omega _{1}^{2}-\omega _{2}^{2}\right) },\,\,\,\,\theta _{10}=\theta _{20}=0 \end{aligned}$$

(45)

Finally, the nonlinear frequencies $\Omega _{j}$ $(j=1,2)$ can be expressed as

$$\begin{aligned} \Omega _{1}&=\omega _{1}-\frac{A^{2}\left( \left( \beta _{5}\omega _{2}^{2}\left( 2\omega _{1}^{2}+\omega _{2}^{2}\right) -\beta _{4}\left( 2\omega _{1}^{4}+4\omega _{2}^{2}\omega _{1}^{2}+3\omega _{2}^{4}\right) \right) \omega _{1}^{2}+3\beta _{3}\left( 2\omega _{1}^{4}+\omega _{2}^{4}\right) \right) }{8\left( 2\omega _{1}^{3}-\beta _{1}\omega _{1}\right) \left( \omega _{1}^{2}-\omega _{2}^{2}\right) {}^{2}} \end{aligned}$$

(46a)

$$\begin{aligned} \Omega _{2}&=\omega _{2}-\frac{A^{2}\left( \left( \beta _{5}\omega _{1}^{2}\left( \omega _{1}^{2}+2\omega _{2}^{2}\right) -\beta _{4}\left( 3\omega _{1}^{4}+4\omega _{2}^{2}\omega _{1}^{2}+2\omega _{2}^{4}\right) \right) \omega _{2}^{2}+3\beta _{3}\left( \omega _{1}^{4}+2\omega _{2}^{4}\right) \right) }{8\left( \omega _{1}^{2}-\omega _{2}^{2}\right) {}^{2}\left( 2\omega _{2}^{3}-\beta _{1}\omega _{2}\right) } \end{aligned}$$

(46b)

Both eigenvalues $\Omega _{1}$ and $\Omega _{2}$ exist to be relative to one single modeshape, and this was also observed by Majkut [72].

4.3 Forced vibration solution

To study the forced vibration response of the nanobeam, the equation of motion (28) is considered with both external harmonic forcing function and damping coefficient and its solution is sought using the MMS. For the primary resonance, i.e., ${\hat{\theta }}\approx \omega _{1}$, assume that the excitation frequency ${\hat{\theta }}$ and the system linear frequency $\omega _{l}$ are approximately the same. The following equation can be expressed as

$$\begin{aligned} {\hat{\theta }}=\omega _{l}+\varepsilon ^{2}\sigma \end{aligned}$$

(47)

where $\sigma$ represents the detuning parameter. An approximate solution is obtained for the ordinary differential equation (ODE) given by (29) using Eq. (31) to derive the $n^{th}$-order differential equations. The only difference with free vibration analysis is that the damping terms $\mu _{1}$ and $\mu _{2}$ and the dimensionless amplitude of the force $\bar{F}_{1}$ are scaled to the third order. Substituting (31) into (29) and gathering like powers of $\varepsilon$ yield the a system of three differential equations

$$\begin{aligned} \varepsilon ^{1}:\ \ \ D_{0}^{4}q_{0}+\beta _{1}D_{0}^{2}q_{0}+\beta _{2}q_{0}=&0 \end{aligned}$$

(48a)

$$\begin{aligned} \varepsilon ^{2}:\ \ \ D_{0}^{4}q_{1}+\beta _{1}D_{0}^{2}q_{1}+\beta _{2}q_{1}=&-4D_{1}D_{0}^{3}q_{0}-2\beta _{1}D_{0}D_{1}q_{0} \end{aligned}$$

(48b)

$$\begin{aligned} \varepsilon ^{3}:\ \ \ D_{0}^{4}q_{2}+\beta _{1}D_{0}^{2}q_{2}+\beta _{2}q_{2}=&-\left( 4D_{2}D_{0}^{3}+6D_{1}^{2}D_{0}^{2}\right) q_{0}-\beta _{1}\left( D_{1}^{2}+2D_{2}D_{0}\right) q_{0}\nonumber \\&-\beta _{4}q_{0}^{2}D_{0}^{2}q_{0}-4D_{1}D_{0}^{3}q_{1}-2\beta _{1}D_{1}D_{0}q_{1}-\beta _{3}q_{0}^{3}\nonumber \\&-\beta _{5}\left( D_{0}q_{0}\right) ^{2}\zeta _{0}-\mu _{1}D_{0}^{3}q_{0}-\mu _{2}D_{0}q_{0}\nonumber \\&+\frac{1}{2}\left( \mu _{3}+\mu _{4}{\hat{\omega }}^{2}\right) \bar{F}_{1}\left( \mathrm {e}^{i{\hat{\theta }}T_{0}}+\mathrm {e}^{-i{\hat{\theta }}T_{0}}\right) \end{aligned}$$

(48c)

Evidently, Eqs. (48a) and (48b) are, respectively, analogous to the case of free vibration equations (32a) and (32b) and hence have identical solutions. Substituting the solutions of equations (48a) and (48b) into the third-order equation (48c) results in the following secular terms:

$$\begin{aligned}&2i\omega _{1}\left( 2\omega _{1}^{2}-\beta _{1}\right) D_{2}A_{1}+i\omega _{1}\left( \mu _{1}\omega _{1}^{2}-\mu _{2}\right) A_{1}+3\left( \beta _{4}\omega _{1}^{2}-\beta _{3}-\frac{1}{3}\beta _{5}\omega _{1}^{2}\right) A_{1}^{2}\bar{A}_{1}\nonumber \\&\quad +2\left[ \beta _{4}\left( \omega _{1}^{2}+2\omega _{2}^{2}\right) -3\beta _{3}-\beta _{5}\omega _{2}^{2}\right] A_{1}A_{2}\bar{A}_{2}+\frac{1}{2}\left( \mu _{3}+\mu _{4}\omega _{1}^{2}\right) \bar{F}\mathrm {e}^{i\sigma T_{2}}=0 \end{aligned}$$

(49a)

$$\begin{aligned}&2i\omega _{2}\left( 2\omega _{2}^{2}-\beta _{1}\right) D_{2}A_{2}+i\omega _{2}\left( \mu _{1}\omega _{2}^{2}-\mu _{2}\right) A_{2}+3\left( \beta _{4}\omega _{2}^{2}-\beta _{3}-\frac{1}{3}\beta _{5}\omega _{2}^{2}\right) A_{2}^{2}\bar{A}_{2}\nonumber \\&\quad +2\left[ \beta _{4}\left( \omega _{2}^{2}+2\omega _{1}^{2}\right) -3\beta _{3}-\beta _{5}\omega _{1}^{2}\right] A_{1}\bar{A}_{1}A_{2}=0 \end{aligned}$$

(49b)

Using the expression of $A_{1}$ and $A_{2}$ provided by Eq. (38) and splitting into imaginary and real components yield a set of equations in which the unknowns are $a_{1}$ and $\theta _{1}$

$$\begin{aligned} \omega _{1}\left( 2\omega _{1}^{2}-\beta _{1}\right) \frac{da_{1}}{dT_{2}}=&-\frac{1}{2}\left( \mu _{3}+\mu _{4}\omega _{1}^{2}\right) \bar{F}\sin \left( -\theta _{1}+\sigma T_{2}\right) +\frac{1}{2}\omega _{1}a_{1}\left( \mu _{2}-\omega _{1}^{2}\mu _{1}\right) \end{aligned}$$

(50a)

$$\begin{aligned} \omega _{1}a_{1}\left( 2\omega _{1}^{2}-\beta _{1}\right) \frac{d\theta _{1}}{dT_{2}}=&-\frac{1}{2}\left( \mu _{3}+\mu _{4}\omega _{1}^{2}\right) \bar{F}\cos \left( -\theta _{1}+\sigma T_{2}\right) +\frac{3}{4}a_{1}\left( \frac{a_{1}^{2}}{2}+a_{2}^{2}\right) \beta _{3}\nonumber \\&-\frac{a_{1}}{2}\left( \frac{3}{4}a_{1}^{2}\omega _{1}^{2}+\frac{1}{2}a_{2}^{2}\omega _{1}^{2}+a_{2}^{2}\omega _{2}^{2}\right) \beta _{4}+\frac{a_{1}}{4}\left( \frac{1}{2}a_{1}^{2}\omega _{1}^{2}+a_{2}^{2}\omega _{2}^{2}\right) \beta _{5} \end{aligned}$$

(50b)

A similar system of differential equations can be obtained for $a_{2}$ and $\theta _{2}$ which can be written as

$$\begin{aligned} \left( 2\omega _{2}^{2}-\beta _{1}\right) \frac{da_{2}}{dT_{2}}=&\frac{1}{2}a_{2}\left( \mu _{2}-\omega _{2}^{2}\mu _{1}\right) \end{aligned}$$

(51a)

$$\begin{aligned} \omega _{2}a_{2}\left( 2\omega _{2}^{2}-\beta _{1}\right) \frac{d\theta _{2}}{dT_{2}}=&\frac{3}{4}a_{2}\left( \frac{a_{2}^{2}}{2}+a_{1}^{2}\right) \beta _{3}-\frac{a_{2}}{2}\left( \frac{3}{4}a_{2}^{2}\omega _{2}^{2}+\frac{1}{2}a_{1}^{2}\omega _{2}^{2}+a_{1}^{2}\omega _{1}^{2}\right) \beta _{4}\nonumber \\&+\frac{a_{2}}{4}\left( \frac{1}{2}a_{2}^{2}\omega _{2}^{2}+a_{1}^{2}\omega _{1}^{2}\right) \beta _{5} \end{aligned}$$

(51b)

Let

$$\begin{aligned} \gamma _{1}=\sigma T_{2}-\theta _{1} \end{aligned}$$

(52)

,

a steady-state condition is sought. Hence, the frequency response equations can be expressed by setting all derivative terms, in Eqs. (50a), (50b), (51a) and (51b), to zero. The resulting equations can be written as

$$\begin{aligned} 0=&-\frac{1}{2}\left( \mu _{3}+\mu _{4}\omega _{1}^{2}\right) \bar{F}_{1}\sin \left( \gamma _{1}\right) +\frac{1}{2}\omega _{1}a_{1}\left( \mu _{2}-\omega _{1}^{2}\mu _{1}\right) \end{aligned}$$

(53a)

$$\begin{aligned} 0=&-\frac{1}{2}\left( \mu _{3}+\mu _{4}\omega _{1}^{2}\right) \bar{F}_{1}\cos \left( \gamma _{1}\right) +\omega _{1}a_{1}\left( 2\omega _{1}^{2}-\beta _{1}\right) \sigma +\frac{3}{4}a_{1}\left( \frac{a_{1}^{2}}{2}+a_{2}^{2}\right) \beta _{3}\nonumber \\&-\frac{a_{1}}{2}\left( \frac{3}{4}a_{1}^{2}\omega _{1}^{2}+\frac{1}{2}a_{2}^{2}\omega _{1}^{2}+a_{2}^{2}\omega _{2}^{2}\right) \beta _{4}+\frac{a_{1}}{4}\left( \frac{1}{2}a_{1}^{2}\omega _{1}^{2}+a_{2}^{2}\omega _{2}^{2}\right) \beta _{5} \end{aligned}$$

(53b)

$$\begin{aligned} 0=&\frac{1}{2}a_{2}\left( \mu _{2}-\omega _{2}^{2}\mu _{1}\right) \end{aligned}$$

(53c)

$$\begin{aligned} 0=&\frac{3}{4}a_{2}\left( \frac{a_{2}^{2}}{2}+a_{1}^{2}\right) \beta _{3}-\frac{a_{2}}{2}\left( \frac{3}{4}a_{2}^{2}\omega _{2}^{2}+\frac{1}{2}a_{1}^{2}\omega _{2}^{2}+a_{1}^{2}\omega _{1}^{2}\right) \beta _{4}\nonumber \\&+\frac{a_{2}}{4}\left( \frac{1}{2}a_{2}^{2}\omega _{2}^{2}+a_{1}^{2}\omega _{1}^{2}\right) \beta _{5} \end{aligned}$$

(53d)

From Eq. (53c), it can be concluded that $a_{2}=0$. In light of this, Eqs. (53a) and (53b) can be further simplified

$$\begin{aligned} \frac{1}{2}\left( \mu _{3}+\mu _{4}\omega _{1}^{2}\right) \bar{F}_{1}\sin \left( \gamma _{1}\right) =&\frac{1}{2}\omega _{1}a_{1}\left( \mu _{2}-\omega _{1}^{2}\mu _{1}\right) \end{aligned}$$

(54a)

$$\begin{aligned} \frac{1}{2}\left( \mu _{3}+\mu _{4}\omega _{1}^{2}\right) \bar{F}_{1}\cos \left( \gamma _{1}\right) =&\omega _{1}a_{1}\left( 2\omega _{1}^{2}-\beta _{1}\right) \sigma +\frac{3}{8}a_{1}^{3}\beta _{3}-\frac{3}{8}a_{1}^{3}\omega _{1}^{2}\beta _{4}+\frac{1}{8}a_{1}^{3}\omega _{1}^{2}\beta _{5} \end{aligned}$$

(54b)

By taking the square and summation of Eqs. (54a) and (54b), the following frequency response equation is obtained:

$$\begin{aligned} \left( \frac{\bar{F}_{1}}{2}\left( \mu _{3}+\mu _{4}\omega _{1}^{2}\right) \right) ^{2}= & {} \left( \frac{1}{2}\omega _{1}a_{1}\left( \mu _{2}-\omega _{1}^{2}\mu _{1}\right) \right) ^{2}\nonumber \\&+\left( \omega _{1}a_{1}\left( 2\omega _{1}^{2}-\beta _{1}\right) \sigma +\frac{1}{8}a_{1}^{3}(3\beta _{3}-3\omega _{1}^{2}\beta _{4}+\omega _{1}^{2}\beta _{5})\right) ^{2} \end{aligned}$$

(55)

5 Numerical solution using DQM

The MMS solution was developed based on linear classical modeshapes defined in Table 1. To assess the accuracy of such assumption, a numerical differential quadrature method (DQM) solution proposed by Trabelssi et al. [44] based on the actual nonclassical modeshapes is employed. The DQM formulation is briefly reviewed in this section. The dynamic response of the nanobeam is governed by two nonlinear partial differential equations (PDEs) (27a) and (27b), each subjected to two boundary conditions. DQM is a high-order method which leverages all the mesh points in the system to interpolate and calculate the derivatives involved in the PDE system. DQM and its related methods have been used several times to analyze the nonlinear response of structures at the nanoscale [43, 44, 73,74,75,76]. Because of its efficiency, DQM was used to discretize the equation of motion in a weight optimization of axially functionally graded nonlinear microbeams [76]. Differential–integral quadrature method (DIQM), another variant of DQM, was exploited to investigate the buckling and post–buckling behaviors of nonlinear carbon nanotubes [75]. Lately, Trabelsi at al. developed a high-order finite element for a nanobeam using DQM matrices to study the dynamic response of a nonlinear nanobeam [45].

In this section, these PDEs are discretized using DQM based on the shifted Chebyshev–Gauss–Lobatto grid points [77]

$$\begin{aligned} \xi _{i}=\frac{1}{2}\left\{ 1-\cos \left( \pi \frac{i-1}{n_x-1}\right) \right\} ,\quad (i=1,\ldots ,n_x) \end{aligned}$$

(56)

where $n_x$ is the number of nodes. Let $Y_{1}$ and $Y_{2}$ be the nodal displacement vectors where the element of each vector is $[Y_{1}]_{i}={\hat{w}}_{i}(t)$ and $[Y_{2}]_{i}={\hat{\phi }}_{i}(t)$. The velocity and acceleration vectors are denoted ${\ddot{Y}}$ and ${\dot{Y}}$, respectively. The discretized equations of motion (27a) and (27b) is given by following system of ODEs:

$$\begin{aligned}&\left( M_{0}-{\hat{\mu }}_{0}M_{2}\right) .{\ddot{Y}}_{1}+{\hat{\mu }}_{f}\left( M_{0}-{\hat{\mu }}_{0}M_{2}\right) .{\dot{Y}}_{1}-\frac{1}{s^{2}}\left( M_{1}.Y_{2}+M_{2}.Y_{1}\right) \nonumber \\&\quad -\kappa \left( i{\mathcal {W}}(\xi ).\left( M_{1}.Y_{1}\right) {}^{2}\right) \left( M_{2}.Y_{1}-{\hat{\mu }}_{0}M_{4}.Y_{1}\right) \nonumber \\&\quad -{\hat{k}}_{s}\left( M_{2}.Y_{1}-{\hat{\mu }}_{0}M_{4}.Y_{1}\right) +{\hat{k}}_{L}\left( Y_{1}-{\hat{\mu }}_{0}M_{2}.Y_{1}\right) \nonumber \\&\quad +{\hat{k}}_{NL}\left( Y_{1}^{3}-3{\hat{\mu }}_{0}\left( 2Y_{1}\left( M_{1}.Y_{1}\right) {}^{2}+Y_{1}^{2}M_{2}.Y_{1}\right) \right) -\left( {\hat{F}}-{\hat{\mu }}_{0}{\hat{F}}''\right) \cos ({\hat{\theta }}{\hat{t}}) = 0 \end{aligned}$$

(57a)

$$\begin{aligned}&m\left( {\ddot{Y}}_{2}-{\hat{\mu }}_{0}M_{2}.{\ddot{Y}}_{2}\right) -M_{2}.Y_{2}+\frac{1}{s^{2}}(M_{1}.Y_{1}+Y_{2}) = 0 \end{aligned}$$

(57b)

where the $m^{th}$ DQM derivative matrices $M_{m}$ are given by [77]. Note that $M_{0}$ is the identity matrix. $i{\mathcal {W}}$ is a vector integral operator, and its expression can be given in [44]. Here, the matrix product of $M_{2}$ and Y is denoted $M_{2}.Y$ and the scalar product of two vectors is $i{\mathcal {W}}.Y$. $M_{2}M_{1}$ or $M_{1}^{2}$ is the Hadamard product. Only S-S and C-C boundary conditions are considered in this study. Their discretized forms are, respectively, given by

$$\begin{aligned} \left[ M_{0}.Y_{1}\right] _{k_{b}}= & {} 0\nonumber \\ \left[ \begin{array}{r} {\hat{\mu }}_{0}\left( {\ddot{Y}}_{1}+mM_{1}.{\ddot{Y}}_{2}+c{\dot{Y}}\right) +M_{1}.Y_{2}\\ -{\hat{\mu }}_{0}\left( \kappa iW(\xi ).\left( M_{1}.Y_{1}\right) {}^{2}M_{2}.Y_{1}-{\hat{k}}_{s}M_{2}.Y_{1}+Y_{1}{\hat{k}}_{L}+Y_{1}^{3}{\hat{k}}_{NL}-{\hat{F}}\cos ({\hat{\theta }}{\hat{t}})\right) \end{array}\right] _{k_{b}}= & {} 0\nonumber \\ \end{aligned}$$

(58)

$$\begin{aligned} -- & {} -\nonumber \\ \left[ M_{0}.Y_{1}\right] _{k_{b}}= & {} 0\nonumber \\ \left[ M_{0}.Y_{2}\right] _{k_{b}}= & {} 0\nonumber \\ \end{aligned}$$

(59)

where $[M_{1}]_{i,j}$ and $[Y_1]_{i}$ designate the (i, j) and (i)element of the matrix $M_{1}$ and $[Y_{1}]$, respectively. Here, $k_{b}$ is either 1 or $n_x$. Further details about the solution procedure can be found in [44].

6 Numerical results and discussion

6.1 Validation studies

The first validation study is performed to check the correctness of the nonlocal nonlinear frequency ratio, which is defined as follows:

$$\begin{aligned} \text {Nonlocal nonlinear frequency ratio} = \frac{\text {Nonlocal nonlinear natural frequency}}{\text {Classical nonlinear natural frequency}} \end{aligned}$$

(60)

For the S-S case, the present study results are given in Table 2 along with those reported in references [78] and [79] for different values of amplitude parameters A and gradation index n. The geometrical configuration of the beam such as length L, breadth b and height h is 10nm, 1nm and 1nm, respectively. The beam material properties used in this study are the same as those of [78]. This validation study does not consider the elastic foundation effects. The obtained results are in agreement with the published results as reported in Table 2.

Table 2 Comparison of the nonlocal nonlinear frequency ratio for the S-S case with those published by Refs. [78] and [79]; ($\mu _{0}=2$nm, ${{\hat{k}}}_{L}=0$, ${{\hat{k}}}_{NL}=0$, ${{\hat{k}}}_{s}=0$)

In the previous validation, it is assumed that the neutral axis and the geometrical axis coincide with each other. The second validation is performed to check the correctness of the linear frequency based on the above assumption. The natural frequency was estimated for various values of the ratio $E_U/E_L$ and for two values of the material gradation index $n=0$ and 4. The properties of the beam are $E_L=210$ GPa and $\rho = 7800 \text {kg}/\text {m}^3$ and are the same used by Eltaher et al. [55]. The beam length is $L = 100$nm, and the width and height of its cross section are chosen such that $b=0.1L$ and $h=0.01L$. The present study results are reported in Table 3 and found to be in good agreement as compared with those of reference [55].

The previous validations were conducted on EBT nanobeams with a length-to-thickness ratio equal to 10. The purpose of the third validation is to assess the accuracy of the nondimensional nonlinear nonlocal frequency for a deep S-S TBT nanobeam with a length-to-thickness ratio varying between 5 and 8. The results obtained using MMS are tabulated in Table 4 and are compared with those published by Refs. [44, 45] using DQM for different values of the inhomogeneity index n, the vibration amplitude A and the nonlocal parameter $\mu _0$. Excellent agreement is achieved between the obtained and published results.

Table 3 Comparison of the nondimensional linear natural frequency obtained for the simply supported beam with shifted neutral axis (NA) with results obtained by Eltaher et al. [55] for different elastic modulus ratios (${{\hat{\mu }}}_0=0$, $L/h=100$, $\rho _{U}/\rho _{L}=1$ and $\lambda = \sqrt{\frac{{{\hat{\omega }}}}{\tau }} L \root 4 \of {\frac{\rho _{L} A}{E_{L} I}}$)

Table 4 Comparison of the nondimensional nonlinear nonlocal frequency for a deep TBT nanobeam obtained using MMS with those published by Refs. [44, 45] using DQM for different values of the inhomogeneity index n; (${\hat{k}}_{s}=5$, ${\hat{k}}_{L}=50, {\hat{k}}_{NL}=50)$

6.2 Parametric study

6.2.1 Free vibration response

In this section, the effect of varying the aspect ratio L/h, material inhomogeneity n, nonlocal parameter ${{\hat{\mu }}}_0$, elastic modulus ratio $E_U/E_L$, amplitude A, surface elastic modulus ratio $E_U^s/E_L^s$ and elastic foundation stiffness coefficients ${\hat{k}}_L$, ${\hat{k}}_s$ and ${\hat{k}}_{NL}$ on the nonlinear frequency of the beam is studied in this section. The results are obtained for S-S and C-C boundary conditions using MMS and accounting for the physical neutral axis and using both MMS and DQM. The parametric study is conducted by considering the graded nanobeam with a beam length of 10 nm. Based on the power-law model given by (1), the bottom surface is enriched with aluminum material properties with an elastic modulus $E=70$ GPa, density $\rho = 2700$ kg/$\hbox {m}^3$ and surface elastic modulus $E_s$=5.1882 N/m. The modeshape functions used to obtain the results are provided in Table 1.

Figure 2a, b depicts the influence of varying the inhomogeneity index n from 1 to 100 and the amplitude A from 0 to 1 on the nonlocal nonlinear frequency versus the beam aspect ratio for the cases where the normalized nonlocal parameter ${\hat{\mu }}_0$ is equal to 0.04. The elastic modulus ratio $E_U/E_L$ was chosen to be 2 and 10 which correspond to the critical cases to investigate the influence of the aspect ratio of the beam on the nondimensional frequency. The upper and lower two plots correspond, respectively, to the S-S and C-C boundary conditions. A substantial variation of the nondimensional frequency in the low aspect ratio range can be observed especially below the value of 10 and regardless of the value of the ratio $E_U/E_L$. As expected, a large value of $E_U/E_L$ amplifies the effect of the inhomogeneity index n. Furthermore, it can be seen that the higher the aspect ratio, the lower the impact of the inhomogeneity index. Such observation is expected since low aspect ratio beams provide higher moment contribution for the unevenly distributed material. In addition, it can be noted that the higher the value of the amplitude, the higher the effect of the inhomogeneity. Moreover, the effect of the inhomogeneity index n seems to be strongly related to $E_U/E_L$ ratio and this is true for both S-S and C-C cases. Indeed, given the nature of the material distribution, it is expected that raising n does not always move the nonlinear frequency toward the same direction. This is clearly illustrated when observing the case of $E_U/E_L=2$ and $A=1$ where the frequency curves order does not follow their inhomogeneity index. Furthermore, when $E_U/E_L$ is raised to a value of 10, the curves presetting the same amplitude but different inhomogeneity index n are affected differently. This can probably be attributed to the fact that for each value of $E_U/E_L$, there is a different value of n that maximizes or minimizes the position of $h_0$ to yield a larger effect of $E_U/E_L$. In the linear case, where $A=0$, the frequency curves split at a value of 10. However, increasing the amplitude drives the splitting value further away. In general, the effect of the amplitude appears to be highly nonlinear.

Fig. 2

Nonlocal nonlinear frequency versus aspect ratio for different values of the inhomogeneity index and amplitude a ${{\hat{\mu }}}_0=0$ and b ${{\hat{\mu }}}_0=0.04$ for both S-S and C-C cases

It is also interesting to explore the influence of considering the physical neutral axis. For this study, the data used to generate Fig. 2a, b, are recreated without considering the physical neutral axis (i.e., the neutral axis is positioned in the center line of the beam). The resulting frequencies are presented in Table 5 as percentage of their corresponding frequencies had the physical neutral axis been adopted. Furthermore, the same data are regenerated while considering a high surface stress ratio. Given the results in Table 5, it can be observed that for a low value of $E_U/ E_L$, the effect of the position of the neutral axis is small. In fact, this variation reaches a maximum at 99.36% for the S-S and 97.39% for the C-C case for the lowest aspect ratio. However, when $E_U/ E_L$ ratio is high, the difference reaches 9% for the C-C case. Interestingly, it can be seen that raising the amplitude or lowering the aspect ratio of the beam widens the variation of the natural frequency which emphasizes the importance of considering the neutral axis especially for the nonlinear results. When exploring the data where the surface stress is accounted, up to a 12% deviation is recorded between frequencies computed with and without accounting for the physical neutral axis . This further highlights the importance of accounting for surface stress when calculating the position of the neutral axis.

Table 5 Effect of neglecting the physical neutral axis location on the natural frequencies

Figure 3a,b depicts the effect of varying the amplitude A from 0 to 1 and the nonlocal parameter ${{\hat{\mu }}}_0$ from 0 to 2 on the nonlocal nonlinear frequency versus the inhomogeneity index n for the cases where the elastic moduli ratio $E_U/E_L$ is equal to 2 and 10, respectively. The beam aspect ratio L/h was chosen to be 6 to represent a deep beam. The upper and lower two plots correspond, respectively, to the S-S and C-C boundary conditions. Unlike the amplitude A, ${{\hat{\mu }}}_0$ does not seem to alter significantly the shape of the frequency curves. It is also observed that the variation of the frequencies registers a minimum especially for high values of the amplitude A. A higher value of $E_U/E_L$ not only boosts the effect of the inhomogeneity index but also moves the position of the minimum. It can also be noted that raising the value of ${{\hat{\mu }}}_0$ not only results in a softening but also increases the effect of the amplitude A as the plot of the same line type is more spread for higher values of ${{\hat{\mu }}}_0$. The frequency curves of C-C case seem to be less affected by the variation of the inhomogeneity index. Here, the correlation between the effect of n and $E_U/E_L$ can clearly be seen when observing the location of the observed minima which is slightly affected by ${{\hat{\mu }}}_0$ and heavily affected by the elastic moduli ratio $E_U/E_L$. These results are in agreement with the observations presented earlier.

Fig. 3

Nonlocal nonlinear frequency versus inhomogeneity index for different values of the amplitude and nonlocal parameter a $E_{U}/E_{L}=2$ and b $E_{U}/E_{L}=10$ for both S-S and C-C cases

Figure 4a, b describes the effect of varying the inhomogeneity index n from 5 to 20 and the amplitude A from 0 to 1 on the nonlocal nonlinear frequency versus the elastic moduli ratio for the cases where the beam aspect ratio L/h is equal to 4 and 8, respectively. The nonlocal parameter ${{\hat{\mu }}}_0$ was chosen to be equal to 2. The upper and lower two plots correspond, respectively, to the S-S and C-C boundary conditions. An aspect ratio L/h ranging between 4 and 8 is chosen. This should lead to a more pronounced effect of $E_U/E_L$. The reduction of the value of L/h does not seem to affect the general evolution of the frequency plots. However, it does highlight that thicker beams are more sensitive to the variation of $E_U/E_L$, especially for the C-C cases. Both the ratio $E_U/E_L$ and the inhomogeneity index n seem to alter the values of the natural frequency in different ways resulting in the occurrence of minima in few curves. Raising the value of the amplitude A mainly exaggerates these effects. This is clearly illustrated in Fig. 5 which shows a rapid increase in the frequencies as A increases especially for the S-S case.

Fig. 4

Nonlocal nonlinear frequency versus elastic moduli ratio for different values of the inhomogeneity index, amplitude and aspect ratio a $L/h=4$ and b $L/h=8$ for both S-S and C-C cases

Fig. 5

Nonlocal nonlinear frequency versus amplitude for different values of the inhomogeneity index and aspect ratio for both S-S and C-C cases

Figure 6a, b represents the effect of varying the inhomogeneity index n from 5 to 20 and the beam aspect ratio L/h from 4 to 8 on the nonlocal nonlinear frequency versus the elastic surface moduli ratio $E_{U}^{s}/E_{L}^{s}$ for the cases where the amplitude A is equal to 0 and 1 and the elastic moduli ratio $E_{U}/E_{L}$ is equal to 2 and 10. Modifying the value of $E_{U}^{s}/E_{L}^{s}$ changes the stiffness distribution across the beam in a different way than $E_{U}/E_{L}$. As indicated in Appendix B, while modifying $E_{U}/E_{L}$ affects the shear stiffness ${\tilde{D}}$, modifying the surface stress ratio $E_{U}^{s}/E_{L}^{s}$ does not. On the other hand, it can be seen that the expression of $\kappa _{0}$ given by (17) indicates that the geometric nonlinearity is directly affected by the surface stress. Figure 6a,b shows significant variation in the frequency as the ratio $E_{U}^{s}/E_{L}^{s}$ increases. This effect tends to be more pronounced for low aspect ratio regardless of the boundary conditions. This effect is slightly influenced by the vibration amplitude especially for the S-S case.

In Fig. 7a,b, the natural frequencies for different surface stiffness ratios, amplitudes, inhomogeneity indices are plotted as a function of the aspect ratio. It can be observed that a low aspect ratio greatly enhances the effect of the surface stress ratio for both C-C and S-S cases. It is important to note that the surfaces stresses have higher lever arm to the neutral axis in deep beams, thereby a higher contribution to the moment. Furthermore, the expression of $h_0$ is dependent on the surface stresses values. These two facts may explain the importance of surface stress in deep beams. A crossing in the frequency is also observed as the aspect ratio is raised and its location seems to be affected by the vibration amplitude A. As stated earlier, this can be traced to the expression of $\kappa _{0}$. This study shows the importance of modeling surface stresses in an FGM beam using Timoshenko beam theory. In fact, since Timoshenko beam theory accounts for shear effects, it is now clearer that the effect of surface stress gradient and gradient elasticity is different than for the Euler–Bernoulli beam theory. This effect is more pronounced for deep beams which further highlights the importance of using Timoshenko beam theory.

Fig. 6

Nonlocal nonlinear frequency versus surface elastic moduli ratio for different values of the aspect ratio, inhomogeneity index, amplitude and elastic moduli ratio a $E_{U}/E_{L}=2$ and b $E_{U}/E_{L}=10$ for both S-S and C-C cases

Fig. 7

Nonlocal nonlinear frequency versus aspect ratio for different values of the surface elastic moduli ratio, amplitude, elastic moduli ratio and inhomogeneity index a $n=5$ and b $n=20$ for both S-S and C-C cases

The effect of the elastic foundation under different boundary conditions on the nonlinear frequency is illustrated in Fig. 8a, b with and without the nonlinear stiffness coefficient ${\hat{k}}_{NL}$, respectively. The plotted results are based on the current MMS formulation in addition to the DQM formulation proposed by Trablelssi et al. [44]. It can be observed that there is a slight increase in the frequency with the increase in amplitude. The net effect of the shear stiffness coefficients dominates the nonlinear frequency. The set of values chosen for ${\hat{k}}_{L}$ and ${\hat{k}}_{S}$ in Fig. 8 is chosen based on the expression of $\beta _2$ and $\beta _3$ in Appendix D. ${\hat{k}}_{L}$ and ${\hat{k}}_{S}$ only appear in the expression of $\beta _2$ and $\beta _3$. It can be seen that the effects of ${\hat{k}}_{L}$ and ${\hat{k}}_{S}$ are comparable except that ${\hat{k}}_{S}$ is multiplied by the second space derivative of the weighted sum of the shape function and few of its space derivative. A rough calculation using the linear modeshapes for both S-S and C-C case shows that the effect of ${\hat{k}}_{S}$ should be about 10 times the effect of ${\hat{k}}_{L}$ for S-S case and around 20 times for the C-C case. This observation can be easily detected in the MMS results since linear modeshape are used for the evaluation of the results. However, while the DQM and MMS produce comparable results for the S-S case, the results for the C-C case are vastly different for both methods. This is most likely due to the fact that for the C-C case the modeshape can no longer be approximated with a linear modeshape. A comparable observation was made by Trabelssi et al. [43] on a similar problem. It can be concluded that these errors occur mainly because MMS assumes the first modeshape function for both S-S and C-C cases which are classical modeshape functions as given in Table 1, but DQM employs a nonclassical modeshape function.

The data presented in Fig. 8 can be used to examine the effect of the nonlinearities on the beam response which is either caused by the van Karman strain nonlinearity or the nonlinear stiffness coefficient ${\hat{k}}_{NL}$ or a combination of both. As stated earlier, this can be achieved by comparing the frequencies obtained for an amplitude equal to and different from zero corresponding to the linear and nonlinear behavior, respectively. When ${\hat{k}}_{NL}$ is set to zero, only the geometric nonlinearity is responsible for the dependence of the frequency on the amplitude. Compared to the linear case, the geometric nonlinearity results in a slight increase in the natural frequency when the vibration amplitude is raised. However, when ${\hat{k}}_{NL}$ is set to 100, the effect of the nonlinear foundation increases the dependence of the natural frequencies on the amplitude making it further depart from the linear case.

Fig. 8

Nonlocal nonlinear frequency versus amplitude for different linear stiffness, shear and nonlinear stiffness coefficients a ${\hat{k}}_{NL}=0$, b ${\hat{k}}_{NL}=100$ for both S-S and C-C cases

Fig. 9

Effect of the aspect ratios at elastic moduli ratio $E_{U}/E_{L}=1$ on the frequency response of FG beam without and with surface effects ($\rho _{U}/\rho _{L}=1$, n= 20, ${\hat{\mu }}_{0}$= 0.02, ${\hat{k}}_{L}$= 10, ${\hat{k}}_{S}$= 5, ${\hat{k}}_{NL}$= 50)

Fig. 10

Effect of the inner material properties on the frequency response of FG beam with surface effects ($\rho _{U}/\rho _{L}=1$,$E_{U}/E_{L}=10$, $E_{U}^{s}/E_{L}^{s}=10$ ,$\frac{L}{h}=6$, ${\hat{k}}_{L}$=10, ${\hat{k}}_{NL}$= 50, ${\hat{k}}_{s}$= 5)

6.2.2 Forced vibration response

The proposed forced vibration study investigates the effects of the aspect ratio, the material inhomogeneity, the nonlocal parameter, the foundation coefficients while considering the effect of surface elasticity on the frequency response curve (FRC) of the nanobeam. The damping coefficient is taken as ${{\hat{c}}}=0.1$, and the force amplitude is selected as ${\bar{F}}_{1}=1$ for the S-S case.

Fig. 11

Effect of the elastic foundation properties on the frequency response of FG beam S-S nanobeam ($L/h=6$,$\rho _{U}/\rho _{L}=1$, n= 20, ${\hat{\mu }}_{0}$= 0.02,$E_{U}/E_{L}=10$, $E_{U}^{s}/E_{L}^{s}=10$ , ${\hat{k}}_{NL}$= 50, ${\hat{k}}_{s}$= 5,${\hat{k}}_{L}$= 10)

The effect of the aspect ratio L/h on the frequency response of the nanobeam under different elastic modulus ratios without and with surface elasticity effects is shown in Fig. 9. It is observed that the effect of surface stress, though small, is noticeable on the FRCs. It is noted that setting $E^S_U/E^S_L=10$ enhances the effect of the aspect ratio. These observations agree with the free vibration results shown in Fig. 2 where low aspect ratio amplifies the surface stress contribution due to higher moment contribution for the unevenly distributed material.

The influence of the inhomogeneity index n and the nonlocal parameter of the beam on the frequency response of the beam is explored in Fig. 10. Different elastic modulus ratios are considered, with or without surface elasticity effects. A relatively low aspect ratio of $L/h=6$ is selected, while elasticity ratio is set to $E_U/E_L=10$. As established in the free vibration response, such a choice should help highlight the effect of the inhomogeneity of the beam material. It can be seen from Fig. 10a that raising the inhomogeneity index n does not always produce the same effect. This is expected since raising n does not always make the beam less homogeneous. Looking back at Figs. 2 and 3 in the free vibration study, a similar behavior was observed where raising the value does not produce a monotonous effect. The effect of the nonlocal parameter on the frequency response under different elastic modulus ratios is depicted in Fig. 10b. As expected, regardless of surface elasticity, raising the nonlocal parameter induces a hardening of the FRC. A similar observation was made by Trabelssi et al. [44].

The effect of the nonlinear foundation is considered in Fig. 11. It can be seen that increasing either the linear stiffness or the shear coefficient softens the FRCs. However, as discussed in the free vibration section, given the expression of $\beta _{2}$ and $\beta _{3}$, the effect of the shear coefficient is more pronounced than the linear stiffness coefficient and is shape function dependent.

The nonlinear stiffness coefficient appears to be the major contributor to the nonlinear response of the FRCs of the nanobeam, as shown in Fig. 11. In fact, for low values of ${\hat{k}}_{NL}$, the FRCs show a very limited hardening. This hardening can be rapidly increased by raising the value ${\hat{k}}_{NL}$.

7 Conclusions

This paper investigates the effects of combining surface elasticity, nonlocality and physical neutral axis location on the dynamic performance of a graded nonlinear Timoshenko deep beam. The principle of virtual displacements was utilized to obtain the equations of motion by considering the surface effects. By employing the method of multiple scales (MMS), a fourth-order nonlinear ordinary differential equation was obtained to yield the nondimensional nonlinear frequencies and the frequency response curves of the beam. Since MMS was derived using linear classical modeshapes, a DQM numerical solution which uses the nonclassical modeshapes was employed to assess the accuracy of the MMS solution. The present study results were validated based on published results. A parametric study was performed to examine the effects of the aspect ratio, surface modulus ratio, the elastic modulus ratio, the nonlocal parameter, the inhomogeneity index, the elastic foundation coefficients on the dynamic behavior of the graded nanobeam. The major findings in this work are outlined as given below

• The nonlinear natural frequency reduces rapidly for low aspect ratios for both S-S and C-C cases.

• The nonlocal parameter reduces the natural frequency, while the amplitude is dependent on n and the ratio $E_U/E_L$.

• For both C-C and S-S cases, the inhomogeneity index slightly decreases and then increases the natural frequency for low values of $E_U/E_L$ and remains insensitive otherwise. The inhomogeneity index effect is also slightly sensitive to the amplitude and $\mu _0$.

• Deeper beams are found to be more sensitive to the variation of $E_U/E_L$ especially for the C-C cases. A low aspect ratio also enhances the effect of the surface stiffness ratio $E_U^s /E_L^s$.

• Unlike the S-S case, a study, based on the expressions of $\beta _2$ and $\beta _3$, revealed that for low aspect ratio the C-C nanobeam modeshape deviates from the classical one.

• A significant variation in the natural frequency is observed as the ratio $E_U^s /E_L^s$ increases especially for low aspect ratio.

• The forced vibration study showed that raising to $E_U^s /E_L^s= 10$ boosts the effect of the aspect ratio.

• The forced vibration study showed that raising the inhomogeneity index n does not always produce the same effect on FRC. This behavior was also observed in the free vibration study.

• As expected, in the forced vibration study, raising the nonlocal parameter results in a hardening of the FRC.

• Given the expression of $\beta _2$ and $\beta _3$, the effect of the shear coefficient on the FRCs is more pronounced than the linear stiffness coefficient and is shape function dependent

• In the forced vibration study, it was observed that nonlinear stiffness coefficient is responsible for most of the nonlinear response of the FRCs of the nanobeam.

• For the Timoshenko beam, the ratio $E_{U}^{s}/E_{L}^{s}$ affects its bending stiffness and does not contribute to its shear stiffness, while the ratio $E_{U}/E_{L}$ alters both the bending and shear stiffness. For the Euler–Bernoulli beam, there are no shear effects accounted in the model.

• Surface stress gradient affects the position of the beam neutral axis and possesses a higher lever arm resulting in a larger moment contribution especially in deep beams.

• The expressions of the nonlinear frequencies $\Omega _{j}$ $(j=1,2)$ given by Eqs. (46a) and (46b) and that of the frequency response curve given by Eq. (55) are validated using the differential quadrature method and can be potentially employed in a design problem of a nanobeam.

Appendices

Expression of the position of the neutral axis appearing in (12):

To determine the neutral axis location, the axial displacement is ignored and higher-order terms are neglected. Thus, Eq. (11) reduces to

$$\begin{aligned} {\tilde{B}}\left( \frac{\partial \phi }{\partial x}\right) =0 \Leftrightarrow {\tilde{B}}=0 \end{aligned}$$

(A.1)

In what follows, ${\tilde{B}}$ is equated to zero. Simplifying (A.1) results in the following expression:

$$\begin{aligned} b\int _{\frac{-h}{2}-h_{0}}^{\frac{h}{2}-h_{0}}E(z)z\,dz+b\left[ E_{U}^{s}\left( \frac{h}{2}-h_{0}\right) +E_{L}^{s}\left( -\frac{h}{2}-h_{0}\right) \right] +2\int _{\frac{-h}{2}-h_{0}}^{\frac{h}{2}-h_{0}}E^{s}(z)z\,dz=0 \end{aligned}$$

(A.2)

Making the following change of variables $z=z_{m}-h_{0}$, Eq. (A.2) can be written as follows:

$$\begin{aligned}&b\int _{\frac{-h}{2}}^{\frac{h}{2}}E(z_{m})(z_{m}-h_{0})\,dz_{m}+b\left[ E_{U}^{s}\left( \frac{h}{2}-h_{0}\right) +E_{L}^{s}\left( -\frac{h}{2}-h_{0}\right) \right] \nonumber \\&\quad +2\int _{\frac{-h}{2}}^{\frac{h}{2}}E^{s}(z_{m})(z_{m}-h_{0})\,dz_{m} = 0 \end{aligned}$$

(A.3)

From Eq. (A.3), the position of the neutral axis can be determined

$$\begin{aligned} h_{0}= & {} \frac{b\int _{\frac{-h}{2}}^{\frac{h}{2}}E(z_{m})z_{m}\,dz_{m}+\frac{h}{2}b\left[ E_{U}^{s}-E_{L}^{s}\right] +2\int _{\frac{-h}{2}}^{\frac{h}{2}}E^{s}(z_{m})z_{m\,}dz_{m}}{b\int _{\frac{-h}{2}}^{\frac{h}{2}}E(z_{m})\,dz_{m}+b\left[ E_{U}^{s}+E_{L}^{s}\right] +2\int _{\frac{-h}{2}}^{\frac{h}{2}}E^{s}(z_{m})\,dz_{m}} \nonumber \\= & {} -\frac{h \left[ \left( b \left( n^2+3 n+2\right) +2 h n\right) \left( E^s_L-E^s_U\right) +b h n (E_L-E_U)\right] }{2 (n+2) \left( b n E^s_L+b E^s_L+b n E^s_U+b E^s_U+2 h n E^s_L+2 h E^s_U+b h n E_L+b h E_U\right) } \end{aligned}$$

(A.4)

Simplified expressions of ${\tilde{A}}$, ${\tilde{D}}$ and ${\tilde{G}}$ appearing in (13):

$$\begin{aligned} {\tilde{A}}= & {} b\int _{-\frac{h}{2}}^{\frac{h}{2}}E(z_{m})\,dz_{m}+2\int _{-\frac{h}{2}}^{\frac{h}{2}}E^{s}(z_{m})dz_{m}+b\left[ E_{U}^{s}+E_{L}^{s}\right] \nonumber \\= & {} \frac{bh\left( nE_{L}+E_{U}\right) }{n+1}+b\left( E_{L}^{s}+E_{U}^{s}\right) +\frac{2h\left( nE_{L}^{s}+E_{L}^{s}\right) }{n+1},\nonumber \\ {\tilde{D}}= & {} b\int _{-\frac{h}{2}}^{\frac{h}{2}}E(z_{m})\left( z_{m}-h_{0}\right) ^{2}\,dz_{m}+2\int _{-\frac{h}{2}}^{\frac{h}{2}}E^{s}(z_{m})\left( z_{m}-h_{0}\right) ^{2}\,dz_{m}\nonumber \\&+b\left[ \left( \frac{h}{2}-h_{0}\right) ^{2}E_{U}^{s}+\left( -\frac{h}{2}-h_{0}\right) ^{2}E_{L}^{s}\right] \nonumber \\= & {} \frac{1}{12}h\left( h^{2}+12h_{0}^{2}\right) \left( bE_{L}+2E_{L}^{s}\right) +\left( -\frac{h^{3}}{n+3}+\frac{\left( h+2h_{0}\right) h^{2}}{n+2}-\frac{\left( h+2h_{0}\right) {}^{2}h}{4(n+1)}\right) \nonumber \\&\left( b(E_{L}-E_{U})+2(E_{L}^{s}-E_{U}^{s})\right) +\frac{1}{4}b\left( \left( h+2h_{0}\right) {}^{2}E_{L}^{s}+\left( h-2h_{0}\right) {}^{2}E_{U}^{s}\right) \nonumber \\ {\tilde{G}}= & {} \frac{K_{s}}{2(1+\nu )}\frac{bh(nE_{L}+E_{u})}{n+1} \end{aligned}$$

(B.1)

Eliminating the axial displacement appearing in (13):

The first assumption along with (8a) results in $M_{xx}^{(0)}$ being a constant. Hence, the following expression is obtained:

$$\begin{aligned} \frac{\partial u}{\partial x}+\frac{1}{2}\left( \frac{\partial w}{\partial x}\right) ^{2}=c_{1}(t) \end{aligned}$$

(C.1)

Integrating the above equation yields the expression of the axial displacement

$$\begin{aligned} u(x,t)=-\int _{0}^{x}\left[ \frac{1}{2}\left( \frac{\partial w(s,t)}{\partial s}\right) ^{2}\right] ds+c_{1}(t)x+c_{2}(t) \end{aligned}$$

(C.2)

where $c_{1}$ and $c_{2}$ are obtained from the second assumption as follows:

$$\begin{aligned} c_{1}(t)=\frac{1}{L}\int _{0}^{L}\left[ \frac{1}{2}\left( \frac{\partial w}{\partial x}\right) ^{2}\right] dx\quad \text{ and }\quad c_{2}(t)=0 \end{aligned}$$

(C.3)

As a result:

$$\begin{aligned} M_{xx}^{(0)}= & {} {\tilde{A}}c_{1}(t) \end{aligned}$$

(C.4a)

$$\begin{aligned} M_{xx}^{(1)}= & {} {\tilde{D}}\frac{\partial \phi }{\partial x} \end{aligned}$$

(C.4b)

where $c_{1}$ is provided by (C.3).

Expressions of $\beta _{i} (i=1,\ldots ,5)$ and $\mu _{i} (i=1,\ldots ,4)$ appearing in (29):

$$\begin{aligned} \beta _{1}&=\frac{1}{\Delta }\int _{0}^{1}\Biggl \{\left[ 1-{\hat{\mu }}_{0}\frac{d^{2}}{d\xi ^{2}}\right] \left( \psi -\left( m+s^{2}\right) \psi ''\right) \nonumber \\&\quad +ms^{2}\left[ {\hat{k}}_{L}-{\hat{k}}_{S}\frac{d^{2}}{d\xi ^{2}}\right] \left( \psi -2{\hat{\mu }}_{0}\psi ''+{\hat{\mu }}_{0}^{2}\psi ^{(4)}\right) \Biggr \}\psi \ d\xi \end{aligned}$$

(D.1a)

$$\begin{aligned} \beta _{2}&=\frac{1}{\Delta }\int _{0}^{1}\Biggl \{\psi ^{(4)}+\left[ {\hat{k}}_{L}-{\hat{k}}_{S}\frac{d^{2}}{d\xi ^{2}}\right] \left( \psi -s^{2}\psi ''-{\hat{\mu }}_{0}\left( \psi ''-s^{2}\psi ^{(4)}\right) \right) \Biggr \}\psi \ d\xi \end{aligned}$$

(D.1b)

$$\begin{aligned} \beta _{3}&=\frac{1}{\Delta }\int _{0}^{1}\Biggl \{-I_{\kappa }\left[ 1-{\hat{\mu }}_{0}\frac{d^{2}}{d\xi ^{2}}\right] \left( \psi ''-s^{2}\psi ^{(4)}\right) +{\hat{k}}_{\text {NL}}\left( \psi {}^{3}-3s^{2}\left( \psi {}^{2}\psi ''+2\psi \psi '{}^{2}\right) \right) \nonumber \\&\quad -3{\hat{\mu }}_{0}{\hat{k}}_{\text {NL}}\left( \psi {}^{2}\left( \psi ''-s^{2}\psi ^{(4)}\right) -12s^{2}\psi '{}^{2}\psi ''+2\psi \left( \psi '{}^{2}-s^{2}\left( 3\psi ''{}^{2}+4\psi ^{(3)}\psi '\right) \right) \right) \Biggr \}\psi \ d\xi \end{aligned}$$

(D.1c)

$$\begin{aligned} \beta _{4}&=\frac{ms^{2}}{\Delta }\int _{0}^{1}\Biggl \{3I_{\kappa }\left( -\psi ''+2{\hat{\mu }}_{0}\psi ^{(4)}-{\hat{\mu }}_{0}^{2}\psi ^{(6)}\right) \nonumber \\&\quad +3{\hat{k}}_{\text {NL}}\left( \psi {}^{3}-6{\hat{\mu }}_{0}\left( \psi {}^{2}\psi ''+2\psi \psi '{}^{2}\right) \right) \nonumber \\&\quad +9{\hat{k}}_{\text {NL}}{\hat{\mu }}_{0}^{2}\left( \psi ^{(4)}\psi {}^{2}+12\psi '{}^{2}\psi ''+2\psi \left( 3\psi ''{}^{2}+4\psi ^{(3)}\psi '\right) \right) \Biggr \}\psi \ d\xi \end{aligned}$$

(D.1d)

$$\begin{aligned} \beta _{5}&=2\beta _{4} \end{aligned}$$

(D.1e)

in which $\Delta =ms^{2}\int _{0}^{1}\Biggl \{\psi -2{\hat{\mu }}_{0}\psi ''+{\hat{\mu }}_{0}^{2}\psi ''''\Biggr \}\psi \ d\xi$ and $I_{\kappa }=\kappa \int _{0}^{1}\left( \frac{d\psi }{d\xi }\right) ^{2}d\xi$.

$$\begin{aligned} \mu _{1}&=ms^{2}\frac{{\hat{c}}}{\Delta }\int _{0}^{1}\Biggl \{\psi -2{\hat{\mu }}_{0}\psi ''+{\hat{\mu }}_{0}^{2}\psi ^{(4)}\Biggr \}\psi d\xi \end{aligned}$$

(D.2a)

$$\begin{aligned} \mu _{2}&=\frac{{\hat{c}}}{\Delta }\int _{0}^{1}\Biggl \{\psi -{\hat{\mu }}_{0}\psi ''-\left( \psi ''-{\hat{\mu }}_{0}\psi ^{(4)}\right) s^{2}\Biggr \}\psi d\xi \end{aligned}$$

(D.2b)

$$\begin{aligned} \mu _{3}&=\frac{1}{\Delta }\int _{0}^{1}\Biggl \{\psi _F-\left( {\hat{\mu }}_{0}+s^{2}\right) \psi _F''+s^{2}{\hat{\mu }}_{0}\psi _F^{(4)}\Biggr \}\psi d\xi \end{aligned}$$

(D.2c)

$$\begin{aligned} \mu _{4}&=-\frac{ms^{2}}{\Delta }\int _{0}^{1}\Biggl \{\psi _F-2{\hat{\mu }}_{0}\psi _F''+{\hat{\mu }}_{0}^{2}\psi _F^{(4)}\Biggr \}\psi d\xi \end{aligned}$$

(D.2d)