1 Introduction

Friction dampers are devices that use dry friction to dissipate energy of a system in order to limit its vibratory response. They work by keeping in contact two surfaces that move relative to each other in order to generate friction. That basic concept has been around for a very long time. An example is the use of leaf springs in horse-drawn carriages in the eighteenth century [10]. Contemporary research dating back to 1930 proposes a mathematical formulation for such a damper [24].

When compared to other means to attenuate vibration, friction dampers stand out by their noteworthy advantages. To name a few, they work in harsh environments and in the absence of electric or hydraulic power; they adapt to a wide excitation bandwidth without tuning; and they can act simultaneously along multiple directions. Consequently, they are used in a variety of applications. Their most common use is in buildings, as a means to prevent damage caused by earthquakes. Considerable research also focuses on vibration isolation of trussed or otherwise bolted structures using solely the induced damping from the joints [53]. Their use is also common in the transportation sector, such as for truck and train damping of road-induced vibrations. Friction damping is also extensively used in turbomachinery, especially on turbine blades and bladed disks [12, 21].

Friction damping can be referred to as frictional damping or Coulomb damping. When the damping comes from the material itself or from a system about which no clear information of the inner dynamics is known, the terms hysteretic damping, complex stiffness, and structural damping may refer to the same phenomenon of dissipation by friction [45].

The relative motion at the point of contact of a friction damper can be linear or rotative, and the contacting surfaces can have curved or planar topologies. Combination with other damping technologies such as eddy currents, viscous dampers, and tuned mass dampers is also common. In such cases, the damper is often said to be semi-active. In other cases, the term semi-active can imply that the clamping force or another geometric parameter is actively controlled. Semi-active dampers are also known as variable or controllable dampers. Macroslip dampers dissipate energy only by Coulomb friction. They thus exhibit a fully sliding displacement between two surfaces. In contrast, microslip dampers dissipate energy by the sole presliding displacement of the contacting surfaces. Consequently, they display no perceivable motion.

This survey concentrates on passive devices which can be installed on a given system; have a low weight; use minimal space; and are efficient at damping frequencies ranging from 10 Hz to 1 kHz. Most attention is given to uniaxial dampers undergoing continuous linear relative movement along planar surfaces. The magnitudes of the motion can go from micro- to macroslip ranges. The aim is to provide a more recent review on friction damping with respect to the currently available one of [21]. Consequently, coverage of friction models is concentrated to those which present compatible characteristics.

First, a short introduction to the challenges linked to the design, modeling, and testing of friction dampers is given in Sect. 2. Section 3 presents the analytical and numerical methods used by various authors. Then, a selection of configurations and parameter identification methods are reported in Sect. 4. Dry friction is given considerable attention, because it is the most important underlying mechanism of friction dampers. Finally, Sect. 5 provides suggestions for modeling and experimental studies of uniaxial planar friction dampers acting on continuously vibrating systems.

2 Considerations for modeling and testing

A few aspects of friction dampers and dry friction are introduced here before presenting the bulk literature. First, the influence of the friction damper on the resonance frequency of an experimental beam setup with the damper at the tip can be considerable [21]. Also, the relation between dissipated energy and displacement magnitude is known to differ between micro- and macroslips regimes. Another difficulty in using the friction dampers is said to come from the inverse dependence of the equivalent viscous damping constant on the amplitude and velocity of the slip displacement [21].

The clamping force and the displacement amplitude have a crucial influence on the resulting damping. For example, if the force is too small, the damping device will absorb insufficient energy. On the contrary, if it is too large, relative movement between the concerned parts vanishes and so does the damping effect.

To ease the comprehension of this review, a set of terms specific to dynamic friction is introduced:

  • Black-box models Empirical models which do not attempt to simulate the inner workings of the friction phenomena;

  • Physics-based models, gray-box models Models based on a logical interpretation of the phenomena;

  • Static models, state-independent models Friction models which have no internal state and where the force opposing motion is usually based on the normal load and/or the contact velocity;

  • Dynamic models, state-dependent models Models that have an internal state variable that usually serves to represent the friction behavior prior to slipping;

  • Coulomb friction Force proportional to the normal contact force and opposite to velocity;

  • Stiction force, break-loose force, slippage load The maximum value of the static friction force that prevents contacting bodies from sliding;

  • Stribeck effect The dependence of the friction force on relative contact velocity; its function is often represented by \(f _ { \mathrm {ss}}(v), g(v)\), or s(v);

  • Viscous friction Friction force calculated as the multiplication of a coefficient by the relative velocity of the contacting surfaces and which is sometimes included in the Stribeck effect; in the LuGre model, its elastoplastic extension is represented by the \(\sigma _2\) coefficient;

  • Bristle deflection Microscopic deformation of a surface while it follows the relative displacement of an adjacent contacting surface usually cannot be measured; in the LuGre model, its elastoplastic extension is represented by the z state variable;

  • Micromotion, presliding, zero-slip behavior, partial sliding, mezzo-sliding State of the contact point when the force between the two bodies is not enough to cause full slipping at the interface and where the contact patch deformation can be elastic and/or plastic; this is also the state where, for the bristle deflection analogy, the bristles are not yet fully deformed;

  • Hysteresis In the case of friction, hysteresis is a form of energy dissipation and is visible by the change in the force–position and force–velocity curves when reversing the movement or velocity; it occurs in both the presliding and fully developed states of the system;

  • Frictional lag Delay that the friction force experiences with respect to velocity; visible as hysteresis in the friction force against velocity curve;

  • Zero-slip displacement, drift, plastic sliding Analytical or numerical effect that causes contacting bodies where friction is measured by a state-dependent model to incur displacement even when the applied force cycle does not exceed the stiction force;

  • Reversal point memory Property of a friction model to reproduce the same force–position trajectory regardless of the number of completed friction cycles;

  • Rate dependence Property of a friction model to show dependence on velocity for the force–position curves; these models thus usually do not show reversal point memory;

  • Dwell time Time during which contacting surfaces remain at a null relative velocity.

Finally, a friction damper designed with adequate contact patch clearance along a plane should be able to damp motion in all directions. This approach is sometimes used for shrouded turbine blade or railway boogie damping. It may be tempting to rely on bidimensional friction models for such cases. However, the accuracy of the latter is dubious and a more in depth discussion on the matter is provided at the end of Sect. 3.2. Nevertheless, modeling relative damper motion along a line can allow to study the response along different directions.

3 Modeling approaches

A proper friction model is necessary in order to properly model friction dampers, as seen by the majority of authors who model such dampers. A non-negligible number of authors rely on Coulomb-type friction models. However, quite often the modeling is concerned with seismic devices which are excited for short time spans. Dynamic models become more important when studying friction dampers acting on continuously vibrating structures. Effectively, their contact patches undergo velocity and direction changes at high frequency and no significant changes in normal forces. From these premises, this article covers more thoroughly dynamic types of friction models.

3.1 Analytical methods

Modeling of the force exchange between two contacting bodies is the basis to evaluating the behavior of friction dampers. Friction is an integral part of life and has been used and studied since ancient civilization. The first documented scientific characterization of the friction forces comes from Leonardo da Vinci [48]. He modeled friction force \(F_\mathrm{f}\) in the direction opposite to motion according to the following equation,

$$\begin{aligned} F_\mathrm{f} = 0.25 F_\mathrm{n} \end{aligned}$$
(1)

where \(F_\mathrm{n}\) is the normal contact force between the materials. It was later discovered that friction force was not always the ratio of normal force. The model thus evolved into the Coulomb version as,

$$\begin{aligned} F_\mathrm{f} = \mu F_\mathrm{n} \end{aligned}$$
(2)

where \(\mu \) is the friction coefficient and depends on the pair of contacting materials. It was then discovered that the friction force resisting motion was greater when the contacting surfaces have no relative movement than when in motion. A binary value was thus proposed for the friction coefficient. Later, it was also discovered that friction forces are velocity dependent, exhibit lag, and have elasticity even when the contacting surfaces are apparently at rest. For example, Dupont et al. [17] report that what was traditionally called static friction is now known as the presliding regime. For metal contacts, this regime extends over several microns of displacement. These are some of the diverse phenomena that can be attributed to friction and of which Table 1 gives a short overview. Consequently, a plethora of different modeling approaches which present themselves to either analytical or numerical analyses was developed. Most approaches that consider dynamic friction behavior, and especially non-harmonic ones, must be solved numerically. A few words are nonetheless first given concerning analytical methods. The most common analytical methods used to solve systems with friction damper are the exact solution and the harmonic balance. However, the harmonic balance can sometimes only lead to the constraint equations for a numerical problem [36].

The exact solution can usually be obtained for steady-state systems. In cases where the system is harmonically excited and the response is antiperiodic, thus periodically oscillating between positive and negative identical cycles, exact solutions can also be obtained. In other cases, solutions were also obtained by piecing together different analytical solutions applied to different time ranges. The exact solution method can be combined with a bifurcation analysis to study the influence of the system parameters on the type of expected response. Sometimes, the generated differential equations are solved by representing them as Fourier series.

The harmonic balance method is used for cases with steady excitation by a single harmonic forcing function. Such is often the case for rotating systems. The method allows obtaining the stiffness and viscous damping coefficients necessary to build an equivalent spring–mass–damper system. It is limited to estimating the steady-state response to sustained harmonic excitation. An example of the harmonic balance method applied to turbomachinery is the work of Charleux et al. [12]. They report that the harmonic balance method is the most used analysis method for steady-state rotating cases. In their work, the friction damping of blade attachments on a rotating disk is analyzed. They also mention that a major challenge comes from the varying pressure on the blade which causes the friction contact force, and pressure, at the root of the blade to vary in time and display non-uniformity. In general, however, difficulties arise from the highly nonlinear behavior, present also in vicinity of equilibrium, as mentioned by Ferri [21] in his review on friction damping.

Finally, an alternative to the harmonic balance is to use multi-harmonic methods with contributions from the stick–slip phenomena. This can also help identify a new resonance frequency. The alternating frequency–time (AFT) method proposed and described by Cameron and Griffin [9] for a friction damper is an example of a multi-harmonic solution. That method allows to quickly obtain a solution to a nonlinear system excited by multiple harmonics by iteratively switching between the time and frequency domains.

3.2 Numerical methods

When an iteration over time is necessary to solve the equations representing the system with friction, numerical methods become necessary. Today, this is most often the case for friction damper analysis. Methods such as numerical integration, multibody dynamics, and finite element analysis are thus often used. A friction model can be applied within any such method. Depending on the integration scheme, some friction models may lend themselves better to the solution. This section presents a sample of models and their usage from the literature. Attention is drawn to models which are suitable for friction damper modeling by properly addressing frequent velocity reversals going through the stick–slip zone.

Time-marching dry friction models can be divided into two categories: static and dynamic. Static models assume that no motion occurs in the contacting materials while they are in the sticking phase. This is the case for the Coulomb model of which a few examples are given in the next paragraphs.

Charleux et al. [12] use the dynamic Lagrangian frequency–time (DLFT) method, which is a formulation of the harmonic balance method. As for the AFT method, it solves the dynamic system by iterating between the frequency and time domains. Thus, the system is assumed to behave periodically. The contact and friction forces are calculated in the time domain. They use a finite element approach and the component modes synthesis to reduce the number of degrees of freedom. The friction force is assumed to depend linearly on the normal contact force, and thus, this model belongs to the category of the Coulomb models. No stick–slip or Stribeck effect is considered, and it is assumed that the rotation leads to macroslip at the blade root. They mention good agreement between their model and their experimental testing. The DLFT method is described in detail by Nacivet et al. [42].

Lopez and Nijmeijer [38] use the Coulomb model to calculate the maximum energy dissipation condition of a friction damper. They report that errors stemming from the simplicity of the Coulomb friction model are mostly present in the zone of high friction coefficient. They attribute this zone to the stick–slip portion of the system and thus mention that the use of a dynamic model such as the LuGre one would improve accuracy in that specific zone. They also mention that errors can come from the viscous damping inherent to bearing lubrication.

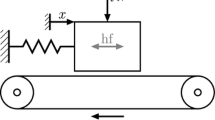
He et al. [26] have a numerical simulation that attempts to reproduce the blade of an aircraft engine. The setup is shown in Fig. 1, where the horizontal portion of the cross represents the platform and the vertical section is the blade. The two lateral masses slip against the horizontal beam and create the friction damping effect. A mathematical representation is shown in Fig. 2, where the y-axis is the radial direction and the x-axis is the tangential direction. They solve for friction using a Coulomb type of model with different stick and slip friction coefficients.

Fig. 1
figure 1

Setup tested by He et al. [26] to represent an aircraft engine. Reprinted according to the terms of the creative commons license

Full size image
Fig. 2
figure 2

Diagram of the setup of He et al. [26]. Reprinted according to the terms of the creative commons license

Full size image

Concluding the static model examples, Ferri [21] mentions that the discontinuity of the Coulomb model with varying friction force values between sticking and sliding regimes is challenging for numerical integration. Consequently, it is difficult to identify whether the contacting surfaces are sliding or not when using the Coulomb model. This can be a major limitation in determining whether a friction damper is actually damping or not. Effectively, no damping is provided when the damper system sticks.

Dynamic models, on the other hand, assume that a small presliding displacement occurs in the sticking phase, as for the Dahl and LuGre models. Such models are quite useful for high-precision control [47] while at above 3 mm/s both static and dynamic models return similar friction forces. Piatkowski [47] also mentions that dynamic models are also adequate when looking at rapid transitions between sticking and slipping states of the contacting bodies. This indicates that they are suitable for friction dampers, which undergo rapid transition between positive and negative velocities. They further add that the dynamic models are more numerically difficult to use and that numerical instabilities can lead to improper adaptation of the model to changes in the normal load if it is not characterized anew. This is not a concern for friction dampers which usually have reasonably constant normal loads. Another example of dynamic model is used by Kang et al. [28] who apply the Bouc–Wen hysteresis model to a friction damper.

The LuGre model [61] is a well-known example of a state-dependent physics-based modeling approach of calculating friction. It has the state variable, z, for which a common, although not fully accurate physical interpretation, exists. The interpretation is that z represents the state of deformation of the bristles that exist at the contact interface. The friction force thus varies prior to slip and is caused by the elastic deformation of these bristles. Once the bristles reach their maximum deformation, slip starts to occur. The friction force of the LuGre model is defined as follows,

$$\begin{aligned} F_\mathrm{f} = \sigma _ { 0} z + \sigma _ { 1} \frac{ \mathrm{d} z }{ \mathrm{d} t } + \sigma _ { 2} v \end{aligned}$$
(3)

where v is the relative velocity between the surfaces and z is the internal state. Although they are not strictly related to the material properties, the three \(\sigma \) parameters can be attributed physical meanings. As such, the stiffness and viscous damping of the bristle are \(\sigma _0\) and \(\sigma _1\), respectively. And, the viscous damping of the contact is \(\sigma _2\). The latter is usually only required for lubricated contacts. The time derivative, \(\dot{z}\), of the internal state is

$$\begin{aligned} \frac{ \mathrm{d} z }{ \mathrm{d} t } = v - \frac{ | v | }{ g ( v ) } z \end{aligned}$$
(4)

where g(v) is the Stribeck curve of friction–velocity dependence. A Stribeck curve proposed by Wit et al. [61] has the following form,

$$\begin{aligned} \sigma _ { 0} g ( v ) = F _ { \mathrm{C} } + ( F _ { \mathrm{S} } - F _ { \mathrm{C} } ) e ^ { - ( v / v _ { \mathrm{s} } ) ^ { 2} } \end{aligned}$$
(5)

while some authors use an exponent other than 2 in the last term, or even a completely different function. The parameters of the LuGre model are thus \(\sigma _0, \sigma _1, \sigma _2\), and the Stribeck curve. In case of dry friction, \(\sigma _2\) is often null. The \(\sigma \)’s cannot be negative. The Stribeck curve, in the presented case, can be obtained by identifying the \(F _ { \mathrm{C} }, F _ { \mathrm{S} }\), and \(v _ { \mathrm{s} }\) parameters. These three parameters are the Coulomb and stiction forces and the Stribeck velocity, respectively.

From a literature review, Coulibaly and Chassaing [14] are able to qualitatively describe the Stribeck curve. They give the description that the coefficient of friction increases with the sliding velocity up to a critical value and then reduces.

Astrom and de Wit [4] recall that in the LuGre model, it is possible to use different values for the positive and negative velocity conditions of the \(\sigma _1\) and \(\sigma _2\) parameters. This permits modeling potentially different contact patch characteristics in the different directions of oscillations of a friction damper. They also define the boundness and dissipativity of the LuGre model. Furthermore, Astrom and de Wit [4] go through a series of system’s analysis methods to deduce which conditions and parameters make the Dahl and LuGre models stable, rate independent, and more.

Cao et al. [11] use the LuGre model to characterize rotational displacement along the circumference of a brake drum to pad contact. Their friction damping system is intended to damp building structures and consists of a converted vehicle braking device. The displacements along the circumference that they observe reach 2.5 mm, which signifies that depending on the type of contact studied, the presliding behavior can apparently extend well beyond a few dozen micrometers. They use LuGre bristle stiffness and friction force (for the Stribeck curve) parameters dependent on the normal load, but not on excitation frequency. Their forward and backward Stribeck curves have different friction force parameters. Finally, their modeling approach comprises three stages of which two are pure elastic displacements and one uses the LuGre model. This allows to include the particular dynamics of the drum brake and its anchor pin. The LuGre portion does, however, cover a substantial portion of the whole traveled distance.

Wojtyra [63] numerically analyzes the classical LuGre model and a modified version. He assesses their response under normal loads that differ from the calibration loads or that are non-constant. They conclude that the variation of the normal load away from what was used experimentally can have a significant influence on the modeled behavior.

Saha et al. [51] develop an alternative LuGre implementation which allows to reproduce hysteresis loops in both clock- and counterclockwise directions. The loops they consider are in terms of friction force against relative velocity. This achievement is obtained by modifying the definition of the internal state variable of the LuGre model. Velde and Baets [57], however, mention that the counterclockwise hysteresis loops do not occur in reality but are rather the result of a non-measured vibration of the sliding friction element. They thus advise using sliding parts with tangential natural frequencies that differ from each other by a factor of at least 5.

Piatkowski [47] mentions that the difficulty of integrating the LuGre model is also related to the damping degree \(\xi \) of the system. It has an influence on numerical stability and is defined as a function of the \(\sigma _0\) and \(\sigma _1\) parameters of the LuGre model,

$$\begin{aligned} \xi = \frac{\sigma _1}{2 \sqrt{m \sigma _0}} \end{aligned}$$
(6)

which can be thought of as the ratio of bristle damping to critical damping. At low values of the damping degree \(\xi \), the LuGre model takes much longer to converge. However, \(\xi \) also has very little influence on the shape of the hysteresis loop. Piatkowski [47] also mentions that characterization of the hysteresis loop parameters of the dynamic friction models are better grasped when taking measurements of slow displacements, with cycle times of at least 10 s.

As an alternative to LuGre, the generalized Maxwell-slip model was developed by Al-Bender et al. [2]. It provides N state variables to allow a better representation of the gradual transition between stick and slip phases. Good results can be obtained with four or more state variables, here called elements. Each of these element has stiffness and viscosity, a gain, and a velocity function. These four parameters must be identified by a nonlinear optimization procedure.

Rizos and Fassois [49] implement a modification of the generalized Maxwell-slip (GMS) model by applying a finite-impulse response filter on both the spring elongation and displacement histories. They thus define the extended model, having the friction force \(f _ { \mathrm{EM} }\). Their modification can be summarized by the following equation,

$$\begin{aligned} f _ { \mathrm{EM} } ( t ) = \sum _ { j = 0} ^ { n } \varvec{\theta } _ { j } ^ { T } \cdot \varvec{\delta } ( t - j ) + \sum _ { j = 0} ^ { n _ { x } } r _ { j } \cdot x ( t - j ) \end{aligned}$$
(7)

where t is time, the vectors \(\varvec{\theta }_j\) and \(r_j\) are the coefficients of the filter, \(\varvec{\delta }\) is the spring deformation vector, and x is the imposed displacement. Ultimately, Rizos and Fassois [49] conclude that their modified Maxwell model yields by far the best representation of the friction forces for their set of validation simulations and experiments. These experiments consist of friction forces in the order of one Newton and with changing directions within a roughly 1 s long sample. They also report that the identification method using a two-phase optimization approach using both linear and nonlinear methods is efficient at finding the accurate friction parameters of the model. Their validation phase is conducted using both randomly generated data from simulation and experimental data from another study [31].

Also, Boegli et al. [6] use an optimization procedure for parameter identification of both LuGre and smoothed GMS friction models. They use the current provided to a translation actuator to estimate the friction force while the position is sampled separately. Their experiment is conducted in 1 dimension, on a line. They use different motion cycles of amplitudes of roughly \(20~\upmu \hbox {m}\) and reaching a total motion of roughly \(200~\upmu \hbox {m}\). Their accelerations reach \(20~\text {mm}/\text {s}^2\) and velocities \(2~\text {mm}/\text {s}\).

In another state-based dynamic friction model, Gastaldi and Gola [22] explore the improvements that a friction model which considers microslip can bring to the modeling of a dry friction damper. They characterize a rotating planar contact both numerically and experimentally. Their numerical model consists of a set of tangential and normal springs which come into contact with the rotating contact surface and manage the normal force and slip delay. They demonstrate that their model is able to reproduce both micro- and macroslip hysteresis loops. They state that reaching a slip phase is necessary to identify the friction coefficients. Finally, they state that their model with microslip prevents an overestimation of the energy dissipated when undergoing small relative displacements, roughly below 25 \(\upmu \)s. Their friction model is shown in Figs. 3 and 4.

Fig. 3
figure 3

Schema of the friction model proposed by Gastaldi and Gola [22]. Reprinted with permission from Elsevier.

Full size image
Fig. 4
figure 4

Functional diagram of the friction model proposed by Gastaldi and Gola [22]. Reprinted with permission from Elsevier.

Full size image

Dupont et al. [17] present an elastoplastic extension of the LuGre model. It adds an elastic zone in the presliding phase in order to remove the numerical drift phenomenon. The friction force is computed using the LuGre model Eq. (3). The state equation, however, becomes

$$\begin{aligned} \dot{ z } = \dot{ x } \left( 1- \alpha ( z ,\dot{ x } ) \frac{ z }{ z _ { \mathrm {ss} } ( \dot{ x } ) } \right) \end{aligned}$$
(8)

where \(\dot{x}\) is the relative contact velocity and is sometimes simply written as v. The variable \(z_{\mathrm{ss}}\) represents the steady-state elastic strain. The function which dictates the transition from elastic to plastic sliding, \({\alpha ( z ,\dot{ x } )}\), is null when either \({\mathrm {sgn}( \dot{ x }) \ne \mathrm {sgn}( z)}\) or \({| z | \le z _ { \mathrm{ba} }}\) is true. When \({\mathrm {sgn}( \dot{ x }) = \mathrm {sgn}( z)}\), the function \(\alpha ( z ,\dot{ x } )\) has a unit value if \({| z | \ge z _ { \mathrm{ss} }(\dot{x})}\) or

$$\begin{aligned} \alpha ( z ,\dot{ x } ) = \frac{ 1}{ 2} \sin \left( \pi \frac{ z - \left( \frac{ z_{\mathrm{ss}} + z _ { \mathrm{ba}} }{ 2} \right) }{ z _ { \mathrm{ss} } - z _ { \mathrm{ba} } } \right) + \frac{ 1}{ 2} \end{aligned}$$
(9)

for all other cases. The variable \(z_{\mathrm{ba}}\), also known as the breakaway displacement, is the stiction zone parameter. It ensures that there is no plastic displacement if the bristle deformation does no overcome its value. Consequently, the condition

$$\begin{aligned} z _ { \mathrm{ba} } \le | z | < z_{\mathrm{ss}} ( \dot{ x } ) \end{aligned}$$
(10)

is respected for that last case. The value of the elastic strain at steady state is

$$\begin{aligned} z_{\mathrm{ss}}(\dot{x}) = \left\{ \begin{array}{lr} { \frac{ f _ { \mathrm {ss} } ( \dot{ x } ) }{ \sigma _ { 0} } ,} &{} { | \dot{ x } | > 0} \\ { \lim _ { x \rightarrow 0^+} \left( \frac{ f _ {\mathrm { ss }} ( \dot{ x } ) }{ \sigma _ { 0} } \right) ,} &{} { \dot{ x } = 0} \end{array} \right. \end{aligned}$$
(11)

where \(f _ { \mathrm {ss}}(\dot{x})\) is the Stribeck velocity function which imposes the friction for a given steady-state relative velocity \(\dot{x}\). The variable \(z_{\mathrm{ba}}\) can be a constant or sometimes a fraction of \(z_{\mathrm{ss}}\). In the works of other authors, the Stribeck function is sometimes identified by g(v) or \(g(\dot{x})\) instead of \(f _ { \mathrm {ss}}\). Both \(z _ { \mathrm{ba} }\) and \(z_{\mathrm{ss}}\) are terms that allow to calibrate the transition between elastic and plastic behavior of the model. Dupont et al. [17] mention that their Stribeck curve is a constant value because they use a lubricant. While Dupont et al. [17] uses a null viscous parameter \(\sigma _2\), Keck et al. [30], which also use the elastoplastic LuGre formulation of Dupont et al. [17], choose to use a non-null \(\sigma _2\) parameter specifically because of the presence of a lubricant. Keck et al. [30] also mention that a common procedure to obtain the Stribeck curve is to record the friction force at different constant velocities and reconstruct the curve from the gathered data. Doing so, they obtain a Stribeck velocity \(v_\mathrm{s}\) in the order of 1 cm/s.

Fig. 5
figure 5

Imposed velocities by Keck et al. [30] to obtain the Stribeck curve. Reprinted with permission from Elsevier

Full size image

Keck et al. [30] also choose to leave the viscous friction out of the Stribeck curve used in their model because it is already considered by the \(\sigma _2\) parameter. To gather constant velocity readings, they run an experiment where the relative velocity of the contacting surfaces is imposed as a stepwise oscillating velocity function. The function, shown in Fig. 5, ensures that the velocities are constant and acceleration effects on friction are null at the point of measurement, which is shown in between the dotted lines on the figure. Keck et al. [30] find a Stribeck function which is not symmetric, nor odd, and thus, the positive and negative portions are not completely equivalent. This recalls what had been alluded by Dupont et al. [17] which uses different positive and negative constant Stribeck curve values. Keck et al. [30] also assume, as for the latter, that the motor inertia can be neglected and thus the motor force can be used as the friction force. Their use of the elastoplastic model is to provide friction compensation for micromotions with direction reversals. They obtain a good correlation with experimental data.

Liu et al. [37] compare the ability of five friction models to reproduce their experimental data. They conclude that the LuGre model is more accurate than the Dahl and Stribeck friction models. Their LuGre model has no absolute value operator on the velocity \(\dot{x}\) in the second term of the state equation as defined with the form of Eq. (4) presented in Sect. 3.2. However, other implementations of the LuGre model, including previous work by the same authors [35], make this term absolute. This absolute value also appears implicitly for the elastoplastic model through the definition of the \(\alpha ( z ,\dot{ x } )\) term’s condition on the equality of \({{\,\mathrm{sgn}\,}}(\dot{x})\) and \({{\,\mathrm{sgn}\,}}(z)\). Liu et al. [37] write that, for their experiment, the Coulomb model and the LuGre elastoplastic extension [17] fail to capture the stick–slip phenomena. However, the elastoplastic model implemented by Liu et al. [37] has small differences with that of Dupont et al. [17]. One is that Liu et al. [37] chose to rely on a non-constant Stribeck curve, having the following function,

$$\begin{aligned} g ( \dot{ x } ) = F _ { \mathrm{c} } + ( F _ { \mathrm{s} } - F _ { \mathrm{c} } ) e ^ { - ( | \frac{ \dot{ x } }{ v _ { s } } | ) ^ { j } } \end{aligned}$$
(12)

where they mention that usually \(j = 2\). The latter should provide increased accuracy of the response. Another difference is that, while they used the stiction zone parameter \(z_{\mathrm{ba}}\) expressed as a percentage of the steady-state elastic strain \(z_{\mathrm{ss}}\) during the calibration, they chose to use a constant value of \(z_{\mathrm{ba}} = 10^{-7}\) mm for the calibrated model. Finally, they also use a microscopic Stribeck velocity, \(v_\mathrm{s} = 16\) nm/s, which makes their Stribeck curve nearly constant even at quite small velocities.

Other authors report that the elastoplastic model properly reproduces the stick–slip effect. For example, Pennestrì et al. [44] report that the elastoplastic model is able to model stiction, and consequently the stick–slip effect. They also write that, among the models they studied, it is one of the only two that avoid numerical drift. Avoiding numerical drift is important when modeling dampers having friction surfaces which undergo frequent traversal of the stick–slip zone. Zhang et al. [65] also report, based on their numerical testing, that both the LuGre and elastoplastic models are able to properly represent the stick–slip phenomenon. They also add that presliding is better modeled and drift is almost eliminated by the use of the elastoplastic model. Marques et al. [41] survey a total of twenty-one friction models in order to assess their applicability to multibody dynamics. They also note that most static friction models are also able to reproduce the stick–slip behavior, Coulomb included. In their work, both LuGre and the elastoplastic model properly reproduce the stick–slip phenomenon. Their tests are conducted at the macro level of displacement.

Marques et al. [41] also conduct an assessment of the solution time required by the different friction models. They report that in the case of the elastoplastic model, an integration algorithm designed for stiff problems is two orders of magnitude faster. They also report that both LuGre and elastoplastic models have similar solution times, with the latter being slightly slower.

Bidimensional dynamic models of dry friction would allow to assess the impact of perpendicular vibrations on friction dampers. However, their current state of development is too prototypal to be used in such a way. They are not thoroughly studied by the scientific community, as noted by Xia [64]. The latter author presents a method to consider dry friction in two dimensions, by introducing a friction vector. The author uses a single equation to compute the unidimensional Coulomb friction force from the magnitude of the resulting velocity vector. Subsequently, the author imposes that this friction force vector be in the direction opposed to velocity. For the particular case where relative velocity is null, the direction of the excitation force determines the friction angle. No experimental validation is provided and the author notes that the implementation would be more complicated for state-dependent friction forces. Fadaee and Yu [20] develop a bidimensional dynamic dry friction model using the same friction angle definition. For the numerical solution, they determine its value from previous timestep data. They also reproduce experimental results for the acceleration of an elastically constrained pin moving in two dimensions on a plane with direction changes. A similar friction angle definition is also used by Kardan et al. [29] who also include planar rotation motion. To do so, they integrate over the rotating contact patch to obtain a set of resulting point translations. An experimental validation is conducted, but limited to the verification of the eccentric force at which the relative velocity becomes non-null. Barber and Wang [5] study the numerical stability of such friction angle methods and warn that some precautions must be taken to ensure numerical stability. Prior work by Sanliturk and Ewins [54] also explored two-dimensional dry friction by implementing a friction angle based on the path of motion.

Although approaches based on friction angles have been used in the works cited in the previous paragraph, they remain one-dimensional models. Their difference is that the friction force is applied along a bidimensional path. This approach works for static friction models but cannot be physically justified for dynamic models. Effectively, the recent work of Wijata et al. [60] mentions that it cannot be applied to models with an internal state. As stated earlier, models which incorporate the bristle deformation analogy such as LuGre and its elastoplastic extension have an internal state. Wijata et al. [60] extend the reset integrator model of friction, which is bristle based, to work for plane motion. They do so by changing the state variable to a state vector having radial and rotational components, which represent strain and rotation of the bristle, respectively. Their stiction model is isotropic, but allows anisotropic friction once the bidimensional force is calculated, as could be done for any of the 2D models previously covered. They provide good experimental correlations for stick–slip transition in 2D for displacements that are, however, much larger than typical presliding displacement. The relative recency and consequent absence of adoption by other authors of the approach by Wijata et al. [60] indicate that care must be taken before assuming it can be easily implemented into any type of friction modeling problem. Furthermore and at the least, numerical instabilities as those pointed out by Barber and Wang [5] may require to be dealt with prior to attempting such an implementation into generic multibody codes.

4 Testing procedures

This section presents a series of configurations studied in the literature. In order to properly test a friction damper, the contributions of friction to its behavior must be carefully assessed. It should also be noted that, as pointed out by Ferri [21], the experimental results of friction damping tests are hard to reproduce. This is caused by the influence of temperature, humidity, and the presence of a memory effect. Thus, experimental setups built with the sole purpose of studying friction are first presented. Then, testing assemblies which concentrate on friction-induced dissipation and dampers are reported. Consequently, this section will report both experiments used to retrieve the parameters of friction models and experiments focusing on the damping properties of friction dampers as a whole. Nevertheless, most studies combine experiments and simulations. Also, summary tables are presented at the end of this section. However, they do not cover every study mentioned here nor limit themselves to those actually mentioned here.

4.1 Friction

Without looking into damping per se, Liu et al. [37] use the piezoelectric stick–slip actuator (PE-SSA) approach to compare the capability and accuracy of different friction models in capturing the viscous, Stribeck, presliding, and hysteresis effects of friction. The PE-SSA approach allows to generate these friction conditions by creating a stick–slip motion between a stage and effector. The experimental setup is shown in Fig. 6 where motion is read by the displacement sensor identified by the number 6. A more thorough description of their test bed is available in another article [34].

Fig. 6
figure 6

Experimental apparatus of Liu et al. [37]. Reprinted according to the terms of the creative commons license

Full size image

Wang et al. [58] use the apparatus depicted in Fig. 7 to assess the influence of external vibrations on the constant friction coefficient of a pair of contacting pads. Referring to the figure, the motion is applied to the upper specimen (6) by a linear motor (2) driving a screw rod (3). The bottom specimen (8) is excited by an electromagnetic modal exciter. They find that external vibrations can significantly reduce the friction within the system.

Fig. 7
figure 7

Experimental apparatus of Wang et al. [58]. Reprinted with permission from Elsevier

Full size image

Lovell et al. [39] use a tribometer of model FALEX ISC-200PC to characterize the friction between a hard carbon steel tool and a softer aluminum surface. A pin is fixed while the disk rotates and they perform tests on a sliding distance of 20 m, to attain steady-state friction conditions. At steady state, the recorded friction coefficient nevertheless varies by values of roughly \(\pm \,10\%\). They study the effects of changing the pin diameter, sliding velocity, lubricant used, and normal load. They evaluate the impact of these parameters by plotting against the shear factor, which relates applied pressure to the shear strength of the soft material. Among their findings, the greatest impacts come from changes in the applied load and changes in the shape of the contacting entities. The influence of sliding speed, in the range they tested, [0.1,0.8] m/s, is negligible.

This type of pin-on-disk apparatus is commonly used in the literature, as pointed out by Philippon et al. [46]. The latter also warn that the equipment used can have a significant influence on the measured friction coefficient. Thus, they instead use a projectile and recipient device to measure the friction coefficient at various velocities and normal loads, as shown in Fig. 8. Their setup allows a course of 30 mm with normal pressures between 10 and 33 MPa. They measure the velocity of the projectile-propelled part using light beams interruption records. They use both an air gun for velocities beyond 10 m/s and a hydraulic jack for velocities below 3 m/s to generate the relative movement between the two specimens. Strain gauges allow them to measure the friction force. Their conclusions are that both normal pressure, and relative velocities have a significant impact on the friction coefficient. They do not attempt to use the results obtained within an analytical or numerical friction model and do not mention dynamic types of friction models. A similar ballistic method is also used by Coulibaly and Chassaing [14] to study the effects of normal pressure, sliding velocity, and temperature of the friction coefficient. These experiments are better described by Chassaing et al. [13] who find increases of temperature beyond \(1000\,^\circ \hbox {C}\) caused by a specimen under normal pressure of 118 MPa sliding 6 cm at 43 m/s.

Fig. 8
figure 8

Experimental apparatus of Philippon et al. [46]. Reprinted with permission from Elsevier

Full size image

Dupont et al. [17] use the x-axis translation of an electrical discharge machining system capable of a displacement resolution of \(0.1~\upmu \hbox {s}\), which allows to study the presliding regime. This numerical control machine is thus used to execute a set of trajectories and record motor current as the friction torque. They test both hysteresis loops that occur inside the presliding regime and others where fully developed sliding is achieved. They, like many others, characterize their model by minimizing the error between modeled and experimental force–displacement curves within an iterative optimization procedure. Also as other authors, they obtain the relative velocities at the point of contact from a filtered numerical integration of the displacement curves. They actually only gather information about the input velocity of their machine and consider the receiving contact patch to be fixed. Their reported data thus present angular displacements while the friction probably mostly emanates from linear displacements of a ball-screw-and-nut transmission. No information is given about the normal load, and they use a null viscous friction parameter.

Saha et al. [51] use the silicon rubber conveyor belt device shown in Fig. 9 to test friction-induced oscillations. They measure the friction force using an indirect measurement. Thus, they obtain the friction force by recording the displacement and acceleration data and applying those to the governing equations of the system to obtain the friction force. Displacement of sliding mass is obtained using a laser and acceleration using an accelerometer.

Fig. 9
figure 9

Experimental apparatus of Saha et al. [51]. Reprinted with permission from Elsevier

Full size image

Amjadian and Agrawal [3] sand their friction pad before each test to avoid the accumulation of residual material which could affect the results. They read the displacements with an LVDT and use linear ball bearings to ensure smooth movement in translation. The displacements are imposed by a linear servo actuator and the forces measured by a load cell. The closer and global views of their experimental setup are shown in Figs. 10 and 11, respectively.

Fig. 10
figure 10

Setup tested by Amjadian and Agrawal [3] to produce planar friction and eddy-current damping. Reprinted with permission from Elsevier

Full size image
Fig. 11
figure 11

Data acquisition devices used by Amjadian and Agrawal [3]. Reprinted with permission from Elsevier

Full size image

Wojewoda et al. [62] use a shaker to provide motion covering the frequency ranges near resonance of the rig. They use an LVDT and an LVT to measure the relative displacement and velocity, respectively. They obtain the friction force by inputting the force read by a force transducer on the vibrating mass into a simplified dynamic model. Lopez and Nijmeijer [38] use a shaker to excite their friction damper setup and warn that although the voltage signal they send to the shaker is sinusoidal, the output force is not, due to its impedance. The normal force they apply is not maintained constant between their various measurements.

Dion et al. [15] heavily criticize that many experiments intended to identify the friction parameters of contacting material couples contain too many uncertainties. They mention, for example, the pin-on-disk and pin-on-plane experiments which depend on the machining process. They also criticize that many experiments are not able to provide repeatable or even constant normal loads. They also mention that many experiments are not able to reproduce high frequencies (>100 Hz) and high amplitude (\(>1\,\upmu \hbox {m}\)) together. Finally, they also criticize the very often important coupling between the friction forces and the inertia of the system which adds noise to the curves then used to characterize a friction model. In the tribometer they designed to avoid these problems, they use four to eight contact surfaces to reduce statistical errors. Dion et al. [15] also mention that plasticity can make the assumption that the friction coefficient does not depend on the normal load invalid. Their testing yields a value of 2 for the exponent of the g(v) function of LuGre. They also report that for their test material, aluminum Al 2017, an apparent pressure beyond 5 MPa damages the material and modifies the friction characteristics. They also find out that the shape and size of the contact area do not influence the friction behavior. They exclude the viscous damping terms of the LuGre model by assuming that they are non-influent for metal to metal contacts. Both Dion et al. [15] and Wang et al. [58] report the roughness of the materials they use for friction. Both Ozaki et al. [43] and Hashiguchi et al. [25] are concerned with stick–slip effects of friction and perform validation experiments at constant velocity.

4.2 Damping

Charleux et al. [12] test the blades of a turbine for the impact of friction. Their setup is under vacuum at 20 mbar to reduce the aerodynamic effects and isolate friction-induced motion. They rotate the main shaft at frequencies between 1000 and 5000 rpm and excite the blades with piezoelectric actuators using a sweep sine frequency. They measure the response with the strain gauges and evaluate the resulting damping from the fundamental frequency and the half-power bandwidth. The latter is also used by Butt and Akl [8] to quantify damping.

Esteves et al. [19] perform an experimental study of a planar linear reciprocating friction contact. This system is thus similar to the friction dampers emphasized by this paper. They obtain a mostly linear relationship between dissipated energy and the volume of material removed. The displacements considered range from 20 to \(60~\upmu \hbox {m}\). Their tests are performed with 2 GPa contact pressure at 10 Hz. The shapes of the force–displacement hysteresis cycles they obtain are highly influenced by the displacement amplitudes. They find considerable influence of humidity and of the molecular content of the atmosphere which can be filled either with oxygen or nitrogen. These influences come from the effects of these atmospherical conditions on oxidation and the resulting quantity of residual powder. They work consequently further highlights the friction damper’s sensibility to environmental conditions and excitation forces.

Lopez and Nijmeijer [38] carry a study on the relationship between the normalized friction force and the energy dissipated by a friction damper modeled as a single DOF system. The normalization consists of a division by the amplitude of the applied harmonic force. Their findings show that there is an optimal friction force which maximizes the energy dissipation for the damper. This force depends only on the motion amplitude and is independent of the excitation frequency and mass of the system. They obtain a maximum of 10% error between their prediction with the Coulomb friction model and the experiment and thus conclude that such simple friction models may be sufficient to calculate the energy dissipation by friction dampers if relative displacements are large. A similar reasoning comes from Peyret et al. [45] for their simulations of a friction damper. They model friction using a Coulomb model and state that sliding speed and thus frequency have a negligible effect of the damping.

Wieczorek et al. [59] study the response of a bridge damped with a semi-active friction damper. The normal force on the damper is varied by a stack of piezoelectric actuators. In their experiments, they impose the movement using a sine signal and record the friction force. The normal force they used for each curve is variable, due to peculiarities of their test bench and the hysteresis of piezoelectric actuators. Effectively, Wieczorek et al. [59] apply 300 V to the actuators to create a clamping force and consequently the initial normal force varies between 46 and 179 N, but is not known exactly.

Tsopelas et al. [56] rely on friction bearings to assist damping the motion of a seismically excited bridge model. The model is 25% the length of the original bridge. They characterize their friction parameters using a velocity-dependent coefficient of friction. They identify the response of their structure using white noise table-induced excitation. The damping provided by their system was enhanced by dissipating energy through viscous dampers. The frequencies at which they test the damper vary between roughly 0.4 Hz and 0.75 Hz.

Lee et al. [33] develop and test a new contact patch material for friction dampers used in building structures. Their design is inspired by automotive braking technology and is able to eliminate wear of the friction pad over the duration of their tests. The friction force they obtain is proportional to their initial clamping force and is not influenced by variations of this force during the tests. They rely on a Coulomb model for their numerical simulation of the damper. They also assess that their damper does not slip under simulated wind vibrations but loses damping capacity with increasing temperatures.

Dowell and Schwartz [16] experimentally determine the damping ratio of a friction-damped beam using the method of logarithmic decrement on the time signal. They find that the magnitude of the exciting force has a nonlinear influence on the shape of the frequency response strain of the beam. In the semi-active experimental friction damper case of Lu et al. [40], the pivot position of a lever arm is controlled to modify the transmitted friction force. Latour et al. [32] use linear variable differential transformers (LVDT) to measure the displacements of their friction damper setup. They apply the simulated seismic loads with hydraulic actuators. They mention that applying an aluminum coating by thermal spray on a steel surface significantly increases the coefficient of friction of a friction damper. However, they find that such a coating quickly degrades at the loading forces they tested. Degradation is notable after roughly 250 mm of cumulated displacement. This is fine for earthquake-resistant structures, but not to damp systems which are subjected to continuous excitation. They also mention that the influence of excitation frequency is not critical because the influence of speed on friction can be neglected.

Amjadian and Agrawal [3] create a dynamic model comprising inertia, eddy currents, and the LuGre friction model to numerically reproduce the behavior of their prototype damper. The nomenclature they use for the description of the magnetic properties of the damper has to be carefully read to avoid confusion with terms using the same letters in the friction literature. They mention that the \(\sigma _2\) parameter of the LuGre model is used to incorporate viscous damping effects typically caused by the lubrication of the contacting specimens and thus choose to set it to zero for their dry friction case. They use a fixed value of 2 for the exponent of the Stribeck curve and 0.01 m/s for the dividing velocity of the same curve. They obtain the LuGre parameters by minimizing the error between the experimentally and numerically determined damper forces from the hysteresis curves. From their tests at 0.1 Hz, 0.5 Hz, and 1.5 Hz, they conclude that the influence of frequency on the LuGre parameters is negligible.

Finally, Table 1 gives an insight on the testing of friction within the context of this review. Table 2 provides an overview of the friction dampers tested in the literature. They both contain articles cited above, chosen based on their relevance to the target of this paper which dampers undergoing continuous one-dimensional sliding between flat surfaces.

Table 1 Friction testing
Full size table
Table 2 Friction damper testing and modeling summary table
Full size table

4.3 Characterizing friction models

When conducting experimental work to identify the parameters of friction models capable of modeling the presliding, it is essential that the corresponding zones of the friction be explored. As a consequence, the literature shows experiments that use very limited movements, in the order of 20–\(200~\upmu \hbox {m}\). This is confirmed by Sun et al. [55] who recall that identifying the effects for which dynamic models exist requires displacements in the range of a few micrometers (\(\upmu \hbox {m}\)). Also, to properly reproduce the response at different velocities, the Stribeck effect must be grasped experimentally. Thus, the range of tested velocities should reach velocities of at least 1 cm/s, unless the Stribeck velocity is already known from the literature. Furthermore, Sun et al. [55] criticize that most experiments used to characterize friction models do not allow variation of the normal force.

Dion et al. [15] argue that most parametric friction models can be identified with a displacement–load hysteresis curve while the velocity–load curve is used to identify the slip behavior.

Rizos and Fassois [49] present three methods to simultaneously obtain the parameters of three dynamic friction models. They are the LuGre [61], the Maxwell [2], and a modified Maxwell model. They obtain the parameters by error reduction from a single displacement–friction force curve. They simulate experimental data numerically by adding noise to the results obtained by the respective friction models. They also validate their method with experimental data which Lampaert et al. [31] graciously provided to them.

Overall, the conclusion on friction identification is the following. Some authors choose to break down the identification process into different steps. For example, they will identify the Stribeck curve separately. However and in any case, they mostly rely on an iterative search for parameters by minimizing the error between the friction forces obtained experimentally and numerically.

5 Discussion and conclusion

A series of simulations and experimental approaches are presented in this document. They evaluate the response of systems to either friction alone or friction damping. Based on these, the following proposed methodology is given as a starting point for numerical simulation and experimental testing of sliding friction dampers for continuously vibrating systems. The choice of friction model and its characterization, experimental testing, and considerations for the modeling of a complete system are given.

5.1 The friction model

A series of dynamic friction models are used for system control. Most applications use small relative contact surface displacements. Thus, LuGre-type models are important in the research area of control systems. When it comes to friction damping, some authors choose to rely upon the simpler Coulomb model. However, they often mention some inaccuracy due to the crude modeling of the stick–slip transition. Numerical difficulties also emanate from the transition between stick and slip. As an alternative, some authors use the LuGre model for friction damping. The original LuGre is very good at representing micromovements, but is known to exhibit drift. This is of smaller importance for control of systems which have feedback corrector loops. This may be significant for a high-frequency damper where the presliding and sliding regimes are crossed many times per second. Many authors extend or inspire themselves from the LuGre to propose drift-free solutions that still properly reproduce frictional lag, presliding, and memory. However, most of these solutions add significant complexity to the model and sometimes many degrees of freedom. Also, there is not much research available on these other models as for the LuGre and its elastoplastic version. One extension which solves the drift issue and adds relatively little complexity to the model is the elastoplastic version. It is thus suggested to opt for the elastoplastic LuGre model of Dupont et al. [17], as presented in Eqs. (8) to (11).

5.2 Characterization and parameters

The normal force between the contacting friction surfaces has an important influence on the results. This force is often hard to experimentally control and monitor. Many authors use the same or a similar normal force for all their test cases, and many do not know its value. The amplitude of the relative surface displacement is another influential factor. Some authors note that the differences between the dynamic friction model parameters obtained by hysteresis loops of experiments conducted at different frequencies, and thus speeds, are negligible. The same, however, cannot be said for the parameters obtained from tests conducted at different oscillation amplitudes or different clamping loads.

It is suggested to rely on a nonlinear optimization algorithm in order to identify the parameters of friction model. The curves that serve the optimization should be displacement–force and/or velocity–force curves covering the proper zones of presliding and fully sliding hysteresis. An alternative parameter identification technique is to separately obtain the Stribeck curve parameters and the other LuGre parameters, as suggested by Keck et al. [30].

Other important aspects that stem from this literature review are the effect of wear, temperature, and humidity. These effects are, however, not directly implemented in the reviewed models. They should thus be considered as having an influence on the parameters of the model itself. Generally, new model parameters should be obtained for each new condition of clamping load, humidity, temperature, and wear. If the clamping force varies, experimental data should be used to validate the approach of multiplying the friction force by the normal clamping force. This will ensure that the magnitude of the variations in the latter only results in linear friction force changes.

5.3 Experiments

When performing experimental tests, the range of displacement amplitudes and clamping forces required by the targeted application should be represented. A study of the influence of wear, temperature, and humidity on the evolution of the friction parameters should also be conducted. Although not optimal, excitation of the test rig may be done at smaller frequencies and velocities than the application. Displacements should cover both presliding and sliding regimes and allow to obtain a Stribeck curve for the full range of predicted velocities. Such small displacement could be imposed by piezoelectric actuators, linear step motors, shakers, or angular motors with screw mechanisms. Care must be taken to read the forces at the proper location, as most motion inducing devices have embedded elasticity and damping. Alternatively, their viscoelastic properties should be modeled during the parameter identification phase. Similar care must also be taken when reading the relative displacement at the contact surfaces. Most authors use LVDTs to measure displacements while some use high-speed cameras. Such high-speed cameras are also used to obtain forces indirectly by inputting the measured movement in a simplified inertial mathematical model. Forces are sometimes measured by load cells or force transducers. It is thus suggested to rely on LVDTs to read displacements and on load cells to measure both tangential and normal forces. Inertial effects should be considered by the identification model. Although not a widespread approach, using repeated and symmetric contacts and avoiding overconstraining the device should reduce identification errors.

5.4 Dynamic modeling

Many authors choose to present their system using a simplified one degree-of-freedom equivalent representation. Quite often that representation has a single mass, a spring, and a damper. They then add friction as an external force. This is a potential source of errors in the characterization phase. Inertia, viscosity, and damping are indeed often present in the experimental devices. A common solution to this is to rely on testing at frequency and amplitude ranges that isolate friction from the other effects. However, to test many different frequency ranges and amplitudes, it is suggested to rely on an approach that can fully model the system at hand. Thus, for high accuracy, the friction model can be implemented into a multibody simulation. The resulting implementation can also be coupled with finite element analysis when deformable parts are present in the vibrating system. Doing so should ensure proper simulation of a damper working under non-harmonic excitation, repeatedly crossing null velocities, and having a slightly variable clamping load.

5.5 Further reading

This survey attempts to give a thorough vision of the modeling and testing of friction dampers. However, it only covers a portion of the literature available for the study of dry friction and friction dampers. A non-exhaustive list of titles is given for readers wishing to further deepen their insight. Al-Bender et al. [1] give a careful introduction to different friction models prior to presenting their own. Pennestrì et al. [44] provide an analysis where different friction models are assessed for their numerical behavior. Astrom and de Wit [4] present a thorough stability analysis of the LuGre friction model. Ferri [21] covers the state of the art of friction damping in the 1990s. Rizvi et al. [50] give an overview of the numerical methods used to solve friction damper systems.