Characterization of industrial low-density polyethylene: a thermal, dynamic mechanical, and rheological investigation

Abstract

The study of commercial low-density polyethylenes (LDPEs) has always focused on the effects of the molecular architecture of the polymer on its shear and extensional rheological properties due to their direct influence on manufacturability. However, the complex morphology of industrial-grade LDPEs also affects the crystallization kinetics and dynamic mechanical properties of the polymers, which are key to the processibility and applications. Therefore, a comprehensive investigation was conducted into the areas of crystallization kinetics, crystallinity, dynamic mechanical, and linear and non-linear shear rheological properties of two industrial-grade LDPEs to build a cohesive insight into the influence of morphology on these material properties. We further analyzed the steady-state and transient shear viscosity data obtained from the two LDPEs in comparison with constitutive model predictions using the hierarchical multi-mode molecular stress function (HMMSF) and found excellent agreement within experimental accuracy between predictions by the HMMSF model and shear stress as well as normal stress data of the LDPEs investigated.

Introduction

In 1898, the accidental side product of Hans von Pechmann’s (1898) investigations into diazomethane brought about the creation of polyethylene (PE). Fast forward from discovery to the present day, PE has become one of the most commonly used plastics globally, with an annual production of nearly 84 million tons in 2014 (Dobbin 2017), with low-density polyethylene (LDPE) taking up 16% of the global production in 2017 (Geyer 2020). The attractiveness of LDPE is owed to its high versatility and adaptability for various manufacturing processes and applications. LDPE produced by the means of free-radical or Ziegler–Natta polymerization leads to wide molecular weight distributions and the formation of short- and long-chain branches. The molecular weight distribution and branching of LDPE contribute to its rheological properties, giving the polymer desirable flow properties when it comes to the formation of films, making them suitable for sterile medical packaging films, plastic bags, and plastic wraps (Malpass 2010).

Therefore, studies on industrial-grade LDPEs have typically focused on the relationship between rheological properties and molecular architecture and their influences on processing performance (Gabriel, et al. 1998; Han and Villamizar 1978; Rasmussen, et al. 2005). The film blowing processibility of LDPE was shown to be dependent on its rheological properties and crystallization behavior (Winter 1983). Preferred polymer properties developed during solidification can be acquired by understanding the crystallization kinetics of polymers, which in turn allows users the ability to design polymers for specific applications (Gahleitner, et al. 2016). It has been shown through molecular dynamics simulation that crystallization kinetics and final morphologies of polyethylene are mainly influenced by branch content, which acts as a defect both in the nucleation and crystal growth process (Gao, et al. 2016). Gao et al. (2016) showed that the crystallization rate and crystallinity of polyethylene decrease while induction time increases as branch content increases. Moreover, during industrial processes, polymers are subjected to high cooling rates coupled with shear and extensional flow that further complicate the crystallization process (Mileva, et al. 2018). The rate of crystallization and crystalline growth can be evaluated quantitatively by methods such as X-ray crystallography, infrared spectroscopy, density analysis (i.e., dilatometry), and microscopic observations (Buchdahl, et al. 1959).

Due to its high industrial demand, there is an interest in investigating LDPE by various techniques that encompass thermal, mechanical, and rheological properties to determine an internal consistency and cohesive understanding of LDPE’s behavior. Dynamic mechanical analysis (DMA) is an effective technique to analyze the mechanical behavior of viscoelastic materials and explain their behavior during processing and applications. The DMA is suitable for glassy polymers, rubbers, and stiff gels (Danielsen, et al. 2021). For example, DMA has been widely used in the analysis of the α, β, and γ relaxations in polyethylene, single-crystal polyethylene, polyethylene copolymer blends, and so on (Khanna et al. 1985; Sinnott 1966; Hoffman et al. 1966). Kline et al. (1956) employed DMA to investigate the effect of branching on dynamic mechanical properties in polyethylene, and results indicated that all three main dispersion regions (α, β, γ), characteristics of polyethylene, are affected to some extent by branching. Kohutiar et al. (2018) used DMA in the study of viscoelastic behaviors of recycled thermoplastic polymers such as low-density polyethylene, polypropylene, and polyethylene terephthalate. DMA also serves as a useful tool in characterizing the interfacial interactions between fillers and polymer matrix, which greatly influence the properties of nanocomposites (Bashir 2021). Robertson et al. (2008) utilized DMA to confirm that two distinct glass transitions ($T_{g}$), shown in filled nanocomposites, were attributed to $T_{g}$ the bulk of polymer and $T_{g}$ the polymer chains located in the interphase region of the nanocomposites.

Oscillatory shear rheology is a technique that relies on similar fundamental concepts as the DMA to analyze the mechanical behavior of materials (Jóźwiak and Boncel 2020). The relaxation behaviors of polymer materials can be characterized using oscillatory shear rheology for a wide range of frequencies by employing the time–temperature-superposition procedure (Dealy and Plazek 2009; Van Gurp and Palmen 1998). Sliozberg et al. (2013) utilized rheology to understand the effect of physical entanglements on the mechanical and rheological properties of polymer gels. The network formation kinetics can be studied by observing the storage (G'), loss modulus (G"), and tan(δ) = G" / G' as a function of time during the gelation process, which helps to associate the development of the network structures with their mechanical responses. Vandiver et al. (2016) reported the effect of hydration on the mechanical properties of a polyethylene-based membrane via oscillatory measurements. The dynamic mechanical testing was conducted while ramping humidity at a constant temperature and by ramping temperature at constant or saturated relative humidity to distinguish mechanical transitions due to hydration and temperature level. The G' and G" showed a sharp decrease during humidification with a reversible transition between the dry and hydrated states. Skrzeszewska et al. (2010) studied the kinetics of transient network formation using oscillatory experiments and found that as the gel point is approached, the elastic properties start to play a more significant role and the loss modulus and storage modulus show very similar power-law behavior with a critical exponent. Constitutive modeling of shear and extensional rheological behavior of polymer is yet another method to relate the effects of morphology to its processibility. A number of constitutive models have been developed for branched polymer melts, such as the pom-pom model of McLeish and Larson (1998) and the molecular stress function (MSF) model of Wagner and coworkers (1979, 2001, 2003,1979). The MSF model was eventually evolved by Narimissa and Wagner into the novel hierarchical multi-mode molecular stress function (HMMSF) model (Narimissa, et al. 2015, 2016; Narimissa and Wagner 2016b, c, 2018), which realizes the fundamental schemes of the integral version of pom-pom models such as hierarchical relaxation and dynamic dilution and takes into account the interchain tube pressure. The model is suitable for predicting extensional and shear rheological behaviors of linear and LCB polymer melts based on their linear-viscoelastic characterization. The HMMSF model has been shown in simulated 3D abrupt contraction flow to have excellent agreement with experimental vortex opening angles and stress birefringence measurements for LDPE melt (Olley, et al. 2022).

This contribution intends to provide a comprehensive investigation of crystallization kinetics, crystallinity, dynamic mechanical, and linear and non-linear shear rheological properties of two industrial-grade LDPEs (1840H and 3020D) to build a cohesive insight into the influence of morphology on these material properties. Due to the immense industrial application of LDPE, the optimization of the processing conditions during extrusion, injection molding, calendaring, etc. is of great importance to polymer processing, and a methodical relationship between molecular-level structure (polydispersity, molar mass distribution, branching, crystallization kinetics, etc.) and the flowability/processability of LDPE is required. Thus, this study provides an in-depth characterization of the two LDPEs by various analytical techniques and an accurate quantification of their rheology by the HMMSF constitutive model. The article is organized as follows: In Sect. 2, we report on the sample preparation and experimental methods used for the various thermal, morphology, mechanical, and shear rheological experiments. We first present in Sect. 3 the crystallinity and crystallization kinetics data of the LDPEs. In the next section, we present the morphology and dynamic mechanical analysis of the LDPEs from well below their glass transition temperature to 100 °C. Section 5 compares and discusses the model predictions of the HMMSF model to the steady-state and transient shear data of the two LDPEs.

Experimental

Materials and sample preparation

LDPE Purell 1840H polymer pellets were purchased from LyondellBasell and LDPE 3020D polymer pellets were provided by Technische Universität Berlin. Based on LyondellBasell’s specifications, the density of polymers is 0.919 g/cm³ and 0.927 g/cm³, for 1840H and 3020D, respectively. The LDPE pellets were dried in a vacuum oven at 50 °C for 24 h to remove moisture. The pellets were then homogenized in a twin-screw extruder at 170 °C before compression molding. Samples for DMA and shear rheological experiments were prepared by compression molding at 150 °C between smooth polytetrafluoroethylene film sheets using extruded LDPE granules. The samples were compression molded for 15 min in a pre-heated hydraulic press before being removed and cooled to room temperature by placing them between water-cooled hydraulic press plates. For the DMA experiments, rectangular samples with a 45-mm length, 12-mm width, and 2-mm thickness were fabricated. Disk-shaped samples with a 25-mm diameter (for parallel-plate) and 15-mm diameter (for cone-partitioned-plate) with a 2-mm thickness were prepared.

Thermal characterization

The thermal properties of extruded LDPE 1840H and LDPE 3020D samples were analyzed using differential scanning calorimetry (DSC25, TA Instruments). To determine the degree of crystallinity (%crystallinity), samples of about 5 mg were heated to 200 °C to erase their thermal history from the extrusion process, and subsequently cooled to − 90 °C, and a second heating cycle was conducted at a temperature range of − 90 to 200 °C. The experiment used a heating rate of 10 °C/min and a cooling rate of 5 °C/min under a nitrogen atmosphere with a flow rate of 50 mL/min. Only the second heating cycle was considered to determine the thermal properties of the samples. In isothermal crystallization experiments of extruded LDPE 1840H and LDPE 3020D samples, samples were heated to 150 °C, which is above their melting point, and held for 5 min to erase the thermal history of the samples before cold quenching at − 50 °C/min to the desired crystallization temperature T_c (ranging from 103 to 106.5 °C) and held at T_c (isothermally) for 30 min.

Molecular weight and branching characterization

The molecular weights and molecular weight distributions of LDPE 1840H and LDPE 3020D were determined by gel permeation chromatography (GPC) using a PL-GPC-200 instrument equipped with a differential detector and two PLgel MIXED-LS 300 × 7.5 mm columns. The measurement was performed at 150 °C with 1,2,4-trichlorobenzene as the eluent at a flow rate of 1 mL/min. Polystyrene was used as a standard for calibration. The branching level CH₃/1000C of LDPEs was calculated using ¹H nuclear magnetic resonance (NMR) data (Zhang et al. 2020). NMR was recorded on a 400-MHz Bruker AVANCE III instrument at 120 °C using deuterated 1,2-dichlorobenzene as a solvent, at a sample concentration of 80 mg/mL.

Dynamic mechanical analysis

DMA of LDPE 1840H and LDPE 3020D was performed using a torsion fixture (rectangle) geometry on an ARES-G2 (TA Instruments) at a temperature range of − 150 to 100 °C, an angular frequency of 1 Hz, and a heating rate of 5 °C/min.

Rheological characterization

A series of rheological characterizations of LDPE 1840H and LDPE 3020D were performed on an ARES-G2 (TA Instruments) with parallel-plate, cone-and-plate, and cone-partitioned-plate (10 mm inner diameter and 0.1 rad angle) fixtures. The linear viscoelastic properties of LDPE melts were obtained using the parallel-plate geometry from a series of multi-wave oscillatory measurements (Holly, et al. 1988) in the air atmosphere. The multi-wave technique was chosen in preference to the small-amplitude oscillatory shear (SAOS) method to shorten the measurement time. This reduces the effects of thermal and thermo-oxidative degradations on the polymers at high testing temperatures. Time-sweep rheometry measurements of neat LDPE 1840H and stabilized LDPE 1840H with Irganox 1076 at temperatures of 190 and 210 °C showed competing degradation mechanisms between thermal and thermo-oxidative degradations which resulted in a slight increase in storage modulus and a decrease in phase angle (Poh, et al. 2022). Over an extended period, thermal degradation takes over as the driving mechanism for degradation, resulting in a sharp increase in storage modulus and a decrease in phase angle. The measurements for LDPE 1840H and 3020D were carried out at 150, 170, 190, 210, and 230 °C with two sets of multi-wave oscillation at each temperature. The fundamental and harmonic frequencies for the multi-wave oscillation are summarized in Table 1. The two sets of multi-wave oscillation would cover an angular frequency range of 0.05 to 256 rad/s. All data for LDPE 1840H and LDPE 3020D were shifted to 150 °C using the time–temperature-superposition procedure. SAOS measurements were performed using the parallel-plate geometry at the reference temperature of 150 °C for LDPE 1840H and LDPE 3020D from an angular frequency range of 0.01 to 400 rad/s to verify the validity of the multi-wave measurements as shown in the Appendix.

Table 1 Fundamental and harmonic frequencies for multi-wave oscillations of LDPE 1840H and LDPE 3020D

Steady-state shear experiments were conducted using parallel-plate, cone-and-plate, and cone-partitioned-plate (10 mm inner diameter and 0.1 rad angle) fixtures with shear rates ranging from 0.001 to 100 s⁻¹ at 150 °C for LDPE 1840H and LDPE 3020D. Rabinowitsch corrections were applied to the parallel-plate measurements (see Eq. (5) of (Keentok and Tanner 1982)). Transient shear experiments were conducted using cone-partitioned-plate with shear rates ranging from 0.01 to 100 s⁻¹ at 150 °C for LDPE 1840H and from 0.001 to 100 s⁻¹ at 150 °C for LDPE 3020D.

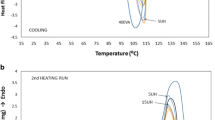
Thermal properties and isothermal crystallization kinetics

During heat scanning of the samples, the following characteristics of the samples were determined: melt temperature ($T_{m}$), cold crystallization temperature ($T_{c}$), endothermic enthalpy of melting ($\Delta H_{m}$), and exothermic enthalpy of crystallization ($\Delta H_{c}$). The DSC results of the second heating cycle are shown in Fig. 1 and Table 2. The percent crystallinity is then determined using the following equation (Menczel, et al. 2009):

$$X_{c} = \frac{{\Delta H_{m} }}{{\Delta H_{m}^{0} }} \times 100\%$$

(1)

where $\Delta H_{m}$ is the enthalpy of fusion, $\Delta H_{m}^{0}$ is the heat of melting of 100% crystalline polymer, and $X_{c}$ is the percentage crystallinity. The theoretical melting enthalpy of 100% crystalline polyethylene is $\Delta H_{m}^{0} =$ 293 J/g (Wunderlich 1990).

Fig. 1

DSC a heating curves and b cooling curves of extruded LDPE 1840H and LDPE 3020D

Table 2 DSC data of LDPE 1840H and LDPE 3020D

The isothermal crystallization kinetics of extruded LDPE 1840H and LDPE 3020D were investigated through DSC at different ranges of isothermal temperatures (103 to 104.5 °C for LDPE 1840H and 105 to 106.5 °C for LDPE 3020D). Figures 2 and 3 present the DSC curves of the samples, showing the crystallization exotherm as a function of time. The crystallization peak shifts to lower values with decreasing isothermal crystallization temperature, indicating that the crystallization rate has increased. The isothermal crystallization kinetics of the LDPE 1840H and LDPE 3020D were analyzed using the Avrami equation as shown in the following expression:

$$1 - V_{c} (t) = \exp ( - kt^{n} )$$

(2)

where $V_{c} (t)$ is the relative volumetric transformed fraction of amorphous to crystalline polymer; $k$ is the growth function rate constant, which is a function of T_c; $n$ is the Avrami index that reflects the crystallization mechanism and dimensionality; and $t$ is the crystallization time. The Avrami index usually has values of an integer between 1 and 4 for different crystallization mechanisms, with 1, 2, and 3 indicating one-, two-, and three-dimensional crystal growth with non-sporadic mechanisms, and 2, 3, and 4 for one-, two-, and three-dimensional growth for sporadic mechanisms (Wunderlich 1973). The relative volumetric transformed fraction $V_{c} (t)$ is calculated as,

$$V_{c} (t) = \frac{{W_{c} }}{{W_{c} + ({{\rho_{c} } \mathord{\left/ {\vphantom {{\rho_{c} } {\rho_{a} }}} \right. \kern-\nulldelimiterspace} {\rho_{a} }})(1 - W_{c} )}}$$

(3)

where $\rho_{\;c}$ and $\rho_{\;a}$ are the fully crystalline (1.004 g/cm³) and fully amorphous polyethylene (0.853 g/cm³) densities (Lorenzo, et al. 2007). $W_{c}$ is the crystalline mass fraction that is calculated with the following equation:

$$W_{c} = \frac{\Delta H(t)}{{\Delta H_{{{\text{total}}}} }}$$

(4)

where $\Delta H_{{{\text{total}}}}$ is the maximum enthalpy value reached at the end of the isothermal crystallization process and $\Delta H(t)$ is the enthalpy variation as a function of time. Applying logarithmic properties to both sides of Eq. (2), the following equation can be obtained,

$$\log \left\{ { - \ln \left[ {1 - V_{c} (t)} \right]} \right\} = \log k + n\log t$$

(5)

Fig. 2

Heat flow versus time during isothermal crystallization of LDPE 1840H at different crystallization temperatures (103, 103.5, 104, and 104.5 °C) by DSC

Fig. 3

Heat flow versus time during isothermal crystallization of LDPE 3020D at different crystallization temperatures (105, 105.5, 106, and 106.5 °C) by DSC

Equation (5) is used to construct the Avrami plot of $\log \left\{ { - \ln \left[ {1 - V_{c} (t)} \right]} \right\}$ against $\log t$ of LDPE 1840H and LDPE 3020D as shown in Fig. 4. The experimental data are obtained from the integration of the DSC isothermal data in Figs. 2 and 3.

Fig. 4

Avrami plot of the experimental data (open symbols) obtained from the isothermal crystallization of a LDPE 1840H and b LDPE 3020D. The solid black line represents the Avrami fit (Eq. (5))

The fitting of the Avrami equation with the experimental data was performed with an Origin plugin developed by Lorenzo et al. (2007). Lorenzo et al. (2007) found good fitting was achieved using a relative volumetric conversion range of 3 to 20% for hydrogenated polybutadiene and showed significant deviations in the predictions of the crystallization half-time $t_{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}}}$ if the experimental data were fitted to the entire conversion range (0 to 100%). However, from our findings, the experimental data for LDPE 1840H and LDPE 3020D were well fitted to a conversion range of 5 to 95%. The calculated Avrami parameters and experimental crystallization half-time $t_{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}}}$ are summarized in Table 3. The Avrami index has often been found to be fractional due to successive or concurrent crystallization mechanisms, incomplete crystallization, and changes in the sample volume during crystallization or annealing. Literature has reported a wide range of Avrami indexes ranging between 1.72 to 4 for polyethylenes which are dependent on the molecular weight and branching of the polymer (Booth and Hay 1971; Gupta, et al. 1994; Hay, et al. 1976; Hillier 1965; Kamal and Chu 1983). It is well documented that the Avrami index of a branched polymer such as low-density polyethylene can be as low as 1 (Buchdahl, et al. 1959; Maderek and Strobl 1983). It was suggested that the dendritic nature of spherulite growth, which would result in a non-uniform density within the spherulites, might be the cause of irregular crystallization seen in LDPE (Banks, et al. 1964; Maderek and Strobl 1983; Strobl, et al. 1983). Isothermal crystallization experiments were conducted on a similar grade but different batch of LDPE 1840H while simultaneously being analyzed by time-resolved small- and wide-angle X-ray scattering, revealing Avrami indexes of 2, 1.6, and 1.4 at temperatures 95, 98, and 100, respectively (Heeley, et al. 2014, 2015).

Table 3 Avrami parameters of LDPE 1840H and LDPE 3020D

Based on Table 3, it is observed that the Avrami index $n$ and growth function rate constant $k$ decrease with increasing crystallization temperature $T_{c}$. This indicates that the rate of nucleation and crystallization decreases with increasing crystallization temperature. The decrease in crystallization rate with increasing crystallization temperature is indicated in crystallization half-time $t_{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}}}$. Based on the comparison between the Avrami constant $k$ and crystallization half-time $t_{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}}}$ of LDPE 1840H and LDPE 3020D, it seems that the crystallization of LDPE 3020D is slightly faster than that of LDPE 1840H, which suggests that LDPE 3020D is less branched than LDPE 1840H (Gao, et al. 2016; Mandelkern 2004). The Avrami index $n$ cannot provide an accurate explanation of the crystallization mechanism of both LDPEs due to its branching.

Figure 5 shows excellent agreement between the isothermal crystallization data of (a) LDPE 1840H and (b) LDPE 3020D with predictions from the Avrami equation (Eq. (5)) based on the Avrami parameters given in Table 3. It is observed that all the characteristic sigmoidal isotherms shift to the right, i.e., to longer times, as the crystallization temperature increases and the crystallization rate is reduced.

Fig. 5

Relative volumetric transformed fraction $V_{c} (t)$ as a function of crystallization time $t - t_{0}$ for isothermal crystallization of a LDPE 1840H (open symbols) at different crystallization temperatures (103, 103.5, 104, and 104.5 °C) and LDPE 3020D (open symbols) at different crystallization temperatures (105, 105.5, 106, and 106.5 °C). The solid black line represents the Avrami fit (Eq. (5)). $t_{0}$ is the initial crystallization time

Morphology and dynamic mechanical analysis

DMA of polymers is mainly governed by two intrinsic (and correlated) properties: (i) the level of branching (long-chain branching (LCB) and short-chain branching (SCB)) and (ii) the degree of crystallinity (%crystallinity). In the case of polyethylene (PE), branching is defined as the ratio of methyl groups per 100 carbon atoms concerning the average length of side branches and number-average molar mass. The degree of crystallinity can be either estimated from the density of PE or, more accurately, computed from the DSC result using the enthalpy of melting and crystallization of polymer (Eq. (1)). The degree of crystallinity based on the density of PE proposed by Sperati et al. (1953) is as shown,

$$\rho=2.0\times10^{-3}\left(\%crystal\right)+0.803$$

(6)

where $\rho$ is the density of the PE. Table 4 reports the molecular characteristics, density, and the %crystallinity of LDPE 1840H and 3020D determined from both Eqs. (1) and (6). It can be observed that the crystallinity determined from the density of the samples agrees with the crystallinity determined from the DSC data in that LDPE 3020D has a higher degree of crystallinity as compared to LDPE 1840H.

Table 4 Molar mass (M_w), polydispersity index (M_w/M_n), degree of branching, density, and percentage crystallinity, $X_{c}$ (Eq. (1)) and $X_{{c,{\text{density}}}}$ (Eq. (6)) of LDPE 1840H and 3020D

The weight-average molar mass (M_w), polydispersity index (PDI), and degree of branching of LDPEs are shown in Table 4. The experimental data from gel permeation chromatography (GPC) indicate that LDPE 3020D has a higher molar mass, as compared to LDPE 1840H, with narrower molecular mass distribution (Figs. 6, 7 and 8; Table 4). Moreover, the calculated results from NMR testing demonstrate that LDPE 3020D is more branched than LDPE 1840H.

Fig. 6

Loss modulus and loss tangent of extruded LDPE 1840H (red line) and LDPE 3020D (blue line) measured by dynamic mechanical analysis at T =  − 150 to 100 °C and frequency of 1 Hz

Fig. 7

Storage modulus of extruded LDPE 1840H (red line) and LDPE 3020D (blue line) measured by dynamic mechanical analysis at T =  − 150 to 100 °C and frequency of 1 Hz

Fig. 8

Molecular weight distribution of extruded LDPE 1840H and 3020D samples

DMA investigates the variation of the following rheological properties as functions of temperature from sub-glass transition temperature (T < T_g) up to the melting points: storage modulus (aka resonant frequency (G')), loss modulus (aka mechanical loss (G")), and internal friction (aka damping factor, loss tangent ($\tan \delta = G\prime \prime /G\prime$)). Figure 6 shows the progress of the mechanical loss (i.e., damping) of LDPE samples as a function of temperature. The maximum testing temperature was fixed at 100 °C to prevent sagging at higher temperatures. Three dispersion regions are marked by the occurrence of damping peaks (in both $G\prime \prime$ and $\tan \delta$ curves), and each dispersion region is indicative of a stand-alone relaxation process. Relaxation/dispersion regions are specified (from high to low temperature) as α-relaxation ($0 \le T_{\alpha } \,[^\circ C] \approx 100$), β-relaxation ($- 92 \le T_{\beta } \,[^\circ C] \approx 0$), and γ-relaxation ($- 150 \le T_{\gamma } \,[^\circ C] \le - 92$) when the temperature range of each relaxation zone is estimated from the inflection points of curves after their peaks.

In γ-relaxation region (Fig. 6), damping peaks (peaks in $G\prime \prime$ and $\tan \delta$) of both samples occur at similar temperatures (− 135 °C for $G\prime \prime$ and − 128 °C for $\tan \delta$). However, the intensity (height) of the loss moduli peaks is markedly higher for LDPE 3020D (i.e., $7.44 \times 10^{7}$ Pa vs. $6.80 \times 10^{7}$ Pa). The occurrence of the γ-relaxation peak is apparent in semi-crystalline polymers and methacrylate esters. According to Hoff et al. (1955) and Kline et al. (1956), this relaxation region is governed by the motion of chain segments within the amorphous phase. As γ-relaxation region is also evident in linear PE, the aforementioned segmental chain motions occur on the backbone rather than the side chains (i.e., branch points do not show motion in this temperature range). Therefore, the extent and intensity of this relaxation region are inversely dependent on the degree of crystallinity of the polymer (i.e., the higher the degree of branching, the larger the amorphous phase). The reduction in the intensity of the damping peak in this region is due to the shortening of the range of relaxation times (i.e., increase in elasticity) because of the greater crystallinity (as favored by the linearity of chains) of polymers; in other words, damping behavior heightens with the expansion of amorphous phase. A competing theory on the origin of the γ-relaxation region was proposed by Hoffman et al. (1966) and Sinnott (1966), stating that γ-relaxation is controlled by defects (i.e., relaxation of loose ends) in the crystalline phase. Later, Khanna et al. (1985) postulated that in PE, the combination of reorientation of loose chain ends inside amorphous and crystalline phases as well as the motion of a short segment (i.e., crankshaft motion of 3 to 4 CH₂ groups inside amorphous phase (Khonakdar, et al. 2004)) is the origin of γ-relaxation. For instance, in the case of high-density PE (HDPE, linear), both storage and loss moduli show higher intensity in the γ-relaxation region, nonetheless, noticeable reduction in peak intensity (c.f. LDPE) along with an increase in peak temperature of the damping factor ($\tan \delta$) is indicative of higher crystallinity of HDPE (see Figs. 2 and 3 of Khanna et al. (1985) and Figs. 6 and 8 of Khonakdar et al. (2004)). As shown in Fig. 6, there is a small difference between the crystallinity of LDPE samples where the intensity of the damping factor of the 3020D sample is slightly higher than 1840H. The marginally higher %crystallinity observed in 3020D is following the study of crystallinity of samples via density and DSC analyses (see Table 4).

The γ-relaxation region is also the region of the glass transition (i.e., change of state from glassy to rubber-elasticity). In the glass transition region, the timescale of chain relaxation equates with that of deformation; hence, deformation (in the form of oscillation in DMA) is converted into internal friction (i.e., non-elastic deformation). Therefore, the loss modulus undergoes a sudden growth (i.e., peak) while the storage modulus shows a steep reduction (Fig. 7). Consequently, for our LDPE samples, the peak temperature in γ-relaxation (i.e., glass transition temperature (T_g)) is higher in damping factor in contrast to the loss modulus (i.e., $T_{{\gamma ,\,\tan \delta_{\max } }} = - 128^\circ C$ and $T_{{\gamma ,\,G\prime \prime_{\max } }} = - 135\,^\circ C$ in Fig. 6). As this subzero temperature is well below the reach of conventional DSC instruments, DMA is the only device capable of measuring the glass transition temperature of LDPE.

The onset of the β-relaxation ($- 92 \le T_{\beta } \,[^\circ C] \approx 0$) region is denoted by the gradual increase in the damping properties of LDPEs following the peak in γ-relaxation, and it continues until the inflection point following the peaks in damping factor and mechanical loss ($T \approx 0$). The intensity of the loss modulus peak is directly associated with the degree of branching (e.g., HDPE lacks a noticeable peak in this region (Khanna, et al. 1985)). Overall, β-relaxation occurs due to the diffusional motion of branch points of segments (on both backbones and arms) in the amorphous matrix (Kline, et al. 1956; Nielsen 1962; Stehling and Mandelkern 1970). It is worth mentioning that some studies consider the peak in this region as the glass transition peak of PE (Davis and Eby 1973; Kline, et al. 1956). In sum, as density and %crystallinity of polymers are inversely related to their degree of branching, the increase in branching results in an increase in the number of amorphous domains, resulting in more pronounced β-relaxation peaks. As shown in Fig. 6, peak temperatures of LDPEs are rather close ($T_{{\beta ,\,G\prime \prime_{\max } }} \approx - 26^\circ C$ and $T_{{\beta ,\,\tan \delta_{\max } }} \approx - 19\,^\circ C$ for 1840H and 3020D, respectively), whereas the higher intensity observed in the loss modulus of 1840H could indicate a higher degree of branching.

The α-relaxation ($0 \le T_{\alpha } \,[^\circ C] \approx 100$) is related to the mobilization of chains in the crystalline phase. It was shown that the temperature of α-relaxation peak ($T_{{\alpha ,\,G\prime \prime_{\max } }}$) in PE is correlated with the thickness of crystals when $T_{{\alpha ,\,G\prime \prime_{\max } }}$ starts from 20 °C (for lamellar thickness $l = 100\mathop {\text{A}}\limits^{ \circ }$) and plateaus at $l > 400\mathop {\text{A}}\limits^{ \circ }$, and $T_{{\alpha ,\,G\prime \prime_{\max } }} = 75^\circ C$ was predicted for infinite lamellar thickness (Khanna, et al. 1985). However, it has been shown that the crystalline structure per se is not governing the α-relaxation as this region is dependent on both crystalline and amorphous phases. Sinnott (1966) and Boyd (1979) showed that the motion of chain folds at crystal surfaces as well as the softening of the amorphous phase are in control of the α-relaxation; i.e., α-relaxation occurs due to the motion of interfacial chains between crystalline and amorphous phases. Moreover, it has been shown that the rate of cooling has a significant impact on the peak temperature of PE (see Table 4 of Khanna et al. (1985)), which is justifiable in the context of variation in the thickness of lamellae (i.e., change in crystallinity/density) due to cooling rates (i.e., quenching vs. slow cooling). According to the peak temperature of loss modulus illustrated in Fig. 6 (i.e., $T_{{\alpha ,\,G\prime \prime_{\max } }} :10\,^\circ C$) and the cited modeling of lamellar thickness and polymer density for PE, it is expected that LDPE samples of this study should possess lamellar thickness $l:50\mathop {\text{A}}\limits^{ \circ }$ and density $\rho :0.92$ g/cm³. The density of LDPE samples reported is in good agreement with the α-relaxation analysis of DMA data. Overall, deduced from the aforementioned relaxation regions, the minor increase in the damping behavior of LDPE 1840H is due to a marginally higher degree of branching and lower %crystallinity of this grade of LDPE.

The elasticity of the samples does not show a considerable variation in the testing temperature range where the storage modulus curve shows four elastic regions based on the inflection points of its corresponding curves (Fig. 7): (a) glassy region ($T \, < - 120^\circ C$), (b) transition region ($- 120^\circ C < T \, \le - 100\,^\circ C$), (c) rubbery region ($- 100^\circ C < T \, \le - 65\,^\circ C$), and (d) secondary transition region ($- 65^\circ C < T \, \le - 20^\circ C$). These results are very close to the LDPE grade LD00BW (density = 0.923 g/cm³) of Khonakdar et al. (2004).

Rheological characterization and modelling

The Hierarchical Multi-mode Molecular Stress Function (HMMSF) model for linear and LCB polymer melts implements the basic ideas of (i) hierarchical relaxation, (ii) dynamic dilution, (iii) interchain tube pressure, and (iv) convective constraint release (Narimissa, et al. 2015, 2016; Narimissa and Wagner 2016a, b, c). The HMMSF model represents a reduced number of well-defined constitutive relations comprising the rheology of both linear and LCB melts.

The extra stress tensor of the Hierarchical Multi-mode MSF (HMMSF) model is given as,

$$\sigma (t) = \sum\limits_{i} {\int\limits_{ - \infty }^{ + \infty } {\frac{{\partial G_{i} (t - t^{\prime})}}{\partial t^{\prime}}f_{i}^{2} (t,t^{\prime}){\mathbf{S}}_{DE}^{IA} (t,t^{\prime})dt^{\prime}} }$$

(7)

Here, ${\mathbf{S}}_{{{\text{DE}}}}^{{{\text{IA}}}}$ is the Doi and Edwards orientation tensor assuming an independent alignment (IA) of tube segments (Doi and Edwards 1986), which is five times the second-order orientation tensor S,

$$\mathrm S_{DE}^{IA}\;(t,t')=5\left\langle\frac{\mathrm u'\mathrm u'}{\mathrm u'^2}\right\rangle=5\mathrm S\left(t,t'\right)$$

(8)

u′ presents the length of the deformed unit vector u′, and the bracket denotes an average over an isotropic distribution of unit vectors at time t′, u(t′), which can be expressed as a surface integral over the unit sphere. The molecular stress functions $f_{i} = f_{i} (t,t\prime )$ are the inverse of the relative tube diameters a_i of each mode i,

$${f}_{i}\left(t,{t}^{\mathrm{^{\prime}}}\right)={a}_{i0}/{a}_{i}\left(t,{t}^{\mathrm{^{\prime}}}\right)$$

(9)

$f_{i} = f_{i} (t,t\prime )$ is a function of both the observation time t and the time of the creation of tube segments by reptation t’. The relaxation modulus G(t) of the melt is represented by discrete Maxwell modes with partial relaxation moduli $g_{i}$ and relaxation times $\tau_{i}$,

$$G(t) = \sum\limits_{j = 1}^{n} {G_{j} (t) = } \sum\limits_{j = 1}^{n} {g_{j} \exp ( - t/\tau_{j} )}$$

(10)

The mass fraction $w_{i}$ of dynamically diluted linear or LCB polymer segments with relaxation time $\tau_{i} > \tau_{D}$ is determined by considering the ratio of the relaxation modulus at a time $t = \tau_{i}$ to the dilution modulus $G_{D} = G(t = \tau_{D} )$,

$$\begin{gathered} w_{i}^{2} = \frac{{G(t = \tau_{i} )}}{{G_{D} }} = \frac{1}{{G_{D} }}\sum\limits_{j = 1}^{n} {g_{j} \exp ( - \tau_{i} /\tau_{j} )\,} \,\,\,\,\,\,{\text{for}}\,\,\,\tau_{i} > \tau_{D} \hfill \\ w_{i}^{2} = 1\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{\text{for}}\,\,\,\tau_{i} \le \tau_{D} \hfill \\ \end{gathered}$$

(11)

It is assumed that the value of $w_{i}$ obtained at $t = \tau_{i}$ can be attributed to the chain segments with relaxation time $\tau_{i}$. Segments with $\tau_{i} < \tau_{D}$ are considered to be permanently diluted, i.e., their weight fractions are fixed at $w_{i} = 1$. Although this may seem to be a very rough estimate, it was shown to be a sufficiently robust assumption to model the rheology of broadly distributed polymers, largely independent of the number of discrete Maxwell modes used to represent the relaxation modulus G(t) (Narimissa, et al. 2015). The evolution equation for the molecular stress function of each mode is expressed as (Narimissa, et al. 2015),

$$\frac{{\partial f_{i} }}{\partial t} = f_{i} ({\mathbf{K}}:{\mathbf{S}}) - \frac{1}{\alpha }(\frac{1}{{\tau_{i} }} + \beta CR)\,\left[ {(f_{i} - 1)(1 - \frac{2}{3}w_{i}^{2} ) + \frac{2}{9}f_{i}^{2} (f_{i}^{3} - 1)w_{i}^{2} } \right]$$

(12)

with the initial conditions $f_{i} (t = t\prime ,t) = 1$. The first term on the right-hand side represents the average affine stretch rate with ${\mathbf{K}}$ the velocity gradient tensor, the second term takes into account Rouse relaxation in the longitudinal direction of the tube, and the third term limits molecular stretch due to the interchain tube pressure in the lateral direction of a tube segment (Wagner, et al. 2005). The topological parameter $\alpha$ depends on the topology (chain architecture) of the melt, with

$$\begin{array}{cc}\alpha =1& \mathrm{for\,\,LCB\,\,melts}\\ \,\,\,\,\,\alpha =1/3& \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\mathrm{for\,\,polydisperse\,\,linear\,\,melts}\end{array}$$

(13)

CR represents a dissipative Constraint Release (CR) term in shear flow (Narimissa and Wagner 2016c) which is zero in extensional flow while in simple shear flow, CR is defined in terms of shear rate $\dot{\gamma }$ and normal components of the orientation tensor,

$$CR=\frac{1}{2}\sqrt{{\overline{\gamma }}^{2}\left|{S}_{11}-{S}_{22}\right|}$$

(14)

, and β is the numerical coefficient of the CR mechanism considered a fitting parameter (see Eq. 14 of (Narimissa and Wagner 2018)).

Figure 9 shows the mastercurve of storage $G\prime$ and loss moduli $G\prime \prime$ of LDPE 1840H and LDPE 3020D at T = 150 °C with the best fit (green lines) of $G\prime$ and $G\prime \prime$ (symbols) using the IRIS software (Winter and Mours 2006). The IRIS software (Winter and Mours 2006) was used to extract the relaxation spectrum from the data and to predict the linear viscoelastic behavior. From the relaxation spectrum, the zero-shear viscosity $\eta_{0} = \sum\limits_{i} {g_{i} \tau_{i} }$ and disengagement time $\tau_{d} = {{\sum\limits_{i} {g_{i} \tau_{i}^{2} } } \mathord{\left/ {\vphantom {{\sum\limits_{i} {g_{i} \tau_{i}^{2} } } {\sum\limits_{i} {g_{i} \tau_{i} } }}} \right. \kern-\nulldelimiterspace} {\sum\limits_{i} {g_{i} \tau_{i} } }}$ of the LDPEs were also calculated and are shown in Table 5. The horizontal shift factors obtained from multi-wave measurements that are used to determine the activation energy in Table 5 are shown in the Appendix.

Fig. 9

Storage (G') and loss (G") moduli of a LDPE 1840H and b LDPE 3020D at 150 °C. Continuous green lines represent fit by discrete relaxation spectrum (Eq. (10) and Table 5) using the IRIS software (Winter and Mours 2006)

Table 5 Discrete relaxation spectrum and zero-shear viscosity of LDPE 1840H and LDPE 3020D at T = 150 °C by us using the IRIS software (green lines), respectively

The multi-wave oscillation measurements were performed on a single sample at a specific temperature resulting in an overall time of approximately 10 min. A multi-wave oscillation is a superposition of the fundamental frequency with the harmonic frequencies that are integer multiples of the fundamental frequency. Therefore, the total time taken for a single multi-wave oscillation is reduced to the time needed for a measurement at the fundamental frequency. To minimize thermal and thermo-oxidative degradation of LDPE 1840H at high temperatures, measurements at each temperature were performed on a new sample. Whereas LDPE 3020 showed sufficient thermal stability for all the multi-wave measurements to be performed on a single sample. The effects of thermal and thermo-oxidative degradation on LDPE 1840H are further discussed in the Appendix.

$${\text{LCBI}} = 1 - \delta (G^{*} = 10^{4} {\text{Pa}})/90^\circ$$

(15)

From the mastercurve of storage G' and loss modulus G" of LDPE 1840 and LDPE 3020D at T = 150 °C, we used the IRIS software (Winter and Mours 2006) to construct van Gurp-Palman plots (vGP), i.e., loss angle $\delta$ as a function of complex modulus G^*, of the samples as illustrated in Fig. 10. Trinkle and coworkers (2001,2002) showed that polydispersity has an inverse relationship with the magnitude of the complex viscosity at δ = 60°. This inverse relationship suggests that the polydispersity of LDPE 1840H may be lower than LDPE 3020D (Fig. 10). The long-chain branching index (LCBI) is also determined from the vGP curves at $G^{*} = 10^{4} {\text{Pa}}$ for the samples, resulting in LCBI = 0.419 for LDPE 1840H and LCBI = 0.462 for LDPE 3020D. LCBI has been shown to correlate with the strain hardening behavior of linear PE in elongational flow (Poh, et al. 2021). The LCBI should be taken only as a rule-of-thumb rather than an accurate measure of branching. The LCBI is based on the relation reported by Garcia-Franco et al. (2008),

Fig. 10

van Gurp-Palmen plot for LDPE 1840H and LDPE 3020D at 150 °C produced by the IRIS software (Winter and Mours 2006) using storage (G') and loss (G") modulus data measured. Horizontal (dashed) and vertical (dashed-dotted) lines denote the complex modulus at δ = 60 (for PDI), and loss angle at G* = 10 kPa (for LCBI, Eq. (15))

Figure 11 shows the steady shear viscosity $\eta$ of LDPE 1840H and LDPE 3020D at T = 150 °C measured using parallel-plate (PP), cone-and-plate (CP), and cone-partitioned-plate (CPP) geometries with Carreau-Yasuda fitting using the IRIS software (Winter and Mours 2006). The steady shear viscosity $\eta$ measured was fitted with the Carreau-Yasuda model (Carreau 1972; Carreau, et al. 1997; Yasuda, et al. 1981) as expressed in the following equation:

$$\eta \left( {\dot{\gamma }} \right) = \frac{{\eta_{0} }}{{\left( {1 + \left( {\lambda \dot{\gamma }} \right)^{a} } \right)^{{{{(n - 1)} \mathord{\left/ {\vphantom {{(n - 1)} a}} \right. \kern-\nulldelimiterspace} a}}} }}$$

(16)

Fig. 11

Comparison between (open symbols) steady shear viscosity data ($\eta$) measured by parallel-plate (PP), cone-and-plate (CP), and cone-partitioned-plate (CPP) of a LDPE 1840H and b LDPE 3020D at 150 °C. Continuous red lines represent the fit by the Carreau-Yasuda model (Eq. (16)) using the IRIS software (Winter and Mours 2006)

The Carreau-Yasuda parameters and the disengagement time $\tau {}_{d}$-IRIS and zero-shear viscosity $\eta_{0}$-IRIS determined from the relaxation spectrum (using the IRIS software) are summarized in Table 6 of LDPE 1840H and LDPE 3020D at 150 °C. It is noted from the steady shear viscosity data that there is a vertical shift in the shear data measured by the cone-partition-plate geometry as compared to parallel-plate and cone-and-plate geometry for both LDPEs (Fig. 11; Table 6).

Table 6 Carreau-Yasuda parameters and disengagement time $\tau {}_{d}$ of LDPE1840H and LDPE3020D at 150 °C

Transient shear tests were performed in the strain rate range of 0.01 to 100 s⁻¹ for LDPE 1840H and 0.001 to 100 s⁻¹ for LDPE 3020D at 150 °C. We note that the first normal stress growth coefficient $\psi_{1}^{ + } (t)$ at strain rates of 0.01 and 0.05 s⁻¹ for LDPE 1840H and 0.001 to 0.01 s⁻¹ for LDPE 3020D (at T = 150 °C) are removed due to normal force transducer limitations resulting in the data being overly scattered. Transient shear viscosity data of LDPE 1840H at T = 150 °C (Fig. 12) shows that steady-state was achieved at all strain rates with no signs of edge fracture while the transient shear data of LDPE 3020D (Fig. 13) at T = 150 °C show signs of edge fracture at strain rates 50 and 100 s⁻¹. We note that the first normal stress difference data of LDPE 3020D at T = 150 °C (Fig. 13b) from strain rates 5 to 100 s⁻¹ has not yet reached steady-state as it has reached the maximum allowable normal force (20 N) of the rheometer. Nonetheless, this would not affect the viscosity measurements as the equation for shear stress does not involve axial force (Macosko and Larson 1994), and it is still well within the maximum torque of the rheometer.

Fig. 12

Comparison between predictions (lines) of the HMMSF model (Eqs. (7) and (12)) with $G_{D} = {\text{ 10,000 Pa}}$ and $\beta = 0.2$ and a shear stress growth coefficient $\eta^{ + } (t)$ data and b first normal stress growth coefficient $\psi_{1}^{ + } (t)$ data of LDPE 1840H at 150 °C. The predictions of higher rates are horizontally shifted in time: (a by a factor of 1.2, 1.5, 1.9, and 2.1 for shear rates 10, 25, 50, and 100 s⁻¹, respectively; b by a factor of 1.2, 1.5, 2, 2.5, 3, and 4 for shear rates 1, 5, 10, 25, 50, and 100 s⁻¹, respectively) to mimic the experimental delay of the stress signal due to limited stiffness of the rheometer

Fig. 13

Comparison between predictions (lines) of the HMMSF model (Eqs. (7) and (12) with $G_{D} = {\text{ 5000 Pa}}$ and $\beta = 0.5$ and a shear stress growth coefficient $\eta^{ + } (t)$ and b first normal stress growth coefficient $\psi_{1}^{ + } (t)$ of LDPE 3020D at 150 °C. The predictions of higher rates are horizontally shifted in time: (a by a factor of 1.3, 1.5, 1.8, 2, and 2.3 for shear rates 5, 10, 25, 50, and 100 s⁻¹, respectively; b by a factor of 1.3, 1.5, 2, 3, and 4 and for shear rates 5, 10, 25, 50, and 100 s⁻¹, respectively) to mimic the experimental delay of the stress signal due to limited stiffness of the rheometer

Figure 12 shows the predictions of growth coefficients of shear stress and normal stress of LDPE 1840H (at T = 150 °C) by the HMMSF model (Eqs. (7) and (12) with $G_{D} = {\text{ 10,000 Pa}}$ and $\beta = 0.2$. The dilution modulus $G_{D}$ was fitted based on the relaxation spectrum and extensional flow data of LDPE 1840H (at T = 150 °C) measured by VADER1000 which would be presented in future studies on the extensional flow measurements of the LDPE. The model is in quantitative agreement with the shear stress growth coefficient $\eta^{ + } (t)$ data (Fig. 12a); however, the model slightly over-predicts the shear viscosity particularly at higher strain rates ($10 - 100{\text{s}}^{ - 1}$). Additionally, the model can predict the occurrence of very weak maxima at low shear rates ($0.5{\text{ and 1}}{\text{s}}^{ - 1}$) and significant maxima at high shear rates ($5 - 100{\text{s}}^{ - 1}$) in the shear stress growth coefficient $\eta^{ + } (t)$ data. The observed experimental delays in the rise time of the normal stress growth coefficient $\psi_{1}^{ + } (t)$ signals are due to the limited stiffness of the instrument, which causes radial inflow of the melt (Meissner 1972; Narimissa and Wagner 2016c). Therefore, in Fig. 12, the predictions of the model were horizontally shifted at high shear rates in time to mimic the experimental delays of the instrument. The predictions for the first normal stress growth coefficient $\psi_{1}^{ + } (t)$ (Fig. 12b) demonstrate quantitative disagreements with the HMMSF model where the model under-predicts the data at all shear rates. It was shown that the apparent normal force measured by the transducer using a cone-partitioned plate is dependent on the sample radii (Schweizer 2003). Moreover, the sample radii (> 15 mm after compression) used in transient shear experiments are much smaller than the bottom plate of the cone-partitioned plate (25 mm), so it can be a challenge to get the sample positioned in the center of the geometry. This can be overcome by extracting the first normal stress different from a series of measurements with different sample radii at each shear rate and Eq. (7) of Schweizer (2003).

Figure 13 shows the predictions of growth coefficients of shear stress and normal stress of LDPE 3020D (at T = 150 °C) by the HMMSF model (Eqs. (7) and (12) with $G_{D} = {\text{ 5000 Pa}}$ and $\beta = 0.5$. The predictions were fitted based on the dilution modulus $G_{D}$ of LDPE 3020D found in Wagner et al. (2022). The model is in quantitative agreement with the shear stress growth coefficient $\eta^{ + } (t)$ data for all the strain rates (Fig. 13a); however, we note that the shear stress growth coefficient $\eta^{ + } (t)$ data for strain rates ($5 - 100{\text{s}}^{ - 1}$) have not yet reach steady state due to normal force limits. Despite reaching the maximum allowable normal force of the rheometer, the shear viscosity measured for shear rates $5 - {100}{\text{s}}^{ - 1}$ still shows qualitative agreement with the predictions of the HMMSF model. Similar experimental delays due to the limited stiffness of the instrument are observed in the transient shear data, therefore, in Fig. 13, the predictions of the model were horizontally shifted at high shear rates in time to mimic the experimental delays of the instrument. Despite the edge fracture of the transient shear data of LDPE 3020D at strain rates $50{\text{ and 100}}{\text{s}}^{ - 1}$, the predictions show good agreement with the maxima of experimental data before edge fracture. The predictions for the first normal stress growth coefficient $\psi_{1}^{ + } (t)$ (Fig. 13b) demonstrate quantitative disagreements with the HMMSF model where the model under-predicts the data at shear rates from 0.05 to 1 s⁻¹. For shear rates $5 - {100}{\text{s}}^{ - 1}$ (Fig. 13b), the disagreement between the model and normal stress data of LDPE 3020D at T = 150 °C is likely caused by the rheometer reaching its maximum allowable normal force (20 N) and apparent normal force measured by the transducer using a cone-partitioned-plate is dependent on the sample radii (Schweizer 2003).

Figure 14 demonstrates the predictions of steady shear viscosity data $\eta$ of LDPE 1840H at 150 °C using HMMSF with $G_{D} = {\text{ 10,000 Pa}}$ (Fig. 13a) and $\beta = 0.2$ and LDPE 3020D at 150 °C using HMMSF with $G_{D} = {\text{ 5000 Pa}}$ and $\beta = 0.5$ (Fig. 14b). The model is in quantitative agreement with the steady shear viscosity data $\eta$ measured for both LDPEs using various configurations of parallel-plate, cone-and-plate, and cone-partitioned-plate geometry, determined from either steady-state or transient shear measurements. For the PP and CP geometries, the steady-state shear viscosity measurements for LDPE 1840H are limited to a shear rate of 10 s⁻¹ due to edge fracture. Steady shear viscosity measurements of LDPE3020D at 150 °C using PP and CP geometry are limited to a shear rate of 3.98 and 1 s⁻¹, respectively, due to the measurements reaching the maximum normal force of the transducer. The safety protocol of the rheometer will end the experiment when it reaches the maximum normal force limit, and a smaller geometry can be used to increase the shear rate range as seen in the CPP measurements. In Fig. 14a, the predicted zero shear viscosity $\eta_{0}$ of LDPE 1840H at 150 °C from the HMMSF model matches well with the measurements from all geometries while at higher shear rates of $5 - {100}{\text{s}}^{ - 1}$ the predictions fit better with the measurements from the cone-partitioned plate. In Fig. 14b, the HMMSF model matches well with shear viscosity $\eta$ measurements of LDPE 3020D at 150 °C using all geometries while at higher shear rates of $5 - {100}{\text{s}}^{ - 1}$, the predictions fit better with the measurements from cone-partitioned-plate. Shear viscosity $\eta$ measurements of LDPE 3020D at 150 °C show that zero shear viscosity $\eta_{0}$ lies after shear rates of $0.01{\text{s}}^{ - 1}$, whereas predictions by HMMSF indicates that the zero shear viscosity $\eta_{0}$ lies in much lower shear rate regions. However, it is important to note that accurate zero-shear viscosity $\eta_{0}$ measurements by the rheometer at low shear rates are challenging due to the limited minimum torque range and torque resolution of the transducer.

Fig. 14

Comparisons between (open symbols) steady shear viscosity data $\eta$ measured by parallel plate (PP), cone and plate (CP), cone-partitioned plate (CPP), and steady-state regions of transient shear viscosity data measured by cone-partitioned plate (CPP-transient) with steady shear viscosity predictions (continuous line) of HMMSF model (Eqs. (7) and (12) of a LDPE 1840H with $G_{D} = {\text{ 10,000 Pa}}$ and $\beta = 0.2$ and b LDPE 3020D with $G_{D} = {\text{ 5000 Pa}}$ and $\beta = 0.5$ at 150 °C using the IRIS software (Winter and Mours 2006)

Figure 15 demonstrates the predictions of the first normal stress coefficient data $\psi_{1}$ of (a) LDPE 1840H at 150 °C using HMMSF with $G_{D} = {\text{ 10,000 Pa}}$ and $\beta = 0.2$, and (b) LDPE 3020D at 150 °C using HMMSF with $G_{D} = {\text{ 5000 Pa}}$ and $\beta = 0.5$. The model is in qualitative agreement with the first normal stress coefficient data, $\psi_{1}$ data measured for both LDPEs using various configurations of parallel-plate, cone-and-plate, and cone-partitioned-plate geometry, determined from either steady-state or transient shear measurements. The rheometer struggles to provide good measurements for the first normal stress coefficient at shear rates > 0.5 s⁻¹ due to the limited normal force range and force resolution of the transducer (Figs. 15a and b). Despite reaching the maximum allowable normal force of the rheometer for shear rates (5 to 100 s⁻¹), Fig. 15, the first normal stress coefficient data shows good agreement with the predictions from HMMSF of LDPE 3020D at 150 °C with $G_{D} = {\text{ 5000 Pa}}$ and $\beta = 0.5$ (Fig. 15b). Further investigations of the time delay seen in the first normal stress growth coefficient $\psi_{1}^{ + } (t)$ of both LDPEs and testing below the maximum allowable normal force of the instrument will be performed in an upcoming study.

Fig. 15

Comparisons between (open symbols) first normal stress coefficient $\psi_{1}$ measured by parallel plate (PP), cone and plate (CP), cone-partitioned plate (CPP), and steady-state region of the first normal stress growth coefficient by cone-partitioned plate (CPP-transient) with the first normal stress coefficient predictions (continuous line) of HMMSF model (Eqs. (7) and (12)) of a LDPE 1840H with $G_{D} = {\text{ 10,000 Pa}}$ and $\beta = 0.2$ and b LDPE 3020D with $G_{D} = {\text{ 5000 Pa}}$ and $\beta = 0.5$ at 150 °C using the IRIS software (Winter and Mours 2006)

1.1. 5.1 A note on LDPE characterization

Incongruities seen between direct (via NMR and GPC) and indirect (via thermal and rheological methods) analyses of branching and dispersity are explicable by the fact that NMR only measures the number of methyl groups regardless of the type of branching; hence, it does not discriminate between SCB and LCB. Also, LCB can have different topologies, e.g., “comb,” “H,” or “tree.” The level of branching (LCB vs. SCB) and topology of the chain leads to different effects in different characterization techniques. For instance, %crystallinity (Eqs. 1 and 6) depends on SCB, LCB, and PDI (i.e., higher PDI means more chain ends, which reduces crystallinity). Thus, a polymer like LDPE 1840H can show stronger strain hardening during extensional flow, which indicates higher LCB, but it may also be affected by larger PDI (i.e., higher dynamic dilution), which is in agreement with the dilution moduli of 1840H vs. 3020D (10,000 Pa and 5,000 Pa, respectively). As indicated by DMA analyses, LDPE 1840H shows slightly lower crystallinity than 3020D due to higher degree of branching and higher PDI (shorter molecules act as softeners). Although the LCBI method (Eq. 15) is merely a rule of thumb (see (Poh, et al. 2021)), it is still in agreement with the NMR results. Alternatively, Trinkle et al. (2002) method of investigating the PDI (refer to Fig. 10) is only valid for similar topologies, which is not the case here. In summary, all analytical results are important for characterization and have to be considered together rather than independently, as, for instance, the rheology of polymers is affected by the combination of branching, topology, and PDI.

Conclusion

In the present study, a comprehensive investigation of the thermal, morphology, mechanical, and shear rheological properties of two industrial-grade LDPEs was conducted using various methods such as isothermal crystallization, gel permeation chromatography, nuclear magnetic resonance, dynamic mechanical analysis, multi-wave oscillatory, steady-state, and transient shear measurements. The crystallization kinetics of the LDPEs revealed similar conclusions as other studies that the Avrami method is not suitable in clarifying the crystallization mechanism of branched polyethylene. According to Gao et al. (2016), a decrease in crystallinity of LDPE is correlated to an increase in branching content. This coincides with our DMA and DSC experiments where the lower density and crystallinity of LDPE 1840H showed a more pronounced β-relaxation peaks due to the increase in the number of amorphous domains caused by a higher degree of branching as compared to LDPE 3020D.

We also present the successful use of multi-wave oscillation to characterize the linear viscoelastic properties of two industrial-grade low-density polyethylene melts. The method significantly reduced experimental time as compared to conventional SAOS methods. The steady-state and transient shear data of LDPE 1840H and LDPE 3020D were also measured by parallel-plate, cone-and-plate, and CPP shear rheometry. The HMMSF model was applied to predict the steady-state and transient shear stress growth data of LDPEs (1840H and 3020D) using the linear viscoelastic properties characterized by multi-wave oscillation. We also discuss the stress growth data of the first normal stress coefficient as measured by cone-partitioned-plate rheometry up to high shear rates of 100 s⁻¹, thereby capturing data with maxima in the high shear flow of LDPE. The transient experimental results of LDPE 3020D at 150 °C showed the limitations of ARES-G2 with CPP geometry in measuring the first normal stress growth coefficient at shear rate > 5 s⁻¹ due to the maximum allowable normal force (20 N). The acceptable shear rate range of CPP geometry is very much dependent on the viscosity of the sample, as seen by LDPE 1840H at 150 °C failing to provide good measurements at shear rates of < 0.01 s⁻¹ and > 5 s⁻¹ for LDPE 3020D at 150 °C. The HMMSF model, with two nonlinear material parameters, namely the dilution modulus $G_{D}$ and constraint release parameter $\beta$, shows excellent agreement within experimental accuracy between predictions by the HMMSF model and shear rheological properties of the tested LDPEs for a wide range of shear rates.

Appendix

Figure 

Fig. 16

Storage (G') and loss (G") modulus as well as loss tangent of two extruded LDPE 1840H samples measured by dynamic mechanical analysis at T =  − 150 to 100 °C and frequency of 1 Hz

16,

Fig. 17

Storage (G') and loss (G") modulus as well as loss tangent of two extruded LDPE 3020D samples measured by dynamic mechanical analysis at T =  − 150 to 100 °C and frequency of 1 Hz Fig 16 and 17 show the storage and loss moduli as well as the damping factor of two specimens of LDPE 1840H and 3020D samples in the temperature range of $T = - 150\,\,{\text{to}}\,\,100^\circ \,C$ at oscillation frequency $1\,{\text{Hz}}$. As shown in Figs. 16 and 17, DMA data show a satisfactory reproducibility for both samples

17,

Fig. 18

Activation energy plots for linear viscoelastic small amplitude oscillatory shear measurements of a LDPE 1840H and b LDPE 3020D. Continuous green lines represent the Arrhenius fit using the IRIS software (Winter and Mours 2006) The activation energy shown in Table 5 is determined from the horizontal shift factors obtained from multi-wave measurements (Fig. 8).

18 and

Fig. 19

Storage (G') and loss (G") moduli of conventional SAOS measurement (square symbol), single sample multi-wave measurement (triangle symbol), and multiple sample multi-wave measurement (circle symbol) of a LDPE 1840H and b LDPE 3020D at a reference temperature of 150 °C. The effects of thermal and thermos-oxidative degradation during the consecutive multi-wave experiment at temperatures of 150, 170, 190, 210, and 230 °C on a single LDPE 1840H sample resulted in the shortening of the lowest frequency range as compared to using a fresh sample for each multi-wave measurement (Fig. 19a). The extended lowest frequency resulted in a longer relaxation time which would improve the predictions from the HMMSF model. LDPE 3020D showed better thermal and thermo-oxidative stability and did not require a fresh sample for each multi-wave measurement at each temperature (Fig. 19b)

19