On the glass transition and correlation functions

Abstract

Correlation functions are the basis for the understanding of many thermodynamic systems that can be directly observed by scattering experiments. In this manuscript, the correlation functions include the steric repulsion of atoms that also leads to distinct shells of neighbors. A free energy is derived on the basis of these assumptions, and in the following the temperature dependence of the density (or specific volume), the typical time scale of the α-relaxation, and the heat capacity. From this, I argue that the glass transition is dominated by the vicinity of a first-order phase transition. While the correlation length stays rather constant in the vicinity of the glass transition, the intensity of the fluctuations is considerably increasing. The scattering amplitude is connected to the cluster size, also introduced in the cooperativity argument. Additionally, correlations of loops are discussed. The additional correlations describe rather small structures. Applying this to scattering intensities, a correlation peak was described that may be connected to the “Boson Peak” or a “cooperativity length.” The new concept of correlation functions on sterically repulsive atoms may find more attention in the wider field of physics.

Introduction

The glass transition has been investigated and discussed over many decades with the result of clear experimental temperature dependencies of the specific volume, the typical time scale of the α-relaxation, and the heat capacity [1, 2] to show either steeper steps, divergencies, or peaks at the glass transition temperature. However, the exact physical meaning of all these observations was left partially unclear such that different authors even contradict each other [3].

Classically, the time scale t of the α-relaxation measured by dielectric spectroscopy or as a viscosity $\eta \sim t$ was empirically described by the Vogel-Fulcher equation [4, 5] as given by:

$$ t=t_{\infty} \exp \left[ \frac{DT_{0}}{T-T_{0}} \right] $$

(1)

The high temperature limit of the time scale is $t_{\infty }$, D is a constant, and T₀ is the Vogel-Fulcher temperature that points towards the glass transition temperature. D is also called the “fragility” parameter [6] that is connected to the degree of deviation from the pure Arrhenius behavior:

$$ t=t_{\infty} \exp \left[ \frac{E_{A}}{k_{B}T} \right] $$

(2)

with E_A being the activation energy and k_B being the Boltzmann constant. Usually, the Vogel-Fulcher temperature T₀ is found approx. 40K below the glass transition temperature T_g. It should be stressed that the glass transition is a thermo-kinetic phenomenon, which means that around T_g and below most observations are dominated by extremely slow processes and the equilibrium is rarely reached.

The scenario becomes even more complicated by the view of Tanaka [7], who argues that most glassy systems deal with two-order parameters: One is connected to the particle density as the most important and most obvious order parameter. The other one is introduced as a directional order parameter which is connected to the molecular anisotropy. For polymers, these fluctuations are connected to the Fischer renormalized behavior [8] (and references herein). While spin glasses are dominated by the directional order parameter, classical colloidal suspensions and simple metals are dominated by the order parameter of the density.

A dynamic model for colloidal suspensions has been developed quite far recently [9]. Astonishingly, hydrodynamic interactions were neglected; thus, the model would be applicable for a wide range of systems. Currently, rheological measurements on aging and creep are in the focus of colloidal glasses [10, 11].

Here, I offer a model free energy that should help to better understand the experimental observations, and therefore is able to go a little deeper consistently within the model. This model considers only density fluctuations, and neglects any directional order parameter. Furthermore, it is less heuristic than free volume models [12] that successfully capture most of the features of the glass transition similarly well. There also exists a lattice theory [13, 14] that captures aspects of density fluctuations through the free volume and aspects of directed bonds, but which stays at a finite expansion level. The important difference of the newly introduced model is the correlation function that covers the steric repulsion of atoms and introduces distinct neighboring shells. I also discuss limits of my model, and accidently came to a motivation of the “Boson Peak” observed in [15] as a matter of the steric repulsions.

Theory

I start with a classical Hamiltonian for a number of N identical particles that interact with each other via a single pair potential V (Δr):

$$ H = T + \underset{i\neq j}{\sum}{V(\mathbf{r}_{i} - \mathbf{r}_{j})} $$

(3)

The kinetic energy T is only needed later for the entropy and heat capacity, and is not of interest for most of the considerations. The partition function of the interactions will then read:

$$ \begin{array}{@{}rcl@{}} Z_{\text{int}} = {\int}_{V} \cdots {\int}_{V} d^{3N} r_{1} \cdots r_{N} \exp \left( -\beta \underset{i\neq j}{\sum}{V(\mathbf{r}_{i} - \mathbf{r}_{j})} \right. \\ \left. -\frac{\beta\mu}{N} \sum\limits_{i,j=1}^{N}{\int d^{3}{\Delta} r \delta(\mathbf{r}_{i}-\mathbf{r}_{j}-{\Delta}\mathbf{r})} \right) \end{array} $$

(4)

Note that the volume V without an argument appears in the limits of the integral. I introduced the chemical potential that I will need later for the grand canonical partition. The potential that is normalized by the thermal energy β^− 1 = k_BT can be split in a short range repulsive and an attractive term of a little longer range, which is usually considerably strong for next neighbors.

$$ \beta V({\Delta}\mathbf{r}) = v_{\text{rep}}({\Delta}\mathbf{r}) + v_{\text{attr}}({\Delta}\mathbf{r}) $$

(5)

The complete repulsive energy is expressed by $\epsilon _{\text {rep}}= {\int \limits } d^{3}r$v_rep(r)/v₀ and normalized by the thermal energy β^− 1. The repulsive term reserves a spherical volume of v₀ = πd³/6 for each particle of diameter d, because the repulsive energy 𝜖_rep takes large values (in A.1, I am more precise and replace v₀ by v_lattice). The attractive potential has a minimum $\min \limits (v_{\text {attr}}) = \epsilon$ that is equally normalized by the thermal energy, and will be used later. I assume that the minimum is taken at the distance d, i.e., v_attr(|r| = d) = 𝜖. In the following, I will understand the theory in terms of a hybrid between a lattice and a continuous theory: The repulsive interaction will reserve distinguished compartments of volume v₀ where only one particle can be present. So, nearest particles build up a lattice if they come close to each other. On the other hand, I treat the parameter r still as a continuous parameter that especially over large distances does not take discrete values anymore. The only important parameter of the potential will be the next neighbor interaction 𝜖 and is the only energetic parameter of interest. This distinction between 𝜖_rep and 𝜖 is not made by most lattice theories, while here I argue that the repulsive term reserves the particle volume and practically is not probed anymore by other particles while the next neighbor interaction is the essential parameter which is probed by neighboring particles. We will see below that our entropic term serves for avoiding highest densities while classical lattice theories achieve the finite compressibility also by choosing rather high repulsive interaction parameters that are included in the overall interaction.

The term with the chemical potential can be expanded as follows:

$$ \begin{array}{@{}rcl@{}} &&\left\langle \exp \left( -\frac{\beta\mu}{N} \sum\limits_{i,j=1}^{N}{\int d^{3}{\Delta} r \delta(\mathbf{r}_{i}-\mathbf{r}_{j}-{\Delta}\mathbf{r})} \right) \right\rangle = \\ &&\left\langle 1 -\frac{\beta\mu}{N} \sum\limits_{i,j=1}^{N}{\int d^{3}{\Delta} r \delta(\mathbf{r}_{i}-\mathbf{r}_{j}-{\Delta}\mathbf{r})} \right. \\ && +\frac{1}{2!}\frac{\beta^{2}\mu^{2}}{N^{2}} \underset{i,j,k,l}{\sum}{\int d^{6}{\Delta} r_{1}{\Delta} r_{2} \cdot} \\ &&\qquad\qquad\qquad\qquad\cdot \delta(\mathbf{r}_{i}-\mathbf{r}_{j}-{\Delta}\mathbf{r}_{1}) \delta(\mathbf{r}_{k}-\mathbf{r}_{l}-{\Delta}\mathbf{r}_{2}) \\ &&\left. -\frac{1}{3!}\frac{\beta^{3}\mu^{3}}{N^{3}} \underset{i,j,k,l,m,n}{\sum}{\int d^{9}{\Delta} r_{1}{\Delta} r_{2}{\Delta} r_{3}\cdots} \right\rangle \end{array} $$

(6)

This expansion is understood in terms of a small chemical potential μ, but the limits arise from other reasons as discussed later. To some extent, this assumption can be seen in parallel to a fugacity f expansion with $f=\exp (-\beta \mu )$ being close to 1, but being applied to the Gibbs’ free energy [16, 17]. In this context, I used the angled brackets to indicate the canonical integral with the thermodynamic weight of the original interaction term. This in particular includes the repulsive term that avoids two particles being at the same origin, and the next neighbor interactions. The different lines of Eq. 6 indicate correlation functions with different degrees. The first line introduces the 2-point correlation function, the next line a 4-point correlation function, and so on. By integrating over all possible particle positions r_i, there are no open ends that can be parameterized, and so only closed loops are considered.

Now, I will factorize the partition function of the above expression in the following simple manner:

$$ \begin{array}{@{}rcl@{}} Z_{\text{int}}&=& \left[ V (1 -\phi) \exp(-\epsilon\frac{z}{2}\phi^{2}) \right]^{N} {\sum}_{l=0}^{\infty}{\frac{1}{l!} (-\beta\mu N \left\langle\varPhi\right\rangle )^{l}} \\ &=& \left[ V (1 -\phi) \exp(-\epsilon\frac{z}{2}\phi^{2}) \exp(-\beta\mu\left\langle\varPhi\right\rangle ) \right]^{N} \end{array} $$

(7)

The first two terms in the bracket arise from the mean field entropy $S/N\sim k_{B}\ln (V(1-\phi ))$ of one component with unoccupied volume (I define ϕ = Nv₀/V). These terms are basically connected to the translational entropy of the particles, but they differ from classical lattice theories which would obtain an expression like V (1 − ϕ)^{1 − 1/ϕ}. The lattice entropy takes the value zero for the density 1, because the discrete packing of particles has only one solution. In my approach, I assumed continuous variables for the particle position, and this results in high entropic pressures due to the confinement. This approach becomes incorrect in the limit of highest densities 1 or extremely high pressures or temperatures towards zero, where quantum mechanical effects would yield a countable number of states and finally lead to a finite entropy that then can be defined as zero. The third factor of Eq. 7 in the bracket represents a mean field expression of the next neighbor interactions (with the coordination number z = 12).

The factorization of the individual correlation functions is not exact, because various indices might take the same values which would complicate the correlation function. First of all, the frequency of indices being different is quite high, especially for the lower degrees of correlation functions. Second, the correlations that are represented by open graphs (Fig. 1) reduce to exactly the factorization, because the order of integrals can be chosen in this way that the graphs are stripped from the outer regions to the inner regions, and each time the exact factor Φ appears. So the exactness of this calculation is only corrupted by closed loops (see A.2). The portion of graphs with closed loops is always low compared with the open graphs, especially for the low degrees of correlations. Another flaw might be that at high degrees of connectivity the actually distinguished number of different paths is limited to the coordination number. Again, this bulkiness effect will eventually need corrections at high degrees of correlations, which can be safely neglected here. So within the considerations of this manuscript, the abovementioned approximation is good, and assumed to be quite precise.

Fig. 1

A selection of open graphs showing the possibility of connectivity. None of them violates the factorization of the corresponding correlation function, because the order of integration allows for stripping the graphs sequentially

The derived correlation function is understood as the following: I consider a chain of particles covering the distance Δr. From this chain, I get a contribution α = ϕ ⋅ (−𝜖) for each particle in the chain accounting for the probability and the energetic contribution of the next neighbors. At this point, the probability α is treated in the sense of classical lattice theories. An energy renormalization to the average contact energy would refine the term α = ϕ ⋅ (−𝜖 + ϕ𝜖) = ϕ(1 − ϕ)(−𝜖). At this point, the correlation function counts additional correlations that are not covered by the mean field expression $\epsilon \frac {z}{2}\phi ^{2}$ of Eq. 7. This correlation function would read then:

$$ \varPhi({\Delta}\mathbf{r}) = \alpha^{n} \quad\text{with}\quad n=g|{\Delta}\mathbf{r}|/d $$

(8)

The factor g takes the possibility for wrinkled paths into account, but still is of the order of unity. The overall estimate is then given by:

$$ \langle \varPhi({\Delta}\mathbf{r}) \rangle = 1+\gamma\cdot\frac{\alpha(1+\alpha)}{(1-\alpha)^{3}} $$

(9)

While Φ(Δr) ⋅〈ϕ〉 = 〈ϕ(r₁)ϕ(r₁ + Δr)〉 is a classical van Hove correlation function [18] of the particle density ϕ (except for the factor of the mean density ϕ = 〈ϕ〉), the integral $\langle \varPhi ({\Delta }\mathbf {r}) \rangle := \int \limits \varPhi (\mathbf {r})d^{3}r$ tells about the cooperativity of correlations. I include every coordination number effect in the prefactor γ including the wrinkledness of the paths. It lies in the range of $\gamma =\sqrt {2}\pi =4.4$ and $\pi \sqrt {27/2}=11.5\approx z$ for simple cubic and hexagonal-packed lattices. Finally, we will see below that the exact number does not play a major role. Apart from the discussion about the coordination number, the explicit presence of the particle at the origin is added to this correlation function. This central particle is always considered, because the original sum of Eq. 6 considers equal indices i,j explicitly. This correlation function describes the cluster size with respect to the average particle density, so to speak the size of enrichments with respect to the background. For the grand canonical partition function, I still need to sum up all possible particle numbers, and so I obtain:

$$ Z_{\text{gc}} = \sum\limits_{N=0}^{\infty}{ Z_{\text{int}}} = \left[ 1 -\frac{V}{V_{0}}(1 -\phi)\exp(-\epsilon\frac{z}{2}\phi^{2} -\beta\mu\langle\varPhi\rangle)\right]^{-1} $$

(10)

The reference volume V₀ is introduced to obtain dimensionless numbers in the partition function. It appears as a constant for derivatives and is set to V at the end of calculations. All of this also guarantees that the abovementioned sum converges to finite numbers. From this, I do the transformation back to obtain the free energy with the parameters T, V, and N (with leading terms only):

$$ F=-k_{B}T\cdot\frac{N}{\langle\varPhi\rangle}\left[\ln\left( \frac{V}{V_{0}}(1 -\phi)\right)-\epsilon\frac{z}{2}\phi^{2}\right] $$

(11)

This free energy basically looks like a mean field expression of interacting particles. But the number of particles appearing in the expression is now divided by the cluster size 〈Φ〉 to yield the effective number of particles. From this, I obtain the equation of state:

$$ -p-\frac{\partial F}{\partial V} = 0 = $$

(12)

$$ -\tilde{p}\langle\varPhi\rangle +\frac{\phi}{1-\phi} +\epsilon z \phi^{3} -\phi^{2}\frac{\partial\ln\langle\varPhi\rangle}{\partial\phi}\left[\ln(1 - \phi) - \epsilon\frac{z}{2}\phi^{2}\right] $$

(13)

Here the scaled pressure is $\tilde {p}=pv_{0}/k_{B}T$. This enables us to calculate the particle density as a function of the scaled parameters $\tilde p$ and 𝜖 (see also Fig. 2). As all of the parameters scale with the reciprocal temperature τ^− 1, I can write $\tilde {p}=\tilde {p}_{0}/\tau$ and 𝜖 = 𝜖₀/τ. This basically leaves the interesting parameter space to be around unity for the considered parameters.

Fig. 2

The equation of state for the parameters 𝜖 = − 0.4 (solid line), − 0.5 (dashed), and − 0.6 (dotted). The other parameters were p = 0.05 and γ = 11.5 (z = 12). One can see that a single state is well defined for smaller neighbor interactions, while for larger interactions phase separation occurs. The interactions for stable phases are indicated by the arrows

An example for such calculations is shown in Fig. 3. The particle density goes up steadily until τ^− 1 ≈ 1.5, where a steeper increase is found. We can see that in this example the increase becomes steeper with higher 𝜖₀. As we will see, this property correlates with the fragility of the glass. For even higher τ^− 1, the density saturates. This overall behavior is well known for the specific volume, which is V/N = v₀/ϕ. I believe that the theory is closer to the observations on the heating cycle compared with the cooling cycle, because cooling towards the glassy state deals with stronger changes in the configuration.

Fig. 3

The particle density as a function of the scaled temperature. The common parameters are $\tilde p_{0}=0.1$ and γ = 11.5 (z = 12). The attractive nearest neighbor interaction 𝜖₀ was − 0.28 (solid line), − 0.25 (dashed), − 0.20 (dotted), and − 0.15 (thin solid)

From the concept of cooperativity [19], a basic equation was derived for the characteristic time t involved in the α-process of the glass-forming system [2, 3, 20, 21]. I finally use the specific entropy of the clusters that were explicitly well explained in [20]:

$$ \ln t = \left( \frac{a}{T\cdot S_{\text{conf}}} \right)^{x} $$

(14)

The parameter a is a free energy and is neglected in the following. The exponent x is mostly found close to 1 in theory and experiments. The configurational entropy is calculated as follows:

$$ \frac{S_{\text{conf}}}{Nk_{B}}=-\frac{1}{Nk_{B}}\frac{\partial F}{\partial T}= $$

(15)

$$ \frac{3}{2}+\frac{1}{\langle\varPhi\rangle} \left[ \left( 1 - \frac{\partial\ln\langle\varPhi\rangle}{\partial\ln T}\right) \left( \ln(1 - \phi) - \epsilon\frac{z}{2}\phi^{2}\right) + \epsilon\frac{z}{2}\phi^{2} \right] $$

(16)

At this point, I come back on the kinetic term, i.e., 3/2, that is needed to be considered, and other terms involving the cluster size. So, the cluster size is highly important, and gives rise to the glassy behavior, but is not directly connected to the “Cooperatively Rearranging Units” [21], i.e., HCode $n_{\text {cluster}}=\langle \varPhi \rangle \not \sim S_{\text {conf}}^{-1}$.

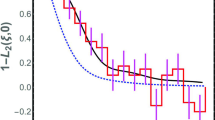
Examples for the relaxation times are depicted in Fig. 4. They are normalized to span the range of 0 to 1. The fragile glass (𝜖 = − 0.28) shows a highly bent curve, while the softer glass (𝜖 = − 0.15) leads to a lower curvature. This is a general observation for glass-forming systems, and the underlying model free energy is capable to connect the fragility of a glass to the simple parameter 𝜖: The nearest neighbor interaction parameter. These curves can also directly be connected to experimental viscosities [22, 23].

Fig. 4

The characteristic time t as a function of the scaled temperature τ₀/τ. The common parameters are $\tilde p_{0}=0.1$ and γ = 11.5 (z = 12). The attractive nearest neighbor interaction 𝜖₀ was − 0.28 (solid line), − 0.25 (dashed), − 0.20 (dotted), and − 0.15 (thin solid)

In more recent discussions of the time scale t [24, 25] as a function of the reciprocal temperature, say τ₀/τ, the magnitude

$$ \left( \frac{\partial \ln(t)}{\partial(\tau_{0}/\tau)} \right)^{-1/2} = \sqrt{\frac{1}{DT_{0}}}\cdot \left( 1-\frac{T_{0}}{T} \right) $$

(17)

is often discussed because more detailed temperature ranges with distinct slopes can be observed more clearly. The Arrhenius behavior would lead to a constant value over a certain temperature range. The corresponding graph to Fig. 4 is displayed in Fig. 5. The classical Vogel-Fulcher region would be found in the range of τ₀/τ = 0.9..1. Towards even lower temperatures τ₀/τ ≈ 1, the behavior flattens as also found in literature for propylbenzene [25] and salol [24]. Towards higher temperatures τ₀/τ = 0.6..0.8, the curve also flattens and is often identified by the Arrhenius behavior with an ideal slope of zero (propylbenzene [25] and salol [24]). At much higher temperatures τ₀/τ < 0.5, the curve takes a higher slope again, which is also found for systems very far from the Vogel-Fulcher temperature [24], namely glycerol and glycols. Here, a rather soft glass behavior might even flatten the original Vogel-Fulcher region τ₀/τ = 0.9..1 more than shown in our graph (Fig. 5) such that the slope might be unified over a larger range τ₀/τ = 0.6..1. More details would be left for a deeper parameter analysis of the whole theory.

Fig. 5

The more detailed derivative of the characteristic time as a function of τ₀/τ for more detailed analysis of nearly straight regions. The common parameters are $\tilde p_{0}=0.1$ and γ = 11.5 (z = 12). The attractive nearest neighbor interaction 𝜖₀ was − 0.28 (solid line), − 0.25 (dashed), − 0.20 (dotted), and − 0.15 (thin solid)

The heat capacity is another relevant function in concert with the glass transition. It is related within our expressions in the following:

$$ \begin{array}{@{}rcl@{}} \frac{C_{p}}{Nk_{B}}&=&\frac{1}{Nk_{B}}\left( \frac{\partial H}{\partial T}\right)_{p} \end{array} $$

(18)

$$ \begin{array}{@{}rcl@{}} &=&\frac{3}{2}-\frac{T}{Nk_{B}}\frac{\partial^{2}F}{\partial T^{2}} +\frac{T\tilde{p}}{\phi^{2}} \frac{\partial\text{eqn}_{13}}{\partial T}/ \frac{\partial\text{eqn}_{13}}{\partial\phi} \end{array} $$

(19)

The explicit use of the left-hand side of Eq. 13 is used for the full expression. The kinetic energy also plays a role, and contributes simply in terms of 3/2. Examples for the calculation are given in Fig. 6. We can see the presence of a more or less pronounced peak, according to the fragility of the glass. I again believe that the theory is closer to the observations on the heating cycle.

Fig. 6

The heat capacity of a glass-forming system as a function of the reduced temperature τ. The common parameters are $\tilde p_{0}=0.1$ and γ = 11.5 (z = 12). The attractive nearest neighbor interaction 𝜖₀ was − 0.28 (solid line), − 0.25 (dashed), − 0.20 (dotted), and − 0.15 (thin solid)

Polymers

The glass transition of polymers has also been in the focus of recent research [26]. The whole concept of the present manuscript might be extended for polymers with little changes (if no directional order parameter is needed [7, 8]). For the equation of state, I find the following (following ref. [17]):

$$ \begin{array}{@{}rcl@{}} 0 &=& -\tilde{p}\langle\varPhi\rangle + \frac{\phi}{N_{\text{pol}}} + \frac{\phi^{2}}{1-\phi} + \epsilon \left( z-2+2N_{\text{pol}}^{-1} \right) \phi^{3} \\ && -\phi^{2}\frac{\partial\ln\langle\varPhi\rangle}{\partial\phi}\bigg(\ln(1-\phi)-\epsilon\left( \frac{z}{2}-1+N_{\text{pol}}^{-1}\right)\phi^{2} \\ && \qquad\qquad\qquad -(1-N_{\text{pol}}^{-1})\ln\frac{z-1}{e} \bigg) \end{array} $$

(20)

The reference unit is a single atom (or monomer). The rather strong change lies in the probabilities for the next neighbor particles. Here the connectivity of the chain plays an important role that is completely independent of the temperature. So I find:

$$ \alpha = \frac{2-2N_{\text{pol}}^{-1}}{4\pi} + \frac{4\pi-2+2N_{\text{pol}}^{-1}}{4\pi} \phi(1-\phi)(-\epsilon) $$

(21)

I calculated some examples for the particle densities as a function of the degree of polymerization N_pol (see Fig. 7). One can see that the glass transition temperature is lowered for the shorter chains. This seems to be the usual case. Here, the glass fragility seems to be changed less (also seen from the heat capacity, not shown) compared with smaller molecules. In parallel, I could find other parameters (smaller 𝜖₀, and higher $\tilde p_{0}$) for the opposite trend. While I predicted now changes for polymeric glasses with the degree of polymerization, a very detailed analysis of the model and experimental data is needed to get the trends correct. At the moment, I leave the results as they are now.

Fig. 7

The particle density as a function of the degree of polymerization, which were chosen N_pol = 500 (solid line), 100 (dashed), and 20 (dotted). The common parameters are 𝜖₀ = − 0.28, $\tilde p_{0}=0.05$ and γ = 11.5 (z = 12). The change of the glass transition temperature is ≈ . 5%

Discussion

Small-angle scattering of glasses would be a measure density fluctuations and, therefore, the correlation function. According to the scenario I have developed here, the scattering function is derived from the Fourier transformation of the correlation function 〈ϕ(r₁)ϕ(r₁ + Δr)〉 =Φ (Δr) ⋅〈ϕ〉, see Eq. 8:

$$ S(Q) = \frac{v_{0} \phi \langle\varPhi\rangle}{(1+A^{2}Q^{2}/2)^{2}} $$

(22)

with the correlation length $A=\sqrt {2}d/(-g\ln \alpha )$. I expect that especially the correlation length and the specific volume deliver the parameters of the presently discussed model. Details about the coordination number of this model could be corrected on the basis of scattering experiments on absolute scale. Furthermore, I believe that the tendency to crystallization might modify the assumed coordination number of the hexagonal packing to a different one. There are not many experiments on this type of scattering [27], because the correlation volumes are small, and the scattering intensities are weak.

I just stress the prediction of this model for the scattering: The correlation length A is rather constant in the vicinity of the glass transition, and the intensity would increase towards the glass transition due to the growing term ϕ (see Fig. 3). The regions of stronger fluctuations are stabilized because a smaller driving force acts towards equilibrium. This, and the bigger cluster size (or bigger “Cooperatively Rearranging Units”) together, is responsible for the strong slowing down of relaxations in a glass. More details about the scattering are discussed in A.3.

Two experimental results might be quite interesting to be compared with Eq. 22 with the correlation length $A=\sqrt {2}d/$$(-g\ln \alpha )$. The diverging intensity towards lower temperatures was confirmed by depolarized light scattering experiments [28]. A dependence of the correlation length A over a wide temperature range has been performed on glycerol confined in zeolites and a scaling exponent of γ₁ = 0.28 was obtained [29]. This can be compared with our theory with $\gamma _{1}=-1/\ln (\alpha )$ by taking ϕ = 0.5 and 𝜖 = − 0.2, I would arrive at a value of γ₁ = 0.33. It should be stressed that this value is only observed over a large temperature range, while close to the glass transition and below the correlation length should be rather constant.

I discuss now the meaning of the glass transition within this model. As we see, that close to 𝜖₀ = − 0.26 the heat capacity diverges, and the specific volume nearly changes stepwise from one to another value. I can also depict the equation of state (Eq. 13) for higher neighbor interactions (see Fig. 2). We see that then a two-phase coexistence between a high density state and a low density state is obtained. While the model is not really capable of predicting the crystalline state correctly, the meaning is as follows: The phase transition between the liquid and crystalline state is close to the glass transition. This causes relatively strong but finite fluctuations of particle density (even though they will be hardly observable due to a small correlation length). The discussed equation of state indicates a first-order phase transition, a diverging heat capacity, and a nearly stepwise change of the specific volume. The interplay of strong fluctuations and large clusters (or “Cooperatively Rearranging Units”) explains the dramatic slowing down of relaxations in a glass, while the correlation length A is growing very slowly as discussed in the literature [30, 31]. Thus, the glass transition can be classified physically on the basis of this model. Apart from that, I hope that this model will be a basis for more detailed models that are capable of quantitative predictions.

In the Appendix, I argue basically for the absence of contributions from loops in the calculation, because they predict a crowdedness that basically cannot appear. From calculations of higher order corrections to the scattering and a heuristic subtraction of the original cluster, I derived an additional scattering function:

$$ S_{\text{BP}}(Q)= v_{0}\phi\langle\varPhi\rangle^{2} \left( \exp(-A^{2}Q^{2})-\exp(-2.62A^{2}Q^{2})\right) \\ $$

(23)

This scattering contribution describes a correlation peak, the intensity of which depends on the magnitude of n_cluster. Thus, a new length scale ℓ = 8.1A appears. While I believe that this feature would stay weak for a pure structural scattering experiment (without energy resolution), the additional correlation might appear in spectroscopic methods, where this finding is called the “Boson Peak.” Polymers might show this feature more often, because the term α includes a contribution of the connectivity. The “Boson Peak” would describe rearrangements of a few neighbors to the actual cluster. In another publication [32], the “cooperativity length” was observed using calorimetric methods and pointed out as a separate, considerably bigger length scale than the bare correlation length. Details about this feature still stay open for discussion. I also would like to stress that I argue here in terms of discretization (or bulkiness) effects that I introduced heuristically (described by the Feynman graphs in Eq. 45), and not in terms of a strict mathematical formalism (that actually contradicts to this view).

Conclusions

While this model contains many detailed relations, I would like to put emphasis on a few aspects that seem to be correctly described by the model. The analysis of the time scale t as a function of the temperature was refined by a special derivative (Eq. 17 and Fig. 5) with higher sensitivity to different regions. Quite quantitatively, the different temperature ranges of locally linear dependencies were identified. The correlation or scattering function grows in amplitude but the correlation length A stays rather constant (see Eq. 22) in the vicinity of the glass transition. The constant length scale is recently discussed in the literature [30, 31]. Over a wider temperature range, the correct scaling exponent of the correlation length is predicted [29]. The predicted and confirmed growing amplitude [28] is connected to a higher susceptibility that slows down the restoring forces. The secondary scattering function is a correlation peak (see Eq. 23) that points towards a much larger length scale compared with the correlation length A. In recent measurements, the “cooperativity length” was identified to be much bigger than the bare correlations [32]. Alternatively, a “Boson Peak” at considerably larger length scales than the atomistic distances [15] is observed in spectrometric experiments. In the latter publication, the atomistic length scales are just not identified as the bare correlations for the glass-forming system. Thus, the new concept of repulsive atoms with distinct neighboring shells is promising in calculating correlation functions for glassy systems and may even be extended to high energy physics when gravitation comes into play. In any case, I am optimistic that the derived correlation functions will shed new light on the physics of glasses and contribute to quite quantitative predictions.

Appendix

Appendix 1. Details for the free energy

The partition function in the canonical ensemble Z_int (4) introduces the chemical potential term βμN by expressing the number of particles N indirectly through the following identity:

$$ \sum\limits_{i,j=1}^{N}{\int d^{3}{\Delta} r \delta(\mathbf{r}_{i}-\mathbf{r}_{j}-{\Delta}\mathbf{r})} = N^{2} $$

(24)

It is implicitly assumed that surface effects can safely be neglected, such that the integral of the δ-function always takes the value 1. The newly introduced δ-function now gives rise to a correlation function Φ(Δr) that we see in the context of the partition with its statistical weight, i.e., the angled brackets mean:

$$ \langle f(\mathbf{r}_{k},\mathbf{r}_{l}) \rangle = {\int}_{V} \cdots {\int}_{V} d^{3N} r_{1} \cdots r_{N} f(\mathbf{r}_{k},\mathbf{r}_{l}) \cdot \exp \left( -\beta \underset{i\neq j}{\sum}{V(\mathbf{r}_{i} - \mathbf{r}_{j})} \right) $$

(25)

and I define Φ as:

$$ \varPhi({\Delta}\mathbf{r}) = \frac{1}{N} \sum\limits_{j=1}^{N}{ \langle \delta(\mathbf{r}_{1}-\mathbf{r}_{j}-{\Delta}\mathbf{r}) \rangle } $$

(26)

where the index 1 is arbitrary because all particles are identical. This correlation function can be interpreted in terms of particle chains (on a lattice) that have probability of α from particle to particle. Then, the correlation function simply takes Φ(Δr) = αⁿ with the number of particles in the chain n = g|Δr|/d. Since the average contact energy is explicitly taken into account in terms of a mean field approach (third term in Eq. 7), the energy in the probability α is renormalized with respect to the average contact energy, and so α = ϕ ⋅ (−𝜖 + ϕ𝜖) = ϕ(1 − ϕ)(−𝜖). The volume integral of the correlation function finally would lead to the expression:

$$ \int d^{3}{\Delta} r \varPhi({\Delta}\mathbf{r}) = 4\pi {\int}_{0}^{\infty} dr r^{2} \alpha^{gr/d} $$

(27)

In the main text, the continuous integral was replaced by a discrete sum using n = gr/d. Thus, the essential term reads:

$$ 4\pi \left( \frac{d}{g}\right)^{3} \sum\limits_{n=0}^{\infty} n^{2}\alpha^{n} = 4\pi \left( \frac{d}{g}\right)^{3} \frac{\alpha(1+\alpha)}{(1-\alpha)^{3}} $$

(28)

These expressions carry units from the volume that originally was avoided by the δ-function. So they need to be normalized by the lattice volume $v_{\text {lattice}}\sim d^{3}$ such that the expressions are dimensionless. Apart from that, the correlation of the central particle is added to the whole correlation function (I write sloppy 〈Φ(Δr)〉) and arrive at Eq. 9. The new parameter γ is defined as 4πd³/(g³v_lattice). For a simple cubic lattice, I arrive at v_lattice = d³ and $g=\sqrt {2}$, so $\gamma = \sqrt {2}\pi = 4.4$. For a hexagonal close-packed (or fcc) lattice, the parameters are v_lattice = a³/4, $d=a/\sqrt {2}$, and $g=2/\sqrt {3}$, so $\gamma = \pi \sqrt {27/2} = 11.5$ (with the fcc unit cell size a³). Note that I took a maximum value for the wrinkledness. It might be discussed if an average value for g between 1 and the maximum value might apply. The additional term 1 arises from the central particle that is present for sure according to the original idea of the δ-function (for i = j). The magnitude 〈Φ〉 can be interpreted as a cluster size which grows from 1 for smallest α (i.e., either 𝜖 = 0 or ϕ = 0 or 1) to bigger values. A rather big value is obtained for 𝜖 = − 0.28 and ϕ = 1/2 that results in 〈Φ〉≈ 2.07 for hexagonal closed packing.

From the grand canonical partition (8) function, I obtain:

$$ \begin{array}{@{}rcl@{}} F_{\text{gc}} & = & -k_{B}T \ln Z_{\text{gc}} \\ &=& k_{B}T\ln\left[ 1-\frac{V}{V_{0}}(1-\phi)\exp(-\epsilon\frac{z}{2}\phi^{2}-\beta\mu\langle\varPhi\rangle)\right] \end{array} $$

(29)

and the number of particles can be calculated according to:

$$ N=\frac{\partial}{\partial\mu}F_{\text{gc}}=\langle\varPhi\rangle\frac{X}{1-X} $$

(30)

I used the definitions:

$$ \begin{array}{@{}rcl@{}} X&=&\frac{V}{V_{0}}(1-\phi)\exp(-\epsilon\frac{z}{2}\phi^{2}-\beta\mu\langle\varPhi\rangle) \end{array} $$

(31)

$$ \begin{array}{@{}rcl@{}} Y&=&\frac{N}{\langle\varPhi\rangle} \end{array} $$

(32)

And so X = Y/(1 + Y ) holds true. The canonical description can be obtained by the free energy that is determined by:

$$ \begin{array}{@{}rcl@{}} F\equiv F_{\mathrm{c}}&=&k_{B}T\ln(1-X)-\mu N \end{array} $$

(33)

$$ \begin{array}{@{}rcl@{}} &=&-k_{B}T\ln(1+Y) \\ & & +\ln\left( \frac{X}{\frac{V}{V_{0}}(1-\phi)\exp(-\epsilon\frac{z}{2}\phi^{2})} \right) \frac{N}{\beta\langle\varPhi\rangle} \end{array} $$

(34)

$$ \begin{array}{@{}rcl@{}} &=&k_{B}T\Big[ Y\ln Y - (1+Y)\ln(1+Y) \\ & & + Y\left( -\ln\left[\frac{V}{V_{0}}(1-\phi)\right]+\epsilon\frac{z}{2}\phi^{2}\right)\Big] \end{array} $$

(35)

$$ \begin{array}{@{}rcl@{}} &\approx & -k_{B}T \frac{N}{\langle\varPhi\rangle} \left( \ln\left[\frac{V}{V_{0}}(1-\phi)\right] - \epsilon\frac{z}{2}\phi^{2}\right) \end{array} $$

(36)

The two logarithmic terms of Y and (1 + Y ) basically cancel out ($\sim -1-\ln Y-1/(2Y)\cdots$) against the much bigger third term of the second last line (large number of particles). In the last line, I obtained (11) of the main text.

Appendix 2. Some missing terms

The approximations so far left some terms disappear, and I tried to argue that I still cover most of the physics of the glass transition. This is quite true, and I will give more details why. So within second-order correlations, a single loop might form. The contribution looks like:

(37)

Here and in the following I neglected details about the combinatorial factors, when N went slowly down to N − 1, N − 2, etc. For the third-order correlation, I could also have a loop coexisting with a single strand. This contribution looks similar:

(38)

The most complicated correlation I consider is a loop consisting of three strands. The contribution is:

(39)

The constant f = 0.00128 results from a numeric integration for the triangular correlation. For this I had to solve the integral:

$$ \begin{array}{@{}rcl@{}} & & 8\pi^{2}\int\limits_{0}^{\infty} z^{2}dz \int\limits_{z/2}^{\infty} r^{2} dr \int\limits_{-1}^{z/2r} d\cos\theta \alpha^{z+r+\sqrt{r^{2}+z^{2}-zr\cos\theta}} \end{array} $$

(40)

$$ \begin{array}{@{}rcl@{}} & & \approx\frac{\gamma^{2}}{2}\sum\limits_{n=0}^{\infty} n^{5}\alpha^{n} {\int\limits_{0}^{2}} \frac{dR}{R^{4}} {\int\limits_{0}^{1}} d\kappa {\cdots} \\ & & \frac{1+R/2}{(1+R^{-1}+\sqrt{1+R^{-2}-(\kappa(1+R/2)-1)R^{-1}})^{6}} \end{array} $$

(41)

The z-axis connects particles 1 and 2, while the third particle is connected to particle 1 along the r-axis. The angles for the z-axis are arbitrary, while this is only the case for the azimuthal angle. The residual polar angle 𝜃 is kept explicitly in the integration. In line 41, the integral limits are made rectangular such that a simple Monte Carlo integration delivers the numerical result of f. The original integral along z was rewritten as a sum, and the term for n = 0 was added separately in Eq. 39.

The terms of order l containing a single loop are small compared with the leading term of order l when the condition below is fulfilled:

$$ N^{2} \gg \frac{l(l+1)}{2\langle\varPhi\rangle} $$

(42)

By assuming a large system, this condition is always fulfilled. The complicated case of small finite volumes [21] cannot be treated here because there are important surface terms apart from the condition above. The condition for the triangle correlation (here I stick to the third-order correlation) reads:

$$ N^{3}\langle\varPhi\rangle^{3} \gg \frac{f}{2} \left( 1+ \gamma^{2}\alpha\frac{1 + 26\alpha + 66\alpha^{2} + 26\alpha^{3} + \alpha^{4}}{(1-\alpha)^{6}} \right) $$

(43)

Again, within my model, the system is large, and so the condition is usually fulfilled (actually more easily than condition 42). Tending towards smaller volumes would also require the neighbor interaction to be attractive enough to have a reasonable system within the approximations.

Appendix 3. The smallness of the loop terms

We have seen that at some point the loop terms might break down the approximation. Here, I would like to argue that a strict mathematical treatment of loops is to be seen with caution, because those correlations would take place on the tiniest spaces, and that cannot appear for particles of finite size. While the open loops extend over a reasonable space, the closed loops do not. So, I discuss a scattering contribution from a triangular correlation, i.e.,

(44)

The dashed line indicates the scattering term. The triangular correlation was calculated similarly as in Eqs. 39-41, where the Q-axis was parallel to the z-axis. The dominating Q-dependence was calculated from a Taylor expansion at small Q. When comparing this result with the original scattering function (22, A is the original correlation length), we see: The structural size does not change dramatically, while the amplitude goes up dramatically. This would mean that there are many more correlations in the tiniest space. Due to my applied continuous space description (used especially here), I artificially find an amplification of correlations for the higher order terms. This means that closed loops violate the concept of discrete particles. One way out, to describe higher order terms (heuristically), might be the subtraction of this crowdedness, i.e., Eq. 23 and:

(45)

I stress that I argue here in terms of discretization (or bulkiness) effects that I introduced heuristically and not in terms of a strict mathematical formalism.