1 Introduction

The Third Pole region contains the largest amount of ice outside of the polar regions and acts as a water tower for highly populated communities, agriculture, and industry downstream (e.g., Immerzeel et al. 2020). An understanding of how the regional water cycle has changed and will change in the future is of high societal importance, however, knowledge of mountain climate is limited by a lack of observations and by the relatively coarse resolution of the models conventionally used for climate simulations. Such models are unable to adequately represent complex orography and associated processes (e.g., Rasmussen et al. 2011; Prein et al. 2013; Ban et al. 2014; Schmidli et al. 2018; Chow et al. 2019; Singh et al. 2021) and also parameterize deep convection, which is a key source of uncertainty (see e.g., Prein et al. 2015; Mooney et al. 2017). Over the Tibetan Plateau (TP), CMIP6 models exhibit pronounced wet, cold, and excess snow biases as well as difficulties in capturing observed trends (Lalande et al. 2021). These biases are in part attributable to their smoothed representation of the orographic barrier (e.g., Lin et al. 2018) and contribute to uncertainty in future projections.

Refining the horizontal resolution of climate models to kilometer-scale (km-scale; grid spacing \(\le 4\) km) has emerged as a promising way forward for understanding present and future mountain climate, due to better-resolved orography and dynamical representation of atmospheric processes. More importantly, this approach allows for explicit simulation of deep convection (often referred to as "convection-permitting" and or "convection-resolving" modelling; e.g., Weisman et al. 1997) and has led to major improvements in regional climate simulations, especially over complex topography. For example, km-scale regional climate models improve the simulation of precipitation diurnal cycle and heavy precipitation, especially on sub-daily time scales (e.g., Ban et al. 2014, 2015; Prein et al. 2015); produce a better representation of cloud cover (e.g., Prein et al. 2013; Hentgen et al. 2019), snow cover (e.g., Rasmussen et al. 2011; Lüthi et al. 2019) and local wind systems like sea-breeze (e.g., Belušić et al. 2018); and, reduce model uncertainties and parameter sensitivities (e.g., Ban et al. 2021; Pichelli et al. 2021).

Recent applications of km-scale regional models over the Third Pole have similarly demonstrated added value for precipitation amount, frequency, intensity, and diurnal timing at the event (Prein et al. 2022a) and seasonal (e.g.,Li et al. 2021) timescales compared to both reanalyses and coarser simulations with parameterized deep convection as well as for spatial and temporal variability of near-surface meteorological fields (e.g., Collier and Immerzeel 2015; Karki et al. 2017; Sugimoto et al. 2021) and orographic effects on water vapor transport (Lin et al. 2018). Although the impact of convection-permitting modeling has been explored over limited domains (e.g., Cai et al. 2021) and for seasonal simulations (e.g., Li et al. 2020; Yun et al. 2020; Li et al. 2021; Sugimoto et al. 2021; Liu et al. 2022; Ma et al. 2023), there is a lack of multi-annual, multi-model and multi-physics ensembles with domains covering all of the Third Pole region, hindering process understanding and leaving gaps in our knowledge of the impact of model uncertainty on simulated mountain climate.

The Coordinated Regional Climate Downscaling Experiment (CORDEX; (Gutowski et al. 2016)) Flagship Pilot Study (CORDEX-FPS) Convection-Permitting Third Pole (CPTP; Prein et al. 2022a) was established in 2019, with the aim of addressing this gap and of improving the understanding of the current and future water cycle and associated processes over the region. In the first phase of the project, Prein et al. (2022a) evaluated an initial model ensemble for three short case studies of different precipitation events: a mesoscale convective system, an exceptionally wet month during the monsoon season, and a large snowfall event, with the km-scale simulations demonstrating similar skill as observations across these varying weather events. Here, we present the second phase of the project, consisting of a 13 member multi-model and multi-physics ensemble of km-scale simulations for one hydrological year (October 2019 to September 2020; hereafter referred to as Water Year 2020 or WY2020). This hydrological year was selected due to improved observational coverage closer to the present and because of the extreme precipitation and flooding that occurred in East Asia in the summer of 2020 related to a record-strong positive Indian Ocean Dipole event (e.g., Zhou et al. 2021). This paper aims to present first results from the simulations and to evaluate ensemble performance and spread compared with available observations on seasonal timescales, with a focus on precipitation as one of the most important variables for understanding the hydroclimate of the Third Pole. The simulations will provide an invaluable resource towards future improvements in the process understanding of the water cycle over this remote but important region.

2 Methods

2.1 Model simulations

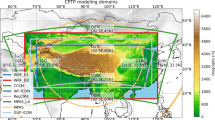
The ensemble consists of 13 simulations run at km-scale grid spacing by 10 research groups for a year-long period, which are listed in Table 1. The simulation domain differs from model to model, with a minimum domain for analysis that encompasses all of the Third Pole as shown in Fig. 1.

The simulation ensemble consists of four models:

  1. 1.

    COSMO-CLM: Consortium for Small-Scale Modeling, run in climate mode (Rockel et al. 2008; Baldauf et al. 2011)

  2. 2.

    ICON-CLM: Icosahedral Nonhydrostatic Weather and Climate Model, run in limited-area climate mode (Pham et al. 2021)

  3. 3.

    MPAS: the Model for Prediction Across Scales (Skamarock et al. 2012)

  4. 4.

    WRF: the Weather Research and Forecasting model (e.g., Skamarock and Klemp 2008; Powers et al. 2017).

A detailed description of the model configurations and physics options is provided in Table 1 of Prein et al. (2022a). For brevity, we refer readers to this paper and specific references therein for more details on the dynamics and physics of each participating model. However, Table 1 reviews key details of the model settings and indicates changes made from Prein et al. (2022a) for the WY2020 simulations.

All models were initialized with and forced at the lateral boundaries by the ERA5 reanalysis (Hersbach et al. 2020) at either hourly or three-hourly temporal resolution (cf. Table 1) from 1 October 2019 to 30 September 2020. Spin-up procedures vary between the models. For COSMO-CLM, soil and snow fields in the 12-km parent and 2.2-km domains were spun up over 1 year and 2 months, respectively. At the start of the WY2020 period, the atmosphere was reinitialized and unrealistic snow depths over the Karakoram were capped at 2 m following Collier et al. (2013). ICON-CLM employed one month of spin-up for both atmosphere and land. For MPAS, a one-year spin-up simulation was run on a global, quasi-uniform 30-km mesh from 1 September 2019 to 31 August 2020. The initial and lower boundary conditions for this spin-up simulation were taken from ERA5. The final land state of the 30-km spin-up simulation was remapped to the 4–32 km variable resolution global grid and used as the initial conditions for another one-month spin-up from 1 September 2020 to 30 September 2020 on the 4–32 km grid. WRF_REF performed a spin-up simulation with a 12-km grid-spacing domain (covering D2 in Fig. 1) that started on the 1st of October 2016 to spin up the soil fields. All other WRF simulations used the same initial and boundary conditions as the WRF_REF simulation.

The multi-model framework, as presented here, permits sampling of uncertainty due to model structure and horizontal grid spacing. Additionally, several sensitivity experiments with WRF were performed (Table 2) to assess uncertainty due to the parameterization of microphysical (MP) and planetary boundary layer (PBL) processes. In all km-scale simulations, cumulus (CU) parameterization was turned off except for one model (WRF_CU_KF, which employed a scale-aware scheme; cf. Table 2), and, therefore, deep convection is explicitly resolved in most simulations. Information on the treatment of shallow convection in each simulation is provided in Table 1 of Prein et al. (2022a). Furthermore, all simulations were allowed to freely evolve in regions away from the lateral boundaries except for one (WRF_NDG, which employed spectral nudging).

We note that there are more simulations performed using the WRF model than with other models due to the CPTP group’s capabilities. However, we follow Ban et al. (2021) and Pichelli et al. (2021) in presenting the mean of all ensemble members regardless of the differing prevalence of modelling systems. We note that the WRF simulations and the processes underlying their differences would benefit from more detailed investigation in future studies, as this analysis is out of the scope of the current study.

2.2 Observational datasets

To evaluate model performance, we used the following satellite-based gridded precipitation products:

  1. 1.

    CHIRPS – a gauge-corrected product based on satellite infrared data. It incorporates several climatologies and in-situ station data to create a gridded rainfall time series. The data span 50\(^{\circ }\)S-50\(^{\circ }\)N and all longitudes. We use data at daily temporal and 0.05\(^{\circ }\) spatial grid spacing (Funk et al. 2015).

  2. 2.

    CMORPH – a product based on passive microwave data. The data consist of satellite precipitation estimates that have been bias-corrected and reprocessed using the Climate Prediction Center (CPC) Morphing Technique (MORPH) to form a global, high-resolution precipitation analysis (Xie et al. 2019). The quality of this data is compromised for snowfall and cold-season precipitation. In particular, it tends to underestimate the precipitation amount during cold seasons over mid- and high latitudes (Xie et al. 2019). We use CMORPH data at 30-min temporal and 8-km spatial grid spacing (Xie et al. 2019).

  3. 3.

    IMERG (Integrated Multi-satellitE Retrievals for GPM) – is the successor to the Tropical Rainfall Measuring Mission (TRMM) and merges multiple satellite inputs of precipitation radar and microwave data (Ma et al. 2016). This dataset has been found to match or exceed the skill of TRMM products in detecting light and solid precipitation on the TP (Ma et al. 2016). We use the L3 V06B product at 30-minute temporal and 0.1\(^{\circ }\) spatial grid spacing (Huffman et al. 2019).

In addition to gridded precipitation datasets, we also use in-situ observations of daily total precipitation and daily near-surface air temperature from the Global Surface Summary of the Day (GSOD) dataset (https://www.ncei.noaa.gov/access/metadata/landing-page/bin/iso?id=gov.noaa.ncdc:C00516; last accessed 1 August 2023). Even though these data are quality controlled prior to release, we impose additional filters based on available metadata in the dataset. For daily minimum, mean, and maximum air temperature, we consider only those days with at least 6 sub-daily observations available. For precipitation, we excluded days when the total precipitation amount was reported in either less than two 6-h reports or one 12-h report or when the station reported 0 mm precipitation on the given day, but sub-daily observations showed that precipitation had occurred. Lastly, for each variable, we discarded stations that had less than 30% (40 days) of available observations per season and/or if the difference in elevation between the ensemble grid (see Sect. 2.3) and observations exceeded 500 m. This filtering process resulted in 247 (220) and 233 (226) GSOD stations for the precipitation (near-surface air temperature) analysis in the cold and warm seasons, respectively. For the remaining stations, we corrected near-surface air temperature for the elevation difference using an environmental lapse rate of \(-\)6.5\(^{\circ }\)C km\(^{-1}\). To extract model data for the station location we use the nearest neighbor interpolation method. We also tested using a 3x3 kernel instead of the nearest neighbor for the GSOD comparison, but it did not significantly affect the results and conclusions, although as expected, metrics like precipitation intensity were lower. For near-surface air temperature, we calculated the mean bias as the ensemble-average minus station data, and for precipitation, the relative bias as the difference between ensemble-average daily mean or heavy precipitation minus the corresponding station data value normalised by the station data. For precipitation, we neglected stations that recorded zero precipitation in a season for computing the relative bias. We note that we did not assess whether the GSOD observations have been assimilated in the reanalysis dataset.

As the above list implies, several observations for the same variable are used to account for observational uncertainty (see e.g., Prein and Gobiet 2017) following previous studies (see e.g.,Ban et al. 2021; Pichelli et al. 2021; Prein et al. 2022b). In such a way, we do not take one observational dataset as ground truth but rather consider the spread between observations and how it relates to the model ensemble prediction.

For completeness, we note some of the well-known observational uncertainties. Satellite estimates provide areal averages that suffer from biases due to complex terrain, which often underestimate the intensity of extreme precipitation events. Even though some of these datasets are corrected using surface rain gauges, they themselves suffer from well-known shortcomings, in particular in complex terrain where station density is sparse in space and time and tends to under-sample high-elevation regions. Station observations also suffer from issues such as undercatch of precipitation, which can reach up to 50% of the total precipitation depending on the season, intensity, region, and altitude (Frei et al. 2003); interpolation effects (Isotta et al. 2014); and inaccurate retrieval of light and solid precipitation (Ma et al. 2016). Since different observational datasets suffer from different shortcomings, it is difficult to select one as a reference. There is also a debate in the literature suggesting that high-resolution models, such as those run at km-scale, may surpass the skill of observations (see e.g., Lundquist et al. (2019)). However, there is not yet a clear way forward to more thoroughly address this issue. We therefore use all of the aforementioned, different observations to check our simulations for physical consistency and to evaluate whether the ensemble captures the observed spatio-temporal characteristics of the variables and statistics of interest.

2.3 Analyses

Our analysis focuses on the warm and cold seasons of June–July–August–September (JJAS) and December–January–February–March (DJFM), respectively, unless otherwise stated, representing two different synoptic situations where precipitation is predominantly related to the South- and East-Asian monsoons and to the westerlies (e.g., Bookhagen and Burbank, 2010). We focus our evaluation on precipitation, where the km-scale simulations are anticipated to add value (see e.g., Prein et al. 2015; Ban et al. 2021), with an emphasis on the warm season, when 60 to 70% of the annual total precipitation falls on the TP (Wang et al. 2018).

For evaluation, all km-scale ensemble members were regridded to a common 0.036x0.036\(^{\circ }\) grid (\(\sim\)4 km), using conservative remapping for precipitation and bilinear interpolation for other variables. Statistics in ERA5 and the gridded observational datasets were computed on their native grids. For creating the Taylor diagrams (Taylor 2001b), all datasets were regridded to the coarsest-resolution grid, that of ERA5. One ensemble member contained negative precipitation values (ICON-CLM; \(\sim\)O(100) kg m\(^{-2}\) hr\(^{-1}\)) which were zeroed prior to using the data.

For precipitation, we further considered the metrics presented in Table 3 following Ban et al. (2021). The monsoonal circulation is characterized by active and break periods consisting of heavy and low rainfall, respectively (e.g., Rajeevan et al. 2010), that are of high societal importance (e.g., Singh et al. 2014). Flooding is often caused by multi-day extreme precipitation (e.g. the flooding in Pakistan in 2022 Nanditha et al. (2023), and in East Asia during the summer of 2020). As such, we analyze wet spells using the three statistics provided in Table 3 considering a length of three days, following Singh et al. (2014).

In addition to the above indices, we evaluate precipitation by calculating the spatial correlation (R) and the standard deviation (STD). The STD is normalized by the standard deviation of reference observations (IMERG) and yields the normalized STD (NSTD). Taylor diagrams are calculated for the mean daily precipitation and heavy precipitation for each season. Using the Law of Cosines, we relate these metrics to infer the centered root mean squared error (CRMSE) to produce Taylor diagrams (after Taylor 2001a):

$$\begin{aligned} CRMSE^{2} = \sigma _{m}^{2} + \sigma _{o}^{2} - 2\sigma _{m}\sigma _{o}R \end{aligned}$$
(1)

Here \(\sigma _{m}\) represents the spatial standard deviation of the modeled and \(\sigma _{o}\) of the observational seasonally averaged mean daily or heavy precipitation.

Furthermore, we analyze the link between temperature and heavy precipitation in observations, ERA5, and the model ensemble. Because of the lack of availability of both temperature and precipitation in other observational datasets, here we focus only on the GSOD observations and daily precipitation data. To provide more robust statistics, we consider the full year of data. We require that valid measurements of temperature and precipitation are available simultaneously for at least 300 days at each considered station. Such a criterion is fulfilled at 198 stations, which are then used for the analysis. As in the previous analyses with station data, ERA5 and the model ensemble gridpoints nearest to each GSOD station are taken into account. After that, for each station, we group daily precipitation data according to the corresponding mean daily temperature following, for example, Ban et al. (2014); Lenderink and van Meijgaard (2008). We use bins of 2\(^\circ\)C, with 1\(^\circ\)C overlap, to derive statistics. Furthermore, from these binned values, we calculate the 80th, the 90th, and the 99th percentiles, which are considered to represent heavy daily precipitation. The percentiles are calculated using all events in a bin (i.e., including dry days, following Schär et al. 2016), but only if there are at least 10 events in that bin. After percentiles are calculated for each station and gridpoint individually, they are averaged and shown only if there are at least 10% of stations and gridpoints with enough data for the calculation of the percentiles in that specific temperature bin. This analysis is shown for an average over all stations over the analysis domain as well as separately for stations above and below 2800 meters, i.e., on and below the TP.

3 Results

3.1 Precipitation

For the evaluation of precipitation, we first consider the spatial representation, focusing on daily metrics due to the greater availability of observational datasets. Figure 2 shows spatial maps of daily precipitation statistics during the cold and warm seasons. The observed spatial patterns are generally well reproduced by both ERA5 and the model ensemble, although there is a large observational spread. However, the ensemble provides some clear improvements compared with the reanalysis, including (i) a reduced wet bias in the eastern Himalaya (northern India) in both seasons and in the central Himalaya in JJAS (Fig. 2a); (ii) a reduced overestimate of wet-day frequency and underestimate of wet-day intensity, along the slopes in DJFM and over much of the analysis domain in JJAS (Fig. 2b,c); and (iii) a better representation of heavy precipitation in the western part of the analysis domain in both seasons (Fig. 2d). Similar patterns and results are obtained when comparing spatial patterns of hourly precipitation statistics (see Fig. S1.1 in the Supplementary Information (SI) Sect. S1). Although at hourly timescales the ensemble simulates clearly higher wet-hour intensities in low-elevation regions in JJAS, it provides much greater improvements in wet-hour frequency, which is largely overestimated in the reanalysis data. Thus, it is clear that the ensemble improves on these biases and has a better representation of spatial patterns of daily and hourly precipitation statistics.

In addition to the ensemble mean, we show the individual models for heavy hourly precipitation in the warm and cold seasons in the SI (Fig. S1.2). It can be seen that even though those individual simulations slightly differ in the intensity of heavy precipitation, the spatial patterns are quite similar. It is also quite notable that no clear differences between different modeling groups or systems are visible and those differences are within the range of the differences for different realizations of one model, i.e., WRF simulations.

Next, we evaluate the spatial representation of seasonal mean and heavy precipitation considering individual members using Taylor Diagrams (Taylor 2001a) as well as compare IMERG with other gridded datasets (Fig. 3). The km-scale simulations show a relatively good performance according to these metrics for both seasons. For mean precipitation, spatial correlation coefficients are generally higher in DJFM, although COSMO-CLM and MPAS are noticeably lower, and most ensemble members have a higher spatial correlation than ERA5, consistent with the predominance of orographic precipitation in this season, which can be better resolved at higher resolutions. Conversely, spatial variability (here spread in the normalized standard deviation) is higher in JJAS, consistent with the greater prevalence of localized convective precipitation on the TP in this season (e.g., Ueno et al. 2001). For heavy precipitation, the results are similar for both seasons, however correlations, NSTDs, and CRMSE values are all lower than for mean precipitation. Noticeably, simulated results have a similar difference to IMERG as CMORPH (except for some simulations with high normalized standard deviations), indicating that the models are close to observational quality with regard to simulating seasonally averaged precipitation patterns. Here, we choose IMERG as the reference dataset against which to correlate the model and other observational datasets, and with which to calculate the CRMSE. There is a strong correlation and low CRMSE between IMERG and CHIRPS, suggesting that taking CHIRPS as the reference dataset would lead to similar patterns in model spread.

In addition to considering gridded precipitation datasets, we evaluate daily precipitation at GSOD station locations. The results for the observational and model datasets are shown in Fig. 4 for mean daily precipitation, while a similar analysis for heavy precipitation is shown in SI Sect. S2. The spatial maps of the relative biases in the ensemble mean and reanalysis (Fig. 4a, b) show large variability, however, some general patterns include: in DJFM, stronger biases overall and a tendency for the ensemble to underestimate both statistics in the western part of the domain and to overestimate them in the eastern part; and in JJAS, to underestimate them in the western and northeastern parts of the analysis domain. The probability density functions (PDFs) are more informative (Fig. 4c), showing that ERA5 slightly overestimates the frequency of lower intensity events and strongly underestimates the frequency of higher intensity events for both seasons, as expected and previously reported for the region at six-hourly timescales by Prein et al. (2022a). In the cold season, the ensemble also simulates fewer of the highest intensity events than GSOD but is in better agreement with the other observational datasets. However, it is noteworthy that GSOD occasionally reports very large daily precipitation totals, exceeding all other datasets. In the warm season, the ensemble (and all other datasets) are much closer to the GSOD PDF, although some members (WRF_CU_KF and ICON-CLM) strongly overestimate peak daily intensities compared with observations.

In addition to daily precipitation statistics, the number of consecutive wet days is also of high societal importance due to impacts such as flooding (e.g., Singh et al. 2014). Thus, we next consider the wet-spell statistics shown in (Fig. 5). The km-scale ensemble represents the spatial patterns and magnitudes of all wet-spell statistics in both seasons better than the driving reanalysis compared with the gridded observations. ERA5 strongly overestimates the average and longest spell length (Fig. 5a,c) along the central and eastern Himalaya in DJFM and over much of the Third Pole region in JJAS, with the overestimate in spell length exceeding \(\sim\)30 days over a large area during the latter season. ERA5 also generally overestimates the number of wet spells (Fig. 5b) compared with the gridded observations. The km-scale ensemble improves on all of the aforementioned biases, although wet-spell statistics are still overestimated over the eastern Himalaya, a feature that may be inherited from the driving reanalysis but may also reflect observational error as discussed at the end of this section. The improved representation of consecutive wet days is relevant for impact studies, as some land-surface and cryospheric models reset snow albedo to that of fresh snow after a certain precipitation threshold is exceeded (e.g., Niu et al. 2011).

In addition to seasonal and daily statistics, we also analyze the sub-diurnal variability of precipitation, focusing on JJAS due to the predominantly convective nature of precipitation. The diurnal cycles of mean precipitation, wet-hour frequency and intensity, and heavy precipitation for the area above 2800 m are shown in Fig. 6. Both the ensemble mean and most individual members capture the salient features of the diurnal cycles of the metrics as represented by the gridded observations (Fig. 6). In particular, the km-scale simulations improve on several issues in the driving reanalysis, including the too-early onset and peak in convective precipitation (Fig. 6a), the constant drizzle in the form of too-frequent wet hours of too-low intensity (Fig. 6b, c), and the underestimation of heavy precipitation (Fig. 6d). These issues are typical of coarser resolution models that parameterize deep convection as ERA5 does (e.g., Ban et al. 2014, 2015). In addition, ERA5 also suffers from constant small precipitation amounts due to data processingFootnote 1. Compared with the gridded observations, the km-scale simulations tend to overestimate night-time precipitation (Fig. 6a) and to underestimate both the wet-hour intensity and the heaviest convective precipitation (Fig. 6c, d),. However, there is large observational spread in the intensity, and spatial maps indicate that on the slopes and low-elevation regions, the models simulate much higher intensities than the gridded datasets (see Fig. S1.2). An outlier in the sub-diurnal analysis is the COSMO-CLM simulation, which shows a delayed onset and peak in precipitation, seemingly due to more frequent light precipitation in the afternoon. However, the COSMO-CLM simulation also provides one of the better representations of wet-hour and heavy precipitation intensity compared with gridded observations (cf. Figure 6c,d). Further details on the delayed onset and peak in mean precipitation in this simulation are provided in SI Sect. S3.

The spatially averaged patterns presented in Fig. 6 mask considerable regional and spatial variability in the timing of the diurnal peak in precipitation, as illustrated by the spatial map of the timing of the diurnal peak shown in Fig. 7. Gridded observations show that the diurnal peak occurs in the early to mid-morning hours on the slopes and to the east of the TP and in the evening on the TP itself. Consistent with previous studies (e.g., Li et al. 2021), these patterns are better captured by the km-scale simulations than the convection-parameterizing reanalysis data. ERA5 tends to simulate peak precipitation too early in the day over high-elevation areas and on the slopes. The high-resolution ensemble is much better in representing these features although the timing of the peak on the slopes is still earlier than observed.

3.2 Temperature

Figure 8 compares daily mean air temperatures in the reanalysis and model datasets with GSOD station data. On average, the ensemble exhibits relatively small warm biases at lower elevations and cold biases at higher elevations on the TP (Fig. 8a), a pattern that is more pronounced in ERA5 and in the warm season. The simulated PDFs of near-surface air temperature of the ensemble and ERA5 generally agree well with GSOD (Fig. 8c) and added value is most apparent for the left tails of the distributions, as ERA5 strongly overestimates the frequency of occurrence of colder temperatures in both seasons. In DJFM, the ensemble also better represents values near the melting point, although there is a clear outlier, WRF_MP_WDM6. This simulation has a cold bias and erroneous peak around the melting point related to simulated snow accumulation at the GSOD station locations (SI Sect. S2), which is much higher than in other simulations during January and February. The relatively deep snowpack in the cold season and at the start of the warm season in ERA5 at GSOD station locations is consistent with the bias towards colder temperatures. In JJAS, the high-resolution ensemble not only improves the left tail of the distribution but also better represents the peak frequency of the temperatures between 25 and 30\(^{\circ }\)C.

Even though there are some improvements in the simulation of the temperature when using high-resolution models, they are not as clear as for the simulation of the precipitation. A smaller added value when simulating daily mean temperature with higher resolution models is not surprising and is consistent with previous studies over other regions (see e.g., Soares et al. 2022). This is especially true for daily mean temperature, while sub-daily values might show different results as they can be influenced by cloudiness and locally developing systems. Due to the lack of sub-daily observations with which to evaluate the diurnal cycle, we examined the diurnal temperature range (calculated as a difference between daily maximum and minimum temperature from the model output and at GSOD stations), however, there were no clear differences in the spatial patterns between the reanalysis and km-scale ensemble during the warm season (not shown).

3.3 Scaling of heavy precipitation with temperature

In the last part of the study, we analyze the combined dependency of precipitation and temperature. With such an analysis, we test the hypothesis originating from the Clausius-Clapeyron (CC) relation, that the equilibrium vapor pressure of the atmosphere increases with temperature at a rate of 7\(\%/1K\). Many studies have argued that this relation sets a scale for the thermodynamically driven increase of precipitation extremes as the atmosphere warms (see e.g., Trenberth et al. 2003; Lenderink and van Meijgaard 2008). We examine if such a relationship can be found in the observations for the Third Pole region, and how it is represented in the reanalysis data and high-resolution ensemble.

In Fig. 9, we show the 80th, 90th, and 99th percentiles as a function of daily mean temperature, averaged over all stations over both the analysis domain and considering high and low elevations separately, and considering all data from WY2020 for more robust statistics. However, we note that this is only one year and further analysis should be done once more data are available.

Overall, the observed scaling shows good agreement with the 7\(\%/1K\) rate given by the CC-relation for temperatures between 0 and 25\(^\circ\)C when averaged across all stations (Fig. 9a), especially for the 99th percentile. The 80th and 90th percentiles show a smaller scaling rate than expected from the CC-relation. Deviations are visible at both ends of the curves, i.e., for the coldest and warmest temperatures. For warmer temperatures, the scaling drops quickly, which is expected, has been reported by other studies, and is most likely due to the lack of available moisture to form heavy and extreme precipitation (see e.g. Prein et al. 2016). However, it is surprising that for colder temperatures, i.e., below 0\(^\circ\)C, the intensity increases with decreasing temperature. More detailed analysis shows that this feature comes from stations above 2800 ms, i.e., on the TP, while stations below 2800 ms exhibit a drop in the scaling for lower temperatures (Fig. 9e,i).

Both the reanalysis and high-resolution model ensemble largely reproduce the observed scaling rates, however, some differences exist. For example, ERA5 produces slightly lower scaling for the 99th percentile and shows a drop in the scaling for stations above 2800 m already around 10\(^\circ\)C, while in the observations this occurs around 15\(^\circ\)C, and this feature is better represented by the high-resolution model ensemble. However, both ERA5 and the ensemble fail to reproduce the observed increase in scaling for temperatures below 0\(^\circ\)C.

4 Discussion and conclusions

In this paper, we presented a novel ensemble of km-scale simulations conducted over the TP region for the hydrological year of October 2019 to September 2020 (WY2020), performed as the second phase of the CORDEX-FPS CPTP project. We analyzed a total of 13 simulations, which were produced by 10 international research groups and configured with a horizontal grid spacing ranging from 2.2 to 4 km. The simulations were completed with four different climate models and driven by ERA5 reanalysis data. We evaluated the km-scale ensemble against available observations and explored the representation of precipitation and near-surface air temperature compared with the driving reanalysis.

We identified a clear improvement in the km-scale ensemble for simulated warm-season precipitation statistics and for wet spells in both the warm and cold seasons. Specifically, we showed an improvement in the simulation of the precipitation diurnal cycle, precipitation frequency, and heavy precipitation, consistent with other regions like the European Alps (e.g., Ban et al. 2021; Pichelli et al. 2021) and seasonal studies over this region (e.g., Li et al. 2020). We also showed for the first time that km-scale models improve the representation of wet-spell statistics over the Third Pole region. This result has important implications for impact assessments using ERA5, particularly those determining flood and water resource risks, as ERA5 considerably overestimates the length, and the number of long, wet spells while underestimating the intensity of wet days compared to both observational datasets and the high-resolution model ensemble (cf. Figs. 2 and 5). The temperature evaluation showed some benefit from the km-scale ensemble in terms of the simulated frequency of colder air temperatures in both seasons, likely related to the unrealistically deep snowpack present in ERA5 in DJFM and at the start of JJAS. The smaller added value is not surprising since the temperature is not as variable as precipitation and is consistent with previous studies over other regions (e.g, Soares et al. 2022). However, it remains to be investigated how other metrics of temperature, such as extremes and the diurnal cycle and range, are represented in such high-resolution model ensembles. As shown by Ban et al. (2014), higher resolution models have the potential to better represent the diurnal temperature range due to a better representation of the diurnal cycle of precipitation. The combined analysis of temperature and heavy precipitation showed that ERA5 has more shortcomings in reproducing the observed scaling of heavy precipitation with temperature than the ensemble mean. Although ERA5 overestimates the frequency of colder temperatures, it underestimates the intensity of heavy precipitation at these temperatures. In addition, it shows the drop in precipitation intensity already around 10°C for stations above 2800 m, while in the observations this occurs around 15°C. While the ensemble mean shows the same performance as ERA5 for colder temperatures, it shows a better performance for warmer temperatures for stations on the TP. The better performance of high-resolution models in reproducing such a relation between temperature and precipitation has also been found in other regions like European Alps (e.g, Ban et al. 2014), and it increases the credibility of such models in projecting changes in heavy and extreme precipitation with further warming of the atmosphere.

Overall, all analyzed metrics show a good performance of the km-scale ensemble and general consistency among ensemble members. However, there are some outliers, which is not surprising since some of the models have been applied for the first time over this region at such high-spatial resolution and over such an extended period of time. Some examples include the highest daily warm-season precipitation intensities simulated by some members (Fig. 4); the delayed diurnal cycle of mean precipitation and wet-hour frequency simulated by COSMO-CLM (Fig. 6a,b); and the bias in the distribution of daily air temperatures in WRF_MP_WDM6 (Fig. 8). Although a detailed analysis of differences between ensemble members is not the focus of the current study, some potential takeaways from the evaluation are that (i) the scale-aware cumulus parameterization (WRF_CU_KF) with this WRF configuration does not lead to a significant improvement compared with other members and produces quite high warm-season intensities (compared with station data (cf. Fig. 4), although this member does not stand out in spatial analyses (cf. Figure S1.2)) and (ii) the WDM6 microphysics scheme with this WRF configuration produces unrealistically high snowfall during the cold season, which was not apparent from previous sensitivity studies focused on the monsoon season (Orr et al. 2017). For the delayed onset and peak in convective precipitation in COSMO-CLM, preliminary analysis indicates that the issue is related to the representation of low clouds (SI Sect. S3). However, it has not been observed over other mountainous areas (e.g., over the European Alps; Ban et al. 2015, 2021) and highlights both the challenges that can arise in transferring regional climate models to a new region (e.g., Prein et al. 2022b), especially at high-spatial resolutions, and the difficulties that general circulation models encounter when using a setup tuned for a specific region or process.

A feature that repeatedly appears in the precipitation evaluation for the region is the large spread in the gridded observations. In general, IMERG has more frequent wet days and hours of lower intensity than CMORPH and CHIRPS (cf. Fig. 2). During the warm season, CMORPH also has localized areas of high values of precipitation statistics due to retrieval errors over lakes (Guo et al. 2017) while during the cold season, it shows unrealistically low statistics over the Karakoram and western Himalaya compared with IMERG and CHIRPS (cf. Fig. 2). These issues are consistent with the CPTP case study evaluation (Prein et al. 2022a) and previous studies indicating that this product has relatively low fidelity over the Third Pole (Guo et al. 2017; Wang et al. 2017). In addition, ERA5 and the ensemble generally show higher precipitation and spell statistics over the eastern Himalaya, where there are known differences between satellite-derived estimates (IMERG) and gauge observations that have been attributed to warm-rain processes (Ma et al. 2016). The spread in gridded observational datasets in this region and the lack of, or difficulty in accessing hourly in-situ observations, represents two huge challenges for the km-scale climate modelling community in assessing the performance of their simulations, both over the Third Pole and over other regions as well. Therefore, there is an urgent need for different communities, not only observational, to address these issues and to provide a standardized way forward for model evaluation, thus making such analyses more consistent across different regions, models, and studies.

The ensemble of high-resolution simulations and analysis presented here lays the foundation for using the WY2020 data to tackle the many open and interesting questions about the hydroclimate of the Third Pole. The ensemble represents a foundational step towards decadal climate simulations at high resolution over this complex region, which will lead to a better understanding of processes and of natural variability in this sparsely observed region, and finally, of how the climate of the Third Pole will change in the future.

Table 1 Participating Models
Full size table
Table 2 WRF sensitivity simulations
Full size table
Table 3 Precipitation & wet-spell statistics analyzed in this study\(^{a}\)
Full size table
Fig. 1
figure 1

The model and analysis domains employed in this study. The green, red, light-blue and orange contours delineate the extent of the km-scale domains for COSMO-CLM, WRF, ICON-CLM, and MPAS, respectively. The dark blue box shows the extent of the analysis domain (70–115E, 25–40N), with surface elevation at 0.036\(^{\circ }\) resolution shaded [m] and the elevation of 2800 m, above which area averages were computed, delineated in dark purple

Full size image
Fig. 2
figure 2

Spatial representation of the daily precipitation statistics presented in Table 3 for the DJFM (top row) and JJAS (bottom row) seasons: a mean; wet-day b frequency and c intensity; and, d heavy precipitation. The panel labelled ’Ensemble’ displays the mean of all km-scale simulations

Full size image
Fig. 3
figure 3

Taylor diagram for DJFM (left column) and JJAS (right column), displaying the spatial pattern correlation, normalized spatial standard deviation, and centered root mean squared error for ERA5 and observations (black symbols) and for the km-scale simulations (colored numbers). The top row shows the seasonal mean daily precipitation and the bottom row the seasonal heavy daily precipitation calculated as the 99th percentile. The marker labelled ENS_MEAN displays the mean of all km-scale simulations

Full size image
Fig. 4
figure 4

Maps of the relative bias [%] of mean daily precipitation in DJFM (left column) and JJAS (right column) for a the ensemble mean and for b ERA5 in comparison with GSOD station data. The marker size indicates the number of valid observations per season. c The probability density functions (PDFs) of daily precipitation amounts comparing GSOD and all other datasets at GSOD station locations. The probabilities were calculated in bins of 5 mm per day to reduce noise. We note that the largest intensities in the GSOD observations during the cold season occur in only few stations towards the Eastern part of the domain

Full size image
Fig. 5
figure 5

Maps of the wet-spell statistics presented in Table 3 for the DJFM (top row) and JJAS (bottom row) seasons: a average spell length, b total number of wet spells longer than 3 days, and c the longest continuous wet spell. The panel labelled ’Ensemble’ displays the mean of all km-scale simulations

Full size image
Fig. 6
figure 6

Diurnal cycles of the following hourly precipitation statistics, averaged over the JJAS season and above 2800 m on the TP: a mean precipitation; wet-hour b frequency and c percentage (expressed relative to the total number of hours in each bin); and d heavy (99th percentile) precipitation. The curve labelled ENS_MEAN displays the mean of all km-scale simulations

Full size image
Fig. 7
figure 7

Map of the timing [in UTC; LT is \(\sim\)UTC+6] of the diurnal maximum in mean three-hourly precipitation totals in the warm season. The contour labels indicate the center point of the three-hour window. The label ’Ensemble’ displays the mean of all km-scale simulations

Full size image
Fig. 8
figure 8

Maps of the average daily bias [\(^{\circ }\)C] of daily mean near-surface air temperature in DJFM (left column) and JJAS (right column) for a the ensemble mean and b ERA5 in comparison with GSOD station data. The marker size indicates the number of valid observations per season. c Same as Fig. 4c but for mean daily air temperatures, calculated for each degree using a ± 2\(^{\circ }\)C window and re-scaled by bin size to result in a cumulative probability of 1

Full size image
Fig. 9
figure 9

Percentiles of daily precipitation as a function of daily mean temperature averaged across a–c all stations, e–g stations below and (i-k) stations above 2800 meters. d, h, l Number of precipitation values in each temperature bin averaged across all stations in all three data sets considered - GSOD station observations, ERA5 reanalysis and high-resolution ensemble simulations. Precipitation intensity is plotted for the 80th, 90th, and 99th percentiles. The shading indicates the range between 10th and 90th percentile calculated over stations for each specific bin and each intensity percentile. The black dash-dotted (dashed) lines are the exponential relations given by a 7\(\%\) (14\(\%\)) increase of precipitation with temperature. The analysis covers the entire WY2020

Full size image