On Networks with Order Close to the Moore Bound

Abstract

The degree/diameter problem for mixed graphs asks for the largest possible order of a mixed graph with given diameter and degree parameters. Similarly the degree/geodecity problem concerns the smallest order of a k-geodetic mixed graph with given minimum undirected and directed degrees; this is a generalisation of the classical degree/girth problem. In this paper we present new bounds on the order of mixed graphs with given diameter or geodetic girth and exhibit new examples of directed and mixed geodetic cages. In particular, we show that any k-geodetic mixed graph with excess one must have geodetic girth two and be totally regular, thereby proving an earlier conjecture of the authors.

1 Introduction

It is often of practical interest to consider networks that include both undirected edges and directed arcs. For example, road networks contain both two-way and one-way streets and websites contain links that are unidirectional and others that are bidirectional. Such networks are represented mathematically by mixed graphs; such graphs have applications in job scheduling [35] and Bayesian inference [15] amongst others. The efficiency of such networks may be measured using such graph parameters as the diameter (longest distance between nodes) or the geodetic girth (which pertains to the uniqueness of short paths between nodes). In this paper we discuss two extremal problems for these parameters in mixed graphs.

In the case of undirected graphs, the degree/diameter problem asks for the largest possible order of a graph with given diameter and maximum degree. The order of such a graph is bounded above by the so-called Moore bound; a survey of this problem can be found in [33]. The degree/girth problem requires the smallest possible order of a graph with given minimum degree and girth; a good survey of this problem is [20]. For this problem the Moore bound now serves as a lower bound on the order. The degree/diameter problem has also been investigated in the setting of directed graphs [33] and mixed graphs [29]. Several recent papers, such as [32, 38], have also discussed a directed analogue of the degree/girth problem called the degree/geodecity problem. In [39] the present authors extended the degree/geodecity problem to mixed graphs and discussed the total regularity of extremal graphs in the degree/diameter and degree/geodecity problems.

The structure of this paper is as follows. Section 2 defines the notation that we will be using and provides some background on the problems that we will discuss. In Sect. 3 we prove the existence of mixed geodetic cages and discuss monotonicity relations. We then present strong new bounds on the excess of totally regular mixed graphs in Sect. 4 and generalise our results to mixed graphs that are not totally regular in Sect. 5, which allows us to prove the non-existence of k-geodetic mixed graphs with excess one for $k \ge 3$, thereby proving a conjecture of the authors in [39]. Employing similar counting arguments, we derive a new upper bound on the order of totally regular mixed graphs with undirected degree and directed degree equal to one in Sect. 6. In Sect. 7 we present new mixed and directed geodetic cages and give upper bounds for some other values of the degrees and geodetic girth using a computer search among mixed Cayley graphs. Finally in Sect. 8 we present figures of some known extremal graphs.

2 Notation

Formally, a mixed graph G consists of a set V(G) of vertices, a set E(G) of undirected edges and a set A(G) of directed arcs. An undirected edge is an unordered pair of vertices, whereas an arc is an ordered pair of vertices. We forbid loops as well as parallel edges and arcs. For any notation not defined here we refer to [4].

Each vertex u is incident with a certain number d(u) of undirected edges; we call this the undirected degree of u. Similarly the number of arcs with initial point u is the directed out-degree of u and is denoted $d^+(u)$, whereas the directed in-degree of u is the number of arcs of G with terminal vertex u and is written $d^-(u)$. If there is an edge between vertices u and v we write $u \sim v$, whereas the presence of an arc from u to v is indicated by $u \rightarrow v$. For any vertex u we set $U(u) = \{ u_1,u_2, \dots , u_r\} = \{ v \in V(G) : u \sim v\}$, $Z^-(u) = \{ v_1,v_2, \dots , v_s\} = \{ v \in V(G) : v \rightarrow u\}$ and $Z^+(u) = \{ u_{r+1}, \dots , u_{r+z}\} = \{ v \in V(G) : u \rightarrow v\}$. If there exist r and z such that for all vertices u we have $d(u) = r, d^+(u) = z$, then G is said to be out-regular. If we also have $d^-(u) = d^+(u) = z$ for all u then we say that G is totally regular. If $G^U$ and $G^Z$ denote respectively the undirected and directed subgraphs (i.e. the subgraphs induced by the edges/arcs), then it can be seen that G is out-regular if and only if $G^U$ is regular and $G^Z$ is out-regular, and G is totally regular if and only if $G^U$ is regular and $G^Z$ is diregular.

A walk W in G is a sequence $u_0u_1 \dots u_{\ell }$ of vertices of G such that for $0 \le i \le \ell -1$ either $u_i \sim u_{i+1}$ or $u_i \rightarrow u_{i+1}$. The length of the walk is $\ell$ and $u_0$ and $u_{\ell }$ are the initial and terminal vertices of W respectively. The walk is non-backtracking if the walk does not cross an edge and then immediately retrace it, i.e. if the walk does not contain a subsequence of three consecutive vertices $u_i \sim u_{i+1} \sim u_i$. We will call a non-backtracking walk in G a mixed path.

The distance d(u, v) from a vertex u to a vertex v is the length of a shortest mixed path with initial vertex u and terminal vertex v. Observe that we can have $d(u,v) \ne d(v,u)$. If there is no mixed path from u to v then we set $d(u,v) = \infty$. The diameter of G is defined to be $diam(G) = \max \{ d(u,v): u,v \in V(G)\}$. Suppose that for any ordered pair of (not necessarily distinct) vertices (u, v) of G there is at most one mixed path from u to v with length $\le k$; then we say that G is k-geodetic. The largest k such that G is k-geodetic is the geodetic girth or geodecity of G.

A mixed Moore graph is an out-regular mixed graph G such that for every pair of vertices u, v of G there is a unique mixed path of length $\le k$ from u to v. We can draw a mixed Moore tree to deduce an upper bound on the order of a mixed graph G with maximum undirected degree r, maximum directed out-degree z and diameter k. Fix a vertex u and call this root vertex Level 0 of the tree. Draw edges from Level 0 to Level 1 from u to all of the undirected neighbours of u and arcs from Level 0 to all of the directed out-neighbours of u. In general, once we have added all vertices at Level t, where $0 \le t \le k-1$, we add the next level to the tree by the following rule for each vertex $u_i$ in Level t:

• Draw arcs from Level t to Level $t+1$ from $u_i$ to all directed out-neighbours of $u_i$.

• If $u_i$ appears in Level t as the terminal vertex of an arc from Level $t-1$ then draw edges from Level t to Level $t+1$ from $u_i$ to all undirected neighbours of $u_i$.

• If $u_i$ appears in Level t as the endpoint of an edge from a vertex $u_j$ in Level $t-1$, then below $u_i$ in the Moore tree draw an edge from $u_i$ to Level $t+1$ to all undirected neighbours of $u_i$ apart from $u_j$.

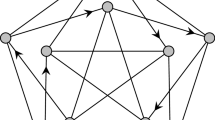
We continue this process until we have a tree of depth k. As G has diameter k all vertices of G are contained in the mixed Moore tree. An example for a mixed graph with maximum undirected degree $r = 3$, maximum directed out-degree $z = 3$ and diameter $k = 2$ is shown in Fig. 1.

Fig. 1

The Moore tree for $r = 3, z = 3, k = 2$

Counting the number of vertices in the Moore tree therefore gives an upper bound (called the mixed Moore bound) on the order of a mixed graph with given diameter. An exact expression for the Moore bound for mixed graphs was derived in [10] using recurrence relations.

Theorem 1

(Mixed Moore bound [10]) The order of a mixed graph with maximum undirected degree r, maximum out-degree z and diameter k is bounded above by

$$\begin{aligned} M(r,z,k) = A\frac{\lambda _1^{k+1}-1}{\lambda _1-1} + B\frac{\lambda _2^{k+1}-1}{\lambda _2-1},\end{aligned}$$

where

$$\begin{aligned} \phi = \sqrt{(r+z-1)^2+4z}, \lambda _1 = \frac{z+r-1+\phi }{2}, \lambda _2 = \frac{z+r-1-\phi }{2}\end{aligned}$$

and

$$\begin{aligned} A = \frac{\phi +(z+r+1)}{2\phi }, B = \frac{\phi -(z+r+1)}{2\phi }.\end{aligned}$$

If $r = 0$ or $z = 0$ then this expression reduces to the undirected and directed Moore bounds respectively.

A graph that meets the mixed Moore bound is called a mixed Moore graph. Recall that a mixed graph G is k-geodetic if and only if for any pair u, v of vertices of G there is at most one mixed path (i.e. non-backtracking mixed walk) of length $\le k$ from u to v in G. It is easily seen that a mixed graph is Moore if and only if it satisfies the following conditions.

Theorem 2

A mixed graph G is Moore if and only if

• G is totally regular with undirected degree r and directed degree z,

• the diameter of G is k, and

• G is k-geodetic.

Mixed Moore graphs with diameter $k = 2$ were first investigated by Bosák in the seventies [5,6,7]. In [7] he proved that any mixed Moore graph is totally regular and used spectral methods to prove that the undirected degree r and directed out-degree z of a mixed Moore graph with diameter two satisfy a very special condition.

Theorem 3

[7] Apart from trivial cases, if there exists a mixed Moore graph with diameter two, undirected degree r and directed out-degree z, then there exists a positive odd integer c such that $c\mathrel {|}(4z-3)(4z+5)$ and $c^2+3 = 4r$.

However, Theorem 3 leaves an infinite number of pairs r, z for which the existence of a mixed Moore graph with undirected degree r, directed out-degree z and diameter two is undecided. The smallest orders not covered by Theorem 3 are displayed in Table 1.

Table 1 Values of r and z not covered by Theorem 3

There is one known infinite family of mixed Moore graphs with diameter two, formed by collapsing all digons in the Kautz digraph K(d, k) into edges. This mixed graph can be described simply. Take an alphabet $\Omega$ of size $z+2$. The vertices of $\mathrm {Kautz}(z)$ are words ab, where $a \not = b$. For all $a,b,c \in \Omega$ with $a \not = b$ and $b\not = c$ we introduce an arc $ab \rightarrow bc$ when $c \not = a$ and an edge $ab \sim ba$. It is easily verified that this yields a mixed Moore graph with undirected degree $r = 1$, directed out-degree z and diameter $k = 2$. In fact it is shown in [24] using spectral techniques that these are the unique mixed Moore graphs with these parameters.

Theorem 4

[24] For all $z \ge 1$ there is a unique mixed Moore graph with undirected degree $r = 1$, directed out-degree z and diameter $k = 2$.

In [7] Bosák identified a further mixed Moore graph with undirected degree $r = 3$, directed out-degree $z = 1$, diameter $k = 2$ and order $M(3,1,2) = 18$. The uniqueness of this graph was proven in [34].

One method of searching for mixed Moore graphs is to restrict the search space to Cayley mixed graphs. By carrying out a computer search for Cayley mixed graphs that meet the Moore bound Jørgensen found two Cayley mixed Moore graphs with undirected degree $r = 3$, directed out-degree $z = 7$, diameter $k = 2$ and order $n = 108$ [26]. However, it has been shown that there are no further Cayley mixed Moore graphs with diameter two and order $\le 485$ [19, 30]. A search using a SAT solver has also completely ruled out the existence of mixed Moore graphs with diameter two and orders 40, 54 or 84 [28].

It is natural to ask whether there exist any mixed Moore graphs with diameter greater than two? It was shown by a counting argument in [34] that the answer to this question is negative, except in trivial cases.

Theorem 5

[34] There are no mixed Moore graphs with diameter $k \ge 3$, except for undirected and directed cycles.

Whilst there remain an infinite number of open cases, it is evident that it is very difficult for a mixed graph to meet the mixed Moore bound. In general the mixed Moore tree of depth k will either not contain all vertices of G (in which case the diameter of G is larger than k) or there will be vertices repeated in the Moore tree (in which case G is not k-geodetic). It is therefore of interest to study the structure of mixed graphs with order close to the mixed Moore bound. To this end in the conditions in Theorem 2 we can either relax the requirement that all of the vertices in the Moore tree be distinct or the requirement that the Moore tree contains all of the vertices of G. This motivates the following definitions.

Definition 1

• A mixed graph with maximum undirected degree r, maximum directed out-degree z, diameter k and order $M(r,z,k)-\delta$ is called an $(r,z,k;-\delta )$-graph and has defect $\delta$. A mixed graph with defect one is called an almost mixed Moore graph.

• A k-geodetic mixed graph with minimum undirected degree r, minimum directed out-degree z and order $M(r,z,k)+\epsilon$ is called an $(r,z,k;+\epsilon )$-graph and has excess $\epsilon$. The smallest possible value of $\epsilon$ such that there exists an $(r,z,k;+\epsilon )$-graph will be written $\epsilon (r,z,k)$. We set $N(r,z,k) = M(r,z,k)+\epsilon (r,z,k)$.

Recent progress on the problem of finding mixed graphs with small defect can be found in [1], in which a $(5,2,2;-4)$-graph is constructed and shown to be optimal. In [16, 31] mixed graphs with given diameter and order asymptotically approaching the Moore bound are constructed using voltage assignments and graphs on alphabets. The cases $\delta = 1$ and $\epsilon = 1$ are of particular interest. It was shown by the present authors that any $(r,z,2;-1)$- or $(r,z,2;+1)$-graph must be totally regular [39]. López and Miret used spectral theory to derive the following necessary condition for the existence of an almost mixed Moore graph with diameter $k = 2$ in [27].

Theorem 6

Let G be a (totally regular) $(r,z,2;-1)$ -graph. Then r is even and one of the following three possibilities holds:

• $r = 2$,

• there exists an odd integer c such that $c^2 = 4r+1$ and $c\mathrel {|}(4z+1)(4z-7)$ , or

• there exists an odd integer c such that $c^2 = 4r-7$ and $c\mathrel {|}(16z^2+40z-23)$.

Using the methods of López and Miret it is possible to show the following result, which we state without proof.

Theorem 7

Let G be a totally regular $(r,z,2,+1)$ -graph. Then either:

• $r = 2$,

• $4r+1 = c^2$ for some $c \in {\mathbb {N}}$ and $c\mathrel {|}(16z^2-24z+25)$ , or

• $4r-7 = c^2$ for some $c \in {\mathbb {N}}$ and $c\mathrel {|}(16z^2+40z+9)$.

It is proven in [11] that there is a unique $(2,1,2;-1)$-graph (displayed in Fig. 2) and in [17] it is shown that there are exactly three $(1,1,3;-1)$-graphs. In [39] a $(2,1,2;+1)$-graph is constructed (see Fig. 3) and is shown to be the unique graph with these parameters; this graph remains the only known mixed graph with excess one.

Fig. 2

A mixed almost Moore graph

Fig. 3

A mixed graph with excess one

If G is an $(r,z,k;-\delta )$-graph, then there will be exactly $\delta$ repetitions in the Moore tree of depth k based at any vertex u. We form a multiset R(u), with a vertex v appearing $t-1$ times in R(u) if it appears t times in the Moore tree; R(u) is called the repeat set of u. Similarly if G is an $(r,z,k;+\epsilon )$-graph then all vertices appearing in the Moore tree based at a vertex u will be distinct, but the tree will not contain all vertices of G. If G is totally regular, then there will be exactly $\epsilon$ vertices v satisfying $d(u,v) \ge k+1$; any such v is an outlier of u and the set O(u) of all outliers of u is the outlier set of u (observe that there are no repetitions in O(u)). For given r, z and k a mixed graph with smallest possible excess is an (r, z, k)-geodetic-cage, or a geodetic cage if the values of the parameters can be inferred from the context (we insert ‘geodetic’ to distinguish such constructions from extremal cycle-avoiding mixed graphs, which are already called mixed cages [2]).

3 Existence of Cages

One subtle point that does not arise in the degree/diameter problem is that it is not immediately clear that cages exist for all values of the degree d and girth g; therefore it is necessary to prove that for any $d \ge 2$ and $g \ge 3$ there exists a graph with degree d and girth g. This result was first shown by Sachs in [36] using a recursive construction. The upper bound in [36] was subsequently improved in a joint paper by Sachs and Erdős [18]. An approachable presentation of these proofs is given in an appendix of [20].

Our first step is therefore to show that geodetic cages exist for all values of the geodetic girth k and the degree parameters r and z. In the purely directed case we obtain the existence of geodetic cages and a good estimate of their order almost for free from a nice family of digraphs called the permutation digraphs. These digraphs were first mentioned in [21] and their properties further developed in [9]. They are defined as follows.

Definition 2

For $d,k \ge 2$ the vertex set of the permutation digraph P(d, k) consists of all sequences $x_0x_1\dots x_{k-1}$ of length k drawn from an alphabet $[d+k] = \{ 0,1,2,\dots , d+k-1\}$ such that for $0 \le i < j \le k-1$ we have $x_i \not = x_j$.

The adjacencies of P(d, k) are defined by

$$\begin{aligned} x_0x_1\dots x_{k-1} \rightarrow x_1x_2\dots x_{k-1}x_k,\end{aligned}$$

where $x_k \in ([d+k] - \{ x_0,x_1,\dots , x_{k-1}\} )$.

It is shown in [9] that permutation digraphs are highly symmetric. The symmetric group on $d+k$ symbols acts on P(d, k) in a natural way by permuting the symbols of the underlying alphabet, meaning that the permutation digraphs are arc-transitive, although not 2-arc-transitive. Their symmetry groups are derived and the Cayley permutation digraphs classified in [9]. The important property of the permutation digraphs from our point of view is that P(d, k) is k-geodetic and for fixed $k \ge 2$ the digraphs P(d, k) have order approaching the directed Moore bound M(d, k) asymptotically from above. The digraph P(2, 2) is displayed in Fig. 4.

Lemma 1

For $d,k \ge 2$ the permutation digraph P(d, k) is diregular with degree d, has geodetic girth k and has order

$$\begin{aligned} {}^{d+k}\!P_{k} = (d+k)(d+k-1)\dots (d+1).\end{aligned}$$

Hence for fixed $k \ge 2$ the excess of P(d, k) is

$$\begin{aligned} ((d+k)(d+k-1)\dots (d+1)) - (d^k+d^{k-1}+\dots +d+1) \sim \left( \frac{k(k+1)}{2}-1\right) d^{k-1} \end{aligned}$$

as $d \rightarrow \infty$.

Proof

For all $d,k \ge 2$ the digraph P(d, k) contains directed cycles of length $k+1$, for example

$$\begin{aligned} 012\dots (k-1) \rightarrow 12\dots (k-1)k \rightarrow 23\dots (k-1)k0 \rightarrow \dots \end{aligned}$$

$$\begin{aligned}\qquad \rightarrow k01\dots (k-2) \rightarrow 012\dots (k-1), \end{aligned}$$

so the geodetic girth of P(d, k) is certainly $\le k$.

By vertex-transitivity of P(d, k), to prove k-geodecity it is sufficient to demonstrate that if P and Q are paths of length $\le k$ in P(d, k) from the vertex $012\dots (k-1)$ to a vertex $x_0x_1\dots x_{k-1}$, then $P = Q$. All vertices at distance $r \le k-1$ from $012\dots (k-1)$ have first symbol r, whereas all vertices at distance k from $012\dots (k-1)$ have a first symbol that does not lie in $\{ 0,1,\dots ,k-1\}$. As $d(01\dots (k-1),x_0x_1\dots x_{k-1}) \le k$ by assumption, it follows that if $x_0 \in \{ 0,1,\dots ,k-1\}$ then both P and Q have length $x_0$, whereas if $x_0 \not \in \{ 0,1,\dots ,k-1\}$ then both P and Q must have length k; in either case $\ell (P) = \ell (Q)$.

If $x_0 = r \in \{ 0,1,\dots ,k-1\}$ then the only path with length r from $01\dots (k-1)$ to $x_0x_1\dots x_{k-1}$ is the path with initial vertex $01\dots (k-1)$ obtained by successively deleting the symbol i on the left-hand side and adding the symbol $x_{k-r+i}$ on the right for $i = 0,1,\dots ,r-1$. If $x_0 \not \in \{ 0,1,\dots ,k-1\}$, then the first arc e of both P and Q must be $012\dots (k-1)\rightarrow 12 \dots (k-1)x_0$. Deleting the arc e from P and Q leaves two paths $P'$ and $Q'$ of length $k-1$ from $12\dots (k-1)x_0$ to $x_0x_1\dots x_{k-1}$; by the above reasoning $P' = Q'$ and hence $P = Q$. $\square$

Fig. 4

P(2, 2)

Lemma 1 shows that a (0, z, k)-geodetic cage exists for all values of $z,k \ge 1$. As the permutation digraphs are diregular, we see that for $d,k \ge 1$ there is also a smallest possible diregular k-geodetic digraph with degree d. By combining this construction with that of Sachs [36] for undirected graphs we can show the existence of mixed geodetic cages for all $r,z,k \ge 1$.

Theorem 8

There exists a mixed geodetic (r, z, k)-cage for all $r, z, k \ge 1$.

Proof

We employ a truncation argument. Let H be an undirected cage with degree r, girth $g = 2k+1$ and order n. Let $H'$ be a directed geodetic cage with geodetic girth k and directed out-degree nz. We form a mixed graph G by identifying each vertex u of $H'$ with an isomorphic copy $H_u$ of H and connecting the copies of H by arcs in accordance with the topology of $H'$; specifically, for each vertex u of $H'$ partition the nz arcs from u in $H'$ into n sets $A_1,A_2,\dots ,A_n$ of z arcs and assign a set $A_i$ of arcs to each of the n vertices in $H_u$, such that if an arc in $A_i$ goes to a vertex v in $H'$, then in G it is directed to any vertex of $H_v$. The resulting mixed graph G obviously has geodetic girth k. A similar construction starting with directed cages substituted for vertices of an undirected cage establishes the other part of the theorem.

$\square$

As in the undirected degree/girth problem, the bounds given in Theorem 8 are much too large to be of any practical help. We also note that by using regular graphs with girth $2k+1$ (which exist by [36]) and diregular k-geodetic digraphs (we can use the permutation digraphs), the truncation argument in Theorem 8 also shows the existence of a smallest totally regular $(r,z,k;+\epsilon )$-graph.

Corollary 1

For all $r,z \ge 1$ and $k \ge 2$ there exists a smallest totally regular $(r,z,k;+\epsilon )$ -graph.

Now that the existence of mixed geodetic cages has been established, the question of monotonicity arises. Intuition suggests that the order of a cage should grow strictly with increasing r, z and k. Monotonicity of the order of cages in the undirected degree/girth problem was proven by Fu, Huang and Rodger [22] and degree monotonicity of undirected cages was discussed in [40], but appears to be a difficult problem. We generalise the approach of [22] to prove strict monotonicity of the order of mixed cages in the geodetic girth k. The following proof also applies to purely directed geodetic cages.

Theorem 9

$N(r,z,k) < N(r,z,k+1)$ for all $k \ge 2$.

Proof

Let G be an $(r,z,k+1)$-cage. Suppose that there exists a vertex u of G with even undirected degree $d(u) = 2t$. Write $U(u) = \{ u_1,u_2, \dots , u_{2t-1},u_{2t}\}$. Define the graph $G'$ as follows: delete u from G, join $u_{2i-1}$ to $u_{2i}$ by an undirected edge for $1 \le i \le t$ and for every vertex $u^-$ in $Z^-(u)$ insert an arc from $u^-$ to some vertex $u^+$ in $Z^+(u)$. This construction is shown in Fig. 5, with the new arcs and edges shown dashed. Call the added arcs and edges new elements.

Suppose that $G'$ is not k-geodetic; let w and $w'$ be vertices of $G'$ with distinct mixed paths P and Q of length $\le k$ from w to $w'$. As each new element in $G'$ can be extended to a walk of length two in G whilst preserving the non-backtracking property and G is $(k+1)$-geodetic, we can assume that the mixed path P contains at least two new elements. Examining a mixed path with length $\le k-2$ between adjacent new elements in P, we see that there exists a non-backtracking closed walk of length k through u in G, which is impossible. Thus G is at least k-geodetic and, having order smaller than the $(r,z,k+1)$-cage G, its geodetic girth must be exactly k.

Thus we can assume that every vertex of G has odd undirected degree. Let $u \sim v$ be an undirected edge of G. Let $U(u) = \{ v,u_1,u_2,\dots , u_{2t}\}$ and $U(v) = \{ u,v_1,v_2,\dots , v_{2s}\}$. Form a new graph $G''$ by deleting u and v and matching up the remaining neighbours of u and v by new elements as in the previous construction, i.e. setting $u_{2i-1} \sim u_{2i}$ for $1 \le i \le t$, $v_{2j-1} \sim v_{2j}$ for $1 \le j \le s$ and inserting an arc from each vertex of $Z^-(u)$ to $Z^+(u)$ and an arc from each vertex of $Z^-(v)$ to $Z^+(v)$. Assuming $k \ge 2$, notice that the sets $U(u)-\{ v\}$, $U(v)-\{ u\}$, $Z^-(u)$, $Z^+(u)$, $Z^-(v)$ and $Z^+(v)$ are pairwise disjoint.

If $G''$ has geodetic girth $\le k-1$, with two distinct mixed paths P and Q from a vertex w to a vertex $w'$, then as before we can assume that P contains two new elements.

Consider consecutive new elements in P. By the preceding argument these new elements cannot be associated with same vertex in G, for example a new edge between undirected neighbours of u and an arc from $Z^-(u)$ to $Z^+(u)$ would yield a contradiction as above. By symmetry we can assume that the first element is associated with u and the second with v; for example, these elements could be a new arc from $Z^-(u)$ to $Z^+(u)$ followed by a new edge in U(v). Looking at the mixed subpath of P between these consecutive new elements, we see that in G there is either a mixed path of length $\le k-2$ from $N^+(u)$ to $N^-(v)$; it follows that there are distinct mixed paths of length $\le k$ from u to v in G, a contradiction, so $G''$ is k-geodetic. $\square$

Fig. 5

The construction in Theorem 9

Applying the procedure of Theorem 9 to a smallest totally regular $(r,z,k;+\epsilon )$-graph (which we know to exist by Corollary 1) by joining vertices of $Z^-(u)$ to $Z^+(u)$ by arcs in a one-to-one fashion, we see that strict monotonicity in the geodetic girth k also holds for the order of smallest possible totally regular $(r,z,k;+\epsilon )$-graphs. Monotonicity in the directed out-degree is simple to demonstrate.

Theorem 10

$N(r,z,k) \le N(r,z+1,k)$. If $r = 0$, then strict inequality holds.

Proof

Let G be an $(r,z+1,k)$-cage. Delete one outgoing arc from every vertex; the resulting graph has minimum undirected degree r, minimum directed out-degree z and, as a subgraph of G, is obviously still k-geodetic. If $r = 0$, then the deleted arcs can be chosen such that the resulting subgraph $G'$ of G contains a source vertex z, i.e. the in-degree of z is zero; deleting z does not decrease the geodetic girth or the minimum out-degree. $\square$

4 Bounds on Totally Regular Mixed Graphs with Small Excess

The proof of the non-existence of mixed Moore graphs [34] uses an argument that admits of very useful generalisations. We now present a counting argument that gives a new bound on the order of totally regular $(r,z,k;\epsilon )$-graphs.

Theorem 11

For $k \ge 3$ , the excess $\epsilon$ of a totally regular $(r,z,k;+\epsilon )$ -graph satisfies

$$\begin{aligned} \epsilon \ge \frac{r}{\phi }\Bigl [\frac{\lambda _1^{k-1}-1}{\lambda _1 - 1}-\frac{\lambda _2^{k-1}-1}{\lambda _2 - 1}\Bigr ], \end{aligned}$$

where

$$\begin{aligned} \phi = \sqrt{(r+z-1)^2+4z}, \\ \lambda _1 = \frac{1}{2}(r+z-1 + \phi ) \end{aligned}$$

and

$$\begin{aligned} \lambda _2 = \frac{1}{2}(r+z-1 - \phi ). \end{aligned}$$

Proof

Let the vertex x be the end-point of an arc in an undirected branch $T(u_i)$ of the Moore tree of depth k based at a vertex u such that $d(u,x) \le k-1$. We will call such a vertex an arrow vertex (with respect to u). All undirected neighbours of the arrow vertex x occur in $T(u_i)$, together with a single vertex of $Z^-(x)$. As G is totally regular, there are $z-1$ vertices of $U(x) \cup Z^-(x)$ that do not occur in $T(u_i)$. Suppose that every vertex of Z(u) can reach x by a mixed path of length $\le k$. As x cannot occur in the directed branches of u, it would then follow that each of the z directed branches must contain a vertex in $U(x) \cup Z^- (x)$; however, as $r+1$ vertices of $U(x) \cup Z^-(x)$ already occur in $T(u_i)$, this means that a vertex is repeated in the Moore tree, which contradicts k-geodecity. Therefore $x \in \bigcup _{u_i \in Z(u_i)}O(u_i)$.

We now count the number of such arrow vertices x. For $1 \le t \le k-1$, let $Z_t$ be the number of vertices in the undirected branches at Level t in the Moore tree based at u that are end-points of arcs emanating from Level $t-1$ and let $U_t$ be the number of vertices in the undirected branches at Level t that are connected by an edge to Level $t-1$. Obviously $U_1 = r, Z_1 = 0$ and $Z_1 = rz$. These numbers satisfy the recurrence relations

$$\begin{aligned} U_{t+1} = (r-1)U_t+rZ_t, Z_{t+1} = zU_t + zZ_t \end{aligned}$$

for $t \ge 1$. It follows that

$$\begin{aligned} Z_{t+2} = zU_{t+1}+zZ_{t+1} = z((r-1)U_t+rZ_t)+zZ_{t+1}.\end{aligned}$$

Substituting using the second relation,

$$\begin{aligned} Z_{t+2} = zZ_{t+1}+rzZ_t+z(r-1)(1/z)(Z_{t+1}-zZ_t) = (r+z-1)Z_{t+1}+zZ_t.\end{aligned}$$

This second-order recurrence relation has characteristic equation

$$\begin{aligned} \lambda ^2 - (r+z-1)\lambda - z = 0,\end{aligned}$$

with solutions $\lambda _1 , \lambda _2$ as given in the statement of the theorem. Observe that the discriminant $\phi ^2 = (r+z-1)^2+4z$ is strictly positive, so $\lambda _1, \lambda _2$ are real and distinct. It follows that

$$\begin{aligned} Z_t = A\lambda _1^t + B\lambda _2^t \end{aligned}$$

for $t \ge 1$ and some constants A and B. Substituting $Z_1 = 0, Z_2 = rz$, we obtain

$$\begin{aligned} Z_t = \frac{rz}{\phi }(\lambda _1^{t-1}-\lambda _2^{t-1})\end{aligned}$$

for $t \ge 1$. Summing, we find that there are

$$\begin{aligned} \sum _{i = 0}^{k-2}\frac{rz}{\phi }(\lambda _1^{i}-\lambda _2^{i}) = \frac{rz}{\phi }\left[ \frac{\lambda _1^{k-1}-1}{\lambda _1 - 1}-\frac{\lambda _2^{k-1}-1}{\lambda _2 - 1}\right] \end{aligned}$$

such vertices. As the union of the outlier sets of the vertices in Z(u) contain a maximum of $z\epsilon$ distinct vertices between them, it follows that

$$\begin{aligned} z\epsilon \ge \frac{rz}{\phi }\left[ \frac{\lambda _1^{k-1}-1}{\lambda _1 - 1}-\frac{\lambda _2^{k-1}-1}{\lambda _2 - 1}\right] \end{aligned}$$

and the result follows. $\square$

Some values of the lower bound in Theorem 11 for $k = 4$ are displayed in Table 2. We are not aware of any instance in which the bound of Theorem 11 is tight. However, as we shall now demonstrate, it does yield a powerful result on mixed graphs with excess one.

Table 2 Lower bound on the excess from Theorem 11 for $k = 4$

Corollary 2

If G is a totally regular $(r,z,k;+1)$-graph with $k \ge 3$, then $r = 1$ and $k = 3$.

Theorem 12

There are no totally regular $(r,z,k;+1)$-graphs for $k \ge 3$.

Proof

Let G be a totally regular $(1,z,3;+1)$-graph. For any vertex $u \in V(G)$ write $u^*$ for the undirected neighbour of u. Let the adjacency matrices of $G, G^U$ and $G^Z$ be $A, A_U$ and $A_Z$ respectively. Fix a vertex u and draw the Moore tree rooted at u. Examination of the Moore tree shows that there are two walks of length $\le 3$ from u to itself (the trivial walk u and the walk $u \sim u^* \sim u$ of length two), two walks of length $\le 3$ from u to $u^*$ ($u \sim u^*$ and $u \sim u^* \sim u \sim u^*$), three walks of length $\le 3$ from u to any directed out-neighbour v of u ($u \rightarrow v, u \sim u^* \sim u \rightarrow v$ and $u \rightarrow v \sim v^* \sim v$) and unique walks of length $\le 3$ from u to the vertices at distance two and three from u. It follows that

$$\begin{aligned} I+A+A^2+A^3 = I+J+A+A_Z-P,\end{aligned}$$

where I is the $n \times n$ identity matrix, J is the all-one matrix and $P_{vv'} = 1$ if $o(v)=v'$ and 0 otherwise. As G is totally regular, J commutes with the left-hand side, I and $A_Z$; therefore $JP = PJ$ and o is a permutation.

Take an edge $uu^*$. The argument of Theorem 11 and the fact that o is a permutation shows that $o(Z^+(u)) = Z^+(u^*)$ and $o(Z^+(u^*)) = Z^+(u)$. Applying this result to an arbitrary directed in-neighbour v of u, we see that there is a path $v \sim v^* \rightarrow o(u)$. Let $w \in Z^+(o(u))$. A diagram of this situation is shown in Fig. 6. There is a path of length three from v to w, so $d(u,w) \ge 3$; in fact, since o is a permutation, we have equality. Since only $r+z-1$ in-neighbours of w lie in the Moore tree rooted at u, it follows that w must be the outlier of an out-neighbour of u. Examining the Moore tree of depth three based at v, we see that if w is an outlier of a vertex in $Z^+(u)$, then it would appear twice in the Moore tree rooted at v, once in the undirected $v^*$-branch and once in the u-branch in $Z^+(u^*)$, violating 3-geodecity. Therefore w is the outlier of $u^*$; as the excess is one, $u^*$ has a unique outlier, so $z = 1$.

Fig. 6

Configuration for Theorem 12 for $z = 2$

We can dispose of the case $r = z = 1, k = 3$ by the argument of Theorem 11. Let $u_8 \sim a, u_8 \rightarrow b, u_9 \rightarrow c, u_{10} \sim d, u_{10} \rightarrow e$; see Fig. 7. Our argument shows that $o(u_2) = u_3$, so

$$\begin{aligned} \{ a,b,c,d,e\} = \{ u,u_1,u_6,u_7,u_{11}\} ,\end{aligned}$$

where $u_{11} = o(u)$. As the undirected neighbours of $u, u_1$ and $u_6$ are accounted for, $\{ b,c,e\} = \{ u,u_1,u_6\}$ and $\{ a,d\} = \{ u_7,u_{11}\}$. We have $\{ c,e\} \not = \{ u,u_1\}$ or there would be a repeat in the Moore tree rooted at $u_5$. $u \not = b$ or else there would be paths $u_4 \sim u_2$ and $u_4 \rightarrow u_8 \rightarrow u \rightarrow u_2$, so $u \in \{ c,e\}$. Thus $u_1 \not \in \{ c,e\}$, so $b = u_1$ and $\{ c,e \} = \{ u,u_6\}$. By 3-geodecity applied to $u_8$, $b = u_1$ implies that $a \not = u_7$, so $a = u_{11} = o(u)$ and hence $d = u_7$. $e \not = u_6$, or $u_{10}$ would have two paths of length $\le 3$ to $u_7$. Therefore $c = u_6, e = u$.

Taking into account all adjacencies, it follows that there are three arcs from $\{ u_6,u_7,u_{11}\}$ to $\{ u_4,u_9,u_{11}\}$. $u_{11} \not \rightarrow u_{11}$ and $u_{11} \not \rightarrow u_4$, or we would have $u_4 \rightarrow u_8 \sim u_{11} \rightarrow u_4$. Hence $u_{11} \rightarrow u_9$. $u_6 \not \rightarrow u_{11}$, or $u_9 \rightarrow u_6 \rightarrow u_{11} \rightarrow u_9$, so $u_6 \rightarrow u_4$ and $u_7 \rightarrow u_{11}$. But now there are paths $u_1 \sim u \rightarrow u_2 \sim u_4$ and $u_1 \rightarrow u_3 \sim u_6 \rightarrow u_4$, contradicting 3-geodecity. As G has even order, G has excess $\epsilon \ge 3$. $\square$

Fig. 7

Moore tree for a 3-geodetic mixed graph with $r = z = 1$

It follows from Corollary 2, Theorem 12 and the results of [39] that any $(r,z,k;+1)$-graph is either totally regular with $k = 2$, satisfying the conditions in Theorem 7, or else $k \ge 3$, $z \ge 2$ and G is not totally regular.

We conclude this section with a result on the connection between outlier sets and automorphisms of mixed graphs with excess one. It is known that the outlier function of a digraph G with excess one is an automorphism if and only if G is diregular [38]. The above results now allow us to extend this result to the more general mixed setting.

Theorem 13

The outlier function of an $(r,z,k;+1)$ -graph G is an automorphism if and only if G is totally regular.

Proof

Suppose firstly that G is not totally regular; recall that G must be out-regular. Let $v' \in S'$. Suppose that o is an automorphism. It follows that $o(v') \in S'$. However, this implies that $o(v')$ has $> r+z$ in-neighbours distributed among the $r+z$ branches of the Moore tree based at $v'$, so that some out-neighbour of $v'$ has $\ge 2$ mixed paths to $o(v')$ with length $\le k$. Thus if o is an automorphism, then G is totally regular.

Now let G be totally regular. Let $k = 2$ and write A for the adjacency matrix of G. Then

$$\begin{aligned} I + A + A^2 = J + rI - P,\end{aligned}$$

where I is the $n \times n$ identity matrix, J is the all-one matrix and $P_{uv} = 1$ if $o(u) = v$ and 0 otherwise. As G is totally regular, both I and J commute with A. Therefore P commutes with A, so that o is an automorphism. There are no totally regular mixed graphs with excess one for $k \ge 3$ by Theorem 12, so the proof is complete. $\square$

5 Excess of Mixed Graphs that are Not Totally Regular

We will now revisit the counting arguments used in the previous section to derive a bound in the more difficult context of mixed graphs that are not totally regular. We will see that a bound for all mixed graphs, totally regular or not, can be achieved by relaxing the bound in Theorem 11 by a factor of $\frac{z}{2r+3z}$. We will need the following result from [39].

Theorem 14

[39] Any $(r,z,k;+1)$-graph must be totally regular if either $k = 2$ or $z = 1$.

Using the new bound presented in the following theorem we will improve on Theorem 14 significantly.

Theorem 15

The excess of any (r, z, k)-cage satisfies

$$\begin{aligned} \epsilon \ge \frac{rz}{(2r+3z)\phi }\Bigl [\frac{\lambda _1^{k-1}-1}{\lambda _1 - 1}-\frac{\lambda _2^{k-1}-1}{\lambda _2 - 1}\Bigr ], \end{aligned}$$

where $\lambda _1, \lambda _2$ and $\phi$ are as defined in Theorem 11.

Proof

Let G be an (r, z, k)-cage. We can assume that the directed subgraph of G is out-regular, by deleting some arcs if necessary. Let the number of arrow vertices in the Moore tree of an out-regular $(r,z,k;+\epsilon )$-graph be A(r, z, k). By the calculation of Theorem 11 we know that

$$\begin{aligned} A(r,z,k) = \frac{rz}{\phi }\Bigl [\frac{\lambda _1^{k-1}-1}{\lambda _1 - 1}-\frac{\lambda _2^{k-1}-1}{\lambda _2 - 1}\Bigr ].\end{aligned}$$

We are therefore aiming to prove that

$$\begin{aligned} \epsilon \ge \frac{1}{2r+3z}A(r,z,k).\end{aligned}$$

We have $\frac{A(r,z,k)}{2r+3z} < \frac{A(r,z,k)}{r}$, where $\frac{A(r,z,k)}{r}$ is the number of arrow vertices per undirected branch of an out-regular $(r,z,k;+\epsilon )$-graph. Thus each branch contains more than $\frac{A(r,z,k)}{2r+3z}$ vertices, so if G contains a vertex u with undirected degree $d(u) \ge r+1$ then the claimed bound holds. Hence we can assume that G is out-regular.

Let the deficiency $\sigma ^-(v)$ of a vertex $v \in S$ be $z - d^-(v)$ and the surplus $\sigma ^+(v')$ of a vertex $v' \in S'$ be $d^-(v')-z$. As G is out-regular we have for the total deficiency $\sigma$

$$\begin{aligned} \sigma = \sum _{v\in S}\sigma ^-(v) = \sum _{v' \in S'}\sigma ^+(v').\end{aligned}$$

As each vertex in $S'$ contributes at least one to $\sigma$, we trivially have $\sigma \ge |S'|$. We will now find an upper bound for $\sigma$ in terms of r, z and $\epsilon$.

Fix a vertex u of G and draw the Moore tree of depth k rooted at u. Write $U(u) = \{ u_1,u_2, \dots , u_r\}$. Let $v \in S$ have deficiency $\sigma ^-(v) = s$. Suppose firstly that $d(u,v) \ge k$ (i.e. either v lies at the bottom of the tree or $v \in O(u)$). Then v can have in-neighbours in at most $r+z-s$ branches of the Moore tree and so lies in the outlier sets of at least s members of $N^+(u)$.

Now suppose that either $u = v$ or $d(u,v) \le k-1$ and v lies in an undirected branch of the tree. At most $z - s$ directed branches of the tree can contain in-neighbours of v (in fact $z-s-1$ branches if v is an arrow vertex), so again v occurs at least s times in the multiset $O(Z^+(u))$.

Lastly we must consider the case that v lies in a directed branch of the tree and $d(u,v) \le k-1$. Consider the Moore tree based at any $u_i \in U(u)$, say $u_1$. v lies in an undirected branch of this tree and so by our previous analysis v occurs at least s times in $O(N^+(u_1))$.

We have now dealt with all members of S. Summing their deficiencies to find $\sigma$ we find that the elements of S appear at least $\sigma$ times in the multiset $O(N^+(u))\cup O(N^+(u_1))$. As this multiset contains $(2r+2z)\epsilon$ elements, we conclude that

$$\begin{aligned} \sigma \le (2r+2z)\epsilon .\end{aligned}$$

We now estimate the size of the set $S'$. Again we consider the Moore tree rooted at u. If an arrow vertex x relative to u lies in $V(G) - S'$, then x cannot have an in-neighbour in every directed branch of the tree and so must be an outlier of at least one directed out-neighbour of u. There are $z\epsilon$ elements in $O(Z^+(u))$, so it follows that at least $A(r,z,k)-z\epsilon$ of the arrow vertices must lie in $S'$. Therefore

$$\begin{aligned} (2r+2z)\epsilon \ge \sigma \ge |S'| \ge A(r,z,k)-z\epsilon .\end{aligned}$$

Rearranging we derive the inequality

$$\begin{aligned} \epsilon \ge \frac{1}{2r+3z}A(r,z,k).\end{aligned}$$

This proves the theorem. $\square$

This result now enables us to rule out the existence of mixed graphs with excess one for $k \ge 4$ and ‘most’ values of r and z for $k = 3$.

Theorem 16

There are no $(r,z,k;+1)$-graphs for $k \ge 4$ or for $k = 3$, $r \ge 4$ and $z > \frac{2r}{r-3}$.

Proof

Setting $\epsilon = 1$ in Theorem 15 shows that if $A(r,z,k) > 2r+3z$, then no $(r,z,k;+1)$-graph can exist. If $k \ge 5$, then

$$\begin{aligned} A(r,z,k) \ge A(r,z,5) = rz^3+2r^2z^2+r^3z-r^2z+rz.\end{aligned}$$

If $z \ge 2$, then this expression obviously exceeds $2r+3z$, so let $z = 1$. Then by Theorem 14G must be totally regular; however, no such graphs exist by Theorem  12.

Let $k = 4$. We have $A(r,z,4) = rz^2+zr^2$. If $r \ge 2$ and $z \ge 2$, then $rz^2+zr^2 \ge 4r + 4z > 2r+3z$. The result follows for $z = 1$ by Theorem 14 and Theorem 12, so we can assume that $r = 1$. We want to show that $z^2 + z > 3z + 2$, i.e. $z^2 - 2z - 2 > 0$. This inequality holds for $z \ge 3$, so this leaves only the pair $(r,z) = (1,2)$ to deal with. However in this case the Moore bound M(1, 2, 4) is even, so that G must have odd order. However, $r = 1$ implies that G has a perfect matching, so this is impossible.

Finally let $k = 3$. We have $A(r,z,3) = rz$, so $A(r,z,3) > 2r+3z$ if and only if $r \ge 4$ and $z > \frac{2r}{r-3}$. $\square$

For $k = 3$ this leaves open the cases $r = 1,2,3$, $r = 4$ and $2 \le z \le 8$, $r = 5$ and $2 \le z \le 5$, $r = 6$ and $2 \le z \le 4$, $r = 7,8$ and 9 and $2 \le z \le 3$ and $r \ge 10$ and $z = 2$. We can deal with the majority of these cases by a slightly more sophisticated method.

Lemma 2

If G is an $(r,z,k;+1)$-graph that is not totally regular, then every vertex $v' \in S'$ has directed in-degree $z+1$. Therefore $\sigma = |S'|$.

Proof

Consider the Moore tree rooted at $v' \in S'$. Each branch of the tree can contain at most one in-neighbour of $v'$ by k-geodecity. Therefore, as $v'$ has at least $r+z+1$ in-neighbours we conclude that each branch contains exactly one in-neighbour of $v'$ and $o(v') \in Z^-(v')$. Hence $v'$ has exactly $r+z+1$ in-neighbours. $\square$

Lemma 3

No $v' \in S'$ is an outlier.

Proof

Assume for a contradiction that G is an $(r,z,k;+1)$-graph in which $o(u) = v'$ for some $u \in V(G)$ and $v' \in S'$. As $v'$ is the outlier of u, no in-neighbour of $v'$ can lie at distance less than k from u. By k-geodecity, we conclude that every branch of the Moore tree rooted at u contains a unique in-neighbour of $v'$ at distance k from u. Therefore we must have $o(u) \in N^-(v')$ to account for the final in-neighbour of $v'$. As $v' = o(u)$, this contradicts k-geodecity. $\square$

Lemma 4

For $k = 3$, if an $(r,z,3;+1)$-graph exists, then $z^2+z+r \ge \sigma \ge z+r$.

Proof

Let G be an $(r,z,3;+1)$-graph. The Moore bound for $k = 3$ is

$$\begin{aligned} M(r,z,3) = r^3+z^3+3rz^2+3r^2z-r^2+z^2+r+z+1.\end{aligned}$$

The order of G is $n = M(r,z,3)+1$. The Moore bound for $k = 2$ is

$$\begin{aligned} M(r,z,2) = r^2+z^2+2rz+z+1.\end{aligned}$$

Fix some $v' \in S'$. By Lemma 3, every vertex of G can reach $v'$ by a mixed path of length $\le 3$. We achieve a lower bound for the number of these vertices by assuming that $S \subseteq N^-(v')$. Taking into account that $v'$ has exactly one extra directed in-neighbour by Lemma 2 and since all vertices of $T_{-3}(v')$ are distinct by 3-geodecity we obtain the following inequality:

$$\begin{aligned} n = M(r,z,3)+1 \ge M(r,z,3)+M(r,z,2) -\sigma (1+r+z). \end{aligned}$$

Rearranging,

$$\begin{aligned} \sigma (1+r+z) \ge M(r,z,2)-1 = r^2+z^2+2rz+z. \end{aligned}$$

Multiplying out, it is easily seen that $\sigma \ge r+z.$ Now we turn to the upper bound. Fix a vertex u and draw the Moore tree based at u. By the argument of Theorem 15, we see that any vertex v in S that lies in $\{ u,o(u) \} \cup N^k(u)$ or any of the undirected branches of the tree must be an outlier of at least $\sigma ^-(v)$ vertices in $N^+(u)$. Therefore these vertices between them contribute at most $r + z$ to the total $\sigma$.

Fix a directed out-neighbour $u^+$ of u and consider the vertices in the Moore tree rooted at $u^+$ at distance $\le 1$ from $u^+$. Any vertex $v \in S$ belonging to this set will be an outlier of at least $\sigma ^-(v)$ vertices in $Z^+(u^+)$. Between them such vertices can therefore contribute at most $z^2$ to the total $\sigma$. Since we have now considered all vertices in G, the conclusion follows. $\square$

Theorem 17

There are no $(r,z,3;+1)$-graphs with $r \ge 2$.

Proof

Suppose that G is an $(r,z,3;+1)$-graph with $r > 1$. We know from Lemma 4 that $z^2+r+z \ge \sigma \ge r+z$, so we can write $\sigma = z^2+r+z-\alpha$, where $0 \le \alpha \le z^2$. Fix an arbitrary vertex u of G and draw the Moore tree rooted at u. There are rz arrow vertices in the tree relative to u, i.e. rz vertices in the set $Z^+(U(u))$. If any of the arrow vertices does not belong to $S'$, then it will be an outlier of a vertex in $Z^+(u)$. It follows that at least $(r-1)z$ of the arrow vertices belong to $S'$. Repeating this reasoning for each vertex in $N^+(u)$ and taking into account that the vertices of $Z^+(u)$ are arrow vertices relative to any vertex in U(u), we see that there are at least

$$\begin{aligned} (r-1)z + (r-1)z + (r-1)(r-2)z + z^2(r-1) = (r-1)(z^2+rz) \end{aligned}$$

vertices of $S'$ in the tree. In fact, if we take u to be an element of $S'$, a valid assumption by Theorem 12, then we can actually deduce that

$$\begin{aligned} \sigma = z^2+r+z -\alpha = |S'| \ge (r-1)(z^2+rz)+1.\end{aligned}$$

Rearranging, we see that $\alpha$ must satisfy

$$\begin{aligned} \alpha \le z^2+r+z-rz^2-r^2z+z^2+rz-1 = -zr^2-(z^2-z-1)r+(2z^2+z-1).\end{aligned}$$

If $r \ge 2$ and $z \ge 2$, then

$$\begin{aligned} \alpha \le -zr^2-(z^2-z-1)r+(2z^2+z-1) \le -4z-2(z^2-z-1)+(2z^2+z-1) = -z+1 < 0, \end{aligned}$$

so it follows that we must have $r = 1$ and, considering the parity of the Moore bound, z must be odd. $\square$

By Theorems 16 and 17 the only remaining open case left for $k \ge 3$ is the question of the existence of a non-totally regular $(1,z,3;+1)$-graph. We finally settle this outstanding problem.

Theorem 18

If G is an $(r,z,k;+1)$-graph, then $k = 2$ and G is totally regular.

Proof

Suppose that G is an $(r,z,k;+1)$-graph with $k \ge 3$. Then by Theorems 16 and 17 we have $r = 1$, $k = 3$ and z is odd. Also G is not totally regular by Theorem 12, so that by Theorem 14 we have $z \ge 3$. Fix a vertex u of G. Let $u^*$ be the undirected neighbour of u and $\{ u_1,u_2,\dots ,u_z\}$ be the set $Z^+(u)$ of directed out-neighbours of u. Draw the Moore tree of depth 3 rooted at u.

By counting the in-neighbours of a vertex $v \in S$ that are available to lie in the directed branches of the tree, it can be seen that v will be the outlier of at least $\sigma ^-(v)$ vertices of $N^+(u)$ unless v lies in $U(Z^+(u))$, i.e. unless v is the undirected neighbour of a directed out-neighbour of u. For example, if $v \in Z^+(u)$, then the vertices $u^*$ and v can reach v by mixed paths of length $\le k$ and v has two in-neighbours already appearing in the tree (one is u and the other is $v^*$ at Level 2), so that v has at most $z-\sigma ^-(v)-1$ further in-neighbours that can lie in the remaining $z-1$ directed branches, so that v is the outlier of at least $\sigma ^-(v)$ vertices in $N^+(u)$. Repeating this analysis for each position in the Moore tree implies the result.

However, if v lies in $U(Z^+(u))$, then we can only say that it will be the outlier of at least $\sigma ^-(v)-1$ vertices of $N^+(u)$ (it can be reached by two vertices of $N^+(u)$ by $\le k$-paths and has a further $z-\sigma ^-(v)$ in-neighbours available for the remaining $z-1$ directed branches). Observe also that if an arrow vertex in the Moore tree lies in S, then this vertex v will be an outlier of at least $\sigma ^-(v)+1$ vertices of $Z^+(u)$.

Summing the deficiencies of all the vertices in S to get the total deficiency $\sigma$, we conclude that there are at most $2z+1$ vertices of S, for at most z vertices of S can lie in $U(Z^+(u))$ and every other vertex v of S is an outlier of at least $\sigma ^-(v)$ vertices in $N^+(u)$ and hence appears at least $\sigma ^-(v)$ times in $o(N^+(u))$, which is a multiset with size $z+1$. We now make this estimate more precise. For any vertex u of G define $\rho (u) = |S \cap U(Z^+(u))|$. Also let $\rho _{\min } = \min \{ \rho (u) : u \in V(G)\}$. If u is a vertex at which this minimum value $\rho _{ \min }$ is achieved, then as there are exactly $\rho _{\min }$ undirected neighbours of $Z^+(u)$ that lie in S, the total deficiency satisfies $\sigma \le z+\rho _{\min } +1$.

Suppose that $\rho _{\min }\ge 1$. For any vertex u, the sets $U(Z^+(u))$, $U(Z^+(u^*))$ and $U(Z^+(u_i))$ for $1 \le i \le z$ are mutually disjoint and each contain at least $\rho _{\min }$ vertices of S, which are distinct by 3-geodecity. Thus

$$\begin{aligned} (z+2)\rho _{\min } \le |S| \le \sigma \le z+\rho _{\min }+1. \end{aligned}$$

(1)

Rearranging, we see that either $\rho _{\min } = 0$ or $\rho _{\min } = 1$. Suppose that $\rho _{\min } = 1$; then we have equality in Equation 1, which implies that $|S| = z+2$ and $\rho (u^*) = \rho (u_i) = 1$ for $1 \le i \le z$. Then as $\rho (u) = 1$, there is a directed out-neighbour of u (say $u_1$) such that $u_1^* \in S$. Applying the same reasoning to $u_1$, we conclude that each of the $z+2$ sets $U(Z^+(u_1))$, $U(Z^+(u_1^*))$ and $U(Z^+(u'))$, where $u'$ is any directed out-neighbour of $u_1$, each contain one element of S; however, including $u_1^*$, we see that there would be at least $z+3$ elements of S in the Moore tree of depth three rooted at $u_1$, a contradiction.

Thus $\rho _{\min } = 0$. Hence by Lemma 4 we have $\sigma = z+1$. As no vertices of S lie in $U(Z^+(u))$, each of the elements $v \in S$ is an outlier of at least $\sigma ^-(v)$ vertices of $N^+(u)$, so that we must have $o(N^+(u)) = S$ as multisets, where $v \in S$ appears $\sigma ^-(v)$ times on the right-hand side. If any arrow vertex v in the Moore tree rooted at u (i.e. any vertex of $Z^+(u^*)$) belongs to S, then this vertex would contribute at least $\sigma ^-(v)+1$ times to the set $o(Z^+(u))$, so that as $\sigma \ge z+1$, in total there would be $\ge z+2$ vertices in $o(N^+(u))$, which is impossible. Furthermore, if an arrow vertex lies in $V(G)-(S \cup S')$, then this vertex would be an outlier of a vertex in $Z^+(u)$, contradicting $o(N^+(u)) = S$. Thus all arrow vertices in the tree belong to $S'$.

Applying the same reasoning to the vertices in $N^+(u)$, we see that if some $w \in N^+(u)$ has $\rho (w) = 0$, then all vertices of $Z^+(w^*)$ would lie in $S'$, so that the Moore tree of depth three rooted at u would contain at least 2z vertices of $S'$, which is strictly greater than $\sigma$ for $z \ge 3$. Thus $U(Z^+(w))$ contains at least one vertex of S for each $w \in N^+(u)$; it follows that each branch of the Moore tree rooted at u contains at least one vertex of S at distance three from u. As $|S| \le \sigma = z+1$, we must have $|S| = z+1$ and each vertex in S has directed in-degree $z-1$.

There are only $z+1$ vertices in S, so we conclude that $\rho (w) = 1$ for each $w \in N^+(u)$. As there is only one vertex of $S'$ not contained in $Z^+(u^*)$, there must be a directed out-neighbour of u, say $u_1$, such that $S' \cap Z^+(u_1^*) = \emptyset$. Since the $z+1$ vertices of S are contained in $U(Z^+(N^+(u)))$, we also have $S \cap Z^+(u_1^*) = \emptyset$, so that $Z^+(u_1^*) \subseteq V(G)-(S \cup S')$. It follows that $Z^+(u_1^*) = o(Z^+(u_1))$. However, as just one vertex of S is contained in $U(Z^+(u_1))$, at least z vertices in $N^+(u_1)$ must have outliers in S, implying that $z = 1$, a contradiction. $\square$

This completes our classification of k-geodetic mixed graphs with excess one for $k \ge 3$. In [39] the authors conjectured that any mixed graph with excess one is totally regular; Theorem 18 proves this conjecture.

6 Bounds on Totally Regular Mixed Graphs with Small Defect

We now return to the degree/diameter problem for mixed graphs and extend the counting arguments from the previous section to deal with totally regular mixed graphs with small defect. The first non-trivial bound for such graphs was derived in [17], where it is shown that for a totally regular $(r,z,k;-\delta )$-graph with $k \ge 3$ the defect is bounded below by the undirected degree r. There is equality for $k = 3$ and hence the bound is tight. We present a new upper bound on the order of totally regular $(1,1,k;-\delta )$-graphs that improves on the result of [17] for $k \ge 4$.

Let G be a totally regular mixed graph with undirected degree $r = 1$, directed degree $z = 1$ and diameter k. We will denote the unique undirected neighbour of a vertex v of G by $v^*$, the directed in-neighbour by $v^-$ and the directed out-neighbour by $v^+$. Since $r = 1$, G contains a perfect matching and must have even order.

For any vertex v of G we make the further definition that $v^1 = (v^+)^*$, that is $v^1$ is the undirected neighbour of the directed out-neighbour of v. We extend this definition as follows. We set $v^0 = v$ and by iteration define $v^s = (v^{s-1})^1$ for $s \ge 2$. By analogy we specify that $v^{-1} = (v^*)^-$, so that $v^-$ is the directed in-neighbour of the undirected neighbour of v. Again we set iteratively $v^{-s} = (v^{-(s-1)})^-$. Notice that $(v^1)^{-1} = (v^{-1})^1 = v$ for all $v \in V(G)$.

We draw the Moore tree of G of depth k based at a vertex u as indicated in Fig. 8. In particular, if a vertex at Level $t \le k-1$ of the tree has both an undirected neighbour and a directed out-neighbour below it at Level $t+1$ of the tree, then we will place the undirected neighbour on the left and label the vertices accordingly. If $k \ge 3$, then there will be vertices repeated in the tree, so that a vertex of G can receive distinct labels in the Moore tree; nevertheless, for counting purposes we will still distinguish between the position labels in the tree. The left-hand side branch beginning at $u_1$ is the undirected branch and the right-hand side branch beginning at $u_2$ is the directed branch.

Fig. 8

The Moore tree for $r = z = 1$ and $k = 5$

To reiterate, an arrow vertex in the Moore tree of G rooted at u is a vertex x at a Level t, $2 \le t \le k-1$, of the tree in the undirected branch such that x appears as the terminal vertex of an arc with its initial vertex at Level $t-1$. Unlike the k-geodetic case, arrow vertices can be equal in G or be equal to a vertex in the directed branch; therefore we will slightly abuse the term ‘arrow vertex’ by associating it, not with a vertex of G, but with a position or label in the tree.

Consider an arrow vertex x at Level t of the Moore tree. Its directed in-neighbour $x^-$ appears at Level $t-1$ and its undirected neighbour $x^*$ at Level $t+1$, so that the entire in-neighbourhood $N^-(x) = \{ x^-,x^*\}$ is also contained in the undirected branch of the Moore tree. As G has diameter k, $u_2$ must be able to reach x by a mixed path of length $\le k$, so it follows that at least one of $x^-,x^*$ also appears in the directed branch of G. For every such occurrence there will be an additional repeat of $u_0$, so that we can bound the defect $\delta$ from below by counting the smallest possible number of positions in the undirected branch such that for every arrow vertex x either $x^*$ or $x^-$ lies in one of these positions. We will call such a set of positions a transversal of the undirected branch.

We will now focus on the undirected branch of the Moore tree. The undirected branch of a Moore tree of depth 8 is shown in Fig. 9. For convenience we use a different labelling of the undirected branch; for example, vertex 1 corresponds to $u_1$ in Fig. 8, 2 to $u_3$, 3 to $u_6$, 5 to $u_{11}$, etc. For the moment we ignore the complication that a vertex of G could appear multiple times as an arrow vertex in this tree. Under this assumption we will show that $\delta$ is bounded from below by the size of a minimum transversal of the Moore tree.

Fig. 9

The undirected branch for $k = 8$

Consider an arrow vertex x at Level t of the tree, where $2 \le t \le k-1$. In the undirected branch shown in Fig. 9 these are vertices 2, 4, 5, 7, 9, 10, 12, 13, 15, 17, 18, 20, 22, 23, 25, 26, 28, 30, 31 and 33. As already noted, either the undirected neighbour $x^*$ or the directed in-neighbour $x^-$ of x must occur in the directed branch of the Moore tree, and each such occurrence counts towards the number of repeats of the root vertex u of the tree. However, the in-neighbourhoods of the arrow vertices overlap; for example, the vertex 8 is an in-neighbour both of the vertex 5 and the vertex 13. We will partition the positions in the undirected branch of the Moore tree corresponding to vertices in the in-neighbourhoods of the arrow vertices into chains.

A chain is a maximal string of vertices in the undirected branch of the Moore tree of the form $v=v^0,v^1,v^2,v^3, \ldots$, where v is an in-neighbour of an arrow vertex. If v is at Level $t \le k-2$, then $v^2$ is at Level $t+2$. For example 1, 3, 8, 21 is a chain which we have labelled (a) in Fig. 9. Every in-neighbourhood of an arrow vertex is contained in a unique chain. Every arrow vertex at Level t, where $2 \le t \le k-2$, is the beginning of a chain, as is the vertex 1. Conversely, by iterating the $^-$ operation on an in-neighbour of an arrow vertex, i.e. considering the sequence of vertices $v,v^{-1},v^{-2}, \dots$, we see that every chain begins either at 1 or an arrow vertex at Level $t \le k-2$. This decomposition is displayed for $k = 8$ in Fig. 10.

Fig. 10

The chain decomposition for $k = 8$

We will call the number of vertices (i.e. positions in the Moore tree) in a chain $v,v^1,v^2,\dots$ the length of the chain. For example, for $k = 8$ the chain 1, 3, 8, 21 has length 4. Let C be a chain of length $\ell$. Any pair of consecutive vertices in C is the in-neighbourhood of an arrow vertex, so at least one of them must appear in the directed branch of the Moore tree. As any vertex in C is contained in two pairs of consecutive vertices of the chain, it follows that the smallest transversal of C, i.e. the smallest number of vertices in the Moore tree that intersect every in-neighbourhood of arrow vertices that is contained in the chain, is $\lceil \frac{\ell }{3}\rceil$ (this follows from the domination number of the path [12]).

The number of chains beginning at Level t of the tree, where $2 \le t \le k-2$, is equal to the number of arrow vertices at Level t. From the calculation of Theorem 11 we know that this number is

$$\begin{aligned} Z_t = \frac{1}{2^{t-1}\sqrt{5} }((1+\sqrt{5})^{t-1}-(1-\sqrt{5})^{t-1}).\end{aligned}$$

The first vertex 1 of the undirected branch is also the first vertex of a chain. We therefore define $Z'_t = 1$ for $t = 1$ and $Z'_t = Z_t$ for $2 \le t \le k-1$. The length of a chain beginning at Level t is $\ell (t) = 1+\lfloor \frac{k-t}{2} \rfloor$. It follows from our argument that the smallest transversal of the undirected branch of the Moore tree has size

$$\begin{aligned} \sum ^{k-2}_{t=1} Z'_t\left\lceil \frac{1}{3} + \frac{1}{3}\left\lfloor \frac{k-t}{2} \right\rfloor \right\rceil .\end{aligned}$$

This expression gives a lower bound for the number of positions in the undirected branch of the Moore tree that are occupied by vertices that also appear in the directed branch. It could happen that these positions in the undirected branch are actually occupied by the same vertex, which would reduce the number of vertices that would have to be repeated in the directed branch.

However, it is easily seen that this does not affect our lower bound for the defect. Let T be the transversal of the undirected branch that is repeated in the directed branch of a largest $(r,z,k;-\delta )$-graph. If s positions of T are occupied by the same vertex v, then v occurs at least once in the directed branch of the Moore tree, but is also repeated at least $s-1$ times in the undirected branch, so that this set of s positions nevertheless contributes at least s to the total defect $\delta$. We have therefore proved the following theorem.

Theorem 19

Any totally regular $(1,1,k;-\delta )$-graph has defect

$$\begin{aligned} \delta \ge \sum ^{k-2}_{t=1} Z'_t\left\lceil \frac{1}{3} + \frac{1}{3}\left\lfloor \frac{k-t}{2} \right\rfloor \right\rceil \end{aligned}$$

for $k \ge 3$.

In Table 3 are summarised the new upper bounds on the order of $(1,1,k;-\delta )$-graphs from Theorem 19. Note that any totally regular mixed graph with undirected degree one must have even order; this is taken into account in the final column of the table.

Table 3 New bounds on $(1,1,k;-\delta )$-graphs

If we allow $\delta (k)$ to denote the lower bound on the defect of a $(1,1,k;-\delta )$ graph from Theorem 19 then the following result shows in a more illuminating manner the rate of growth of $\delta (k)$.

Theorem 20

For $k \ge 1$ we have

$$\begin{aligned} \delta (k+6) = \delta (k)+F_{k-1}+F_{k+4} ,\end{aligned}$$

where $F_0 = F_1 = 1, F_2 = 2, F_3 = 3, F_4 = 5, \dots$ is the Fibonacci sequence.

Proof

Take a Moore tree of a $(1,1,k;-\delta )$-graph and increase its depth by six. Then each of the pre-existing chains in the Moore tree of depth k are lengthened by three, so that each such chain contributes one more to the sum in Theorem 19. There are $F_{j-2}$ chains that begin at Level $j \ge 2$ in the undirected branch of such a Moore tree, with one chain beginning at Level 1. Therefore there are

$$\begin{aligned} 1+F_0+F_1+F_2+\dots +F_{k-5}+F_{k-4} = F_{k-2}\end{aligned}$$

chains present in the tree of depth k. Hence the chains in the tree of depth k contribute $\delta (k) + F_{k-2}$ to the sum in Theorem 19. There are $F_{k-3}$ vertices at Level $k-1$ and $F_{k-2}$ vertices at Level k that grow into chains with length four in the depth $k+6$ tree, each of which contribute two to the sum. Finally for $i = 1,2,3,4$ there are $F_{k+i-2}$ vertices at Level $k+i$ that grow into chains of length not exceeding three, each of which contributes one to the sum for the depth $k+6$ tree. In total, this gives $\delta (k+6) = \delta (k) +F_{k-1}+F_{k+4}$. $\square$

7 Directed and Mixed Cages

We summarise here the results of a computer search for the smallest possible digraphs of given d, k and mixed graphs for certain values of r, z, k. For digraphs without undirected edges, we adopt the usual notation where the (out)-degree is denoted by d; such a graph could equally be viewed as a mixed graph with $r=0$ and $z=d$. Such searches quickly become computationally infeasible as the order of the graphs grows. In many cases we can obtain a useful upper bound on the order of cages by restricting the search space to Cayley graphs; thus we present tables of the smallest Cayley graphs separately from tables of smallest general graphs.

Recall that a Cayley graph $\mathrm {Cay}(G,S)$ of a group G and subset $S\subseteq G$ has vertex set the elements of the group G, and a (directed) arc from x to xs for every $s\in S$. If the set S contains involutions or inverse pairs, then the resulting directed 2-cycles in the Cayley graph are considered to be undirected edges. Thus a mixed Cayley graph of order n, undirected degree r and directed degree z is constructed from a group G of order n, together with a set S such that S contains exactly r elements whose inverse is also in S, and z elements whose inverse is not. To ensure the resulting Cayley graph is connected, we insist that $\langle S\rangle =G$.

The Cayley graph search was carried out using GAP [23] and proceeded by examining each possible group in increasing order, starting from the Moore bound for given r, z, k. The geodecity of such a graph is then the largest value of k for which all possible words of length $\le k$ in the generating set S have different values. (We consider only reduced words, i.e. words in which a generator is not immediately followed by its inverse.) It is well known that if $\phi$ is an automorphism of the group G, then the Cayley graphs $\mathrm {Cay}(G,S)$ and $\mathrm {Cay}(G,\phi (S))$ are isomorphic. This provides a very useful means to cut down the search space for Cayley graphs, since only orbit representatives of possible generating sets need be considered.

The general graph search was carried out using a bespoke C program, the output of which was tested against the Cayley graph search to ensure correct functioning. The program proceeds by starting with a Moore tree for given values of r and z, then adding vertices and arcs and/or edges to obtain a graph of order n. As each arc/edge is added, the graph obtained is tested to ensure it still has geodecity at least k; if not, the search backtracks and tries another arc/edge.

Selected output graphs from the search are illustrated in Sect. 8.

7.1 Digraphs

Table 4 shows the results of the Cayley digraph search. For $d=2$ we were able to complete the search for all groups of order less than 1024, so the results presented are known to be optimal. For higher degrees the search space becomes increasingly large, and so for degrees 5 and 6 we were only able to search far enough to determine the smallest digraphs of geodecity 2.

Table 4 Smallest Cayley digraphs of given degree d and geodecity k

The general graph search results in Table 5 show a similar pattern, although because the search space is very much larger than in the Cayley case the range of values for which we are able to determine the order of cages is quite restricted.

Table 5 Smallest digraphs of given degree d and geodecity k (* = smallest known)

7.2 Mixed Graphs

The Cayley graphs in Table 6 were again found by searching groups of increasing order until the first Cayley graph with the required geodecity was found. Thus the entries in this table are all minimal. The search for general graphs is again much more difficult. We have been able to find bounds for the orders of some cages, but the search space is so large that only a few provably minimal entries are known.

Table 6 Smallest Cayley mixed graphs of given degree parameters and geodecity k

Table 7 Smallest mixed graphs of given degree parameters and geodecity k (* = smallest known)

8 Figures of Some Known Cages

Fig. 11

Two digraphs with $d = 2$, $k = 2$ and excess $\epsilon = 2$

Fig. 12

Two digraphs with $d=2,k=3,\epsilon =5$

Fig. 13

The unique extremal digraph $d=3,k=2,n=16$

Fig. 14

Two mixed graphs with $r=1,z=1,k=3,\epsilon =5$

Fig. 15

A mixed graph with $r=1,z=1,k=4,\epsilon =11$

Fig. 16

The extremal mixed graph $r=2,z=2,k=2,n=21$